Value for Money? Array Genomic Hybridization for Diagnostic Testing for Genetic Causes of Intellectual Disability

Abstract

Array genomic hybridization (AGH) provides a higher detection rate than does conventional cytogenetic testing when searching for chromosomal imbalance causing intellectual disability (ID). AGH is more costly than conventional cytogenetic testing, and it remains unclear whether AGH provides good value for money. Decision analytic modeling was used to evaluate the trade-off between costs, clinical effectiveness, and benefit of an AGH testing strategy compared to a conventional testing strategy. The trade-off between cost and effectiveness was expressed via the incremental cost-effectiveness ratio. Probabilistic sensitivity analysis was performed via Monte Carlo simulation. The baseline AGH testing strategy led to an average cost increase of $217 (95% CI $172–$261) per patient and an additional 8.2 diagnoses in every 100 tested (0.082; 95% CI 0.044–0.119). The mean incremental cost per additional diagnosis was $2646 (95% CI $1619–$5296). Probabilistic sensitivity analysis demonstrated that there was a 95% probability that AGH would be cost effective if decision makers were willing to pay $4550 for an additional diagnosis. Our model suggests that using AGH instead of conventional karyotyping for most ID patients provides good value for money. Deterministic sensitivity analysis found that employing AGH after first-line cytogenetic testing had proven uninformative did not provide good value for money when compared to using AGH as first-line testing.

Main Text

Intellectual disability (ID) is a life-long condition that has significant impact on the affected person and his or her family.^1–3 Clinical geneticists seek to establish the cause of a child's disability to provide accurate genetic counseling, prognosis, and management. A chromosomal abnormality is the most commonly recognized cause of ID,^4,5 and cytogenetic analysis is the standard clinical approach to identifying chromosomal abnormalities. Conventional cytogenetic analysis employs a karyotype to assay the entire genome (some 6000 million base pairs [6000 Mb] of DNA in a single test) but cannot detect chromosomal rearrangements smaller than 5–10 Mb. Fluorescence in situ hybridization (FISH) and subtelomeric FISH have much better resolution, but these approaches provide information on just one or a few specific locations in the genome.

Array genomic hybridization (AGH) can identify submicroscopic chromosomal imbalance 100 or more times smaller than that detectable by standard cytogenetic analysis anywhere in the genome. Recent studies suggest that AGH can detect a causal chromosomal abnormality in twice as many patients as karyotyping.^6,7 As a result, many laboratories are now offering AGH as a clinical test, and some clinical geneticists advocate the use of AGH instead of conventional cytogenetic analysis for evaluating children with ID.^8–10

The cost of AGH, however, is substantially more than that of conventional cytogenetic analysis, and there is limited evidence on whether a diagnostic testing strategy that includes AGH will provide good value for money.¹¹ This report examines the cost-benefit of a testing strategy that includes the use of AGH (henceforth referred to as the AGH testing strategy or AGH testing pathway) against a conventional cytogenetic testing strategy to identify chromosomal imbalance causing ID.

A decision analytic model (Figure 1) was used to synthesize the economic and clinical outcomes accrued to a hypothetical cohort of individuals with idiopathic ID undergoing a conventional or AGH testing strategy. The time horizon of the model was 1 year. In the AGH testing pathway, children who were not suspected of having a trisomy had AGH testing as first-line. For those children with suspected trisomy 21 (MIM #190865), trisomy 18, or trisomy 13, a karyotype was used as first line, followed by AGH if a diagnosis was not established. Trisomy 21, 18, or 13 were included in the economic model because AGH can be applied to these patients if karyotyping does not establish a diagnosis. If an imbalance was detected by AGH, targeted FISH (in the parents and child) and karyotyping (in the child) was used to confirm the finding.

Figure 1.

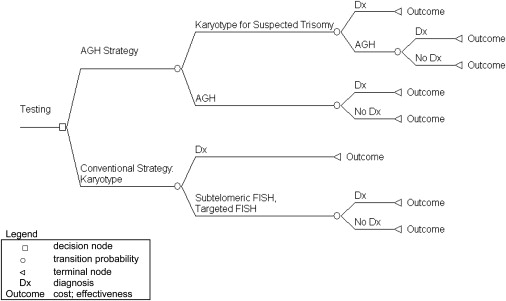
Decision Analytic Model

Legend: open square, decision node; open circle, transition probability; left open triangle, terminal node; Dx, diagnosis; outcome, cost; effectiveness.

The first-line genetic test in the conventional testing pathway was karyotyping; the probability of receiving a genetic diagnosis with a karyotype differed between those with and without suspected trisomy 21, 18, or 13. If a karyotype did not provide a diagnosis, it was assumed that testing with either targeted FISH (via single or multiple probes) or subtelomeric FISH was conducted. Identified chromosomal abnormalities of unknown clinical relevance after FISH were assumed to require targeted FISH testing of both parents to establish whether the chromosomal abnormality occurred de novo.

Health care economic evaluations should examine both the costs and consequences of competing testing strategies.¹² Mean cost and cost differences (ΔC) were examined from the perspective of the British Columbia Ministry of Health Services. The Ministry of Health insures residents of British Columbia for medically required services provided by clinicians and other health care practitioners, including laboratory services and diagnostic procedures. Consequences include the clinical or personal utility associated with a strategy.¹³ In this analysis, consequences were measured via (1) incremental effectiveness (ΔE), which represented clinical utility and was calculated as the number of additional diagnoses provided by AGH; and (2) incremental benefit (ΔWTP), which is a metric that combines clinical and personal utility with preferences from a discrete choice experiment (DCE).¹⁴ Examining issues surrounding value for money implies that a trade-off may exist between increased effectiveness and cost. The metrics used to investigate value for money were the incremental cost-effectiveness ratio (ICER; ΔC/ΔE) and the net benefit of AGH versus conventional testing (ΔWTP-ΔC).

The transition probabilities populating the decision model were informed through published literature or chart review. The proportion of children having a karyotype for suspected trisomy 21, 18, or 13 and the probability of receiving a genetic diagnosis for these individuals were taken from a study by Rauch et al.⁴ The probability of establishing a diagnosis with a karyotype in those without trisomy 21, 18, or 13 came from van Karnebeek et al.¹⁵

The probability of undergoing targeted or subtelomeric FISH testing after receiving no causal genetic diagnosis with karyotyping was estimated through chart review. The chart review utilized medical records maintained at the Provincial Medical Genetics Programme at Children's & Women's Hospital in Vancouver, Canada. For inclusion in the review, individuals were required to be between the ages of 5 and 10 years, have moderate to severe ID, and live in metro Vancouver. Moderate to severe ID was defined as being at least four standard deviations below the mean on standardized developmental tests recorded in the chart. Eligible families of children with ID were contacted via mail; informed consent to use the data was obtained from 162 families. Ethics approval for the chart review was granted by the Behavioral Research Ethics Board, University of British Columbia.

The conditional probability of receiving a diagnosis with targeted FISH subsequent to karyotyping was informed with a substudy by Rauch et al.,⁴ and the conditional probability of receiving a diagnosis with subtelomeric FISH was obtained from a retrospective study of individuals who had such testing after cytogenetic analysis had failed to provide a diagnosis.¹⁶

The AGH testing pathway requires the number of genetic diagnoses provided by AGH after karyotyping and when AGH is used as first-line testing. For the former, the probability of diagnosis was obtained by pooling data from several published reports examining AGH for idiopathic ID.^17–26 The number of genetic diagnoses obtained when AGH is used as a first-line test is difficult to establish because published studies use AGH for patients who have undergone clinical evaluation and initial cytogenetic testing. We assumed that AGH would identify each of the diagnoses obtained by karyotyping. This probability was then added to the conditional estimate of obtaining a diagnosis with AGH.

In the cost analysis, resource utilization associated with laboratory testing (excluding cytogenetic, FISH, or array testing) and individual clinical assessments was informed through the chart review. The chart review included the utilization of other laboratory tests; visits to general practitioners, pediatricians, and other specialists; and individual developmental assessments (e.g., for autism, delayed development of speech, etc.). The resource utilization of each case was subsequently divided into the laboratory or clinical assessments before initial cytogenetic analysis, and laboratory or clinical assessment after initial cytogenetic analysis if a diagnosis was or was not obtained. Unit costs attached to resource utilization and for cytogenetic and FISH testing were obtained from the Medical Services Plan (MSP) fee schedule available from the Ministry of Health. The MSP fee schedule lists the actual reimbursements that the Ministry of Health pays for health services that are insured. The cost for AGH testing was obtained from the Cytogenetics Laboratory at the British Columbia Children's Hospital because AGH is not currently covered in the MSP fee schedule; the fee used in the model is the reimbursement paid by the insurer. All costs are reported in 2007 Canadian dollars.

Combining the clinical and personal utility of genetic testing was achieved by using the willingness to pay (WTP) for a gain in the probability of obtaining a causal genetic diagnosis for ID, which was valued via data from families of children with ID as reported by Regier et al.¹¹ The present study uses the econometric results of Regier et al.,¹¹ but our estimate of WTP will differ because the number of additional genetic diagnoses is predicted by the decision analytic model (Regier et al.¹¹ assume a rate of diagnosis). To calculate benefit, we generated a WTP estimate for each testing pathway with the multiple alternatives approach.¹¹

The decision analytic model was programmed via TreeAge Pro (TreeAge Pro Inc, Williamstown, MA, USA). A number of deterministic sensitivity analyses informing the uncertainty surrounding key assumptions were undertaken. (1) Multiplex ligation-dependent probe amplification (MLPA) is an inexpensive alternative to subtelomeric FISH. A sensitivity analysis was conducted to include MLPA instead of subtelomeric FISH in the conventional testing strategy; we assumed that the approaches would have identical rates of diagnosis, but the cost of MLPA was $40. (2) Cytogenetic laboratories can employ a strategy where AGH is used after a normal karyotype for children without suspected trisomy 21, 18, or 13. The cost-benefit of this strategy was examined against (i) the conventional testing strategy defined in the baseline analysis; and (ii) the AGH testing strategy defined in the baseline analysis. (3) The final sensitivity analysis examined the cost-benefit of an AGH testing strategy versus a conventional strategy solely for those individuals without suspected trisomy 21, 18, or 13.

Probabilistic sensitivity analysis was conducted to account for the joint sampling uncertainty of the parameters in the decision model. Probabilistic sensitivity analysis requires assigning distributions to each uncertain parameter. The beta distribution was specified for the probability of obtaining a diagnosis and for the probability of transitioning to subsequent genetic testing.²⁷ The cost associated with laboratory testing was assumed to follow the gamma distribution.²⁸ Uncertainty was propagated throughout the decision analytic model via Monte Carlo simulation with 10,000 draws taken from the input distributions. The decision uncertainty surrounding the adoption of an AGH testing strategy was examined with the cost-effectiveness acceptability curve (CEAC). The CEAC plots the probability that an AGH strategy will be cost effective at a given threshold of WTP that decision makers may have for an effectiveness gain, which is denoted as λ. In the context of this analysis, λ represents decision makers' WTP for an additional genetic diagnosis. For each analysis we report the λ that suggests there is a 95% probability that an AGH strategy will be cost effective.

The results of the decision model for each transition probability are presented in Table 1. In the conventional testing strategy, the mean probability that karyotyping establishes a diagnosis was 0.161 (95% confidence interval [CI] 0.127–0.196); 0.161 is the sum of 0.095 (0.128 × 0.741 in Table 1) for trisomy cases and 0.065 (0.872 × 0.075 in Table 1) for nontrisomy cases. The conditional probability of receiving a diagnosis with either subtelomeric or targeted FISH testing after failing to receive a diagnosis with an initial karyotype was 0.032 (95% CI 0.024–0.043). The overall probability of establishing a diagnosis in the conventional testing pathway was 0.192 (95% CI 0.159–0.228).

Table 1.

Transition Probabilities in the Decision Model

Parameter	Mean (Standard Error)	95% CI	Reference Number
Probability of Receiving First Line Genetic Test
Karyotype for trisomy 21, 13, or 18	0.128 (0.013)	0.103–0.157	4
Karyotype (conventional testing strategy)/GH (AGH testing strategy)	0.872 (0.014)	0.845–0.898	4
Conditional Probability after Karyotype and Not Receiving a Diagnosis (Conventional Testing Strategy)
Targeted FISH	0.561 (0.04)	0.485–0.637	chart review
Subtelomeric FISH	0.439 (0.04)	0.365–0.516	chart review
Probability of Receiving a Genetic Diagnosis
Karyotype for suspected syndrome (trisomy 21; trisomy 13; trisomy 18)	0.741 (0.05)	0.634–0.835	4
Karyotype	0.075 (0.016)	0.046–0.109	15
Subtelomeric FISH	0.026 (0.002)	0.023–0.029	16
Targeted FISH	0.047 (0.006)	0.031–0.066	4
AGH (first line test)	0.202 (0.018)	0.178–0.229	assumption
AGH (second line test)	0.126 (0.013)	0.101–0.153	17–26
Cost of Genetic Testing
Karyotype	$280	N/A	MSP
FISH (single probe)	$187	N/A	MSP
Targeted FISHa	$221 (9.8)	$202–$240	MSP
Subtelomeric FISH	$444	N/A	MSP
AGH	$710	N/A	current cost
Cost of Laboratory Testingb
Before cytogenetic testing	$1054 (66)	$928–$1191	chart review
After first cytogenetic test with diagnosis	$742 (143)	$489–$1042	chart review
After first cytogenetic test without diagnosis	$1227 (144)	$951–$1528	chart review

Abbreviations: CI, confidence interval; FISH, fluorescent in situ hybridization; MSP, Medical Services Plan; N/A, not applicable as these costs are charged to the British Columbia Ministry of Health and there is no variance in payment. All costs are in 2007/2008 Canadian dollars.

^aThese costs and CIs are derived from the percentage of individuals having a test after karyotyping as identified by the chart review: 45% had 1 targeted FISH, 5.6% had 2 targeted FISH, 1.4% had 3 targeted FISH.

^bDoes not include the cost of cytogenetic analysis.

In the AGH testing strategy, 0.099 (95% CI 0.077–0.123) diagnoses would be established via karyotyping or AGH (if the karyotype was negative) for individuals who were suspected of having trisomy 21, 18, or 13. For nontrisomy cases, the probability of establishing a diagnosis when AGH was used as first-line was 0.18 (95% CI 0.157–0.205); 0.18 is from 0.872 × 0.202 in Table 1. The probability of establishing a causal diagnosis in the AGH testing pathway was 0.275 (95% CI 0.245–0.306).

Table 1 also presents the cost of laboratory investigations and other clinical visits or developmental tests estimated in the model. The mean per patient cost of genetic testing for ID in the conventional testing pathway was $572 (95% CI $553–$592); when all other costs for laboratory and individual assessments were included, the mean was $2763 (95% CI $2499–$3052). In the AGH testing pathway, the average per patient cost of genetic testing for ID alone was $829 (95% CI $805–$855), and the total per patient cost of all testing was $2980 (95% CI $2727–$3254).

Table 2 summarizes the mean costs, effects, and benefits of each strategy. The incremental cost of AGH including genetic testing and other laboratory and clinical assessments was $217 (95% CI $172–$261) more for the AGH strategy. The incremental probability of obtaining a diagnosis provided by undertaking an AGH strategy (ΔE) was 0.082 (95% CI 0.044–0.119): the model predicts that an additional 8.2 children in 100 tested will receive a causal diagnosis.

Table 2.

Cost-Effectiveness Results and Sensitivity Analyses

Baseline Analysis
	Mean AGH Strategy (95% CI)	Mean Conventional Strategy (95% CI)	Mean Difference (95% CI)
Cost	$2980 ($2727–$3254)	$2763 ($2499–$3052)	$217 ($172–$261)
Effectiveness	0.275 (0.245–0.306)	0.192 (0.159–0.228)	0.082 (0.044–0.119)
ICER	$2646 ($1619–$5296)
Benefit	$1053 ($432–$1828)
Net benefit	$836 ($203–$1616)
Sensitivity Analysis 1
	Mean AGH Strategy (95% CI)	Mean Conventional Strategy (95% CI)	Mean Difference (95% CI)
Cost	$2980 ($2727–$3254)	$2615 ($2351–$2903)	$366 ($322–$409)
Effectiveness	0.275 (0.245–0.228)	0.192 (0.159–0.228)	0.082 (0.049–0.142)
ICER	$4463 ($2962–$8446)
Benefit	$1053 ($432–$2828)
Net benefit	$687 ($58–$1464)
Sensitivity Analysis 2 (i)
	Mean Karyotype/AGH Strategy (95% CI)	Mean Conventional Strategy (95% CI)	Mean Difference (95% CI)
Cost	$3090 ($2837–$3367)	$2763 ($2499–$3052)	$327 ($291–$365)
Effectiveness	0.267 (0.230–0.304)	0.192 (0.159–0.228)	0.074 (0.051–0.099)
ICER	$4418 ($3226–$6432)
Benefit	$948 ($445–$1563)
Net benefit	$621 ($114–$1234)
Sensitivity Analysis 2 (ii)
	Mean Karyotype/AGH Strategy (95% CI)	Mean AGH Strategy (95% CI)	Mean Difference (95% CI)
Cost	$3090 ($2837–$3367)	$2980 ($2727–$3254)	$110 ($73–$143)
Effectiveness	0.267 (0.23–0.304)	0.275 (0.245–0.228)	−0.008 (−0.030–0.0189)
ICER	−$13,750 weak dominance
Net benefit	−214 (−$567–$169)
Sensitivity Analysis 3
	Mean AGH Strategy (95% CI)	Mean Conventional Strategy (95% CI)	Mean Difference (95% CI)
Cost	$3065 ($2801–$3350)	$2832 ($2554–$3138)	$233 ($183–$281)
Effectiveness	0.201 (0.176–0.229)	0.110 (0.081–0.145)	0.091 (0.048–0.132)
ICER	$2766 ($1543–$5267)
Benefit	$1117 ($423–$1984)
Net benefit	$884 ($179–$1757)

Abbreviations: ICER, incremental cost-effectiveness ratio; CI, confidence interval; benefit is measured in willingness to pay; all money estimates are in 2007/2008 Canadian dollars

AGH is incrementally more costly and more effective, and decision makers will need to make a judgment regarding whether the additional diagnoses provided by the AGH strategy warrant the additional costs. The ICER characterizes the value for money trade-off. The ICER was $2646 (95% CI $1619–$5296) when all costs were included in the analysis. This suggests that the health care payer will have to spend $2646 (95% CI $1619–$5296) per additional diagnosis. We do not know decision makers' WTP for an additional diagnosis (λ) and we cannot say how the statistical uncertainty affects the value for money trade-off. For the latter, the CEAC gives the exact probability that an AGH testing strategy will be cost effective at different thresholds of λ (Figure 2). AGH will reach a 95% probability of being cost effective when λ = $4550.

Figure 2.

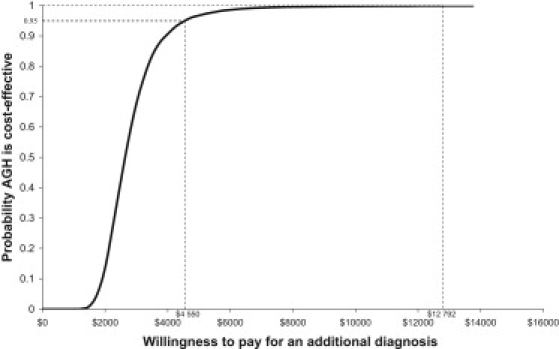
Cost-Effectiveness Acceptability Curve of Maximum Willingness to Pay for an AGH Testing Strategy versus a Conventional Testing Strategy

By using the preferences of parents who have a child with ID, we estimated that WTP was $1053 (95% CI $432–$1828) for an additional 8.2 diagnoses for every 100 children who are tested. For comparability with the ICER, the WTP for an increase in the rate of diagnosis can be converted into the WTP per additional diagnosis by dividing the WTP result by the increased probability of diagnosis. The WTP per diagnosis was calculated as $12,792 (95% CI $6,508–$19,207). The CEAC (Figure 2) shows that there is more than a 99% probability that the AGH testing strategy is cost effective at this threshold of WTP. The net benefit statistic also suggested that AGH was cost beneficial (Table 2). Given an incremental cost of $217 (95% CI $172–$261), the expected net benefit per child tested was $836 (95% CI $203–$1616), which is significantly different from no difference in net benefit.

The results of the sensitivity analyses are presented in Table 2. Sensitivity analysis 1 examined using MLPA instead of subtelomeric FISH. The mean cost in the conventional strategy was $2615 (95% CI $2351–$2903). The ICER was $4463 (95% CI $2962–$8446) and there was a 95% probability that AGH is cost effective when λ = $7500. The net benefit using parents' WTP for an additional 8.2 diagnoses was $687 (95% CI $58–$1464), which suggests that the AGH strategy remains an attractive option when MLPA is used.

Sensitivity analysis 2 (i) examined the scenario where AGH is employed subsequent to initial karyotyping versus conventional cytogenetic testing. This AGH strategy had an average cost of $3090 (95% CI $2837–$3367) and an incremental effectiveness of 0.074 (95% CI 0.051–0.099) when compared to the conventional strategy in the baseline analysis. The ICER was $4418 (95% CI $3226–$6432) and there was a 95% probability AGH is cost effective when λ = $6000. Using parents' WTP, the benefit was $948 (95% CI $445–$1563) and the net benefit was $621 (95% CI $114–$1234). Sensitivity analysis 2 (ii) examined AGH after karyotyping against the AGH strategy defined in the base case analysis. The AGH subsequent to karyotyping strategy resulted in a statistically significant cost increase of $110 (95% CI $73–$143) and a nonstatistically significant decrease in effectiveness. Employing AGH subsequent to karyotyping is unlikely to provide good value for money compared to the baseline AGH strategy and only reaches a 20% probability of being cost effective when λ = $50,000; it never reaches a 95% probability of cost effectiveness.

Sensitivity analysis 3 examined an AGH testing strategy solely for those individuals without suspected trisomy. The AGH strategy in this scenario resulted in a statistically significant cost increase of $233 (95% CI $183–$281); AGH also resulted in 0.091 (95% CI 0.048–0.132) additional diagnoses. The ICER was $2766 (95% CI $1543–$5267) and there was a 95% probability AGH is cost effective if λ = 4500. The benefit and net benefit of this AGH strategy was $1117 (95% CI $423–$1984) and $884 ($179–$1757), respectively. The AGH strategy remains cost beneficial when those with suspected trisomy are excluded from the analysis.

In summary, we used decision modeling to examine whether an AGH strategy in comparison to a conventional strategy for detecting chromosomal imbalance causing ID provides good value for money. The AGH strategy resulted in a statistically significant increase in costs, clinical effectiveness, and benefit within the first year after a child undergoes genetic evaluation for ID. In the context of the commonly cited WTP threshold of $50,000 (i.e., λ = 50,000) for an effectiveness gain,²⁹ the baseline ICER of $2646 (95% CI $1619–$5296) per additional diagnosis suggests that the AGH strategy offers good value for money. Probabilistic sensitivity analysis revealed that there is a 95% probability that AGH is cost effective when λ = $4550, which is below the $50,000 threshold. However, we do not know λ and, therefore, we used preferences of families with children who have ID to establish WTP. The model predicted that the WTP for an additional diagnosis was $12,792 (95% CI $6,508–$19,207). At this threshold, the probability that AGH is cost effective is more than 99%. The net benefit statistic was $836 (95% CI $203–$1616). The ICER and net benefit statistics therefore suggest that an AGH testing strategy is expected to be cost beneficial and will provide good value for money assuming a time horizon of 1 year.

The sensitivity analyses examined how the ICER and net benefit statistics differed across critical model assumptions. The conclusion that AGH is cost beneficial did not change in our sensitivity analyses. Our results suggest that AGH testing after a karyotype for each individual versus the use of AGH as first-line diagnostic test defined in the baseline analysis resulted in costs that exceeded benefits overall because AGH after a karyotype increases average costs by $110 (95% CI $73–$143) per patient without significantly changing effectiveness. The use of AGH after an initial karyotype on all individuals cannot be recommended according to our analysis.

This economic evaluation was conducted according to current methodological guidelines,²⁸ but there are a number of caveats. First, the cost of the AGH test is likely to decrease as the technology becomes widely adopted. In the case of British Columbia, the cost of AGH will decrease if AGH is covered under the MSP program. This will serve to improve the cost-benefit of AGH and our analysis is therefore conservative with respect to this assumption. Second, effectiveness was not measured by using the quality adjusted life years (QALY) metric, which is currently recommended to inform resource allocation decisions (National Institute for Health and Clinical Excellence). The QALY was not used because of methodological concerns surrounding the use of preference-based quality of life measurements in children.³⁰ It may be feasible, however, to measure the QALY for parents whose children do or do not have a diagnosis for their ID, which remains a future avenue for research.

The third caveat is that there are a number of whole-genome array platforms available to diagnose ID. We used the term “AGH” in the generic sense to encompass the class of array technologies that detect submicroscopic copy number variants. Our analysis does not address the cost-benefit of any specific array platform. Fourthly, given our short-term time horizon, we excluded future economic costs and benefits associated with a diagnosis or lack of a diagnosis of ID. This includes the costs and benefits associated with more accurate genetic counseling. It is uncertain what effect these omissions will have on the ICER. Research that projects costs and effects over a longer time horizon is warranted.

The fifth caveat is related to the chart review and our inclusion criteria of children between the ages of 5 and 10. This age range was desirable because these children are more likely to have gone through the full array of laboratory and other testing associated with their ID, but was limited because children dying before the age of 5 were excluded from the analysis. Although this limitation is unlikely to affect the ICER, it may have implications for the mean cost per patient and the sampling uncertainty surrounding the cost estimates.

Finally, when an economic evaluation uses an intermediate outcome such as the additional number of genetic diagnoses, statements regarding cost effectiveness require the assumption of a particular range of WTP for a diagnosis among decision makers. In our analysis, this was addressed via the CEAC; any statement we made regarding cost effectiveness was thus limited to conclusions surrounding the CEAC. We instead made statements regarding cost-benefit and value for money, which are broader in scope because they enable resource allocation decisions to be made both within health care and across all sectors of the economy.¹²

In conclusion, our analysis suggests that AGH testing for ID provides good value for money when compared to conventional karyotyping followed by FISH. Our decision models also suggest that obtaining a karyotype on all children with ID and then testing with AGH if the cytogenetic analysis does not provide a diagnosis is not cost beneficial when compared to using AGH as first-line diagnostic testing.

Web Resources

The URLs for data presented herein are as follows:

• National Institute for Health and Clinical Excellence, http://www.nice.org/uk/media/B52/A7/TAMethodsGuideUpdatedJune2008.pdf

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/