Detecting Coevolution through Allelic Association between Physically Unlinked Loci

Abstract

Coevolving interacting genes undergo complementary mutations to maintain their interaction. Distinct combinations of alleles in coevolving genes interact differently, conferring varying degrees of fitness. If this fitness differential is adequately large, the resulting selection for allele matching could maintain allelic association, even between physically unlinked loci. Allelic association is often observed in a population with the use of gametic linkage disequilibrium. However, because the coevolving genes are not necessarily in physical linkage, this is not an appropriate measure of coevolution-induced allelic association. Instead, we propose using both composite linkage disequilibrium (CLD) and a measure of association between genotypes, which we call genotype association (GA). Using a simple selective model, we simulated loci and calculated power for tests of CLD and GA, showing that the tests can detect the allelic association expected under realistic selective pressure. We apply CLD and GA tests to the polymorphic, physically unlinked, and putatively coevolving human gamete-recognition genes ZP3 and ZP3R. We observe unusual allelic association, not attributable to population structure, between ZP3 and ZP3R. This study shows that selection for allele matching can drive allelic association between unlinked loci in a contemporary human population, and that selection can be detected with the use of CLD and GA tests. The observation of this selection is surprising, but reasonable in the highly selected system of fertilization. If confirmed, this sort of selection provides an exception to the paradigm of chromosomal independent assortment.

Introduction

Coevolving genes are expected to undergo compensatory mutations to maintain their interaction. Over evolutionary time, accumulation of compensatory mutations at two loci would result in correlation of phylogenetic distances between the loci. Methods have been developed for detecting coevolution by testing for high correlation of phylogenetic distance matrices between gene families, genes, or gene domains.^1–6 These methods have successfully identified known coevolving gene families and previously unknown candidate coevolving genes.

In addition to detecting correlated phylogenetic distances, some models of coevolution predict allelic association within a population.⁷ Numerous experimental studies have shown evidence of coevolution-induced allelic association in several systems. Self-incompatibility mating systems require polymorphic self-recognition proteins on both sperm and eggs. Genes encoding self-recognition proteins are in physical linkage in sea squirts,⁸ Brassica,⁹ and Aspergillus nidulans,¹⁰ allowing compatible self-recognition genes to be transmitted together so that outcrossing is maintained over generations. Conversely, sea urchin eggs preferentially bind sperm with a sperm-recognition gene allele like their own, even though that gene is not expressed in eggs.¹¹ It has been proposed that physical linkage between the polymorphic gamete-recognition genes maintains the observed allelic association.¹¹ In abalone, physically unlinked gamete receptor genes were recently found to be in linkage disequilibrium (LD).⁶ More generally, genome-wide studies of LD have found that, even across chromosomes, functionally related genes have higher LD than do functionally unrelated genes in Drosophila¹² and between inbred mouse lines¹³ (however, see ¹⁴). This increased association may facilitate efficient interactions between polymorphic genes in an interacting group. In humans, HLA and KIR are well established as interacting immune-response loci under intense diversifying selection. Although these genes are on different chromosomes, their allele frequencies are significantly correlated within human populations, as one would expect under intense selection for allele matching.¹⁵

In all of the examples above, selective advantage of paired alleles resulted in allelic association, sometimes even in the absence of physical linkage. Most cases of selective advantage for specific allele pairing would be resolved with fixation of the optimal allele pair.⁷ For sustained selection-induced allele pairing, additional forces must maintain polymorphism. Allele-pairing selection may occur in gamete recognition because the process is obviously essential for gene transmission, requires interaction between sperm and egg receptor genes, and is subject to complex selective forces culminating in sexual conflict.¹⁶

Comprehension of these selective forces requires an explanation of the mechanics of gamete recognition. In humans, an egg is contained in a plasma membrane that is surrounded by a glycoprotein shell, the zona pellucida (ZP). A sperm binds to the ZP, releases enzymes to break through the ZP, travels through the ZP, binds to the plasma membrane, and finally fuses with the egg to fertilize it.¹⁷ If more than one sperm fuses with the egg, the polyspermy zygote is inviable. To prevent this, after a sperm fuses with the egg, the ZP is modified in the cortical reaction to prevent more sperm from reaching the egg. To avoid polyspermy, a fit sperm receptor allele will bind sperm slowly, to minimize the chance that multiple sperm bind before the cortical reaction completes. At the same time, the only sperm to pass on genetic information is the first fertilizer. This sperm competition for quick egg recognition means that a fit egg receptor binds very quickly. These opposing interests create sexual conflict, causing successive waves of selection at each locus. When polyspermy rates are high, slower-binding sperm receptors have a selective advantage. Then egg receptor alleles that quickly bind to the increasingly common sperm receptors have a selective advantage, increasing polyspermy rates and starting the cycle again.¹⁸ All the while, the interaction between loci is maintained, resulting in rapid coevolution between polymorphic loci.

In this paper, we explore the ramifications of coevolution between the genes mediating sperm-ZP binding in humans. Specifically, the ZP-located protein ZP3 (MIM 182889) has been shown to mediate sperm binding to the ZP¹⁹ and is in the top 10% of divergent (but still alignable) genes between humans and rodents.²⁰ Additional studies have shown that some strongly conserved sites form regions of exposed hydrophobic residues involved in ZP3 polymer formation²¹ and that sites under the intense positive selective pressure are in regions implicated in species-specific gamete recognition.²² The corresponding egg receptor on sperm has been less clearly identified. However, ZP3R has been proposed to bind ZP3.^23–26 Because ZP3 and ZP3R are putative interactors mediating gamete recognition, are polymorphic among humans, and are located on different chromosomes, they are excellent candidates for coevolution-induced allelic association. We show evidence of current genotype pairing selection between ZP3 and ZP3R, as observed in intergenic allelic association.

We propose allelic association as an indicator of selection for allele pairing. The most commonly used form of allelic association is gametic LD, which quantifies the sum of association between maternal alleles and association between paternal alleles at two loci.²⁷ Although LD is typically thought of as a measure of recombination rate correlated with physical distance, LD was originally devised to detect allelic association due to epistatic selection.^28,29 In this study, we are interested in association between paternal egg receptor (ZP3R) alleles and maternal sperm receptor (ZP3) alleles, which is quantified in a specific nongametic allelic association, rather than gametic LD. We consider population-based data, in which there is no gametic phase information, preventing direct measurement of the relevant specific nongametic allelic association.

Instead of haplotypic gametic or nongametic LD, we use genotypic association measures, which include the relevant nongametic allelic association along with other allelic associations. Specifically, we use composite linkage disequilibrium (CLD)³⁰ as a general measure of additive association and genotype association (GA)³¹ as a measure of association in genotype pairs. CLD quantifies additive co-occurence of alleles in genotypes at two loci, whereas GA measures departures from independence of genotypes between two loci. Here, we describe these measures and their results regarding the allelic association between ZP3 and ZP3R as compared to both the asymptotic null expectation and empirical distribution.

Subjects and Methods

Data

The Wellcome Trust Case Control Consortium (WTCCC) kindly provided us with the genotype calls using the Affymetrix 500K SNP genotyping platform for 1504 individuals in the 1958 Birth Cohort study.³² We used the same quality-control procedures on the data as did the WTCCC study, leaving 1480 individuals.³² Genes of interest were represented by sets of SNPs over these 1480 individuals.

To ensure genotyping probe-binding specificity for the SNPs examined around the candidate genes, we ran blastn searches on each 25-mer probe, using a small word size (7) and no filtering or masking. We found no extraneous exact probe matches, nor any near matches between the chromosomes containing ZP3 and ZP3R; chromosomes 7 and 1, respectively.

Candidate Gene SNPs

A subset of SNPs from the Affymetrix 500K genotyping platform act as a proxy for functionally distinct alleles of ZP3 and ZP3R. To choose SNPs representative of alleles encoding structurally distinct proteins, we use SNPs in a local region defined by high LD around the gene. Although the Affymetrix 500K SNPs are relatively dense genome-wide, they are too sparse to allow accurate assessment of fine-scale LD structure. Therefore, gene regions were determined by LD calculated with the use of the more densely genotyped HapMap CEU group (Utah residents with ancestry from northern and western Europe).³³ The exact regions used were the smallest regions extending no further than 100 kb up- and downstream of the gene, including all SNPs in high LD with a SNP in the gene itself. We quantify high LD as r² > 0.8, with r² defined³⁰ as

$$r^2=\frac{{\left({\tilde{p}}_{AB}-{\tilde{p}}_A{\tilde{p}}_B\right)}^2}{{\tilde{p}}_A\left(1-{\tilde{p}}_A\right){\tilde{p}}_B\left(1-{\tilde{p}}_B\right)}$$

in which ${\tilde{p}}_A$ is the observed minor allele frequency (MAF) at one locus, ${\tilde{p}}_B$ is the observed MAF at the other locus, and ${\tilde{p}}_{AB}$ is the observed double minor allele haplotype frequency.

Applying this SNP selection method to ZP3 and ZP3R produces 13 and 28 SNPs, respectively, all genotyped in the 1958 Birth Cohort. Monomorphic SNPs in the 1958 Birth Cohort are eliminated, leaving ten SNPs to represent ZP3 and 26 to represent ZP3R.

There is LD within these SNP sets, preventing assumptions of independence. To decrease dependence between SNPs, we use tag SNPs identified through an ad hoc method. The SNP having r² > 0.8 with the highest number of other SNPs is chosen as a tag SNP for all of those SNPs. If there are multiple SNPs having r² > 0.8 with the same number of SNPs, the tag SNP is chosen randomly. This process is repeated until all SNPs in the locus are tagged, resulting in seven and nine SNPs in ZP3 and ZP3R, respectively. These tag SNPs do not eliminate dependency between tests, but they do reduce both gross differences in representation of different LD blocks and the total number of tests computed between SNP sets.

Empirical Comparisons

We evaluate the extremity of allelic association between the candidate genes by using an empirical framework to account for background genomic levels of allelic association between physically unlinked loci. We consider two different data types for empirical comparison: SNPs and genes.

In the SNP-wise method, the association tests between SNP pairs in our candidate genes are compared to the distribution of association tests between all SNPs on the chromosomes of the candidate genes; chromosomes 1 and 7. So, an empirical allelic association p value is calculated for each SNP pair between the candidate genes. While this method provides a simple estimation of the significance of association between candidate gene SNPs, it does so independently for each SNP pair, ignoring dependencies within each candidate gene.

To account for LD within each candidate gene, we compare the distribution of test statistics between SNPs in the candidate genes with the distributions of test statistics from SNP pairs between other genes on chromosomes 1 and 7. These distribution-distribution comparisons incorporate LD within genes.

For this purpose, a gene is defined as the set of overlapping transcripts from the same strand, as defined in the UCSC Genome Browser's “known genes” list downloaded in September 2007 from NCBI build 36.³⁴ There are 1662 such genes on chromosome 1 and 769 genes on chromosome 7. The SNPs included to describe each gene were identified in a manner similar to that of those for the candidate genes, in which the total genetic distance across the gene approximates that of the candidate gene.

Allelic Association Tests

We are interested in whether there is allelic association between the maternally inherited ZP3 and paternally inherited ZP3R. Clearly, conventional gametic LD will not detect this specific association. Nongametic LD may be more appropriate for this application. However, because we use population data, rather than family data, gametic phase can not be determined, so it is not possible to directly measure either gametic or nongametic LD. Instead, we measure both general allelic association, using CLD, and association between genotype pairs, in a measure that we call genotype association (GA). Each measure quantifies the sum of several specific associations, including the association between maternal ZP3 and paternal ZP3R.

Note that if there is diploid expression in gametes so that both transmitted and nontransmitted protein alleles are present, noninherited maternal ZP3 and paternal ZP3R may play a role in sperm-egg recognition. The data set used here is population-based and thus lacks noninherited allele information, so we focus on inherited genes.

Composite Linkage Disequilibrium

General allelic association between a pair of SNPs is quantified by CLD. An estimate of CLD has been previously given³⁵ as

$${\widehat{\mathrm{\Delta }}}_{AB}=\frac{1}{n}{n}_{AB}-2{\tilde{p}}_A\tilde{p}$$

in which

$$n_{AB}=2n_{AABB}+n_{AABb}+n_{AaBB}+\frac{1}{2}{n}_{AaBb}$$

The hypothesis that CLD is zero, indicating no allelic association, can be tested with the test statistic

$$X_1^2=\frac{n{\widehat{\mathrm{\Delta }}}_{AB}^2}{\left({\tilde{p}}_A{\tilde{p}}_a+{\tilde{p}}_{AA}-{\tilde{p}}_A^2\right)\left({\tilde{p}}_B{\tilde{p}}_b+{\tilde{p}}_{BB}-{\tilde{p}}_B^2\right)}$$

which is approximately χ² distributed with one degree of freedom. The CLD method tests for additive association of the A and B alleles in a two-locus genotype.

Genotype Association

Not all selective scenarios that create genotypic association may be detected with the CLD method. For example, if AA and –b tend to co-occur and –a and BB tend to co-occur, the net association measured in ${\widehat{\mathrm{\Delta }}}_{AB}$ would be very small, despite strong genotype associations. To address this possibility, we use a standard contingency table for independence between the two genotypes (Table 1), resulting in the chi-square distributed test statistic with four degrees of freedom:

$$X_4^2=n(\frac{{\left({\tilde{p}}_{AABB}-{\tilde{p}}_{AA}{\tilde{p}}_{BB}\right)}^2}{{\tilde{p}}_{AA}{\tilde{p}}_{BB}}+\frac{{\left({\tilde{p}}_{AABb}-{\tilde{p}}_{AA}{\tilde{p}}_{Bb}\right)}^2}{{\tilde{p}}_{AA}{\tilde{p}}_{Bb}}+\frac{{\left({\tilde{p}}_{AAbb}-{\tilde{p}}_{AA}{\tilde{p}}_{bb}\right)}^2}{{\tilde{p}}_{AA}{\tilde{p}}_{bb}}+\frac{{\left({\tilde{p}}_{AaBB}-{\tilde{p}}_{Aa}{\tilde{p}}_{BB}\right)}^2}{{\tilde{p}}_{Aa}{\tilde{p}}_{BB}}+\frac{{\left({\tilde{p}}_{AaBb}-{\tilde{p}}_{Aa}{\tilde{p}}_{Bb}\right)}^2}{{\tilde{p}}_{Aa}{\tilde{p}}_{Bb}}+\frac{{\left({\tilde{p}}_{Aabb}-{\tilde{p}}_{Aa}{\tilde{p}}_{bb}\right)}^2}{{\tilde{p}}_{Aa}{\tilde{p}}_{bb}}+\frac{{\left({\tilde{p}}_{aaBB}-{\tilde{p}}_{aa}{\tilde{p}}_{BB}\right)}^2}{{\tilde{p}}_{aa}{\tilde{p}}_{BB}}+\frac{{\left({\tilde{p}}_{aaBb}-{\tilde{p}}_{aa}{\tilde{p}}_{Bb}\right)}^2}{{\tilde{p}}_{aa}{\tilde{p}}_{Bb}}+\frac{{\left({\tilde{p}}_{aabb}-{\tilde{p}}_{aa}{\tilde{p}}_{bb}\right)}^2}{{\tilde{p}}_{aa}{\tilde{p}}_{bb}})$$

Table 1.

Genotype-Count Contingency Table

	nBB	nBb	nbb
nAA	nAABB	nAABb	nAAbb
nAa	nAaBB	nAaBb	nAabb
naa	naaBB	naaBb	naabb

Note that when there are zero instances of any one-locus genotype, a GA statistic would have fewer than four degrees of freedom. Those cases have been excluded from further analysis in this discussion.

Permutation Testing Scheme

The CLD and GA test statistics measure allelic association, but they are also dependent on marginal one-locus genotype counts. To control for the one-locus genotype counts, X₁² and X₄² are used as test statistics in permutation tests. For each permutation, the individual identities corresponding to multimarker genotypes for one locus are held fixed, while the individual identities for the other locus are shuffled. Intralocus allelic association is maintained, and only interlocus allelic association is randomized. The permutation p value for a SNP pair is the proportion of permuted data sets resulting in X₁² or X₄² larger than those calculated from the original observed data. Permutation p values approximate exact p values, which are the probabilities of an allelic association at least as strong as that observed, given the marginal genotypes at each locus. We use the permutation approximation of exact tests here because the large sample size (n = 1480) precludes complete enumeration of all two-locus data sets.

Addressing Power

The chance of falsely rejecting the hypothesis of allelic independence is set by our choice of significance level, and the probability of correctly rejecting the hypothesis can be addressed by power calculations. In order to study power, we need to specify an alternative hypothesis, and we do so by invoking a model of selection.

Using a simple selective model, we calculate expected genotype counts for a range of selective coefficients, including no selection. Both CLD and GA tests are applied to the expected genotype counts, and test power and type I error are calculated for each test. Below, we present a simple selective model used to generate genotype counts and methodology both for calculating power exactly and for estimating power asympototically.

Simulating Selection

As in Lewontin's simulations,^28,29 we simulate selection on a system with two loci, ZP3R-like A expressed in sperm and ZP3-like B expressed in eggs, each with two alleles, A/a and B/b. Because selection occurs when egg and sperm encounter each other and attempt fertilization, we consider gamete pair frequencies, meaning the joint frequency of egg ZP3 and sperm ZP3R alleles. At the start of the simulation, gamete pair frequencies are uniformly distributed such that each gamete pair has frequency of 1/16 in individuals. Gamete pair encounter frequencies are calculated under random mating with equal numbers of male and female individuals, as the product of individual gamete frequencies in the current generation. Not all gamete pair encounters lead to successful fertilization, and some gamete pair alleles may recognize each other better than others. To simulate this differential fertilization success, gamete pair encounter frequencies are multiplied by their respective adaptive values to obtain gamete pair frequencies in the next generation.

In this model, we assume haploid expression, meaning that only the transmitted allele is expressed in a gamete. So, gamete pairs with the alleles sperm A, egg B and sperm a, egg b are equally fit, with adaptive values of 1.0, whereas pairs sperm A, egg b and sperm a, egg B are equally less fit, with adaptive values of 1.0-s, in which s is the selective coefficient. The adaptive values of all gamete pairs are listed in Table 2.

Table 2.

Adaptive Values of All Gamete Pairs

	Sperm
Egg	AB	Ab	aB	ab
AB	1	1	1-s	1-s
Ab	1-s	1-s	1	1
aB	1	1	1-s	1-s
ab	1-s	1-s	1	1

To clarify the simulation process, we demonstrate the calculations over a generation. Say in the current generation the single contributing gamete frequencies and gamete pair frequencies in individuals are

These current-generation gamete pair frequencies can be summed appropriately, producing the single-gamete frequencies contributing to the next generation. For example, the frequency of eggs or sperm with gametic haplotype AB will be

$$p_{AB}^{\prime egg}=p_{AB\text{.}AB}+\frac{1}{2}\left(p_{AB\text{.}Ab}+p_{AB\text{.}aB}+p_{Ab\text{.}AB}+p_{aB\text{.}AB}\right)+\frac{1}{4}\left(p_{AB\text{.}ab}+p_{Ab\text{.}aB}+p_{aB\text{.}Ab}+p_{ab\text{.}AB}\right)\text{.}$$

The gamete pair encounter frequencies for the next generation are the product of the individual-gamete frequencies. For example, the probability of an AB egg encountering an AB sperm is p′_AB^eggp′_AB^sperm. At this point, selection for gamete receptor matching is applied. In the case of the AB egg and AB sperm, the egg B and sperm A match, so the adaptive value used is 1.0 and the next-generation gamete pair frequency in individuals is p′_AB.AB = 1.0(p′_AB^eggp′_AB^sperm). For an AB egg and an aB sperm, the egg B and sperm a do not match, so their adaptive value is 1.0 − s and p′_AB.aB = (1.0 – s)(p′_AB^eggp′_aB^sperm). All of the next next-generation genotype frequencies are normalized so that they sum to 1.0.

In this study, 50 generations were simulated, at which point the gamete pair frequencies were stable. Because of the symmetry in selection on each allele, the allele frequencies remain at 0.5.

Calculating Power

The power of a Fisher's exact test for gametic LD can be computed for particular disequilibrium parameters.³⁶ Similarly, the power of a Fisher's exact test for either CLD or GA can be computed with the use of the genotype-frequency matrix F expected under some selective coefficient s:

$$F=\left[\begin{array}{ccc}{p}_{AABB}& p_{AABb}& p_{AAbb}\\ p_{AaBB}& p_{AaBb}& p_{Aabb}\\ p_{aaBB}& p_{aaBb}& p_{aabb}\end{array}\right]$$

Because the row and column sums of F are constrained to the one-locus frequencies, the matrix can be specified by the four entries p_AABB, p_AABb, p_AaBB, and p_AaBb. Note that the matrix is described in the four parameters

$$\begin{array}{c}\kappa =\frac{p_{AABB}{p}_{aabb}}{p_{AAbb}{p}_{aaBB}}\\ \lambda =\frac{p_{AABb}{p}_{aabb}}{p_{AAbb}{p}_{aaBb}}\\ \mu =\frac{p_{AaBB}{p}_{aabb}}{p_{Aabb}{p}_{aaBB}}\\ \nu =\frac{p_{AaBb}{p}_{aabb}}{p_{Aabb}{p}_{aaBb}}\end{array}$$

Given these genotype frequencies, the probability of the genotype-count matrix

$$C=\left[\begin{array}{ccc}{n}_{AABB}& n_{AABb}& n_{AAbb}\\ n_{AaBB}& n_{AaBb}& n_{Aabb}\\ n_{aaBB}& n_{aaBb}& n_{aabb}\end{array}\right]$$

with marginal genotype-count arrays M = [n_AA, n_Aa, n_aa], [n_BB, n_Bb, n_bb] follows the multinomial probability-density function and can be computed as

$$\begin{array}{c}P\left(C\right|M,F)=\frac{n!}{\prod _i{C}_i}\prod _i{F}_i^{C_i}\\ =\frac{n!}{n_{AABB}!n_{AaBB}!\dots n_{aabb}!}{\kappa }^{n_{AABB}}{\lambda }^{n_{AABb}}{\mu }^{n_{AaBB}}{\nu }^{n_{AaBb}}\cdot \frac{1}{T}\end{array}$$

in which i indexes all C_i and F_i, which are two-locus genotype counts and frequencies in C and F, respectively, that are constrained by the one-locus marginals. The same constraint hold for normalizing factor T:

$$\begin{array}{c}T=\sum _{i}P\left(C_i|M,F\right)\\ =\sum _{n_{AABB},n_{AABb},n_{AaBB},n_{AaBb}}\frac{n!}{n_{AABB}!\dots n_{aabb}!}{\kappa }^{n_{AABB}}{\lambda }^{n_{AABb}}{\mu }^{n_{AaBB}}{\nu }^{n_{AaBb}}\text{.}\end{array}$$

For the power computation, the marginal one-locus genotype counts M are held fixed while all joint two-locus genotype-count matrices C are enumerated and P(C|M, F) are calculated. The GA Fisher's exact test p value of each individual joint genotype-count matrix C with P(C|M, F) = q is the sum of P(C|M, F) for all C where P(C|M, F) ≤ q. With p computed for every matrix C, the exact power of the GA exact test is the sum of P(C|M, F) for all possible C with p ≤ α. The exact type I error rate is computed the same way, in which s = 0.

For the CLD test, the exact p value of each individual joint genotype-count matrix C with P(C|M, F) = q and X₁² = x is then the sum of P(C|M, F) for all C where X₁² ≥ x. The exact power of the CLD test is the sum of P(C|M, F) for all joint genotype-count matrices where p ≤ α and the type I error rate is the same sum computed when s = 0.

Estimating Power Asymptotically

Calculating the power of these exact tests can be prohibitively slow with a large sample size. As an alternative, we quickly estimate power by using theoretical test statistic distributions under the alternative hypothesis. Under the alternative hypothesis with genotype frequency matrix F, X₁² is approximately chi-square distributed with one degree of freedom and noncentrality parameter

$${\lambda }_1=\frac{{\Delta }_{AB}^2}{(p_A{p}_a+p_{AA}-p_A^2)(p_B{p}_b+p_{BB}-p_B^2)}$$

whereas X₄² is chi-square distributed with four degrees of freedom and noncentrality parameter

$${\lambda }_4=n\left(\frac{{\left(p_{AABB}-p_{AA}\ast p_{BB}\right)}^2}{p_{AA}\ast p_{BB}}+\frac{{\left(p_{AABb}-p_{AA}\ast p_{Bb}\right)}^2}{p_{AA}\ast p_{Bb}}+\frac{{\left(p_{AAbb}-p_{AA}\ast p_{bb}\right)}^2}{p_{AA}\ast p_{bb}}+\frac{{\left(p_{AaBB}-p_{Aa}\ast p_{BB}\right)}^2}{p_{Aa}\ast p_{BB}}+\frac{{\left(p_{AaBb}-p_{Aa}\ast p_{Bb}\right)}^2}{p_{Aa}\ast p_{Bb}}+\frac{{(p_{Aabb}-p_{Aa}\ast p_{bb})}^2}{p_{Aa}\ast p_{bb}}+\frac{{\left(p_{aaBB}-p_{aa}\ast p_{BB}\right)}^2}{p_{aa}\ast p_{BB}}+\frac{{\left(p_{aaBb}-p_{aa}\ast p_{Bb}\right)}^2}{p_{aa}\ast p_{Bb}}+\frac{{\left(p_{aabb}-p_{aa}\ast p_{bb}\right)}^2}{p_{aa}\ast p_{bb}}\right)\text{.}$$

The power of each test is the area right of the critical value under the corresponding noncentral chi-square distribution with parameters obtained via simulated one- and two-locus genotype frequencies. This assumes that the test statistics follow their expected asymptotic distributions. In fact, because genetic data are discrete, the resulting test statistics are discrete and their distribution only approximates the asymptotic expectation.³⁶ Power computed asymptotically is not the true exact power for our analysis with 1480 individuals; however, it provides an adequate approximation.

Results

SNP Pair Analysis

Both X₁² and X₄² were used as association measures in 1000-iteration permutation tests between each tag SNP pair in ZP3 and ZP3R. Because we are considering seven SNPs representing ZP3 and nine SNPs representing ZP3R, a full test yields a matrix of 63 test statistics. Table 3 and Table 4 show these permutation p value tables using X₁² and X₄², respectively. In Table 4, some results are excluded because the GA test is defined only when both SNPs tested have at least one observed instance of each genotype.

Table 3.

CLD-Based Permutation p Values between Tag SNPs in ZP3R and ZP3

	ZP3
ZP3R	rs2868371	rs6978009	rs10156094	rs1860148	rs868269	rs1019096	rs2298691
rs3813948	0.62	0.13	0.38	0.41	0.49	0.57	0.30
rs8942	0.06	0.02	0.15	0.70	0.01	0.76	0.14
rs2491395	0.00	0.01	0.06	0.99	0.24	0.23	0.04
rs4844573	0.03	0.09	0.47	0.59	0.28	0.58	0.18
rs11120277	0.43	0.46	0.02	0.38	0.32	0.03	0.57
rs10746451	0.03	0.29	0.55	0.08	0.50	0.53	0.15
rs7543834	0.85	0.25	0.03	0.33	0.33	0.24	0.29
rs7516640	0.09	0.19	0.67	0.19	0.49	1.00	0.28
rs11120512	0.34	0.88	0.50	0.14	0.82	0.87	0.18

p values below 0.05 are indicated in bold font.

Table 4.

GA-Based Permutation p Values between Tag SNPs in ZP3R and ZP3

	ZP3
ZP3R	rs2868371	rs6978009	rs10156094	rs1860148	rs1019096	rs2298691
rs3813948	0.92	0.36	0.91	0.41	0.14	0.73
rs8942	0.21	0.20	0.52	1.00	0.72	0.67
rs2491395	0.02	0.03	0.39	0.72	0.34	0.25
rs4844573	0.05	0.09	0.50	0.50	0.26	0.43
rs10746451	0.19	0.08	0.43	0.29	0.34	0.22
rs7516640	0.29	0.29	0.03	0.45	0.02	0.53
rs11120512	0.81	0.92	0.79	0.24	0.52	0.49

p values below 0.05 are indicated in bold font.

Of the 63 and 42 permutation p values based on X₁² and X₄², ten (15.9%) and five (11.9%) are significant, respectively, with α = 0.05. If the allelic association tests were independent and followed the asymptotic distribution assuming no allelic association, we would expect 5% of tests to be significant, so the observed p values are enriched for significance. The use of tag SNPs decreases dependence between tests; however, there is still LD within each gene. Because of this dependence, these significance proportions can not be directly compared to the expectation under independence, but they do suggest a high rate of allelic association. Dependence within each locus is further addressed in the Gene Pair Analysis section.

SNPs with low MAFs are more likely to have genotyping errors, and these errors have greater effects on allelic association calculations for low-MAF SNPs. To check that the associations observed between ZP3 and ZP3R can not be explained by low-MAF genotyping errors, SNPs with MAF below 0.05 were excluded from the LD-blocked SNP sets. Of the remaining tests, 14.3% and 11.9% of SNP pairs were found to be significantly associated via permutation tests based on X₁² and X₄², respectively. The similar percentage in significance without low-MAF SNPs confirms that the observed associations are not due to low-MAF SNP-genotyping error.

We ran a similar analysis on a secondary candidate gene pair implicated in maternal-fetal interactions: GHR (MIM 600946) and GH2 (MIM 139240).³⁷ The fetus releases GH2 into the mother, where it is detected by GHR, in order to alter its environment to its benefit, which is not necessarily in the mother's interest.³⁷ For example, it is in the fetus's interest to maximize nutrient uptake from the mother's blood, whereas it is in the mother's interest to keep enough nutrients to remain healthy. This conflict may cause similar selective patterns as in fertilization. With the use of permutation p values based on X₁² and X₄², 17.3% and 6.8%, respectively, of tag SNP pairs are significantly associated (Tables S3 and S4, available online). With exclusion of SNPs with MAF below 0.05, the results were similar, with 18.2% and 6.8% of tag SNP pairs shown by X₁² and X₄², respectively, to be significantly associated. Histograms of GHR-GH2 test statistics are compared to the asymptotic expectations and empirical distributions in Figure S1.

Conditioning on the marginal one-locus SNP genotypes in each gene, we've shown that SNPs in ZP3 and ZP3R are more associated than expected under independence. We are also interested in whether ZP3 and ZP3R have high allelic association in comparison to background genomic association levels. To test empirical allelic association, permutation p values were computed for all SNP pairs between chromosomes 1 and 7. Figure 1 shows the full distribution of the ZP3-ZP3R allelic association test statistics in comparison with the empirical SNP pair results and asymptotically expected null test statistic distributions. The ZP3-ZP3R test statistics are shifted right of the asymptotic null chi-square distributions and of the empirical test statistics. The quantile-quantile (Q-Q) plots in Figure 2 provide a visual comparison of ZP3-ZP3R p values and the same number of p values from random SNP pairs between chromosomes 1 and 7. CLD is higher in the candidate genes than in the random SNP pairs, but GA appears to be more similarly distributed between the candidates and random SNP pairs.

Figure 1.

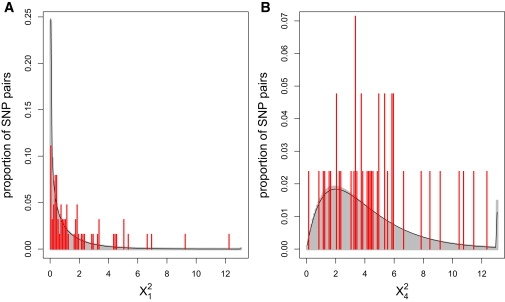
CLD and GA Test Statistic Distributions

The black curve shows the asymptotically expected null test statistic distribution, the gray bars are histograms of the empirical distribution of the test statistics between all SNP pairs on chromosomes 1 and 7, and the red bars are a histogram of test statistics between SNPs in ZP3 and ZP3R for (A) X₁² and (B) X₄².

Figure 2.

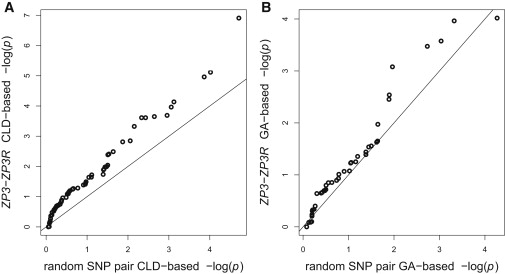
Q-Q Plot Comparing ZP3-ZP3R with Random SNP Pairs

The Q-Q plots compare the (A) X₁²-based and (B) X₄²-based permutation p values between ZP3-ZP3R and an equal number of random SNP pairs between chromosomes 1 and 7.

Gene Pair Analysis

To control for LD within each locus, we compare the observed test statistics between SNPs in ZP3 and ZP3R with test statistics between SNPs in random gene pairs between chromosomes 1 and 7. As an example, we examine the association comparison between ZP3-ZP3R and a single random gene pair: DPY19L1 on chromosome 7 and PIP5K1A on chromosome 1. The random gene pair choice was constrained to genes with numbers of typed SNPs similar to those in the candidate genes. DPY19L1 has 26 SNPs, whereas PIP5K1A has ten.

Permutation tests based on both X₁² and X₄² were performed between every SNP pair in ZP3-ZP3R and in DPY19L1-PIP5K1A. The results are compared in Q-Q plots in Figure 3, which shows more significant p values in the candidate gene pair as compared to the random gene pair. In this random example, 15.9% of X₁²-based p values and 11.9% of X₄²-based p values between ZP3 and ZP3R are significant, whereas zero p values based on either X₁² or X₄² between DPY19L1 and PIP5K1A are significant, with α = 0.05.

Figure 3.

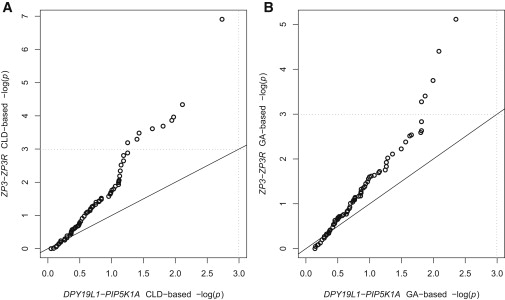
Q-Q Plot Comparing ZP3-ZP3R with Random Gene Pairs

These Q-Q plots compare the (A) X₁²-based and (B) X₄²-based permutation p values between ZP3-ZP3R and PIP5K1A-DPY19L1. The dotted lines indicate significance thresholds with α = 0.05.

The ZP3-ZP3R and DPY19L1-PIP5K1A test statistic distribution comparison is a useful example, but is only a single comparison. To better understand the genomic empirical extremity of our candidate gene pair test statistics, we compare the candidate gene pair test distributions to many random gene pair test distributions. Because these gene pair comparisons are meant to control for intragenic LD, all SNPs are included, rather than tag SNPs only. We visually compare the permutation p value distribution of the candidate gene pair with many random gene pairs simultaneously, by plotting the cumulative distribution functions (CDFs) of – log(p) for candidate and random gene pairs on the same plot (Figure 4). When one CDF is below and to the right of another CDF, the first distribution has greater values than the second.

Figure 4.

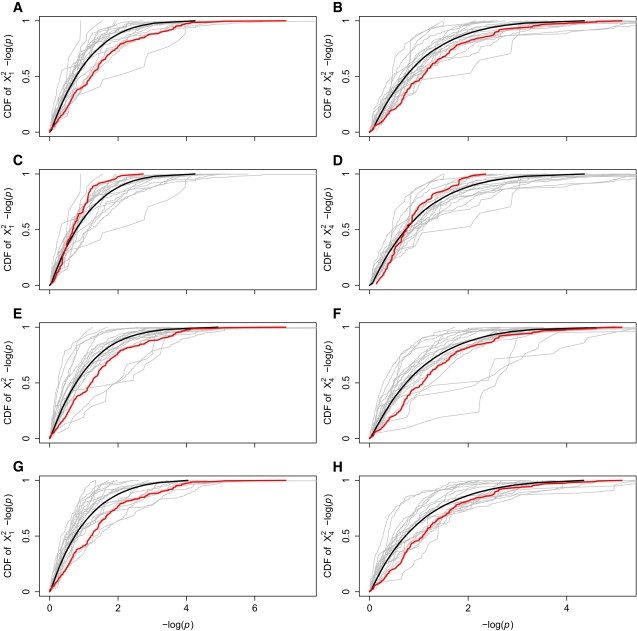
Comparative Gene Pair CDFs

These plots show the cumulative distribution functions (CDFs) of permutation – log(p) computed between the gene pair of interest in red, 20 comparison gene pairs in gray, and the average CDF of all comparison gene pairs in black. In the top row, – log(p) between ZP3R and ZP3 (red) is compared to – log(p) between random gene pairs on chromosomes 1 and 7 (gray) and the average comparative gene pair – log(p) distribution (black) for (A) X₁²-based and (B) X₄²-based permutation p values. In the second row, – log(p) between PIP5K1A and DPY19L1 (red) is compared to – log(p) between random gene pairs on chromosomes 1 and 7 (gray) and the average comparative gene pair – log(p) distribution (black) for (C) X₁²-based and (D) X₄²-based permutation p values. In the third row, – log(p) in ZP3R-ZP3 (red) are compared to – log(p) between ZP3R and 20 genes on chromosome 7 (gray) and the average – log(p) distribution between ZP3R and chromosome 7 genes (black) for (E) X₁²-based and (F) X₄²-based permutation p values. In the bottom row, – log(p) in ZP3R-ZP3 (red) is compared to – log(p) between ZP3 and 20 genes on chromosome 1 (gray) and the average – log(p) distribution between ZP3R and chromosome 7 genes (black) for (G) X₁²-based and (H) X₄²-based permutation p values.

In Figures 4A and 4B, the ZP3-ZP3R – log(p) CDF in red is to the right of most random gene pair CDFs and the average random gene pair curve, showing that the – log(p) distribution in candidate gene pairs is shifted right of both individual random gene pairs and random gene pairs on average. Although only 20 individual random gene pair CDFs are shown in each plot in Figure 4, the average CDF curves are calculated with the use of all 769 random gene pairs between chromosomes 1 and 7. Figures 4C and 4D show the same random gene pair CDFs with the DPY19L1-PIP5K1A distribution highlighted in red, illustrating that DPY19L1-PIP5K1A p values are distributed much like other random gene pairs. It may be that the unusual association in ZP3-ZP3R is due to some unknown feature of either ZP3 or ZP3R, independent of their relationship to each other. To check that possibility, the ZP3-ZP3R p value distribution is compared to ZP3R paired with chromosome 7 genes and to ZP3 paired with chromosome 1 genes. Figures 4E and 4F compare the ZP3-ZP3R to ZP3R-chromosome 7 genes, and Figures 4G and 4H compare ZP3-ZP3R to ZP3-chromosome 1 genes. In each case, the ZP3-ZP3R p value distributions are shifted more significantly in comparison to the candidate versus random gene p value distributions.

A one-sided Kolmogorov-Smirnov (KS) test can be used to quantitatively test the hypothesis that the candidate gene pair p value distribution is significantly lower than the distribution resulting from a random gene pair. We performed such KS tests to compare p value distributions between ZP3-ZP3R and the 769 random gene pairs. Just as shown in Figure 4, we performed three analogous sets of KS tests for comparison: between fixed DPY19L1-PIP5K1A and the 769 random gene pairs, between fixed ZP3-ZP3R and ZP3R paired with 769 chromosome 7 genes, and between fixed ZP3-ZP3R and ZP3 paired with 1662 chromosome 1 genes. Table 5 shows the proportions of each set of KS tests in which the fixed p value distribution is significantly (α = .05) lower than the comparison p value distribution. For both CLD- and GA-based permutation tests, the proportion of tests rejected in the null DPY19L1-PIP5K1A comparison is significantly lower than in the ZP3-ZP3R comparisons.

Table 5.

Significant KS Test Rates

	X12-Based	X42-Based
ZP3R-ZP3 versus chr1-chr7 gene pairs	0.760	0.740
PIP5K1A-DPY19L1 versus chr1-chr7 gene pairs	0.295	0.476
ZP3R-ZP3 versus ZP3R-chr7 genes	0.818	0.811
ZP3R-ZP3 versus ZP3-chr1 genes	0.803	0.738

The proportions of significant KS tests with $\alpha =0.05$ are shown for $X_1^2$-based permutation and $X_4^2$-based permutation tests (row 1) comparing the ZP3-ZP3R results to chromosome 1–7 random gene pairs, (row 2) comparing DPY19L1-PIP5K1A to chromosome 1–7 random gene pairs, (row 3) comparing ZP3-ZP3R to ZP3R paired with chromosome 7 genes, and (row 4) comparing ZP3-ZP3R to ZP3 paired with chromosome 1 genes. All KS tests are against the alternative hypothesis that the fixed gene pair p values are more significant than the varying gene pair p values.

We again used one-sided KS tests to test the hypothesis that the p value distributions for each random gene pair are lower than those of the candidate genes. With the use of CLD- and GA-based p values, 8.2% and 7.6% of random gene pair p value distributions were significantly lower than the ZP3-ZP3R distributions, respectively.

The KS test results support the hypothesis that the candidate gene p value distributions are lower than random gene pair p value distributions, indicating unusual allelic association between ZP3 and ZP3R. The comparisons of ZP3-ZP3R with each ZP3 and ZP3R paired with other genes show that the unusual association in ZP3-ZP3R is not due to some feature of either gene on its own but, rather, is specific to ZP3 and ZP3R.

Power Analysis

Because of the surprising nature of the observed allelic association and proposed causal coevolution, it is important to confirm the biological plausibility of selection causing allelic association and of that allelic association being detected by the tests that we applied. We use our selection model to numerically calculate the effect of allele-matching selection on gamete pair frequencies over generations. The resulting expected gamete pair frequencies under selection are used as parameters in power calculations. The selective model used in this analysis is a vast simplification of the complex dynamics involved in fertilization protein evolution; however, it provides a rough approximation that we can use to assess the plausibility of detecting coevolution via allelic association in biological data.

Power curves for the exact and asymptotic tests are shown under various s and n in Figure 5. For a high but biologically reasonable s of 0.1,³⁸ with a sample size of n = 1480, the asymptotic CLD test has a power of 0.525 and the asymptotic GA test has a power of 0.327. The causal coevolving polymorphisms are likely to be in LD with the SNPs examined, adding another step of association and potentially decreasing power in the applied tests. At the same time, the tests actually used in this analysis are permutation tests, which approximate the more powerful exact test, rather than the less powerful chi-square tests used in the power calculation. Although these power estimates are approximate, they indicate that it is feasible that these tests could detect allelic association caused by biologically plausible levels of selection.

Figure 5.

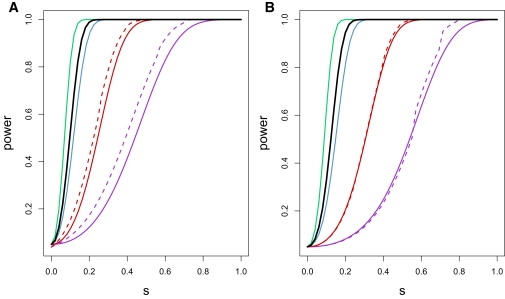
Power Curves

Assuming the selective model described in the text, the exact power of the exact test and the asymptotically derived power of the asymptotic tests were computed for both (A) X₁² and (B) X₄² for 50 values of s ranging from 0 to 1. The dashed curves show exact power, and the solid curves show asymptotically estimated power. Violet, red, blue, black, and green curves are calculated with the use of n = 50, 200, 1000, 1480, and 3000, respectively.

Using the same exact test methods with s = 0, we calculated the type I error rates for n = 50, 200 as 4.0% and 3.9%, respectively. Because of computational limitations, we were unable to perform the exact test for larger value of n; however in the cases computed, the false-positive rate is below the expected nominal level of 5.0%.

Family-Based Power Estimation

Our analysis applies a population-based approach. However, a family-based design could provide additional information, including parental nontransmitted alleles and transmitted alleles. Power in several family-based approaches was estimated with the use of the simulation framework described above, in which individuals are simulated and random gametes encounter one another. The selective coefficient s is applied to random gamete encounter zygote formation, so that some, but not all, random gamete encounters result in a trio. This trio set is used to estimate power via several different family-based methods.

Particularly fertile couples may have better-matched ZP3 and ZP3R alleles than particularly infertile couples. It is possible that expression is diploid during gametogenesis, so that proteins expressed from nontransmitted ZP3 and ZP3R alleles are present in gametes. In that case, the association of interest is between the maternal ZP3 and paternal ZP3R genotypes, which could be evaluated with CLD and GA tests.

In the case of haploid expression in gametes, one would expect transmission disequilibrium of better-matching allele pairs. To test this possibility, the observed and possible transmitted gamete allele pairs are totaled over all trios and tested for association via a standard chi-square test.

The trio set was used for calculation of CLD and GA between maternal ZP3 and paternal ZP3R and the transmission test. The simulation was repeated 10, 000 times with a selective coefficient of s = 0.1 and a sample size of 900 trios, resulting in power estimates of 16.8%, 12.3%, and 9.7%, respectively.

Discussion

Our results support unusual allelic association between ZP3 and ZP3R, as quantified by both CLD and GA tests. Alleles of ZP3 and ZP3R are nonrandomly associated, as shown via permutation methods, and their association is empirically unusual, as shown in genomic comparisons. We explore the plausibility of mechanisms apart from coevolution causing allelic association in ZP3-ZP3R.

In previous genome-wide studies, allelic association between physically unlinked loci has been explained by mismapped SNPs³⁹ (R. Lawrence et al., 2007, Genet. Epidemiol., abstract). In this study, the genotyping probes for each SNP examined in ZP3 and ZP3R were checked for sequence similarity with other regions in the genome. No sequence similarity between the probes and the regions around ZP3 and ZP3R was found, so the observed allelic association was not caused by SNP mismapping.

Population structure could also cause allelic association between physically unlinked loci. Allelic association would be observed if the alleles at each locus have different frequencies in different populations and those populations are pooled together. In this analysis, ZP3 and ZP3R are associated as compared to other genes in the same individuals. It is not likely that population structure would cause allelic association in our candidate gene pair but not in other gene pairs in the same population.

It is possible that ZP3 and ZP3R are statistical outliers that we expect under no selection and are associated simply by chance. However, given our limited single-hypothesis candidate gene approach, we find that unlikely. Having ruled out other causes for allelic association, we propose that the observed association is a result of selection for allele pairing.

Previously, it had not been clear what degree of selective pressure would be necessary for detectable allelic association. Our power analysis shows that allelic association can be maintained with a realistic level of selective pressure for allele matching. Given our sample size, test power is not high enough to reliably detect selection-induced allelic associations, but power is high enough so that a significant association cannot be immediately dismissed as an artifact.

The field has yet to identify a gene pair that is certainly coevolving in which both genes are polymorphic. In the absence of a clear positive control, we performed preliminary tests on GHR and GH2, a secondary candidate gene pair that may mediate fetal-maternal interactions. This candidate gene pair showed some association, similar to ZP3-ZP3R. A collection of unusually associated candidate gene pairs supports the hypothesis that coevolution results in slight, if not blatant, association.

To further support the hypothesis that ZP3-ZP3R association is biological in nature, we would like to perform an amino-acid-level analysis of the structural allelic differences driving selection. Unfortunately, the data used here are too sparse for such a fine-scale analysis. Finer-scale variation or sequence data is necessary to understand the local LD structure and identify causal variants. In lieu of sequence data at ZP3 and ZP3R, we do note that of the five nonsynonymous SNPs in ZP3, four fall in or near a sperm-binding region, as one would expect for functionally distinct sperm-binding alleles.^21,34 Because ZP3R was more recently identified as a gene, it has been less thoroughly sequenced, and no nonsynonymous SNPs are known in ZP3R as of yet.³⁴

A different study design using family data would enable different analyses considering full parental genotypes and transmission. To investigate the feasiblity of family-based studies, we performed power estimations, showing insufficient power with currently available data sets. As larger densely genotyped family data sets are available, it will be interesting to apply family-based methods to investigate selection for allelic association.

Despite the coarse, limited data analyzed, the observed results indicate that coevolution causes allelic association between physically unlinked gamete receptor genes. The fact that there could be allelic association between physically unlinked loci is quite surprising. The Mendelian model indicates that for each generation, genes on separate chromosomes are inherited independently, and thus the allele pairs would be randomized every generation. Strong selective force is required to maintain association between alleles randomized during each generation. Fertilization is a likely point for this powerful selection, given that unsuccessful fertilization negates further gene transfer. Additionally, it may be adventageous for egg and sperm receptors to increase or decrease allele frequencies independently, which is only possible in the absence of physical linkage. By contrast, in self-infertility systems, in which both coinheritance and correlation of allele frequencies are favored, recognition genes are often found in physical linkage.^8–10

We speculate that there are a few other biological points where allele-pairing selection plays such a powerful role. For example, in host-pathogen invasion, only pathogens that can successfully recognize their specific host can invade and reproduce, so allelic association may exist between host and pathogen receptor genes. It is also possible that allelic association is maintained at low levels between interacting genes or gene groups as a result of weak allele-matching selection.

The implications of rapidly coevolving gamete-recognition genes in structured populations deserve some exploration. Theoretical and empirical work has shown that gamete-recognition genes in isolated populations could diverge to the point of speciation.^6,7 In humans, population differentiation is relatively recent and migration rates are high enough so that the vast majority of variation is shared across populations.⁴⁰ However, given that there is some isolation, gamete receptor allele frequencies are likely to vary across subpopulations, so the frequency-dependent selection on any given allele will vary in different subpopulations. If an individual from an external subpopulation joins a given subpopulation, his or her genotype may be selected for or against, depending on the allelic context of the given subpopulation.

Chromosome transmission is widely assumed to be random. If there are cases in which selection is strong enough to create nonrandom chromosome transmission, the current model of large-scale genome structure needs to be revisited. For example, in GWAS, a signal for association at a SNP is assumed to be due to some nearby variant. Nonrandom chromosome transmission implies that such an association peak may not be due to a physically linked variant but rather to an unlinked, but associated variant. Further exploration of the extent of interchromosomal allelic association is necessary to determine the relevance of this possibility in functional genetic studies.

Web Resources

The URLs for data presented herein are as follows:

• International HapMap Project, http://hapmap.org

• Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim

• UCSC Genome Browser, http://genome.ucsc.edu