Quantitative Three Dimensional Structure Linear Interaction Energy Model of 5'-O-[N-(Salicyl)sulfamoyl]adenosine and the Aryl Acid Adenylating Enzyme MbtA

Abstract

MbtA (a salicyl AMP ligase) is a key target for the design of new antitubercular agents. Based on structure activity relationship (SAR) data generated in our laboratory, a structure-based model is developed to predict the binding affinities of arylacid-AMP bisubstrate inhibitors of MbtA. The approach described takes advantage of the linear interaction energy (LIE) technique to derive linear equations relating ligand structure to function. Using only two parameters derived from molecular dynamics simulations good correlation (R² = 0.70) was achieved for a set of 31 inhibitors with binding affinities spanning six orders of magnitude. The results were applied to understand the effect of steric and heteroatom substitutions on bisubstrate ligand binding and to predict second generation inhibitors of MbtA. The resulting model was further validated by chemical synthesis of a novel inhibitor with a predicted LIE binding affinity of 1.6 nM and a subsequently determined experimental K_i^app of 0.7 nM.

Introduction

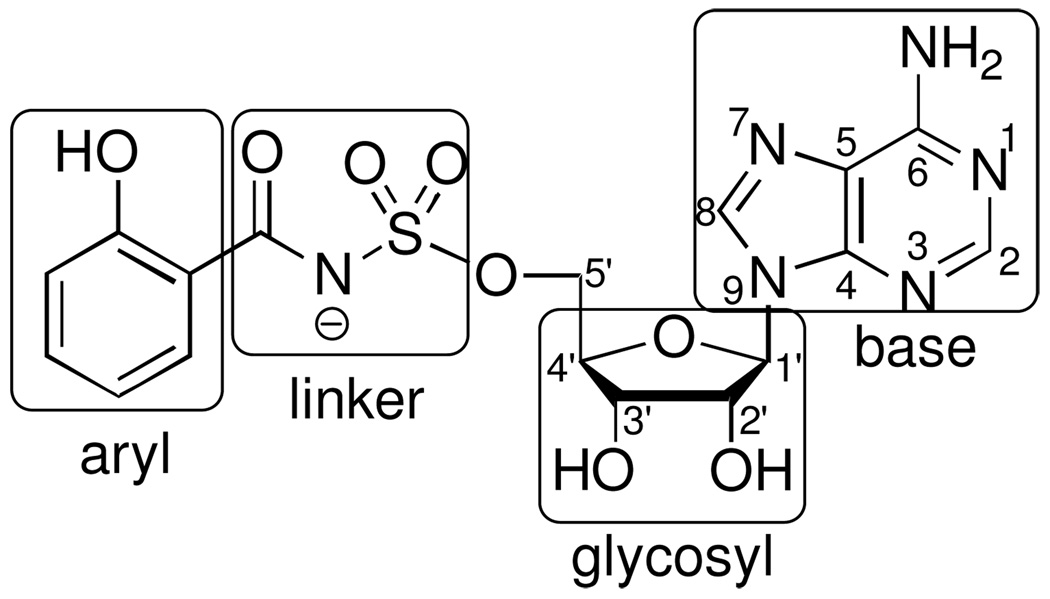
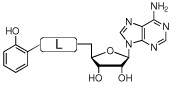
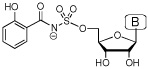
Iron is an essential nutrient for almost all known organisms; however, its concentration in serum and human body fluids is approximately 10⁻²⁴ M, which is far too low to support bacterial colonization and growth.¹ In order to overcome this iron limitation, many bacterial pathogens such as Mycobacterium tuberculosis, the causative agent of tuberculosis (TB), synthesize small molecule iron-chelators termed siderophores for iron acquisition.² Consequently, siderophore biosynthesis has emerged as a promising biochemical pathway for antibiotic development.³ The availability of detailed structural and biochemical information for aryl acid adenylation enzymes (AAAE’s), which catalyze the first step in biosynthesis of aryl-capped siderophores, has made these enzymes attractive targets.^4–6 5'-O-[N-(Salicyl)sulfamoyl]adenosine (1, Sal-AMS, Figure 1), a rationally designed bisubstrate analogue, is the prototypical AAAE inhibitor that has been shown to potently inhibit AAAE’s from numerous organisms.^7–9 As shown in Figure 1, Sal-AMS is comprised of four modules: aryl, linker, glycosyl, and nucleobase. We have systematically and methodically examined the impact of each module on enzyme inhibition of the AAAE known as MbtA from M. tuberculosis as well as antitubercular activity to provide comprehensive structure-activity-relationships (SAR). ^10–15

Figure 1.

Structure of Sal-AMS (1).

The ability to predict the binding affinity of new compounds can be of substantial benefit during the optimization phase of drug development. While the difference in free energy of binding could be calculated exactly for two related molecules it is in practice, an intractable problem to consider large numbers of ligands in this manner. The free energy perturbation method (FEP), for instance, requires dozens of converged molecular dynamics (MD) simulations for each ligand. On the other hand, the literature contains a number of reports where a predictive binding model is constructed using experimental binding affinities to weight theoretical interaction energies.^16–19 Within such linear interaction energy (LIE) approximations, binding affinities are estimated after only one ligand-receptor and one ligand-solvent simulation for each additional compound. The resulting models often display high correlation and, in contrast to some activity relationship models, have the advantage of being structure-based and therefore serve as interpreters and guides for rational drug design. While most such studies utilize crystal structures, there are examples in the literature where homology models have been substituted with good results.^{20, 21}

We present a structure based analysis and linear LIE model for the Sal-AMS scaffold with emphasis on providing a quantitative model for predicting binding affinities and a grounded physical interpretation of the SAR to guide future synthesis. Modifications of the nucleobase are of particular interest as this moiety represents the best opportunity for improving potency and increasing specificity and lipophilicty. The linker and glycosyl regions are also examined as variation of these moieties may be required to modify the number of hydrogen bond donors and acceptors or otherwise tune pharmacokinetic properties.

Computational Methods

Receptor and Ligand Starting Structures

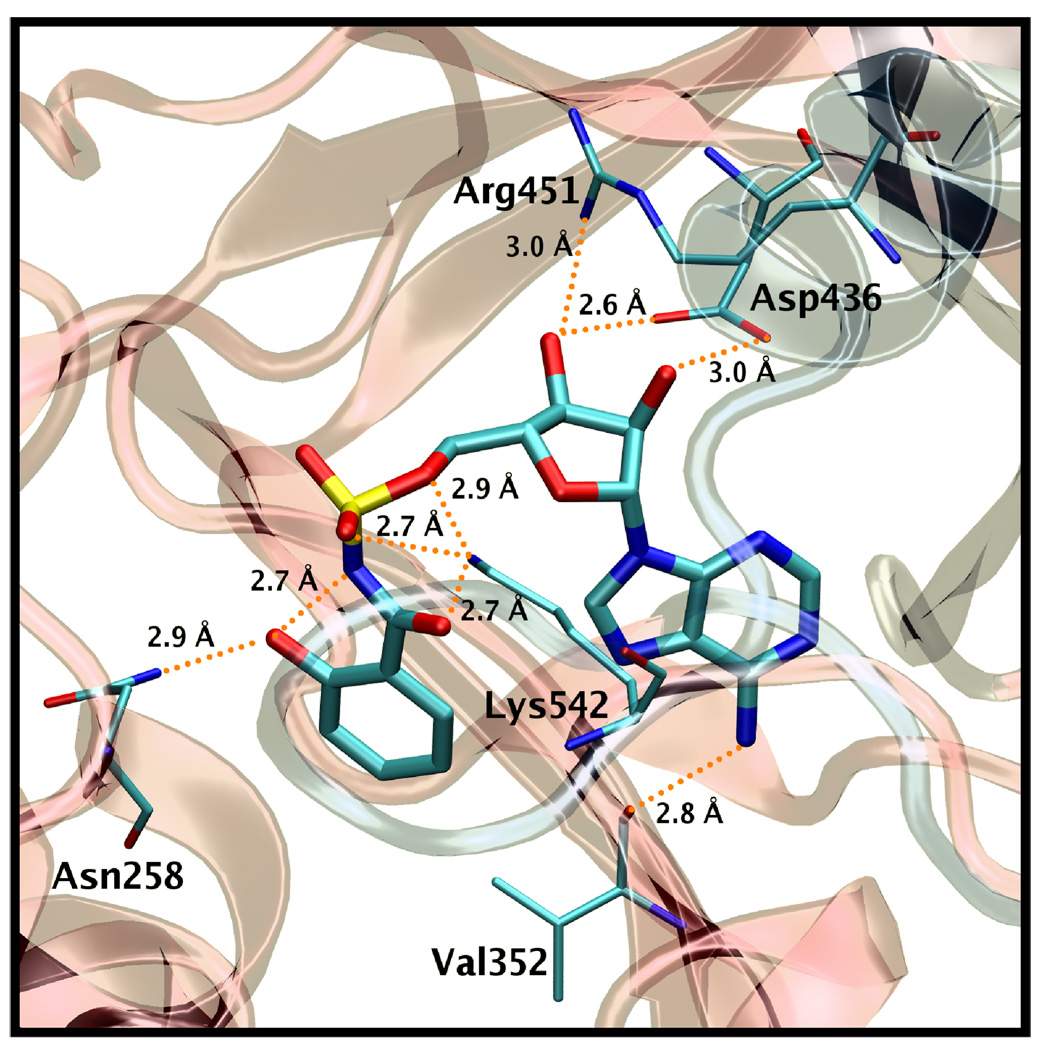
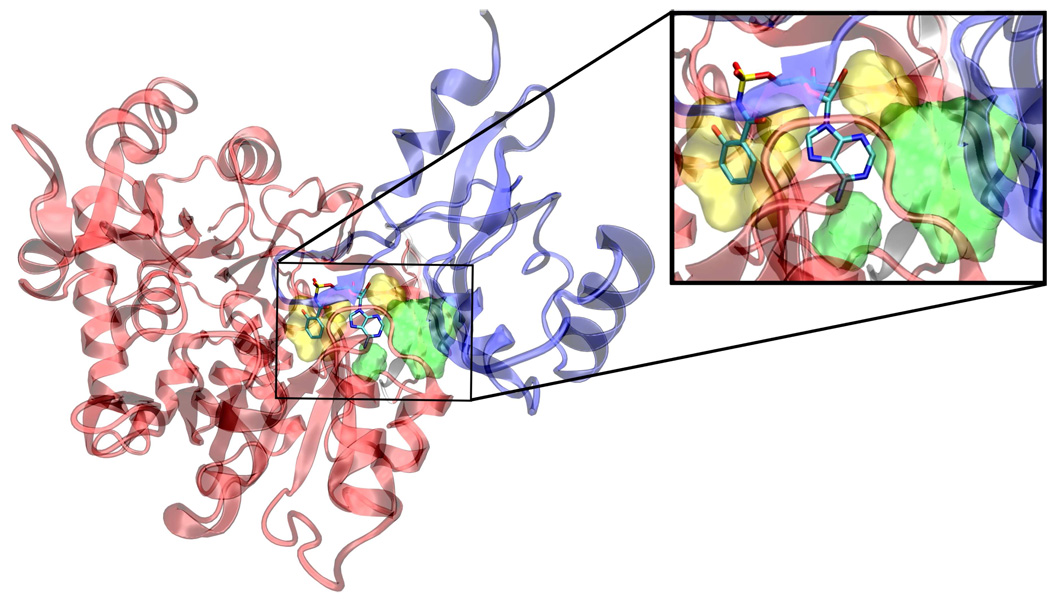
Although a crystal structure for MbtA is not yet available we have detailed the construction of a homology model in a previous publication.¹⁰ Our homology model is based on the co-crystal structure of DhbE with an adenylated 2,3-dihydroxybenzoic acid (2,3-DHB).²² DhbE shares 42% sequence identity with MbtA, but almost absolute conservation of active site residues. Thus, 16 of the 21 residues within 4 Å of the adenylated ligand are identical in MbtA and the remaining 5 changes are conservative mutations. Three of these mutations in MbtA (Y236F, S240C, V337L) map to the aryl acid substrate binding pocket and are responsible for conferring selectivity to the native substrate salicylic acid (Sal) over 2,3-DHB. The predicted binding conformation of Sal-AMS within the homology model is shown in Figure 2.

Figure 2.

Sal-AMS (1) displayed in tube representation bound in a homology model of the MbtA binding site.¹⁰ The N-terminal domain residues are presented in red ribbon, the C-terminal domain in blue. Residues that make important electrostatic contacts with the ligand are presented in tube representation. The orange dotted lines are possible hydrogen bonds. Hydrogens are not shown for clarity.

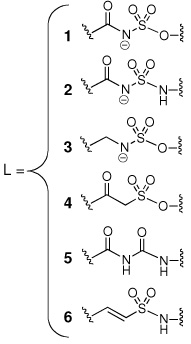
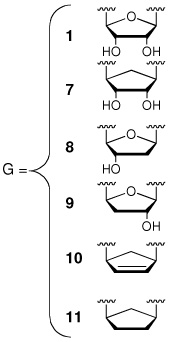
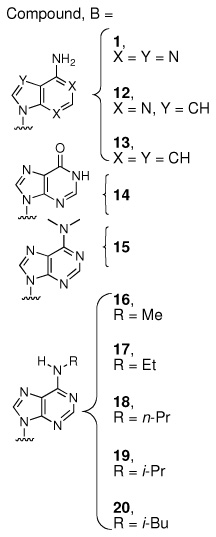
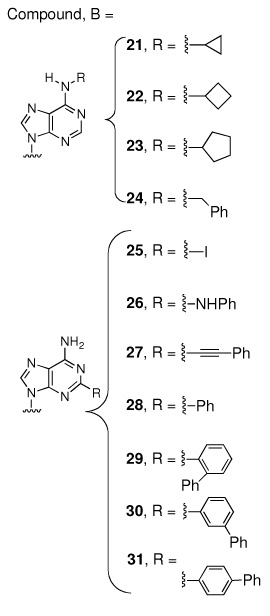
The ligand Sal-AMS (1) assumes a relatively compact form when bound to the receptor as compared to the extended conformations that are possible in solution phase. Sal-AMS forms an internal hydrogen bond between the 2-hydroxy and negatively charged nitrogen atom of the acylsulfamate linker, which enforces a coplanar arrangement of the aryl moiety and linker carbonyl. The aryl binding pocket is largely nonpolar and only a single hydrogen bond between the carboxamide side chain of Asn258 and the aryl hydroxyl group of 1 is predicted. The linker moiety of 1 interacts with conserved Lys542 (protonated) via a network of three hydrogen bonds and electrostatically with the negatively charged sulfamate as shown in Figure 2. The glycosyl moiety adopts a 3’-endo pucker and both 2’- and 3’- hydroxyl groups are predicted to form a bidentate hydrogen bond with Asp436. Deletion of either hydroxyl group in 8 and 9 (Table 1) does not disturb binding affinity while deletion of both oxygen atoms in analogue 10 results in an approximate 10-fold loss in binding affinity. The interactions of the nucleobase are largely hydrophobic with a single predicted hydrogen bond between the exocyclic N-6 amino group and Val352, which is further supported by the 238-loss in binding affinity when the N-6 amino group is replaced with an oxygen atom. Significantly, no electrostatic interactions of the purine N-1 and N-3 atoms are observed, and the N-7 shows poor hydrogen bonding geometry with Gly330 and Gly354. A small pocket vicinal to the N-6 amino group enables binding of no more than three carbon atoms, while the interdomain region of the receptor adjacent to the C-2 purine position is flexible as predicted by molecular dynamics simulations and can accommodate bulky substituents. A major consequence of the significant and relatively rigid hydrogen bonding structure is that the core of the ligand scaffold can be considered anchored by these contacts and has little room for adjustment. For substituents added to the core to have the desired effect of improving potency they must readily access the available binding pockets from their attachment to the core without disrupting the structure apparent in Figure 2. Compounds 16 and 28 are representative ligands that do exactly that, accessing the N-6 and C-2 binding clefts, respectively.

Table 1.

LIE coefficients for various receptor and ligand groups. ^a

Model	A = αΔGvdW + βΔGEl + γ			Number of Compounds	R2
	α	β	γ
I	X	6.49e-3	−8.22	31	0.66
N I	1.04e-2	1.31e-2	−8.36	25	0.71
L I	1.58e-2	4.98e-3	−8.23	6	0.99
II	1.37e-2	7.48e-3	−8.48	31	0.70
B II	1.64e-2	1.14e-2	−8.66	21	0.81

^aN, L, and B refer to nucleoside, linker, and base compound sets. I and II refer to truncation procedures 1 and 2, respectively. α and β have units of 1/(kJ/mol) so that multiplication by an interaction energy in kJ/mol results in a pure number. γ is unitless. A is an estimation of log(K_i^app). X indicates that the coefficient was statistically insignificant.

While the model was found to be somewhat sensitive to starting structures (due to the relatively rigid conformation of the core scaffold discussed above) most ligands have only one conformation of interest. The active conformation of the ligand Sal-AMS was constructed in the homology model by mutation of DhbE’s adenylated natural substrate 2,3-DHB and subsequent minimization. Ligands with large adenine C-2 substituents result in significant changes of nearby residues such as Lys332 and Val448. A second homology model differing from the DhbE crystal structure, but allowing for the exceptional potency of compounds 25–31 was used to model these ligands. Briefly, the largest difference involves the loss of a hydrogen bond between the two residues mentioned above and relaxation of the receptor’s tertiary structure around the bulkier ligands. MD simulations indicate that the C-2 position, despite having little obvious room for substitution in the DhbE crystal structure, is located in an extremely flexible region of the protein at the seam of the two domains and linker and thus very amenable to substitution.¹⁰ As this work progressed it was found that ligands with relatively small modifications of 1 could be studied effectively with the C-2 pocket residues optimized in either conformation.

Molecular Dynamics

Two molecular dynamics simulations are necessary to estimate the binding affinity of a single ligand (ligand in receptor, ligand in solvent). Two truncation procedures were applied to the homology model before MD simulation. In the first, all residues within 10 Å of the ligand were included in the calculation, and 21 complete residues, those with any atom 3 Å or closer to Sal-AMS (1) after a frozen-protein minimization, were allowed to move freely through the course of the simulation. The outer shell was frozen. After minimization and a 25 ps equilibrium run, data was sampled every 25 fs and averaged over the entire simulation. In the second procedure, all residues within 14 Å of the ligand were included in the simulation. The 33 residues with any atom within 4 Å of 27 (the largest ligand) were allowed to move freely while the outer shell was frozen. To eliminate possible differences due to the conformation of side chains near the C-2 pocket, the second truncation procedure was only applied to the more permissive homology model, which was used with all of the ligands. After an identical equilibrium run data averaged over the entire simulation was collected. In every case a GB/SA²³ implicit solvation model was used to approximate the effects of solvent. The running average of the forcefield terms was collected and examined at 10, 25, and 50 ns for each ligand. As the terms changed very little between the 25 and 50 ns simulations no longer calculations were completed.

LIE Terms

The MD-LIE terms collected in this work differ only by which truncation procedure was used and length of simulation. All of the MD models reported utilize values from the 50 ns simulation of the ligand in solution (implicit solvation) and the electrostatic and van der Waals terms from increasingly lengthy simulations of the complexes to yield the ΔG_vdW and ΔG_El terms of Equation 1. MD calculations were completed with MacroModel²⁴ 9.1 using the OPLS forcefield.²⁵

Results and Discussion

The most basic LIE model is given below in Equation 1 where A is a free energy, IC₅₀, K_D or some other experimentally measured indication of binding affinity, ΔG_vdW and ΔG_El are the forcefield determined van der Waals and electrostatic interaction energies of the receptor-ligand complex, and α, β, and γ are constants usually derived through multivariate regression to best fit the available data.

$$\mathrm{A}=\mathrm{\alpha }\mathrm{\Delta }{\mathrm{G}}_{\text{vdW}}+\mathrm{\beta }\mathrm{\Delta }{\mathrm{G}}_{\text{El}}+\mathrm{\gamma }$$ (1)

The ΔG_vdW term approximates nonpolar binding contributions while ΔG_El accounts for electrostatic free energy differences of the ligand-solvent and ligand-receptor complexes. Each represents the difference in interaction energy of the ligand in (a) the receptor environment and (b) the solvent environment. While the constants are typically unique for each receptor and forcefield, once α, β, and γ are established an affinity prediction for a new compound can be determined with minimal effort, requiring only the relevant interaction energy calculation. We chose to transform the interaction energies calculated from the MD simulations (ΔG_vdW and ΔG_El) into values relative to 1 (the parent compound) before further processing. As a result the ideal value of γ is the experimental log(K_i^app) of compound 1 (−8.3). Variation in the binding affinity estimation, A, for each compound is determined by the first two terms. For example, desolvating an additional hydrophobic group relative to 1, as in the case of 28, results in a negative ΔG_vdW and correspondingly lower (better binding) estimation of A. An additional term fitting the difference in solvent accessible surface area (SASA) is sometimes included to further improve correlation; however, we found no significant improvements when including a SASA term possibly due to the polar nature of the ligands (a dipole moment of 16.8 D, for instance, was calculated for a compact solution phase conformation of 1 at the B3LYP^{26, 27} level of theory and a basis set^28,29 designed for calculating dipole moments) or the van der Waals issues with some ligands growing too large for the pocket discussed below. More recently, specific receptors have been studied with linear response methods that replace the fitted van der Waals and electrostatic terms with a QM/MM interaction energy.^{30, 31} The QM/MM interaction energy was calculated for each ligand at both minimized and time averaged single points by treating the protein with the OPLS forcefield and the ligand at B3LYP/6-31G*³² level of theory. While trends were noted for specific ligand sets the QM/MM interaction energy was incapable of describing all or even most of the ligand binding in even a qualitative sense. We concluded that in this case evaluation of a relatively large ensemble is more important for estimating binding affinities than highly accurate studies on a single or smaller number of structures. Furthermore, attempts to correlate binding affinity with short 10–50 ps MD simulations featuring the entire unrestricted MbtA protein resulted in worse correlation than longer simulations (150–300 ps) in a truncated receptor.

Initially, a poor correlation was noted when including all active ligands in a single model and we opted to separate the inhibitors based on the modular structure of Sal-AMS. The analogues were separated into groups corresponding to modifications in the aryl, linker, glycosyl, and base moieties. Most of the error in a unified model resulted from compounds featuring modifications of the aryl ring. Due to the conjugated nature of the salicyl moiety much of the modulation in potency caused by substitution of the aryl ring may be indescribable by classical physics, instead requiring electronic structure and polarization effects. For example, substituting the paraposition of the aryl ring with the isosteric methyl and trifluoromethyl groups results in a 380-fold difference in potency suggesting force fields based methods may be incapable of describing the phenomena without highly specific reparameterization. Regardless, almost every modification (> 20) on the ring has resulted in a significant loss of potency and the focus of this work is on the adenosine binding site.²² The linker is a critically important region as it must be metabolically stabile and correctly position the aryl and nucleoside moieties in their respective binding pockets.¹³ A systematic series of six compounds differing only in the linker feature widely varying potencies ranging from 3.8 nM to 143 µM.^{9,11, 13–15} The complete final set of compounds that we investigated additionally includes 25 inhibitors with modifications of the glycosyl and nucleobase groups. All K_i^app values were determined using an ATP pyrophosphate exchange assay under identical assay conditions and tight-binding inhibition observed for many of the most potent compounds was accounted for using the analysis of Morrison.¹⁴ Therefore differences in binding affinity as measured by the assay are representative of differences in free energy. The binding affinities of the inhibitors span six orders of magnitude with K_i^app values ranging from 270 pM to 143 µM.

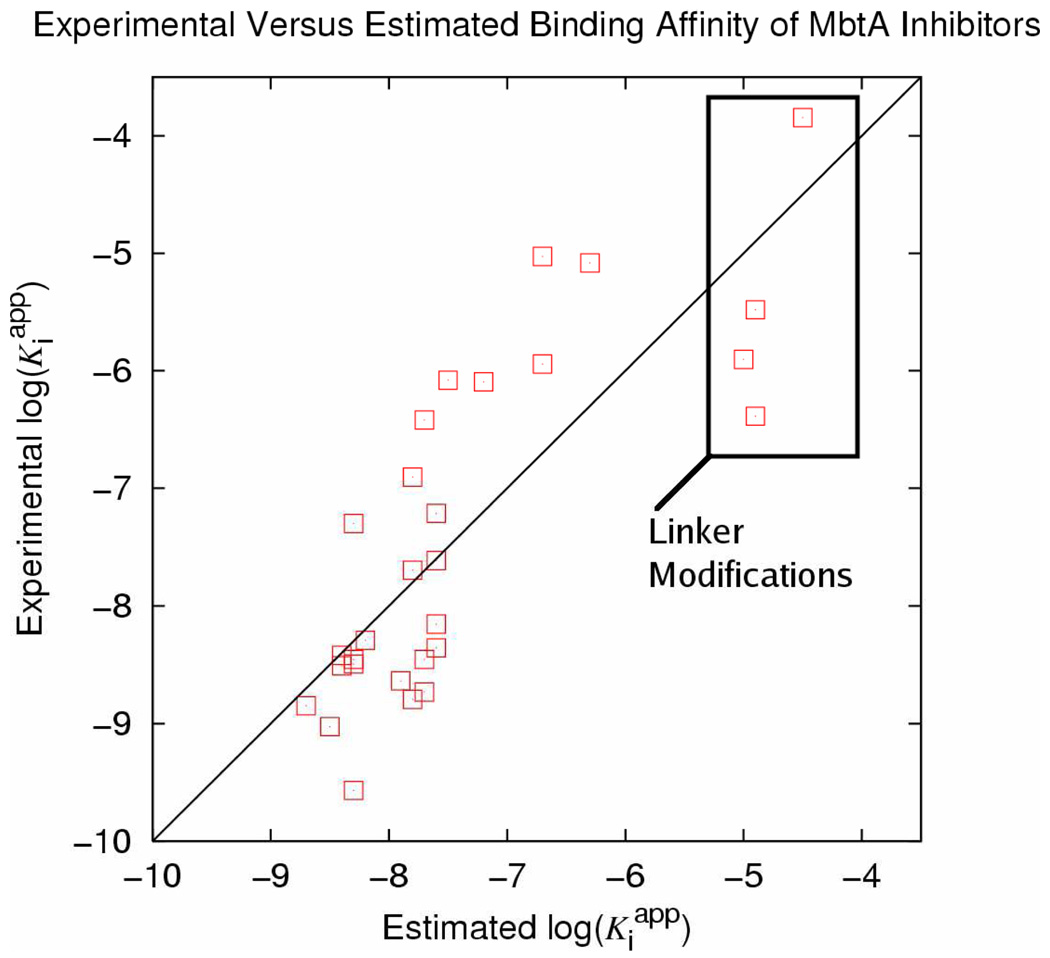
The smaller of the two receptor models (truncation procedure 1) has the distinct advantage of being much more computationally efficient allowing longer simulation times while simultaneously converging in fewer time steps due to the fewer degrees of freedom. Evaluation of Equation 1 using 150 ps simulations of all ligand-receptor complexes results in an R² value of 0.66. Experimental log(K_i^app) are plotted against those predicted by the equation in Figure 3. The resulting coefficients necessary to predict binding affinity are presented in Table 1. The structures of these compounds are reported in Table 2 along with the K_i^app and log(K_i^app) used to construct the model.

Figure 3.

LIE Model of all compounds within the small receptor model. The boxed ligands all feature modifications of the linker such that the charged nitrogen is removed.

Table 2.

Experimental and calculated log(K_i^app) values.^a

Entry	Kiapp (nM)	log(Kiapp)	Calculated log(Kiapp)	Entry	Kiapp (nM)	log(Kiapp)	Calculated log(Kiapp)
	5.1b	−8.3	−8.5		5.1b	−8.3	−8.5
	3.8b	−8.4	−8.4		2.3b	−8.6	−8.3
	410c	−6.4	−4.9		3.5b	−8.5	−8.3
	3,300d	−5.5	−5.0		3.2b	−8.5	−8.3
	1,250e	−5.9	−6.5		830b	−6.1	−7.6
	143,000c	−3.8	−5.1		61b	−7.2	−7.3
Entry	Kiapp (nM)	log(Kiapp)	Calculated log(Kiapp)	Entry	Kiapp (nM)	log(Kiapp)	Calculated log(Kiapp)
	5.1b	−8.3	−8.5		1.85f	−8.7	−7.8
	24.3f	−7.6	−8.3		124f	−6.9	−7.0
	20.1f	−7.7	−8.1		9,410f	−5.0	−4.9
	802f	−6.1	−8.0		8,260f	−5.1	−6.0
	380f	−6.4	−7.9		3.03f	−8.5	−8.3
	1.6f	−8.8	−8.6		0.94f	−9.0	−8.7
	4.4f	−8.4	−8.0		0.40f	−9.4	−8.4
	3.5f	−8.5	−7.8		0.27f	−9.6	−9.1
	7.0f	−8.2	−7.9		47f	−7.3	−6.9
	1140f	−5.9	−6.2		1.4f	−8.9	−8.7
					0.99f	−9.0	−8.2

^aCalculated using interaction energies from 150 ps MD simulations and truncation procedure II (α = 1.37e-2, β = 7.48e-3, γ = −8.48) described in text.

^bRef. ⁹.

^cRef. ¹².

^dRef. ¹⁵.

^eRef. ¹¹.

^fRef. ¹⁰.

Examination of the coefficients reveals that the intercept constant, γ, maintains a very reasonable value of −8.22. As the interaction energies of Equation 1, ΔG_vdW and ΔG_El, were transformed into values relative to Sal-AMS (1) before further statistical analysis the ideal value of γ is the log(K_i^app) of Sal-AMS (the relative ΔG and ΔG_El terms are always zero for this compound). The K_i^app values of the additional compounds are then modulated by the ΔG_vdW and ΔG_El terms. The coefficients α and β are both always positive indicating that the model responds intuitively to the ΔG terms rewarding compounds that are predicted to interact more strongly with the receptor with greater binding affinities. Closer inspection, however, reveals that α is nearly statistically insignificant and that most of the correlation is due to the electrostatic term. The most important reason for this phenomenon appears to be due to compounds 15–24, where a series of aliphatic and aromatic groups are appended onto the N-6 position of the purine. The removal of these hydrophobic groups from solution results in increasingly favorable ΔG_vdW contributions. The binding affinity, however, shows a correlated decrease as the substituents grow larger than 3 carbon atoms. The isobutyl, cyclobutyl, cyclopentyl, and benzyl substituents are larger than the volume available in the N-6 pocket and significantly displace the nucleoside (RMS of heavy base atoms 1.6–1.9 Å) making room for the large hydrophobic groups. As the more polar glycosyl and linker regions are displaced an energetic penalty is partially expressed in the electrostatic term, recovering correlation though in a non-physical manner resulting from unrealistic binding modes.

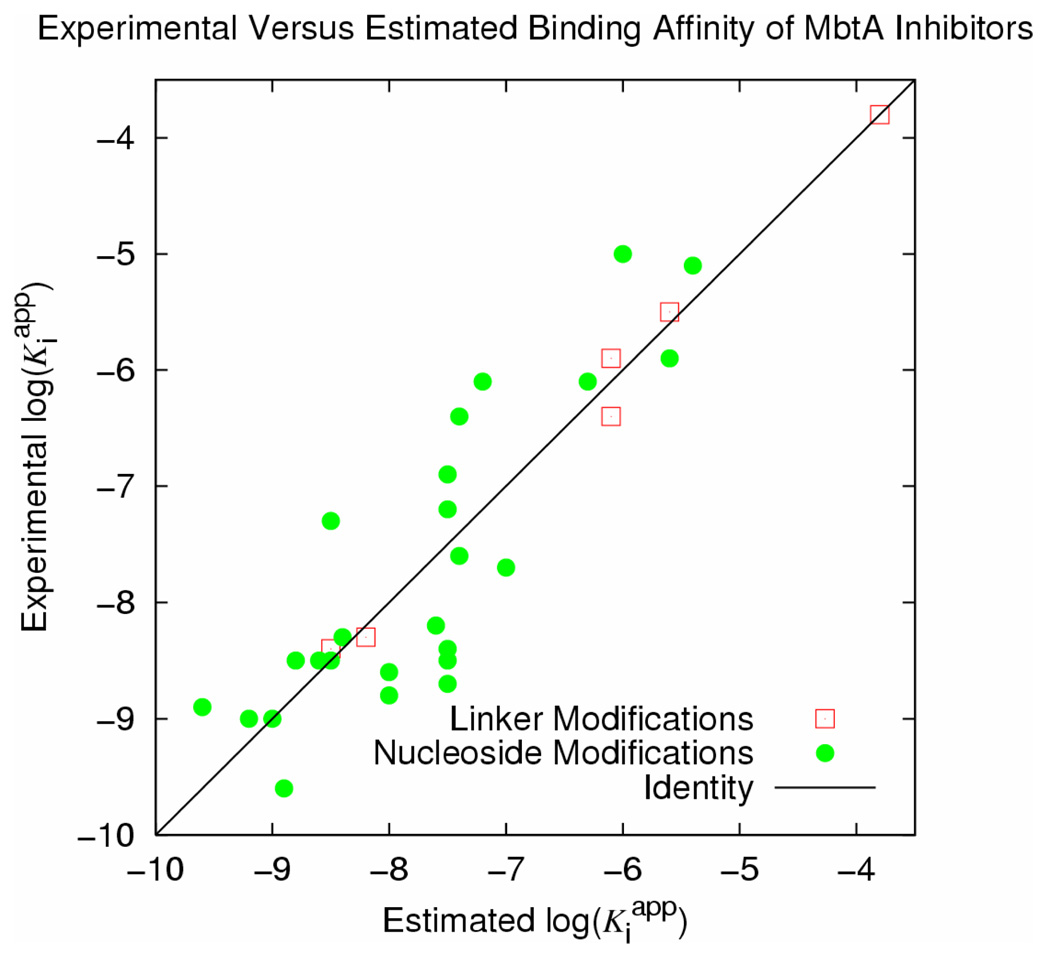
Further examination of Figure 3 reveals that even for compounds without large substituents the electrostatic term alone is not an adequate predictor of activity. Four ligands included in the set modify the linker such that the negatively charged nitrogen is either removed from the scaffold or has neighboring atoms modified such that it is neutral within the receptor. Removing the compounds with linker modifications increases the R² to 0.71 for the remaining set (Figure 4). While most of the correlation is still due to the electrostatic term, α increases to a meaningful value of 1.04e-2. Increasing simulation time to 300 ps resulted in no significant changes to the model and only very slightly improved R² to 0.72. Simulations longer than 300 ps did not improve correlation. The six compounds with varying linker groups (1–6) when treated separately from the nucleoside modifications demonstrate an extremely high R² of 0.99. While the correlation would undoubtedly decrease with a larger set of compounds, the physically sensible values of the coefficients (α = 1.58e-2, β = 4.98e-3, γ = −8.23) and individual R² values resulting from ΔG_vdW and ΔG_El of 0.39 and 0.82, respectively, indicates that this small receptor model should be a reasonable starting point for interpretation of any similar future modifications. It also implies that differences in charge or protonation state may require re-parameterizing the electrostatic coefficient or properly accounting for this effect by electrostatic continuum calculations.

Figure 4.

Plots of the estimated versus experimental binding affinities for MbtA Inhibitors using model I after 150 ps molecular dynamics simulations. The linker set (6 compounds, hollow red squares) and nucleoside set (25 compounds, filled green circles) are treated separately (see Table 1, LI and NI, respectively). The solid identity line represents the point where prediction is equal to the experimental value.

Several issues were noted that indicate a larger, more flexible model may be important to provide a fully rational interpretation of the binding affinity data. Charge-charge interactions in particular are long range, suggesting that a larger protein shell may be necessary if ligands with different charges are to be included in a single model. Additionally, the relatively poor correlation of the van der Waals term and observation that several N-6 and C-2 substituents are large enough to extend well beyond the volume occupied by 1 indicate that it may be important to extend the shell of residues allowed to move. To address these deficiencies a study similar to that described above was completed, though modeling all residues with any atom closer than 14 angstroms and allowing 33 residues in an expanded inner shell to move freely. Interestingly, many aspects of the model were improved. The van der Waals term is considerably more significant, demonstrating an R² of 0.33. The electrostatic term continues to correlate well, R² = 0.56, and remain independent of the van der Waals term demonstrated by the cross correlation between the two of only 0.08. Furthermore, the improvement from using both terms over the entire set of 31 ligands is clear with an R² of 0.70 and standard deviation of 0.85 log units. The leave-group-out (or leave-one-out) cross validation method was run for 100 cycles with group sizes of 1, 2, 4, and 9. That is, 100 (or 31 for a group size of 1) randomly selected groups of molecules of the appropriate size were treated as a test set with the remainder serving as a training set. The average correlation coefficient (q²) of the test sets was generally near and did not fall below 0.60 in any of the validation tests. Furthermore, manually breaking the ligands into a trainer and test set of 21 and 10 ligands (chosen to represent modifications of the linker, glycosyl, and base subunits) yields R² values of 0.69 and 0.59, respectively, in line with the leave-group-out analysis.

Correlation can be increased further if the ligands are broken into sets that split away the four compounds with very different electrostatic properties. While all parameters are allowed to re-optimize freely, the van der Waals term encouragingly varies little between groups while the electrostatic coefficient adjusts significantly accounting for the difference in electrostatic interaction energies between charged and non-charged species. Finally, issues apparent in the smaller, less flexible receptor model have been addressed. The N-6 pocket appears to be more realistically modeled, as the substituents that crowd the small cleft no longer displace a large part of the ligand resulting in electrostatic penalties, but instead see van der Waals energetic penalties consistent with steric crowding. The electrostatic term of the four neutral ligands does not fit well with the remainder of the set, but reduced significance of ΔG_El with respect to ΔG_vdW resulting from the larger, more flexible receptor allows for the full set to be included in a unified model and still exhibit quite reasonable predictive power. For affinity predictions of new molecules, however, a model trained with only the most closely related compounds appears to be the wisest course of action. For example, to investigate dual modifications of the scaffold at the purine N-6 and C-2 positions a priori we would consider only the 21 compound subset representing single modifications at these positions.

Conclusions

We have presented the first computational analysis of MbtA and analogues based on 5'-O-[N-(salicyl)sulfamoyl]adenosine, a promising class of new antibacterial compounds with a novel mechanism of action. The LIE model provides a clear framework for both qualitatively predicting trends and quantitatively estimating binding affinities of related compounds within MbtA using only two short MD simulations. The improvements in predictive power realized with a larger, more flexible protein model speaks well for the applicability of structure based design and interpretation for MbtA inhibitors within our homology model. Moreover, it seems reasonable to expect that similar methods should be applicable to a number of homologous aryl acid adenylating enzymes such as BasE, YbtE, VibE, PchD, and EntE (from the pathogens Acinetobacter baumannii, Yersinia pestis, Vibrio cholerae, Pseudomonas aeruginosa, and Escherichia coli, respectively).

Figure 6 presents an amalgamation of experimental and theoretical work, summarizing the structure activity relationship data used in the development of the LIE model. The schematic shows where the scaffold can be most easily modified to favorably access additional volume within MbtA and improve potency and specificity. As a final check of the applicability of the model, we have applied the LIE analysis to predict the binding affinity of a compound not included in the initial training set that includes modifications to both the N-6 and C-2 positions. The binding affinity of N-6-cyclopropyl-2-phenyl-Sal-AMS was estimated using the LIE model to be 1.6 nM, indicating the activity would fall between that of 23 and 28. This compound, the first dual modification of the scaffold, has been synthesized and found to have a K_i^app of 0.7 nM.³³ The analog is approximately twice as potent as 23 but 3-fold less active than 28, in concert with the LIE predicted result. Additional applications of the LIE model are currently underway to guide the synthesis of even more diverse Sal-AMS analogs and, based the results presented here, significant gains in potency is expected.

Figure 6.

Sal-AMS (1) docked in the MbtA homology model. The protein is represented as a ribbon diagram, N-terminal red, C-terminal blue. The ligand is shown in a tube representation and colored by element. The green surfaces expose volumes that, when filled with hydrophobic groups, improve potency and specificity. The larger of the two is the C-2 cleft (accessed by compounds 25–31) while the smaller is the N-6 pocket (accessed by compounds 16–24). Filling the yellow volumes results in a reduction in potency.

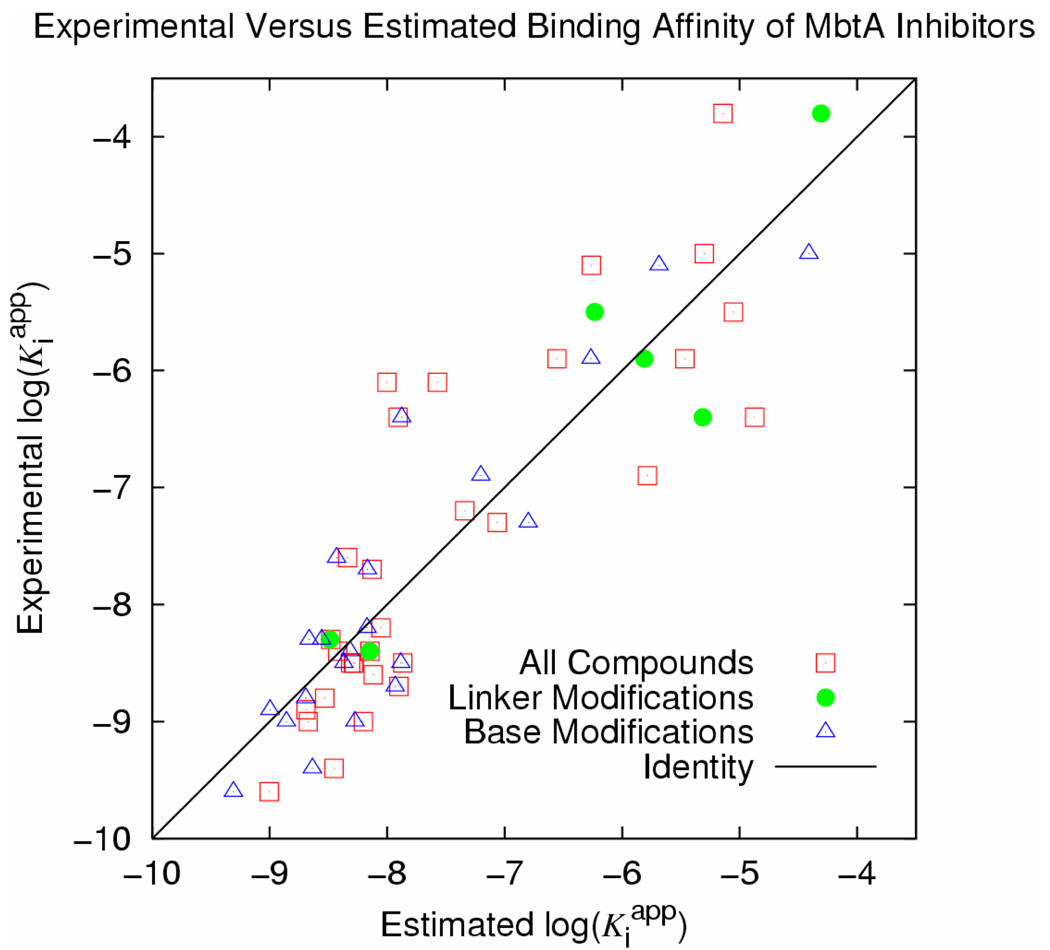
Figure 5.

Predicted activity versus experimental log(K_i^app). All compounds are included in a single set (hollow red squares), though improvement is still noted by clustering ligands into groups based on which region of the scaffold was modified (linker, filled green circles and base modifications separately as hollow blue triangles). R² (all compounds, log(K_i^app) = 0.0137ΔG_vdW + 0.00748ΔG_El − 8.48) = 0.70.

ABBREVIATIONS

AAAE

aryl acid adenylating enzyme

ATP

adenosine triphosphate

FEP

free energy perturbation

K_i^app

apparent inhibition constant

LIE

linear interaction energy

MD

molecular dynamics

MM

molecular mechanics

PDB

protein data bank

QM

quantum mechanics

QSAR

quantitative structure activity relationship

RMSD

root mean square deviation

SAR

structure activity relationships

Sal-AMS

5’-O-[N-(salicyl)sulfamoyl]adenosine

TB

tuberculosis.