Mother's Genome or Maternally-Inherited Genes Acting in the Fetus Influence Gestational Age in Familial Preterm Birth

Abstract

Objective

While multiple lines of evidence suggest the importance of genetic contributors to risk of preterm birth, the nature of the genetic component has not been identified. We perform segregation analyses to identify the best fitting genetic model for gestational age, a quantitative proxy for preterm birth.

Methods

Because either mother or infant can be considered the proband from a preterm delivery and there is evidence to suggest that genetic factors in either one or both may influence the trait, we performed segregation analysis for gestational age either attributed to the infant (infant's gestational age), or the mother (by averaging the gestational ages at which her children were delivered), using 96 multiplex preterm families.

Results

These data lend further support to a genetic component contributing to birth timing since sporadic (i.e. no familial resemblance) and nontransmission (i.e. environmental factors alone contribute to gestational age) models are strongly rejected. Analyses of gestational age attributed to the infant support a model in which mother's genome and/or maternally-inherited genes acting in the fetus are largely responsible for birth timing, with a smaller contribution from the paternally-inherited alleles in the fetal genome.

Conclusion

Our findings suggest that genetic influences on birth timing are important and likely complex.

Introduction

Preterm birth is a major public health concern. In the United States, 12.8% of births occur before term (<37 weeks) [1]. Infants born before term have an increased risk of neonatal mortality as well as serious health problems, such as respiratory illness, blindness and cerebral palsy [2]. Moreover, the severity and incidence of these problems worsen with decreasing gestational age [3]. The impact of this disorder grows with the increasing rate of preterm birth in recent decades [2].

A wealth of evidence supports maternal genetic influences on preterm birth. For example, birth timing is highly consistent across pregnancies in the same woman [4,5,6,7,8,9]. Moreover, the most likely age for a recurrent preterm birth to a given mother is the same week as the first preterm birth [6, 9, 10] suggesting that factors that are stable over time, such as genetics, affect birth timing. Additionally, mothers and daughters [11], and sisters [9] share risk for delivering preterm. Heritability studies in twins indicate that genes account for about 30% of variation in preterm delivery [12, 13] and child's gestational age as continuous trait [12, 14], when the mother is considered the proband of a delivery. Similar studies comparing full and half siblings for children's gestation age estimated that 14% of variation may be due to maternal genetic factors [15].

Several lines of evidence further suggest that fetal genetic effects may influence birth timing. First, fetal genes that are paternally imprinted mainly control placental and fetal membrane growth [16]. Because the placenta and fetal membranes likely play a role in preterm birth, fetal genes controlling these tissues may also contribute. Additionally, a study comparing the correlation in gestational age between full and half siblings suggests that preterm birth is influenced in part by fetal genetic factors [15]. Lastly, several studies suggest that paternity affects risk for the disorder. For example, several studies indicate that partner changes between pregnancies reduced risk of preterm birth [17, 18]; however, changes in paternity may reflect association with long interpregnancy intervals rather than paternity effects per se. Paternal race also has been associated with preterm birth risk. Previous studies observed that preterm birth rates are highest when both parents are Black and remain higher when one parent is Black, whether that parent is the mother or father [19, 20], suggesting that fetal race also influences birth timing. However, father's family history of preterm birth has been shown to have only a weak association with risk. While an early study of a Norwegian birth registry demonstrated a correlation between father and children's gestational ages [21], a more recent and extensive study of this registry suggested fathers contributed little to no risk to preterm delivery [22]. Similarly, a recent study [14] suggested that paternal genetics contributed little to gestational age, but could not refute the possible role of maternally-inherited genes expressed in the fetus. Hence, while paternally-inherited genes may contribute little to preterm birth or other disorders, maternally-inherited genes expressed in the fetus may still be important. Together, these data suggests that the fetal genome may contribute to birth timing, motivating further study defining the infant as the proband.

While multiple lines of evidence suggest genetic contributors are important in preterm birth, a specific mode of inheritance has not been identified. No prominent simple Mendelian pattern of inheritance has been observed in multiplex pedigrees identified to date. Modeling procedures used by twin studies suggest that additive genetic factors and environmental risk factors that are not shared between siblings both influence preterm birth [12,13,14]. Moderate values of lambda sibling (λ_S), a measure of risk to siblings of affected individuals compared to the population risk for a disorder, estimated for preterm birth (λ_S (95% CI): 4.3 (4.0–4.6)) [23] are also consistent with complex genetic and environmental etiologies [24]. Moreover, association studies have reported gene-gene [25, 26] and gene-environment [27,28,29] interactions with preterm birth. Together, these studies imply that the etiology of preterm birth likely involves genetic as well as environmental factors in complex interactions. However, there has not been a systematic study of possible genetic models for preterm birth to date.

In this study, we performed segregation analyses to identify the best fitting genetic model for gestational age, a quantitative proxy for preterm birth. Because either mother or infant can be considered the proband from a preterm delivery, and there is evidence to suggest that genetic factors in either one or both may influence the trait, we performed segregation analysis for gestational age as a quantitative trait either attributed to the infant, infant's gestational age, or to the mother, by averaging the gestational ages at which her children were delivered, using 96 multiplex preterm families. We also tested parent of origin models for infant's gestational age to examine whether mother's genotype is the sole determinant of variation in this trait. Additionally, as pregnancies in which either the mother [4, 7] or father [19, 20] is Black are at increased risk for preterm delivery, we performed segregation analysis for each phenotype in the total sample, as well as stratified by Black and White race, to test for heterogeneity between these two groups.

Material and Methods

Proband mother-infant pairs were initially identified through premature birth of a live singleton fetus before 37 weeks of gestation [30] by review of delivery logs at university medical center hospitals at Washington University and University of Helsinki or by self-identification through the study's website from 2003 to October 2007. To avoid misclassification bias at borderline gestational ages, we defined preterm birth as <35 weeks in the US cohort and <36 weeks in the Finland cohort. Our gestational age criterion was less stringent in the Finland cohort due to the high number of early ultrasounds performed, leading to more accurate gestational ages in this cohort. To include only families with spontaneous onset of preterm singleton birth, the following mother-infant pairs were further excluded: elective deliveries without spontaneous onset of labor and deliveries in which either maternal (e.g. systemic infection) or fetal (e.g. malformation) disease with known predisposition to premature birth was indicated. Families were extended through affected individuals on both maternal and paternal sides until no additional first degree relatives were identified as either mother or infant of a preterm delivery. Families were recruited into the study only if two or more members were mothers and/or infants of preterm deliveries. 55 families were recruited from the US, of which 31 were Black and 24 were White. 41 White families were recruited from Finland. In the US cohort, families ranged from 9 to 36 individuals with phenotypic information with a median family size of 18 individuals. In the Finland cohort, families ranged from 8 to 73 individuals with phenotypic information with a median family size of 16 individuals. Informed consent was obtained from participants and the study was approved by the institutional review board of Washington University School of Medicine and the ethics committee of Helsinki University Central Hospital.

From the US cohort, an individual's gestational age was calculated based on his or her mother's self report of expected due dates and actual delivery dates for a pregnancy or of how many weeks early that family member was born. For all individuals born at the Washington University School of Medicine, gestational ages were verified from medical records. From the Finland cohort, an individual's gestational age was obtained from medical records. Individuals for whom pedigree information indicated that they were born <35 or <36 weeks without a specific gestational age designated were assigned a gestational age of 34 or 35 weeks, respectively. Similarly, those individuals indicated as ‘term’ were designated 40 weeks. Infant's gestational age was treated as a quantitative trait, which was standardized to a normal distribution (μ = 0, σ = 1) prior to any analysis. A total of 1378 individuals had non-missing phenotypes, with a median of 13 individuals per family (range 3–80). The number of sibpairs with phenotypic information for this phenotype was 309, with a median of 3 sibpairs per family (range 1–7). The median number of generations with phenotypic information was 3 (range 1–5).

For both cohorts, a variable representing the average gestational age of all children born to a given mother was constructed. For mothers who had one or more children born before 37 weeks, this variable was calculated as the mean of the gestational ages for all children born to that woman. Mothers who gave birth to all of their children at term (>37 weeks) were assigned a value of 40 weeks. Mothers for whom one or more children had missing gestational ages were coded as missing. Additionally, all males and females who had not yet given birth were coded as missing. This phenotype was treated as a quantitative trait, which was standardized to a normal distribution (μ = 0, σ = 1) prior to any analysis. Univariate statistics and standardizations for each phenotype were performed with SAS language v. 9.1.3 for Linux OS (SAS Institute, Cary, N.C., USA). A total of 404 individuals had non-missing phenotypes, with a median of 4 individuals per family (range 1–17). The number of sibpairs with phenotypic information for this phenotype was 309, with a median of 0 sibpairs per family (range 0–5). The median number of generations with phenotypic information was 2 (range 1–4).

We used the Pedigree Analysis Package (PAP), Version 5.0 [31] to perform segregation analysis. Under the mixed Mendelian model (model 1), the phenotype is influenced by a major gene, polygenic background and an untransmitted environmental component. The major gene is biallelic (A, a), with allele A, occurring at frequency p, associated with lower trait values. Mean values for the three genotypes (μ_AA, μ_Aa, μ_aa, where the order of the means is constrained to be μ_AA ≤ μ_Aa ≤ μ_aa) and a common standard deviation for all genotypes are estimated. Parent-to-offspring transmission probabilities for the three genotypes (τ_AA, τ_Aa, and τ_aa) also are included in the model. τ_AA, τ_Aa, and τ_aa designate the probability of transmitting allele A for the genotypes AA, Aa, and aa, with Mendelian expectations of 1, 0.5, 0, respectively. When the τ's are set equal to p, there is no transmission of the major effect. Polygenic heritability (H) after accounting for the putative major gene effect was also estimated. For parent of origin models, heterozygotes who inherited A from their mother (Aa) and heterozygotes who inherited A from their father (aA) are distinguished from one another and allowed to have different means. Many of the free τ's models did not converge initially. In order to estimate these models, τ_AA and τ_aa were fixed to 1 and 0, respectively, and likelihoods calculated under these additional assumptions were used for the analysis.

All parameters were estimated using a maximum likelihood method. Nested models representing null hypotheses were tested against a more general model using a likelihood ratio test (LRT), in which the difference between negative twice the log-likelihood (–2 ln L) values for two models approximates a chi-square distribution with degrees of freedom (d.f.) equal to the number of independent parameter restrictions. The most parsimonious model of those not rejected by likelihood ratio test (p > 0.01) was determined using Akaike's Information Criterion (AIC) [32], which is computed as −2 ln L of the model plus twice the number of parameters estimated. The model with the lowest AIC indicates the most parsimonious fit to the observed data.

To account for the ascertainment of the families, the likelihood of each model was conditioned on the likelihood of the proband's phenotype under the model, an appropriate correction for the manner in which these families were extended [33]. While our criterion required 2 or more preterm first degree relatives for a family to be enrolled in the study, the ascertainment scheme is approximately equivalent to single ascertainment [34]. Because not all preterm deliveries in the metropolitan St. Louis or Finnish health care systems occurring during the study period were captured under our ascertainment scheme, the probability that a family was identified through multiple probands is small and should be proportional to the number of affected deliveries in a family, as expected under single ascertainment [35]. Under single ascertainment, conditioning on the proband's phenotype is sufficient to adjust for the ascertainment of families [35]. Hence, analyses for infant's gestational age were corrected for the proband infant's gestational age jointly with preterm birth (<37 weeks) affection status. Similarly, analyses attributing gestational age to the mother were corrected for the proband mother's average gestational age of children jointly with her preterm birth (<37 weeks) affection status.

To test genetic heterogeneity among races, we used the heterogeneity χ² test [36, 37] in which the −2 ln L value under the best fitting model for the combined data is subtracted from the summation of −2 ln L values for stratified analyses to obtain the test statistic. This test statistic approximates a χ² distribution with d.f. equal to K*J – K where J is the number of subgroups and K is the number of parameters in the model.

Results

Modeling of Gestational Age Attributed to the Infant

We first analyzed gestational age of the infant. The number of subjects and descriptive statistics for this phenotype are shown in table 1. Table 2 presents the LRTs and AIC values for segregation analysis of infant's gestational age for 17 models of inheritance. The parameter estimates for segregation analysis of infant's gestational age are listed in table 3. The hypotheses of no familial resemblance (model 2), no major gene effect (model 3), and no multifactorial effect (model 4) are rejected, suggesting the presence of both a major gene and a multifactorial effect. Additionally, the equal τ's hypotheses (models 10, 12 and 14) are rejected for the mixed, recessive mixed and dominant mixed models, respectively. In the free τ's models, the estimated τ_Aa differed from 0.5, expected under the Mendelian model, and fit the data better than their respective general models (models 1, 7 and 8) for all groups. Together, this evidence supports a genetic component for preterm birth transmitted from parents to offspring and suggests that the transmitted effect is complex. Similar models were tested for general parent of origin effects, as well as maternal-specific and paternal-specific effects under Mendelian transmission (models 15–17). The parent of origin model (model 15) best fit the data as judged by AIC values and was chosen as the most parsimonious model (table 2). This model suggests that, when attributing gestational age to the infant of a delivery, genetic factors influence this trait and the parent from whom such factors are inherited influences the overall trait value.

Table 1.

General characteristics of the study subjects as a single cohort and stratified by race

	Combined	Blacks	Whites
Infant's gestational age
Numbers (<37 weeks)	1,130 (33.63%)	301 (41.53%)	829 (30.76%)
Mean	37.12	36.12	37.49
Standard deviation	4.09	4.83	3.73
Kurtosis	1.73	0.24	2.47
Skewness	–1.45	–1.08	–1.58
Mother's average gestational age
Numbers (<37 weeks)	191 (54.97%)	48 (70.83%)	143 (49.65%)
Mean	35.69	34.22	36.19
Standard deviation	4.24	4.45	4.07
Kurtosis	–0.24	–0.66	0.17
Skewness	–0.76	–0.32	–0.95

Table 2.

Segregation analysis of infant's gestational age in 96 multiplex families (n = 1,224 nonfounders)

	Model	Estimated parameters	‘-2 ln L’	Test	χ2	d.f.	p value	AIC
1	Mixed	6	2,266.85					2,278.85
2	Sporadic	2	2,754.87	2 vs. 1	488.02	4	<0.001	2,758.87
3	Multifactorial	3	2,690.72	3 vs. 1	423.87	3	<0.001	2,696.72
4	Additive	5	2,303.33	4 vs. 1	36.48	1	<0.001	2,313.33
5	Recessive	4	2,545.26	5 vs. 1	278.41	2	<0.001	2,553.26
6	Dominant	4	2,305.64	6 vs. 1	38.79	2	<0.001	2,313.64
7	Mixed recessive	5	2,544.08	7 vs. 1	277.23	1	<0.001	2,554.08
8	Mixed dominant	5	2,270.77	8 vs. 1	3.92	1	0.05	2,280.77
9	Mixed free τ's	9	2,100.61	1 vs. 9	166.24	3	<0.001	2,118.61
10	Mixed equal τ's	6	2,354.73	10 vs. 9	254.12	3	<0.001	2,366.73
11	Recessive free τ's	8	2,291.99	7 vs. 11	252.09	3	<0.001	2,307.99
12	Recessive equal τ's	5	2,354.73	12 vs. 11	62.74	3	<0.001	2,364.73
13	Dominant free τ's	8	2,106.20	8 vs. 13	164.57	3	<0.001	2,122.20
14	Dominant equal τ's	5	2,354.73	14 vs. 13	248.53	3	<0.001	2,364.73
15	Parent of origin1	6	2,078.97					2,090.97
16	Maternal	4	2,320.79	16 vs. 15	260.83	3	<0.001	2,328.79
17	Paternal	4	2,356.23	17 vs. 15	296.27	3	<0.001	2,364.23

¹Most parsimonious model.

Table 3.

Parameter estimates for segregation analysis of infant's

	Model	A allele frequency p	Transmission		probabilities		Mean values for		genotypes		Common standard deviation, σ	Heritability H
			τAA	τAa	τaA	τaa	μAA	μAa	μaA	μaa
1	Mixed	0.27	[1]	[0.5]	[0.5]	[0]	-1.73	0.52a	[μAa]	0.37a	0.56	0.38
2	Sporadic	[1]	[1]	[0.5]	[0.5]	[0]	0.01	[μAA]	[μAA]	[μAA]	0.92	[0]
3	Multi-factorial	[1]	[1]	[0.5]	[0.5]	[0]	0.24	[μAA]	[μAA]	[μAA]	0.91	0.33
4	Additive	0.27	[1]	[0.5]	[0.5]	[0]	-1.82	0.46a	[μAa]	0.31a	0.56	[0]
5	Recessive	0.03	[1]	[0.5]	[0.5]	[0]	-1.55	[μAA]	[μAa]	0.32	0.71	[0]
6	Dominant	0.26	[1]	[0.5]	[0.5]	[0]	-1.84	0.39	[μAa]	[μAa]	0.57	[0]
7	Mixed-recessive	0.03	[1]	[0.5]	[0.5]	[0]	-1.56	[μAA]	[μAa]	0.33	0.71	0.05
8	Mixed-dominant	0.27	[1]	[0.5]	[0.5]	[0]	-1.75	0.45	[μAa]	[μAa]	0.56	0.36
9	Mixed-free τ's	0.05	1.00	0.99	[τaa]	0.16	-1.60	0.42	[μAa]	0.58	0.55	0.42
10	Mixed-equal τ's	0.33	[p]	[p]	[p]	[p]	-1.84	0.40	[μAa]	0.40	0.58	0.28
11	Recessive free τ's	0.01	0.98	0.70	[τaa]	0.04	-1.77	[μAA]	[μAa]	0.42	0.57	0.25
12	Recessive equal τ's	0.06	[p]	[p]	[p]	[p]	-1.84	[μAA]	[μAa]	0.40	0.58	0.28
13	Dominant free τ's	0.05	1.00	0.98	[τaa]	0.16	-1.56	0.49	[μAa]	[μAa]	0.55	0.40
14	Dominant equal τ's	0.33	[p]	[p]	[p]	[p]	-1.84	0.40	[μAa]	[μAa]	0.58	0.28
15	Parent of origin1	0.20	[1]	[0.5]	[0.5]	[0]	-2.38	-0.69	0.60	0.58	0.37	[0]
16	Maternal	0.09	[1]	[0.5]	[0.5]	[0]	-1.71	[μAA]	0.40	[μAa]	0.57	[0]
17	Paternal	0.12	[1]	[0.5]	[0.5]	[0]	-1.81	0.39	[μAA]	[μAa]	0.57	[0]

A bracketed number (e.g. [1]) denotes that the parameter was set and not estimated.

¹Most parsimonious model.

^aParameter estimates are approximately equal within standard error.

Modeling of Gestational Age Attributed to the Mother

We also analyzed gestational age attributed to the mother, by averaging the gestational ages at which her children were delivered (see table 1). Table 4 presents the likelihood ratio tests and AIC values for segregation analysis on mother's average gestational age of children for 14 models of inheritance. The parameter estimates for the combined dataset are listed in table 5. The hypotheses of no familial resemblance (model 2), no major gene effect (model 3), and no multifactorial effect (model 4) are rejected, suggesting the presence of both a major gene and a multifactorial effect. The equal τ's (models 10, 12 and 14) are rejected. None of the free τ's models (models 9, 11 and 13) converged initially. In order to estimate these models, τ_AA and τ_aa were fixed to 1 and 0, respectively. Only τ_Aa was estimated and, in each case, differed from 0.5, expected under the Mendelian model. Additionally, the free τ's models fit the data better than their respective general models (models 1, 7 and 8), perhaps suggesting that the major effect observed is more complex than the single biallelic locus modeled here. Together, this evidence supports a genetic component for preterm birth transmitted from parents to offspring and suggests that the transmitted effect is complex. The mixed free τ's model (model 9) best fit the data as judged by the AIC values and was chosen as the most parsimonious model (table 4). This model suggests that a complex genetic model most likely best accounts for variation in gestational age, when the trait is attributed to the mother of a delivery.

Table 4.

Segregation analysis of mother's average gestational age of children in 96 multiplex families (n = 192 nonfounders)

	Model	Estimated parameters	‘–2 ln L’	Test	χ2	d.f.	p value	AIC
1	Mixed	6	175.06					187.06
2	Sporadic	2	222.42	2 vs. 1	47.36	4	<0.001	226.42
3	Multifactorial	3	216.37	3 vs. 1	41.31	3	<0.001	222.37
4	Additive	5	181.57	4 vs. 1	6.50	1	0.01	191.57
5	Recessive	4	187.88	5 vs. 1	12.82	2	0.002	195.88
6	Dominant	4	182.62	6 vs. 1	7.55	2	0.02	190.62
7	Mixed recessive	5	186.70	7 vs. 1	11.63	1	<0.001	196.70
8	Mixed dominant	5	175.68	8 vs. 1	0.62	1	0.43	185.68
9	Mixed free τ's1,2	7	153.94	1 vs. 9	21.13	3	<0.001	167.94
10	Mixed equal τ's	6	173.56	10 vs. 9	19.62	3	<0.001	185.56
11	Recessive free τ's2	6	184.09	7 vs. 11	2.60	3	0.46	196.09
12	Recessive equal τ's	5	173.56	12 vs. 11	-10.54	3	n/a	183.56
13	Dominant free τ's2	6	157.15	8 vs. 13	18.53	3	<0.001	169.15
14	Dominant equal τ's	5	173.56	14 vs. 13	16.40	3	<0.001	183.56

¹Most parsimonious model.

²Indicates the model did not converge on its own. τ_AA was set equal to 1 and τ_aa set equal to 0 in order to estimate the model.

Table 5.

Parameter estimates for segregation analysis of mother's average gestational age of children in 96 multiplex families (n = 192 nonfounders)

	Model	A allele frequency p	Transmission probabilities			Mean values for genotypes			Common standard deviation, σ	Heritability H
τAA	τAa	τaa	μAA	μAa	μaa
1	Mixed	0.27	[1]	[0.5]	[0]	-1.02	0.89	0.99	0.45	0.58
2	Sporadic	[1]	[1]	[0.5]	[0]	0.55	[μAA]	[μAA]	0.87
3	Multifactorial	[1]	[1]	[0.5]	[0]	0.74	[μAA]	[μAA]	0.86	0.44
4	Additive	0.25	[1]	[0.5]	[0]	-1.28	0.72	0.94	0.48	[0]
5	Recessive	0.04	[1]	[0.5]	[0]	-0.94	[μAA]	0.89	0.49
6	Dominant	0.28	[1]	[0.5]	[0]	-1.08	0.87	[μAa]	0.48
7	Mixed-recessive	0.04	[1]	[0.5]	[0]	-1.06	[μAA]	0.91	0.47	0.43
8	Mixed-dominant	0.28	[1]	[0.5]	[0]	-1.01	0.94	[μAa]	0.45	0.59
9	Mixed free τ's1,2	0.16	[1]	0.77	[0]	-1.01	0.87	1.08	0.44	0.52
10	Mixed equal τ's	0.40	[p]	[p]	[p]	-1.00	0.92	0.92	0.45	0.61
11	Recessive free τ's2	0.02	[1]	0.66	[0]	-0.85	[μAA]	0.91	0.49	0.02
12	Recessive equal τ's	0.08	[p]	[p]	[p]	-1.00	[μAA]	0.92	0.45	0.61
13	Dominant free τ's2	0.18	[1]	0.75	[0]	-0.96	0.96	[μAa]	0.44	0.54
14	Dominant equal τ's	0.40	[p]	[p]	[p]	-1.00	0.92	[μAa]	0.45	0.61

A bracketed number (e.g. [1]) denotes that the parameter was set and not estimated.

¹Most parsimonious model.

²Indicates the model did not converge on its own. τAA was set equal to 1 and τaa set equal to 0 in order to estimate the model.

Heterogeneity between Blacks and Whites

Since pregnancies in which either the mother [4, 7] or father [19, 20] is Black are at increased risk for preterm delivery, we tested for evidence of genetic heterogeneity between these two groups. Segregation analyses of infant's gestational age and mother's average gestational age over all her children also were performed in Black and White subgroups. Table 1 documents the number of subjects and descriptive statistics for both phenotypes by race. The segregation analyses of infant's gestational age supported similar conclusions in the combined sample and Black and White subgroups. However, several results differed in the segregation analysis of mother's average gestational age of children when the sample was stratified by Black and White race, compared to the combined sample. In the race-stratified samples, final estimates of the free τ's models had higher −2 ln likelihoods than did similar models with fewer parameters, indicating that the maximum likelihood was not reached. As a result, the equal τ's hypotheses (models 10, 12 and 14) and the free τ's hypotheses (models 9, 11 and 13) were not rejected for the mixed, recessive mixed and dominant mixed models, respectively, in Black and White subgroup analysis. The best fitting model according to AIC values was the mixed equal τ's model and was selected as the most parsimonious model in both race subgroups (data not shown).

To test formally for heterogeneity between Blacks and Whites, we used the heterogeneity χ² test [36, 37] in which the −2 ln L value under a given model for the combined data is subtracted from the summed −2 ln L values from stratified analyses. For infant's gestational age, evidence for genetic heterogeneity among races was observed when comparing values under the multifactorial model (χ² = Σ(698.07 Black + 2010.02 White) − 2690.72 combined = 17.37, 3 d.f., p = 0.0006). Of note, parameter estimates for Blacks and Whites differed, particularly estimates of p, H and μ_AA which were generally higher in Blacks than Whites. For the multifactorial model, H was estimated as 0.46 (95% CI: 0.27–0.65) for Blacks and 0.23 (95% CI: 0.13–0.33) for Whites. While these point estimates are quite different, the 95% CI overlap, indicating that this difference may not be statistically significant. For mother's average gestational age of children, evidence for genetic heterogeneity among races was observed when comparing values under the multifactorial model (χ² = Σ(54.92 Black + 213.58 White) − 216.37 combined = 52.13, 3 d.f., p = 2.81 × 10^–11). Of note, parameter estimates for Blacks and Whites differed, particularly estimates of H, which are generally higher in Blacks than Whites. For the mixed free τ's model, H was estimated as 0.70 (95% CI: 0–1) for Blacks and 0.23 (95% CI: 0–0.57) for Whites. As the 95% confidence intervals overlap, this difference is not significant in the sample size analyzed here.

Discussion

Preterm birth likely has a complex etiology involving both genetic and environmental risk factors, based on evidence from previous studies. This study is the first to explicitly test different modes of inheritance for birth timing, by assessing gestational age as a phenotype of either mother or infant. These data lend further support to a genetic component contributing to birth timing since sporadic (i.e. no familial resemblance) and nontransmission models, in which gestational age is attributed to environmental factors alone, are strongly rejected (tables 2 and 4). Our findings suggest that genetic influences on birth timing are important and likely complex.

For infant's gestational age, the parent of origin model (model 15) best fit the data according to the AIC values and was chosen as the most parsimonious model (table 2). Based on the mean estimates for AA, Aa, aA and aa under this model (table 3), it appears that this parent of origin effect is largely maternal. Heterozygotes who inherit the A allele from their mother (Aa) have a mean closer to, but not equal to, AA. Under a strict maternal model, AA and Aa would be equivalent, since mother's A allele would be expected to be the sole determinant of phenotype. In contrast, heterozygotes who inherited the A allele from their father (aA) have a mean that is approximately equivalent to that of aa, suggesting that father's A allele has little effect on phenotype. A model in which the maternally-inherited allele was the sole determinant of the phenotype (model 16) did not fit the data better than the parent of origin model in which the entire genotype was considered. Importantly, father's genes also affect phenotype in this model, aligning with previous work showing paternity [17, 18] as well as paternal race [19, 20] influence preterm birth risk. Hence, both maternal and paternal alleles seem to contribute to infant's gestational age, with maternally-inherited alleles having a stronger effect on phenotype than those inherited from the father. This finding may support previous studies that have observed stronger effects of mother's race [19, 20] and family history on risk for preterm birth [22] than those of the father. These data suggest that maternally-inherited genes acting in the fetus and/or maternal genes acting in the mother are largely responsible for birth timing; however, these two possibilities are not easily distinguished. Maternal genetic effects can create the same pattern of phenotypic variation as genomic imprinting [38]. These two classes of effects can be distinguished by comparing the offspring of heterozygous mothers [38]; however, such comparisons are not possible in our dataset in which individuals were assigned probabilities for each possible genotypic state, rather than having known genotypes measured empirically. Previous studies in cattle [39, 40] have observed maternal genetic effects on gestational age, but did not consider parent of origin effects. Consequently, further study is needed to determine whether maternal effects or imprinting account for our observations. In either case, considering the mother of a preterm delivery as proband may be most useful in identifying genetic contributions to preterm birth.

Segregation analysis of mother's average gestational age of children also supported a complex genetic model. The mixed free τ's model (model 9) best fit the data according to the AIC values and was chosen as the most parsimonious model (table 4). This model, in combination with results from LRTs, suggests that genetic influences on birth timing are important and likely complex. Importantly, fewer individuals are informative when mother is considered the proband in a preterm delivery (fig. 1), and the smaller sample size affects the power of the analysis. As a result, the parameter and likelihood estimates made when considering mother as proband are more affected by sampling variance; however, conclusions made by comparing across models should be less affected by sample size.

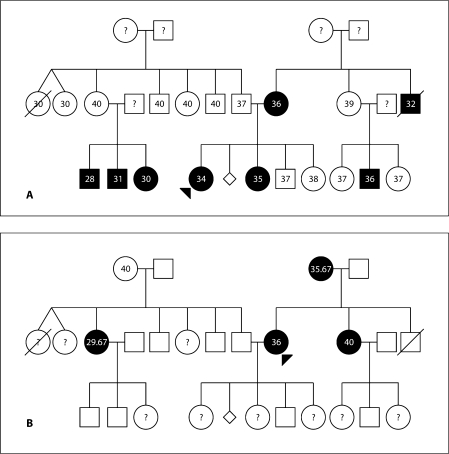
Fig. 1.

A representative pedigree of familial preterm birth with gestational age in weeks of each individual indicated. Question marks indicate that the gestational age for that individual is unknown. Panel A depicts the pattern of affection status (<37 weeks) if the infant is considered pro-band of a preterm delivery. Panel B depicts the pattern of affection status (<37 weeks) if the mother is considered proband of a preterm delivery. Multiple births are excluded due to the likelihood of singleton and multiple births having different mechanisms for early birth.

Overall, mother-based and infant-based analyses both support the importance of genetic factors, perhaps primarily acting in the mother or maternally-inherited alleles acting in the fetus, in birth timing. The genetic component influencing preterm birth likely involves many genes in interaction with environmental and other genetic factors. These results are consistent with previous studies suggesting that genes and environments [12,13,14], as well as gene-gene [25, 26] and gene-environment [27,28,29] interactions influence preterm birth. Estimates from the multifactorial model (model 3, tables 2 and 4) indicate 30–40% of variation in gestational age, attributed to either mother or infant, can be explained by genetics, consistent with estimates from previous twin studies [12, 14]. As twins may not be representative of the population as a whole, our heritability estimates corroborate the general importance of genetics in birth timing. Heritability estimates were generally higher in mother-based analyses (0.44 (95% CI: 0.11–0.77)) than in infant-based analysis (0.33 (95% CI: 0.24–0.42)), but not significantly different (tables 3, 5). While many genes may be contributing to the observed genetic influence on birth timing, the moderate heritability observed suggests that the cumulative effect of these genes accounts for an important amount of variation in gestational age.

Although alternative methods for segregation analysis exist, we considered PAP to be the best method for our primary goal of identifying the best-fitting genetic model for birth timing. Using PAP, we were able compare models directly and identify the most parsimonious model. In contrast, Markov Chain Monte Carlo (MCMC) methods, such as those used by the Loki [41] and Morgan [42] packages, generate a series of posterior probabilities for various models, but no one model is identified as superior. Moreover, MCMC methods model several Mendelian loci simultaneously but do not include a polygenic component, which we wanted to include in the models we examined. Furthermore, one cannot correct for ascertainment within MCMC analysis, in contrast to PAP. One of the disadvantages of using PAP exclusively was that we were not able to estimate the approximate number of loci contributing to birth timing, as could be done with MCMC methods. Additionally, MCMC methods may be better at handling large, complex pedigrees than PAP [43]; however, since our families were relatively small and simple (e.g. containing no inbreeding), we did not consider this a limitation.

We have likely enriched for genetic and/or common environmental effects by using 96 multiplex families, all of whom were recruited based on having two or more first degree relatives delivered preterm. These multiplex families provided a large sample size from which genetic effects could be examined. However, the ascertainment scheme also introduces bias, as the families were not collected randomly and may overestimate the importance of certain genetic models. To minimize errors due to such bias, all analyses were corrected for ascertainment by conditioning on the initial proband, either the mother or the offspring depending which phenotype was considered, that led to the ascertainment of the family, assuming single ascertainment. However, if our assumption of single ascertainment is incorrect, conditioning on probands in this manner may create bias in estimating model parameters [44], leading to inaccurate conclusions about the best-fitting model for familial preterm birth. Because we believe our ascertainment scheme is consistent with single ascertainment, these results appear to be most appropriate for modeling genetic effects in familial preterm birth. Yet, it is possible that our conclusions drawn from familial cases of preterm birth may not generalize to all instances of this disorder. Familial cases of preterm birth may have a different genetic contribution than isolated cases, perhaps having different etiologies than isolated cases.

This study is also limited by the phenotypes studied. Information on gestational age was collected by self-report data from questionnaires for many individuals used in this analysis. While it was possible to verify gestational ages from medical records in some cases, including all births delivered at the participating institutions, many gestational ages could not be verified and may be subject to reporting errors. Additionally, many individuals for whom we could not verify precise gestational ages were reported as ‘full term’ and assigned gestational age of 40 weeks. While this is the most likely gestational age for infants to be born [6], we may lose some variability in the overall distribution of gestational age by doing so. As modeling of trait variance is essential to segregation analysis, this approach also may have affected our results.

Our findings suggest that genetic influences on birth timing are important. Modeling for both mother and infant phenotypes indicate that a genetic component influences gestational age and is complex in nature. In analyses using either mother or infant as proband, monogenic Mendelian models were strongly rejected, suggesting that a single gene model cannot fully explain birth timing in these families. A number of genes probably contribute to the genetic influence on birth timing and preterm birth described. Analyses of gestational age attributed to the infant support a model in which mother's genome and/or maternally-inherited genes acting in the fetus are largely responsible for birth timing, with a smaller contribution from the paternally-inherited alleles in the fetal genome. Hence, considering the mother of a preterm delivery as proband may be more useful in identifying specific genetic contributions to preterm birth. Interestingly, results from the heterogeneity χ² test comparing race-stratified analyses suggest that genetic influences on birth timing may differ between Blacks and Whites. Hence, in future association studies, race-stratified analyses or population stratification corrections may improve our ability to identify specific genes associated with preterm birth. Overall, as multiple genes in the mother's genome may explain the bulk of genetic influences on birth timing, future studies to identify specific genes influencing preterm birth perhaps will be most fruitful by using large scale studies of mothers’ genomes.