Logical-Rule Models of Classification Response Times: A Synthesis of Mental-Architecture, Random-Walk, and Decision-Bound Approaches

Abstract

We formalize and provide tests of a set of logical-rule models for predicting perceptual classification response times (RTs) and choice probabilities. The models are developed by synthesizing mental-architecture, random-walk, and decision-bound approaches. According to the models, people make independent decisions about the locations of stimuli along a set of component dimensions. Those independent decisions are then combined via logical rules to determine the overall categorization response. The time course of the independent decisions is modeled via random-walk processes operating along individual dimensions. Alternative mental architectures are used as mechanisms for combining the independent decisions to implement the logical rules. We derive fundamental qualitative contrasts for distinguishing among the predictions of the rule models and major alternative models of classification RT. We also use the models to predict detailed RT distribution data associated with individual stimuli in tasks of speeded perceptual classification.

A fundamental issue in cognitive science concerns the manner in which people represent categories in memory and the decision processes that they use to determine category membership. In early research in the field, it was assumed that people represent categories in terms of sets of logical rules. Research focused on issues such as the difficulty of learning different rules and on the hypothesis-testing strategies that might underlie rule learning (e.g., Bourne, 1970; Levine, 1975; Neisser & Weene, 1962; Trabasso & Bower, 1968). Owing to the influence of researchers such as Posner and Keele (1968) and Rosch (1973), who suggested that many natural categories have “ill-defined” structures that do not conform to simple rules or definitions, alternative theoretical approaches were developed. Modern theories of perceptual classification, for example, include exemplar models and decision-bound models. According to exemplar models, people represent categories in terms of stored exemplars of categories, and classify objects based on their similarity to these stored exemplars (Hintzman, 1986; Medin & Schaffer, 1978; Nosofsky, 1986). Alternatively, according to decision-bound models, people may use (potentially complex) decision bounds to divide up a perceptual space into different category regions. Classification is determined by the category region into which a stimulus is perceived to fall (Ashby & Townsend, 1986; Maddox & Ashby, 1993).

Although the original types of logical rule-based models no longer dominate the field, the general idea that people may use rules as a basis for classification has certainly not disappeared. Indeed, prominent models that posit rule-based forms of category representation, at least as an important component of a fuller system, continue to be proposed and tested (e.g., Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Erickson & Kruschke, 1998; Feldman, 2000; Goodman, Tenenbaum, Feldman, & Griffiths, 2008; Nosofsky, Palmeri, & McKinley, 1994). Furthermore, such models are highly competitive with exemplar and decision-bound models, at least in certain paradigms.

A major limitation of modern rule-based models of classification, however, is that, to date, they have not been used to predict or explain the time course of classification decision making.¹ By contrast, one of the major achievements of modern exemplar and decision-bound models is that they provide detailed quantitative accounts of classification response times (RTs) (e.g., Ashby, 2000; Ashby & Maddox, 1994; Cohen & Nosofsky, 2003; Lamberts, 1998, 2000; Nosofsky & Palmeri, 1997a).

The major purpose of the present research is to begin to fill this gap and to formalize logical-rule models designed to account for the time course of perceptual classification. Of course, we will not claim that the newly developed rule models provide a reflection of human performance that holds universally across all testing conditions and participants. Instead, according to modern views (e.g., Ashby & Maddox, 2005), there are multiple systems and modes of classification, and alternative testing conditions may induce reliance on different classification strategies. Furthermore, even within the same testing conditions, there may be substantial individual differences in which classification strategies are used. Nevetheless, it is often difficult to tell apart the predictions from models that are intended to represent these alternative classification strategies (e.g,. Nosofsky & Johansen, 2000). By studying the time course of classification, and requiring the models to predict classification RTs, more power is gained in telling the models apart. Thus, the present effort is important because it will provide a valuable tool and a new arena in which rule-based models can be contrasted with alternative models of perceptual category representation and processing.

As will be seen, en route to developing these rule-based models, we combine two major general approaches to the modeling of RT data. One approach has focused on alternative “mental architectures” of information processing (e.g., Kantowitz, 1974; Schweickert, 1992; Sternberg, 1969; Townsend, 1984). This approach asks questions such as whether information from multiple dimensions is processed in serial or parallel fashion, and whether the processing is self-terminating or exhaustive. The second major approach uses “diffusion” or “random-walk” models of RT, in which perceptual information is sampled until a criterial amount of evidence has been obtained to make a decision (e.g., Busemeyer, 1985; Link, 1992; Luce, 1986; Ratcliff, 1978; Ratcliff & Rouder, 1998; Townsend & Ashby, 1983). The present proposed logical-rule models of classification RT will combine the mental-architecture and random-walk approaches within an integrated framework (for examples of such approaches in other domains, see Palmer & Mclean, 1995; Ratcliff, 1978; Thornton & Gilden, 2007). Fific, Nosofsky, and Townsend (2008, Appendix A) applied some special cases of the newly proposed models in preliminary fashion to assess some very specific qualitative predictions related to formal theorems of information processing. The present work has the far more ambitious goals of: i) using these architectures as a means of formalizing logical-rule models of classification RT; ii) deriving an extended set of fundamental qualitative contrasts for distinguishing among the models; iii) comparing the logical-rule models to major alternative models of classification RT; and iv) testing the ability of the logical-rule models to provide quantitative accounts of detailed RT distribution data and error rates associated with individual stimuli in tasks of speeded classification.

Conceptual Overview of the Rule-Based Models

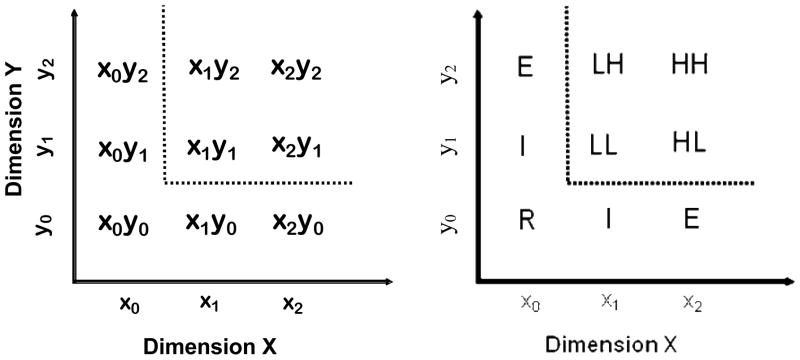
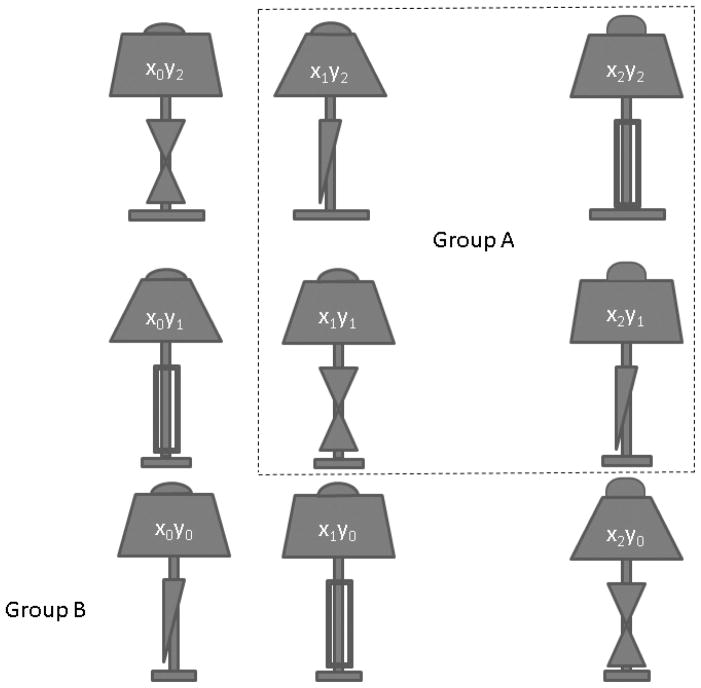
It is convenient to introduce the proposed rule-based models of classification RT by means of the concrete example illustrated in Figure 1 (left panel). This example turns out to be highly diagnostic for distinguishing among numerous prominent models of classification RT and will guide all of our ensuing empirical tests. In the example, the stimuli vary along two continuous dimensions, x and y. In the present case, there are three values per dimension and the values are combined orthogonally to produce the 9 total stimuli in the set. The four stimuli in the upper right quadrant of the space belong to the “target” category (A), whereas the remaining stimuli belong to the “contrast” category (B).

Figure 1.

Left Panel: Schematic illustration of the structure of the stimulus set used for introducing and testing the logical-rule models of classification. The stimuli are composed of two dimensions, X and Y, with three values per dimension, combined orthogonally to produce the nine members of the stimulus set. The stimuli in the upper-right quadrant of the space (x1y1, x1y2, x2y1, and x2y2) are the members of the “target” category (Category A), whereas the remaining stimuli are the members of the “contrast” category (Category B). Membership in the target category is described in terms of a conjunctive rule, and membership in the contrast category is described in terms of a disjunctive rule. The dotted boundaries illustrate the decision boundaries for implementing these rules. Right Panel: Shorthand nomenclature for identifying the main stimulus types in the category structure.

Following previous work, by a “rule” we mean that an observer makes independent decisions regarding a stimulus’s value along multiple dimensions and then combines these separate decisions by using logical connectives such as “AND”, “OR”, and “NOT” to reach a final classification response (Ashby & Gott, 1988; Feldman, 2000; Nosofsky, Clark, & Shin, 1989). The Figure 1 category structure provides an example in which the target category can be defined in terms of a conjunctive rule. Specifically, a stimulus is a member of the target category if it has a value greater than or equal to x1 on Dimension x AND greater than or equal to y1 on Dimension y. Conversely, the contrast category can be described in terms of a disjunctive rule: A stimulus is a member of the contrast category if it has value less than x1 on Dimension x OR has value less than y1 on Dimension y. A reasonable idea is that a human classifier may make his or her classification decisions by implementing these logical rules.

Indeed, this type of logical rule-based strategy has been formalized, for example, within the decision-boundary framework (e.g., Ashby & Gott, 1988; Ashby & Townsend, 1986). Within that formalization, one posits that the observer establishes two decision boundaries in the perceptual space, as is illustrated by the dotted lines in Figure 1. The boundaries are orthogonal to the coordinate axes of the space, thereby implementing the logical rules described above. That is, the vertical boundary establishes a fixed criterion along Dimension x and the horizontal boundary establishes a fixed criterion along Dimension y. A stimulus is classified into the target category if it is perceived as exceeding the criterion on Dimension x AND is perceived as exceeding the criterion on Dimension y; otherwise, it is classified into the contrast category. In the language of decision-bound theory, the observer is making independent decisions along each of the dimensions and then combining these separate decisions to determine the final classification response.

Decision-bound theory provides an elegant language for expressing the structure of logical rules (as well as other strategies of classification decision making). In our view, however, to date, researchers have not offered an information-processing account of how such logical rules may be implemented. Therefore, rigorous processing theories of rule-based classification RT remain to be developed. The main past hypothesis stemming from decision-bound theory is known as the “RT-distance hypothesis” (Ashby, Boynton, & Lee, 1994; Ashby & Maddox, 1994). According to this hypothesis, classification RT is a decreasing function of the distance of a stimulus from the nearest decision bound in the space. In our view, this hypothesis seems most applicable in situations in which a single decision bound has been implemented to divide the psychological space into category regions. The situation depicted in Figure 1, however, is supposed to represent a case in which separate, independent decisions are made along each dimension, with these separate decisions then being combined to determine a classification response. Accordingly, a fuller processing model would formalize the mechanisms by which such independent decisions are made and combined. As will be seen, our newly proposed logical-rule models make predictions that differ substantially from past distance-from-boundary accounts.

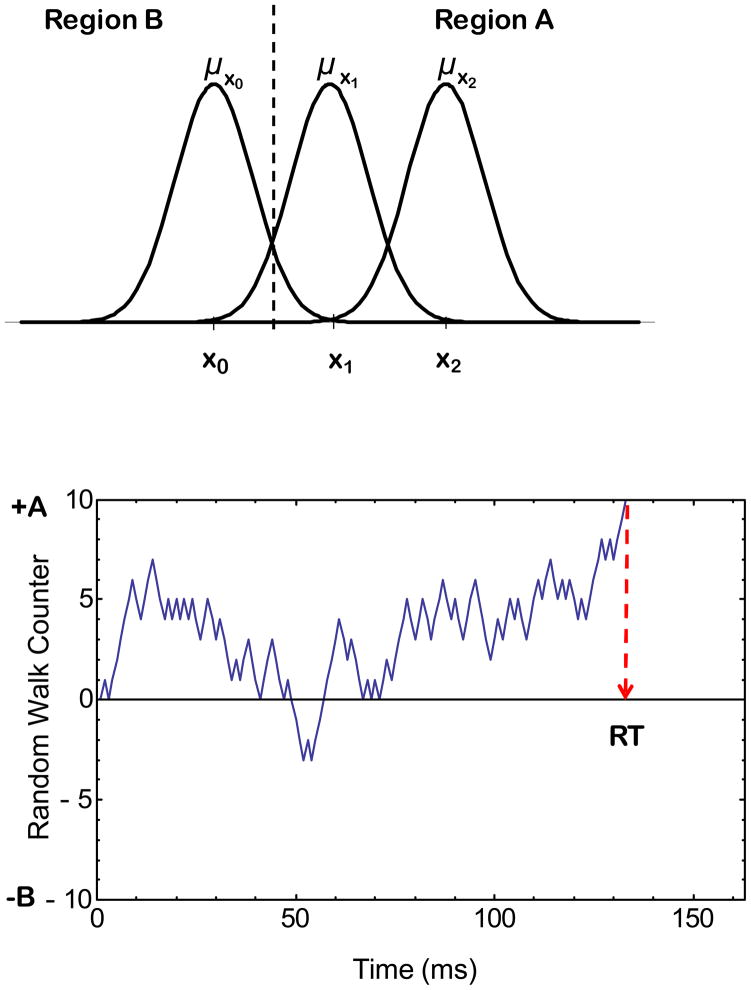
To begin this effort of developing these rule-based processing models, we combine two extremely successful general approaches to the modeling of RT data, namely random-walk and mental-architecture approaches. In the present models, the independent decisions along Dimensions x and y are each presumed to be governed by a separate, independent random-walk process. The nature of the process along Dimension x is illustrated schematically in Figure 2. In accord with decision-bound theory, on each individual dimension, there is a (normal) distribution of perceptual effects associated with each stimulus value (top panel of Figure 2). Furthermore, as illustrated in the figure, the observer establishes a decision boundary to divide the dimension into decision regions. On each step of the process, a perceptual effect is randomly and independently sampled from the distribution associated with the presented stimulus. The sampled perceptual effects drive a random-walk process (bottom panel of Figure 2). In the random walk, there is a counter that is initialized at zero, and the observer establishes criteria representing the amount of evidence that is needed to make an A or B decision. If the sampled perceptual effect falls in Region A, then the random-walk takes a unit step in the direction of criterion A; otherwise, it takes a unit step in the direction of criterion B. The sampling process continues until either Criterion A or B has been reached. The time to complete each individual-dimension decision process is determined by the number of steps that are required to complete the random walk. Note that, in accord with the RT-distance hypothesis, stimuli with values that lie far from the decision boundary (i.e., x2 in the present example) will tend to result in faster decision times along that dimension.

Figure 2.

Schematic illustration of the perceptual-sampling and random-walk processes that govern the decision process on Dimension X.

The preceding paragraph described how classification decision making takes place along each individual dimension. The overall categorization response, however, is determined by a mental architecture that implements the logical rules by combining the individual-dimension decisions. That is, the observer classifies a stimulus into the target category (A) only if both independent decisions point to region A (such that the conjunctive rule is satisfied). By contrast, the observer classifies a stimulus into the contrast category (B) if either independent decision points to B (such that the disjunctive rule is satisfied).

In the present research, we consider five main candidate architectures for how the independent decisions are combined to implement the logical rules. The candidate architectures are drawn from classic work in other domains such as simple detection and visual/memory search (Sternberg, 1969; Townsend, 1984). To begin, processing of each individual dimension may take place in serial fashion or in parallel fashion. In serial processing, the individual-dimension decisions take place sequentially. A decision is first made along one dimension, say, Dimension x; then, if needed, a second decision is made along Dimension y. By contrast, in parallel processing, the random-walk decision processes operate simultaneously, rather than sequentially, along Dimensions x and y.² A second fundamental distinction pertains to the stopping rule, which may be either self-terminating or exhaustive. In self-terminating processing, the overall categorization response is made once either of the individual random-walk processes has reached a decision that allows an unambiguous response. For example, in Figure 1, suppose that stimulus x0y2 is presented, and the random-walk decision process on Dimension x reaches the correct decision that the stimulus falls in Region B of Dimension x. Then the disjunctive rule that defines the contrast category (B) is already satisfied, and the observer does not need to receive information concerning the location of the stimulus on Dimension y. By contrast, if an exhaustive stopping rule is used, then the final categorization response is not made until the decision processes have been completed on both dimensions.

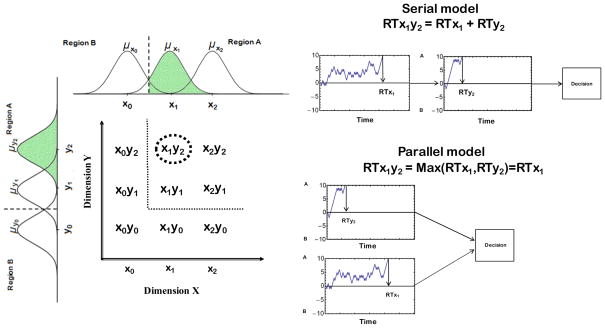
Combining the possibilities described above, there are thus far four main mental architectures that may implement the logical rules -- serial exhaustive, serial self-terminating, parallel exhaustive, and parallel self-terminating. It is straightforward to see that if processing is serial exhaustive, then the total decision time is just the sum of the individual-dimension decision times generated by each individual random walk. Suppose instead that processing is serial self-terminating. Then, if the first processed dimension allows a decision, total decision time is just the time for that first random walk to complete; otherwise, it is the sum of both individual-dimension decision times. In the case of parallel exhaustive processing, the random walks take place simultaneously, but the final categorization decision is not made until the slower of the two random walks has completed. Therefore, total decision time is the maximum of the two individual-dimension decision times generated by each random walk. And in the case of parallel self-terminating processing, total decision time is the minimum of the two individual-dimension decision times (assuming that the first-completed decision allows an unambiguous categorization response to be made). A schematic illustration of the serial-exhaustive and parallel-exhaustive possibilities for stimulus x1y2 from the target category is provided in Figure 3.

Figure 3.

Schematic illustration of the serial-exhaustive and parallel-exhaustive architectures, using stimulus x1y2 as an example. In the serial example, we assume that Dimension X is processed first. The value x1 lies near the decision boundary on Dimension X, so the random-walk process on that dimension tends to take a long time to complete. The value y2 lies far from the decision boundary on Dimension Y, so the random-walk process on that dimension tends to finish quickly. For the serial-exhaustive architecture, the two random walks operate sequentially, so the total decision time is just the sum of the two individual-dimension random-walk times. For the parallel-exhaustive architecture, the two random walks operate simultaneously, and processing is not completed until decisions have been made on both dimensions, so the total decision time is the maximum (i.e., slower) of the two individual-dimension random-walk times.

Finally, a fifth possibility that we consider in the present work is that a “coactive” mental architecture is used for implementing the logical rules (e.g., Diederich & Colonius, 1991; Miller, 1982; Mordkoff & Yantis, 1993; Townsend & Nozawa, 1995). In coactive processing, the observer does not make separate “macro-level” decisions along each of the individual dimensions. Instead, “micro-level” decisions from each individual dimension are pooled into a common processing channel, and it is this pooled channel that drives the macro-level decision-making process. Specifically, to formalize the coactive rule-based process, we assume that the individual dimensions contribute their inputs to a pooled random-walk process. On each step, if the sampled perceptual effects on Dimensions x and y both fall in the target-category region (A), then the pooled random walk steps in the direction of criterion A. Otherwise, if either sampled perceptual effect falls in the contrast category region (B), then the pooled random walk steps in the direction of criterion B. The process continues until either criterion A or B has been reached.

Regarding the terminology used in this article, we should clarify that when we say that an observer is using a “self-terminating” strategy, we mean that processing terminates only when it has the logical option to do so. For example, for the Figure-1 structure, in order for an observer to correctly classify a member of the target category into the target category, logical considerations dictate that processing is always exhaustive (or coactive), because the observer must verify that both independent decisions satisfy the conjunctive rule. Therefore, for the Figure-1 structure, the serial exhaustive and serial self-terminating models make distinctive predictions only for the members of the contrast category (and likewise for the parallel models). All models assume exhaustive processing for correct classification of the target-category members.

Finally, note that for all of the models, error probabilities and RTs are predicted using the same mechanisms as correct RTs.³ For example, suppose that processing is serial self-terminating and that Dimension x is processed first. Suppose further that x0y2 is presented (see Figure 1), but the random-walk leads to an incorrect decision that the stimulus falls in the target-category region (A) on Dimension x. Then processing cannot self-terminate, because neither the disjunctive rule that defines Category B nor the conjunctive rule that defines Category A has yet been satisfied. The system therefore needs to wait until the independent decision process on Dimension y has been completed. Thus, in this case, the total (incorrect) decision time for the serial self-terminating model will be the sum of the decision times on Dimensions x and y.

Free Parameters of the Logical-Rule Models

Specific parametric assumptions are needed to implement the logical-rule models described above. For purposes of getting started, we introduce various simplifying assumptions. First, in the to-be-reported experiments, the stimuli will vary along highly separable dimensions (Garner, 1974; Shepard, 1964). Furthermore, preliminary scaling work indicated that adjacent dimension values were roughly equally spaced. Therefore, a reasonable simplifying assumption is that the psychological representation of the stimuli mirrors the 3×3 grid structure illustrated in Figure 1. Specifically, we assume that associated with each stimulus is a bivariate normal distribution of perceptual effects, with the perceptual effects along Dimensions x and y being statistically independent for each stimulus. Furthermore, the means of the distributions are set at 0, 1, and 2, respectively, for stimuli with values of x0, x1, and x2 on Dimension x; and likewise for Dimension y. All stimuli have the same perceptual-effect variability along Dimension x, and likewise for Dimension y. To allow for the possibility of differential attention to the component dimensions, or that one dimension is more discriminable overall than the other, the variance of the distribution of perceptual effects (Figure 2, top panel) is allowed to be a separate free parameter for each dimension, σ_x² and σ_y², respectively.

In addition, to implement the perceptual-sampling process that drives the random walk (Figure 2, top panel), the observer establishes a decision-bound along Dimension x, D_x, and a decision-bound along Dimension y, D_y. Furthermore, the observer establishes criteria, +A and −B, representing the amount of evidence needed for making an A or a B decision on each dimension (Figure 2, bottom panel). A scaling parameter k is used for transforming the number of steps in each random walk into milliseconds.

Each model assumes that there is a residual base time, not associated with decision-making processes (e.g., reflecting encoding and motor-execution stages). The residual base-time is assumed to be log-normally distributed with mean μ_R and variance σ_R².

Finally, the serial self-terminating model requires a free parameter p_x representing the probability that, on each individual trial, the dimensions are processed in the order x-then-y (rather than y-then-x).

In sum, in the present applications, the logical-rule models use the following 9 free parameters: σ_x², σ_y², D_x, D_y, +A, −B, k, μ_R and σ_R². The serial self-terminating model also uses p_x. The adequacy of these simplifying assumptions can be assessed, in part, from the fits of the models to the reported data. Some generalizations of the models are considered in later sections of the article.

Fundamental Qualitative Predictions

In our ensuing experiments, we test the Figure-1 category structure under a variety of conditions. In all cases, individual subjects participate for multiple sessions and detailed RT-distribution and error data are collected for each individual stimulus for each individual subject. The primary goal is to test the ability of the alternative logical-rule models to quantitatively fit the detailed RT-distribution and error data and to compare their fits with well known alternative models of classification RT. As an important complement to the quantitative-fit comparisons, it turns out the Figure-1 structure is a highly diagnostic one for which the alternative models make contrasting qualitative predictions of classification RT. Indeed, as will be seen, the complete sets of qualitative predictions serve not only to distinguish among the rule-based models, but also to distinguish the rule models from previous decision-bound and exemplar models of classification RT. By considering the patterns of qualitative predictions made by each of the models, we gain insight into the reasons why one model might yield better quantitative fits than the others. In this section, we describe these fundamental qualitative contrasts. They are derived under the assumption that responding is highly accurate, which holds true under the initial testing conditions established in our experiments.

Target-Category Predictions

First, consider the members of the target-category (A). The category has a 2×2 factorial structure, formed by the combination of values x1and x2 along Dimension x, and y1 and y2 along Dimension y. Values of x1 and y1 along each dimension lie close to their respective decision boundaries, so tend to be hard to discriminate from the contrast category values. We will refer to them as the “low-salience” (L) dimension values. The values x2 and y2 lie farther from the decision boundaries, so are easier to discriminate. We will refer to them as the “high-salience” values (H). Thus, the target-category stimuli x1y1, x1y2, x2y1, and x2y2 will be referred to as the LL, LH, HL, and HH stimuli, respectively, as depicted in the right panel of Figure 1. This structure forms part of what is known as the double-factorial paradigm in the information-processing literature (Townsend & Nozawa, 1995). The double-factorial paradigm has been used in the context of other cognitive tasks (e.g., detection and visual/memory search) for contrasting the predictions from the alternative mental architectures described above. Here, we take advantage of these contrasts for helping to distinguish among the alternative logical rule-based models of classification RT. In the following, we provide a brief summary of the predictions along with intuitive explanations for them. For rigorous proofs of the assertions (along with a statement of more technical background assumptions), see Townsend and Nozawa (1995).

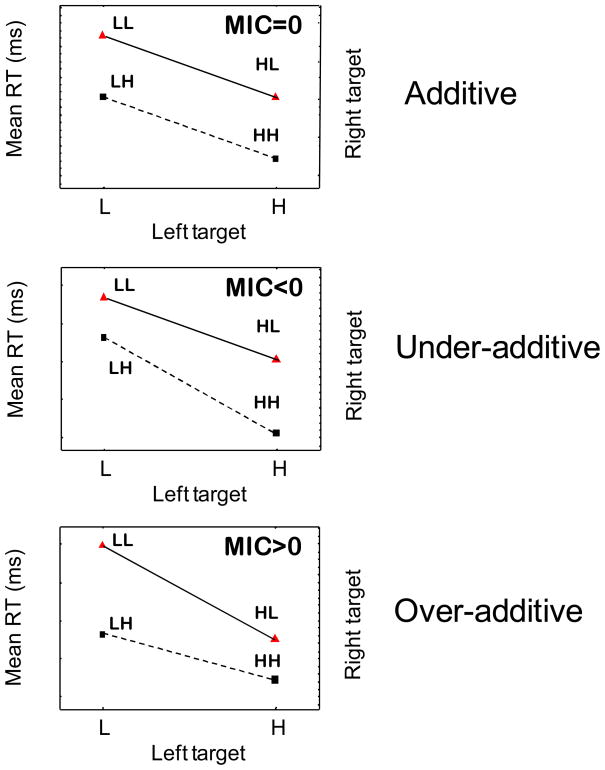
To begin, assuming that the H values are processed more rapidly than are the L values (as is predicted, for example, by the random-walk decision process represented in Figure 2), then there are three main candidate patterns of mean RTs that one might observe. These candidate patterns are illustrated schematically in Figure 4. The patterns have in common that LL has the slowest mean RT, LH and HL intermediate mean RTs, and HH the fastest mean RT. The RT patterns illustrated in the figure can be summarized in terms of an expression known as the mean interaction contrast (MIC):

$$\text{MIC}=[\text{RT}(\text{LL})-\text{RT}(\text{LH})]-[\text{RT}(\text{HL})-\text{RT}(\text{HH})],$$ (1)

where RT(LL) stands for the mean RT associated with the LL stimulus, and so forth. The MIC simply computes the difference between: the distance between the leftmost points on each of the lines [RT(LL)-RT(LH)] and the distance between the rightmost points on each of the lines [RT(HL)-RT(HH)]. It is straightforward to see that the pattern of “additivity” in Figure 4 is reflected by an MIC equal to 0. Likewise, “under-additivity” is reflected by MIC<0, and “over-additivity” is reflected by MIC>0.

Figure 4.

Schematic illustration of the three main candidate patterns of mean RTs for the members of the target category, assuming that the “high-salience” values on each dimension are processed more quickly than are the “low-salience” values. The patterns are summarized in terms of the mean-interaction-contrast, MIC = [RT(LL)-RT(LH)] − [RT(HL)-RT(HH)]. When MIC=0 (top panel), the mean RTs are “additive”; when MIC<0 (middle panel), the mean RTs are “under-additive”; and when MIC>0 (bottom panel), the mean RTs are “over-additive”.

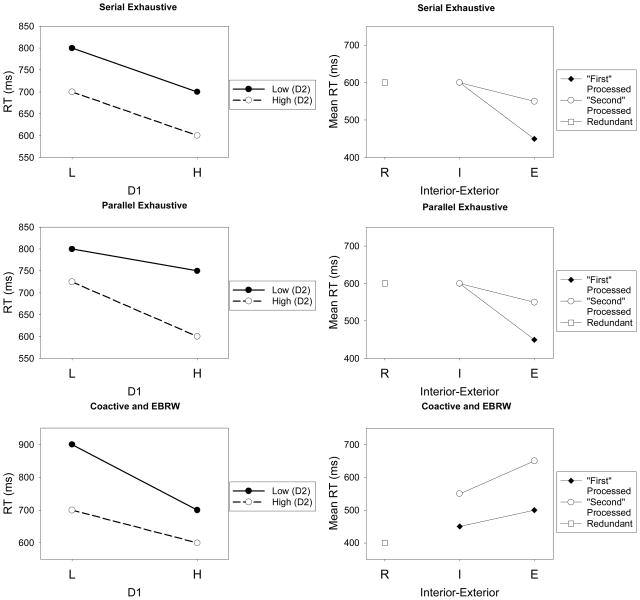
The serial rule models predict MIC=0, that is, an additive pattern of mean RTs. Recall that, for the Figure-1 structure, correct classification of the target-category items requires exhaustive processing, so the serial self-terminating and serial-exhaustive models make the same predictions for the target-category items. In general, LH trials will show some slowing relative to HH trials due to slower processing of the x dimension. Likewise, HL trials will show some slowing relative to HH trials due to slower processing of the y dimension. If processing is serial exhaustive, then the increase in mean RTs for LL trials relative to HH trials will simply be the sum of the two individual sources of slowing, resulting in the pattern of additivity that is illustrated in Figure 4.

The parallel models predict MIC<0, that is, an under-additive pattern of mean RTs. (Again, correct processing is always exhaustive for the target category items, so in the present case there is no need to distinguish between the parallel-exhaustive and parallel self-terminating models.) If processing is parallel-exhaustive, then processing of both dimensions takes place simultaneously; however, the final classification decision is not made until decisions have been made on both dimensions. Thus, RT will be determined by the slower (i.e, maximum time) of the two individual-dimension decisions. Clearly, LH and HL trials will lead to slower mean RTs than will HH trials, because one of the individual-dimension decisions will be slowed. LL trials will lead to the slowest mean RTs of all, because the more opportunities for an individual decision to be slow, the slower on average will be the final response. The intuition, however, is that the individual decisions along each dimension begin to “run out of room” for further slowing. That is, although the RT distributions are unbounded, once one individual-dimension decision has been slowed, the probability of sampling a still slower decision on the other dimension diminishes. Thus, one observes the under-additive increase in mean RTs in the parallel-exhaustive case.

Finally, Townsend and Nozawa (1995) have provided a proof that the coactive architecture predicts MIC>0, i.e., the over-additive pattern of mean RTs shown in Figure 4. Fific et al. (2008, Appendix A) corroborated this assertion by means of computer-simulation of the coactive model. Furthermore, their computer simulations showed that the just-summarized MIC predictions for all of these models hold when error rates are low (and, for some of the models, even in the case of moderate error rates).

A schematic summary of the target-category mean RT predictions made by each of the logical-rule architectures is provided in the left panels of Figure 5. We should note that the alternative rule models make distinct qualitative predictions of patterns of target-category RTs considered at the distributional level as well (see Fific et al., 2008, for a recent extensive review). However, for purposes of getting started, we restrict initial consideration to comparisons at the level of RT means.

Figure 5.

Summary predictions of mean RTs from the alternative logical-rule models of classification. The left panels show the pattern of predictions for the target-category members, and the right panels show the pattern of predictions for the contrast-category members. Left panels: L = low-salience dimension value, H = high-salience dimension value, D1 = Dimension 1, D2 = Dimension 2. Right panels: R = redundant stimulus, I = interior-stimulus, E = exterior stimulus.

Contrast-Category Predictions

The target-category contrasts summarized above are well known in the information-processing literature. It turns out, however, that the various rule-based models also make contrasting qualitative predictions for the contrast-category, and these contrasts have not been considered in previous work. Although the contrast-category predictions are not completely parameter free, they hold over a wide range of the plausible parameter space for the models. Furthermore, parameter settings that allow some of the models to “undo” some of the predictions then result in other extremely strong constraints for telling the models apart. We used computer simulation to corroborate the reasoning that underlies the key predictions listed below. To help keep track of the ensuing list of predictions, they are summarized in canonical form in the right panels of Figure 5. The reader is encouraged to consult Figures 1 and 5 as the ensuing predictions are explained.

For ease of discussion (see Figure 1, left and right panels), in the following we will sometimes refer to stimuli x0y1 and x0y2 as the left-column members of the contrast category; to stimuli x1y0 and x2y0 as the bottom-row members of the contrast category; and to stimulus x0y0 as the redundant (R) stimulus. Also, we will sometimes refer to stimuli x0y1 and x1y0 as the interior (I) members of the contrast category, and to stimuli x0y2 and x2y0 as the exterior (E) members (see Figure 1, left and right panels). In our initial experiment, subjects are provided with instructions to use a fixed-order serial self-terminating strategy as a basis for classification. For example, they may be instructed to always process the dimensions in the order x-then-y. In this case, we will refer to Dimension x as the first-processed dimension and to Dimension y as the second-processed dimension. Of course, for the parallel and coactive models, the dimensions are assumed to be processed simultaneously. Thus, this nomenclature refers to the instructions, not to the processing characteristics assumed by the models.

As will be seen, in Experiment 1, RTs were much faster for contrast-category stimuli that satisfied the disjunctive rule on the first-processed dimension as opposed to the second-processed dimension. To allow each of the logical-rule models to be at least somewhat sensitive to the instructional manipulation, in deriving the following predictions, we assume that the processing rate on the first-processed dimension is faster than on the second-processed dimension. This assumption was implemented in the computer simulations by setting the perceptual noise parameter in the individual-dimension random walks (Figure 2) at a lower value on the first-processed dimension than on the second-processed dimension.

Fixed-Order Serial Self-Terminating Model

Suppose that an observer makes individual dimension decisions for the contrast category in serial self-terminating fashion. For starters, imagine that the observer engages in a fixed order of processing by always processing Dimension x first and then, if needed, processing Dimension y. Note that presentations of the left-column stimuli (x0y1 and x0y2) will generally lead to a correct classification response after only the first dimension (x) has been processed. The reason is that the value x0 satisfies the disjunctive OR rule, so processing can terminate after the initial decision. (Note as well that this fixed-order serial self-terminating model predicts that the redundant stimulus, x0y0, which satisfies the disjunctive rule on both of its dimensions, should have virtually the same distribution of RTs as do stimuli x0y1 and x0y2.) By contrast, presentations of the bottom-row stimuli (x1y0 and x2y0) will require the observer to process both dimensions in order to make a classification decision. That is, after processing only Dimension x, there is insufficient information to determine whether the stimulus is a member of the target category or the contrast category (i.e., both include members with values greater than or equal to x1 on Dimension x). Because the observer first processes Dimension x and then processes Dimension y, the general prediction is that classification responses to the bottom-row stimuli will be slower than to the left-column stimuli. More interesting, however, is the prediction from the serial model that RT for the exterior stimulus x2y0 will be somewhat faster than for the interior stimulus x1y0. Upon first checking Dimension x, it is easier to determine that x2 does not fall to the left of the decision criterion than it is to determine the same for x1. Thus, in the first stage of processing, x2y0 has an advantage compared to x1y0. In the second stage of processing, the time to determine that these stimuli have value y0 on Dimension y (and so are members of the contrast category) is the same for x1y0 and x2y0. Because the total decision time in this case is just the sum of the individual-dimension decision times, the serial self-terminating rule model therefore predicts faster RTs for the exterior stimulus x2y0 than for the interior stimulus x1y0.

In sum (see Figure 5, top-right panel), the fixed-order serial self-terminating model predicts virtually identical fast RTs for the exterior, interior, and redundant stimuli on the first-processed dimension; slower RTs for the interior and exterior stimuli on the second-processed dimension; and, for that second-processed dimension, that the interior stimulus will be somewhat slower than the exterior one.

Mixed-Order Serial Self-Terminating Model

A more general version of the serial self-terminating model assumes that instead of a fixed order of processing the dimensions, there is a mixed probabilistic order of processing. Using the reasoning above, it is straightforward to verify that (except for unusual parameter settings) this model predicts an RT advantage for the redundant stimulus (x0y0) compared to all other members of the contrast category; and that both exterior stimuli should have an RT advantage compared to their neighboring interior stimuli. Also, to the extent that one dimension tends to be processed before the other, stimuli on the first-processed dimension will have faster RTs than stimuli on the second-processed dimension. (See Figure 5.)

Parallel Self-Terminating Model

The parallel-self-terminating rule-based model yields a markedly different set of qualitative predictions than does the serial self-terminating model. According to the parallel-self-terminating model, decisions along dimensions x and y are made simultaneously, and processing terminates as soon as a decision is made that a stimulus has either value x0 or y0. Thus, total decision time is the minimum of those individual-dimension processing times that lead to contrast-category decisions. The time to determine that x0y1 has value x0 is the same as the time to determine that x0y2 has value x0 (and analogously for x1y0 and x2y0). Thus, the parallel self-terminating rule model predicts identical RTs for the interior and exterior members of the contrast category, in marked contrast to the serial self-terminating model. Like the mixed-order serial model, it predicts an RT advantage for the redundant stimulus x0y0, because the more opportunities to self-terminate, the faster the minimum RT tends to be. Also, as long as the rate of processing on each dimension is allowed to vary as described above, it naturally predicts faster RTs for stimuli that satisfy the disjunctive rule on the “first-processed” dimension rather than on the “second-processed” one.

Serial Exhaustive Model

For the same reason as the serial self-terminating model, the serial exhaustive model (Figure 5, fourth row) predicts longer RTs for the interior stimuli on each dimension than for the exterior stimuli. Interestingly, and in contrast to the previous models, it also predicts a longer RT for the redundant stimulus than for the exterior stimuli. The reasoning is as follows. Because processing is exhaustive, both the exterior stimuli and the redundant stimulus require that individual-dimension decisions be completed on both dimensions x and y. The total RT is just the sum of those individual-dimension RTs. Consider, for example, the redundant stimulus (x0y0) and the bottom-row exterior stimulus (x2y0). Both stimuli are the same distance from the decision bound on Dimension y, so the independent decision on Dimension y takes the same amount of time for these two stimuli. However, assuming a reasonable placement of the decision bound on Dimension x (i.e., one that allows for above-chance performance on all stimuli), then the exterior stimulus is farther than is the redundant stimulus from the x boundary. Thus, the independent decision on Dimension x is faster for the exterior stimulus than for the redundant stimulus. Accordingly, the predicted total RT for the exterior stimulus is faster than for the redundant one. Analogous reasoning leads to the prediction that the left-column exterior stimulus (x0y2) will also have a faster RT than the redundant stimulus. The predicted RT of the redundant stimulus compared to the interior stimuli depends on the precise placement of the decision bounds on each dimension. The canonical predictions shown in the figure are for the case in which the decision bounds are set midway between the means of the redundant and interior stimuli on each dimension.

Parallel-Exhaustive Model

The parallel-exhaustive model (Figure 5, Row 5) requires that both dimensions be processed, and the total decision time is the slower (maximum) of each individual-dimension decision time. For the interior stimuli and the redundant stimulus, both individual-dimension decisions tend to be slow (because all of these stimuli lie near both the x and y decision bounds). However, for the exterior stimuli, only one individual-dimension decision tends to be slow (because the exterior stimuli lie far from one decision bound, and close to the other). Thus, the interior stimuli and redundant stimulus should tend to have roughly equal RTs that are longer than those for the exterior stimuli. Again, the precise prediction for the redundant stimulus compared to the interior stimuli depends on the precise placement of the decision bounds on each dimension. The canonical predictions in Figure 5 are for the case in which the decision bounds are set midway between the means of the redundant and interior stimuli.

Coactive Rule-Based Model

Just as is the case for the target category, the coactive model (Figure 5, Row 6) yields different predictions than do all of the other rule-based models for the contrast category. Specifically, it predicts faster RTs for the interior members of the contrast category (x1y0 and x0y1) than for the exterior members (x2y0 and x0y2). The coactive model also predicts that the redundant stimulus will have the very fastest RTs. The intuitive reason for these predictions is that the closer a stimulus gets to the lower left-corner of the contrast category, the higher is the probability that at least one of its sampled percepts will fall in the contrast-category region. Thus, the rate at which the pooled random walk marches towards the contrast-category criterion tends to increase. The same intuition can explain why contrast-category members that satisfy the disjunctive rule on the “first-processed” dimension are classified faster than those on the “second-processed” dimension (i.e., by assuming reduced perceptual variability along the first-processed dimension).

Comparison Models and Relations Among Models

As a source of comparison for the proposed logical rule-based models, we consider some of the major extant alternative models of classification RT.

RT-Distance Model of Decision-Boundary Theory

Recall that in past applications, decision-bound theory has been used to predict classification RTs by assuming that RT is a decreasing function of the distance of a percept from a multidimensional decision boundary. To provide a process interpretation for this hypothesis, and to improve comparability among alternative models, Nosofsky and Stanton (2005) proposed a random-walk version of decision-bound theory that implements the RT-distance hypothesis (see also Ashby, 2000). We will refer to the model as the RW-DFB (random-walk, distance-from-boundary) model. The RW-DFB model is briefly described here for the case of stimuli varying along two dimensions. The observer is assumed to establish (two-dimensional) decision boundaries for partitioning perceptual space into decision regions. On each step of a random-walk process, a percept is sampled from a bivariate normal distribution associated with the presented stimulus. If the percept falls in region A of the two-dimensional space, then the random-walk counter steps in the direction of criterion A, otherwise it steps in the direction of criterion B. The sampling process continues until either criterion is reached. In general, the farther a stimulus is from the decision boundaries, the faster are the RTs that are predicted by the model. (Note that, in our serial and parallel logical-rule models, this RW-DFB process is assumed to operate at the level of individual dimensions, but not at the level of multiple dimensions.)

A wide variety of two-dimensional decision boundaries could be posited for the Figure-1 category structure, including models that assume general linear boundaries, quadratic boundaries, and likelihood-based boundaries (see, e.g., Maddox & Ashby, 1993). Because the stimuli in our experiments are composed of highly separable dimensions, however, a reasonable representative from this wide class of models assumes simply that the observer uses the orthogonal decision boundaries that are depicted in Figure 1. (We consider alternative types of multidimensional boundaries in our General Discussion. Crucially, we will be able to argue that our conclusions hold widely over a very broad class of random-walk, distance-from-boundary models.)

Given the assumption of the use of these orthogonal decision boundaries, as well as our previous parametric assumptions involving statistical independence of the stimulus representations, it turns out that, for the present category structure, the coactive rule-based model is formally identical to this previously proposed multidimensional RW-DFB model.⁴ Therefore, the coactive model will serve as our representative of using the multidimensional RT-distance hypothesis as a basis for predicting RTs. Thus, importantly, comparisons of the various alternative serial and parallel rule models to the coactive version can provide an indication of the utility of adding “mental-architecture” assumptions to decision-boundary theory.

EBRW Model

A second comparison model is the exemplar-based random walk (EBRW) model (Nosofsky & Palmeri, 1997a,b; Nosofsky & Stanton, 2005), which is a highly successful exemplar-based model of classification. The EBRW model has been discussed extensively in previous reports, so only a brief summary is provided here. According to the model, people represent categories by storing individual exemplars in memory. When a test item is presented, it causes the stored exemplars to be retrieved. The higher the similarity of an exemplar to the test item, the higher is its retrieval probability. If a retrieved exemplar belongs to Category A, then a random-walk counter takes a unit step in the direction of criterion A; otherwise it steps in the direction of criterion B. The exemplar-retrieval process continues until either criterion A or criterion B is reached. In general, the EBRW model predicts that the greater the “summed similarity” of a test item to one category, and the less its summed similarity to the alternative category, the faster will be its classification RT.

In the present applications, the EBRW uses 8 free parameters (see Nosofsky & Palmeri, 1997a, for detailed explanations): an overall sensitivity parameter c for measuring discriminability between exemplars; an attention-weight parameter w_x representing the amount of attention given to Dimension x; a background-noise parameter back; random-walk criteria +A and −B; a scaling constant k for transforming the number of steps in the random walk into milliseconds; and residual-time parameters μ_R and σ_R² that play the same role in the EBRW model as in the logical rule-based models. Adapting ideas from Lamberts (1995), Cohen and Nosofsky (2003) proposed an elaborated version of the EBRW that includes additional free parameters for modeling the time course with which individual dimensions are perceptually encoded. For simplicity in getting started, however, in this research we limit consideration to the baseline version of the model.

We have conducted extensive investigations that indicate that, over the vast range of its parameter space, the EBRW model makes predictions that are similar to those of the coactive rule model for the target category (i.e, overadditivity in the MIC). These investigations are reported in Appendix A. In addition, like the coactive model, the EBRW model predicts that, for the contrast category, the interior stimuli will have faster RTs than will the exterior stimuli; and that the redundant stimulus will have the fastest RTs of all. The intuition, as can be gleaned from Figure 1, is that the closer a stimulus gets to the lower-left corner of the contrast category, the greater is its overall summed similarity to the contrast-category exemplars. Finally, the EBRW model can predict faster RTs for contrast-category members that satisfy the disjunctive rule on the first-processed dimension by assigning a larger “attention weight” to that dimension (Nosofsky, 1986).

Because the EBRW model and the coactive rule model make the same qualitative predictions for the present paradigm, we expect that they may yield similar quantitative fits to the present data. However, based on previous research (Fific et al., 2008), we do not expect to see much evidence of coactive processing for the highly separable-dimension stimuli used in the present experiments. Furthermore, as can be verified from inspection of Figure 5, the EBRW model makes sharply contrasting predictions from all of the other logical-rule models of classification RT. Thus, to the extent that observers do indeed use logical rules as a basis for the classification in the present experiments, the results should clearly favor one of the rule-based models compared to the EBRW model.⁵

Free Stimulus-Drift-Rate Model

As a final source of comparison, we also consider a random-walk model in which each individual stimulus is allowed to have its own freely estimated step-probability (or “drift rate”) parameter. That is, for each individual stimulus i, we estimate a free parameter p_i that gives the probability that the random-walk steps in the direction of criterion A. This approach is similar to past applications of Ratcliff’s (1978) highly influential diffusion model. (The diffusion model is a continuous version of a discrete-step random walk.) In that approach, the “full” diffusion model is fitted by estimating separate drift-rate parameters for each individual stimulus or condition, and investigations are then often conducted to discover reasons why the estimated drift rates may vary in systematic ways (e.g., Ratcliff & Rouder, 1998). The present free stimulus-drift-rate random-walk model uses 14 free parameters: the 9 individual stimulus step-probability parameters; and 5 parameters that play the same role as in the previous models -- +A, −B, k, μ_R and σ_R².

The free stimulus-drift-rate random-walk model is more descriptive in form than are the logical-rule models or the EBRW model, in the sense that it can describe any of the qualitative patterns involving the mean RTs that are illustrated in Figure 5. Nevertheless, because our model-fit procedures penalize models for the use of extra free parameters (see the Model-Fit section for details), the free stimulus-drift-rate model is not guaranteed to provide a better quantitative fit to the data than do the logical rule models or the EBRW model. To the extent that the logical-rule models (or the EBRW model) capture the data in parsimonious fashion, they should provide better penalty-corrected fits than does the free stimulus-drift-rate model. By contrast, dramatically better fits of the free stimulus-drift-rate model could indicate that the logical-rule models or exemplar model are missing key aspects of performance.

Finally, it is important to note that, even without imposing a penalty for its extra free parameters, the free stimulus-drift-rate model could in principle provide worse absolute fits to the data than do some of the logical-rule models.⁶ The reason is that our goal is to fit the detailed RT-distribution data associated with the individual stimuli. Although the focus of our discussion has been on the predicted pattern of mean RTs, there is likely to also be a good deal of structure in the RT-distribution data that is useful for distinguishing among the models. For example, consider a case in which an observer uses a mixed-order serial self-terminating strategy. In cases in which Dimension x is processed first, then the left-column members of the contrast category should have fast RTs. But in cases in which Dimension x is processed second, then the left-column members should have slow RTs. Thus, the mixed-order serial self-terminating model allows the possibility of observing a bimodal distribution of RTs.⁷ By contrast, a random-walk model that associates a single “drift rate” with each individual stimulus predicts that the RT distributions should be uni-modal in form (see also Ashby et al., 2007, p. 647). As will be seen, there are other aspects of the RT distribution data that also impose interesting contraints on the alternative models.

Ratcliff and McKoon (2008) have recently emphasized that single-channel diffusion models are appropriate only for situations in which a “single stage” of decision making governs performance. To the extent that subjects adopt the present kinds of logical rule-based strategies in our classification task, “multiple stages” of decision making are taking place, so even the present free stimulus-drift-rate model may fail to yield good quantitative fits.

Experiment 1

The goal of our experiments was to provide initial tests of the ability of the logical-rule models to account for speeded classification performance, using the category structure depicted in Figure 1. Almost certainly, the extent to which rule-based strategies are used will depend on a variety of experimental factors. In these initial experiments, the idea was to implement factors that seemed strongly conducive to the application of the rules. Thus, the experiments serve more in the way of “validation tests” of the newly proposed models, as opposed to inquiries of when rule-based classification does or does not occur. If preliminary support is obtained in favor of the rule-based models under these initial conditions, then later research can examine boundary conditions on their application.

Clearly, one critical factor is whether the category structure itself affords the application of logical rules. Because for the present Figure-1 structure, an observer can classify all objects perfectly with the hypothesized rule-based strategies, this aspect of the experiments would seem to promote the application of the rules. The use of more complex category structures might require that subjects supplement a rule-based strategy with the memory of individual exemplars, exceptions-to-the-rule, more complex decision boundaries, and so forth.

A second factor involves the types of dimensions that are used to construct the stimuli. In the present experiments, the stimuli varied along a set of highly separable dimensions (Garner, 1974; Shepard, 1964). In particular, following Fific et al. (2008), the stimuli were composed of two rectangular regions, one to the left and one to the right. The left rectangle was a constant shade of red and varied only in its overall level of saturation. The right rectangle was uncolored and had a vertical line drawn inside it. The line varied only its left-right positioning within the rectangle. One reason why we used these highly separable dimensions was to ensure that the psychological structure of the set of to-be-classified stimuli matched closely the schematic 3×3 factorial design depicted in Figure 1. A second reason is that use of the rule-based strategies entails that separate independent decisions are made along each dimension. Such an independent-decisions strategy would seem to be promoted by the use of stimuli varying along highly separable dimensions. That is, for the present stimuli, it seems natural for an observer to make a decision about the extent to which an object is saturated, to make a separate decision about the extent to which the line is positioned to the left, and then to combine these separate decisions to determine whether or not the logical rule is satisfied.

Finally, to most strongly induce the application of the logical rules, subjects were provided with explicit knowledge of the rule-based structure of the categories and were provided with explicit instructions to use a fixed-order serial self-terminating strategy as a basis for classification. The instructions spelled out in step-by-step fashion the application of the strategy (see Method section). Of course, there is no certainty that observers can follow the instructions, and there is a good possibility that other automatic types of classification processes may override attempts to use the instructed strategy (e.g., Brooks, Norman, & Allen, 1991; Logan, 1988; Logan & Klapp, 1991; Palmeri, 1997). Nevertheless, we felt that the present conditions could potentially place the logical-rule models in their best possible light and that it was a reasonable starting point. In a subsequent experiment, we test a closely related design, with some subjects operating under more open-ended conditions.

Method

Subjects

The subjects were 5 graduate and undergraduate students associated with Indiana University. All subjects were under 40 years of age and had normal or corrected-to-normal vision. The subjects were paid $8 per session plus up to a $3 bonus per session depending on performance.

Stimuli

Each stimulus consisted of two spatially separated rectangular regions. The left rectangle had a red hue that varied in its saturation and the right rectangular region had an interior vertical line that varied in its left-right positioning. (For an illustration, see Fific et al, 2008, Figure 5.)

As illustrated in Figure 1, there were nine stimuli composed of the factorial combination of three values of saturation and three values of vertical-line position. The saturation values were derived from the Munsell color system and were generated on the computer by using the Munsell color conversion program (WallkillColor, version 6.5.1). According to the Munsell system, the colors were of a constant red hue (5R) and of a constant lightness (value 5), but had saturation (chromas) equal to 10, 8, and 6 (for dimension values x0, x1, and x2, respectively). The distances of the vertical line relative to the leftmost side of the right rectangle were 30, 40, and 50 pixels (for dimension values y0, y1, and y2, respectively). The size of each rectangle was 133 × 122 pixels. The rectangles were separated by 45 pixels and each pair of rectangles subtended a horizontal visual angle of about 6.4 degrees and a vertical visual angle of about 2.3 degrees. The study was conducted on a Pentium PC with a CRC monitor, with display resolution 1024 × 768. The stimuli were presented on a white background.

Procedure

The stimuli were divided into two categories, A and B, as illustrated in Figure 1. On each trial, a single stimulus was presented, the subject was instructed to classify it into Category A or B as rapidly as possible without making errors, and corrective feedback was then provided.

The experiment was conducted over 5 sessions, one session per day, with each session lasting approximately 45 minutes. In each session, subjects received 27 practice trials and then were presented with 810 experimental trials. Trials were grouped into six blocks, with rest breaks in between each block. Each stimulus was presented the same number of times within each session. Thus, for each subject, each stimulus was presented 93 times per session and 465 times over the course of the experiment. The order of presentation of the stimuli was randomized anew for each subject and session. Subjects made their responses by pressing the right (Category A) and left (Category B) buttons on a computer mouse. The subjects were instructed to rest their index fingers on the mouse buttons throughout the testing session. RTs were recorded from the onset of a stimulus display up to the time of a response. Each trial started with the presentation of a fixation cross for 1770 ms. After 1070 ms from the initial appearance of the fixation cross, a warning tone was sounded for 700 ms. The stimulus was then presented on the screen and remained visible until the subject’s response was recorded. In the case of an error, the feedback “INCORRECT” was displayed on the screen for 2 sec. The inter-trial interval was 1870 msec.

At the start of the experiment, subjects were shown a picture of the complete stimulus set (in the form illustrated in Figure 1, except with the actual stimuli displayed). While viewing this display, subjects read explicit instructions to use a serial self-terminating rule-based strategy to classify the stimuli into the categories. [Subjects 1 and 2 were given instructions to process Dimension y (vertical-line position) first, whereas Subjects 3–5 were given instructions to process Dimension x (saturation) first.] The instructions for the “saturation-first” subjects were as follows:

We ask you to use the following strategy ON ALL TRIALS to classify the stimuli. First, focus on the colored square. If the colored square is the most saturated with red, then classify the stimulus into Category B immediately. If the colored square is not the most saturated with red, then you need to focus on the square with the vertical line. If the line is furthest to the left, then classify the stimulus into Category B. Otherwise classify the stimulus into Category A. Make sure to use this same sequential strategy on each and every trial of the experiment.

Analogous instructions were provided to the subjects who processed Dimension y (vertical-line position) first. Finally, because the a priori qualitative contrasts for discriminating among the models are derived under the assumption that error rates are low, the instructions emphasized that subjects needed to be highly accurate in making their classification decisions. In a subsequent experiment, we also test subjects with a speed-stress emphasis and examine error RTs.

Results

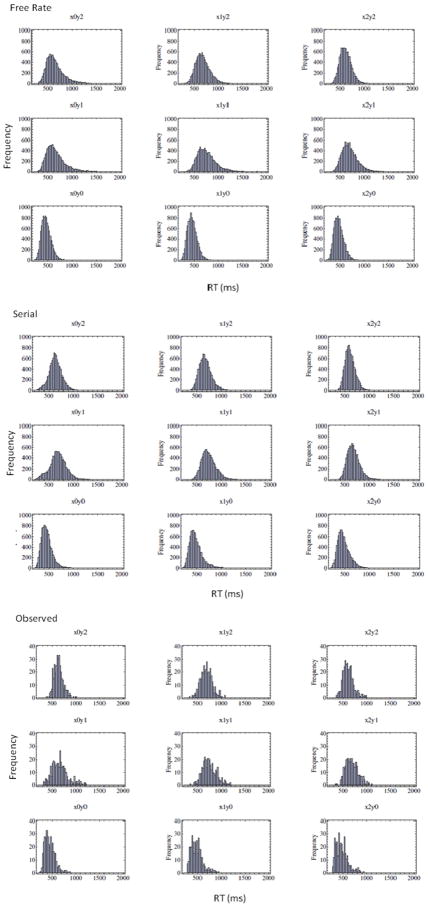
Session 1 was considered practice and these data were not included in the analyses. In addition, conditionalized on each individual subject and stimulus, we removed from the analysis RTs greater than 3 standard deviations above the mean and also RTs of less than 100 msec. This procedure led to dropping less than 1.2% of the trials from analysis.

We examined the mean correct RTs for the individual subjects as a function of sessions of testing. Although we observed a significant effect of sessions for all subjects (usually, a slight overall speedup effect), the basic patterns for the target-category stimuli and contrast-category remained constant across sessions. Therefore, we combine the data across Sessions 2–5 in illustrating and modeling the results.

The mean correct RTs and error rates for each individual stimulus for each subject are reported in Table 1. In general, error rates were low and mirrored the patterns of mean correct RTs. That is, stimuli associated with slower mean RTs had a higher proportion of errors. Therefore, our initial focus will be on the results involving the RTs.

Table 1.

Experiment 1, Mean Correct RTs and error rates for individual stimuli, observed and best-fitting model predicted.

Subject 1
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	501	585	564	637	467	476	578	552	446
RTParallel Self-Terminating	491	590	580	631	469	468	565	564	467
p(e) Observed	.00	.02	.00	.01	.00	.01	.03	.01	.00
p(e) Parallel Self-Terminating	.00	.01	.00	.01	.00	.00	.00	.00	.00
Subject 2
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	609	682	687	748	476	479	635	658	452
RT Serial Self-Terminating	618	681	674	737	478	476	632	686	480
p(e) Observed	.00	.04	.01	.04	.02	.03	.03	.02	.01
p(e) Serial Self-Terminating	.00	.04	.03	.08	.01	.01	.02	.02	.00
Subject 3
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	596	664	665	709	707	721	559	548	531
RT Serial Self-Terminating	606	659	658	707	699	745	548	553	534
p(e) Observed	.01	.00	.01	.01	.01	.02	.01	.00	.00
p(e) Serial Self-Terminating	.00	.00	.00	.01	.01	.01	.00	.00	.00
Subject 4
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	590	618	619	657	624	657	424	423	432
RT Serial Self-Terminating	591	617	620	647	628	659	431	433	432
p(e) Observed	.00	.01	.01	.03	.02	.04	.01	.01	.00
p(e) Serial Self-Terminating	.00	.01	.01	.02	.01	.01	.00	.00	.00
Subject 5
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	546	618	596	687	630	615	484	481	464
RT Serial Self-Terminating	548	626	596	674	611	658	478	481	476
p(e) Observed	.00	.02	.01	.05	.02	.03	.01	.00	.00
p(e) Serial Self-Terminating	.00	.04	.01	.05	.03	.03	.00	.00	.00

Note. p(e) = proportion of errors. RT = mean correct response time.

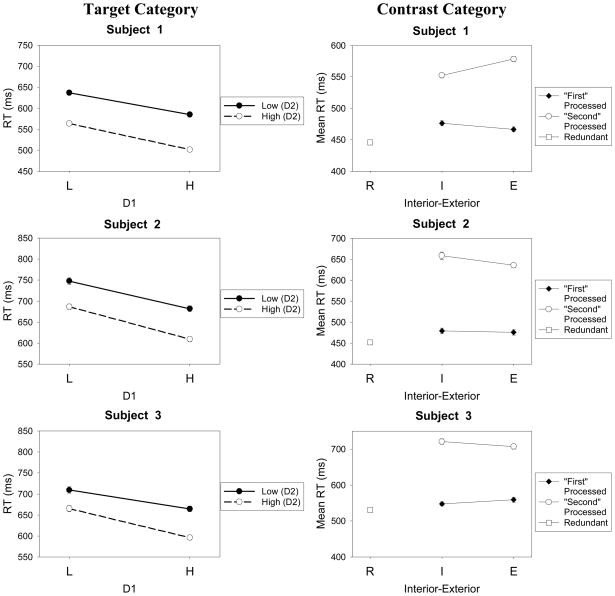
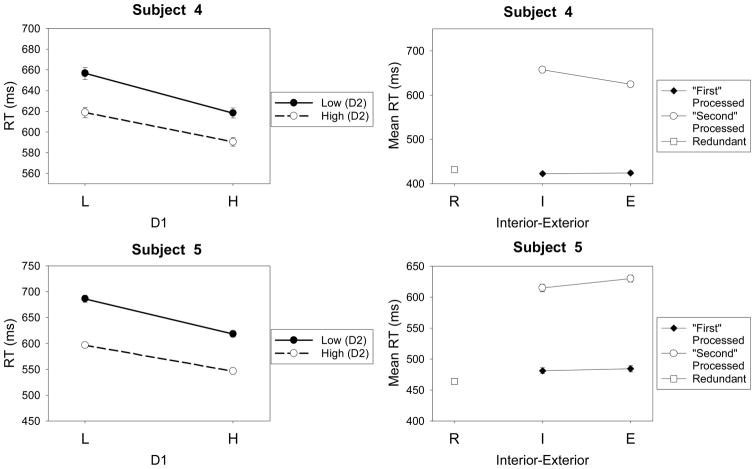
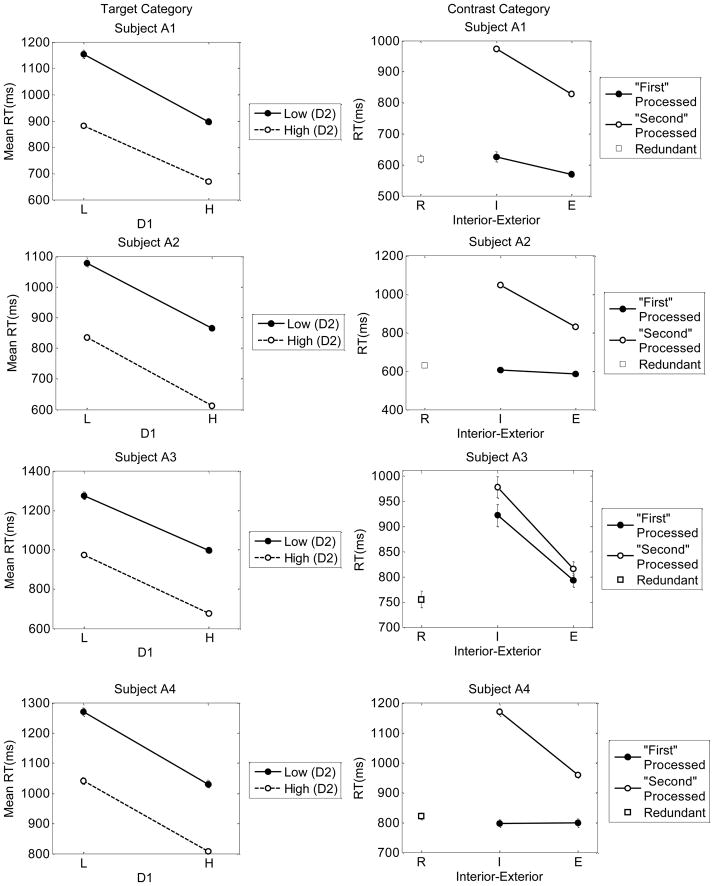
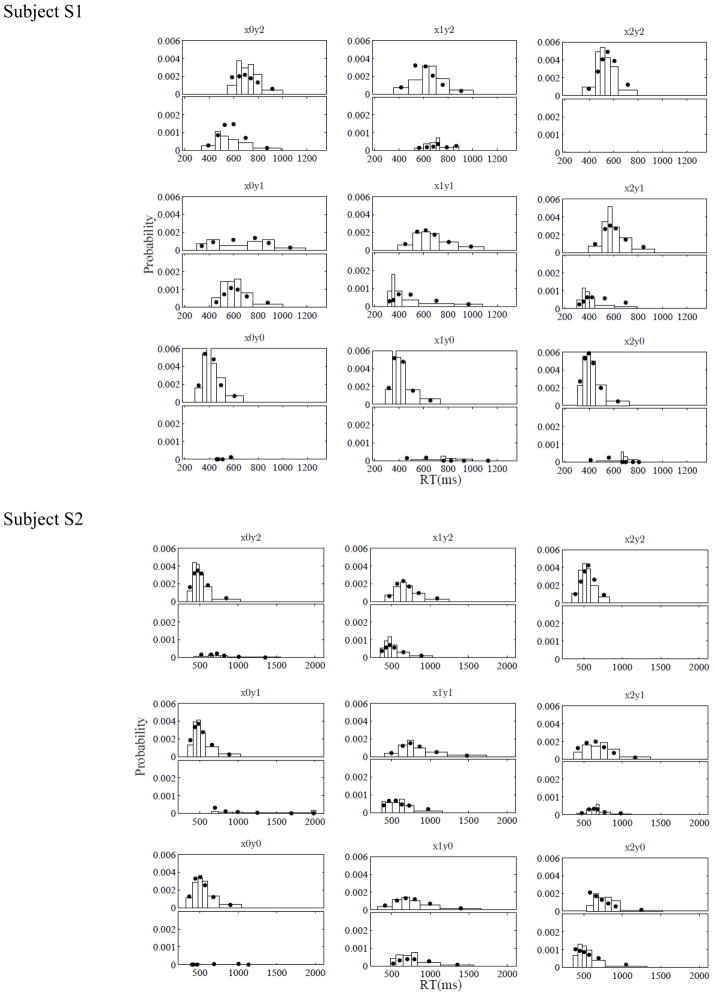
The mean correct RTs for the individual subjects and stimuli are displayed graphically in the panels in Figure 6. The left panels show the results for the target-category stimuli and the right panels show the results for the contrast-category stimuli. Regarding the contrast-category stimuli, for ease of comparing the results to the canonical-prediction graphs in Figure 5, the means in the figure have been arranged according to whether a stimulus satisfied the disjunctive rule on the instructed “first-processed” dimension or the “second-processed” dimension. For example, Subject 1 was instructed to process Dimension y first. Therefore, for this subject, the interior and exterior stimuli on the “first-processed” dimension are x1y0 and x2y0 (see Figure 1).

Figure 6.

Observed mean RTs for the individual subjects and stimuli in Experiment 1. Error bars represent one standard error. Left panels show the results for the target-category stimuli and right panels show the results for the contrast-category stimuli. Left panels: L = low-salience dimension value, H = high-salience dimension value, D1 = Dimension 1, D2 = Dimension 2. Right panels: R = redundant stimulus, I = interior stimulus, E = exterior stimulus.

Regarding the target-category stimuli, note first that for all five subjects, the manipulations of salience (high versus low) on both the saturation and line-position dimensions had the expected effects on the overall pattern of mean RTs, in the sense that the high-salience (H) values led to faster RTs than did the low-salience (L) values. Regarding the contrast-category stimuli, not surprisingly, stimuli that satisfied the disjunctive rule on the first-processed dimension were classified with faster RTs than those on the second-processed dimension. These global patterns of results are in general accord with the predictions from all of the logical-rule models as well as the EBRW model (compare to Figure 5).

The more fine-grained arrangement of RT means, however, allows for an initial assessment of the predictions from the competing models. To the extent that subjects were able to follow the instructions, our expectation is that the data should tend to conform to the predictions from the fixed-order serial self-terminating model of classification RT. For Subjects 2, 3 and 4, the overall results seem reasonably clear-cut in supporting this expectation (compare the top panels in Figure 5 to those for Subjects 2–4 in Figure 6). First, as predicted by the model, the mean RTs for the target category members are approximately additive (MIC=0). Second, for the contrast-category members, the mean RTs for the stimuli that satisfy the disjunctive rule on the first-processed dimension are faster than those for the second-processed dimension. Third, for those stimuli that satisfy the disjunctive rule on the second-processed dimension, RTs for the exterior stimulus are faster than for the interior stimulus (whereas there is little difference for the interior and exterior stimuli that satisfy the disjunctive rule on the first-processed dimension). Fourth, the mean RT for the redundant stimulus is almost the same as (or perhaps slightly faster than) the mean RTs for the stimuli on the first-processed dimension. These qualitative patterns of results are all in accord with the predictions from the fixed-order serial self-terminating model. Furthermore, considered collectively, they violate the predictions from all of the other competing models.

The results for Subjects 1 and 5 are less clear-cut. On the one hand, for both subjects, the mean RTs for the target category are approximately additive, in accord with the predictions from the serial model. (There is a slight tendency towards under-additivity for Subject 1 and towards over-additivity for Subject 5.) In addition, for the contrast category, both stimuli that satisfy the disjunctive rule on the first-processed dimension are classified faster than those on the second-processed dimension. On the other hand, for stimuli in the contrast category that satisfy the disjunctive rule on the second-processed dimension, RTs for the external stimulus are slower than for the internal one, which is in opposition to the predictions from the serial self-terminating model. The qualitative results from these two subjects do not point in a consistent, converging direction to any single one of the contending models (although, overall, the serial and parallel self-terminating models appear to be the best candidates). We revisit all of these results in the section on Quantitative Model Fitting.

We conducted various statistical tests to corroborate the descriptions of the data provided above. The main results are reported in Table 2. With regard to the target-category stimuli, for each individual subject, we conducted three-way ANOVAs on the RT data using as factors session (2–5), level of saturation (H or L), and level of vertical-line position (H or L). Of course, the main effects of saturation and line position (not reported in the table) were highly significant for all subjects, reflecting the fact that the H values were classified more rapidly than were the L values. The main effect of sessions was statistically significant for all subjects, usually reflecting either a slight speeding up or slowing down of performance as a function of practice in the task. However, there were no interactions of session with the other factors, reflecting that the overall pattern of RTs was fairly stable throughout testing.

Table 2.

Experiment 1 statistical-test results table.

Target-Category Factor			Contrast-Category Comparisons
Subject 1	df	F	Subject 1	M	t
Session	3	24.33 **	E1-I1	−9.6	−1.70
Sat. × LP	1	1.73	E2-I2	25.9	4.46 **
Sat. × LP × Session	3	0.59	E1-R	20.8	4.20 **
Error	1401		I1-R	30.5	6.21 **
Subject 2	df	F	Subject 2	M	t
Session	3	2.86 *	E1-I1	−3.7	−0.39
Sat. × LP	1	.80	E2-I2	−23.0	−2.18 *
Sat. × LP × Session	3	.21	E1-R	23.7	2.72 **
Error	1373		I1-R	27.4	3.14 **
Subject 3	df	F	Subject 3	M	t
Session	3	82.44 **	E1-I1	11.4	1.26
Sat. × LP	1	3.52±	E2-I2	−13.5	−1.31
Sat. × LP × Session	3	.04	E1-R	28.2	3.27 **
Error	1392		I1-R	16.8	2.22 *
Subject 4	df	F	Subject 4	M	t
Session	3	139.74 **	E1-I1	1.5	0.32
Sat. × LP	1	1.21	E2-I2	−33.0	−4.55 **
Sat. × LP × Session	3	.71	E1-R	−7.5	−1.52
Error	1386		I1-R	−9.0	−1.85±
Subject 5	df	F	Subject 5	M	t
Session	3	8.88 **	E1-I1	3.0	0.44
Sat. × LP	1	2.63	E2-I2	15.0	1.80±
Sat. × LP × Session	3	.92	E1-R	20.4	3.23 **
Error	1383		I1-R	17.4	2.84 **

Note. Sat. = Saturation, LP = Line Position, E1 = Exterior stimulus on first-processed dimension, I1 = Interior stimulus on first-processed dimension, E2 = Exterior stimulus on second-processed dimension, I2 = Interior stimulus on second-processed dimension, R = redundant stimulus, M = Mean RT difference (ms).

^**p<.01,

^*p<.05,

^±p<.075.

For the contrast-category t-tests, the df vary between 687 and 712, so the critical values of t are essentially z.

The most important question is whether there was an interaction between the factors of saturation and line position. The interaction test is used to assess the question of whether the mean RTs show a pattern of additivity, under-additivity, or over-additivity. The interaction between level of saturation and level of line position did not approach statistical significance for Subjects 1, 2, 4 or 5, supporting the conclusion of mean RT additivity. This finding is consistent with the predictions from the logical rule models that assume serial processing of the dimensions. The interaction between saturation and line position was marginally significant for Subject 3, in the direction of under-additivity. Therefore, for Subject 3, the contrast between the serial versus parallel-exhaustive models is not clear-cut for the target-category stimuli.

Regarding the contrast-category stimuli, we conducted a series of focused t-tests for each individual subject for those stimulus comparisons most relevant to distinguishing among the models. The results, reported in detail in Table 2, generally corroborate the summary descriptions that we provided above. Specifically, for all of the subjects, the RT difference between the interior and exterior stimulus on the first-processed dimension was small and not statistically signficant; the redundant stimulus tended to be classified significantly faster than both the interior and exterior stimuli; and, in the majority of cases, the exterior stimulus was classified significantly faster than was the interior stimulus on the second-processed dimension.

Quantitative Model-Fitting Comparisons

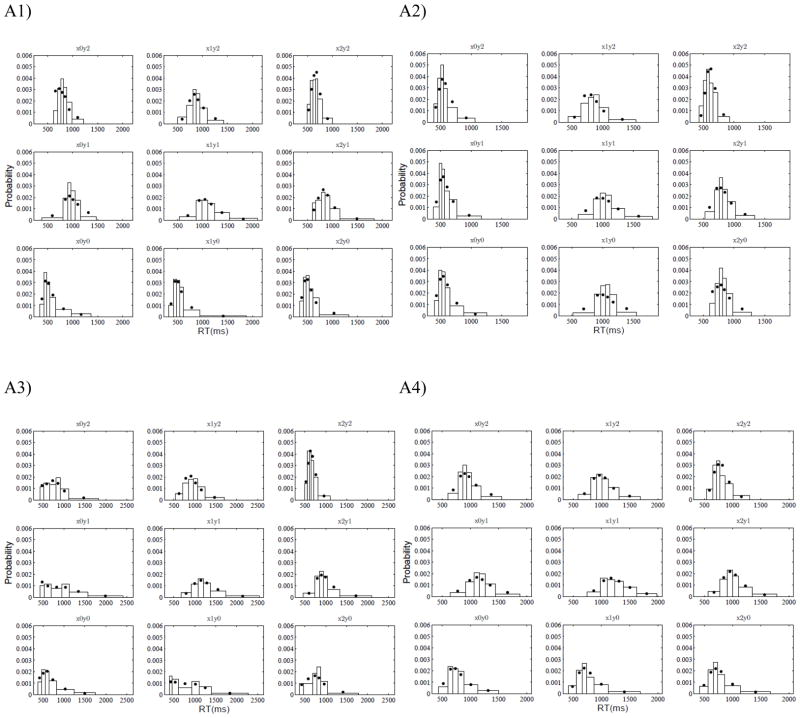
We turn now to the major goal of the studies, which is to test the alternative models on their ability to account in quantitative detail for the complete RT-distribution and choice-probability data associated with each of the individual stimuli. We fitted the models to the data by using two methods. The first was a minor variant of the method of quantile-based maximum-likelihood estimation (QMLE) (Heathcote, Brown, & Mewhort., 2002). Specifically, for each individual stimulus, the observed correct RTs were divided into the following quantile-based bins: the fastest 10% of correct RTs, the next four 20% intervals of correct RTs, and the slowest 10% of correct RTs. (The observed RT-distribution data, summarized in terms of the RT cutoffs that marked each RT quantile, are reported for each individual subject and stimulus in Appendix B.) Because error proportions were low, it was not feasible to fit error-RT distributions. However, the error data still provide a major source of constraints, because the models are required to simultaneously fit the relative frequency of errors for each individual stimulus (in addition to the distributions of correct RTs).

Table B1.

Correct RT quantiles and error probabilities for each individual stimulus and subject in Experiment 1.

Stimulus	RT Quantiles
	.1	.3	.5	.7	.9	N	p(e)
Sub 1
x2y2	419	466	494	535	600	358	.00
x2y1	459	525	578	628	711	357	.02
x1y2	446	505	547	603	711	355	.00
x1y1	505	583	632	691	768	358	.01
x2y0	391	421	452	488	575	357	.00
x1y0	395	428	460	503	582	353	.01
x0y2	489	535	565	603	689	355	.03
x0y1	460	506	544	590	651	353	.01
x0y0	383	413	442	467	516	357	.00
Sub 2
x2y2	482	545	595	656	744	354	.00
x2y1	523	598	672	749	864	356	.04
x1y2	533	621	682	750	834	355	.01
x1y1	577	659	728	810	940	358	.04
x2y0	332	401	455	527	634	353	.02
x1y0	338	396	465	527	632	352	.03
x0y2	514	581	626	673	767	354	.03
x0y1	468	557	644	721	889	357	.02
x0y0	333	388	436	500	581	356	.01
Sub 3
x2y2	486	529	574	629	738	356	.01
x2y1	527	584	640	711	858	356	.00
x1y2	515	575	639	711	866	352	.01
x1y1	550	616	681	758	906	354	.01
x2y0	563	634	692	748	888	356	.01
x1y0	553	624	689	780	938	359	.02
x0y2	422	478	541	595	720	351	.01
x0y1	429	487	533	588	686	352	.00
x0y0	427	481	514	556	658	355	.00
Sub 4
x2y2	502	544	577	630	694	356	.00
x2y1	505	566	613	659	731	355	.01
x1y2	521	560	606	663	737	354	.01
x1y1	533	593	641	694	799	354	.03
x2y0	528	569	611	650	745	354	.02
x1y0	540	596	642	701	801	355	.04
x0y2	355	390	417	446	503	352	.01
x0y1	357	389	414	446	490	352	.01
x0y0	361	395	421	449	513	355	.00
Sub 5
x2y2	456	505	536	573	642	356	.00
x2y1	486	552	606	668	766	357	.02
x1y2	495	544	585	633	727	355	.01
x1y1	535	611	666	747	863	359	.05
x2y0	518	570	618	666	768	356	.02
x1y0	494	537	592	669	778	360	.03
x0y2	387	432	467	509	600	358	.01
x0y1	390	426	467	505	602	356	.00
x0y0	379	420	457	490	556	359	.00

Note. N = total number of non-excluded trials for each stimulus. p(e) = probability of an error.

We conducted extensive computer searches (a modification of Hooke and Jeeves, 1961) for the free parameters in the models that maximized the multinomial log-likelihood function:

$$lnL=\sum _{i=1}^{n}ln\left(N_i!\right)-\sum _{i=1}^n\sum _{j=1}^{m+1}ln\left(f_{ij}!\right)+\sum _{i=1}^n\sum _{j=1}^{m+1}{f}_{ij}•ln\left(p_{ij}\right)$$ (2)

where N_i is the number of observations of stimulus i (i=1,n); f_ij is the frequency with which stimulus i had a correct RT in the j’th quantile (j=1,m) or was associated with an error response (j=m+1); and p_ij (which is a function of the model parameters) is the predicted probability that stimulus i had a correct RT in the j’th quantile or was associated with an error response.

Speckman and Rouder (2004) have criticized use of the QMLE method because it does not provide a true likelihood. In brief, they note that the multinomial likelihood (Equation 2) is based on category bins set a priori at fixed widths and having variable counts, whereas quantile-based bins have variable widths and fixed counts (for further details, see Speckman & Rouder, 2004; for a reply, see Heathcote & Brown, 2004). To address this concern, we also fitted all of the RT-distribution data by dividing the RTs into fixed-width bins (of 100 msec), ranging from zero to 3000, and again searched for the free parameters that maximized the Equation-2 likelihood function with respect to these fixed-width bins. The two methods provided identical qualitative patterns of results in terms of the assessed model fits for each subject’s data. Because the quantile-based method remains the more usual approach in the field, we report those results in the present article. The results from the alternative fixed-width bin approach are available from the authors on request.

To take into account the differing number of free parameters for some of the models, we used the Bayesian Information Criterion (BIC) (Wasserman, 2000). The BIC is given by

$$\text{BIC}=-2ln(\text{L})+\text{P}·ln(\text{M}),$$ (3)

where ln(L) is the (maximum) log-likelihood of the data; P is the total number of free parameters in the model; and M is the total number of observations in the data set. The model that yields the smallest BIC is the preferred model. In the BIC, the term P·ln(M) penalizes a model for its number of free parameters. Thus, if two models yield nearly equivalent log-likelihood fits to the data, then the simpler model with fewer free parameters is preferred.

Modern work in mathematical psychology makes clear that the overall flexibility of a model is not based only on its number of free parameters but on its functional form as well (e.g., Myung, Navarro, & Pitt, 2006). Therefore, use of the BIC is not a perfect solution for evaluating the quantitative fits of the competing models. Nevertheless, at the present stage of development, we view it as a reasonable starting tool. In addition, as will be seen, the BIC results tend to closely mirror the results from the converging sets of qualitative comparisons that distinguish among the predictions from the models. That is, the model that yields the best BIC fit tends to be the one that yielded the best qualitative predictions of the pattern of RT data.

We generated quantitative predictions of the RT-distribution and choice-probability data by means of computer simulation (the source codes for the simulations are available at http://www.cogs.indiana.edu/nosofsky/). We used 10,000 simulations of each individual stimulus to generate the predictions for that stimulus (so that 90,000 simulations were used to generate the predictions for the entire data set for each individual subject). Furthermore, we used 100 different random starting configurations of the parameter values for each individual model in our computer searches for the best-fitting parameters.

The BIC fits of the models are reported for each individual subject in Table 3A. As can be seen, the serial self-terminating model yields, by far, the best BIC fits for Subjects 2 and 4. This result is not surprising because all of the focused qualitative comparisons pointed in the direction of the serial self-terminating model for those two subjects. (Furthermore, taken collectively, the qualitative comparisons strongly violated the predictions from the competing models.) The serial self-terminating model also yields the best fits for Subjects 3 and 5, although the fit advantages are not as dramatic for those two subjects. Only for Subject 1 was the serial self-terminating model not the favored model. Here, the pattern of mean RTs for the contrast category pointed away from the serial model and was in greater overall accord with the parallel self-terminating model.

Table 3.

Table 3A. Experiment 1, BIC fits for all of the baseline models for each subject.
Sub	Serial Self-Terminating		Parallel Self-Terminating		Serial Exhaustive		Parallel Exhaustive
	−ln L	BIC	−ln L	BIC	−ln L	BIC	−ln L	BIC
1	295	671	267	607	440	953	571	1214
2	235	551	389	850	507	1087	690	1453
3	204	489	225	523	327	727	447	967
4	248	577	452	976	619	1310	1046	2165
5	215	511	251	575	437	946	668	1409
Mean	240	560	317	706	446	1005	685	1442

Sub	Coactive		EBRW		Free Stimulus Rate
	−ln L	BIC	−ln L	BIC	−ln L	BIC
1	338	749	342	749	271	655
2	440	952	423	910	364	840
3	259	591	289	643	216	544
4	481	1035	535	1134	345	802
5	315	702	333	731	248	608
Mean	367	806	384	833	289	690

Table 3B. Experiment 1, BIC fits for some elaborated rule-based models.
Sub	Serial, Attention-Switch		Serial, Free Dim. Rate		Coactive, Free Dim. Rate
	−ln L	BIC	−ln L	BIC	−ln L	BIC
1	254	605	270	637	290	669
2	201	499	232	561	389	867
3	195	486	184	464	237	562
4	169	435	211	520	368	826
5	208	512	202	502	267	623
Mean	205	507	220	537	310	709

Note. −ln L = negative ln-likelihood, BIC = Bayesian Information Criterion. Best BIC fits are indicated by boldface type.

Note. −ln L = negative ln-likelihood, BIC = Bayesian Information Criterion.

It should be noted that, for all subjects, the parallel-exhaustive, serial-exhaustive, coactive, and EBRW models yielded quite poor fits to the data. The parallel-exhaustive and serial-exhaustive models had great difficulty accounting for the pattern that, for the contrast category, both stimuli on the instructed “first-processed” dimension were classified more rapidly than those on the “second-processed” dimension (compare Figures 5 and 6). In addition, their prior predictions of slow RTs for the redundant stimulus were violated dramatically as well. The coactive rule model and the EBRW model yielded poor fits because: i) they predicted incorrectly that the target-category stimuli would show an over-additive pattern of mean RTs; and ii) they predicted incorrectly that the interior members of the contrast category would tend to be classified more rapidly than were the exterior members (compare Figures 5 and 6). Thus, in the present experiment, the logical-rule models fared much better than did two of the major previous models of classification RT, namely the EBRW model and the random-walk distance-from-boundary model (represented here in terms of the coactive model).

The best-fitting parameter estimates from the favored models are reported in Table 4. In general, these parameter values are highly interpretable. In all cases, for example, the decision boundaries (D_x and D_y) that implement the logical rules and that underlie the random-walk decision-making process (Figure 2, top panel) are located approximately midway between the means of the x0/x1 values and the y0/y1 values, as seems sensible. In addition, according to the parameter estimate p_x, Subjects 3–5 almost always processed the dimensions in the order x-then-y, as they were instructed to do. (According to the parameter estimate, Subject 3 very occasionally processed the dimensions in the order y-then-x, which explains the small predicted and observed redundancy gain for the redundant stimulus for that subject’s data.). By comparison, Subject 2 almost always processed the dimensions in the order y-then-x, as that subject was instructed to do. (The estimated p_x for Subject 1 was .144, which is also in accord with the instructions; however, the model fits suggest that Subject 1 may have engaged in parallel processing of the dimensions.)

Table 4.

Experiment 1, best-fitting parameters for only the best-fitting model for each subject.

Sub.	σx	σy	Dx	Dy	+A	−B	μR	σR	k	px
1	1.90	0.42	0.51	0.90	14	13	442.0	66.7	2.04	-----
2	0.56	0.54	0.44	0.49	3	2	336.7	96.2	47.43	0.002
3	0.24	0.39	0.74	0.57	2	3	306.4	94.0	75.12	0.891
4	0.20	0.38	0.72	0.46	2	2	272.8	66.4	79.64	1.000
5	0.46	0.71	0.57	0.52	3	3	356.5	64.7	30.96	0.976

Note. For Subjects 2–5, the best-fitting model is the serial self-terminating rule model. For Subject 1, the best-fitting model is the parallel self-termianating rule model.

The predicted mean RTs and error probabilities from the best-fitting models are reported along with the observed data in Table 1. Inspection of the table indicates that the models are doing a very good job of quantitatively fitting the observed mean RTs and error rates at the level of individual subjects and individual stimuli.

Interestingly, in the present experiment, the free stimulus-drift-rate model provided worse BIC fits than did the preferred logical-rule model for all five subjects (see Table 3A). A straightforward interpretation is that, under the present experimental conditions, the extra parameters provided to the free stimulus-drift-rate model are not needed, and the logical-rule models provide a parsimonious description of the observed performances. Even stronger, however, is the fact, for each of the five subjects, the preferred logical-rule model provided a better absolute log-likelihood fit than did the free stimulus-drift-rate model. That is, even without imposing the penalty term associated with the BIC, the best-fitting logical-rule model is preferred. Apparently, the logical-rule models are capturing aspects of the shapes of the RT distributions that the free stimulus-drift-rate model fails to capture. (To preview, the serial rule model will be seen to provide a better account of the relative skew of some of the distributions.) Before addressing this point in more detail, we first consider some elaborations of the rule-based models.

Elaborated Rule-Based Models and Shapes of RT Distributions

Although members from the class of logical-rule models are already providing far better accounts of the RT data than are important extant alternatives, there is still room for improvement. In this section we briefly consider some elaborations of the logical-rule models. One purpose is to achieve yet improved accounts of the data and to gain greater insight into why the models are providing relatively good fits. A second purpose is to gain more general evidence for the utility of the logical-rule models by relaxing some of the assumptions of the baseline models.

Attention-Switching

We begin by focusing on the serial-self-terminating model, i.e., the model that is intended to reflect the instructed strategy that was provided to the subjects. Recall that to foster conditions that would likely be conducive to serial rule-based processing, we used stimuli that varied along highly separable dimensions. Indeed, the stimuli were composed of spatially separated components. A likely mechanism that was left out of the modeling is that subjects would need to shift their attention from one spatial component to another in order to implement the rules. Furthermore, there is much evidence that shifting spatial attention takes time (e.g., Sperling & Weichselgartner, 1995). Even under conditions involving spatially overlapping dimensions, it may take time for shifts of dimensional attention to occur. Therefore, with the aim of providing a more complete description of performance, we elaborated the serial-self-terminating model by adding an attention-shifting stage.⁸ Specifically, we augmented the serial model by including a log-normally distributed attention-shift stage. Thus, the total classification RT would be the sum of decision-making times on each processed dimension, the residual base time, and the time to make the attention shift. Note that the attention-shift stage is not redundant with the residual base time. In particular, it occurs only for stimuli that require both dimensions to be processed (i.e, all members of the target category, and the members of the contrast category on the second-processed dimension). This elaboration of the serial model required the addition of two free parameters, the mean μ_AS and variance σ_AS² of the log-normal attention-shift distribution.

The fits of the serial self-terminating attention-shift model are reported in Table 3B. The table indicates that, even when penalizing the attention-shift model for its extra free parameters by using the BIC measure, it provides noticeably better fits than did the baseline serial model for three of the five subjects, and about equal fits for the other two (compare to results in Table 3A). These results confirm the potential importance of including assumptions about attention shifting in complete models of the time course of rule-based classification.⁹

The fits of the attention-switching, serial self-terminating rule model rule are illustrated graphically in Figure 7, which plots the predicted RT distributions for each individual subject and stimulus against the observed RT distributions. Although there are some occasional discrepancies, the overall quality of fit appears to be quite good. Thus, not only does the model account for the main qualitative patterns involving the mean RTs, it captures reasonably well the shapes of the detailed individual-stimulus RT distributions. None of the other models, including the free stimulus-drift-rate model, came close to matching this degree of fit across the five subjects.

Figure 7.

Experiment 1. Fit (solid dots) of the serial self-terminating model (with attention switching) to the detailed RT distribution data (open bars) of the individual subjects. Each cell of each panel shows the RT distribution associated with an individual stimulus. Within each panel, the spatial layout of the stimuli is the same as in Figure 1.

A remaining question is why is the serial rule model providing better fits to the RT classification data than is the free stimulus-drift-rate model? Recall that the free stimulus-drift-rate model can describe any pattern of mean RTs, so the answer has something to do with the models’ predictions of the detailed shapes of the RT distributions. To provide some potential insight, Figure 8 shows in finer detail the predicted and observed RT distributions for Subject 2, where the improvement yielded by the serial attention-shift model relative to the free stimulus-drift-rate model was quite noticeable.

Figure 8.

Detailed depiction of the predicted and observed individual-stimulus RT distributions for Subject 2 of Experiment 1. Each bar of each histogram represents the predicted or observed number of entries in a 100-msec interval. Top panel: predictions from free stimulus-drift-rate model, Middle panel: predictions from serial self-terminating model with attention-switching, Bottom panel: observed data. Within each panel, the spatial layout of the stimuli is the same as in Figure 1.

Consider first the free stimulus-drift-rate model’s predictions of the RT distributions for the interior and exterior members of the contrast category (Figure 8, top panel). Recall that, for Subject 2, Dimension Y was the first-processed dimension and Dimension X was the second-processed dimension. The predicted RT distributions for the contrast-category members on the second-processed dimension (x0y1 and x0y2) are of course pushed farther to the right than are those on the first-processed dimension (x1y0 and x2y0). Furthermore, as is commonly the case for single-decision-stage random-walk and diffusion models, the predicted RT distributions are all positively skewed (e.g., see Ratcliff & Smith, 2004). It is clear from inspection, however, that the predicted degree of skewing is greater for the slower (i.e. left-column) members of the contrast category. By contrast, while also predicting positively skewed distributions, the serial attention-shift model (Figure 8, middle panel) makes the opposite prediction with regard to the degree of skewing. For that model, it is the fast (bottom-row) members of the contrast category (x1y0 and x2y0) that are predicted to have the greater degree of positive skewing. The predicted RT distributions for the slow (left-column) members of the contrast category (x0y1 and x0y2) are more symmetric and bell-shaped.

The observed RT distribution data for Subject 2 are shown in the bottom panel of Figure 8. Inspection of the figure reveals greater positive skewing for the fast members of the contrast category than for the slow ones. This observation is confirmed by calculation of skew statistics for the RT distributions, which are summarized in Table 5. Indeed, as reported in Table 5, we observed this same overall pattern of predicted and observed results for all five of our subjects. That is, for each subject, the fast members of the contrast category showed, on average, greater skewing than did the slow members. Furthermore, for each subject, the serial self-terminating attention-shift model predicted correctly this direction of magnitude of skewing. By contrast, the free stimulus-drift-rate model predicted the opposite direction of magnitude of skewing for each subject.¹⁰

Table 5.

Summary Skew Statistics for Interior and Exterior Stimuli Along the First-Processed (Fast) and Second-Processed (Slow) Dimensions in Experiment 1.

Sub	Observed		Free Stimulus-Drift Rate		Serial with Attention Switch
	Slow	Fast	Slow	Fast	Slow	Fast
1	0.59	0.92	1.03	0.45	1.12	1.53
2	0.71	0.99	1.53	0.65	0.20	1.14
3	0.71	1.33	0.95	0.54	1.98	2.43
4	0.76	1.06	0.55	0.51	0.74	0.84
5	0.94	1.42	1.59	0.49	1.00	1.38

Why does the serial rule model often predict that it is the slower stimuli that are more symmetric and bell-shaped? The reason probably stems, at least in part, from the fact that it is summing RT distributions from separate stages to generate its predictions of the overall classification RT distribution. Although the predicted outcome of the summing process will depend on the detailed properties of the individual-stage distributions, the intuitive reasoning here follows the central limit theorem. That theorem roughly states that the sum of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. For the serial attention-shift rule model, the predicted RT distribution for the slow stimuli is a sum of four component RT distributions: the residual base time, the attention-shift time, and two decision-stage times. By comparison, it is a sum of only two component RT distributions for the fast stimuli. Thus, the serial rule model allows that the RT distributions for the slow stimuli may turn out to be more bell-shaped.¹¹

Relaxing the Signal-Detection Assumptions

Our fits of the logical rule models have used a signal-detection approach to predicting the random-walk drift rates associated with each of the dimension values. On the one hand, in our view, using some approach to constraining the drift rates seems reasonable: If a random-walk model is to provide a convincing account of the data, then the drift rates should be meaningfully related to the structure of the stimulus set. On the other hand, there are other approaches to predicting the drift rates, and it is reasonable to ask whether our conclusions may rest too heavily on the particular signal-detection approach that we used.

For example, one of the main results of our model fitting was that the serial self-terminating rule model yielded dramatically better fits to the data than did the random-walk distance-from-boundary model (i.e, the coactive model). This result provided evidence of the utility of extending decision-boundary accounts of classification RT with more detailed assumptions about mental architectures. However, perhaps the coactive model fitted poorly because our signal-detection approach to predicting the drift rates was badly flawed. To address this concern, in this section we report fits of generalizations of the serial-rule and coactive models that relax the signal-detection assumptions. In particular, we now allow the drift rates associated with each individual dimension value to be free parameters. That is, for each model, there are three freely varying drift-rate parameters associated with the values on Dimension X, and three freely varying drift-rate parameters associated with the values on Dimension Y. In all other respects, the serial-rule and coactive models are the same as before.¹² Note that this generalization adds a total of two free parameters to each logical-rule model. Whereas the rule models with the signal-detection assumptions used two free parameters to predict the dimensional drift rates on each dimension (D_x and σ_x on Dimension X, and D_y and σ_y on Dimension Y), the generalizations estimate three free drift-rate parameters per dimension.

The fits of these generalized versions of the serial self-terminating and coactive models are reported in Table 3B. The results are clear-cut. Even allowing a completely free drift rate for each individual dimension value, the coactive model continues to provide dramatically worse fits than does the serial self-terminating rule model. Also, although the fits of the generalized serial model are better than those of the baseline serial model (compare results across Tables 3A and 3B), these improvements tend to be relatively small, suggesting that the signal-detection approach to constraining the drift rates provides a reasonable approximation.

Experiment 2

The purpose of Experiment 2 was to extend the tests of the logical-rule models of classification RT while simultaneously meeting various new theoretical and empirical goals. As described in greater detail below, a first goal was to obtain more general evidence of the potential applicability of the models by testing “whole object” stimuli composed of an integrated set of parts instead of the “separate object” stimuli from Experiment 1. A second goal was to fine-tune the category structure to yield even stronger and more clear-cut contrasts among the competing models than we achieved in the previous experiment. A third goal was to test for the operation of the logical-rule models under conditions in which subjects were not provided with explicit instructions for use of a particular processing strategy. And a fourth goal was to test the logical-rule models with regard to some intriguing predictions that they make involving predicted patterns of error RTs compared to correct RTs.

In the present experiment, we used the same logical category structure as in Experiment 1. However, now the stimuli were a set of schematic drawing of lamps, as depicted in Figure 9. The stimuli varied along four trinary-valued dimensions: width of base, degree of curvature (or tallness) of the top finial, shape of the body of the lamp, and shape of the shade of the lamp. Only the first two dimensions (width of base and curvature of finial) were relevant to the logical category structure. We varied the other dimension values (shape of body and shade) only to increase the overall category size and to possibly discourage exemplar-memorization processes in classification. Importantly, as in Experiment 1, the relevant dimension values that compose the stimuli continue to be located in spatially non-overlapping regions, which we believe should foster observers’ use of a serial, logical-rule strategy. In the present case, however, we achieve more generality than in Experiment 1, because the separate dimension values compose familiar, whole objects. Indeed, these types of lamp stimuli (as well as other object-like stimuli composed of spatially separated parts) have been used extensively in past research in the classification-RT and object-recognition literatures.

Figure 9.

Illustration of the “lamp” stimuli used in Experiment 2.

Second, although the basic category structure is the same as in Experiment 1, note that we greatly reduced the overall discriminability between the dimension values that define the contrast-category and those that define the low-salience values of the target category (see Figure 9). The schematic structure of this modified design is shown in Figure 10. The logical rules that define the categories are the same as before. However, because of the modified spacings between the dimension values, the difference between the processing rates associated with the “low-salience” and “high-salience” values should be magnified relative to Experiment 1. The upshot is that the design should provide much stronger quantitative differences in the classification RTs of various critical stimuli to allow stronger contrasts among the models. For example, one of the critical qualitative contrasts that separates the serial self-terminating, coactive, and parallel self-terminating rule models is the pattern of mean RTs for the interior and exterior stimuli on the “second-processed” dimension (see Figure 5): The serial model predicts faster RTs for the external stimulus, the coactive model predicts faster RTs for the interior stimulus, and the parallel model predicts equal RTs. These predictions depend, however, on the processing rate for the low-salience dimension values being slower than the processing rate for the high-salience dimension values. By magnifying these processing rate differences, the present modified design should thereby yield stronger contrasts among the models.

Figure 10.

Schematic illustration of the category structure and spacings between dimension values for the stimuli used in Experiment 2.

Third, we varied the instructions provided to different subjects. The first two subjects received instructions that were analogous to those from Experiment 1, with one instructed to process the dimensions in the order y-then-x and the other in the order x-then-y. The second two subjects were also provided with knowledge about the logical rules that defined the categories prior to engaging in the classification task. However, they were not provided with any instructions for use of a particular processing strategy as a basis for classification. Instead, they were free to use whatever classification strategy they chose, including not using a logical rule-based strategy at all.

Because the critical RT contrasts that distinguish among the models assume accurate responding, the instructions for these first four subjects continued to emphasize that responding be extremely accurate. Therefore, we will refer to these four subjects as the “accuracy” subjects. To investigate some further theoretical predictions from the logical-rule models, we also tested two subjects under speed-stress conditions. These subjects were instructed to respond as rapidly as possible, while keeping their error rates to acceptable levels (see Method section for details). The goal here was to generate error-RT data that would be suitable for model fitting. These “speed” subjects were provided with explicit instructions to use a fixed-order serial self-terminating strategy, as was the case for the subjects in Experiment 1. As will be seen, although some of the previous qualitative contrasts among the models no longer hold under conditions with high error rates, the serial-rule model makes a new set of intriguing predictions regarding the relationship between correct and error RTs. Moreover, these predictions vary in an intricate way across the individual stimuli that compose the categories. Beyond testing these new predictions, the aim was also to test whether the serial logical-rule model could simultaneously fit complete distributions of correct and error RTs.

Method

Subjects

The subjects were 6 undergraduate and graduate students associated with Indiana University. All subjects were under 40 years of age and had normal or corrected-to-normal vision. The subjects were paid $8 per session plus a $3 bonus per session depending on performance.

Stimuli

The stimuli were drawing of lamps composed of four parts (see Figure 9): a finial (or top piece) that varied in amount of curvature (or tallness or area); a lamp shade that varied in the angle at which the sides connected the bottom of the shade to the top of the shade; the design or body of the lamp, which varied in three qualitatively different forms; and the base of the lamp, which varied in width. The shade and body of the lamp were irrelevant dimensions and varied in nondiagnostic fashion from trial to trial. The shade and the body together were 385 pixels tall and 244 pixels at the widest point (the bottom of the shade piece).

The two relevant dimensions were the finial and the base. The combination of values on these dimensions formed the category space, as shown in Figures 9 and 10. The finial curvature was created by drawing an arc inside of a 60 pixel-wide rectangle that had a variable height: 15, 17, or 24 pixels. The base was a rectangle with a 20-pixel height and variable width: 95, 105, and 160 pixels. The stimuli were assigned to Categories A and B as illustrated in Figure 9 (with the shade and body dimensions varying randomly across trials and being irrelevant to the definition of the categories).

Procedure

In each session, participants completed 27 practice trials (3 repetitions of the 9 main stimulus types) followed by 6 blocks of 135 experimental trials (810 trials in total). Because the stimuli were composed of four trinary-valued dimensions, there was a total of 81 unique stimulus tokens. Each of the 81 tokens was presented 10 times in each session. Within each block of 135 trials, each of the 9 critical stimulus types was presented 15 times. For each individual subject and session, the ordering of presentation of the stimuli was randomized within these constraints. There were 5 sessions in total, with the first session considered practice.

Subjects initiated each trial by pressing a mouse key. A fixation cross then appeared for 1770 ms. After 1070 ms from the initial appearance of the fixation cross, a warning tone was sounded for 700 ms. Following the warning tone, a stimulus was presented and remained onscreen until the participant made a response. If the response was incorrect or the response took longer than 5 s, feedback (‘WRONG’ or ‘TOO SLOW’) was presented for 2 s. Participants were then shown instructions to press a mouse key to advance to the next trial.

Using the same procedure as in Experiment 1, all subjects were provided with explicit knowledge about the logical rules that defined the category structure prior to engaging in the classification task.

There were four “accuracy” subjects, who we will denote as Subjects A1-A4. The accuracy subjects were instructed to classify the stimuli without making any errors. They understood, however, that their RTs were being measured, so they needed to make their responses immediately once they had made a classification decision. The first two accuracy subjects (A1 and A2) were given explicit instructions for using a fixed-order, serial self-terminating strategy to apply the classification rules. These instructions were directly analogous to the ones we already presented in the Method section of Experiment 1. Subject A1 was provided with instructions to process the dimensions in the order y-then-x (base followed by finial), whereas Subject A2 processed the dimensions in the reverse order.

Although the second two accuracy subjects (A3 and A4) were provided with knowledge of the logical category structure prior to engaging in the classification task, they were not provided with any instructions for use of a particular processing strategy. They were instructed to formulate some single strategy for categorizing the items during the first session. Then, in Sessions 2–5, they were instructed to maintain that strategy (whatever that may be) on all trials.

There were two “speeded” subjects (S1 and S2). The speeded subjects were given explicit instructions to use a fixed-order serial self-terminating processing strategy for applying the rules (as in Experiment 1), with S1 processing the dimensions in the order y-then-x and S2 processing the dimensions in the order x-then-y. In the first session, to ensure that the speeded subjects understood the rules and the intended strategy, they were instructed to categorize the stimuli without making any errors. (Subject S1 received two sessions of this preliminary accuracy training, as this subject had some difficulty during the first session in discriminating the stimulus dimensions.) Then, in Sessions 2 to 5, the speed subjects were instructed to respond as fast as possible, while trying to keep their error rate at about 15 total errors per block.

Results and Theoretical Analysis, Accuracy Subjects

In this section we report and analyze the results from the four accuracy subjects. As was the case in Experiment 1, the practice session (Session 1) was not included in the analyses. RTs associated with error responses were not analyzed. In addition, conditionalized on each individual subject and stimulus, we removed from the analysis correct RTs greater than 3 standard deviations above the mean and also RTs of less than 150 msec. This latter procedure led to dropping less than 2% of the trials from analysis. Due to computer/experimenter error, the data from 81 trials from the first block of Session 2 of Subject A2 are missing.

Mean RTs

The mean correct RTs and error rates for each individual stimulus for each subject are reported in Table 6. (The detailed RT distribution data for each individual subject and stimulus are reported in Appendix B.) As intended by the nature of the design, error rates are very low. The mean RTs for the individual subjects and stimuli are displayed graphically in the panels in Figure 11. The left panels show the results for the target-category stimuli and the right panels show the results for the contrast-category stimuli. The format for displaying the results is the same as used in Experiment 1. Comparing the observed data to the canonical-prediction graphs in Figure 5, the results are clear-cut: For each subject, the results point strongly toward a form of the serial self-terminating rule model. First, as can be seen in the left panels of Figure 11, the mean RTs for the target category members are very close to additive (MIC=0). Second, as can be seen in the right panels, for those contrast-category stimuli that satisfy the disjunctive rule on the second-processed dimension, RTs for the exterior stimulus are markedly faster than for the interior stimulus. In addition, for Subjects A1, A2, and A4, there is little difference among the RTs for the redundant stimulus and the interior and exterior stimuli on the first-processed dimension. The overall combined pattern of results for these subjects is indicative of a fixed-order, serial self-terminating, rule-based processing strategy. This strategy was the instructed one for Subjects A1 and A2, and was apparently the strategy of choice for un-instructed Subject A4. Interestingly, for Subject A3, the mean RTs on the faster-processed dimension also show the pattern in which in the exterior stimulus is classified markedly faster than is the interior stimulus. Furthermore, for this subject, the redundant stimulus has the fastest mean RT among all of the contrast-category members. This combined pattern of results is indicative of a mixed-order, serial self-terminating, rule-based processing strategy. Apparently, Subject A3 chose to vary the order of processing the dimensions in applying the logical rules.

Table 6.

Experiment 2, Accuracy Subjects: Mean Correct RTs and error rates for individual stimuli, observed and best-fitting baseline model predicted.

Subject A1
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	668	895	882	1160	566	625	825	974	607
RT Serial Self-Terminating	677	917	882	1129	617	618	783	1005	618
p(e) Observed	.01	.04	.02	.12	.04	.04	.02	.01	.00
p(e) Serial Self-Terminating	.00	.04	.03	.08	.01	.00	.01	.01	.00
Subject A2
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	611	834	866	1077	828	1045	583	606	631
RT Serial Self-Terminating	622	819	879	1079	811	1048	590	604	604
p(e) Observed	.00	.01	.05	.02	.02	.01	.01	.01	.00
p(e) Serial Self-Terminating	.00	.00	.01	.02	.00	.00	.00	.00	.00
Subject A3
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	676	997	973	1275	793	922	816	978	755
RT Serial Self-Terminating	692	991	973	1269	822	951	833	979	771
p(e) Observed	.01	.04	.03	.07	.03	.04	.01	.03	.00
p(e) Serial Self-Terminating	.00	.05	.04	.08	.02	.02	.02	.02	.00
Subject A4
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
RT Observed	808	1031	1041	1270	799	797	958	1169	822
RT Serial Self-Terminating	815	1029	1035	1247	820	819	970	1184	822
p(e) Observed	.00	.01	.01	.05	.03	.01	.02	.03	.00
p(e) Serial Self-Terminating	.00	.02	.02	.04	.01	.01	.01	.01	.00

Note. RT = mean correct response time, p(e) = probability of error.

Figure 11.

Observed mean RTs for the individual subjects and stimuli in Experiment 2. Error bars represent one standard error. Left panels show the results for the target-category stimuli and right panels show the results for the contrast-category stimuli. Left panels: L = low-salience dimension value, H = high-salience dimension value, D1 = Dimension 1, D2 = Dimension 2. Right panels: R = redundant stimulus, I = interior stimulus, E = exterior stimulus.

We conducted the same statistical tests as described previously in Experiment 1 to corroborate the descriptions of the data provided above. The results of the tests are reported in Table 7. The most important results are that: i) the interaction between level of finial and level of base did not approach statistical significance for Subjects A2, A3, or A4, and was only marginally significant for Subject A1, supporting our summary description of an additive pattern of mean RTs for the target-category members; and ii) for all subjects, mean RTs for the external stimulus on the second-processed dimension were significantly faster than for the internal stimulus on that dimension. Some of the other results are more idiosyncratic and difficult to summarize: they basically bear on whether the pattern of data is more consistent with a pure, fixed-order serial strategy or a mixed-order serial strategy for each individual subject. Whereas the qualitative patterns of results are generally consistent with the predictions from either a fixed-order or mixed-order serial self-terminating rule strategy, they strongly contradict the predictions from all of the competing rule models as well as the exemplar model.

Table 7.

Experiment 2, Accuracy Subjects, statistical-test results table.

Target-Category Factor			Contrast-Category Comparisons
Subject A1	df	F	Subject A1	M	t
Session	3	33.76**	E1 - I1	−55.72	−3.31**
Base × Finial	1	4.00*	E2 - I2	−145.97	−14.13**
Session × Base × Finial	3	1.65	E1 – R	−49.26	−3.37**
Error	1288		I1 – R	6.46	.33
Subject A2	df	F	Subject A2	M	t
Session	3	65.54**	E1 - I1	−22.15	−2.20*
Base × Finial	1	.91	E2 - I2	−217.57	−21.89**
Session × Base × Finial	3	1.76	E1 – R	−47.44	−4.00**
Error	1375		I1 – R	−25.29	−2.10*
Subject A3	df	F	Subject A3	M	t
Session	3	39.30**	E1 - I1	−129.52	5.08**
Base × Finial	1	.39	E2 - I2	−162.19	−6.45**
Session × Base × Finial	3	.78	E1 – R	38.00	1.75±
Error	1346		I1 – R	167.52	6.18**
			E2 – R	61.18	2.84**
			I2 – R	223.37	8.29**
Subject A4	df	F	Subject A4	M	t
Session	3	77.14**	E1 - I1	2.32	0.13
Base × Finial	1	.06	E2 - I2	−211.83	−14.7**
Session × Base × Finial	3	2.24±	E1 - R	−22.17	−1.32
Error	1373		I1 - R	−24.49	−1.48

Note: E1 = Exterior stimulus on first-processed dimension, I1 = Interior stimulus on first-processed dimension, E2 = Exterior stimulus on second-processed dimension, I2 = Interior stimulus on second-processed dimension, R = redundant stimulus, M =Mean RT difference (ms).

^**p<.01,

^*p<.05,

^±p<.075.

For the contrast-category t-tests, the df vary between 650 and 705, so the critical values of t are essentially z.

Quantitative Model Fitting

We fitted the models to the complete distributions of correct RT data and to the error proportions by using the same methods as described in Experiment 1.¹³ The model fits are reported in Table 8A. The results are clear-cut: The serial self-terminating rule model provides, by far, the best BIC fit to each of the individual subjects’ data. Furthermore, the advantages in fit for the serial self-terminating model are far more pronounced than was the case in Experiment 1, a result that attests to the more diagnostic nature of the modified category structure used in the present experiment. Although we are fitting complete RT distributions, we summarize the predictions from the best-fitting serial self-terminating model in terms of the predicted mean RTs and error rates for each stimulus, which are reported along with the observed data in Table 6. Inspection of the table indicates that the model is providing extremely accurate predictions of each individual subject’s data at the level of the mean RTs. The best-fitting parameters, reported in Table 9, are easily interpretable. For example, the table indicates that Subjects A1, A2, and A4 processed the dimensions in a nearly fixed order across trials (p_x near 0 or 1), whereas Subject A3 used a mixed-order strategy (p_x = .448).

Table 8.

Table 8A. Experiment 2, Accuracy Subjects: BIC fits for the baseline models.
Sub	Serial Self-Terminating		Parallel Self-Terminating		Serial Exhaustive		Parallel Exhaustive
	−ln L	BIC	−ln L	BIC	−ln L	BIC	−ln L	BIC
A1	465	1009	791	1655	822	1716	1114	2299
A2	358	796	560	1193	625	1323	859	1791
A3	257	594	386	844	418	908	542	1157
A4	250	581	439	951	476	1024	618	1308
Mean	333	745	544	1161	585	1243	783	1639

Sub	Coactive		EBRW		Free Stimulus Rate
	−ln L	BIC	−ln L	BIC	−ln L	BIC
1	877	1827	1006	2007	706	1523
2	820	1712	964	1992	422	958
3	570	1213	644	1353	344	801
4	553	1179	635	1335	379	871
Mean	705	1483	812	1672	463	1038

Table 8B. Experiment 2, Accuracy Subjects: BIC fits for some elaborated rule-based models.
Sub	Serial, Attention-Switch		Serial, Free Dim. Rate		Coactive, Free Dim. Rate
	−ln L	BIC	−ln L	BIC	−ln L	BIC
A1	271	639	367	829	831	1750
A2	303	704	348	787	670	1429
A3	221	539	254	606	549	1187
A4	207	511	240	576	537	1162
Mean	251	598	302	700	647	1382

Note. Sub = Subject, −ln L = negative ln-lilkelihood, BIC = Bayesian Information Criterion. Best BIC fit is indicated by boldface type.

Note. −ln L = negative ln-likelihood, BIC = Bayesian Information Criterion.

Table 9.

Experiment 2, Best-Fitting Parameters for the Serial Self-Terminating Model.

Sub.	σx	σy	Dx	Dy	+A	−B	μR	σ R	k	px
A1	1.890	0.988	15.970	10.027	6	4	364.5	88.4	25.955	0.000
A2	1.992	2.845	16.672	9.900	24	16	542.1	105.0	1.650	0.913
A3	3.325	1.723	15.650	9.824	12	5	415.9	109.6	11.440	0.448
A4	2.603	1.234	15.782	9.922	9	5	563.2	126.6	14.049	0.000
S1	2.292	0.652	16.358	10.519	1	4	278.9	53.2	29.742	0.000
S2	2.397	1.628	16.279	9.832	3	3	364.1	64.6	27.229	1.000

Note.

For S1, p_B = .023, μ_AS = 232.0, σ _AS = 62.1, −ln L = 455, BIC = 1015.

For S2, p_B = .160, μ_AS = 79.0, σ _AS = 125.9, −ln L = 396, BIC = 897.

We also fitted the elaborated versions of the serial self-terminating and coactive models that we described in Experiment 1. The fits of these elaborated models are reported in Table 8B. As was the case in Experiment 1, elaborating the serial self-terminating model with a dimensional attention-switching stage yields even better accounts of the data than does the baseline model, as measured by the BIC statistic. And, once again, relaxing the signal-detection constraints from the serial and coactive models (by allowing freely estimated dimension-rate parameters) does nothing to change the pattern of results: Regardless of whether one adopts the signal-detection constraints or estimates freely varying dimension-rate parameters, the serial self-terminating model yields dramatically better fits to the data compared to the coactive model.

Finally, as was the case in Experiment 1, not only does the serial self-terminating model yield better fits than do any of the alternative rule models or the exemplar model, it continues to yield better absolute log-likelihood fits than does the free stimulus-drift-rate model, which can describe any pattern of results involving the mean RTs. Thus, the serial self-terminating rule model again appears to be capturing important aspects of the detailed RT distribution data that the free stimulus-drift rate model fails to capture. This latter result attests to the importance of combining mental-architecture assumptions with the random-walk modeling in the present design.

The predicted RT distributions from the serial self-terminating model (with attention-switching) are shown along with the observed RT distributions for each of the individual subjects and stimuli in Figure 12. Although there are a couple of noticeable deviations (e.g., the first quantile for Stimulus x0y2 of Subject A1, and the first quantile for Stimulus x2y0 of Subject A2), overall the model is doing a very good job of capturing the detailed shapes of the individual-stimulus RT-distribution data. None of the alternative models came close to matching this degree of predictive accuracy.

Figure 12.

Experiment 2, Accuracy Subjects. Fit (solid dots) of the serial self-terminating model (with attention switching) to the detailed RT distribution data (open bars) of the individual accuracy subjects (A1–A4). Each cell of each panel shows the RT distribution associated with an individual stimulus. The spatial layout of the stimuli is the same as in Figure 1.

Results and Theoretical Analysis, Speed Subjects

In general, in the information-processing literature, the modeling of error RTs poses a major challenge to formal theories, and a key issue is whether models can account for relationships between correct RTs and error RTs. There are two main mechanisms incorporated in standard single-decision-stage random-walk and diffusion models that allow for rigorous quantitative accounts of such data (e.g., see Ratcliff, Van Zandt, & McKoon, 1999). First, when there is variability in random-walk criterion settings across trials, the models tend to predict fast error responses and slow correct responses. Second, when there is variability in drift rates across trials, the models tend to predict the opposite.

The present logical-rule models of classification RT inherit the potential use of these mechanisms involving criterial and drift-rate variability. In this section, however, we focus on a more novel aspect of the models’ machinery. In particular, because they combine mental-architecture assumptions with the random-walk modeling, even the baseline versions of the present logical-rule models (i.e., without drift-rate and criterial variability) predict intriguing and intricate relations between correct and error RTs that vary across individual stimuli within the category structures.

We bring out these predictions with respect to the serial self-terminating model, which corresponds to the instructed strategy for our two speed-stress subjects. The overall category structure is illustrated again in Figure 13, but now with respect to explaining predicted patterns of correct and error RTs. The top panel illustrates the main pattern of a priori predictions for correct and error RTs for the case in which the subject processes the dimensions in the order y-then-x (as Subject S1 was instructed to do). Suppose that one of the bottom-row members of the contrast-category (x1y0 or x2y0) is presented. If the subject decides correctly that the stimulus falls below the decision-bound on Dimension Y (D_Y), then he or she will make a correct classification response in this first decision-making stage, because the disjunctive rule will have been immediately satisfied. By contrast, if the first stage of decision making leads to an incorrect judgment (i.e., that the stimulus lies above D_Y), then no rule will have yet been satisfied, so the subject will need to evaluate the stimulus on Dimension X. The most likely scenario is that, in this next stage, the subject judges correctly that the stimulus falls to the right of Decision-Bound X (D_X). Combining the initial incorrect decision with the subsequent correct one, the outcome is that the subject will incorrectly classify the stimulus into the target category, a sequence that will have encompassed two stages of decision making. The upshot is that the model predicts that, for these bottom-row contrast-category members, error RTs should be substantially slower than correct RTs.

Figure 13.

Schematic illustration of the main predicted pattern of mean error RTs from the serial self-terminating rule model for the speeded subjects tested in Experiment 2. Stimuli enclosed by rectangles denote cases in which the mean error RT is predicted to be much slower than is the mean correct RT. Stimuli enclosed by circles denote cases in which the mean error RT is predicted to be much faster than is the mean correct RT.

Whereas the serial self-terminating rule model predicts slow error RTs for the bottom-row contrast-category members, it predicts fast error RTs for the members of the target category that border them (i.e., x1y1 and x2y1). If presented with either one of these stimuli, and the subject judges incorrectly that they fall below D_Y, then the subject will immediately and incorrectly classify them into the contrast category (thinking that the disjunctive rule has been satisfied). Error responses resulting from this process undergo only a single stage of decision making. By contrast, to correctly classify x1y1 and x2y1 into the target category, the subject needs to undergo both decision-making stages (to verify that the conjunctive rule is satisfied). In sum, assuming the processing order y-then-x, the serial self-terminating model predicts that, for stimuli x1y1 and x2y1, error RTs will be substantially faster than correct RTs.

Although the model predicts differences between correct and error RTs for the remaining stimuli in the category structure as well, they tend to be far smaller in magnitude than the fundamental predictions summarized above. The reason is that the kinds of error responses that result in changed sequences of decision making are either much rarer for the remaining stimuli in the set, or else would not change the number of decision-making stages that are required to make a response. The major summary predictions are illustrated schematically in the top panel of Figure 13, where a solid square denotes a very slow error response and a solid circle denotes a very fast error response. Analogous predictions are depicted in the bottom panel of Figure 13, which assumes the processing order x-then-y instead of the processing order y-then-x.

Before turning to the data, we introduce an extension to the logical-rule models, required to handle a final aspect of the correct and error RTs. To preview, an unanticipated result was that, for the external stimulus on the second-processed dimension (e.g., x0y2 in the top panel of Figure 13), error RTs were much faster than correct RTs. As an explanation for the finding (which concurs with our own subjective experience in piloting the task), we hypothesize that, especially under speed-stress conditions, subjects occasionally bypass the needed second stage of decision making. For example, when stimulus x0y2 is presented, there is a strong decision that the value y2 does not fall below the decision-bound D_Y. This strong initial “no” decision (with respect to the disjunctive rule that defines the contrast category) then leads the observer to immediately classify the stimulus into the target category, without checking its value on Dimension X to determine if the conjunctive rule has been satisfied. Thus, we add a single free parameter to the serial self-terminating rule model, p_B, representing the probability that this bypass process takes place. Note that the same bypass process applies to all stimuli that have this extreme value on the first-processed dimension (e.g., x0y2, x1y2, and x2y2 in the top panel of Figure 13). In the case just described, it leads to fast errors; whereas in the other cases, by chance, it works to increase slightly the average speed of correct responses. The fast-error prediction made by the bypass process is illustrated schematically in terms of the dashed circles in the panels of Figure 13.

Mean RTs and Error Rates

The mean correct RTs, error RTs, and error rates for each of the stimuli for each speed subject are reported in Table 10. (The detailed RT distribution quantiles are reported in Appendix B.) As predicted by the serial self-terminating model (see Figure 13, top panel), for Subject S1, the bottom-row members of the contrast category (x1y0 and x2y0) have much slower error RTs than correct RTs (average t(352)=−10.97, p<.001); the bordering members of the target category (x1y1 and x2y1) have much faster error RTs than correct RTs (average t(356)=10.77, p<.001); and for external stimulus x0y2, the error RT is significantly faster than is the correct RT (t(354)=11.58, p<.001). An analogous pattern of results is observed for Subject S2, who processed the dimensions in the order x-then-y (for predictions, see Figure 13, bottom panel): The left-column members of the contrast category (x0y1 and x0y2) have much slower error RTs than correct RTs (average t(350)=−15.14, p<.001); the bordering members of the target category (x1y1 and x1y2) have much faster error RTs than correct RTs (average t(352)=8.54, p<.001); and the external stimulus x2y0 has a much faster error RT than a correct RT (t(353)=12.16, p<.001). For the remaining stimuli, the differences between the mean correct and error RTs were either much smaller in magnitude, or were based on extremely small sample sizes. Finally, we should note that the overall patterns of correct RTs are similar in most respects to those of the accuracy subjects reported in the previous section; one difference, however, is that, for both speed subjects, the external stimulus on the second-processed dimension does not have a faster mean correct RT than does the internal stimulus. As will be seen, this result too is captured fairly well by the serial rule model when applied under speed-stress conditions.¹⁴

Table 10.

Experiment 2, Speed Subjects: Mean Correct RTs, Error RTs, and error rates for the individual stimuli, observed and predicted.

Subject S1
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
Mean Correct RT Observed	540	610	646	675	431	435	724	679	431
Mean Correct RT Predicted	564	627	613	681	429	433	710	690	431
Mean Error RT Observed	573	434	704	507	668	782	582	622	512
Mean Error RT Predicted	----	538	736	587	573	633	590	659	612
p(e) Observed	.003	.168	.092	.270	.025	.039	.256	.388	.011
p(e) Predicted	.000	.218	.062	.274	.064	.054	.398	.292	.026
Subject S2
	x2y2	x2y1	x1y2	x1y1	x2y0	x1y0	x0y2	x0y1	x0y0
Mean Correct RT Observed	550	720	709	854	798	778	520	542	562
Mean Correct RT Predicted	579	669	736	848	748	807	536	539	553
Mean Error RT Observed	526	673	543	609	577	793	822	1190	675
Mean Error RT Predicted	----	725	581	668	625	883	701	803	856
p(e) Observed	.008	.081	.246	.268	.352	.288	.077	.068	.008
p(e) Predicted	.000	.101	.192	.287	.389	.225	.073	.062	.023

Quantitative Model Fitting

We fitted the serial self-terminating rule model to the complete distributions of correct and error responses of each subject. (The model fits reported here made allowance for the attention-shift stage.) The criterion of fit was essentially the same as described in the previous sections (see Equations 2 and 3), except now the Equation-2 expression is expanded to include the complete distribution of error responses into individual RT quantiles. Because there are 9 stimuli, each with 6 correct RT quantiles and 6 error RT quantiles, and because the probabilities across all 12 quantiles for a given stimulus must sum to 1, the model is being used to predict 99 degrees of freedom in the data for each subject.

The predicted mean correct and error RTs for each stimulus, as well as the predicted error rates, are shown along with the observed data in Table 10. Inspection of the table indicates that the model predicts extremely accurately the mean correct RTs for each individual subject and stimulus, and does a reasonably good job of predicting the error rates. (One limitation is that it over-predicts the error rate for Stimulus x0y2 of Subject S1.) The model also does a reasonably good job of predicting mean error RTs associated with individual stimuli that have large error rates (i.e., adequate sample sizes). Of course, for stimuli with low error rates and small sample sizes, the results are more variable. In all cases, the model predicts accurately the main qualitative patterns of results involving the relations between correct and error RTs that were depicted in Figure 13. The best-fitting parameters and summary-fit measures are reported in Table 9.

The complete set of predicted correct and error RT distributions are shown along with the observed distributions in Figure 14. With respect to Subject S1, a noticeable limitation is the one we described previously, namely that the model overpredicts the overall error rate for Stimulus x0y2. For Subject S2, a limitation is that the model overpredicts the proportion of entries in the fastest quantiles for Stimulus x2y0. Natural directions for extensions of the model are to make allowance for drift-rate variability and criterion-setting variability across trials. In our view, however, the baseline model is already providing a very good first-order account of the individual subject/individual-stimulus correct and error RT-distribution data. An interesting question for future research is whether some extended version of a free stimulus-drift-rate model that makes allowance for criterial and drift-rate variability could fit these data. Regardless, such a model does not predict a priori the intricate pattern of correct and error RTs successfully predicted by the serial logical-rule model in the present study.

Figure 14.

Experiment 2, Speed Subjects. Fit (solid dots) of the serial self-terminating model (with attention switching) to the detailed RT distribution data (open bars) of the individual speed subjects (S1 and S2). Each cell of each panel shows the RT distributions associated with an individual stimulus. The top distribution in each cell corresponds to correct RTs and the bottom distribution in each cell corresponds to error RTs. The spatial layout of the stimuli is the same as in Figure 1.

General Discussion

Summary of Contributions

To summarize, the goal of this work was to begin the development of logical rule-based models of classification RT and to conduct initial tests of these models under simplified experimental conditions. The idea that rule-based strategies may underlie various forms of classification is a highly significant one in the field. In our view, however, extant models have not addressed in rigorous fashion the cognitive processing mechanisms by which such rules may be implemented. Thus, the present work fills a major theoretical gap and provides answers to the question: If logical rule-based strategies do indeed underlie various forms of classification, then what would the patterns of classification RT data look like? Furthermore, because the predictions from rule-based models and various alternatives are often exceedingly difficult to distinguish based on choice-probability data alone, the present direction provides potentially highly valuable tools for telling such models apart.

Another significant contribution of the work was that, en route to developing these rule-based classification RT models, we further investigated the idea of combining mental-architecture and random-walk/diffusion approaches within an integrated framework. In our view, this integration potentially remedies limitations of each of these major approaches when applied in isolation. Past applications of mental-architecture approaches, for example, have generally failed to account for error processes, and the impact of errors on the RT predictions from mental-architecture models is often difficult to assess. Conversely, random-walk/diffusion approaches are among the leading process models for providing joint accounts of correct and error RT distributions; however, modern versions of such models are intended to account for performance involving “single-stage” decision-making processes. Various forms of cognitive and perceptual decision making, such as the present forms of logical-rule evaluation, may entail multiple decision-making stages. Thus, the present type of integration has great potential utility.

Relations to Previous Work

Mental Architectures and Decision-Bound Theory

The present logical rule-based models have adopted the assumption that a form of decision-bound theory operates at the level of individual dimensions. Specifically, the observer establishes a criterion along each individual dimension to divide it into category regions (Figure 2, top panel). Perceptual sampling along that dimension then drives the random-walk process that leads to decision making on that individual dimension. Unlike past applications of decision-bound theory, however, multidimensional classification decisions are presumed to arise by combining those individual-dimension decisions via mental architectures that implement the logical rules.

As noted earlier, past applications of decision-bound theory have assumed that multidimensional classification RT is some decreasing function of the distance of a stimulus to some multidimensional boundary. Furthermore, as we previously explained, the coactive rule model turns out to provide an example of a random-walk implementation of this multidimensional distance-from-boundary hypothesis. Specifically, the coactive model arises when the multidimensional boundary consists of two linear boundaries that are orthogonal to the coordinate axes of the space. In the present work, a major finding was the superior performance of some of the serial and parallel-processing rule-based models compared to this coactive one. Those results can be viewed as providing evidence of the utility of adding alternative mental-architecture assumptions to the standard decision-bound account.

A natural question is whether alternative versions of distance-from-boundary theory might provide improved accounts of the present data, without the need to incorporate mental-architecture assumptions such as serial processing or self-terminating stopping rules. In particular, the orthogonal decision bounds assumed in the coactive model are just a special case of the wide variety of decision bounds that the general theory allows. For example, one might assume instead that the observer adopts more flexible quadratic decision boundaries (Maddox & Ashby, 1993) for dividing the space into category regions.

The use of more flexible, high-parameter decision bounds would undoubtedly improve the absolute fit of a standard distance-from-boundary model to the classification RT data. Recall, however, that we have already included in our repertoire of candidate models the free stimulus-drift-rate model, in which each individual-stimulus drift rate was allowed to be a free parameter. A random-walk version of distance-from-boundary theory (Nosofsky & Stanton, 2005) is just a special case of this free stimulus-drift-rate model, regardless of the form of the decision boundary. We found that, under the present conditions, the logical-rule models outperformed the free stimulus-drift-rate model. It therefore follows that they would also outperform random-walk versions of distance-from-boundary theory that made allowance for more flexible decision bounds.

Decision-Tree Models of Classification RTs

In very recent work, Lafond, Lacouture, and Cohen (2009) have developed and tested decision-tree models of classification RTs. Following earlier work of Trabasso, Rollins, Shaughnessy (1971), the basic idea is to represent a sequence of feature tests in a decision tree (e.g., Hunt, Marin, & Stone, 1966). Free parameters are then associated with different paths of the tree. These parameters correspond to the processing time for a given feature test or to some combination of those tests. The models can be used to predict the time course of implementing classification rules of differing complexity.

On the one hand, Lafond et al. have applied these decision-tree models to category structures with rules that are more complex than the conjunctive and disjunctive rules that were the focus of the present research. In addition, the most general versions of their models allow separate free parameters to be associated with any given collection of feature tests. In these respects, their approach has more generality than the present one.

On the other hand, their modeling approach has been applied only in domains involving binary-valued stimulus dimensions. In addition, their specific decision-tree applications assumed what was essentially a fixed-order serial self-terminating processing strategy (with free parameters to “patch” some mis-predictions from the strong version of that model -- see Lafond et al. for details). By contrast, our development makes allowance for different underlying mental architectures for implementing the logical rules. Another unique contribution of the present work was the derivation of fundamental qualitative contrasts for distinguishing among the alternative classes of models (whereas Lafond et al. relied on comparisons of quantitative fit). Finally, whereas Lafond et al.’s models are used for predicting mean RTs, the present models predict full correct and error RT distributions associated with each of the individual stimuli in the tasks. Thus, the decision-tree models of Lafond et al. and the present mental-architecture/random-walk models provide complementary approaches to modeling the time course of rule-based classification decision making.

Higher-Level Concepts

In the present work, our empirical tests of the logical-rule models involved stimuli varying along highly salient primitive dimensions. Furthermore, the minimum-complexity classification rules were obvious and easy to implement. We conducted the tests under these highly simplified conditions because the goals were to achieve sharp qualitative contrasts between the predictions from the models, and to use the models to provide detailed quantitative fits to the individual-stimulus RT distributions of the individual subjects. In principle, however, the same models can be applied in far more complex settings in which classification is governed by application of logical rules. For example, rather than being built from elementary primitive features, the stimuli may be composed of emergent, relational dimensions (Goldstone, Gentner, & Medin, 1991), or the features may even be created as part of the category-learning process itself (Schyns, Goldstone, & Thibaut, 1998). Likewise, rather than relying on minimum-complexity rules, the observer may induce more elaborate rules owing to the nature of hypothesis-testing processes (Nosofsky et al., 1994) or the influence of causal theories and prior knowledge (Murphy & Medin, 1985; Pazzani, 1991). In a sense, the present theory starts where these other theoretical approaches leave off. Whatever the building blocks of the stimuli and the concepts may be, an observer needs to decide in which region of psychological space the building blocks of a presented stimulus fall. The time course of these decision processes can be modeled in terms of the random-walk components of the present synthesized approach. Given the outcomes of the individual decisions, they are then combined via an appropriate mental architecture to produce the classification choice and RT. The candidate architectures will vary depending on the logical rules that the observer induces and uses, but the modeling approach is essentially the same as already illustrated herein.

Directions of Future Research

In this article, our empirical tests of the logical-rule RT models were more in the way of “validation testing” rather than testing for generality of rule-based classification processes. That is, we sought to arrange conditions that would likely be maximally conducive to rule-based classification processing and to evaluate the models under such conditions. Even under these validation-testing conditions, the proposed rule models did not provide complete accounts of performance (although they far outperformed the major extant approaches in the field). In these final sections, we outline two major directions for continued research. First, we consider further possible elaborations of the rule-based models that might yield even better accounts of performance. Second, we describe some new paths of empirical research that are motivated by the present work.

Directions for Generalization of the Models

As acknowledged earlier in our article, our present implementations assumed that the random-walk decision processes along each dimension had fixed criterion settings. Also, we did not allow for drift-rate variability across trials. To provide more complete accounts of performance, these simplifying assumptions almost certainly need to be relaxed. Based on extensive analysis of speed-accuracy trade-off data, for example, there is overwhelming evidence from past applications of random-walk and diffusion models that criterion settings and drift rates vary across trials. Our focus in the present article was to point up novel aspects of the predictions of our logical-rule models for correct and error RTs, but complete models would need to incorporate these other sources of variability. A closely related issue is that the present work ignored consideration of trial-to-trial sequential effects on classification decision making, which are known to be pronounced (e.g., Stewart, Brown, & Chater, 2002).

Another possible avenue for improvement lies in our assumption that the random-walk processes along each dimension operated independently. In more complicated versions of the models, forms of cross-talk might take place (e.g., Mordkoff & Yantis, 1991; Townsend & Thomas, 1994). In these cases, perceptual processing and decision outcomes along one dimension might influence the processing and decision-making along the second dimension. The coactive architecture provides only an extreme example in which inputs from separate dimensions are pooled into a common processing channel. A wide variety of intermediate forms of dimensional interactions and cross-talk can also be posited.

The present development also ignored the possible role of working-memory limitations in applying the logical-rule strategies. In the present cases, applications of the logical rules required only one or two stages of decision making, and observers were highly practiced at implementing the logical-rule strategies. In our view, under these conditions, working-memory limitations probably do not contribute substantially relative to the other components of processing that we modeled in the present work. However, for more complex rule-based problems requiring multiple stages of decision making, or for inexperienced observers, they would likely play a larger role. So, for example, for more complex multiple-stage problems, forms of forgetting or back-tracking might need to be included in a complete account of rule-based classification.

Finally, another avenue of research needs to examine the possibility that the present rule-based strategies are an important component of classification decision making but that they operate in concert with other processes. For example, consider Logan’s (1988) and Palmeri’s (1997) models of automaticity in tasks of skilled performance. According to these approaches, initial task performance is governed by explicit cognitive algorithms. However, following extensive experience in a task, there is a shift to the retrieval of specific memories for past skilled actions. In the present context, observers may simply store the exemplars of the categories in memory, with automatic retrieval of these exemplars then influencing classification responding. Thus, performance may involve some mix of rule-based responding (the “algorithm”) and the retrieval of remembered exemplars (cf. Johansen & Palmeri, 2002).

Directions of New Empirical Research

In conducting the present validation tests, the idea was to assess model performance under conditions that seemed highly conducive to logical rule-based processing. To reiterate, we do not claim that rule-based processing is even a very common classification strategy. Instead, our work is motivated by the age-old idea in the categorization literature that, under some conditions, some human observers may develop and evaluate logical rules as a basis for classification. Until very recently, however, rule-based theories have not specified what classification RT data should look like. The present work was aimed at filling that gap. Using RT data, we now have tools that we can use to help assess the conditions under which rule-based classification does indeed occur and which individual observers are using them.

Natural lines of inquiry for future empirical work include the following. In our validation testing conditions, we used category structures in which observers could achieve excellent performance through use of the simple rule-based strategies. Would observers continue to use rule-based strategies with more complex category structures in which use of such rules might entail some losses in overall accuracy? In our tests, we used stimuli composed of spatially separated components. The idea was to maximize the chances that observers could apply the independent decisions related to assessing each component part of the logical rules. Would such rule-based strategies also be observed in conditions involving spatially overlapping dimensions or even integral-dimension stimuli? In our tests, most observers were given explicit instructions to follow serial self-terminating strategies to implement the rules (although some subjects were left to their own devices). We provided such instructions because they seemed to us to be the most natural rule-based processing strategy that an observer might use or could exert top-down control over. If instructed to do so, could observers engage in parallel-processing implementations instead? Finally, in our tests, all observers had knowledge of the rule-based structure of the categories prior to engaging in the classification tasks. Would logical-rule use continue to be observed under alternative conditions in which subjects needed to learn the structures via induction over training examples? These questions can now be addressed with the new theoretical tools developed in this work.

Table B2.

RT quantiles and error probabilities for each individual stimulus and subject in Experiment 2.

Stimulus	RT Quantiles
	.1	.3	.5	.7	.9	N	p(e)
Sub A1
x2y2	552	605	657	708	800	347	.01
x2y1	661	774	856	947	1146	339	.04
x1y2	680	804	870	946	1091	342	.02
x1y1	875	990	1105	1239	1535	349	.12
x2y0	419	476	540	617	947	339	.04
x1y0	417	478	540	617	947	340	.04
x0y2	698	763	814	877	982	355	.02
x0y1	802	906	967	1044	1159	341	.01
x0y0	430	481	546	661	972	357	.00
Sub A2
x2y2	497	552	595	653	731	356	.00
x2y1	679	757	812	889	1019	353	.01
x1y2	645	766	858	941	1095	354	.05
x1y1	847	961	1049	1145	1360	354	.02
x2y0	693	764	812	873	976	354	.02
x1y0	863	968	1044	1117	1225	357	.01
x0y2	454	506	546	614	771	353	.01
x0y1	480	521	567	649	766	351	.01
x0y0	471	521	573	654	878	352	.00
Sub A3
x2y2	561	608	655	713	813	354	.01
x2y1	743	852	940	1048	1337	351	.04
x1y2	713	851	962	1070	1241	354	.03
x1y1	909	1084	1206	1366	1737	354	.07
x2y0	476	686	795	877	1049	352	.03
x1y0	457	604	927	1102	1398	355	.04
x0y2	519	655	804	908	1113	349	.01
x0y1	528	700	950	1122	1569	354	.03
x0y0	460	551	649	818	1242	356	.00
Sub A4
x2y2	552	605	657	708	800	347	.01
x2y1	661	774	856	947	1146	339	.04
x1y2	680	804	870	946	1091	342	.02
x1y1	875	990	1105	1239	1535	349	.12
x2y0	419	476	540	617	947	339	.04
x1y0	417	478	540	617	947	340	.04
x0y2	698	763	814	877	982	355	.02
x0y1	802	906	967	1044	1159	341	.01
x0y0	430	481	546	661	972	357	.00

Stimulus	RT Quantiles
	Correct Trials					Error Trials
	.1	.3	.5	.7	.9	.1	.3	.5	.7	.9	N	p(e)
Sub S1
x2y2	451	492	529	576	638	573	573	573	573	573	358	.00
x2y1	506	555	588	647	750	342	368	400	448	607	357	.20
x1y2	476	588	646	704	810	599	656	704	732	847	358	.09
x1y1	511	584	652	728	884	339	367	426	562	849	359	.27
x2y0	348	384	413	453	539	460	662	680	715	800	353	.03
x1y0	346	377	413	453	572	498	743	782	865	993	355	.04
x0y2	627	667	718	763	832	449	496	559	641	756	356	.26
x0y1	383	484	712	837	937	495	551	607	658	758	358	.39
x0y0	346	383	414	460	534	462	467	484	535	620	356	.01
Sub S2
x2y2	436	490	535	587	690	418	474	560	583	599	358	.01
x2y1	480	594	715	812	970	535	602	663	697	846	357	.08
x1y2	526	616	685	768	935	401	454	497	569	735	354	.25
x1y1	586	703	783	943	1223	418	509	598	664	791	354	.27
x2y0	627	692	778	859	971	422	476	534	605	780	355	.35
x1y0	506	631	731	866	1129	555	650	754	833	1135	354	.29
x0y2	410	451	494	551	660	615	678	769	866	1148	352	.08
x0y1	413	461	507	576	742	746	925	1064	1435	1949	351	.07
x0y0	407	477	535	602	752	399	437	494	876	1131	354	.09

Note. N = total number of non-excluded trials. p(e) = probability of error.

Appendix A

EBRW Predictions of the Mean Interaction Contrast

We conducted extensive investigations into the predictions that the exemplar-based random-walk (EBRW) model makes for the mean interaction contrast (MIC) for the target-category members. These investigations follow in the spirit of earlier investigations made by Thomas (2006) for the EBRW and other process-oriented RT models for the closely related additive-factors paradigm. The present EBRW predictions are based on analytic formulas for mean RTs (Nosofsky & Palmeri, pp. 269–270) and did not require computer simulation. For each set of parameter values, we generated the EBRW predictions of mean RTs for the LL, LH, HL, and HH members of the target category and then computed MIC = RT(LL)-RT(LH)-RT(HL)+RT(HH). The coordinate values of the stimuli were as given in Figure 1. A city-block metric (Shepard, 1964) was used for computing distances among the stimuli. The qualitative pattern of results is the same if a Euclidean distance metric is used instead.

The parameters of greatest interest for the MIC are c and A. Here, we report predictions for cases in which the sensitivity parameter c varies between 1.0 and 5.0 in increments of .2 and in which the criterion parameter A varies between 3 and 8 in increments of 1. (The criterion parameter B was set equal to A.) As c and A increase, predicted accuracy gets higher. For predictions of present interest, boundary conditions need to be established on c and A. If these parameters both take on values that are too small, then error rates get exceedingly high; whereas if these parameters both take on values that are too large, then predicted accuracy exceeds realistic bounds (i.e., the model predicts that observers will never make any errors). For the present report, we focus mainly on cases in which error rates for the LL stimulus (i.e., the most difficult stimulus to classify) vary between .01 and .20.

In the investigations in this appendix, we report results in which the attention weight parameter is set at w_x=.50. As long as w_x is not too extreme (i.e., close to 0 or 1), the EBRW’s predictions of the MIC remain essentially the same. (If w_x were too extreme, then observers would be unable to discriminate between the target and contrast category members, so those cases are of limited interest.) The MIC predictions are also unaffected by the magnitude of the residual-stage parameters μ_R and σ_R. The background-noise parameter is set at back=0. As back increases, predicted accuracy decreases. As long as back is set at values that produce reasonable predictions of accuracy, the predictions for the MIC are unaffected.

To generate the MIC predictions, we needed to decide the magnitude of the scaling parameter k. The scaling parameter simply transforms the mean number of steps in the random walk, which have arbitrary time units, into milliseconds. The value of k has no influence on the direction of the MIC (i.e., less than zero, equal to zero, or greater than zero), only on its absolute magnitude. To make things comparable across the different values of c and A, for each combination of those parameters we set the scaling constant k at the value that produced a 200 msec difference between the predicted mean RTs of the LL and the HH stimuli. Thus, the predicted magnitude of underadditivity (MIC<0) or overaddivity (MIC>0) is measured relative to this constant 200 msec difference.

The results are shown in Table A1. The table shows, for each combination of c and A, the predicted MIC value and also the predicted error rate associated with the LL stimulus. Note that for the upper-left cells in the table (i.e., the region demarcated by the hashed lines), error rates for the LL stimulus exceed .20. As can be seen, as long as error rates on the LL stimulus are low to moderate (i.e., less than .20), then the EBRW predicts an overadditive MIC (MIC>0), which is the same qualitative signature produced by the coactive model. For higher error rates (upper-left cells of the table), the MIC switches to being underadditive (MIC<0). Again, the same pattern occurs for the coactive model. (Intuitively, this pattern may be thought of as a speed-accuracy tradeoff in which random-walk paths for the LL stimulus that would have resulted in very long RTs result in errors instead.) Although not shown in the table, for combinations in which the magnitude of c and A are both very large, the predicted MIC eventually changes from being overadditive to additive; however, these parameter-value combinations lead to unrealistic predictions in which the observer never makes any errors.

Table A1.

Predictions from the EBRW Model of Mean RT Interaction Contrasts and Error Rates for the LL Stimulus as a Function of c and A.

	A
	3	4	5	6	7	8
c
1.2	−41.8	−18.4	4.3	24.6	41.9	56.3
	.37	.33	.29	.25	.22	.19
1.4	−27.0	−.1	23.5	42.7	57.7	69.2
	.32	.26	.22	.18	.14	.11
1.6	−14.4	14.0	36.6	53.5	65.7	74.4
	.27	.21	.16	.12	.09	.06
1.8	−3.9	24.4	45.0	59.3	68.8	75.2
	.22	.16	.11	.08	.05	.04
2.0	4.6	31.8	50.0	61.6	68.8	73.3
	.19	.12	.08	.05	.03	.02
2.2	11.3	36.7	52.3	61.6	67.0	70.1
	.15	.09	.05	.03	.02	.01
2.4	16.4	39.6	52.8	60.1	64.0	66.1
	.12	.07	.04	.02	.01	.01
2.6	20.1	41.0	52.1	57.6	60.4	61.8
	.10	.05	.02	.01	.01	.00
2.8	22.8	41.3	50.4	54.6	56.5	57.4
	.08	.03	.02	.01	.00	.00
3.0	24.4	40.8	48.1	51.3	52.6	53.2
	.06	.02	.01	.00	.00	.00
3.2	25.3	39.6	45.5	47.9	48.8	49.1
	.05	.02	.01	.00	.00	.00
3.4	25.6	38.0	42.7	44.5	45.0	45.3
	.04	.01	.00	.00	.00	.00
3.6	25.5	36.2	39.9	41.1	41.5	41.6
	.03	.01	.00	.00	.00	.00
3.8	25.0	34.1	37.0	37.9	38.2	38.2
	.02	.01	.00	.00	.00	.00
4.0	24.2	32.0	34.3	34.9	35.0	35.1
	.02	.00	.00	.00	.00	.00
4.2	23.2	29.8	31.6	32.0	32.1	32.2
	.01	.00	.00	.00	.00	.00
4.4	22.1	27.7	29.0	29.4	29.4	29.4
	.01	.00	.00	.00	.00	.00
4.6	20.9	25.6	26.7	26.9	26.9	26.9
	.01	.00	.00	.00	.00	.00
4.8	19.7	23.6	24.4	24.6	24.6	24.6
	.01	.00	.00	.00	.00	.00

Note. Top line in each cell gives the mean RT interaction contrast. Bottom line in each cell gives the error rate on the LL stimulus. Hashed lines at upper left of table demarcate the region where the LL stimulus has a predicted error rate greater than .20.