Predicting the emergence of human hantavirus disease using a combination of viral dynamics and rodent demographic patterns

F SAUVAGE; M LANGLAIS; D PONTIER

doi:10.1017/S0950268806006595

. 2006 Jun 6;135(1):46–56. doi: 10.1017/S0950268806006595

Predicting the emergence of human hantavirus disease using a combination of viral dynamics and rodent demographic patterns

F SAUVAGE ¹, M LANGLAIS ², D PONTIER ^1,^*

PMCID: PMC2870550 PMID: 16753079

SUMMARY

The paper proposes a model explaining the spatial variation in incidence of nephropathia epidemica in Europe. We take into account the rodent dynamic features and the replicative dynamics of the virus in animals, high in the acute phase of newly infected animals and low in the subsequent chronic phase. The model revealed that only vole populations with multi-annual fluctuations allow for simultaneously high numbers of infected rodents and high proportions of those rodents in the acute excretion phase during the culminating phase of population build-up. This leads to a brief peak in exceptionally high concentrations of virus in the environment, and thereby, to human exposure. Such a mechanism suggests that a slight ecological disturbance in animal–parasite systems could result in the emergence of human diseases. Thus, the potential risk for public health due to several zoonotic diseases may be greater than previously believed, based solely on the distribution of human cases.

INTRODUCTION

The relationship between the natural circulation of pathogens and the incidence of diseases in human populations is far from being fully understood [1, 2]. In particular, the emergence of human diseases has often been found to be more spatially restricted than the distribution of the reservoir host, e.g. the Puumala virus-mediated nephropathia epidemica (NE) in Western Europe [3, 4]. However, concluding to the absence of the pathogen in the reservoir host could be misleading as it is only the areas of human disease emergence that are generally probed. For example, the ubiquity of the Sin Nombre virus in the reservoir species was unexpectedly found over an extremely wide region, including cities [3, 5]; whereas the 1993 outbreak of Hantavirus Pulmonary Syndrome (HPS) in the United States was very focused. The available data do not enable us to exclude such a situation in Europe, i.e. that the virus is present, although discrete, in a broader area than the recognized endemic zone of NE.

Hantavirus is an ancient genus that has radiated simultaneously with the evolution of specific rodent species [3, 6]. There is physically no geographical barrier to prevent dispersal of rodents through Western Europe and thus to prevent dispersal of the virus, given the time period involved. In addition, the virus survived crashes in the Northern Europe vole populations at host population sizes smaller than those observed in the stable populations in the southwestern regions [7]. Hence, we may assume that the virus is present in the southern populations of bank voles, Clethrionomys glareolus, but has not been isolated due to the absence of human cases of haemorrhagic fever with renal syndrome (HFRS) and the lack of investigation.

Thus, other factors may explain the existing distribution of human zoonosis. NE cases occur in regions where bank-vole populations are subject to cyclic dynamics, such as in Fennoscandia [1, 4, 8], or to large multi-annual fluctuations (i.e. populations show dramatic density fluctuations over several years), as in Belgium [9]. Southern bank-vole populations do not exhibit such fluctuations but occur at stable densities from one year to the next [7]. We hypothesize that the vole demographic pattern affects the Puumala virus dynamics, allowing in the cyclic case the human contamination which is prevented in the stable vole populations. Our hypothesis is based on the observation made by Gavrilovskaya et al. [10] that infected voles excrete much more virus during the first month than during the chronic phase of infection. In a widely fluctuating population during the expansion phase, there would be a marked and, even more important, a fast increase in local population density which is favourable to direct viral transmission, and a large cohort of susceptible young animals could become infected virtually simultaneously. This could lead to a large population of animals infected for less than 1 month, with subsequently high levels of viral shedding that exceed the threshold for human dead-end infections. More stable populations undergoing only seasonal variation in numbers are unlikely to generate large increases in the relative proportion of newly infected animals, even at high densities, that would prevent the intense peaks of viral contamination necessary for human infection. Returning to the HPS case in the United States, the explosive increase in the deer mouse population may have provided ideal conditions for amplification of the viral load in the environment.

Here, we used a mathematical model to test whether our hypothesis is sufficient to explain the observed transition between endemic and sporadic HFRS that occurs in France. We explicitly included vole population dynamics and the two-phase excretion pattern in infected reservoir hosts together with two forest-use patterns of the potential target human population. The proposed mechanism involving a brief, intense peak in viral concentrations could explain the emergence pattern of several other zoonotic diseases. Thus, the potential area of human epidemic disease could be much wider than initially envisioned, and may have implications for the handling of emerging zoonoses by public health officials.

HYPOTHESES UNDERLYING THE MODEL

Our model contained two subsections, the first describing the demography and infection of the bank-vole reservoir and the second describing the access of humans to the forest and subsequent human infection. In this scenario, the rodents build up a level of environmental contamination that allows the virus to spill over into the human population.

Bank-vole population subsection

The hypotheses and parameterization of the first subsection of the model, describing the hantavirus–bank-vole population dynamics, based on experimental data from our field studies and from literature as defined in Sauvage et al. [11]. The model was based on a classical compartmental SI procedure [12]. Bank voles were considered to be chronic excretors because they generally remain seropositive for life and a high concordance between serological and PCR results suggests persistence of viral production [13]. For a better understanding of the mechanism, the population was not structured in space or by age, since differences in prevalence among age classes result from behaviours not crucial for the hypothesis. However, two classes of infected animals were considered. After infection, animals remained in the newly infected class for 1 month before progressing to the chronically infected class. The susceptible class of uninfected animals contained all newborn offspring because vertical transmission has not been described [14]. The demographic patterns do not result from infection by hantaviruses, since the virus has no reported effect on either the bank vole's fecundity or survival, that was definitely confirmed for natural populations [14]. Consequently, we were only interested in describing accurately the demographic patterns, whatever their causes, to assess how they drive the infection. All bank voles were considered to be reproductively active, since we included no age class. The same mortality term, corrected for carrying capacity, was applied to all three infection classes.

Infection of the susceptible animals placed them in the newly infected class because we did not consider ‘exposed’ animals as a separate category. Infection resulted from (a) direct exposure to a newly infected subject, (b) direct exposure to a chronically infected subject, or (c) indirect contact through contaminated soil litter [11]. Viral excretion by newly infected animals in class I was much higher than that of chronically infected animals in class II [10]. This had consequences for the practical means of transmission between infected and susceptible bank voles. We considered that chronically infected animals could only transmit the virus through very close contacts, whereas the newly infected animals were more widely contagious. Whether a density-dependent or a frequency-dependent transmission is more accurate to model the Puumala virus circulation in bank-vole populations is discussed (e.g. in ref. [2]), but here we considered that the overall incidence would result from a combination of the different routes of viral transmission described above. All bank-vole populations fluctuate throughout the year and each transmission route is more or less important depending on the demographic stage of the bank-vole population. Thus, a single incidence term could not describe the incidence satisfactorily, as reported by Begon et al. [15] for the cowpox–bank vole system. We therefore used a density-dependent transmission for the spread from newly infected rodents, which are widely contagious because they shed large amount of virus in saliva, urine and faeces, and a frequency-dependent transmission for the spread from chronically infected rodents, which requires a close contact, e.g. through biting during mating encounters and through burrow sharing during winter, as the viral shedding becomes much lower [13, 14, 16, 17]. The rate of these types of close encounters involving a chronically infected vole should change relatively little at differing population densities since the number of neighbours can be considered to remain close for a wide range of population densities [18]. The different rates of viral excretion by the two classes of infected animals also affected the amount of ground contamination through urine and faecal deposits; newly infected animals excreted more virus than chronically infected animals. Infectious virus was lost from the soil at a breakdown rate corresponding to viral survival outside the host. We considered that human contamination could only occur through contact with contaminated ground.

Human population subsection

To the above model, we added a village near the forest populated by the infected bank voles. The village included two population groups of humans with different potential exposure rates, according to behaviour. One part of the population consisted of forest workers, such as foresters and hunters, with frequent visits to the forest and a high encounter risk with potentially contaminated soil. All other village inhabitants were considered to visit the forest only infrequently for recreational purposes. We made this distinction because NE has been described as an occupational disease strongly linked to the duration and nature of activities in a forest setting [4, 19]. We estimated a standard duration (in days) for a visit to the forest, and therefore all people returned from the forest to the village at the same standard rate. We did not consider person-to-person transmission because it has never been described in clinical situations [14, 20]. On their return to the village, infected subjects recovered at the same rate and they represented the total number of NE cases because re-infection has not been observed. We modelled the human population dynamics as constant with no births or mortality, since we wished to focus on the short-term dynamics of the disease. In fact, the seasonality of recreational human activities in the forest should strengthen the coincidence of infection in the two host species: the peak in risky autumn activities, such as mushroom picking, hunting and firewood collection, corresponds to maximum vole densities at the end of the reproductive season. Here, we only considered constant recreational behaviour throughout the year.

CONSTRUCTION OF THE MODEL

Bank-vole dynamics submodel

The bank-vole population dynamics were expressed as:

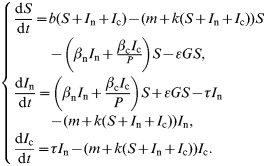$\left\{ \openup 2pt{\matrix { {\displaystyle { {{\rm d}S} \over {{\rm d}t}} \equals b\lpar {S \plus I_{\rm n} \plus I_{\rm c} } \rpar \minus \lpar {m \plus k\lpar {S \plus I_{\rm n} \plus I_{\rm c} } \rpar \rpar} S}\hfill \cr \qquad\ {\minus \left( {\beta _{\rm n} I_{\rm n} \plus {\displaystyle{\beta _{\rm c} I_{\rm c} } \over P}} \right)S \minus \epsiv GS\comma } \hfill \cr {\displaystyle{{{\rm d}I_{\rm n} } \over {{\rm d}t}} \equals \left( {\beta _{\rm n} I_{\rm n} \plus {{\beta _{\rm c} I_{\rm c} } \over P}} \right)S \plus \epsiv GS \minus \tau I_{\rm n}}\hfill \cr \qquad\ { \minus \lpar {m \plus k\lpar {S \plus I_{\rm n} \plus I_{\rm c} } \rpar} \rpar I_{\rm n} \comma } \hfill \cr {\displaystyle{{{\rm d}I_{\rm c} } \over {{\rm d}t}} \equals \tau I_{\rm n} \minus \lpar {m \plus k\lpar {S \plus I_{\rm n} \plus I_{\rm c} } \rpar} \rpar I_{\rm c}.} \hfill \cr} } \right.$

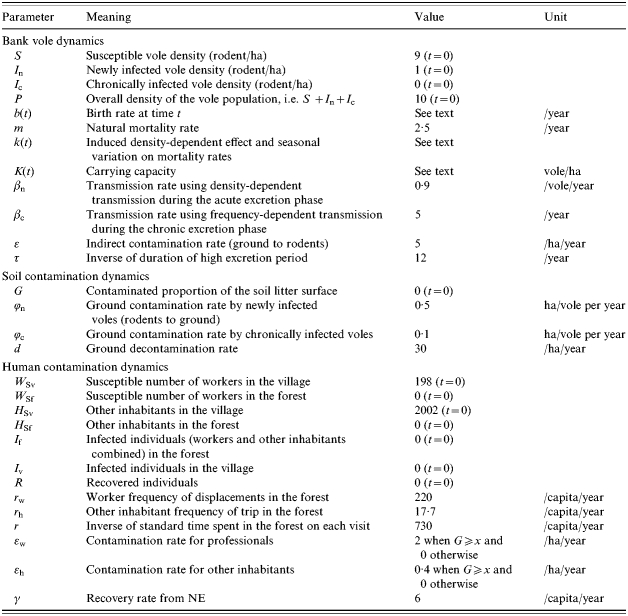
The model's parameters are described in the Table and followed those described in Sauvage et al. [11]. Parameters b and k are functions of time. They integrated respectively the seasonal variations linked to the reproductive season or the possible multi-annual variations of the environmental carrying capacity, which is responsible for multi-annual fluctuations of the rodent population's density.

Table.

Symbols, meanings, values and units of the model parameters, gathered by subsection

graphic file with name S0950268806006595_tab1.jpg

Open in a new tab

The function used to express the birth rate b(t) is the following:

$b\lpar t \rpar \equals 7\! \cdot\! 5\,\lsqb {\left\vert {\sin \, \lpar {2\pi \lpar {t \minus 0\! \cdot\! 15} \rpar} \rpar} \right\vert \plus \sin \, \lpar {2\pi \lpar {t \minus 0\! \cdot\! 15} \rpar} \rpar} \rsqb\comma$

which is periodic with a period of 1 year, and is zero over 6 months (October–March). This birth function allows for a 6-month-long breeding season and implies five litters of five offspring per female per breeding season [21], considering a balanced sex ratio. There was no density dependence incorporated because Verhagen et al. [22] reported only a weak relation between litter size and density. The coefficient value was adapted from Sauvage et al. [11] since we do not take any age structure into account; m=2·5, for an almost 5-month turnover of the population.

Another point which needs further explanations is the parameter k(t), the density-dependent effect and seasonal variation on mortality rate. It corresponds to the mean growth rate of the bank-vole population by the forest carrying capacity: k(t)=10−m/K(t), where K(t) is the environment carrying capacity (see ref. [11]). This parameter is of crucial importance. It was cyclic with a 3-year period (coinciding with the variation in seed production) in the northern part of the bank-vole distribution [7, 23] or constant for the southern part of the distribution [7]. Thus, we built two models where all parameters were similar except the carrying capacity value. Here,

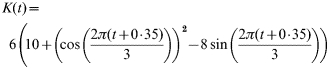$\eqalign{\tab K \lpar t \rpar \equals\cr\tab\enspace 6\left(\hskip-2 10 \plus\hskip-1 \left(\hskip-2{\cos \left( {2\pi \lpar {t \plus 0\! \cdot\! 35} \rpar} \over 3}} \right)}\! \right)^{\setnum{2}} }\right \hskip-1\left \minus 8\sin \left( {{{2\pi \lpar {t \plus 0\! \cdot\! 35} \rpar} \over 3}} \right)}\!\right)}$

for the cyclic population; and K(t)=35 for the stable population.

Throughout the text, β (β_n and β_c) refer to a direct transmission rate and ε (ε, ε_w and ε_h) to an indirect one. The direct transmission contact rates, β_n and β_c, are unknown in bank-vole populations. They were calibrated using Begon et al.'s [15] estimate in the bank vole–cowpox system. β_n was the direct transmission rate from newly infected rodents. β_c was the transmission rate from chronically infected voles, which is directly affected by the number of different neighbours met per vole per year [24]. This number conditions the transmission opportunities through close enough contact for Puumala virus transmission between infected and susceptible voles.

ε=5: the incidence contact rate of indirect transmission; we took a conservative indirect contact rate assuming that on average each point of the area is visited once every 73 days, i.e. 365/73=5 visits per unit of area and per year.

Site contamination/decontamination dynamics allowed the spread of infection from rodents to humans. The modelling process was similar to that used by Berthier et al. [25] (see Table for parameter description):

${{{\rm d}G} \over {{\rm d}t}} \equals \lpar {\phiv _{\rm n} I_{\rm n} \plus \phiv _{\rm c} I_{\rm c} } \rpar \lpar {1 \minus G} \rpar \minus {\rm d}G\comma$

where φ_n, the proportion of territory contaminated by one newly infectious individual per year, and φ_c the equivalent rate for chronically infected voles, were estimated from Rozenfeld et al. [17]. The value of φ_n is higher than that of φ_c because newly infected voles release viruses in higher quantities and through more routes than do chronically infected rodents. Rozenfeld et al. [17] showed a strategic choice of scent marks deposited by male bank voles on their territory borders, their feeding points area and even their rivals’ burrows. These marked areas are more probably explored by other bank voles; and d=30: the reciprocal of the virus survival of about 12 days outside the host [26], e.g. in the ground.

Addition of the human population dynamics

The dynamics of NE infection in humans were written using a SI model with indirect transmission and for a two-host sub-population, forest workers W and others H (See Table for parameter description):

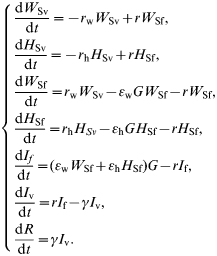$\left\{\openup 3.55pt {\matrix{ {\displaystyle{{{\rm d}W_{{\rm Sv}} } \over {{\rm d}t}} \equals \minus r_{\rm w} W_{{\rm Sv}} \plus rW_{{\rm Sf}} \comma } \hfill \cr {\displaystyle{{{\rm d}H_{{\rm Sv}} } \over {{\rm d}t}} \equals \minus r_{\rm h} H_{{\rm Sv}} \plus rH_{{\rm Sf}} \comma } \hfill \cr {\displaystyle{{{\rm d}W_{{\rm Sf}} } \over {{\rm d}t}} \equals r_{\rm w} W_{{\rm Sv}} \minus \epsiv _{\rm w } GW_{{\rm Sf}} \minus rW_{{\rm Sf}} \comma } \hfill \cr {\displaystyle{{{\rm d}H_{\rm Sf} } \over {{\rm d}t}} \equals r_{\rm h} H_{Sv} \minus \epsiv _{\rm h} GH_{{\rm Sf}} \minus rH_{{\rm Sf}} \comma } \hfill \cr {\displaystyle{{{\rm d}I_{f} } \over {{\rm d}t}} \equals \lpar {\epsiv _{\rm w} W_{{\rm Sf}} \plus \epsiv _{\rm h} H_{{\rm Sf}} } \rpar G \minus rI_{\rm f} \comma } \hfill \cr {\displaystyle{{{\rm d}I_{\rm v} } \over {{\rm d}t}} \equals rI_{\rm f} \minus \gamma I_{\rm v} \comma} \hfill \cr {\displaystyle{{{\rm d}R} \over {{\rm d}t}} \equals \gamma I_{\rm v}.} \hfill \cr} } \right.$

We consider a threshold for human contamination (as it is described for other diseases, e.g. see ref. [27] for tuberculosis or ref. [28] for tularaemia in both animals and humans). Such a threshold results in null values for ε_w and ε_h when G⩽0·08. G becomes the threshold value of the index of environment contamination required for humans to become infected. Such a threshold represents the fact that humans breathe 1·5 m above the forest litter compared to rodents. Moreover, the high host specificity of hantaviruses [29] should reduce the effective infectivity of the virus when humans are exposed to infectious aerosols – as is the case, e.g. of tularemia [28]. I _f represents the number of people acquiring the virus in the forest. Briefly after they come back to town and are actually diseased people I _v. As NE is contracted only once a life, they are removed from the system and accumulate in the R class as they recover. The R class equals the total number of NE cases since the beginning of the simulation, I _f and I _v representing the actual numbers of diseased people in the forest and town respectively at the considered moment.

Simulation results were examined after trajectories had reached a stable periodic state. For the initial set of conditions, we considered a rodent population composed of nine susceptible individuals per hectare and one newly infectious vole per hectare plus a human population of 2200 persons containing 9% of forest workers, which was similar to the population structure of one of the most affected town in the Ardennes, Monthermé [30].

Elasticity and sensitivity analyses

Some demographic and epidemiological parameters were poorly known and the periodic dynamics made the model analytically intractable. We thus conducted numerical elasticity analyses [11]. We observed the relative effect of each parameter on changes in maximum proportion of newly infected rodents, rodent and human prevalences and contaminated proportion of the soil.

Once we identified the parameters that mainly influence the model output variables, we realized bivariate sensitivity analyses within the following range of parameter values: 0–5 for the professional transmission rate ε_w and 0–2 for the transmission rate during the acute excretion phase β_n. This helps us to define whether and how public health policies should manage the epidemic course in humans. Models and simulations were performed with matlab [31].

RESULTS

Bank vole–hantavirus system

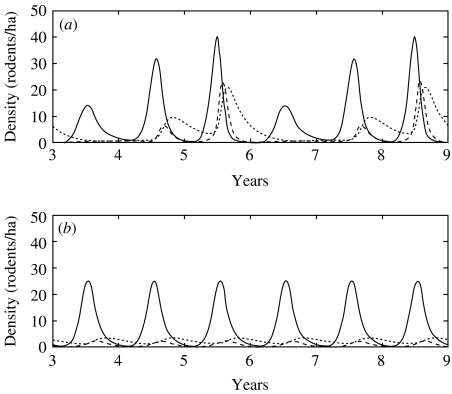
In the multi-annually fluctuating population, the maximum overall prevalences were 6% in the first year, 30% in the second year and 50% the peak year. Population peaks in vole densities, maximum densities of infected voles and maximum relative proportions of newly infected voles occurred simultaneously (Fig. 1 a).

When the carrying capacity was constant, the maximum prevalence reached 17% [but at a time when there were few rodents in the population (Fig. 1 b)]. The virus persisted in the stable vole population but at far lower levels than in the cyclic vole population. Densities of voles in the acute phase of infection did not reach even one tenth of the maximum densities achieved in the cyclic population.

Impact on proportion of contaminated ground surface

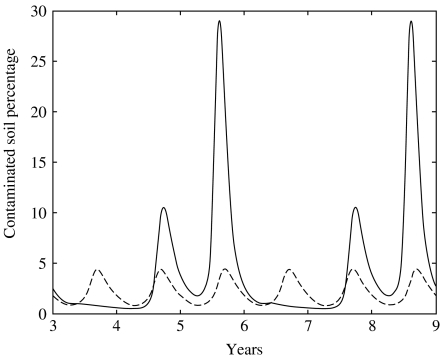
In the cyclic population, the proportion of contaminated area fluctuated with the same pattern as that of infected voles (Fig. 2). The contaminated proportions fluctuated within a range of 0·48 to 29·1%. During the second year of the cycle, the contaminated soil proportion transitorily exceeded the threshold value during the months of September and October. In the second year, the proportion reached 10·6%. These proportions never fell to zero, which means that the ground could play the role of reservoir for the virus. In the case without multi-annual variations, the proportion of contaminated soil never exceeded 4·5% or fell below 0·8% (Fig. 2).

Human infection dynamics

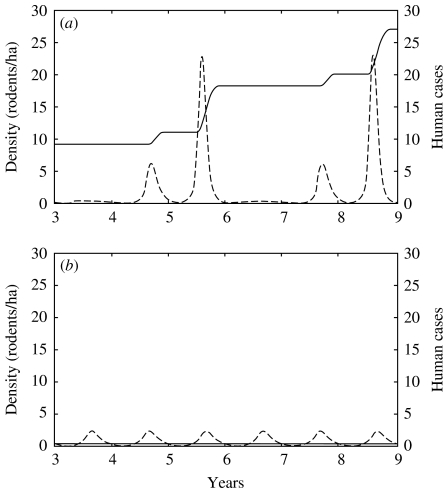
The number of human contaminations coincided with the proportion of contaminated ground surface. Near the cyclic vole population, the threshold for human infection can be reached (Figs 2 and 3 a). There was actually a peak of NE cases in the third year of the vole cycle and the epidemic event began the previous autumn, as observed in the field [32, 33]. This pattern was the same for both human groups (forest workers vs. other inhabitants). Intensity of forest use modified the number of NE cases per group during this peak year, which reached six overall (Fig. 3 a). After 9 years (i.e. three cycles), 27 persons had acquired infection. The prevalence of HFRS in the highly exposed human population was 1·23%. These results were similar to those reported by Penalba et al. [30].

Fig. 3 — Density per hectare of voles in acute phase of infection (– – – –), and total number of human cases since the introduction of the virus (––––). The two parts of the figure distinguish whether the population of voles presents peaks of high density (a) or a more stable pattern (b).

With a constant carrying capacity, there was no multi-annual peak in density of voles and soil contamination remained very low and below the human infection threshold (Fig. 3 b).

Elasticity and sensitivity analyses

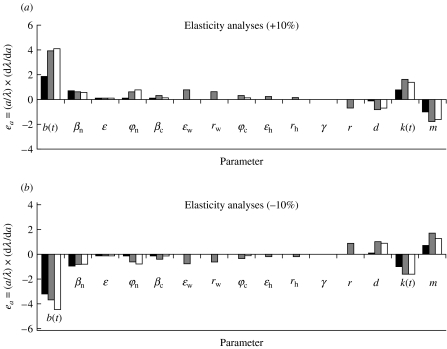
Results of the elasticity analyses are presented in Fig. 4 and the correspondence between numbers and parameters is presented in the Table. As in Sauvage et al. [11], the model was more sensitive to those parameters that affected the number of bank voles. These parameters are the birth rate and the environment carrying capacity. Actually, the host reservoir dynamics drove the infection in humans through the proportion of contaminated soil. In addition, the number of human NE cases after three cycles appeared to be affected by the transmission rate between voles during the acute phase of viral excretion and by the transmission rate of the disease to the forest professional fraction of the human population.

Inline graphic — Elasticity values for 15 parameters of the model with the cyclic vole population, using a variation of ±10%. We present the impact on maximum population density reached during the peak year, on estimated maximum prevalence and on the final number of human HFRS cases. In the scale formula e _a, a denotes the parameter and λ the model output considered. The higher the absolute value of the elasticity, the more sensitive is the model to the corresponding parameter. ■, Prevalence in rodents; , prevalence in humans; □, ground.

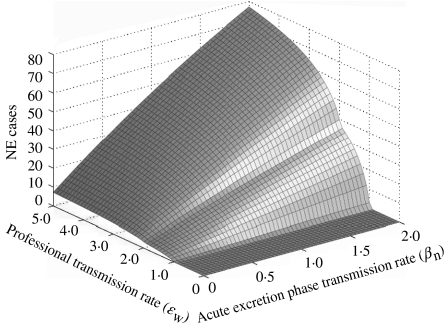
We then analysed the co-influence of (i) the carrying capacity for bank voles and the vole birth rate (Fig. 5), and (ii) the transmission rate during the acute excretion phase in bank voles and the human professional transmission rate (Fig. 6) on the final number of NE cases. The bivariate analyses revealed that slight differences from the bank-vole birth rate and the forest carrying-capacity values used in the model drives a huge gradient on the predicted epidemic pattern in humans. The final predicted number of human cases grew linearly with the acute phase transmission rate but presented an irregular pattern variation with the professional transmission rate.

Fig. 6 — Bivariate sensitivity of the final number of nephropathia epidemica (NE) cases in humans. The surface shows the variations of human cases with the acute transmission rate in bank voles and with the professional transmission rate.

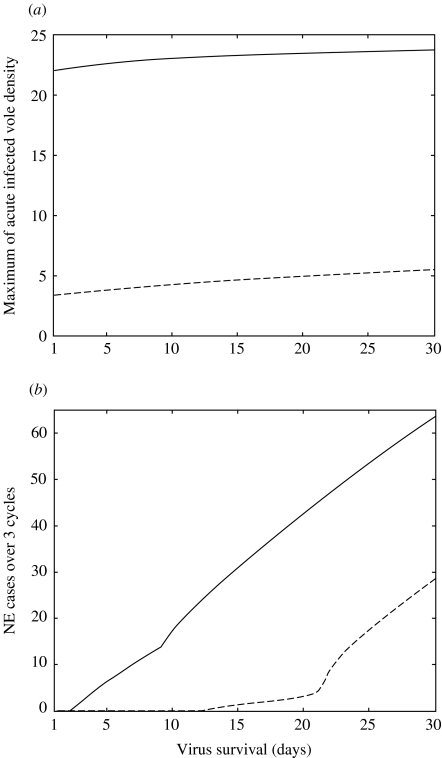
We presented in Fig. 7 the sensitivity to the length of the virus survival in the soil litter of the maximum density of bank voles in acute phase of infection and of the final number of NE cases in humans. We observed that the predicted maximum densities of bank vole in the acute phase of infection were quite robust for both bank-vole populations to variations in the virus survival. Otherwise, the predicted number of NE cases varies greatly according to the virus survival. The situation near the seasonal population was particularly interesting: the threshold for human contamination cannot be reached for a survival below 12 days, some contaminations can occur for a survival between 13 and 21 days and their number greatly increases over 21 days.

DISCUSSION

Disease agents in a reservoir host may persist for very long periods below the threshold level for cross-species transmission. A change in the demography of the reservoir host that leads to a rapid increase in host density can result in a peak of the infectious agent produced by newly infected hosts. Hence, in order to evaluate the risk for humans, host density or prevalence are not good estimators: it is the speed of the host population increase that allows or not the sufficiently high density of newly infected voles for human contamination. Such a mechanism explains the observed NE distribution, since only cyclic vole populations exhibit such a rapid build-up on a regular pattern. It also reveals that if the parasite is present, a single event yielding a sudden peak in the reservoir host density would be sufficient for the disease outbreak in humans, in an area of otherwise stable host populations. This mechanism may explain other pathogen outbreaks, such as the mysterious epidemic that decimated the native Mexican population in the 16th century [34]. The epidemic followed exceptional climatic conditions where prolonged droughts gave way to abundant precipitation. During the droughts, humans and rodents were forced into unusual proximity around the few sources of water. When rainfall returned, the rodent population would have exploded in response to increased food resources, providing ideal conditions for the amplification of a rodent virus above the threshold for human infection. Such explosive changes in rodent demography appear to have preceded the 1545 and 1576 Cocoliztli epidemics. Similar conditions occurred before the 1993 HPS outbreak and following epidemics, driven by the high rainfall and cooler temperature of El-Niño southern oscillation (ENSO) [35]. These outbreaks may be a re-emergence of the disease that is suspected to have caused the extinction of the Anasazi Native American civilization [36]. Bubonic plague may also be another example: devastating outbreaks of disease affected European populations from the 14th to the 16th centuries and the bacterium is still widespread throughout rodent populations in the Americas, southern Africa and Asia [2]. Stapp et al. [37] reported the correlation between ENSO events and plague outbreaks in colonies of black-tailed prairie dogs.

The present study aimed to identify those aspects of the epidemiology of hantavirus infections in bank voles that are associated with increased risk of emergence of human disease. Our previously untested hypothesis linked the multi-annually fluctuating demography of bank voles and the temporal pattern of Puumala virus excretion with the risk of transmission to humans. Sensitivity analyses revealed the major impact of bank-vole peaks of density on the course of NE epidemics. Strikingly, maximum annual incidences of NE of ∼40/100 000 on average have been reported in northern Fennoscandia, with levels as high as 90/100 000 in Finland [1, 33] where bank-vole populations exhibit up to 500-fold changes in density. In the Ardennes region, the maximum annual incidence during the 1993 epidemic outbreak was 13·3/100 000 in France, 30/100 000 in the most affected village [30] and 12·1/100 000 in Belgium [19]. The corresponding peaks in population densities of bank voles never exceeded 100 rodents/ha [9]. These studies all indicate the importance of the amplitude of the peak phase in vole population levels for the risk of human contamination. Also the coincidence of maximum rodent numbers with incidence of human disease explains the simultaneous peaks in infection rates of human subjects and reservoir bank voles [1, 32]. We have tested our hypothesis by constructing a model of Puumala virus–bank vole interactions, including demographic variations and the risk of human infection through inhalation of contaminated rodent excreta in the air.

Our model showed that the course of Puumala virus infections in both humans and bank voles were highly dependent upon variability in vole demography. An explosive spread of the rodent infection, with up to 20% of soil litter being contaminated, occurred during the peak year of the vole cycle. Such a build-up of the rodent populations, and the concomitant increase in the environmental contamination, resulted in an increasing risk of human contamination, according to observations [32]. The model also showed that stable populations of bank voles could carry the virus persistently, but that the relatively high proportion of chronically infected animals excreting low levels of virus did not cause the threshold for human infection to be attained. The contamination risk of humans living in vicinity of stable vole populations was low, due to low environmental viral concentrations. The absence of NE cases in southern France probably results from relatively stable bank-vole demography [7] rather than an absence of virus. The diagnoses of only two NE cases in the stable vole population area strengthen this hypothesis. Conversely, if the bank-vole population dynamics were to change suddenly, for whatever reason, viral excretion could reach threshold levels and potentially cause a health emergency. If the mechanism we describe above can be generalized to many or even all hantaviral infections, then the potential area at risk for emerging hantavirus disease should be greatly extended. Disturbances in stable demographic patterns of reservoir rodents could lead to new emergence of potential and previously unrecognized pathogens. In addition, sensitivity of the model to the length of virus survival highlighted that factors increasing virus survival outside its host may greatly facilitate human contaminations. If factors allowing for rodent density bursts and an increased virus survival are the same, they may act in synergy to lead to NE emergence.

In conclusion, we suggest that it is imperative to establish the true rate of Puumala virus infection in bank voles of southern France, as a measure of the risk that would incur following a disturbance to vole demography. The mechanism that we examined here of increased human exposure due to explosive reservoir dynamics should be added to the various factors already recognized in pathogen emergence [38–44]. Disturbances to reservoir demography can have many causes, such as environmental change due to human activities or climatic disasters. Such events act through modifications in distribution and dynamics of pathogens and their vectors. Recent pathogen emergence in wildlife and humans [38, 43] represent an additional, hidden cost of wildlife habitat alteration. The precise mechanism of emergence often remains poorly understood for a wide variety of vector-borne diseases. Our model of hantavirus emergence from rodent populations suggests that the consequence of disturbing events on the demographic characteristics of intermediate and reservoir hosts should be studied as a potential risk indicator.

ACKNOWLEDGMENTS

We thank T. Greenland, N. G. Yoccoz, J. M. Gaillard, N. Bahi-Jaber and S. Devillard for helpful comments on an earlier version. This study was financed by the Institut National de la Santé et de la Recherche Médicale (INSERM); the Centre National de la Recherche Scientifique (CNRS), and the Agence Nationale de la Recherche (ANR) ‘Programme Santé-Environnement et Santé-Travail’.

DECLARATION OF INTEREST

None.

REFERENCES

1.Olsson GE et al. Demographic factors associated with hantavirus infection in bank voles (Clethrionomys glareolus) Emerging Infectious Diseases. 2002;8:924–929. doi: 10.3201/eid0809.020037. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Keeling MJ, Gilligan CA. Bubonic plague: a metapopulation model of a zoonosis. Proceedings of the Royal Society of London Series B. 2000;267:2219–2230. doi: 10.1098/rspb.2000.1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Schmaljohn C, Hjelle B. Hantaviruses: a global disease problem. Emerging Infectious Diseases. 1997;3:95–104. doi: 10.3201/eid0302.970202. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Olsson GE et al. Human hantavirus infections, Sweden. Emerging Infectious Diseases. 2003;9:1395–1401. doi: 10.3201/eid0911.030275. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Shope RE. A midcourse assessment of hantavirus pulmonary syndrome. Emerging Infectious Diseases. 1999;5:172–174. doi: 10.3201/eid0501.990124. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Asikainen K et al. Molecular evolution of Puumala hantavirus in Fennoscandia: phylogenetic analysis of strains from two recolonization routes, Karelia and Denmark. Journal of General Virology. 2000;81:2833–2841. doi: 10.1099/0022-1317-81-12-2833. [DOI] [PubMed] [Google Scholar]
7.Yoccoz NG, Hansson L, Ims RA. Geographical differences in size, reproduction and behaviour of bank voles in relation to density variations. Polish Journal of Ecology. 2000;48:63–72. [Google Scholar]
8.Niklasson B et al. Temporal dynamics of Puumala virus antibody prevalence in voles and of nephropathia epidemica incidence in humans. American Journal of Tropical Medicine and Hygiene. 1995;53:134–140. doi: 10.4269/ajtmh.1995.53.134. [DOI] [PubMed] [Google Scholar]
9.Escutenaire S et al. Spatial and temporal dynamics of Puumala hantavirus infection in red bank vole (Clethrionomys glareolus) populations in Belgium. Virus Research. 2000;67:91–107. doi: 10.1016/s0168-1702(00)00136-2. [DOI] [PubMed] [Google Scholar]
10.Gavrilovskaya IN et al. Pathogenesis of hemorrhagic fever with renal syndrome virus infection and mode of horizontal transmission of hantavirus in bank voles. Archives of Virology. 1990:57–62. ; Suppl. 1: [Google Scholar]
11.Sauvage F et al. Modelling hantavirus in cyclic bank voles: the role of indirect transmission on virus persistence. Journal of Animal Ecology. 2003;72:1–13. [Google Scholar]
12.Anderson RM, May RM. Population biology of infectious diseases: Part 1. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
13.Escutenaire S et al. Behavioral, physiologic, and habitat influences on the dynamics of Puumala virus infection in bank voles (Clethrionomys glareolus) Emerging Infectious Diseases. 2002;8:930–936. doi: 10.3201/eid0809.010537. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Bernshtein AD et al. Dynamics of Puumala hantavirus infection in naturally infected bank voles (Clethrionomys glareolus) Archives of Virology. 1999;144:2415–2428. doi: 10.1007/s007050050654. [DOI] [PubMed] [Google Scholar]
15.Begon M et al. The population dynamics of cowpox virus infection in bank voles: testing fundamental assumptions. Ecology Letters. 1998;1:82–86. [Google Scholar]
16.Verhagen R et al. Ecological and epidemiological data on hantavirus in bank vole populations in Belgium. Archives of Virology. 1986;91:193–205. doi: 10.1007/BF01314280. [DOI] [PubMed] [Google Scholar]
17.Rozenfeld FM, Le Boulenge E, Rasmont R. Urine marking by male bank voles (Clethrionomys glareolus Schreber, 1780; Microtidae, Rodentia) in relation to their social rank. Canadian Journal of Zoology. 1987;65:2594–2601. [Google Scholar]
18.Bujalska G, Tamarin R, Ostfeld R, Pugh S, Bujalska G. Social System and Population Cycles in Voles. Basel: ALS-Verlag, Birkhauser-Verlag; 1990. Social system of the bank vole Clethrionomys glareolus; pp. 155–167. , pp. [Google Scholar]
19.Crowcroft NS et al. Risk factors for human hantavirus infection: Franco-Belgian collaborative case-control study during 1995–1996 epidemic. British Medical Journal. 1999;318:1737–1738. doi: 10.1136/bmj.318.7200.1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Hart CA, Bennett M. Hantavirus infections: epidemiology and pathogenesis. Microbes and Infection. 1999;1:1229–1237. doi: 10.1016/s1286-4579(99)00238-5. [DOI] [PubMed] [Google Scholar]
21.Innes DGL, Millar JS. Life histories of Clethrionomys and Microtus (Microtinae) Mammal Review. 1994;24:179–207. [Google Scholar]
22.Verhagen R, Leirs H, Verheyen W. Demography of Clethrionomys glareolus, Belgium. Polish Journal of Ecology. 2000;48:113–123. [Google Scholar]
23.Heyman P et al. Incidence of hantavirus infections in Belgium. Virus Research. 2001;77:71–80. doi: 10.1016/s0168-1702(01)00267-2. [DOI] [PubMed] [Google Scholar]
24.Mironov A, Tamarin R, Ostfeld R, Pugh S, Bujalska G. Social System and Population Cycles in Voles. Basel: ALS-Verlag, Birkhauser-Verlag; 1990. Spatial and temporal organization of populations of the bank vole; pp. 181–193. , pp. [Google Scholar]
25.Berthier K et al. Dynamics of a feline virus with two transmission modes within exponentially growing host populations. Proceedings of the Royal Society of London Series B. 2000;267:2049–2056. doi: 10.1098/rspb.2000.1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Kallio E. 2nd European Meeting on Viral Zoonoses. 2003. Stability of Puumala-virus outside the host. , St Raphaël, 27–30 September . [Google Scholar]
27.Collard JMet al. Biosafety in laboratories manipulating Mycobacterium tuberculosis or specimens potentially contaminated with the tuberculose bacilli. Abstract for the 4th Symposium of the National Committee of Microbiology, Brussels, 22 March 1996
28.Patrick W, Layne SI, Beugelsdijk TJ, Patel CKN. Firepower in the Lab: automation in the fight against infectious diseases and bioterrorism. Washington: Joseph Henry Press; 2001. Biological warfare scenarios; pp. 215–224. , pp. [Google Scholar]
29.Monroe M et al. Genetic diversity and distribution of Peromyscus-borne hantaviruses in North America. Emerging Infectious Diseases. 1999;5:75–86. doi: 10.3201/eid0501.990109. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Penalba C, Galempoix J-M, Lanoux P. Epidemiology of hantavirus infections in France [in French] Médecine et Maladies Infectieuses. 2001;31:272–284. [Google Scholar]
31.MathWorks, Inc 2000. . Matlab, the language of technical computing. Version 6, Release 12,
32.Sauvage F et al. Puumala hantavirus infection in humans and in the reservoir host, Ardennes region, France. Emerging Infectious Diseases. 2002;8:1509–1511. doi: 10.3201/eid0812.010518. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Brummer-Korvenkotio M, Henttonen H, Vaheri A. Hemorrhagic fever with renal syndrome in Finland: ecology and virology of nephropathia epidemica. Scandinavian Journal of Infectious Diseases. 1982;36:88–91. [PubMed] [Google Scholar]
34.Acuna-Soto R et al. Megadrought and megadeath in 16th Century Mexico. Emerging Infectious Diseases. 2002;8:360–362. doi: 10.3201/eid0804.010175. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Yates T et al. The ecology and evolutionary history of an emergent disease: Hantavirus Pulmonary syndrome. Bioscience. 2002;52:989–998. [Google Scholar]
36.Chastel C. Were hantaviruses eventually responsible for the lost Anasazi culture? Acta Virologica. 1998;42:353. [PubMed] [Google Scholar]
37.Stapp P, Antolin MF, Ball M. Patterns of extinction in prairie dog metapopulations: plague outbreaks follow El Nino events. Frontiers in Ecology and the Environment. 2004;2:235–240. [Google Scholar]
38.Morse SS. Factors in the emergence of infectious diseases. Emerging Infectious Diseases. 1995;1:7–15. doi: 10.3201/eid0101.950102. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Daszak P, Cunningham AA, Hyatt AD. Emerging infectious diseases of wildlife-threats to biodiversity and human health. Science. 2000;287:443–449. doi: 10.1126/science.287.5452.443. [DOI] [PubMed] [Google Scholar]
40.Daszak P, Cunningham AA, Hyatt AD. Anthropogenic environmental change and the emergence of infectious diseases in wildlife. Acta Tropica. 2001;78:103–116. doi: 10.1016/s0001-706x(00)00179-0. [DOI] [PubMed] [Google Scholar]
41.Mayer JD. Geography, ecology and emerging infectious diseases. Social Science & Medicine. 2000;50:937–952. doi: 10.1016/s0277-9536(99)00346-9. [DOI] [PubMed] [Google Scholar]
42.Ostfeld RS, Keesing F. The function of biodiversity in the ecology of vector-borne zoonotic diseases. Canadian Journal of Zoology. 2000;78:2061–2078. [Google Scholar]
43.Patz JA et al. Effects of environmental change on emerging parasitic diseases. International Journal of Parasitology. 2000;30:1395–1405. doi: 10.1016/s0020-7519(00)00141-7. [DOI] [PubMed] [Google Scholar]
44.Dobson A, Foufopoulos J. Emerging infectious pathogens of wildlife. Philosophical Transactions of the Royal Society of London Series B. 2001;356:1001–1012. doi: 10.1098/rstb.2001.0900. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref001] 1.Olsson GE et al. Demographic factors associated with hantavirus infection in bank voles (Clethrionomys glareolus) Emerging Infectious Diseases. 2002;8:924–929. doi: 10.3201/eid0809.020037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref002] 2.Keeling MJ, Gilligan CA. Bubonic plague: a metapopulation model of a zoonosis. Proceedings of the Royal Society of London Series B. 2000;267:2219–2230. doi: 10.1098/rspb.2000.1272. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref003] 3.Schmaljohn C, Hjelle B. Hantaviruses: a global disease problem. Emerging Infectious Diseases. 1997;3:95–104. doi: 10.3201/eid0302.970202. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref004] 4.Olsson GE et al. Human hantavirus infections, Sweden. Emerging Infectious Diseases. 2003;9:1395–1401. doi: 10.3201/eid0911.030275. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref005] 5.Shope RE. A midcourse assessment of hantavirus pulmonary syndrome. Emerging Infectious Diseases. 1999;5:172–174. doi: 10.3201/eid0501.990124. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref006] 6.Asikainen K et al. Molecular evolution of Puumala hantavirus in Fennoscandia: phylogenetic analysis of strains from two recolonization routes, Karelia and Denmark. Journal of General Virology. 2000;81:2833–2841. doi: 10.1099/0022-1317-81-12-2833. [DOI] [PubMed] [Google Scholar]

[ref007] 7.Yoccoz NG, Hansson L, Ims RA. Geographical differences in size, reproduction and behaviour of bank voles in relation to density variations. Polish Journal of Ecology. 2000;48:63–72. [Google Scholar]

[ref008] 8.Niklasson B et al. Temporal dynamics of Puumala virus antibody prevalence in voles and of nephropathia epidemica incidence in humans. American Journal of Tropical Medicine and Hygiene. 1995;53:134–140. doi: 10.4269/ajtmh.1995.53.134. [DOI] [PubMed] [Google Scholar]

[ref009] 9.Escutenaire S et al. Spatial and temporal dynamics of Puumala hantavirus infection in red bank vole (Clethrionomys glareolus) populations in Belgium. Virus Research. 2000;67:91–107. doi: 10.1016/s0168-1702(00)00136-2. [DOI] [PubMed] [Google Scholar]

[ref010] 10.Gavrilovskaya IN et al. Pathogenesis of hemorrhagic fever with renal syndrome virus infection and mode of horizontal transmission of hantavirus in bank voles. Archives of Virology. 1990:57–62. ; Suppl. 1: [Google Scholar]

[ref011] 11.Sauvage F et al. Modelling hantavirus in cyclic bank voles: the role of indirect transmission on virus persistence. Journal of Animal Ecology. 2003;72:1–13. [Google Scholar]

[ref012] 12.Anderson RM, May RM. Population biology of infectious diseases: Part 1. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]

[ref013] 13.Escutenaire S et al. Behavioral, physiologic, and habitat influences on the dynamics of Puumala virus infection in bank voles (Clethrionomys glareolus) Emerging Infectious Diseases. 2002;8:930–936. doi: 10.3201/eid0809.010537. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref014] 14.Bernshtein AD et al. Dynamics of Puumala hantavirus infection in naturally infected bank voles (Clethrionomys glareolus) Archives of Virology. 1999;144:2415–2428. doi: 10.1007/s007050050654. [DOI] [PubMed] [Google Scholar]

[ref015] 15.Begon M et al. The population dynamics of cowpox virus infection in bank voles: testing fundamental assumptions. Ecology Letters. 1998;1:82–86. [Google Scholar]

[ref016] 16.Verhagen R et al. Ecological and epidemiological data on hantavirus in bank vole populations in Belgium. Archives of Virology. 1986;91:193–205. doi: 10.1007/BF01314280. [DOI] [PubMed] [Google Scholar]

[ref017] 17.Rozenfeld FM, Le Boulenge E, Rasmont R. Urine marking by male bank voles (Clethrionomys glareolus Schreber, 1780; Microtidae, Rodentia) in relation to their social rank. Canadian Journal of Zoology. 1987;65:2594–2601. [Google Scholar]

[ref018] 18.Bujalska G, Tamarin R, Ostfeld R, Pugh S, Bujalska G. Social System and Population Cycles in Voles. Basel: ALS-Verlag, Birkhauser-Verlag; 1990. Social system of the bank vole Clethrionomys glareolus; pp. 155–167. , pp. [Google Scholar]

[ref019] 19.Crowcroft NS et al. Risk factors for human hantavirus infection: Franco-Belgian collaborative case-control study during 1995–1996 epidemic. British Medical Journal. 1999;318:1737–1738. doi: 10.1136/bmj.318.7200.1737. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref020] 20.Hart CA, Bennett M. Hantavirus infections: epidemiology and pathogenesis. Microbes and Infection. 1999;1:1229–1237. doi: 10.1016/s1286-4579(99)00238-5. [DOI] [PubMed] [Google Scholar]

[ref021] 21.Innes DGL, Millar JS. Life histories of Clethrionomys and Microtus (Microtinae) Mammal Review. 1994;24:179–207. [Google Scholar]

[ref022] 22.Verhagen R, Leirs H, Verheyen W. Demography of Clethrionomys glareolus, Belgium. Polish Journal of Ecology. 2000;48:113–123. [Google Scholar]

[ref023] 23.Heyman P et al. Incidence of hantavirus infections in Belgium. Virus Research. 2001;77:71–80. doi: 10.1016/s0168-1702(01)00267-2. [DOI] [PubMed] [Google Scholar]

[ref024] 24.Mironov A, Tamarin R, Ostfeld R, Pugh S, Bujalska G. Social System and Population Cycles in Voles. Basel: ALS-Verlag, Birkhauser-Verlag; 1990. Spatial and temporal organization of populations of the bank vole; pp. 181–193. , pp. [Google Scholar]

[ref025] 25.Berthier K et al. Dynamics of a feline virus with two transmission modes within exponentially growing host populations. Proceedings of the Royal Society of London Series B. 2000;267:2049–2056. doi: 10.1098/rspb.2000.1248. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref026] 26.Kallio E. 2nd European Meeting on Viral Zoonoses. 2003. Stability of Puumala-virus outside the host. , St Raphaël, 27–30 September . [Google Scholar]

[ref027] 27.Collard JMet al. Biosafety in laboratories manipulating Mycobacterium tuberculosis or specimens potentially contaminated with the tuberculose bacilli. Abstract for the 4th Symposium of the National Committee of Microbiology, Brussels, 22 March 1996

[ref028] 28.Patrick W, Layne SI, Beugelsdijk TJ, Patel CKN. Firepower in the Lab: automation in the fight against infectious diseases and bioterrorism. Washington: Joseph Henry Press; 2001. Biological warfare scenarios; pp. 215–224. , pp. [Google Scholar]

[ref029] 29.Monroe M et al. Genetic diversity and distribution of Peromyscus-borne hantaviruses in North America. Emerging Infectious Diseases. 1999;5:75–86. doi: 10.3201/eid0501.990109. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref030] 30.Penalba C, Galempoix J-M, Lanoux P. Epidemiology of hantavirus infections in France [in French] Médecine et Maladies Infectieuses. 2001;31:272–284. [Google Scholar]

[ref031] 31.MathWorks, Inc 2000. . Matlab, the language of technical computing. Version 6, Release 12,

[ref032] 32.Sauvage F et al. Puumala hantavirus infection in humans and in the reservoir host, Ardennes region, France. Emerging Infectious Diseases. 2002;8:1509–1511. doi: 10.3201/eid0812.010518. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref033] 33.Brummer-Korvenkotio M, Henttonen H, Vaheri A. Hemorrhagic fever with renal syndrome in Finland: ecology and virology of nephropathia epidemica. Scandinavian Journal of Infectious Diseases. 1982;36:88–91. [PubMed] [Google Scholar]

[ref034] 34.Acuna-Soto R et al. Megadrought and megadeath in 16th Century Mexico. Emerging Infectious Diseases. 2002;8:360–362. doi: 10.3201/eid0804.010175. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref035] 35.Yates T et al. The ecology and evolutionary history of an emergent disease: Hantavirus Pulmonary syndrome. Bioscience. 2002;52:989–998. [Google Scholar]

[ref036] 36.Chastel C. Were hantaviruses eventually responsible for the lost Anasazi culture? Acta Virologica. 1998;42:353. [PubMed] [Google Scholar]

[ref037] 37.Stapp P, Antolin MF, Ball M. Patterns of extinction in prairie dog metapopulations: plague outbreaks follow El Nino events. Frontiers in Ecology and the Environment. 2004;2:235–240. [Google Scholar]

[ref038] 38.Morse SS. Factors in the emergence of infectious diseases. Emerging Infectious Diseases. 1995;1:7–15. doi: 10.3201/eid0101.950102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref039] 39.Daszak P, Cunningham AA, Hyatt AD. Emerging infectious diseases of wildlife-threats to biodiversity and human health. Science. 2000;287:443–449. doi: 10.1126/science.287.5452.443. [DOI] [PubMed] [Google Scholar]

[ref040] 40.Daszak P, Cunningham AA, Hyatt AD. Anthropogenic environmental change and the emergence of infectious diseases in wildlife. Acta Tropica. 2001;78:103–116. doi: 10.1016/s0001-706x(00)00179-0. [DOI] [PubMed] [Google Scholar]

[ref041] 41.Mayer JD. Geography, ecology and emerging infectious diseases. Social Science & Medicine. 2000;50:937–952. doi: 10.1016/s0277-9536(99)00346-9. [DOI] [PubMed] [Google Scholar]

[ref042] 42.Ostfeld RS, Keesing F. The function of biodiversity in the ecology of vector-borne zoonotic diseases. Canadian Journal of Zoology. 2000;78:2061–2078. [Google Scholar]

[ref043] 43.Patz JA et al. Effects of environmental change on emerging parasitic diseases. International Journal of Parasitology. 2000;30:1395–1405. doi: 10.1016/s0020-7519(00)00141-7. [DOI] [PubMed] [Google Scholar]

[ref044] 44.Dobson A, Foufopoulos J. Emerging infectious pathogens of wildlife. Philosophical Transactions of the Royal Society of London Series B. 2001;356:1001–1012. doi: 10.1098/rstb.2001.0900. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Predicting the emergence of human hantavirus disease using a combination of viral dynamics and rodent demographic patterns

F SAUVAGE

M LANGLAIS

D PONTIER

SUMMARY

INTRODUCTION