Skip to main content
PMC home page
Epidemiology and Infection logoLink to Epidemiology and Infection
. 2006 Jun 26;135(2):181–194. doi: 10.1017/S0950268806006716

Randomization and baseline transmission in vaccine field trials

C J Struchiner 1,*, M E Halloran 2
PMCID: PMC2870563  PMID: 17291359

SUMMARY

In randomized trials, the treatment assignment mechanism is independent of the outcome of interest and other covariates thought to be relevant in determining this outcome. It also allows, on average, for a balanced distribution of these covariates in the vaccine and placebo groups. Randomization, however, does not guarantee that the estimated effect is an unbiased estimate of the biological effect of interest. We show how exposure to infection can be a confounder even in randomized vaccine field trials. Based on a simple model of the biological efficacy of interest, we extend the arguments on comparability and collapsibility to examine the limits of randomization to control for unmeasured covariates. Estimates from randomized, placebo-controlled Phase III vaccine field trials that differ in baseline transmission are not comparable unless explicit control for baseline transmission is taken into account.

INTRODUCTION

‘The only general way rigorously to exclude the biasing effects of other factors is to base allocation decisions as to which intervention is applied to a particular individual or group on a random mechanism’ [1]. The statement is motivated by the independence of the treatment assignment mechanism and the outcome of interest, as well as other covariates, in randomized trials. Randomization also allows, on average, for a balanced distribution of any covariates, observed or not, in the vaccine and placebo groups. Thus, the treatment groups are seen as comparable. Baseline transmission, pre-existing immunity and individual responsiveness are examples of possibly relevant factors. For these reasons, randomization, in addition to double-masking, are usually proposed as good research practices for valid clinical trials [2].

Randomization, however, does not guarantee that the estimated effect is an unbiased estimate of the biological effect of interest. The ability of randomization to control for confounding has been challenged from at least two perspectives. Greenland & Robins [3] and Greenland [4] state the problem from the perspective of potential outcomes and show that effect measures can be confounded even if the treatment assignment mechanism is random. Gail and colleagues [5–8] examine the effects of omitting a covariate that has the same distribution among exposed and unexposed subjects from regression analyses of cohort data. They describe the conditions under which a balanced covariate can be omitted without biasing the estimates.

These results also hold in randomized Phase III vaccine efficacy field trials. A new dimension is added when the covariate being considered is the natural challenge to infection, such as an infectious mosquito bite or a sexual contact, which is assigned by nature to the study participants. Although the efficacy estimate can be based on parameters such as the transmission probability that are conditional on exposure to infection [9], a special case being the secondary attack rate [10, 11], most vaccine studies do not collect information on the number of infectious challenges. Thus, most efficacy estimates are based on unconditional parameters such as incidence density, hazard rates, or incidence proportion [12]. Measures of vaccine efficacy expressed as functions of the incidence proportion [13] or hazard rates [14] depend on the level of transmission.

In this paper we focus on the role and limits of randomization in studies based on unconditional estimators of vaccine efficacy that do not explicitly take into account the number of exposures to infection that each person has [9]. Based on a simple model of the biological efficacy of interest, we extend the arguments of Greenland and Gail on comparability and collapsibility, respectively, to examine the limits of randomization to control for unmeasured covariates in vaccine field studies. We show that randomization does not guarantee easily interpretable estimates of vaccine efficacy within trials or across sites. A series of examples illustrates the extent of the bias possible under a number of plausible biological assumptions. Estimates from randomized, placebo-controlled Phase III field trials that differ in baseline transmission are not comparable unless baseline transmission and pre-existing immunity are taken into account.

STOCHASTIC RISK MODEL

Consider a double-blind vaccine trial of N subjects from the study population with vaccine randomly assigned to N1 subjects and placebo to N0 subjects. For simplicity, we consider estimating the effect of vaccine compared to placebo on the binary outcome of either becoming infected or not. To begin with, we set infection equal to disease. The pre-vaccination covariates represent the values of variables describing the individuals in the population, such as age, gender, genetic composition, pre-existing immunity. The values of any particular covariate may or may not be measured and recorded, depending on the design of the study. For example, we might not measure and record the antibody titre for each person before we begin the study.

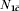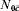For simplicity, consider a binary covariate, C, where a portion of the population has C=c and the rest has C \equals \bar{c}. Let N1c and N0c be the number in the vaccinated and unvaccinated groups with covariate value C=c, and N_{\setnum{1}\bar{c}} and N_{\setnum{0}\bar{c}} be the number in the vaccinated and unvaccinated groups with C \equals \bar{c}, respectively (Table 1).

Table 1.

Example tables template

graphic file with name S0950268806006716_tab1.jpg

Open in a new tab

Individual measures

Under a stochastic risk model, let the probability of being infected per potentially infective contact for an unvaccinated person be r0i and the probability of not being infected after one contact be 1−r0i. This is similar to the stochastic risk model of Greenland [4], except here the risk is conditional on a potentially infective contact. All individuals in whom the infection was not successful at the time of the infective contact return to the pool of individuals at risk to become infected. Analogously, let the probability that a vaccinated individual becomes infected after one exposure to infection be r1i and of not being infected be 1−r1i. The unknown probabilities r0i and r1i are called the individual transmission probabilities per potentially infectious contact. An individual thus has two different potential transmission probabilities, one with and one without the vaccine. Which of these potential transmission probabilities determines the stochastic risk for an individual depends on whether the individual is assigned to vaccine or placebo.

Assume that the vaccine has the effect of reducing the transmission probability in an individual i by a multiplicative factor βi from r0i to r1i=βir0i, where βi could be specific to each individual. The effect of vaccination compared to no vaccination on infection outcome given one specified exposure to infection may be measured in terms of 1 minus the individual transmission probability ratio or the individual transmission probability difference:

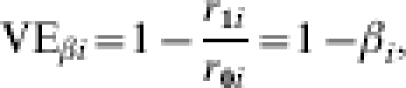{\rm VE}_{\beta i} \equals 1 \minus {{r_{\setnum{1}i} } \over {r_{\setnum{0}i} }} \equals 1 \minus \beta_{i} \comma
D_{i} \equals r_{\setnum{0}i} \minus r_{\setnum{1}i} \equals r_{\setnum{0}i} \lpar 1 \minus \beta_{i} \rpar.

The vaccine efficacy (VE) based on the ratio will be undefined if the transmission probability with no vaccine is zero. Under the multiplicative model, the risk difference depends on r0i whereas VEβi does not. Below, we also use the notation r0i=TP0i, r1i=TP1i, and βi=TPRi, as equivalent for the transmission probabilities in the unvaccinated and vaccinated individual i, and the individual transmission probability ratio.

Special role of exposure to infection

The infection outcomes in an individual would generally depend on whether a person is exposed to infection at all, the size of the inoculum, and how often the person is challenged. The probability of not being infected after the first contact, but then being infected after the second contact is (1−r0i)r0i, and so forth for any number of potentially infective contacts, so that the probability of an individual becoming infected during a study depends on the number of exposures during the study. In this paper, we assume that all exposures to infection are equivalent. We assume that the susceptibility remains the same after being exposed to infection post-randomization.

If infection or disease is an outcome of interest, the individual must receive an infectious challenge to contribute information to the study. In controlled settings with a curable disease, following vaccine and placebo allocation, individuals are sometimes challenged with a known amount of inoculum. In this case, treatment consists of both the vaccine allocation and the infectious challenge. In field trials, often individuals are not exposed to infection. These individuals are recipients of incomplete treatment and are uninformative with respect to the effect of the vaccine on infection and disease. That is, in evaluating prophylactic vaccines, there are actually two levels of treatment. The first is to give either the vaccine or placebo, which we can assign randomly to people. The second is the exposure to infection, which in field trials is assigned by nature [9].

Population measures

The fundamental problem of causal inference [9, 15] is that we cannot observe the individual i both with the vaccine and the placebo, not to mention at a specified exposure to infection, so we cannot observe the effect of the vaccine compared to placebo in the individual. What we can observe is the difference in the average observable outcomes in those who actually received placebo and the average observable outcomes in those who actually received the vaccine. Since we cannot estimate the βi for each person, we do a study in a population to estimate the average effect of the vaccine compared to the placebo. The parameter of interest is the average multiplicative effect, 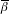\overline\beta, or the average difference in the transmission probabilities, 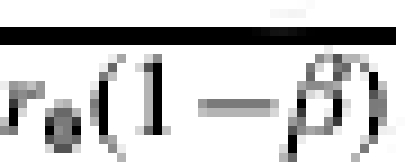\overline{r_{\setnum{0}} \lpar 1 \minus \beta \rpar}, of the vaccine in the population if the people were vaccinated compared to if they were unvaccinated.

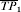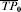Let a1 and a0 denote the expected number of cases in the vaccinated and unvaccinated groups, respectively, at the end of the study. The proportion expected to develop the infection if each individual in the group receives one exposure to infection is the average transmission probability, \overline{TP}_{\setnum{1}} and \overline{TP}_{\setnum{0}}, which is the expected number of infections divided by the number of exposures to infection:

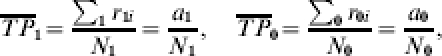\overline{TP}_{\setnum{1}} \equals {{\sum\nolimits_{\setnum{1}} r_{\setnum{1}i} } \over {N_{\setnum{1}} }} \equals {{a_{\setnum{1}} } \over {N_{\setnum{1}} }}\comma \quad \overline{TP}_{\setnum{0}} \equals {{\sum\nolimits_{\setnum{0}} r_{\setnum{0}i} } \over {N_{\setnum{0}} }} \equals {{a_{\setnum{0}} } \over {N_{\setnum{0}} }}\comma

where ∑1 and ∑0 denote summation over the vaccinated and unvaccinated groups, respectively. The proportion of the population expected to develop infection by the end of the study is the attack rate, cumulative incidence, or incidence proportion, denoted IP1 and IP0, respectively:

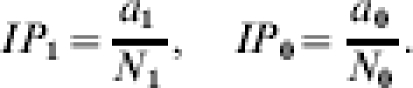IP_{\setnum{1}} \equals {{a_{\setnum{1}} } \over {N_{\setnum{1}} }}\comma \quad IP_{\setnum{0}} \equals {{a_{\setnum{0}} } \over {N_{\setnum{0}} }}.

The incidence proportions are interpreted as the average unconditional risks in the vaccinated and unvaccinated groups, respectively.

Vaccine efficacy (VE) estimated from the relative average transmission probability is

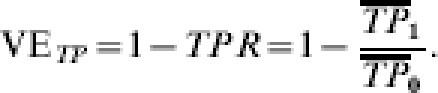{\rm VE}_{TP} \equals 1 \minus TPR \equals 1 \minus {{\overline{TP}_{\setnum{1}} } \over {\overline{TP}_{\setnum{0}} }}.

a1c and b1c denote the number of vaccinated people with covariate value C=c at the end of the study who develop infection or do not, respectively, and a0c and b0c denote the number of unvaccinated people with covariate value C=c who develop infection or do not, respectively. The analogous notation is used in the stratum with C \equals \bar{c} (Table 1). Let R=IP1/IP0. The crude measurable VE estimated from the ratio of the incidence proportions in the vaccinated group compared to the unvaccinated group is (Table 1):

\eqalign {{\rm VE}_{R} \equals \tab 1 \minus R \equals 1 \minus {{IP_{\setnum{1}} } \over {IP_{\setnum{0}} }} \equals 1 \minus {{a_{\setnum{1}} \sol N_{\setnum{1}} } \over {a_{\setnum{0}} \sol N_{\setnum{0}} }} \cr\equals\tab 1 \minus \left( {{{a_{\setnum{1}c} \plus a_{\setnum{1}\bar{c}} } \over {N_{\setnum{1}} }}\hskip-2\Big/ \hskip-1{{a_{\setnum{0}c} \plus a_{\setnum{0}\bar{c}} } \over {N_{\setnum{0}} }}} \right).

The crude risk difference measured by the difference in the incidence proportion in the vaccinated compared to the unvaccinated group is (Table 1):

IP_{D} \equals {{a_{\setnum{0}} } \over {N_{\setnum{0}} }} \minus {{a_{\setnum{1}} } \over {N_{\setnum{1}} }} \equals {{a_{\setnum{0}c} \plus a_{\setnum{0}\bar{c}} } \over {N_{\setnum{0}} }} \minus {{a_{\setnum{1}c} \plus a_{\setnum{1}\bar{c}} } \over {N_{\setnum{1}} }}.

Greenwood & Yule [16] discuss the different interpretation of the ratio and difference measures for vaccines for the incidence proportion.

The far right columns in Table 1 give the vaccine efficacy based on the crude incidence proportion ratio, the crude incidence proportion difference, and the crude odds ratios. The question of interest in this paper is to what extent, even under randomization, does the estimated efficacy measure the effect of interest? 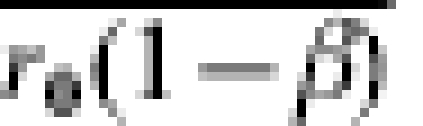In particular, if no information on actual exposure to infection is gathered, to what extent does VER estimate 1 \minus \bar{\beta} or IPD estimate \overline{r_{\setnum{0}} \lpar 1 \minus \beta \rpar}?

Randomization and comparability of treatment groups

Randomization is supposed to ensure that the vaccine and placebo groups are comparable in that the experience of the group with the vaccine would have been the same as the group that did not receive the vaccine had the vaccinated group in fact received the placebo, and vice versa. Randomization coupled with blinding is also supposed to ensure that post-randomization exposure to infection is balanced.

Under randomization, it should not matter which of the groups receives the vaccine or placebo. Following Greenland & Robins [3], we say there is no confounding due to lack of comparability if, in the absence of vaccination, the average risk would have been the same among the people who in fact were vaccinated and those who were not vaccinated. 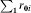Under the assumption of comparability of the two groups, we can replace the experience of the unvaccinated group with the experience of the vaccinated group if it had not been vaccinated, so that \sum\nolimits_{\setnum{0}} r_{\setnum{0}i} \sol N_{\setnum{0}} \equals \sum\nolimits_{\setnum{1}} r_{\setnum{0}i} \sol N_{\setnum{1}}. Here \sum\nolimits_{\setnum{1}} r_{\setnum{0}i} denotes the experience that the vaccinated group would have had if they had not been vaccinated and exposed just once to infection. By balancing the distribution of observed and unobserved covariates in a study, randomization is supposed to ensure that the vaccinated and unvaccinated groups are comparable. The expected proportion of the unvaccinated and vaccinated groups in either level of a binary covariate should be the same in both groups,

{{N_{\setnum{1}c} } \over {N_{\setnum{1}} }} \equals {{N_{\setnum{0}c} } \over {N_{\setnum{0}} }}\comma \quad {{N_{\setnum{1}\bar{c}} } \over {N_{\setnum{1}} }} \equals {{N_{\setnum{0}\bar{c}} } \over {N_{\setnum{0}} }}.

The conditions for comparability rely on the assumption that the outcome in each individual is independent of the outcomes and treatment assignments in the other individuals. The independence is part of the stable unit treatment value assumption (SUTVA) [17]. Halloran & Struchiner [9] consider consequences of the violation of SUTVA in more detail. If we imagine that a small proportion of the population is vaccinated in the trial, then the violations would be minimal.

Limits of comparability with one homogeneous exposure to infection

In this section, we assume that everyone is exposed exactly once to infection during the study. If the trial participants were each to receive a single infectious challenge (infected mosquito bite), the expected incidence proportion ratio equals the expected average transmission probability ratio:

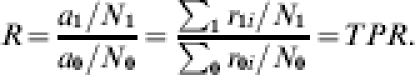R \equals {{a_{\setnum{1}} \sol N_{\setnum{1}} } \over {a_{\setnum{0}} \sol N_{\setnum{0}} }} \equals {{\sum\nolimits_{\setnum{1}} r_{\setnum{1}i} \sol N_{\setnum{1}} } \over {\sum\nolimits_{\setnum{0}} r_{\setnum{0}i} \sol N_{\setnum{0}} }} \equals TPR.

Following the arguments of Greenland [4], even under the assumption of comparability, and exactly one exposure to infection per person, the ratio of the incidence proportions (average transmission probabilities) is not equal to the average of the individual ratios of the transmission probabilities, 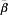\bar{\beta}. Formally, assuming comparability, the expected incidence proportion ratio (ratio of the average transmission probabilities) is

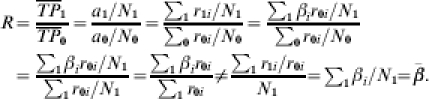\eqalign{\hskip-2 R \equals \tab {{\overline{TP}_{\setnum{1}} } \over {\overline{TP}_{\setnum{0}} }} \equals {{{\textstyle{{a_{\setnum{1}} }\sol {N_{\setnum{1}} }}}} \over {{\textstyle{{a_{\setnum{0}} } \sol {N_{\setnum{0}} }}}}} \equals {{{\textstyle{{\sum\nolimits_{\setnum{1}} r_{\setnum{1}i} } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{\sum\nolimits_{\setnum{0}} r_{\setnum{0}i} } \sol {N_{\setnum{0}} }}}}} \equals {{{\textstyle{{\sum\nolimits_{\setnum{1}} \beta_{i} r_{\setnum{0}i} } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{\sum\nolimits_{\setnum{0}} r_{\setnum{0}i} } \sol {N_{\setnum{0}} }}}}} \cr\equals \tab {{{\textstyle{{\sum\nolimits_{\setnum{1}} \beta_{i} r_{\setnum{0}i} } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{\sum\nolimits_{\setnum{1}} r_{\setnum{0}i} } \sol {N_{\setnum{1}} }}}}} \equals {{{\sum\nolimits_{\setnum{1}} \beta_{i} r_{\setnum{0}i} } \over {\sum\nolimits_{\setnum{1}} r_{\setnum{0}i} }}} \ne {{{\sum\nolimits_{\setnum{1}} {{{{r}_{\setnum{1}i} } \sol {{r}_{\setnum{0}i} }}}} \over {N_{\setnum{1}} }}} \equals {\textstyle{{\sum\nolimits_{\setnum{1}} \beta_{i} } \sol {N_{\setnum{1}} }}}\hskip-2 \equals \bar{\beta }.}

The inequality is true in general, unless the r1i/r0i=β are the same for all i in the vaccinated group, a very strong assumption. In other words, the previous expressions indicate that the population level measure of efficacy based on either the transmission probability or the incidence proportion cannot be interpreted as the average, among the study population, of the individual effect of the vaccine, except in the unlikely case that β=r1i/r0i for each individual i in the population. In general, the expected value of R is biased for the average effect of the vaccine in the vaccinated group, 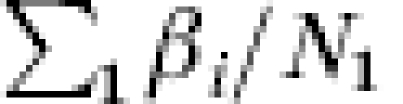\sum\nolimits_{\setnum{1}} \beta_{i} \sol N_{\setnum{1}}, in randomized double-blind, Phase III vaccine trials.

In contrast, under the assumption of comparability, the difference IPD of the incidence proportions (or average transmission probabilities) in the unvaccinated and vaccinated groups is equal to the average of the individual differences in the transmission probabilities, even when individuals have different vaccine responses βi:

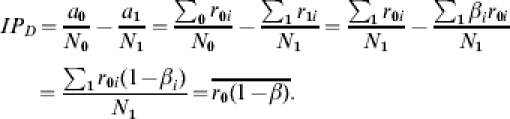\openup3\eqalign{\tab\displaystyle{ IP_{D} \equals {{a_{\setnum{0}} } \over {N_{\setnum{0}} }} \minus {{a_{\setnum{1}} } \over {N_{\setnum{1}} }} \equals {{\sum\nolimits_{\setnum{0}} r_{\setnum{0}i} } \over {N_{\setnum{0}} }} \minus {{\sum\nolimits_{\setnum{1}} r_{\setnum{1}i} } \over {N_{\setnum{1}} }} \equals {{\sum\nolimits_{\setnum{1}} r_{\setnum{0}i} } \over {N_{\setnum{1}} }} \minus {{\sum\nolimits_{\setnum{1}} \beta_{i} r_{\setnum{0}i} } \over {N_{\setnum{1}} }} } \cr \tab\quad\hskip6{\equals {{\sum\nolimits_{\setnum{1}} r_{\setnum{0}i} \lpar 1 \minus \beta_{i} \rpar } \over {N_{\setnum{1}} }} \equals \overline{r_{\setnum{0}} \lpar 1 \minus \beta \rpar}.}

Comparability-based confounding: homogeneous effect; two or more exposures to infection

To illustrate confounding due to unmeasured post-vaccination exposure to infection, we assume for simplicity that the effect of the vaccine on susceptibility is the same in everyone, that is βi=β for each individual i, but that everyone receives two challenges to infection (see also [13]). We assume that the first contact with the infective agent does not leave an immune memory. If everyone is challenged twice, then the expected number of cases in the unvaccinated group is the number of people expected to get infected from the first challenge plus the number of people expected to get infected from the second challenge, 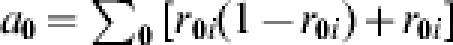a_{\setnum{0}} \equals \sum\nolimits_{\setnum{0}} \lsqb r_{\setnum{0}i} \lpar 1 \minus r_{\setnum{0}i} \rpar \plus r_{\setnum{0}i} \rsqb. The number of cases in the vaccinated group is a_{\setnum{1}} \equals \sum\nolimits_{\setnum{1}} \lsqb r_{\setnum{1}i} \lpar 1 \minus r_{\setnum{1}i} \rpar \plus r_{\setnum{1}i} \rsqb. Under the assumption of comparability of the vaccinated and unvaccinated groups:

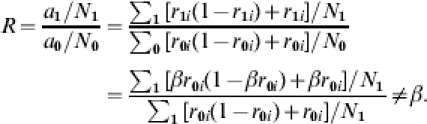\openup3\eqalign{R \equals{{{\textstyle{{a_{\setnum{1}} } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{a_{\setnum{0}} } \sol {N_{\setnum{0}} }}}}} \equals\tab {{{\textstyle{{\sum\nolimits_{\setnum{1}} \lsqb r_{\setnum{1}i} \lpar 1 \minus r_{\setnum{1}i} \rpar \plus r_{\setnum{1}i} \rsqb } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{\sum\nolimits_{\setnum{0}} \lsqb r_{\setnum{0}i} \lpar 1 \minus r_{\setnum{0}i} \rpar \plus r_{\setnum{0}i} \rsqb } \sol {N_{\setnum{0}} }}}}} \cr\equals\tab {{{\textstyle{{\sum\nolimits_{\setnum{1}} \lsqb \beta r_{\setnum{0}i} \lpar 1 \minus \beta r_{\setnum{0}i} \rpar \plus \beta r_{\setnum{0}i} \rsqb } \sol {N_{\setnum{1}} }}}} \over {{\textstyle{{\sum\nolimits_{\setnum{1}} \lsqb r_{\setnum{0}i} \lpar 1 \minus r_{\setnum{0}i} \rpar \plus r_{\setnum{0}i} \rsqb } \sol {N_{\setnum{1}} }}}}} \ne \beta.

If we had information on the number of exposures to infection and knew after which exposure each person becomes infected, we could use the transmission probability ratios to estimate the effect of the vaccine, although even the ratio 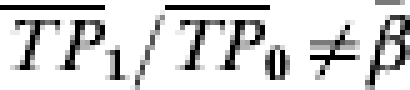\overline{TP}_{\setnum{1}} \sol \overline{TP}_{\setnum{0}} \ne \bar{\beta} unless βi=β.

If the investigator did not have access to information on exposure to infection, as in field trials based on unconditional parameters such as incidence proportion, he or she would report vaccine efficacy as 1−(a1/N1)/(a0/N0)≠1−β. Thus, exposure to infection can be a confounder even in a double-blind, placebo-controlled trial in which randomization ensures comparability, and in particular, when the exposure to infection is not only comparable in the two groups, but homogeneous within groups. This result holds even if the transmission probability is homogeneous for everyone.

As a corollary to this result, since the number of challenges to infection, assigned by nature in field trials, depends on the baseline transmission level, two different randomized, double-blind, placebo-controlled studies taking place in sites that differ by the level of transmission would report different estimates of vaccine efficacy even if the level of protection conferred by the vaccine to a specified challenge to infection is the same in both studies.

The previous result is easily extended to the more realistic situation that in field conditions, nature provides the infection challenge and, thus, some individuals are not challenged at all, some are challenged just once, and some are challenged twice or more. In the general case, the inequality holds even if r0i=r0, and r1i=r1. A similar argument could be constructed to show that the difference of IP0−IP1 does not equal the average difference in susceptibility in the vaccinated compared to the unvaccinated groups, 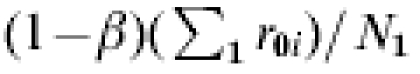\lpar 1 \minus \beta \rpar \lpar \sum\nolimits_{\setnum{1}} r_{\setnum{0}i} \rpar \sol N_{\setnum{1}}. In summary, the population measure of R does not estimate β, and there can be confounding even when (1) the study is randomized, (2) the multiplicative effect of the vaccine is the same for all individuals, i.e. there is no heterogeneity in vaccine efficacy, (3) comparability is preserved, i.e. controls describe what would have happened to the vaccinated group if they had not been vaccinated, (4) the amount of infectious challenge is the same among vaccinated and unvaccinated, and (5) whether SUTVA is violated or not.

Collapsibility with balance of unmeasured covariates

Because on average, randomization achieves balance of pre-vaccination covariates, under certain conditions [5–8], a covariate can be omitted from the analysis without changing the value of the regression parameter of interest. In this case, the analysis is said to be collapsible with respect to the covariates, and such covariates are called non-confounders. The discussions related to collapsibility and omitting a balanced covariate from regression models are concerned with statistical bias and are model-dependent [18]. Greenland [19] argues against the identification of effects with regression model coefficients, since that results in model dependence of causal concepts such as ‘effect’ and ‘confounder’ which is undesirable and unnecessary. Randomized clinical trials analysed with linear or multiplicative models yield unbiased estimates of regression coefficients which, however, are not necessarily appropriate estimates of the individual biological effect of a vaccine [20].

Collapsibility-based confounding

Suppose that the stratum-specific incidence proportion ratio for the jth stratum is Rj=IP0j/IP1j, where the jth stratum is defined in terms of the number j of exposures to infection, j=0, …, J, where J is the maximum number of exposures possible in the study, and,

k \equals R_{\setnum{1}} \equals \cdots \equals R_{j} \equals \cdots \equals R_{J}.

As seen earlier, this assumption cannot be true even if there is a common multiplicative effect of the vaccine, β=r1i/r0i for all i, because then the Rj would differ. Thus, neither the crude measure of effect, nor the adjusted measure of effect once baseline transmission level is controlled for, are easily interpretable.

Interpretation of a multiplicative measure of efficacy, even in the absence of confounding defined in terms of collapsibility [18], is problematic unless one makes the very unlikely assumptions that the biological effect is the same for all individuals and that study participants could be challenged at most once, in which case all people in the study would share the same value of the covariate defined by the number of exposures to infection.

Heterogeneity of effect: effect modification

We now consider the special case that there are strata within which the effect of the vaccine is homogeneous, but that it varies among subgroups. This heterogeneity of effect is called effect modification in the epidemiological literature. Of actual interest would be estimation of the different efficacies in each strata. If it is not possible to stratify on the relevant variable, then the efficacy measure will be a summary measure under heterogeneity [21]. The estimated crude efficacy will depend on the proportional composition of the population of each subgroup in which the vaccine has a different effect.

Examples

We present several examples of how unmeasured covariates, and in particular, unmeasured pre-vaccination or post-vaccination exposure to infection, could alter the estimates of vaccine efficacy even if the field trial were randomized. In every case considered, the vaccine trial is a randomized, double-blind, placebo-controlled trial. In developing these examples, we had in mind an infection like malaria, although the results are quite general. For those readers who know the malaria literature, the transmission probability, TP0, or r0, corresponds to the b in the usual malaria models, the probability that a sporozoite-positive mosquito bite results in successful infection.

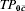In the examples, the covariate C can play several different roles. If C is related to a pre-vaccination covariate that affects susceptibility, then the risk of infection per potentially infective contact in the unvaccinated group with C=c is TP0c and in the unvaccinated group with covariate value C \equals \bar{c} is TP_{\setnum{0}\bar{c}} (Table 1). 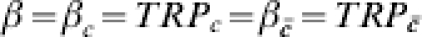If the vaccine effect is the same at both covariate levels, then \beta \equals \beta_{c} \equals TRP_{c} \equals \beta_{\bar{c}} \equals TRP_{\bar{c}}.

If the vaccine effect is related to C, then TPRc=βc=TP1c/ TP0c. The effect of the vaccine in the stratum with C \equals \bar{c} is TPR_{\bar{c}} \equals \beta_{\bar{c}} \equals TP_{\setnum{1}\bar{c}} \sol TP_{\setnum{0}\bar{c}}. In this case, there would be two measures of effect of interest that would be measurable if it were possible to stratify on the covariate C. 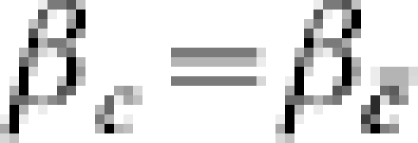The covariate C could also be related only to the number of post-vaccination exposures to infection with a homogeneous effect of vaccination, so that TP_{\setnum{0}\bar{c}} \equals TP_{\setnum{0}c}, and \beta_{c} \equals \beta_{\bar{c}}. Table 1 is a template for the examples.

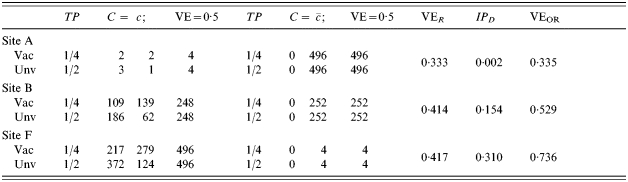
C is post-vaccination challenge; homogeneous VE; infectious challenge as a confounder

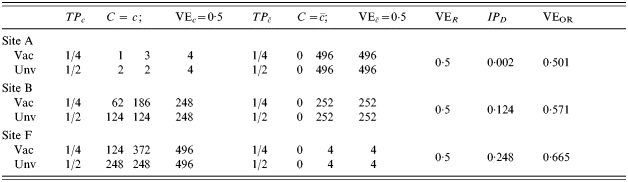
Consider a vaccine candidate that is being evaluated in different trials, possibly on different continents (Table 2). Let the trial sites be designated by capital letters, such as A, B, and F. In Table 2, we consider a situation in which the response to the vaccine is actually homogeneous within each trial site and across each trial site, but that not everyone gets exposed to infection. Thus, C=c denotes being exposed to infection just once, while C \equals \bar{c} denotes not being exposed to infection. The transmission probability in the unvaccinated susceptibles, TP0=0·5, and the effect of the vaccine in reducing the transmission probability, TPR=TP1/TP0=0·5, are the same for all study participants in all three sites. Thus, {\rm VE}_{c} \equals {\rm VE}_{\bar{c}}. In Table 2, the proportion receiving exactly one exposure to infection (C=c) increases from 3% in site A to 97% in site F. The estimated efficacy based on VER is 0·5 regardless of the proportion exposed to infection during the trial, so that under this multiplicative effect model, heterogeneous exposure to infection does not act as a confounder if the maximum number of exposures to infection is 1. The IPD increases from 0·002 at site A to 0·248 in site F, reflecting that the vaccine is more important as a public health tool when more people are exposed to infection.

Table 2.

Homogeneous pre-vaccination susceptibility among sites, homogeneity of vaccine effect within sites, no boosting, and increasing Nc; infectious challenge as a confounder, one exposure to infection in stratum C=c and 0 otherwise (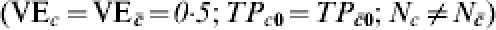{\rm VE}_{c} \equals {\rm VE}_{\bar{c}} \equals {\it 0\cdot5}\semi \,TP_{c\setnum{0}} \equals TP_{\bar{c}\setnum{0}} \semi \,N_{c} \ne N_{\bar{c}})

graphic file with name S0950268806006716_tab2.jpg

Open in a new tab

In Table 3, those people who are exposed to infection (C=c) are exposed twice, compared to only once in Table 2. Otherwise the situations in Tables 2 and 3 are the same. This situation illustrates exposure to infection as a confounder, since the expected VER decreases from 0·5 in site A in Table 2 to 0·333 at site A in Table 3. At site F, the VER decreases from 0·5 in Table 2 to 0·417 in Table 3. In Table 3, the change in IPD from site A to site F is greater than in the situation of lower transmission in Table 2.

Table 3.

Homogeneous pre-vaccination susceptibility among sites, homogeneity of vaccine effect within sites, no boosting, and increasing Nc; infectious challenge as a confounder, two exposures to infection in stratum C=c and 0 otherwise (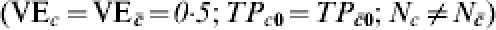{\rm VE}_{c} \equals {\rm VE}_{\bar{c}} \equals {\it 0\cdot5}\semi \,TP_{c\setnum{0}} \equals TP_{\bar{c}\setnum{0}} \semi \,N_{c} \ne N_{\bar{c}})

graphic file with name S0950268806006716_tab3.jpg

Open in a new tab

C is related to heterogeneous VE; effect modification

In Table 4, we assume that in all sites, an immunologically naive susceptible person has a probability of r0i=r0=TP0=1·0 of becoming infected after one exposure to infection. The vaccine effect is heterogeneous. The heterogeneous response could be due to a covariate unrelated to history of exposure to infection, such as genetic composition or gender. One half of the population has C=c and the vaccine reduces the transmission probability by 0·5, so that TPRc=0·5, and VEc=0·5. 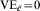One half of the population has C \equals \bar{c} and the vaccine has no effect in this group, so that {\rm VE}_{\bar{c}} \equals 0. The average efficacy of the vaccine on the transmission probability is 0·25. The average transmission probability difference is also 0·25.

Table 4.

Heterogeneous pre-vaccination susceptibility among sites; heterogeneity of vaccine effect within sites and confounding from exposure to infection; no boosting; increasing proportion exposed to infection in trial (A: 1/125, once; B: 1/2, once; F: 1/1, once; G: 2; H: 3; I: 4; J: 5; K: 6; L: 7; M: 8) ({\rm VE}_{c} \equals {\it 0\cdot5}\semi \,{\rm VE}_{\bar{c}} \equals {\it 0}\semi \,TP_{c\setnum{0}} \equals TP_{\bar{c}\setnum{0}} \equals {\it 1}\semi\,N_{c} \equals N_{\bar{c}} \equals {\it 500})

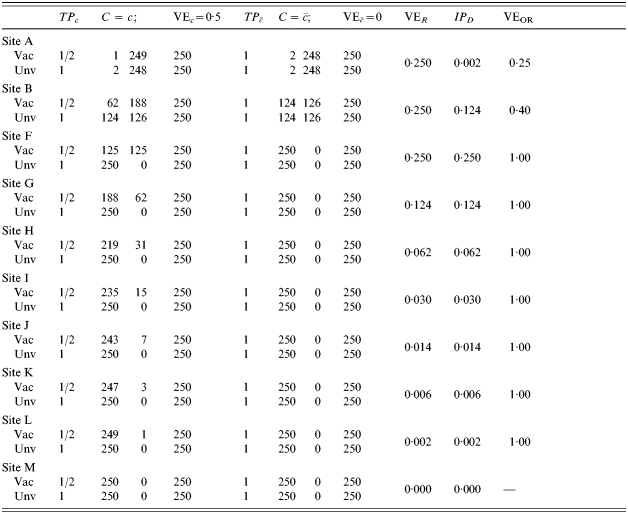
graphic file with name S0950268806006716_tab4.jpg

Open in a new tab

In Table 4, the number of exposures to infection per person increases from top to bottom, with equal probability of being exposed in the vaccinated and unvaccinated groups and at the different levels of C. That is, exposure to infection is independent of both vaccine status and C. In site A, only 1 in 125 are exposed to infection once, the others not at all. In site B, one-half are exposed once, and one-half not at all. In site F, everyone is exposed once. In sites G to M, the number of exposures to infection per person increases from two to eight. When the number of exposures to infection is ⩽1 (sites A, B, F), vaccine efficacy measured by VER does not change for different proportions of the population exposed to infection and equals the average of the effect of the vaccine in the two strata. Efficacy measured by the IPD increases until both measures based on ratio and difference are equal when the whole population is exposed just once (site F). Under these conditions, the expected crude incidence proportion ratio equals the average effect in the population, and the same for the differences of the two. Efficacy measured as 1−OR decreases as the level of exposure to an infective contact increases, and, as expected, it approaches the measure based on the incidence proportion ratio when the disease is rare.

Proceeding down Table 4, after all individuals were exposed to an infective contact once, we mimic a second round of contacts assuming that the first round leaves no immune memory. This is represented at site G in Table 4, in which from the 125 subjects that had not yet shown the outcome of interest, half of them (to the nearest integer) succumb to the infection. Successive rounds of contacts follow until after eight exposures to infection (M), all study participants present the outcome of interest. All three measures of efficacy progress towards the null when transmission increases. The decrease in estimated efficacy would also occur if the vaccine effect were homogeneous.

If we conducted a study of the vaccine in three different sites, say in sites A, G and L, and estimated vaccine efficacy from VER, we would expect three different estimates of the efficacy of the vaccine, namely 0·25, 0·124, and 0·002, even though the vaccine had exactly the same effect in each population, and the study is randomized and balanced. The difference among sites would be due to differences in post-vaccination exposure to infection in the three sites and not differences in the immune protection conferred by the vaccine.

C related to infection history: pre-vaccination heterogeneity, heterogeneity of effect, boosting

In the example in Table 5, the covariate C is related both to pre-vaccination susceptibility and to the heterogeneous response of the vaccine. We let c and \bar{c} denote previous exposure to infection and no previous exposure to infection, respectively, whereby we assume that half of each population has the covariate value C=c and half has C \equals \bar{c}. Suppose that in the three trial sites A, B, and F, the susceptibility of immunologically naive unvaccinated susceptibles is the same, with TP_{\setnum{0}\bar{c}} \equals 0\cdot5. That is, if we took the naive susceptibles from A, B, and F and challenged them with infection, then the transmission probability for each of the three groups would be the same, namely 0·5.

Table 5.

Heterogeneous pre-vaccination susceptibility among sites, heterogeneity of vaccine effect within sites, and boosting, all modulated by infection history; everyone exposed once to infection (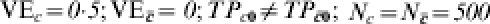{\rm VE}_{c} \equals {\it 0\cdot5}\semi \, {\rm VE}_{\bar{c}} \equals \,{\it 0}\semi \,TP_{c\setnum{0}} \ne TP_{\bar{c}\setnum{0}} \semi\,N_{c} \equals N_{\bar{c}} \equals {\it 500})

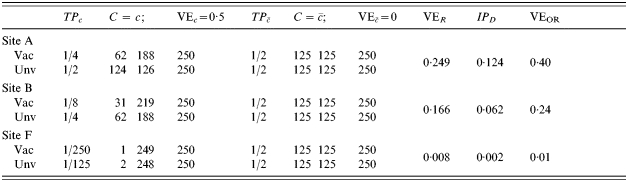
graphic file with name S0950268806006716_tab5.jpg

Open in a new tab

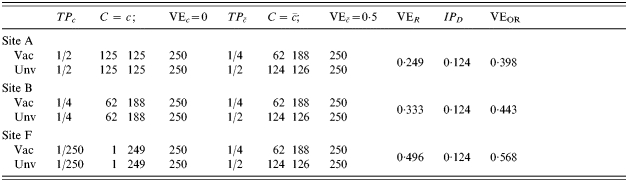
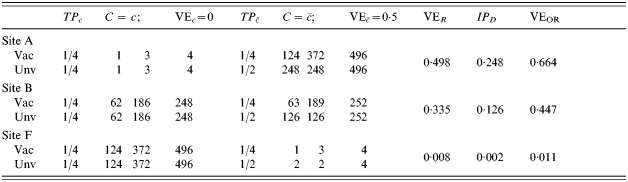
In the people with previous exposure to infection, however, the transmission probability ranges from 0·5 (no change over naive) in site A, to 0·25 at site B to 1/125 at site F. Now assume that the vaccine has an effect only in people who were previously exposed to infection. That is, perhaps the vaccine boosts pre-existing immunity, but has no effect on naive susceptibles. The effect of the vaccine in the previously exposed groups is assumed to be the same in each of the three trial sites, while it has no effect in the naive susceptibles. That is, the biological efficacy of the vaccine in the three trial sites is identical, with 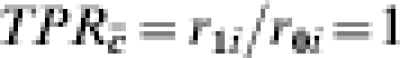TPR_{\bar{c}} \equals r_{\setnum{1}i} \sol r_{\setnum{0}i} \equals 1 and TPRc=r1i/r0i=0·5 at each site, and the proportion with each covariate is exactly half at each site. At site B, the multiplicative protection conferred by previous exposure to infection is the same as the protection conferred by vaccine in those people in whom it has an effect. In Table 5, we further assume that each person is exposed exactly once to infection The number of cases among the unvaccinated individuals in the C=c stratum, that is, those with decreased susceptibility before being vaccinated, decreases from site A to site F. Despite the effect of the vaccine actually being the same in sites A, B, and F of Table 5, the exposure to infection being exactly the same, and the distribution of C being exactly the same, the estimated efficacy of the vaccine decreases from 0·249 at site A to 0·008 at site F, depending on how susceptible those with pre-vaccination immunity are.

C related to infection history: pre-vaccination heterogeneity, heterogeneity of effect, no boosting

In Table 6, we find exactly the same pre-vaccination baseline situations in sites A and B, and half in F as described in Table 5. Assume, however, that the vaccine provides no additional protection to people who were previously exposed, C=c, but that it has an effect in naive susceptible people. In Table 6, the effect of pre-existing exposure to infection on VER is opposite to that in Table 5, and VER increases from 0·249 at site A to 0·496 at site F. Once again the biological effect of the vaccine is the same in the different sites, but if we do not stratify on pre-existing immunity, we get very different efficacy estimates. How the efficacy estimates vary depends on whether the vaccine has greater or lesser effect in the people who had previous exposure. Vaccine efficacy measured as the risk difference, IPD, however, is constant as long as exposure to infection is the same at all sites.

Table 6.

Heterogeneous pre-vaccination susceptibility among sites, heterogeneity of vaccine effect within sites, all modulated by infection history, and no boosting; everyone exposed once to infection (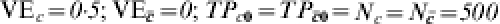{\rm VE}_{c} \equals {\it 0\cdot5}\semi \,{\rm VE}_{\bar{c}} \equals \,{\it 0}\semi\, TP_{c\setnum{0}} \ne TP_{\bar{c}\setnum{0}} \semi \,N_{c} \equals N_{\bar{c}} \equals {\it 500})

graphic file with name S0950268806006716_tab6.jpg

Open in a new tab

Varying the proportion with covariate C, boosting or no boosting

Tables 7 and 8 represent a comparison analogous to that between Tables 5 and 6, respectively. However, in Tables 7 and 8, the relative pre-vaccination susceptibilities are the same in all three sites, but the fraction of the population with the low pre-vaccination susceptibility varies among the different trial sites A, B, and F. Again, we can imagine that the low pre-vaccination susceptibility in the group with C=c comes from immunity acquired due to exposure to infection prior to the vaccine trial. For simplicity, we assume that protection conferred by naturally acquired immunity is the same as that conferred by the vaccine in groups where the vaccine has an effect, so 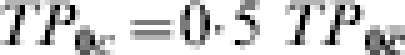TP_{\setnum{0}c} \equals 0\cdot5\ TP_{\setnum{0}\bar{c}} prior to vaccination. The proportion of the population with pre-vaccination immunity (C=c) varies from 1% to 2% in trial site A to 50% in trial site B to 97–98% in trial site F.

Table 7.

Homogeneous pre-vaccination susceptibility among sites, heterogeneity of vaccine effect within sites, boosting, and increasing Nc, all modulated by infection history; everyone exposed once to infection ({\rm VE}_{c} \equals {\it 0\cdot5}\semi\,{\rm VE}_{\bar{c}} \equals \,{\it 0}\semi\, TP_{c\setnum{0}} \ne TP_{\bar{c}\setnum{0}} \semi \,N_{c} \ne N_{\bar{c}})

graphic file with name S0950268806006716_tab7.jpg

Open in a new tab

Table 8.

Homogeneous pre-vaccination susceptibility among sites, heterogeneity of vaccine effect within sites, and increasing Nc, all modulated by infection history, and no boosting; everyone exposed once to infection (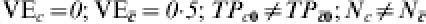{\rm VE}_{c} \equals {\it 0}\semi \,{\rm VE}_{\bar{c}} \equals \,{\it 0\cdot5}\semi \,TP_{c\setnum{0}} \ne TP_{\bar{c}\setnum{0}} \semi \,N_{c} \ne N_{\bar{c}})

graphic file with name S0950268806006716_tab8.jpg

Open in a new tab

In Table 7, we assume that the vaccine has no effect in the naive susceptibles, while reducing susceptibility by 50% in those with previous immunity. In Table 8, the vaccine has no additional effect in those with previous immunity, but reduces susceptibility by 50% in the naive susceptibles. Since the distribution of the covariate C in the populations A, B, and F varies, then the population average biological effect varies. In Table 7, it varies from about 0·01 at site A to 0·48 at site F, and vice versa in Table 8. This is reflected in the crude VER when each person is exposed once to infection. Thus, how the estimate of the vaccine efficacy varies will depend on the proportion with pre-existing immunity and how the vaccine interacts with this.

Effect in naive susceptibles and boosting

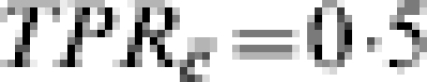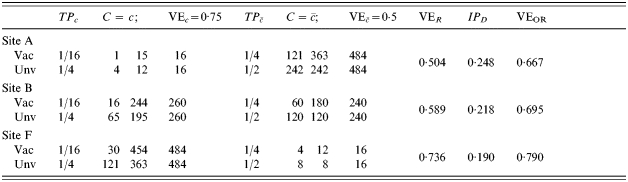
In Table 9, we consider a different biologically plausible situation. Suppose that the vaccine has an effect both in naive susceptibles and in people with previous exposure to infection, but due to immune boosting, the efficacy in those with previous immunity is greater. Assume that the vaccine reduces susceptibility by TPR_{\bar{c}} \equals 0\cdot5 in the immunologically naive, and TPRc=0·75 in those people with previous immunity. We assume that previous exposure reduces susceptibility by 0·5, so TP_{\setnum{0}c} \equals 0\cdot5\,TP_{\setnum{0}\bar{c}}. The proportion in each of the three trial sites with previous immunity (C=c) varies from about 3% in site A to 50% in site B to 97% in site F. With exactly one infectious exposure to infection, the estimated vaccine effect based on VER varies correspondingly from 0·504, close to the biological efficacy in the immunologically naive group, to 0·736, close to the biological efficacy in the previously exposed group. Once again, at the individual level, the efficacy is the same in all three trial sites given the previous immune status of the individual. If no one had had previous exposure to infection, the biological efficacy would have been exactly the same for everyone. The previous exposure acts as an effect modifier of the vaccine, and the final estimate of efficacy depends on the proportion of previously exposed people in the population.

Table 9.

Homogeneous pre-vaccination susceptibility among sites, heterogeneity of vaccine effect within sites, boosting, and increasing Nc, all modulated by infection history; everyone exposed once to infection (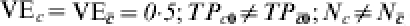{\rm VE}_{c} \equals {\it 0\cdot75}\semi \,{\rm VE}_{\bar{c}} \equals \,{\it 0\cdot5}\semi \,TP_{c\setnum{0}} \ne TP_{\bar{c}\setnum{0}} \semi \,N_{c} \ne N_{\bar{c}})

graphic file with name S0950268806006716_tab9.jpg

Open in a new tab

Varying susceptibility, vaccine response and exposure to infection

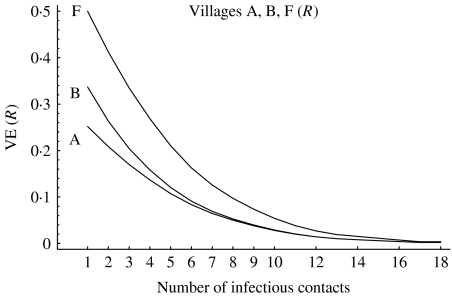
As a final example we consider the situation described in Table 6 for the three vaccine trial sites, but now let the number of exposures per person vary from 1 up to 16 (Fig.). The situation in which everyone is exposed once corresponds to that in Table 6. As the number of exposures per person increases, all the estimates of VER go towards 0. Suppose that site F with a low pre-vaccination susceptibility (pre-existing immunity) also has the higher transmission with a higher number of exposures, say five, during the trial compared with just one in sites A and B. The estimated efficacy will be only 0·25 in site F, while it will be 0·25 in site A and 0·35 in site B. Thus, the difference in transmission level will make the crude efficacy in the three sites seem more similar than it would have been if everyone had had just one exposure to infection. If, on the other hand, transmission is higher in sites A and B than at site F, say five in A and B and one at F, then the difference in transmission will accentuate the differences between the sites. The estimates of VER at sites A and B will both be <0·20, while at site F it is ∼0·50. Of course, none of the expected efficacy estimates takes into account the underlying heterogeneity and do not give an estimate of the actual biological efficacy of the vaccine in the two strata at each site, which is exactly the same for all three sites. This could be part of the explanation for the difference between the South American SPf66 [22, 23] vaccine trials and the trials in The Gambia [24].

Fig.

Fig

Open in a new tab

Vaccine efficacy estimates crossover.

Discussion

The results on the role and limits of randomization for both testing of null hypotheses and for estimates of effect in clinical trials in non-infectious disease are generally applicable to vaccine field trials. Randomization generally ensures that the treatment assignment mechanism is independent of the outcome of interest and of covariates relevant in determining this outcome. It is a good way to prevent additional problems of interpretation being introduced by the researcher and thus adding to the credibility of the study. We have shown, however, that randomization in vaccine field trials does not guarantee that the estimated parameters are biologically meaningful. Nor does randomization guarantee that the estimates are unbiased, unconfounded, or insensitive to baseline transmission. The special role of exposure to infection and the availability of the additional conditional parameters such as the transmission probability in infectious diseases adds another layer of complexity to choice and interpretation of efficacy estimates.

We have not considered the role of randomization under Bayesian inference in this paper. Lindley & Novick [25] argue that randomization is not necessary, because inference is conditional on the observed data. From a subjective Bayesian standpoint, however, they add that randomization is good so that the treatment assignment should appear to be unconnected with any relevant factor and that other people will believe the results. Rubin [15, 26] argues that randomization is good because it simplifies the analysis for Bayesian inference by making the ignorability of the treatment assignment mechanism explicit. However, even under Bayesian inference, randomization does not guarantee that an estimate has a biologically meaningful interpretation.

For purposes of presentation, we have assumed a very simple multiplicative model of protective effects and not differentiated between infection and disease. The relation between the possibly unobservable biological efficacy of the vaccine and the efficacy as measured by the observable outcome may be much more complex and can depend on many factors [14, 27]. A simple extension of the model is to assume that the vaccine does not influence the probability of becoming infected, but that it reduces the probability of developing disease, thus the probability of being ascertained as a case, once successfully infected. More complex models of within-host interactions of the infectious agent with the immune system and their consequences for design of vaccine efficacy trials and their interpretation would be worthwhile exploring.

We have focussed on the incidence proportion, that is, the attack rates, in the development here. Most of the same points will hold for vaccine efficacy measures based on incidence rates, that is, Poisson regression, or hazard rates. Some of the particular results and sensitivity to assumptions of multiplicative vs. additive or heterogeneous effects of the vaccine will vary. Some methods are available for estimating the vaccine efficacy parameters from time-to-event data in the presence of heterogeneity [28–30]. Heterogeneity must also be differentiated from waning efficacy [31, 32] Additional methods to estimate vaccine efficacy from prevalence data are presented in [33–36].

Meaningful interpretation of vaccine efficacy estimates, even in randomized, double-blind, placebo-controlled field trials, remains a challenge. As Savage [37] wrote: ‘whether one is a Bayesian or not, there is still a good deal to clarify about randomization’.

ACKNOWLEDGEMENTS

The research was partially supported by the Brazilian Research Council (CNPq), FAPERJ, and NIH NIAID R01-AI32042.

DECLARATION OF INTEREST

None.

References

  1. Smith PG, Morrow RH. Methods for Field Trials of Interventions Against Tropical Diseases: A Toolbox. Oxford: Oxford University Press; 1991. [Google Scholar]
  2. Efron B. Forcing a sequential experiment to be balanced. Biometrika. 1971;58:403–417. [Google Scholar]
  3. Greenland S, Robins JM. Identifiability, exchangeability, and epidemiologic confounding. International Journal of Epidemiology. 1986;15:412–418. doi: 10.1093/ije/15.3.413. [DOI] [PubMed] [Google Scholar]
  4. Greenland S. Interpretation and choice of effect measures in epidemiologic analyses. American Journal of Epidemiology. 1987;125:761–768. doi: 10.1093/oxfordjournals.aje.a114593. [DOI] [PubMed] [Google Scholar]
  5. Gail MH, Moolgavkar SH, Prentice RL. Modern Statistical Methods. New York: Wiley; 1986. Adjusting for covariates that have the same distribution in exposed and unexposed cohorts; pp. 3–18. , pp. [Google Scholar]
  6. Gail MH. The effect of poofing across strata in perfectly balanced studies. Biometrics. 1988;44:151–162. [Google Scholar]
  7. Gail MH, Tan WY, Piantadosi S. The effect of omitting covariates on tests for no treatment effect in randomized clinical trials. Biometrika. 1988;75:57–64. [Google Scholar]
  8. Gail MH, Wieand S, Piantadosi S. Biased estimates of treatment effect in randomized experiments with non-linear regressions and omitted covariates. Biometrika. 1984;71:431–444. [Google Scholar]
  9. Halloran ME, Struchiner CJ. Causal inference for infectious diseases. Epidemiology. 1995;6:142–151. doi: 10.1097/00001648-199503000-00010. [DOI] [PubMed] [Google Scholar]
  10. Fine PEM, Clarkson JA, Miller E. The efficacy of pertussis vaccines under conditions of household exposure: Further analysis of the 1978–80 PHLS-ERL study in 21 area health authorities in England. International Journal of Epidemiology. 1998;17:635–642. doi: 10.1093/ije/17.3.635. [DOI] [PubMed] [Google Scholar]
  11. Halloran ME, Préziosi M-P, Chu H. Estimating vaccine efficacy from secondary attack rates. Journal of the American Statistical Association. 2003;98:38–46. [Google Scholar]
  12. Halloran ME, Longini IM, Struchiner CJ. Design and interpretation of vaccine field studies. Epidemiologic Reviews. 1999;21:73–88. doi: 10.1093/oxfordjournals.epirev.a017990. [DOI] [PubMed] [Google Scholar]
  13. Halloran ME et al. Direct and indirect effects in vaccine field efficacy and effectiveness. American Journal of Epidemiology. 1991;133:323–331. doi: 10.1093/oxfordjournals.aje.a115884. [DOI] [PubMed] [Google Scholar]
  14. Struchiner CJ et al. Malaria vaccines: lessons from field trials. Cadernos de Saúde Pública. 1994;10:310–326. doi: 10.1590/s0102-311x1994000800009. (Suppl. 2): [DOI] [PubMed] [Google Scholar]
  15. Rubin DB. Bayesian inference for causal effects: the role of randomization. Annals of Statistics. 1978;7:34–58. [Google Scholar]
  16. Greenwood M, Yule UG. The Statistics of anti-typhoid anti-cholera inoculations, and the interpretation of such statistics in general. Proceedings of the Royal Society Medicine. 1915;8:113–194. [PMC free article] [PubMed] [Google Scholar]
  17. Rubin DB. Discussion of ‘Randomization analysis of experimental data in the Fisher randomization test’ by Basu. Journal of the American Statistical Association. 1980;75:591–593. [Google Scholar]
  18. Greenland S. Absence of confounding does not correspond to collapsibility of the rate ratio or rate difference. Epidemiology. 1996;7:498–501. [PubMed] [Google Scholar]
  19. Greenland S. Confounding in epidemiologic studies. Biometrics. 1984;45:1309–1310. [Google Scholar]
  20. Rhodes PH, Halloran ME, Longini IM. Counting process models for differentiating exposure to infection and susceptibility. Journal of the Royal Statistical Society B. 1996;59:751–762. [Google Scholar]
  21. Greenland S. Interpretation and estimation of summary ratios under heterogeneity. Statistics in Medicine. 1982;1:217–227. doi: 10.1002/sim.4780010304. [DOI] [PubMed] [Google Scholar]
  22. Noya O et al. A population-based clinical trial with the SPf66 synthetic P. falciparum malaria vaccine in Venezuela. Journal of Infectious Diseases. 1994;170:396–402. doi: 10.1093/infdis/170.2.396. [DOI] [PubMed] [Google Scholar]
  23. Valero MV et al. Vaccination with SPf66, a chemically synthesised vaccine, against Plasmodium falciparum malaria in Colombia. Lancet. 1993;341:705–710. doi: 10.1016/0140-6736(93)90483-w. [DOI] [PubMed] [Google Scholar]
  24. D’Alessandro U et al. Efficacy trial of malaria vaccine SPf66 in Gambian infants. Lancet. 1995;346:462–467. doi: 10.1016/s0140-6736(95)91321-1. [DOI] [PubMed] [Google Scholar]
  25. Lindley DV, Novick MR. The role of exchangeability in inference. Annals of Statistics. 1981;9:45–58. [Google Scholar]
  26. Rubin DB. Practical implications of modes of statistical inference for causal effect and the critical role of the assignment mechanism. Biometrics. 1991;47:1213–1234. [PubMed] [Google Scholar]
  27. Breslow NE, Storer BE. General relative risk functions for case-control studies. American Journal of Epidemiology. 1985;122:149–162. doi: 10.1093/oxfordjournals.aje.a114074. [DOI] [PubMed] [Google Scholar]
  28. Brunet RC, Struchiner CJ, Halloran ME. On the distribution of vaccine protection under heterogeneous response. Mathematical Biosciences. 1993;116:111–125. doi: 10.1016/0025-5564(93)90063-g. [DOI] [PubMed] [Google Scholar]
  29. Halloran ME, Longini IM, Struchiner CJ. Estimability and interpretation of vaccine efficacy using frailty mixing models. American Journal of Epidemiology. 1996;144:83–97. doi: 10.1093/oxfordjournals.aje.a008858. [DOI] [PubMed] [Google Scholar]
  30. Longini IM, Halloran ME. A frailty mixture model for estimating vaccine efficacy. Applied Statistics. 1996;45:163–175. [Google Scholar]
  31. Durham LK et al. Estimation of vaccine efficacy in the presence of waning: application to cholera vaccines. American Journal of Epidemiology. 1998;147:948–959. doi: 10.1093/oxfordjournals.aje.a009385. [DOI] [PubMed] [Google Scholar]
  32. Kanaan MN, Farrington CP. Estimation of waning vaccine efficacy. Journal of the American Statistical Association. 2002;97:389–397. [Google Scholar]
  33. Brunet RC, Struchiner CJ. Rate estimation from prevalence information on a simple epidemiologic model for health interventions. Theoretical Population Biology. 1996;50:209–226. doi: 10.1006/tpbi.1996.0029. [DOI] [PubMed] [Google Scholar]
  34. Struchiner CJ et al. On the use of state-space models for the evaluation of health interventions. Journal of Biological Systems. 1995;3:851–865. [Google Scholar]
  35. Brunet RC, Struchiner CJ. A non-parametric method for the reconstruction of age- and time-dependent incidence from the prevalence data of irreversible diseases with differential mortality. Theoretical Population Biology. 1999;56:76–90. doi: 10.1006/tpbi.1999.1415. [DOI] [PubMed] [Google Scholar]
  36. Brunet RC, Struchiner CJ. A method for estimating time dependent intervention benefits under arbitrarily varying age and exogenous components of hazard. Lifetime Data Analysis. 2001;7:377–392. doi: 10.1023/a:1012548815575. [DOI] [PubMed] [Google Scholar]
  37. Savage LJ. The Foundations of Statistical Inference. London: Methuen; 1962. [Google Scholar]

Articles from Epidemiology and Infection are provided here courtesy of Cambridge University Press

RESOURCES