Contact tracing strategies in heterogeneous populations

SUMMARY

Contact tracing is a well-established disease control measure that seeks to uncover cases by following chains of infection. This paper examines mathematical models of both single-step and iterative contact tracing schemes and analyses the ability of these procedures to trace core groups and the sensitivity of the intervention to the timescale of tracing. An iterative tracing process is shown to be particularly effective at uncovering high-risk individuals, and thus it provides a powerful public health tool. Further targeting of tracing effort is considered. When the population exhibits like-with-like (assortative) mixing the required effort for eradication can be significantly reduced by preferentially tracing the contacts of high-risk individuals; in populations where individuals have reliable information about their contacts, further gains in efficiency can be realized. Contact tracing is, therefore, potentially an even more potent tool than its present usage suggests.

Introduction

Contact tracing is a sophisticated control measure, applicable to a wide range of infectious diseases. It has been used to combat infections such as smallpox, SARS, tuberculosis, and a large number of sexually transmitted diseases (STDs) [1–9]. Unlike common control tools such as vaccination or public health campaigns, contact tracing is a multi-stage process potentially requiring a large investment of health-care provider time. The first stage of contact tracing requires the diagnosis of an infected index case; then any likely contacts of this index case must be determined, notified, and treated; any contacts subsequently found to be infected become new index cases and the process is repeated [1, 4, 9]. Because of the time and resources that contact tracing requires, mathematical models can be useful in attempting to understand and explain when and whether contact tracing is a successful strategy.

Previous modelling work has investigated the use of contact tracing in the context of a number of infectious diseases, in particular smallpox [5, 10–13] and STDs [6, 14–17]. In the latter instance contact tracing has been applied for many years whereas in the former it is under consideration as an emergency measure to deal with a new outbreak of infection. It has been suggested that, when symptoms can be easily identified and when contact tracing can be carried out iteratively and rapidly, it can be a highly effective measure [15–17]. In the case of STDs, contact tracing is particularly useful for uncovering asymptomatic cases (which can, nevertheless, be identified in the laboratory), thus providing a way of treating individuals who would otherwise remain infectious in the population [18].

The extent to which the idealized contact-tracing procedure described above is possible varies with circumstances and with the characteristics of the infection against which it is used. For instance, when there is no curative treatment available identified cases may need to be quarantined rather than treated [13]. If there is no quick and reliable diagnostic test it may be necessary to isolate all contacts, whether infected or not, until the emergence, or otherwise, of symptoms demonstrates their infection status [5, 10]. These time delays and the large numbers of patients involved make it difficult to maintain chains of contact tracing and to trace quickly in such circumstances.

In this paper we consider the factors that make contact tracing successful and examine the robustness of the intervention when these factors are removed. We focus specifically on the iterative properties of contact tracing and the speed at which contacts can be notified. We consider the possibility of further targeting tracing efforts. In certain circumstances, by preferentially tracing particular contacts, the intervention effort required to eradicate infection can be reduced.

Methods

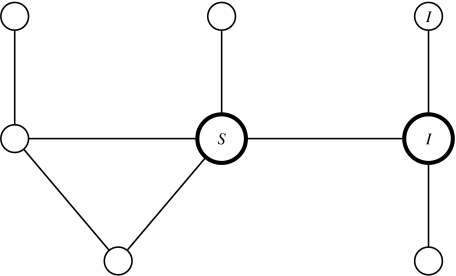
Contact tracing is intrinsically linked to networks of interactions within populations, such as sexual partnership networks for STDs [7, 19–21]. Transmission of infection takes place through inter-person connections [6, 7, 19–22] and these established links also allow the progress of infection to be traced. We define a mixing network to be the set of all individuals and all links between individuals that could allow transmission of infection – a sexual mixing network would contain information about sexual partnerships (Fig. 1). Contact tracing cannot be attempted without knowledge of the contacts of an individual, whether social or sexual, and obtaining this information is a vital step in the tracing process; we therefore use network modelling methods to study this intervention.

Fig. 1.

An example of a simple mixing network. Individuals are represented by circles, partnerships by lines. The infection status of three individuals is included for illustration. The two highlighted individuals contribute 1 towards [SI], the number of susceptible–infected partnerships; along with the individual top right they comprise a SII triple.

We use pair-wise models [23] as a robust method of representing epidemics within a mixing network. Pair-wise models treat connected pairs of individuals as their basic variable and therefore lie between the more usual random mixing approaches [24, 25] and full stochastic simulations of complete networks [12, 26]. By explicitly modelling the essential unit of disease transmission – an interaction between an infected and a susceptible individual – pair-wise models are able to include the mixing behaviour observed in networks and can capture, to a large extent, the spread of infection on networks. Although they cannot include much of the large-scale structure of networks, pair-wise models can capture the local network structure, which is of primary importance in disease transmission, and they have been demonstrated to be accurate and adaptable tools [14]. Pair-wise models can readily be parameterized once the distribution of partnerships (who mixes with whom) in the population is known, and therefore do not require complex and time-consuming evaluation of complete mixing networks. Pair-wise models retain the flexibility of more conventional approaches, and have been adapted to study heterogeneous populations, monogamous interactions, and contact tracing [14, 15, 17, 27, 28].

In this paper we consider simple infections in which individuals can be in one of two states: susceptible or infectious [24, 25]. Individuals become infected at a rate τ per infected partner and recover at rate g, following which they are once again susceptible. This form of highly simplified susceptible–infected–susceptible (SIS) model is appropriate for many common STDs such as chlamydia and gonorrhoea [24, 25], and provides a framework within which further complexities can be introduced. Births and deaths are ignored, and the mixing network is assumed to remain fixed. We define the infection parameter, r, via r=τ/g. The notation used in this paper is listed in the Table.

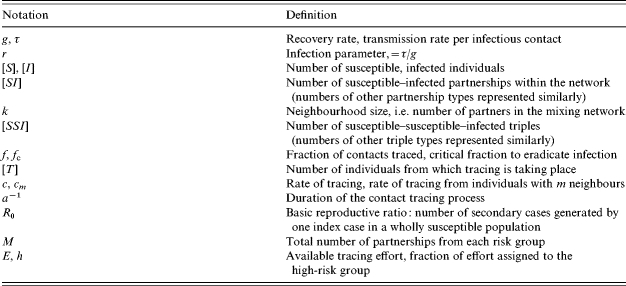
Table.

List of notation

We denote by [S] the number of susceptible individuals and by [I] the number of infected individuals, and consider how these numbers will change over time. [I] will decrease owing to recovery and will increase when infection is transmitted. Within a mixing network, infection can only spread between network neighbours. We denote by [SI] the number of connections within the network between a susceptible and an infected individual; it is only along these connections that infection can be transmitted. We can now form differential equations for the evolution of the numbers of susceptible and infected individuals [23]:

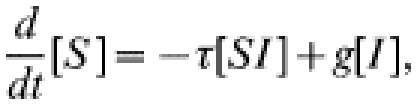(1)

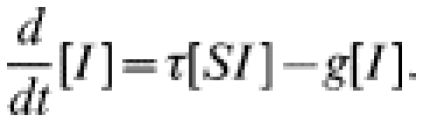(2)

To be iterated, we must also calculate how [SI], the number of susceptible–infected pairs, changes over time; [SI] increases when infection is introduced into a susceptible–susceptible pair (which can take place if one of the susceptibles has an infected partner) or if recovery occurs within an infected–infected pair; [SI] decreases if the susceptible individual becomes infected – either from within the pair or by an external partner – or if the infected individual recovers.

We can now write a differential equation describing the dynamics of [SI]:

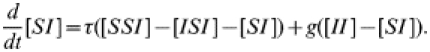(3)

Here [SSI] is the number of triples within the network consisting of a central susceptible individual with a susceptible and an infected partner, and [ISI] similarly. Within this equation they relate to infection entering the pair of interest from outside. The three pair terms in this equation relate to within-pair processes (infection or recovery). See Figure 1 for an illustration of these definitions.

As with the equations for d/dt[S] and d/dt[I], new terms, the triples, have been introduced. We could continue the process, modelling these in terms of triples and quadruples, but this would rapidly become unfeasible, requiring both a large number of equations and a great deal of data to parameterize. Instead, in order to close the system, triples are evaluated in terms of pairs and singles using the moment closure approximation

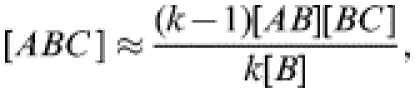(4)

where A, B, and C can represent either S or I. k is the neighbourhood size (i.e. the number of contacts) of the central type-B individual [23]. The approximation is derived as follows: an [ABC] triple requires an [AB] pair; the B individual in any such pair has (k−1) further contacts. Out of a total of k[B] contacts of type-B individuals within the population, [BC] are with type-C individuals, thus any one contact has a probability of [BC]/k[B] of being with a type-C individual. Combining these gives the approximation.

The system can easily be extended to consider populations containing individuals with a range of neighbourhood sizes [14]; the complete set of equations is given in the Appendix.

In this paper we adapt this set of equations to consider two distinct contact tracing approaches: single-step and iterative tracing. In the former case a proportion of the partners of index cases is treated concurrently with the index patient, thus resulting in the recovery of pairs of individuals; this is an appropriate model for certain STD situations when patients and their partners attend a clinic together, but does not allow infected contacts to become new index cases. The second model includes the iterative behaviour of tracing, with the infected partners of any diagnosed cases being sought for treatment and further tracing; in the iterative model, contact tracing behaves as a hyperparasite of infection, spreading through the infected portion of the mixing network.

Contact tracing

Single-step contact tracing

In this model, briefly introduced elsewhere [14], some fraction, f, of the contacts of an index case receive treatment at the same time as the index patient. Thus, a recovery ‘event’ may involve more than one individual leaving the infected class. Similar single-step approaches have been suggested by other authors [5, 6, 10, 13], particularly in contexts where there is no simple and rapid diagnostic test available and where chains of tracing are, therefore, not seen. It is most applicable in circumstances where formal contact tracing procedures are not carried out but when two individuals in a partnership seek treatment together. The governing equations for single-step tracing are:

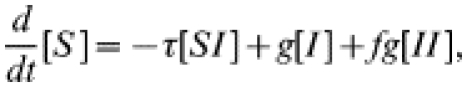(5)

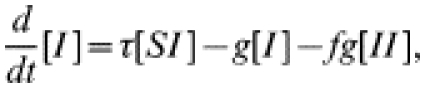(6)

the extra recovery term resulting from those occasions when two individuals are treated at once. As above, the system is closed by modelling the dynamics of pairs within the network and applying the moment closure approximation (see Appendix for the complete set of equations).

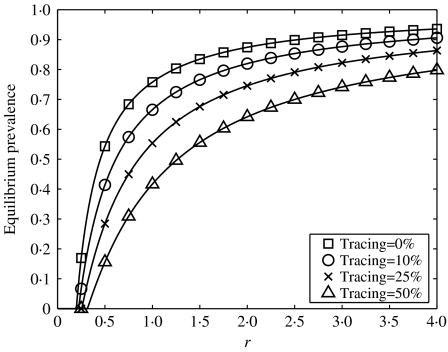
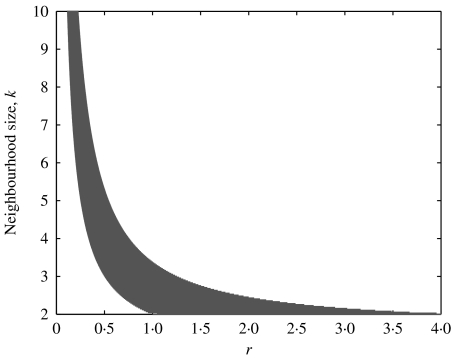
As shown in Figure 2, the additional recovery through contact tracing results in a reduction in equilibrium prevalence. It might be hoped that by sufficiently increasing the tracing fraction single-step tracing can eradicate infection altogether. However, this is not necessarily the case. For example, in a homogeneous population, in which each individual has k contacts, eradication is only possible rk(rk²−rk−r−2k)<1. As Figure 3 shows, there is only a relatively small region of parameter space in which single-step tracing can drive infection from the system. When contact tracing is restricted to a single step it can only have a limited effect on the impact of a pathogen.

Fig. 2.

Equilibrium prevalence plotted against the infection parameter, r, for a range of tracing fractions, f, in a single-step tracing model, g=1 throughout, with r varied by altering τ. A heterogeneous network was used to parameterize the model, with individuals of neighbourhood size ranging from 1 to 13.

Fig. 3.

The region in parameter space for which single-step tracing can eradicate infection in a homogeneous network with uniform neighbourhood size k, shown in grey. Above the shaded region infection persists whatever the tracing fraction; below the shaded region persistence is impossible even when there is no tracing.

Iterative contact tracing

The more usual form of contact tacing, as carried out by GUM clinics, is an iterative process: any infected contacts of an index case are treated as new index cases, and their contacts are also sought. In this way contact tracing spreads through the population, following chains of infection. To represent iterative contact tracing this model, introduced in ref. [15], includes an extra tracing class (denoted T): following treatment individuals enter this tracing class and their contacts are traced. Any successfully traced contacts likewise enter the tracing class. We assume that tracing takes place at rate c and that the tracing process has a duration a⁻¹, after which individuals return to the susceptible class. The governing equations for numbers in each class are:

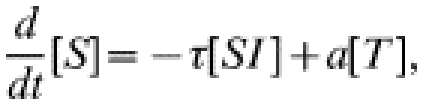(7)

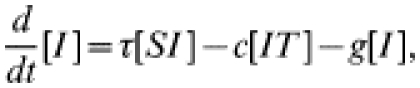(8)

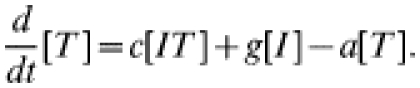(9)

The c[IT] terms represent contact tracing from individuals in the tracing class, T, leading to the removal of infected individuals into the tracing class. Once again, the dynamics of pairs are modelled explicitly, making use of the moment closure approximation (see Appendix for the complete set of equations). In this model tracing occurs iteratively, with each index case being-capable of generating further index cases [16, 17, 28]; the tracing class behaves as a hyperparasite within the system, passing between infected individuals.

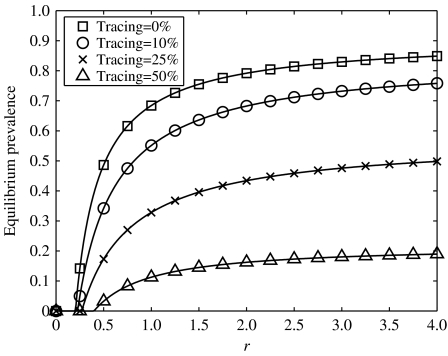
We see from Figure 4 that iterative tracing is an effective control measure leading to a large reduction in infection prevalence. Comparing Figures 2 and 4 shows that iterative tracing has a much more dramatic impact than single-step tracing. As has been shown previously [15, 16], when the tracing process is rapid compared with the dynamics of infection (c and a are much larger than τ and g) the critical tracing fraction – the fraction of contacts, f_c, that must be traced to eradicate infection – is given by f_c=1−1/R₀, where R₀ is the basic reproductive ratio – the average number of new cases generated by an infected individual in an otherwise susceptible population. This relationship holds in a wide range of scenarios, including heterogeneous populations and asymptomatic infections [15], and has a relatively simple explanation: for eradication, each infection must generate no more than one untraced case, i.e. (1−f_c)R₀<1⇛f_c>(1−1/R₀). Immediately a difference between single-step and iterative tracing emerges: in the latter case it is always possible to eradicate infection.

Fig. 4.

Equilibrium prevalence plotted against the infection parameter, r, for a range of tracing fractions in an iterative tracing model, g=1 throughout, with r varied by altering τ. The tracing fraction is given by c/(c+a). The same network was used as in Figure 2.

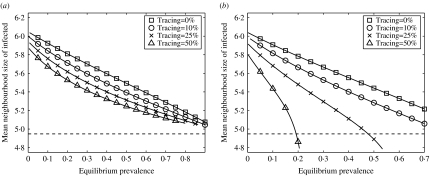
Part of the power of contact tracing comes from its ability to target interventions towards the most high-risk parts of the network; contact tracing involves surveying the partners of infected cases and thus it tends to focus on high-risk individuals. Such individuals, especially when they mix with each other to form high-risk core groups, tend to dominate the dynamics of infection; disease is concentrated in core groups, particularly when population prevalence is low [25, 29–32]. Contact tracing alters the distribution of infection within the population because individuals at highest risk of infection are also the most likely to be traced. We use the mean number of contacts of infected individuals in a heterogeneous network as a measure of the influence of core groups – the higher this number, the more infection is restricted to high-risk individuals – plotted in Figure 5 against equilibrium prevalence to examine how contact tracing affects the distribution of infection.

Fig. 5.

Mean neighbourhood size of infected individuals plotted against equilibrium prevalence for a range of tracing fractions, using the simulation results shown in Figures 2 and 4. (a) Single-step tracing; (b) iterative tracing. Also shown (dashed line) is the mean neighbourhood size of the population.

In all cases, as anticipated, the greater the prevalence, the less it is concentrated in the core groups. When tracing is considered, the results differ greatly between the two forms of contact tracing. Single-step tracing has little effect on the distribution of infection through the population, whereas iterative tracing greatly reduces the dominance of core groups. By repeatedly following links from infected cases, iterative tracing results in intervention efforts naturally focusing on areas of the network where prevalence is highest, allowing the most dominant individuals to be contacted and treated. Because iterative tracing effectively targets high-risk parts of the mixing network, the ability of core groups to sustain infection is reduced, greatly aiding the eradication of infection. By contrast, in single-step tracing the core groups retain much of their dominance and eradication is consequently much more difficult.

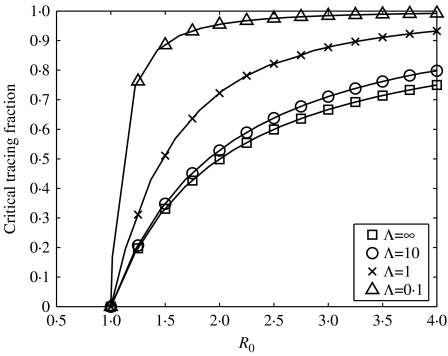
Another issue affecting the success of contact tracing is the speed at which tracing is carried out; for instance, it is of little benefit to trace all partners of an index case if tracing does not occur until infection has already spread many further steps through the population [13]. The expression above for the critical tracing fraction depends on tracing being carried out before secondary cases have had a chance to transmit infection; if tracing is slower we would expect to have to trace more individuals to eradicate infection. Figure 6 demonstrates the larger tracing fraction required to eradicate infection as the speeds of transmission and tracing become similar. Although eradication remains possible, the critical tracing fraction becomes so large that it will seldom be attainable in practice. Thus, contact tracing requires both rapid diagnostic tests and capable and well-resourced health services.

Fig. 6.

Critical tracing fraction necessary to eradicate infection for the iterative tracing model plotted against R₀ for a range of timescale separations. The timescale separation, Λ, is defined by the ratio of the tracing and infection timescales: g=1 and a=Λ×g throughout; R₀ and tracing fraction are varied by changing τ and c respectively.

Targeted contact tracing

We have noted that contact tracing directs intervention efforts towards at-risk parts of the mixing network, the neighbourhood of infected individuals. We now examine the possibility of further targeting interventions, thus avoiding expending effort on subsections of the population where infection is rare.

To investigate the value of targeted contact tracing we consider a simplified population structure, consisting of two groups with different mixing properties, one high-risk (with 10 contacts) and one low-risk (with four contacts). The numbers of individuals in each group are selected so that each group has the same total number of contacts, M. We include variation in population mixing patterns by adjusting the assortativity of the population [19, 33]. Assortativity is a measure of the extent to which similar individuals interact; the more assortative the population, the more the mixing is ‘like with like’. In this two-group model mixing can range from completely assortative, when all links are within group, to completely disassortative, when all links are between individuals in different groups. We note that high assortativity leads to high R₀ whereas prevalence is maximized at some intermediate assortativity [24, 30, 33]. The first result arises because of the dominance of the high-risk group during the early stages of an epidemic: the more coherent this group, the higher R₀. In contrast, prevalence is maximized when there is both a sufficiently distinct core group to sustain high levels of infection within itself and enough contact between the core and non-core for disease to be widespread in the general population. The more assortative the population the greater the segregation of the groups and thus the greater the unevenness of the distribution of infection.

Tracing effort can be apportioned in various ways from entirely directed towards one group to entirely directed towards the other. Use of a simplified population allows all possible choices of intervention targeting to be tested simply by allowing the fraction of effort applied to the high-risk group to vary between zero and one. We look here at two means of targeting tracing: targeting according to the characteristics of the index case, and targeting according to the characteristics of the contact.

First we consider interventions that alter the rate at which tracing is carried out from index cases. We write c_m as the rate at which individuals are traced from an index case with m partners, and allow this parameter to differ between the two groups, depending on how tracing-effort is apportioned. Specifically, if the available effort, E, has a fraction h assigned to the high-mixing group, c_high is increased by hE/M (the denominator is in place since the effort is split between all links that might be traced from this group). When h=1 all effort is spent tracing the contacts of the high-risk group.

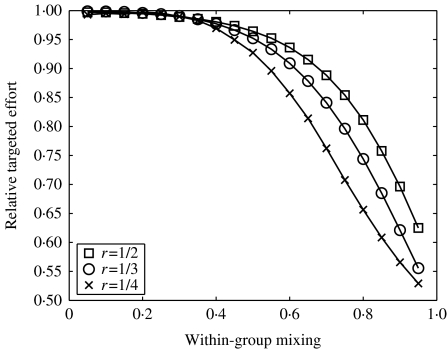
Figure 7 shows the effort required to eradicate infection when contact tracing is targeted compared to the effort required when tracing is uniformly applied. We see that in some cases there is very little difference between the two approaches. However, targeted contact tracing is worthwhile when the population is assortative, and the lower the pre-intervention level of infection the greater the improvement. It is optimal to direct tracing efforts preferentially towards the contacts of core group individuals. This can be explained as follows: for tracing from one group to be more beneficial than tracing from another, the groups must have partners with different levels of infection. The prevalence in the neighbourhood of an index case will depend partly on the index case itself, but will also depend on the properties of the individuals in the neighbourhood – if the neighbourhood consists of high-risk individuals, for instance, then they are likely to have been infected via other sources. Thus, targeting is likely to be useful when the population is non-randomly mixed, i.e. either assortative or disassortative. Moreover, for it to be worthwhile to contact particular groups the prevalence of infection must differ between groups. Therefore, although disassortative mixing allows for particular types of individual to be contacted, the relatively even distribution of infection means that targeting is of little worth. Assortatively mixed populations, however, display unevenly distributed infection, so core group individuals should be sought, and this can be achieved through tracing from other core group members. The fact that targeting becomes more beneficial at lower levels of pre-intervention prevalence supports this argument – when prevalence is low the distribution of infection is more uneven.

Fig. 7.

The effect of mixing pattern on the required effort to eradicate infection, using the iterative tracing model in a simplified population consisting of two types of individual. Relative targeted effort is defined to be the effort needed when tracing is optimally targeted divided by the effort required when tracing is applied uniformly. Within-group mixing is defined to be the proportion of contacts that are between individuals in the same group. In this case, effort is targeted according to the properties of the index case.

We can conclude that there are occasions when contact tracing should be targeted. We have also seen instances when targeting is not worthwhile and, indeed, the effort involved in attempting to target interventions may be such as to negate any positive effect. Targeting is only noticeably beneficial in assortative populations and it is unclear whether human mixing networks, whether social or sexual, are sufficiently assortative for targeted tracing to be recommended [1, 29, 34, 35]. An adequate answer depends on a far more thorough understanding of the patterns of population mixing and the limitations and constraints inherent in human interactions.

In principle, adjusting the tracing rate according to the characteristics of the index case should be achievable; index cases are seen by the health services and can be interviewed to determine their relevant properties. Alternatively, we can consider targeting tracing depending on the characteristics not of the index but of the contact: for example by attempting preferentially to trace core group individuals. This requires that index cases can be questioned not only about the identities and numbers of their contacts, but also about their contacts’ attributes. To work effectively, this approach requires that individuals have good knowledge about their partners and that they are prepared to divulge this information.

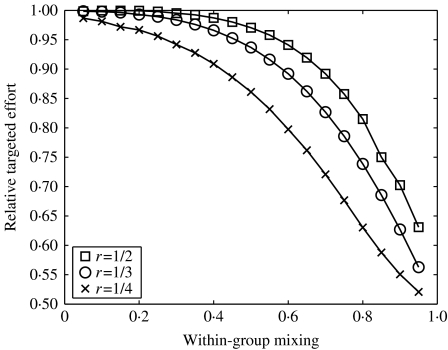
To examine this option requires only the smallest of adjustments to the model: c_m becomes the rate with which individuals with m partners are traced. We see from Figure 8 that, once again, there are situations when this form of targeting is highly beneficial. As before, the less even the spread of infection the greater the benefit of targeting contact tracing, but here we do not require such highly assortative populations to make targeting worthwhile. Previously, only in such cases was it possible to be know which individuals were being traced, but if tracing is carried out according to the properties of contacts, then it is always possible to specifically target core groups. If it is possible to trace based on the properties of contacts then the range of circumstances in which significant savings can be made is noticeably extended.

Fig. 8.

The effect of assortativity on the required effort to eradicate infection. As in Figure 7, but here effort is targeted according to the properties of the contact.

Discussion

Contact tracing is potentially a potent disease control measure. To operate at its fullest efficiency it requires sophisticated and highly trained operatives, capable of gathering the necessary information, coordinating efforts, and contacting individuals. Contact tracing relies on networks of interactions for its success and therefore requires network-based modelling techniques to capture the tracing process. Here we have used pair-wise models of epidemics on networks to examine single-step and iterative contact-tracing schemes.

Through the construction of models of contact tracing we have seen that to be successful contact tracing must be carried out rapidly and must act iteratively. When these conditions are met the impact on infection prevalence is great; the natural targeting of tracing efforts towards the at-risk neighbourhood of infected index cases allows core group individuals to be uncovered and treated. The automatic targeting of contact tracing is a property of the intervention that emerges over a series of tracing steps. A single-step tracing scheme is therefore unable to access core groups as effectively: the failure to trace the partners of all uncovered cases means that infection can be rapidly reintroduced. Indeed, it is only for a very limited range of infection parameters that single-step tracing can eradicate infection, whereas iterative contact tracing is much more broadly effective.

Despite the targeting inherent in contact tracing, there are circumstances in which further focusing of the intervention significantly reduces the tracing effort required to eradicate infection. In assortative networks, where mixing tends to be between individuals with similar characteristics, great savings are possible. In such networks the distribution of infection is highly skewed towards the core group – a lack of interaction between the groups means that prevalence in the general population is lower – and since the contacts of core individuals tend also to be in the core, preferential tracing from the core group allows tracing to target the areas of the network where infection is most likely to be found. In randomly mixed networks, where the neighbourhoods of all individuals have broadly similar properties, there is little to be gained from tracing preferentially from particular individuals. In disassortative networks prevalence is reasonably constant across the population so there are no obvious desirable targets for tracing.

When tracing can be adjusted according to the characteristics of the target individual rather than the index case, there is a greater range of populations in which eradication effort is reduced. In this case, core individuals can be specifically targeted and so long as there is an uneven distribution of infection this proves beneficial. In particular, this form of tracing confers an advantage in randomly mixed populations, not seen when tracing rates depend on the properties of the index case alone. Although tracing according to the properties of the target is an attractive proposition, it is unclear to what extent it is practical. Studies have suggested that, in sexual mixing networks, individuals are not well-informed about their partners’ behaviour [36, 37], but, dependent on the biases present in individuals’ perceptions, there may be sufficient information for targeted tracing to be feasible. Furthermore, there are cases where risk is highly correlated with characteristics such as occupation, ethnicity, or place of residence [20, 30, 32, 38], in which case relevant information about contacts may be more readily available. Further network studies are needed to clarify these issues, but it certainly appears that with good network knowledge and considered use of available resources traditional methods of disease control can be improved.

Appendix

SIS governing equations

For completeness, the full set of pair-wise equations for an SIS type infection in a heterogeneous network is given below. In such a population, where the neighbourhood size varies, individuals are labelled acccording to both their infection status and their neighbourhood size. Thus, [S^m] is the number of susceptible individuals with m contacts and [S^mIⁿ] is the number of pairs consisting of a susceptible with m contacts and an infected with n contacts. Other terms are defined analogously. All triples in the system are evaluated in terms of pairs and singles using the moment closure approximation:

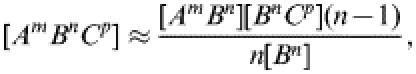(10)

where A, B, and C can be either S or I. This approximation is derived from the same reasoning as outlined in the main text.

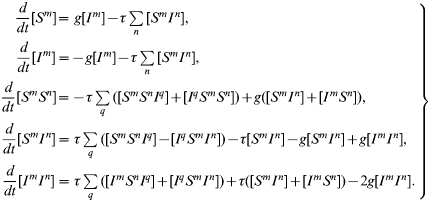(11)

In order to parameterize the system it is necessary to know the number of partnerships within the network between individuals of all neighbourhood sizes; that is to say, we need to know [mn], the number of pairs within the network consisting of one individual with m contacts and one with n contacts (ignoring infection status), for all values of m and n. This information can be obtained by counting pairs within a specific mixing network or can be determined to represent a population of interest. For example, in the targeted tracing section we consider a population consisting of two groups, one with 10 contacts and one with 4; by setting [4 10] (the number of between-group contacts) appropriately we can obtain a population with a required level of between-group mixing.

Governing equations for single-step contact tracing

As described in the main text, the equations governing the dynamics of the numbers of susceptible and infected individuals in the presence of single step contact tracing are

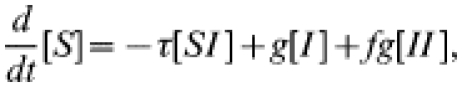(12)

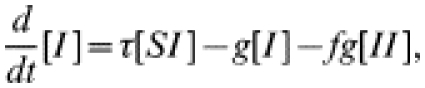(13)

where f is the fraction of contacts that are traced. As in the tracing-free SIS case, we must form similar equations for the behaviour of the various pair types; reasoning as before gives

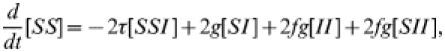(14)

(15)

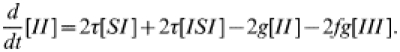(16)

Exactly the same moment closure approximation as used previously closes the system and allow it to be iterated.

Governing equations for iterative tracing

As described in the main text, the equations governing the dynamics of the numbers of susceptible, infected, and tracing individuals in the presence of iterative contact tracing are

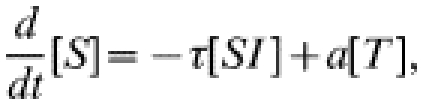(17)

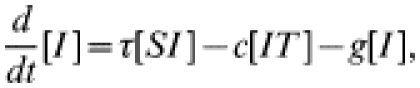(18)

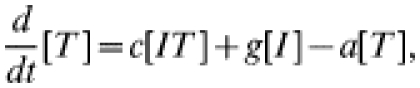(19)

where c is the tracing rate and a⁻¹ the tracing duration. Again, we form equations for the behaviour of pairs.

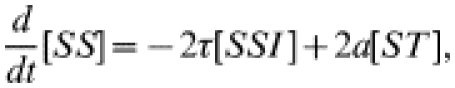(20)

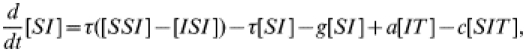(21)

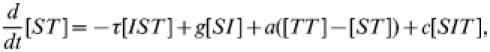(22)

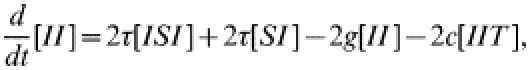(23)

(24)

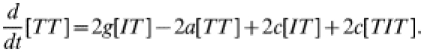(25)

Exactly the same moment closure approximation as used previously closes the system and allow it to be iterated.

DECLARATION OF INTEREST

None.