Scenarios of diffusion and control of an influenza pandemic in Italy

C RIZZO; A LUNELLI; A PUGLIESE; A BELLA; P MANFREDI; G SCALIA TOMBA; M IANNELLI; M L CIOFI DEGLI ATTI

doi:10.1017/S095026880800037X

. 2008 Feb 14;136(12):1650–1657. doi: 10.1017/S095026880800037X

Scenarios of diffusion and control of an influenza pandemic in Italy

C RIZZO ^1,^2,^*, A LUNELLI ³, A PUGLIESE ³, A BELLA ¹, P MANFREDI ⁴, G SCALIA TOMBA ⁵, M IANNELLI ³, M L CIOFI DEGLI ATTI ¹, on behalf of the EPICO Working Group

PMCID: PMC2870775 PMID: 18272019

SUMMARY

To predict the spread of a pandemic strain of influenza virus in Italy and the impact of control measures, we developed a susceptible–exposed, but not yet infectious–infectious–recovered, and no longer susceptible (SEIR) deterministic model with a stochastic simulation component. We modelled the impact of control measures such as vaccination, antiviral prophylaxis and social distancing measures. In the absence of control measures, the epidemic peak would be reached about 4 months after the importation of the first cases in Italy, and the epidemic would last about 7 months. When combined, the control measures would reduce the cumulative attack rate to about 4·2%, at best, although this would require an extremely high number of treated individuals. In accordance with international findings, our results highlight the need to respond to a pandemic with a combination of control measures.

INTRODUCTION

Following the emergence in 1997 of a new strain of avian influenza, A(H5N1), which is capable of infecting humans [1], and the spread of this strain to Europe in 2005 [2], concerns were raised over the occurrence of a pandemic caused by A(H5N1) or a closely related strain [3, 4]. Consequently, countries have been urged to strengthen their preparedness for an influenza pandemic [5], an important aspect of which is predicting the spread of infection.

According to the predictive models used to date [6–12], influenza would spread worldwide over a period of 2–6 months, depending on the basic reproductive number (R₀), and reducing transmission would entail combining control measures, specifically, reducing contacts and performing both antiviral prophylaxis (AVP) and vaccination [7–9, 11, 13].

We developed a SEIR (susceptible–exposed, but not yet infectious–infectious–recovered, and no longer susceptible) deterministic model with a stochastic simulation component to predict the spread of pandemic influenza in Italy and to evaluate the impact of vaccination, AVP and social distancing measures.

METHODS

The SEIR model

We developed a SEIR model in which the population is structured according to age and region of residence. We defined six age classes: infants (0–2 years), children (3–14 years), teenagers (15–18 years), young adults (19–39 years), adults (40–64 years) and the elderly (⩾65 years). In the model, the national population (56 995 744 inhabitants) was also distributed in Italy's 20 regions, according to national demographic data obtained from the 2001 Census [14]. The contact matrix was defined by considering, separately, household, school/work-place and random contacts, and by using data on household composition, school attendance, and employment status. The transportation matrix was defined using data on national airline traffic [15]. The model consists of a system of differential equations, reported in the Appendix.

We also introduced a stochastic component that takes into account all of the random effects that are important during a pandemic's initial and final stages, when the number of infected individuals would be low. Precisely, whenever the deterministic prediction of the number of infected individuals in an age class/region was below the threshold value of 10, it was replaced by a Poisson variable with the same mean. In each simulation, the pandemic began with the introduction of five infected adults in the Lazio Region, where Rome's intercontinental airport is located.

Based on published studies [16] and using the method described by Diekmann & Heesterbeek [17], we computed an R₀ of 1·8, which, when applying the contact matrix, corresponds to a cumulative infected attack rate (AR) of 35%.

Based on the literature [6, 8, 18], in the model we assumed an incubation period of 1 day and an infectious period of 3·9 days. The results were obtained by averaging over 200 simulations for each scenario. For all of the results, the 5–95 percentile values of the AR estimates were within 11%.

Control measures

We considered both single and combined control measures, most of which are included in the Italian National Plan for preparedness and response to an influenza pandemic [19]. We assumed that two doses of vaccine would be administered, 1 month apart. The target population was divided into four categories: (I) personnel providing essential services (15% of the working population, aged 25–60 years) [14]; (II) elderly persons (aged ⩾65 years); (III) children and adolescents (aged 2–18 years); and (IV) adults (aged 40–64 years). We assumed a vaccination coverage of 60% of the target population, based on the 2005–2006 national influenza coverage [20]. We assumed that a period of 2 weeks would be necessary for administration of the vaccine to each target category. For vaccine effectiveness (VE) we made two different assumptions: (1) VE of 70% for all categories; and (2) VE of 50% for all categories; for both assumptions, we assumed that the VE would be reached starting 15 days after the second dose.

We considered different scenarios of vaccine availability; in one scenario, adequate VE would be reached 4 months after the first national case; in the second scenario, it would be reached after 5 months. An adequate VE at 4 months would be feasible only if the first dose contained an avian virus precursor of the pandemic strain [3], followed by a dose of pandemic vaccine; the actual VE of this regimen was assumed to be equal to that of two doses of the pandemic vaccine.

The AVP for uninfected individuals was assumed to reduce susceptibility by 30% and infectiousness by 70% [8]. We considered the administration of one course of antiviral drugs. We assumed that AVP would be provided to all household contacts of 80% of the clinical cases (66% of all infected individuals). We considered administration of AVP for the entire epidemic period; however, since the feasibility of actually doing this would be limited, we also considered other scenarios, i.e. administering AVP only for 2, 4, 8, or 16 weeks after the occurrence of the first Italian case. AVP was assumed to reduce the transmission rate among household contacts, based on the consideration that those household contacts already infected at the time of starting AVP would have a reduced infectiousness, therefore it would be as if only a fraction of them were actually infected; those not yet infected when starting AVP would benefit from both lower susceptibility and lower infectiousness.

We considered the nationwide closure of all schools, public offices, and public meeting places (e.g. restaurants, cinemas, and churches). We simulated the closure of schools for 3 weeks, public offices for 4 weeks and public meeting places for 8 weeks. We assumed that these measures would be introduced simultaneously, at different times (i.e. 2, 4 or 8 weeks after the start of the pandemic). In the model, school closure would reduce the contacts among children and teenagers (the school component of the transmission rate) by 75%; workplace closure would reduce the job component of the transmission rate by 16%; closure of public meeting places would reduce the random component of the transmission rate by 50%.

Sensitivity analysis

We evaluated how the results would change depending on different levels of pathogen transmissibility, with a resulting R₀ value of 1·6, 1·8 or 2·0. We also considered the resulting AR for the three R₀ values for the baseline scenario and for scenarios that differed in terms of the specific control measures adopted.

RESULTS

Baseline dynamics

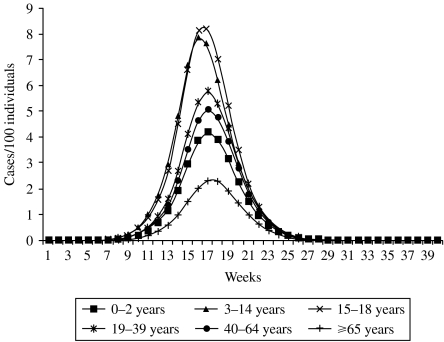
In the absence of control measures, the epidemic peak would be reached about 4 months after the identification of the first case, with a total of 3 million cases during the peak week. The epidemic would be over in 7 months, with a cumulative infected attack rate (AR) of 35% (about 20 million cases). The dynamics of the epidemic were similar in all age groups, whereas the AR varied markedly by age group. The incidence would be particularly high among those aged 15–18 years, with a AR of 54% (Fig. 1).

Fig. 1 — Weekly attack rate, by age group, with no control measures.

Because of the model's stochastic component, the introduction of few infectious individuals in the population did not always result in an outbreak; in fact, in around 40% of the simulations, the number of infected individuals in the early stages of the pandemic was insufficient for sustaining transmission, and the epidemic expired spontaneously.

Single control measures

The impact of single control measures is shown in Table 1. The introduction of control measures frequently increased the probability of stochastic extinction of the pandemic. Vaccination seems to be the most effective measure, especially when VE is reached at 4 months. Vaccinating three of the four target categories (i.e. personnel providing essential services; elderly persons; and those aged 2–18 years) would reduce the AR from 35% to 25%, with almost 5 million cases avoided by treating about 17 million individuals. Vaccinating the fourth target category (i.e. the 40–64 years age group) would not result in an important additional reduction in the AR. If protective VE were reached at 5 months (two doses of pandemic vaccine), vaccinating all four categories, the AR would be 32·5%. Assuming a VE of 50% for all categories would not greatly affect the AR; in fact, the AR would be only 2 or 3 percentage points higher than the AR when assuming a 70% VE for all categories (Table 1).

Table 1.

Effectiveness of single control measures on the dynamics of an influenza pandemic with an R₀ of 1·8 and an attack rate of 35%, for different values of vaccine effectiveness (VE)

graphic file with name S095026880800037X_tab1.jpg

Open in a new tab

n.a., Not applicable.

For age categories see text (Control measures section).

Value in parentheses represent the 5–95 percentile values of the attack rate estimates.

Social distancing measures and AVP were not effective in reducing the AR. However, providing AVP for 16 weeks after the identification of the first Italian cases and implementing social distancing measures starting at week 4 or week 8 would delay the epidemic peak by 1 or 3 weeks, respectively.

Combined control measures

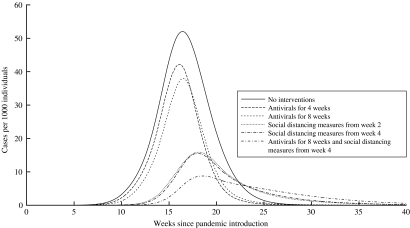
The combination of control measures would be more effective than single measures (Tables 2 and 3). The highest reduction (from 35% to 4·2%) would be obtained by starting social distancing measures at week 4, providing AVP throughout the entire epidemic, and performing vaccination with a VE of 70% at 4 months (when combining measures, we assumed that vaccination would be provided for all categories). This would allow for 17 million cases to be avoided by vaccinating around 26 million individuals and by providing AVP to about 3 million individuals. The AR would be higher (11%) if VE were reached at 5 months, avoiding 13 million cases by treating 25 million individuals and 7 million individuals with vaccine and AVP respectively (Table 2). Providing AVP for 16 weeks, instead of for the entire epidemic period, would increase the AR to 8·4% or 16·6% if VE were reached at 4 or 5 months, respectively. However, this would determine an important reduction in the number of treated individuals (about 150 000). Combining control measures would also increase the probability of stochastic extinction during the initial phases of the epidemic, due to a low number of infectious individuals. A VE of 50% for all categories considered would affect the AR estimates, but only when considering adequate VE at 4 months. In fact, the AR would be 6–8 percentage points higher than the AR assuming a VE of 70%, with a remarkable difference in terms of the number of avoided cases (Table 3). The impact of combined control measures (pre-pandemic vaccine in all categories and AVP and/or social distancing measures), compared to the baseline dynamics of the influenza pandemic, is shown in Figure 2.

Table 2.

Effectiveness of combined control measures on the dynamics of an influenza pandemic with an R₀ of 1·8 and an attack rate of 35%, with 70% vaccine effectiveness (VE)

graphic file with name S095026880800037X_tab2.jpg

Open in a new tab

Value in parentheses represent the 5–95 percentile values of the attack rate estimates.

Table 3.

Effectiveness of combined control measures on the dynamics of an influenza pandemic with an R₀ of 1·8 and an attack rate of 35%, with 50% vaccine effectiveness (VE)

graphic file with name S095026880800037X_tab3.jpg

Open in a new tab

Value in parentheses represent the 5–95 percentile values of the attack rate estimates.

Fig. 2 — Impact of different combinations of control measures considering the use of a pre-pandemic vaccine provided to all categories (I–IV).

Sensitivity analysis

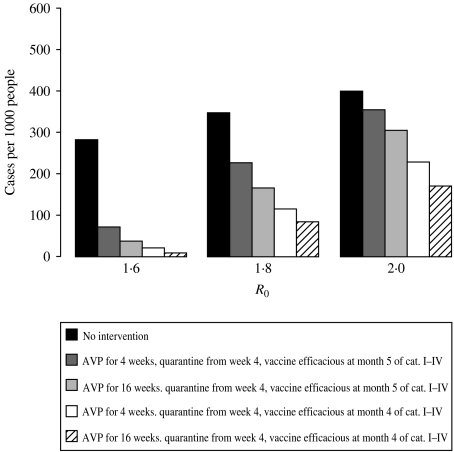
The results of the sensitivity analysis are shown in Figure 3. For R₀=1·6, the epidemic could be mitigated with moderate efforts; all strategies would be successful independently of the timing of vaccination, of the duration of providing AVP, and of the timing of social distancing measures. For R₀=1·8, vaccinating the target categories with a pre-pandemic vaccine, providing AVP for 16 weeks, and implementing social distancing measures for 4 weeks would reduce the AR from 35% to10%. For R₀=2, this combination of control measures would result in a less marked decrease in the AR, from 42% to about 20%.

Fig. 3 — Total attack rates for different values of R₀, with no control measures or selected control measures.

CONCLUSIONS

Our results, considering an R₀ value of 1·8, confirmed the need to combine different control measures [7–9]. In fact, none of the single measures was shown to be effective in containing the pandemic, with the AR decreasing at most from 35% to 24%. Combining measures would be more effective, especially if using the pre-pandemic vaccine (reaching VE at 4 months). In this case, the AR would be 4·2%, but this would require an extremely high number of AVP doses. Providing AVP for 16 weeks only would increase AR to 8·4%, which is similar to that observed during severe seasonal epidemics [21], with a considerable reduction in the number of doses provided. Moreover, if the time to reach adequate VE were 5 months, assuming a different VE (i.e. 70% or 50% in all categories) would not substantially affect the AR. However, if the time to reach adequate VE were 4 months, a VE of 70% would result in an AR of 4·2%, compared to 11·0% if assuming a VE of 50% (i.e. a 50% difference in the AR). In any case, using a less effective vaccine (i.e. with a VE of 50%) would nonetheless allow the pandemic to be contained, with an AR below 18% (range 11·0–18·1%).

Combining different measures markedly increased the probability of stochastic extinction during the early phases of the pandemic. To the best of our knowledge, most of the SEIR models used to simulate a pandemic do not consider the stochastic factors, which can strongly influence the dynamics of the pandemic in its early phases. However, we assumed that no other infectious individuals would enter the country after the few initial cases. If we were to assume that infectious individuals continued to enter the country, then stochastic extinction would be less important.

Another important finding is that the decrease in the AR would depend on which target groups were vaccinated. If a pandemic were to occur, vaccine supplies would be limited and the target groups would have to be prioritized (i.e. personnel of essential services, elderly persons and persons with chronic disease, children and young adults, and healthy adults) [19], requiring the vaccination of 26 million persons with two doses, that would be very difficult to put in practice if a pandemic did occur. However, as reported in other studies [9], our results showed that, independently of the VE, the vaccination of children and young adults would considerably reduce the incidence in other age groups (i.e. resulting in ‘herd immunity’), probably because of the important role of children and adolescents in the spread of influenza, as also observed in inter-pandemic periods [22].

In interpreting our results, some limitations need to be considered. First, we assumed that AVP provided to household contacts would decrease transmission within households but not in other contexts, which could have resulted in an underestimate of the effect of this measure. Second, the parameters used in our model obviously influenced the time estimated for the pandemic to evolve, although our estimate is similar to those obtained in other studies based on deterministic SEIR models on a global [13] or local [23] scale or individual-based models [6–9]. We examined this issue by performing a sensitivity analysis; clearly, the success of control strategies would be strongly influenced by the R₀: for R₀=1·6, all strategies would be quite successful, whereas for R₀=2 only the combined strategy with a pre-pandemic vaccine would satisfactorily mitigate the pandemic. Although the absolute effect of control strategies is strongly influenced by the different values of R₀, the relative worth of strategies are independent from the different R₀ values.

Another important limitation is that mathematical models cannot take into account the fact that the past influenza pandemics in Europe and Italy occurred over two consecutive winters, with the highest AR in the second winter [24–26]. This two-wave pattern is probably an effect of the closing of schools during the summer. Thus our model probably depicts a ‘worst case scenario’, which could be useful in evaluating control measures [9].

Our simulations show that appropriate and prompt measures, when combined, could be effective in containing an influenza pandemic. Timing is also essential, and measures that at first glance appear to be less important, such as increasing social distancing, could be extremely useful in delaying the epidemic peak and thus providing more time for vaccines to be produced. Implementing such measures, however, would entail organizing a variety of both medical and non-medical resources, and some measures, such as the closure of schools, would also have a social impact.

ACKNOWLEDGEMENTS

This work has been partially funded by the EPICO Project, of the Provincia Autonoma di Trento, Italy. The authors thank Mark Kanieff for revising the manuscript.

APPENDIX

The equations of the model are

$\left. {\matrix{ {\dot{S}\hskip 1pt_{i}^{p} \equals \minus \dot{S}\hskip 1pt_{i}^{p} \sum\limits_{j\comma q} {\beta \hskip 1pt_{i\comma j}^{p\comma q} \displaystyle{{I\hskip 1pt _{j}^{q} } \over {N\hskip 1pt_{j}^{q} }}} } \hfill \cr {\dot{E}\hskip 1pt_{i}^{p} \equals \dot{S}\hskip 1pt_{i}^{p} \sum\limits_{j\comma q} {\beta \hskip 1pt_{i\comma j}^{p\comma q} \displaystyle{{I\hskip 1pt_{j}^{q} } \over {N\hskip 1pt_{j}^{q} }}} \minus \eta E\hskip 1pt_{i}^{p} } \hfill \cr {\dot{I}\hskip 1pt_{i}^{p} \hskip2pt \equals \eta E\hskip 1pt_{i}^{p} \minus \gamma I\hskip 1pt_{i}^{p} } \hfill \cr {\dot{R}\hskip 1pt_{i}^{p} \hskip-1pt \equals \gamma I\hskip 1pt_{i}^{p} } \hfill \cr} } \right\}\hfill$

where 1/η and 1/γ represent, respectively, the mean length of the latent and the infectious periods and β_i,j^p,q is the transmission rate between an individual of class i in region p and an individual of class j in region q.

DECLARATION OF INTEREST

None.

REFERENCES

1.Li KS et al. Genesis of a highly pathogenic and potentially pandemic H5N1 influenza virus in eastern Asia. Nature. 2004;430:209–213. doi: 10.1038/nature02746. [DOI] [PubMed] [Google Scholar]
2.World Health Organization. Outbreak news. Avian influenza, Turkey – update. Weekly Epidemiological Record. 2006;81:42–43. [Google Scholar]
3.Monto AS. Vaccines and antiviral drugs in pandemic preparedness. Emerging Infectious Diseases. 2006;12:55–60. doi: 10.3201/eid1201.051068. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Stephenson I et al. Development and evaluation of influenza pandemic vaccines. Lancet Infectious Diseases. 2006;6:71–72. doi: 10.1016/S1473-3099(06)70364-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Influenza Team ECDPaC. Pandemic preparedness in the European Union – multi-sectoral planning needed. Eurosurveillance. 2007;12 : E070222.1. [PubMed] [Google Scholar]
6.Ferguson NM et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
7.Ferguson NM et al. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Longini IM et al. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
9.Germann TC et al. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences USA. 2006;103:5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Carrat F et al. A ‘small-world-like’ model for comparing interventions aimed at preventing and controlling influenza pandemics. BMC Medicine. 2006;4:26. doi: 10.1186/1741-7015-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Colizza V et al. Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Medicine. 2007;4:e13. doi: 10.1371/journal.pmed.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Cooper BS et al. Delaying the international spread of pandemic influenza. PLoS Medicine. 2006;3:e212. doi: 10.1371/journal.pmed.0030212. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Flahault A et al. Strategies for containing a global influenza pandemic. Vaccine. 2006;24:6751–6755. doi: 10.1016/j.vaccine.2006.05.079. [DOI] [PubMed] [Google Scholar]
14.Istituto Nazionale di statistica 2001. http://dawinci.istat.it/daWinci/jsp/MD/dawinciMD.jsp. http://dawinci.istat.it/daWinci/jsp/MD/dawinciMD.jsp . 14th Italian Population and Housing Census. ISTAT . ). Accessed 1 May 2007.
15.Istituto Nazionale di statistica http://www.istat.it/dati/catalogo/20060509_01/inf0606statistiche_trasporto_aereo03.pdf. http://www.istat.it/dati/catalogo/20060509_01/inf0606statistiche_trasporto_aereo03.pdf . Air transport statistics: 2003. ISTAT 2006 ( ). Accessed 1 May 2007.
16.Glezen WP. Emerging infections: pandemic influenza. Epidemiologic Reviews. 1996;18:64–76. doi: 10.1093/oxfordjournals.epirev.a017917. [DOI] [PubMed] [Google Scholar]
17.Diekmann O, Heesterbeek JAP. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. New York, NY: Wiley; 2000. [Google Scholar]
18.Flahault A et al. Modelling the 1985 influenza epidemic in France. Statistics in Medicine. 1988;7:1147–1155. doi: 10.1002/sim.4780071107. [DOI] [PubMed] [Google Scholar]
19.Ministero della Salute http://www.ministerosalute.it/imgs/C_17_pubblicazioni_511_allegato.pdf. http://www.ministerosalute.it/imgs/C_17_pubblicazioni_511_allegato.pdf . National plan for preparedness and response to an influenza pandemic ( ). Accessed 1 May 2007.
20.Ministero della Salute 2005. http://www.ministerosalute.it/promozione/malattie/malattie.jsp. http://www.ministerosalute.it/promozione/malattie/malattie.jsp . Influenza vaccination coverage, ). Accessed 1 May 2007.
21.Bella A 2005. FLU-ISS. A sentinel surveillance network for influenza relying on general practitioners and pediatricians. Report for the period 2004–2005. ISS, . Report No. 22.
22.Brownstein JS, Kleinman KP, Mandl KD. Identifying pediatric age groups for influenza vaccination using a real-time regional surveillance system. American Journal of Epidemiology. 2005;162:686–693. doi: 10.1093/aje/kwi257. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Roberts MG et al. A model for the spread and control of pandemic influenza in an isolated geographical region. Journal of the Royal Society Interface. 2007;4:325–330. doi: 10.1098/rsif.2006.0176. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Viboud C et al. Influenza epidemics in the United States, France, and Australia, 1972–1997. Emerging Infectious Diseases. 2004;10:32–39. doi: 10.3201/eid1001.020705. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Viboud C et al. Multinational impact of the 1968 Hong Kong influenza pandemic: evidence for a smoldering pandemic. Journal of Infectious Diseases. 2005;192:233–248. doi: 10.1086/431150. [DOI] [PubMed] [Google Scholar]
26.Rizzo C et al. Trends for influenza-related deaths during pandemic and epidemic seasons, Italy, 1969–2001. Emerging Infectious Diseases. 2007;13:694–699. doi: 10.3201/eid1305.061309. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref001] 1.Li KS et al. Genesis of a highly pathogenic and potentially pandemic H5N1 influenza virus in eastern Asia. Nature. 2004;430:209–213. doi: 10.1038/nature02746. [DOI] [PubMed] [Google Scholar]

[ref002] 2.World Health Organization. Outbreak news. Avian influenza, Turkey – update. Weekly Epidemiological Record. 2006;81:42–43. [Google Scholar]

[ref003] 3.Monto AS. Vaccines and antiviral drugs in pandemic preparedness. Emerging Infectious Diseases. 2006;12:55–60. doi: 10.3201/eid1201.051068. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref004] 4.Stephenson I et al. Development and evaluation of influenza pandemic vaccines. Lancet Infectious Diseases. 2006;6:71–72. doi: 10.1016/S1473-3099(06)70364-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref005] 5.Influenza Team ECDPaC. Pandemic preparedness in the European Union – multi-sectoral planning needed. Eurosurveillance. 2007;12 : E070222.1. [PubMed] [Google Scholar]

[ref006] 6.Ferguson NM et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]

[ref007] 7.Ferguson NM et al. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref008] 8.Longini IM et al. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]

[ref009] 9.Germann TC et al. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences USA. 2006;103:5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref010] 10.Carrat F et al. A ‘small-world-like’ model for comparing interventions aimed at preventing and controlling influenza pandemics. BMC Medicine. 2006;4:26. doi: 10.1186/1741-7015-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref011] 11.Colizza V et al. Modeling the worldwide spread of pandemic influenza: baseline case and containment interventions. PLoS Medicine. 2007;4:e13. doi: 10.1371/journal.pmed.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref012] 12.Cooper BS et al. Delaying the international spread of pandemic influenza. PLoS Medicine. 2006;3:e212. doi: 10.1371/journal.pmed.0030212. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref013] 13.Flahault A et al. Strategies for containing a global influenza pandemic. Vaccine. 2006;24:6751–6755. doi: 10.1016/j.vaccine.2006.05.079. [DOI] [PubMed] [Google Scholar]

[ref014] 14.Istituto Nazionale di statistica 2001. http://dawinci.istat.it/daWinci/jsp/MD/dawinciMD.jsp. http://dawinci.istat.it/daWinci/jsp/MD/dawinciMD.jsp . 14th Italian Population and Housing Census. ISTAT . ). Accessed 1 May 2007.

[ref015] 15.Istituto Nazionale di statistica http://www.istat.it/dati/catalogo/20060509_01/inf0606statistiche_trasporto_aereo03.pdf. http://www.istat.it/dati/catalogo/20060509_01/inf0606statistiche_trasporto_aereo03.pdf . Air transport statistics: 2003. ISTAT 2006 ( ). Accessed 1 May 2007.

[ref016] 16.Glezen WP. Emerging infections: pandemic influenza. Epidemiologic Reviews. 1996;18:64–76. doi: 10.1093/oxfordjournals.epirev.a017917. [DOI] [PubMed] [Google Scholar]

[ref017] 17.Diekmann O, Heesterbeek JAP. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. New York, NY: Wiley; 2000. [Google Scholar]

[ref018] 18.Flahault A et al. Modelling the 1985 influenza epidemic in France. Statistics in Medicine. 1988;7:1147–1155. doi: 10.1002/sim.4780071107. [DOI] [PubMed] [Google Scholar]

[ref019] 19.Ministero della Salute http://www.ministerosalute.it/imgs/C_17_pubblicazioni_511_allegato.pdf. http://www.ministerosalute.it/imgs/C_17_pubblicazioni_511_allegato.pdf . National plan for preparedness and response to an influenza pandemic ( ). Accessed 1 May 2007.

[ref020] 20.Ministero della Salute 2005. http://www.ministerosalute.it/promozione/malattie/malattie.jsp. http://www.ministerosalute.it/promozione/malattie/malattie.jsp . Influenza vaccination coverage, ). Accessed 1 May 2007.

[ref021] 21.Bella A 2005. FLU-ISS. A sentinel surveillance network for influenza relying on general practitioners and pediatricians. Report for the period 2004–2005. ISS, . Report No. 22.

[ref022] 22.Brownstein JS, Kleinman KP, Mandl KD. Identifying pediatric age groups for influenza vaccination using a real-time regional surveillance system. American Journal of Epidemiology. 2005;162:686–693. doi: 10.1093/aje/kwi257. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref023] 23.Roberts MG et al. A model for the spread and control of pandemic influenza in an isolated geographical region. Journal of the Royal Society Interface. 2007;4:325–330. doi: 10.1098/rsif.2006.0176. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref024] 24.Viboud C et al. Influenza epidemics in the United States, France, and Australia, 1972–1997. Emerging Infectious Diseases. 2004;10:32–39. doi: 10.3201/eid1001.020705. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref025] 25.Viboud C et al. Multinational impact of the 1968 Hong Kong influenza pandemic: evidence for a smoldering pandemic. Journal of Infectious Diseases. 2005;192:233–248. doi: 10.1086/431150. [DOI] [PubMed] [Google Scholar]

[ref026] 26.Rizzo C et al. Trends for influenza-related deaths during pandemic and epidemic seasons, Italy, 1969–2001. Emerging Infectious Diseases. 2007;13:694–699. doi: 10.3201/eid1305.061309. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Scenarios of diffusion and control of an influenza pandemic in Italy

C RIZZO

A LUNELLI

A PUGLIESE

A BELLA

P MANFREDI

G SCALIA TOMBA

M IANNELLI

M L CIOFI DEGLI ATTI

SUMMARY

INTRODUCTION