Dynamics of Salmonella transmission on a British pig grower-finisher farm: a stochastic model

A A HILL; E L SNARY; M E ARNOLD; L ALBAN; A J C COOK

doi:10.1017/S0950268807008485

. 2007 May 3;136(3):320–333. doi: 10.1017/S0950268807008485

Dynamics of Salmonella transmission on a British pig grower-finisher farm: a stochastic model

A A HILL ^1,^*, E L SNARY ¹, M E ARNOLD ¹, L ALBAN ², A J C COOK ¹

PMCID: PMC2870814 PMID: 17475090

SUMMARY

Previous modelling studies have estimated that between 1% and 10% of human salmonella infections are attributable to pig meat consumption. In response to this food safety threat the British pig industry have initiated a salmonella monitoring programme. It is anticipated that this programme will contribute to achieving a UK Food Standards Agency target for reducing salmonella levels in pigs at slaughter by 50% within 5 years. In order to better inform the monitoring programme, we have developed a stochastic transmission model for salmonella in a specialist grower-finisher pig herd, where data from a Danish longitudinal study have been used to estimate some of the key model parameters. The model estimates that about 17% of slaughter-age pigs will be infected with salmonella, and that of these infected pigs about 4% will be excreting the organism. In addition, the model shows that the most effective control strategies will be those that reduce between-pen transmission.

Introduction

There were 16 343 laboratory-confirmed cases of salmonellosis reported in the United Kingdom in 2003 [1]. It is estimated that only one in three cases in the community are reported, suggesting an annual public health burden of around 50 000 cases per year [2]. The most frequent serovar (65%) to be isolated from human cases is Salmonella Enteritidis, which is commonly associated with poultry. The second most commonly isolated human serovar, Salmonella Typhimurium (~14% of cases), is found in all farmed livestock and is the most commonly isolated serovar from pigs [3], in which species it seldom provokes clinical disease. In a recent abattoir survey, Salmonella spp. were isolated from 122 of 520 (23%) randomly selected samples of caecal contents and 67 of these isolates were identified as S. Typhimurium (55%) [4]. If these organisms persist and contaminate the end meat product they may then cause illness in the human population. In response to the results of the abattoir survey, the UK Food Standards Agency (FSA) have now set a target of reducing the prevalence of salmonella in caecal contents taken from pigs at slaughter by 50% by 2010 [5], in order to reduce the risk of human salmonellosis through consuming British pig meat.

Previous to the FSA target, the British Pig Executive (BPEx) introduced the Zoonoses Action Plan (ZAP) Salmonella Monitoring Programme in June 2002 for pigs supplied to quality-assured abattoirs in Great Britain, and in January 2003 ZAP was extended to all producers in Northern Ireland [6]. ZAP Salmonella uses an indirect lipopolysaccharide mix-salmonella meat-juice enzyme-linked immunosorbent assay (MJE) which detects antibodies against groups B and C₁ salmonella. Results from individual samples and positive and negative controls are converted to a sample-to-positive ratio (S/P ratio) and the result is interpreted as negative if it is ⩽0·25 and positive if it is >0·25 (this is roughly equivalent to an optical density percentage of 40%, i.e. OD 40%). From July 2003 all herds where at least 15 samples had been tested in the preceding 3 months were assigned a ZAP level (either 1, 2 or 3). Farms where the incidence of MJE-positive tests is greater than 65% (ZAP level 2 or 3) are required to act within a restricted time-frame to reduce the prevalence of MJE-positive tests, or else be suspended from Quality Assurance schemes, thus losing access to quality-assured abattoirs and potentially having to accept lower prices for their produce.

Two significant questions that cannot be answered by the introduction of a MJE-based monitoring programme at slaughter are (i) whether reductions in overall MJE prevalence in British pigs at slaughter translates into a reduction in the prevalence of salmonella-infected or salmonella-contaminated pigs at slaughter and (ii) what effect reductions in the prevalence of salmonella infection/contamination in pigs at slaughter has on the risk of human salmonella infection from consuming pig meat (and consequently the number of human salmonella cases per year). Any field study attempting to answer these two questions would be technically and logistically difficult and prohibitively expensive. However, the recent progress in the field of quantitative microbiological risk assessment allows these two questions to be investigated within a reasonable time-frame and budget. Models based on data from the Dutch, Danish and British pig industries have estimated that 1–10% of human salmonella cases may be attributable to pig meat consumption [7–9]. A previous farm-to-consumption microbiological risk assessment (MRA) for S. Typhimurium in British pig meat [9] estimated that a reduction of 50% in the prevalence of S. Typhimurium infection in slaughter-age pigs (but before they are transported to the abattoir) would reduce the number of human S. Typhimurium cases attributable to pig meat by a similar percentage.

In this paper we report updates to the farm transmission module from the MRA for S. Typhimurium in British pig meat [9], which has increased confidence in the model's estimation of the prevalence of salmonella infection in slaughter-age pigs immediately prior to transport. We have also investigated what reductions in MJE prevalence per farm are estimated by the model given a range of percentage reductions in the prevalence of salmonella infection per farm in slaughter-age pigs. The model considers grower-finisher production, where pigs are introduced at about 30 kg and raised to slaughter weight (~95 kg). We further assume that the system is continuously stocked, with pigs entering and leaving the farm every week, so that pigs of varying ages are always present. Within the model, we relate salmonella infection (in slaughter-age pigs immediately prior to their transport to the abattoir) with MJE test results at slaughter. This serological response model also allows the use of the large dataset generated by the ZAP programme to estimate transmission parameters.

METHODS

Farm characteristics

There is significant variation between British pig farms in management practices and housing, which may impact the dynamics of salmonella transmission within a herd. Factors which could affect salmonella transmission include, among others, inside/outside production, the number of houses on-farm, the number of weaner sources used, and whether the pigs are all of the same age or not (that is all-in-all-out vs. continuous production) [10].

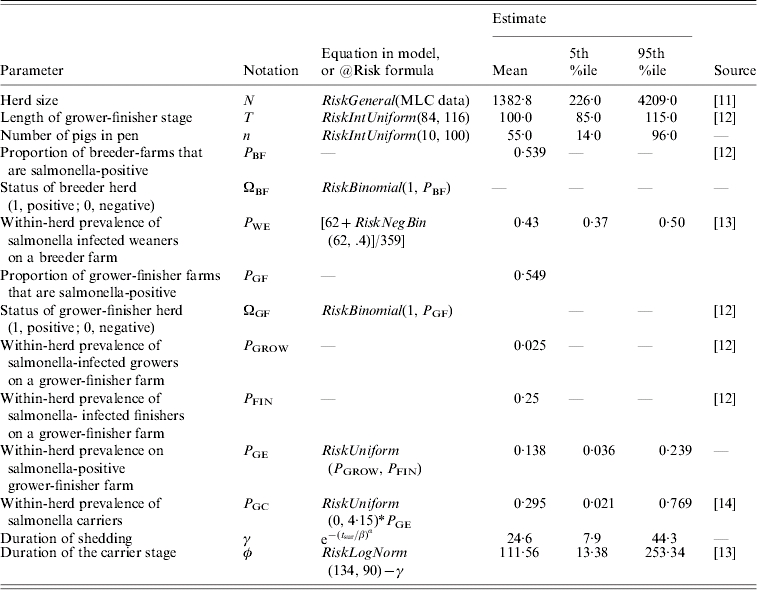
To reduce the complexity of modelling this significant between-farm variability, a ‘typical’ method of grower-finisher production in British was developed with the aid of informal expert opinion. This assumed ‘typical’ farm has the following attributes: inside production; exclusive grower-finisher farm (that is weaners are sourced from other farms); and a continuous system of production. We further consider only one building within this typical farm, which we assume is divided into two rows of pens separated by a feeding passage. Within the model, the population consists of N pigs and these are divided into sub-populations of n pigs per pen. The number of pens, ν, is equal to N/n. The probability distribution describing the herd size, N, is described from data collected by the UK Meat and Livestock Commission [11]; n is estimated using informal expert opinion (see Table).

Table.

Estimates for model variables and parameters used to initialize the settings of each model farm (i.e. each iteration of the simulation model), except for the last two rows, which are used to describe the duration of shedding and the duration of carriage respectively

graphic file with name S0950268807008485_tab1.jpg

Open in a new tab

Initial conditions of model

We have modelled continuous production, where pigs of varying age are reared at the same time; therefore, because the farm is never empty, there is no natural starting point for the model. We have assumed that the model starts (time t=0, t₀) when a new batch of weaners is placed within a randomly selected pen on the typical farm, denoted as pen [i_w]. Infected weaners within the new batch placed within pen [i_w] may infect a previously salmonella-negative herd, or increase the burden of salmonella within a positive herd. The salmonella status of the weaners entering the farm at t₀ and placed in pen [i_w] is determined by the status of the breeder herd supplying the weaners, which can either be positive or negative. This status (Ω_BF) is randomly assigned according to the proportion of British breeder farms that are salmonella-positive, P_BF (see Table for example of random assignation). The farm may already be infected at t₀ by those pigs present on the farm before the new weaners arrive; therefore, the status of the grower-finisher herd before t₀ (Ω_GF) is randomly assigned, similar to Ω_BF, according to the percentage of grower-finisher farms that are salmonella-positive, P_GF. P_BF and P_GF are described using the same British observational study [12] (see Table).

Given a salmonella-positive herd, pigs are defined by one of four states: susceptible; infected and excreting salmonella (an excretor); infected and non-excreting (a carrier); or immune. Importantly, carrier or immune pigs will not contribute to infection of other pigs, and are not themselves susceptible. However, carriers may contribute to the infection of susceptibles during transport from farm to abattoir, where stress may cause these carrier pigs to re-excrete salmonella in their faeces. Due to a current lack of data, intermittent shedding has not been included in this version of the model.

Individual pig status in a salmonella-positive finishing herd is randomly assigned in a similar manner as for herd status: for excretor status, weaners within pen [i_w] are assigned according to the within-herd prevalence of salmonella infection amongst weaners, P_WE. Likewise, for pigs within any other pen, excretor status is assigned according to the within-herd prevalence of salmonella excretion for grower-finisher pigs, P_GE. P_WE and P_GE are estimated using the same British observational study mentioned above [12]. The rectal swab used within this study was considered to have a low sensitivity (~40%) and as such we have estimated P_WE and P_GE in a similar fashion to a previous study (i.e. using a negative binomial distribution to estimate the number of false negatives, see Table) [13]. The observational study gives the within-herd prevalence for growers (P_GROW) and finishers (P_FIN) separately: P_GROW and P_FIN are estimated in a similar fashion to P_WE, and the within-herd prevalence of salmonella for grower/finishers (after adjustment for the poor sensitivity of the test used in the observational study), P_GE, is assumed to be between these two values (see Table). For pigs on the farm before t₀, carrier status may also be assigned (to those not already assigned excretor status) by applying a probability of carriage, P_GC. A Danish expert opinion workshop [14] was used to estimate the ratio of shedding to carrier pigs, P_GC, assuming that this Danish study is also applicable to British finisher farms.

Continuous production

Given a continuous system of production in this model, we assume that pigs in pens other than [i_w] will be taken to slaughter before the batch of new weaners reach slaughter age, at time T. For simplicity, it is assumed that each batch of market-weight pigs taken off the farm can be represented by the removal of one entire pen. Consequently, if it is assumed there is a constant period t_R between the removal of each batch of market-weight pigs, then t_R =T/υ−1, where T is the time (in days) between t₀ and slaughter age of the weaners introduced to the farm at time t₀. During the finishing period pigs in each newly occupied pen are assigned a salmonella status in exactly the same manner as for weaners introduced into pen [i_w] at t₀. Therefore, the prevalence of infection may be reduced or increased due to the continual removal and addition of pigs to the farm.

Transmission of salmonella, and change in infection status, during finishing period

The number of susceptibles, excretors, immune and carriers pigs in pen i at time t, are defined as S_i(t), E_i(t), I_i(t) and C_i(t), respectively.

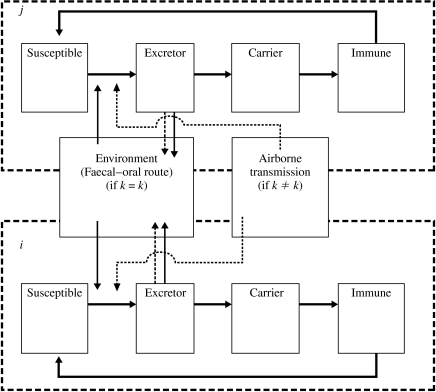
Salmonella is thought to be transmitted between pigs primarily by the faecal–oral route. We assume this route may transmit infection both within and between pens. Airborne transmission may also occur, although this route will be less important [15]. A schematic diagram of salmonella transmission and the resulting phases of infection is shown in Figure 1. The following sections describe how the model was constructed to describe the transition between infection states for individual pigs.

Fig. 1 — Structure of the transmission model used to analyse the within- and between-pen transmission of salmonella for pens i and j; method (and likelihood) of salmonella transmission from one pen depends on whether the pen is in the same row as the pen from which the infection is being transmitted (i.e. row k_i=k_j), or a different row (i.e. k_i≠k_j).

Susceptible→Excreting

The probability of infection, during one time-step, of a susceptible animal within a population containing one or more infected individuals, was derived by Reed & Frost [16, 17]. This probability of infection is governed by the probability of an ‘effective contact’ between a susceptible and infected animal. An effective contact is defined as ‘contact such that, if it occurs between an infectious case and a susceptible, it will produce a new case’ [17]. We assume each susceptible pig has ‘contact’ with every salmonella-excreting pig on the farm either by direct physical contact, contact with contaminated faeces or airborne transmission of salmonella. We assume that the probability of an effective contact depends on the distance between individual pigs, which can be adequately represented by the spatial location of the pens containing the susceptible and excreting pigs in question. Therefore, the probability of a susceptible pig in pen i becoming infected because of E_j(t) excreting pigs in pen j during the period [t, t+1], P_ij(t), is given by:

$P_{ij} \lpar t\rpar \equals 1 \minus \lpar 1 \minus p_{ij} \rpar ^{E_{j} \lpar t\rpar } \comma \hfill$

(1)

where p_ij is the pen-dependent probability of effective contact. The probability of effective contact is assumed to be highest between susceptible and excreting pigs within the same pen, denoted as p_w; the probability of effective contact for pigs between neighbouring pens is denoted as p_b. We assume the probability of transmission between pigs decreases with increasing distance from pen i (i.e. the pen containing the susceptible pig). Moreover, if the row in which the excreting pigs reside, k_j, is different to the row in which the susceptible resides (k_i), we assume the likelihood of transmitting infection is significantly decreased. Therefore, using provided informal expert opinion on how p_ij varies according to distance between pens i and j, p_ij is determined in the following way:

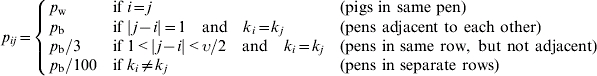$p_{ij} \equals \left\{ {\matrix{ {p_{\rm w} } \hfill \tab {{\rm if}\;i \equals j} \hfill \tab {\lpar {\rm pigs\ in\ same\ pen}\rpar } \hfill \cr {p_{\rm b} } \hfill \tab {{\rm if}\;\vert \hskip1j \minus i\vert \equals 1 \quad {\rm and}\quad k_{i} \equals k_{j} } \hfill \tab {\lpar {\rm pens\ adjacent\ to\ each\ other}\rpar } \hfill \cr p_{\rm b} \sol 3 \hfill \tab {{\rm if}\;{\rm 1} \lt \vert \hskip1j \minus i\vert \lt \upsilon \sol 2 \quad {\rm and} \quad k_{i} \equals k_{j} } \hfill \tab {\lpar {\rm pens\ in\ same\ row\comma \ but\ not\ adjacent}\rpar } \hfill \cr p_{\rm b}\sol100 \hfill \tab {{\rm if}\;k_{i} \ne k_{j} } \hfill \tab {\lpar {\rm pens\ in\ separate\ rows}\rpar } \hfill \cr} } \right.$

The time-step [t, t+1] must be approximately equal to the incubation period; for salmonella infection in pigs, the incubation period is around 24–48 h [18]; therefore the time-step has been set as one day.

Estimating p_w and p_b

No data were available to directly estimate the within- and between-pen probabilities of transmission given an effective contact, p_w and p_b. Therefore, we used maximum-likelihood methods to estimate these two parameters. Using the model developed to relate serological response to infection (see below) we were able to estimate MJE prevalence per farm as a model output, thereby allowing us to use the large dataset provided by the ZAP Salmonella programme, which gives the distribution of MJE prevalence by farm, as the ‘observed data’ from which we can derive the likelihood function for [p_w, p_b].

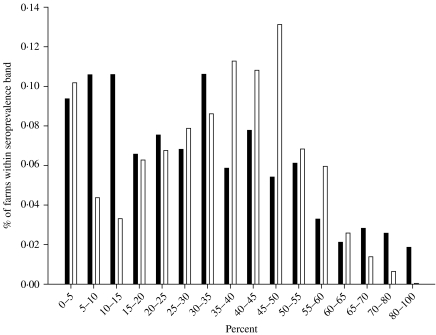
Analysis of the ZAP Salmonella programme test results, by those farms which matched our ‘typical’ model farm, produced the distribution of MJE prevalence by farm in Figure 2. The dataset was binned into 16 categories by multiples of five percentage points each, such that there were at least five farms within each category Δ_q (where q=1, 2, …, 16) (see Fig. 2).

Fig. 2 — Farm-level distribution of MJE prevalence at slaughter for farms matching model farm: observed data from ZAP programme (■), simulated using transmission model and MLE value for [p_w, p_b] (□).

For discrete distributions (the ZAP dataset) and discrete parameter space [p_w, p_b] the log-likelihood function is:

$l\lpar \hskip1p_{\rm w} \comma \ p_{\rm b} \rpar \equals \sum\limits_{q \equals \setnum{1}}^{\setnum{16}} {n_{q} \log \vert \hat{p}_{q} \vert } \comma$

where n_q is the number of farms where the observed MJE prevalence falls within Δ_q and 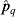$\hat{p}_{q}$ is the likelihood of a MJE prevalence result within Δ_q, given [p_w, p_b]. Simulating over 3000 iterations, the likelihood 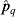$\hat{p}_{q}$ is given by n_q/3000. 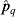$\hat{p}_{q}$ is calculated for each combination of values of [p_w, p_b] considered. The maximum-likelihood estimate (MLE) for [p_w, p_b] was then obtained from the resulting log-likelihood computations for each combination of [p_w, p_b].

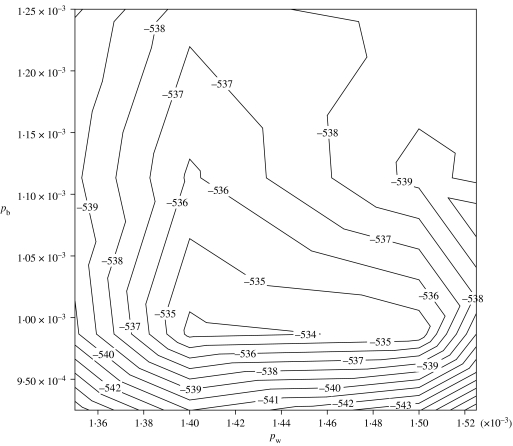
In order to ensure there was only one unique MLE, a grid search over the possible range of [p_w, p_b] was carried out. Only one maxima was found, with both p_w and p_b in the order of magnitude 10⁻³. By reducing the range of [p_w, p_b] and the step between each combination of [p_w, p_b] in subsequent grid searches, the precision of the MLE [p_w, p_b] was iteratively increased. The MLE is thus described as [1·4×10⁻³, 9·0×10⁻⁴] (95% confidence region shown in Fig. 3).

Fig. 3 — Likelihood contour plot describing the 95% confidence region of the MLE (>−536) for the two transmission parameters p_w and p_b.

Excreting→Carrier

The duration of shedding salmonella, γ, between pigs is highly variable [19]; as such, the probability of transition between excreting and carrier states per day, P_γ(t_s), is assumed dependent on the time since infection, t_s.

The distribution for γ was generated from individual pig data using a Danish longitudinal study, which took monthly faecal and blood samples from three herds, for a total of 180 finisher pigs. Assumptions made when analysing the data in the original study [19] were made again; we also assumed this dataset was applicable to British pig herds. Due to data censoring (e.g. pigs still excreting salmonella on the last sampling date of the study) standard survival analysis methods were employed. We assume that the duration of shedding is Weibull-distributed [20], where the survival function is given by 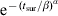${\rm e}^{ \minus \lpar {{t_{\rm sur} \sol \beta } \rpar^{\alpha}}$ , α and β are shape parameters, and t_sur is the survival time. The probability of transfer between excretor and carrier status t_s days after infection, P_γ(t_s), can be given by 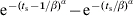${\rm e}^{ \minus \lpar {{t_{\rm s} \minus \setnum{1}} \sol \beta } \rpar^{\alpha } } \minus {\rm e}^{ \minus \lpar {{t_{\rm s} \sol \beta } \rpar^{\alpha}}$ . 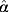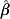The MLE of α and β, $\hat{\alpha}$ and $\hat{\beta}$ , equal 2·36 and 27·80, respectively. As such, the average duration of shedding salmonella is estimated to be 24·6 days. We appreciate that excretion occurs intermittently during this assumed period.

Carrier→(Immune)→Susceptible

Due to a lack of data quantifying the immune phase, we assume the length of immunity is 10 days beyond the end of the carrier period, similar to the length of passive immunity conferred to a newborn piglet from a sow's antibodies [21]. This assumption has been investigated through sensitivity analysis.

Similar for the transition between excreting and carrier pigs, there is a natural distribution for the duration of carriage, φ. The probability density function for φ is defined as previously described by ref. [13] (see Table). The corresponding descending cumulative density function (DCDF) for [φ+10] can be used to estimate the probability of transition between carrier status back to susceptible status, P_φ(t_c), where P_φ(t_c) is equal to the difference between the value of the DCDF at [t_c] and [t_c−1].

Modelling serological response

Distributions for the time taken from infection for a pig to show a MJE-positive response, and the length of time that serological response remains above the MJE test cut-off, were estimated using data from the same study from which the duration of shedding was estimated [19]. The Danish study quoted MJE results in terms of optical densities, and as stated above, we have assumed that a serological result of >OD 40% from the Danish study would test MJE positive in the British ZAP programme (i.e. S/P >0·25). Similar to the above methods for estimating P_γ(t_s), we assumed that the time it takes from infection to MJE positivity is Weibull-distributed, as is the time that a pig's serological response will remain above the MJE test cut-off. Hence the probabilities of an infected pig testing MJE positive t_s days after infection, P_s(t_sero), and the probability of that serological response falling below the MJE cut-off t_d days after seroconversion, P_d(t_d), were estimated using the same methods as that for duration of shedding. For the time to MJE positivity, the MLE for 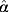$\hat{\alpha}$ =3·28 and 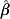$\hat{\beta}$ =64·75, and for the duration of MJE positivity, $\hat{\alpha}$ =3·30 and $\hat{\beta}$ =79·82, respectively. Therefore, the average time to a serological response that will test as MJE positive is 58·0 days, and the average time a serological response to infection remains above the MJE cut-off is 69·7 days. 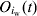At any time t, the number of MJE-positive pigs in pen [i_w] is denoted as $O_{i_{{\rm w}} } \lpar t\rpar$ . The estimated model prevalence of MJE-positive pigs per batch at T, π_p(T), is given by:

$\pi _{\rmrho } \lpar T\hskip1\rpar \equals {{O_{i_{\rm w} } \lpar T\hskip1\rpar } \over n}\comma \hfill$

(2)

Construction and simulation of model

The simulation model was constructed using Microsoft Excel (Microsoft Corporation, Redmond, WA, USA), Visual Basic Editor for Applications (VBA) and the risk analysis software @Risk 4.5 (Palisade Corporation, Ithaca, NY, USA). The simulation model was run using Latin Hypercube sampling methods until the mean and standard deviation of the model output had converged (<1·5% change from the previous 100 iterations). Values for N, n, Ω_BF and Ω_GF were randomly selected from the corresponding @Risk probability distributions inputted into the model spreadsheet to describe between-farm variability. The stochastic transmission model, which was developed within VBA, then describes the within-farm variability. Sensitivity analysis was carried out on parameters with uncertain estimates.

The model is run in 1-day steps, from the time weaners are introduced to pen [i_w] at t₀ until the time they reach slaughter age (T), but before they are taken from their pen, weighed and transported to the abattoir. At each time-step, for each susceptible pig on the farm at time t, the probability of becoming infected with salmonella from excreting pigs in its own pen (i=j) is calculated using equation (1); whether or not the pig becomes infected is determined by using the VBA random number generator (i.e. if the random number generated is less than the probability of infection at t, p_ij(t), the pig is infected). If the pig remains susceptible, the model then calculates the probability of salmonella infection due to excreting pigs within another pen (i≠j), and hence determines whether or not the pig becomes infected using similar methods as those described above. The model loops through each pen until either the pig becomes infected or all pigs in all pens have been considered for that pig and time-step; the next susceptible pig is then considered. Similarly, for excreting, carrier states and seroconversion, random number generators are used to determine whether transition between states occurs for each pig in that infection state.

Model output

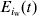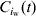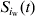At each time-step, the model updates the number of excretors, carriers and susceptibles in pen [i_w], $E_{i_{{\rm w}} } \lpar t\rpar$ , $C_{i_{{\rm w}} } \lpar t\rpar$ and $S_{i_{{\rm w}} } \lpar t\rpar$ , respectively, by summing the number of excretors, carriers and susceptibles within pen [i_w] at the end of the period [t, t+1]. The prevalence of susceptible pigs, π_s(t), the prevalence of excreting pigs at time t, π_e(t), and the prevalence of carrier pigs at time t, π_c(t), in pen [i_w] are given by equation 3(a–c) respectively.

$\pi _{\rm s} \lpar t\rpar \equals {{S_{i_{{\rm w}} } \lpar t\rpar } \over n}\comma \hfill$

(3a)

$\pi _{\rm e} \lpar t\rpar \equals {{E_{i_{{\rm w}} } \lpar t\rpar } \over n}\comma \hfill$

(3b)

$\pi _{\rm c} \lpar t\rpar \equals {{C_{i_{{\rm w}} } \lpar t\rpar } \over n}\comma \hfill$

(3c)

The average prevalence of infection at time t, π_i(t), is given in equation (4).

$\pi _{\rm i} \lpar t\rpar \equals \pi _{\rm e} \lpar t\rpar \plus \pi _{\rm c} \lpar t\rpar \comma \hfill$

(4)

From this information, we can describe the epidemic curve within this pen over the course of the finishing period. Further, the model updates the number of pigs within each infection status for every other pen, hence we can also provide the prevalence of susceptible, excreting and carrier pigs for the whole herd if necessary.

Modelling of control strategies

For farms with a high percentage of MJE-positive tests, and which therefore face possible withdrawal of their Quality Assured status, assistance is available from their veterinarian, and if required vets and microbiologists from the Veterinary Laboratories Agency. Control programmes will be designed by their veterinarian; however, while these programmes will be tailored for each individual farm, most will include strategies such as those given in government advice [22] and include all-in-all-out production, increased biosecurity and dietary changes.

The value of the probability of an effective contact (either within- or between-pen) encompasses all of the factors which contribute to the likelihood of infection given a positive farm, which include the number of salmonella present in contaminated faeces, the immunity of the pig to infection, and the level of biosecurity on the farm. Therefore, within the model any method that may be used to reduce (or indeed increase) the prevalence of salmonella infection may be represented by a change in the values for the probabilities of an effective contact, p_w and p_b. As such, we investigated the effects of control strategies on the prevalence of salmonella infection and the prevalence of MJE-positive pigs by reducing the values of p_w and p_b.

RESULTS

Epidemic curve

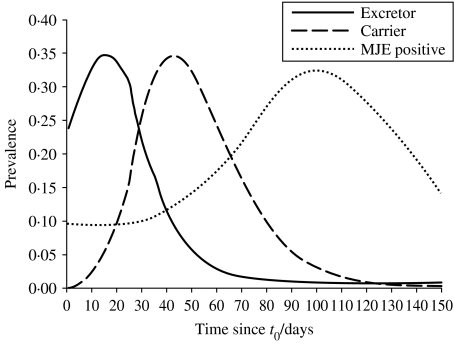
The mean epidemic curves for excretion and carriage are shown in Figure 4. On average, there is a brief increase in the prevalence of excretion after the weaners enter the farm at t₀, followed by a gradual decrease over time until slaughter age (T). The prevalence of carriage increases sharply until about 50 days after the pigs arrive on the farm; after this time the prevalence of carrier pigs decreases rapidly, although it remains higher than excretion until beyond typical slaughter age. The average prevalence of salmonella excretion for pigs of slaughter age, immediately prior to transport to the abattoir [given by equation (3b)] is 4·1% (5th and 95th percentiles of 0·0% and 18·2%, respectively). The mean prevalence of carrier pigs at slaughter age, given by equation (3c), is 11·6% (0·0%, 35·7%). The MJE prevalence [given by equation (2)] is 33·6% (0·0%, 59·2%). It is worth noting that within the model the prevalence of salmonella infection for pigs sent to slaughter is widely variable, ranging from 0% (even if the pigs come from a salmonella-positive farm) to over 50%.

Fig. 4 — Mean prevalence of salmonella-infected pigs for excreting (π_e(t)), carrier (π_c(t)) and MJE-positive (π_p(t)) stages over time t predicted from the model. Slaughter occurs between T=84 and 116 days (between dashed lines).

Validation

During a recent British survey of 93 abattoirs [4] Salmonella spp. were isolated from 124 (23·4%) of 529 intestinal samples (5th and 95th uncertainty percentiles: 20·6%, 26·6%). However, these samples may have contained salmonella which were simply passing through the digestive tract of the pig, rather than salmonella that had truly colonized the animal. Therefore, the true prevalence of salmonella infection may be significantly lower. The predicted average prevalence of salmonella infection at slaughter age [from equation (4)], π_i(T), is 15·7%. This result is lower than that from the abattoir survey and this discrepancy may be explained because of the possibility of environmental salmonella simply passing through the gut and also because the prevalence of salmonella infection is thought to significantly increase during the stressful period of transport from farm to abattoir [10]. Therefore the model result is considered reasonable.

Sensitivity analysis: effect of immunity duration on prevalence of infection at slaughter age

We could not find any relevant data to estimate the length of a pig's immunity to salmonella infection once recovered (or indeed whether immunity was complete or partial). However, within the baseline model we assume a pig will remain completely immune to infection for 10 days after full recovery (i.e. there is no chance of re-infection during this period). The effect of this assumption on the prevalence of infection at slaughter age, π_i(T), has been investigated through sensitivity analysis by varying the period of immunity from 0 to 50 days. This analysis showed that above a value of 2 days for the length of immunity, there is no significant change in the estimate of π_i(T). This result occurs because beyond 2 days only very small numbers of pigs in the model will go through the whole infection cycle and become re-infected before T. Assuming no period of immunity the average prevalence of salmonella infection at slaughter age (i.e. before transport and lairage) would be over 22%.

Scenario analysis: effect of reducing p_w and p_b

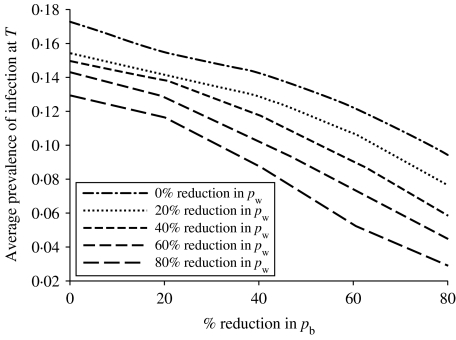
An important aspect of this model is to predict the response to control strategies. Currently, the two transmission parameters encapsulate all known risk factors for salmonella transmission on a pig farm that may be used to develop control strategies (e.g. feed, vermin, and building types). That is, the transmission parameters are estimated bearing in mind the frequency of exposure to all reported risk factors for salmonella infection in pigs and the strength of association between these risk factors and salmonella infection. As such, the effects of theoretical reductions in the values of p_w and p_b on the mean prevalence of infection (excretion and carriage) at slaughter age were investigated to establish the relationship between the model outputs and the transmission parameters p_w and p_b (see Fig. 5). The best fit to the 3D plot in Figure 5 is the linear equation 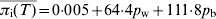$\overline{\pi _{\rm i} \lpar T\hskip 1\rpar } \equals 0 {\cdot} 005 \plus 64 {\cdot} 4p_{\rm w} \plus 111 {\cdot} 8p_{\rm b}$ (R²=0·968). An important result is that 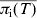$\overline{\pi _{\rm i} \lpar T\hskip1\rpar}$ is more dependent on p_b than p_w, i.e. controlling between-pen transmission has a greater effect on infection levels in slaughter-age pigs than controlling within-pen transmission of salmonella. For example, reducing p_w by 50% results in a 14% lowering in the average prevalence of infection; but reducing p_b by 50% lowers the average prevalence of infection by almost 23%.

Fig. 5 — The average prevalence of infection at slaughter age T, π_i(T), decreases with increasing percentage reductions in the between-pen transmission parameter p_b; the value of the average prevalence of infection also depends on the within-pen transmission parameter p_w, where each line on the graph represents a certain percentage reduction of p_w. The relationship between π_i(T), p_b and p_w is well described by the two-parameter linear equation 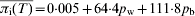$\overline{\pi _{\rm i} \lpar T\hskip1\rpar } \equals 0 {\cdot} 005 \plus 64 {\cdot} 4p_{\rm w} \plus 111 {\cdot} 8p_{\rm b}$ (R²=0·968).

The average prevalence of infection at slaughter age T, π_i(T), decreases with increasing percentage reductions in the between-pen transmission parameter p_b; the value of the average prevalence of infection also depends on the within-pen transmission parameter p_w, where each line on the graph represents a certain percentage reduction of p_w. The relationship between π_i(T), p_b and p_w is well described by the two-parameter linear equation $\overline{\pi _{\rm i} \lpar T\hskip1\rpar } \equals 0 {\cdot} 005 \plus 64 {\cdot} 4p_{\rm w} \plus 111 {\cdot} 8p_{\rm b}$ (R²=0·968).

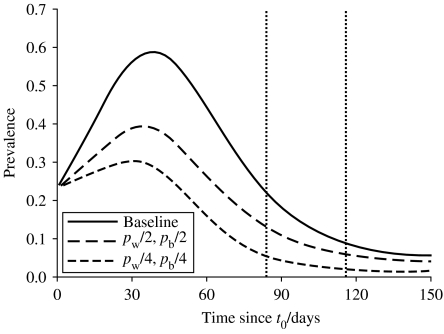
Further investigation of the model shows that the highest infection levels of pigs at slaughter results from those farms where infection occurred after t₀ – which is biologically plausible as pigs have less time to clear infection before slaughter if the epidemic starts nearer slaughter age. Therefore, reducing the number of pens which are infected during the growing-finishing stage has a major role in reducing the prevalence of infection in slaughter-age pigs. There is a linear relationship between p_w and π_i(T), and between p_b and π_i(T). The effect of these linear relationships on the average epidemic curve is shown in Figure 6.

Fig. 6 — Average prevalence of infected pigs over time; each curve represents the spread of salmonella within pen [i_w] given the baseline and theoretical reduction of both p_w and p_b. (dashed vertical lines represent boundaries of slaughter age: 864–116 days).

A recognized problem for schemes such as the ZAP programme is that testing for MJE-positive pigs, rather than for salmonella infection, provides an indication of the situation on the farm during the entire rearing period of the tested pigs: it is a relatively insensitive indicator of the true prevalence of infection at slaughter, which is the important factor in terms of reducing human salmonellosis. A generally poor correlation between herd serology and carcass contamination has been observed in the United Kingdom [23], although a positive, linear correlation between herd serology and the prevalence of salmonella-positive caecal contents and carcass swabs was found in Denmark [24]. If there is a linear correlation between herd serology and salmonella-positive caecal contents it would suggest that reducing the average MJE prevalence would also reduce the prevalence of salmonella infection in pigs at slaughter. We investigated the relationship between the average prevalence of salmonella-infected, slaughter-age pigs per farm and the average MJE prevalence per farm, as described by the model results, to establish the relationship between these two key parameters in British production.

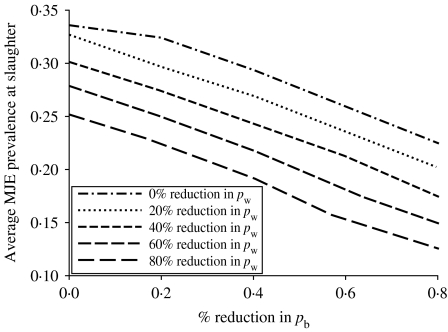
Assuming any change in the prevalence of salmonella infection during transport and lairage is proportional to the prevalence of infection in pigs immediately prior to transport, then we estimate that a 46% reduction in the average MJE prevalence at slaughter per farm observed by the ZAP programme will achieve the FSA target of a 50% reduction in the incidence of salmonella-contaminated caecal contents. 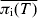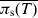However, beyond this percentage reduction (~46%) in MJE prevalence, the relationship between $\overline{\pi _{\rm i} \lpar T\hskip1\rpar}$ and $\overline{\pi _{\rm s} \lpar T\hskip1\rpar}$ becomes increasingly sensitive to the value of p_w and even more so to p_b (see Fig. 7). As a result, a reduction in the prevalence of salmonella infection in slaughter-age pigs, because of control strategies targeting within-pen transmission, but especially those targeting between-pen transmission, will not translate into a similar reduction in MJE prevalence. For example, reducing both p_b and p_w by 70% reduces the average prevalence of infection at slaughter by around 70%, but reduces MJE prevalence by only 57%.

Fig. 7 — Similar to Figure 5 the average MJE prevalence at slaughter age T, π_p(T), decreases with increasing percentage reductions in the between-pen transmission parameter p_b and also with the within-pen transmission parameter p_w. As with the average prevalence of infection at slaughter age, the relationship between π_p(T), p_b and p_w can also be reasonably described by a linear equation.

DISCUSSION

We have developed an individual-based, stochastic transmission model for the dynamics of salmonella infection within a typical British specialist grower-finisher herd, using inside housing and continuous production methods. There are several examples of previous work in a similar field of study to our own, which have all estimated the prevalence of salmonella infection in slaughter-age pigs. Our model was originally based on a deterministic transmission model for a large British finisher herd [9], and is now similar to a recent stochastic SIR model used within a larger Dutch model that estimates the number of salmonella-contaminated pig carcasses immediately after slaughter [25]. Where our model differs from the Dutch SIR model is that the latter is largely based on expert opinion, and assumes that the likelihood of transfer between states (e.g. excretor to carrier) is exponentially distributed. We have assumed that the transfer between states are Weibull-distributed (a much more flexible distribution that can be fitted to the survival curve better than an exponential), and by using a recent longitudinal study to describe the likelihood of transfer between the infection states excretor, carrier and susceptible, and using maximum likelihood to estimate the two transmission probabilities p_w and p_b, we have removed most of the need for expert opinion.

We have described the epidemic curve for salmonella infection under the specified farm conditions of the model. The prevalence of infection for pigs (of slaughter age) per farm is widely variable, ranging from 0% (even if the pigs come from a salmonella-positive farm) to over 50%, with an average of about 17%. The prevalence of infection may be further categorized by those pigs that are excreting salmonella, and those which are carriers. The ratio of excretion to carrier state also varies widely; however, on average, prevalence of carriage is roughly double that of excretion for slaughter-age pigs.

We could find no evidence in the published literature for the length of active immunity to salmonella infection conferred to a recovered pig through salmonella antibodies still present in its body (or even whether immunity is conferred). In order to include the effect of any immune response within the model we assumed that the length of immunity is similar to that of a newborn piglet's passive immunity to infection (~10 days). Sensitivity analysis shows that only a duration of immunity shorter than 2 days would significantly alter the estimated prevalence of salmonella infection at slaughter age. The maximum average prevalence of infection would rise to over 22% if there is no immunity conferred to recovered pigs. From our model validation, we think that the inclusion of a 10-day immunity period is plausible (assuming our model is correct), because not including immunity produces a value for the average prevalence of infection that is as high as the validation estimate (which leaves no room for a significant increase in the prevalence of infection during transport). Better parameter estimation of the duration of infection (particularly the carriage phase) could mean the model output (the prevalence of infection at slaughter) becomes more sensitive to our assumptions regarding immunity. If this situation occurs further research into the duration of any (full or partial) immunity post-recovery from salmonella infection would be of use for further refinement of the model, and would almost certainly be required for an extension of the model to include sows in breeding herds (which live longer and have the potential to initiate infection in weaners).

The parameters p_w and p_b were considered in a scenario analysis. It was concluded that the most important parameter in terms of controlling salmonella levels within a positive herd, is the probability of an effective contact between a susceptible pig in one pen and excreting pigs within another, p_b. This parameter is the most important because it determines how many pigs are infected within the later stages of the finisher period, and therefore how rapidly the prevalence of infection tails off.

The model suggests that to reduce the levels of salmonella infection in pigs of slaughter age efforts should be made to reduce transmission between pens as well as within pens. Efforts should also be focused on reducing the number of pigs that are infected towards the end of the finishing period (e.g. by controlling bird/rodent access to feed, and maintaining a strict biosecurity barrier between pens). Although the scenario analysis shows that controlling p_b has the largest effect on the prevalence of salmonella infection in slaughter-age pigs, it must be remembered that several assumptions are made which may alter this conclusion in later versions of the model. One assumption that may influence the conclusions of the scenario analysis is that once infected a pig will excrete salmonella in its faeces and that the duration of excretion and the number of salmonella that are excreted will not alter with age, up to the point of slaughter. No direct evidence has been found to dispute this assumption, but it is biologically plausible that as a pig grows older it may excrete fewer salmonella once infected. Without further research it is not possible to include a possibly age-dependent probability of excretion given infection: the model can be easily updated should this research be carried out.

Other assumptions include that pigs will be finished in one pen only, and that only one pen of pigs is sent to slaughter at a time. In addition, it was necessary to use informal expert opinion to estimate the probability of effective contact for pigs within distant pens. As with an age-dependent probability of excretion given infection, this expert opinion can be replaced with experimental or field data as it becomes available. The mixing of pigs during rearing, weighing and in transport will serve to increase transmission of salmonella [26]; because of the importance of between-pen transmission the mixing of pigs also warrants further investigation although it will increase the complexity of the model.

At present, the fit between the observed and predicted model distributions of MJE prevalence per farm is not statistically significant; however, we believe that further development of the model will improve this goodness of fit. In particular, the current version of the model uses a number of assumptions to replace scarce data and simplify the initial introduction of salmonella to the farm. An example is that a farm may only become infected through the introduction of salmonella-positive pigs: breaches in biosecurity such as contaminated feed or wildlife access to the pig house have not yet been considered. Observational and experimental data have recently become available to be used within the next version of the model, which will also include salmonella infection in breeding herds. We believe that these updates will allow the timing and source of salmonella infection to be modelled more accurately, and that modelling the source of infection will be crucial in improving the current model's predictions against observation.

Despite the current model's limitations, we have successfully shown that there is a linear relationship between average MJE prevalence over all farms and the average prevalence of salmonella infection within slaughter-age pigs per farm. This result agrees with previous research [24], and shows the probable reduction in infection levels at slaughter, given that the ZAP programme and proposed control strategies record a reduction in the average MJE prevalence for British farms. Work will now continue in order to determine (a) what effect these control strategies will have on reducing both salmonella and MJE prevalence and (b) what practical control strategies will be most cost-effective in reducing salmonella levels in British pigs. Importantly, the results of this work will feed into an updated MRA in order to investigate the effects of the ZAP programme (and associated control strategies) on the risk of human salmonella illness due to domestic pig meat consumption in Great Britain.

ACKNOWLEDGEMENTS

We thank Sandy Miller (VLA), Rob Davies (VLA), John Goodman (Meat & Livestock Commission) and Paul Blanchard (Frank Wright – BASF) for their invaluable advice and assistance in this work. This work has been funded by the Department for Environment, Food and Rural Affairs (Defra).

DECLARATION OF INTEREST

None.

REFERenceS

1.Zoonoses report United Kingdom 2003 2004. http://www.defra.gov.uk/animalh/diseases/zoonoses/zoonoses_reports/zoonoses2003.pdf. http://www.defra.gov.uk/animalh/diseases/zoonoses/zoonoses_reports/zoonoses2003.pdf . Defra . ). Accessed 19 September 2005.
2.Food Standards Agency London: Stationery Office; 2000. . A report of the study of infectious intestinal disease in England. FSA, ). Accessed 19 September 2005. [Google Scholar]
3.Veterinary Laboratories Agency 2005. http://www.defra.gov.uk/corporate/vla/science/science-salm-rep04.htm. http://www.defra.gov.uk/corporate/vla/science/science-salm-rep04.htm . Salmonella in livestock 2004. VLA, ). Accessed 19 September 2005.
4.Teale CJ, Milnes A, Stewart I National Agricultural Centre; Stoneleigh Park, UK: 2004. . Antimicrobial resistance in zoonotic and commensal organisms in animals at slaughter in GB in 2003. Conference Proceedings of Antimicrobial Resistance – from Farm to Fork and Beyond, , December . [Google Scholar]
5.Food Standards Agency 2005. http://www.food.gov.uk/multimedia/pdfs/task0503.pdf. http://www.food.gov.uk/multimedia/pdfs/task0503.pdf . Food Standards Agency strategic targets, ). Accessed 19 September 2005.
6.BPEX . ZAP SALMONELLA – A zoonoses action plan for the British Pig Industry. Meat & Livestock Commission, 2002http://v2.mlc.org.uk/downloads/pdfs/ZAP%20Salmonella.pdf). Accessed 19 September 2005.
7.Berends B et al. Impact on human health of Salmonella spp. on pork in The Netherlands and the anticipated effects of some currently proposed control strategies. International Journal of Food Microbiology. 1998;44:219–229. doi: 10.1016/s0168-1605(98)00121-4. [DOI] [PubMed] [Google Scholar]
8.Hald T et al. A bayesian approach to quantify the contribution of animal-food sources to human salmonellosis. Risk Analysis. 2004;24:255–269. doi: 10.1111/j.0272-4332.2004.00427.x. [DOI] [PubMed] [Google Scholar]
9.Hill Aet al. A ‘farm-to-consumption’ risk assessment for Salmonella Typhimurium in pigs. VLA; 2003 [Google Scholar]
10.Berends B et al. Identification and quantification of risk factors in animal management and transport regarding Salmonella spp. in pigs. International Journal of Food Microbiology. 1996;30:37–53. doi: 10.1016/0168-1605(96)00990-7. [DOI] [PubMed] [Google Scholar]
11.Meat & Livestock Commission. Pig Yearbook. Snowdon: MLC; 2003. [Google Scholar]
12.Davies R, McLaren I, Bedford S. Epidemiological studies of multiresistant Salmonella Typhimurium in Pigs (OZ0134). Report to GB Department of Environment, Food and Rural Affairs 2002
13.Ivanek R et al. A mathematical model for the transmission of Salmonella Typhimurium within a grower-finisher pig herd in Great Britain. Journal of Food Protection. 2004;67:2403–2409. doi: 10.4315/0362-028x-67.11.2403. [DOI] [PubMed] [Google Scholar]
14.Stark KDC et al. Differences and similarities among experts opinions on Salmonella enterica dynamics in swine pre-harvest. Preventative Veterinary Medicine. 2002;53:7–20. doi: 10.1016/s0167-5877(01)00278-1. [DOI] [PubMed] [Google Scholar]
15.Proux K et al. Contamination of pigs by nose-to-nose contact or airborne transmission of Salmonella Typhimurium. Veterinary Research. 2001;32:591–600. doi: 10.1051/vetres:2001148. [DOI] [PubMed] [Google Scholar]
16.Abbey H. An examination of the Reed–Frost theory of epidemics. Human Biology. 1952;24:201–233. [PubMed] [Google Scholar]
17.Bailey N. The Mathematical Theory of Infectious Diseases. 2nd edn. London and High Wycombe: Charles Griffin & Company Ltd; 1975. [Google Scholar]
18.Straw B Diseases of Swine. 8th edn. Ames: Iowa State University Press; 1999. [Google Scholar]
19.Kranker S et al. Longitudinal study of Salmonella enterica subtype Typhimurium infection in three Danish farrow-to-finish swine herds. Journal of Clinical Microbiology. 2003;41:2282–2288. doi: 10.1128/JCM.41.6.2282-2288.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Collett D. Modelling Survival Data in Medical Research. 1st edn. London: Chapman & Hall; 1996. [Google Scholar]
21.Varley M, Wiseman J. The Weaner Pig: Nutrition and Management. Wallington: CABI Publishing; 2001. [Google Scholar]
22.Ministry of Agriculture, Fisheries and Food and the Scottish Executive Rural Affairs Department MAFF Publications; 2000. . Code of practice for the prevention and control of salmonella on pig farms . [Google Scholar]
23.Davies R et al. Evaluation of the use of pooled serum, pooled muscle tissue fluid (meat juice) and pooled faeces for monitoring pig hers for salmonella. Journal of Applied Microbiology. 2003;95:1016–1025. doi: 10.1046/j.1365-2672.2003.02070.x. [DOI] [PubMed] [Google Scholar]
24.Sorenson LL et al. The correlation between salmonella serology and isolation of salmonella in Danish pigs at slaughter. Veterinary Microbiology. 2004;101:131–141. doi: 10.1016/j.vetmic.2004.02.016. [DOI] [PubMed] [Google Scholar]
25.van der Gaag MA et al. A state-transition simulation model for the spread of salmonella in the pork supply chain. European Journal of Operational Research. 2004;156:782–798. [Google Scholar]
26.Nollet N et al. Distribution of salmonella strains in farrow-to-finish pig herds: a longitudinal study. Journal of Food Protection. 2005;68:2012–2021. doi: 10.4315/0362-028x-68.10.2012. [DOI] [PubMed] [Google Scholar]

[ref001] 1.Zoonoses report United Kingdom 2003 2004. http://www.defra.gov.uk/animalh/diseases/zoonoses/zoonoses_reports/zoonoses2003.pdf. http://www.defra.gov.uk/animalh/diseases/zoonoses/zoonoses_reports/zoonoses2003.pdf . Defra . ). Accessed 19 September 2005.

[ref002] 2.Food Standards Agency London: Stationery Office; 2000. . A report of the study of infectious intestinal disease in England. FSA, ). Accessed 19 September 2005. [Google Scholar]

[ref003] 3.Veterinary Laboratories Agency 2005. http://www.defra.gov.uk/corporate/vla/science/science-salm-rep04.htm. http://www.defra.gov.uk/corporate/vla/science/science-salm-rep04.htm . Salmonella in livestock 2004. VLA, ). Accessed 19 September 2005.

[ref004] 4.Teale CJ, Milnes A, Stewart I National Agricultural Centre; Stoneleigh Park, UK: 2004. . Antimicrobial resistance in zoonotic and commensal organisms in animals at slaughter in GB in 2003. Conference Proceedings of Antimicrobial Resistance – from Farm to Fork and Beyond, , December . [Google Scholar]

[ref005] 5.Food Standards Agency 2005. http://www.food.gov.uk/multimedia/pdfs/task0503.pdf. http://www.food.gov.uk/multimedia/pdfs/task0503.pdf . Food Standards Agency strategic targets, ). Accessed 19 September 2005.

[ref006] 6.BPEX . ZAP SALMONELLA – A zoonoses action plan for the British Pig Industry. Meat & Livestock Commission, 2002http://v2.mlc.org.uk/downloads/pdfs/ZAP%20Salmonella.pdf). Accessed 19 September 2005.

[ref007] 7.Berends B et al. Impact on human health of Salmonella spp. on pork in The Netherlands and the anticipated effects of some currently proposed control strategies. International Journal of Food Microbiology. 1998;44:219–229. doi: 10.1016/s0168-1605(98)00121-4. [DOI] [PubMed] [Google Scholar]

[ref008] 8.Hald T et al. A bayesian approach to quantify the contribution of animal-food sources to human salmonellosis. Risk Analysis. 2004;24:255–269. doi: 10.1111/j.0272-4332.2004.00427.x. [DOI] [PubMed] [Google Scholar]

[ref009] 9.Hill Aet al. A ‘farm-to-consumption’ risk assessment for Salmonella Typhimurium in pigs. VLA; 2003 [Google Scholar]

[ref010] 10.Berends B et al. Identification and quantification of risk factors in animal management and transport regarding Salmonella spp. in pigs. International Journal of Food Microbiology. 1996;30:37–53. doi: 10.1016/0168-1605(96)00990-7. [DOI] [PubMed] [Google Scholar]

[ref011] 11.Meat & Livestock Commission. Pig Yearbook. Snowdon: MLC; 2003. [Google Scholar]

[ref012] 12.Davies R, McLaren I, Bedford S. Epidemiological studies of multiresistant Salmonella Typhimurium in Pigs (OZ0134). Report to GB Department of Environment, Food and Rural Affairs 2002

[ref013] 13.Ivanek R et al. A mathematical model for the transmission of Salmonella Typhimurium within a grower-finisher pig herd in Great Britain. Journal of Food Protection. 2004;67:2403–2409. doi: 10.4315/0362-028x-67.11.2403. [DOI] [PubMed] [Google Scholar]

[ref014] 14.Stark KDC et al. Differences and similarities among experts opinions on Salmonella enterica dynamics in swine pre-harvest. Preventative Veterinary Medicine. 2002;53:7–20. doi: 10.1016/s0167-5877(01)00278-1. [DOI] [PubMed] [Google Scholar]

[ref015] 15.Proux K et al. Contamination of pigs by nose-to-nose contact or airborne transmission of Salmonella Typhimurium. Veterinary Research. 2001;32:591–600. doi: 10.1051/vetres:2001148. [DOI] [PubMed] [Google Scholar]

[ref016] 16.Abbey H. An examination of the Reed–Frost theory of epidemics. Human Biology. 1952;24:201–233. [PubMed] [Google Scholar]

[ref017] 17.Bailey N. The Mathematical Theory of Infectious Diseases. 2nd edn. London and High Wycombe: Charles Griffin & Company Ltd; 1975. [Google Scholar]

[ref018] 18.Straw B Diseases of Swine. 8th edn. Ames: Iowa State University Press; 1999. [Google Scholar]

[ref019] 19.Kranker S et al. Longitudinal study of Salmonella enterica subtype Typhimurium infection in three Danish farrow-to-finish swine herds. Journal of Clinical Microbiology. 2003;41:2282–2288. doi: 10.1128/JCM.41.6.2282-2288.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref020] 20.Collett D. Modelling Survival Data in Medical Research. 1st edn. London: Chapman & Hall; 1996. [Google Scholar]

[ref021] 21.Varley M, Wiseman J. The Weaner Pig: Nutrition and Management. Wallington: CABI Publishing; 2001. [Google Scholar]

[ref022] 22.Ministry of Agriculture, Fisheries and Food and the Scottish Executive Rural Affairs Department MAFF Publications; 2000. . Code of practice for the prevention and control of salmonella on pig farms . [Google Scholar]

[ref023] 23.Davies R et al. Evaluation of the use of pooled serum, pooled muscle tissue fluid (meat juice) and pooled faeces for monitoring pig hers for salmonella. Journal of Applied Microbiology. 2003;95:1016–1025. doi: 10.1046/j.1365-2672.2003.02070.x. [DOI] [PubMed] [Google Scholar]

[ref024] 24.Sorenson LL et al. The correlation between salmonella serology and isolation of salmonella in Danish pigs at slaughter. Veterinary Microbiology. 2004;101:131–141. doi: 10.1016/j.vetmic.2004.02.016. [DOI] [PubMed] [Google Scholar]

[ref025] 25.van der Gaag MA et al. A state-transition simulation model for the spread of salmonella in the pork supply chain. European Journal of Operational Research. 2004;156:782–798. [Google Scholar]

[ref026] 26.Nollet N et al. Distribution of salmonella strains in farrow-to-finish pig herds: a longitudinal study. Journal of Food Protection. 2005;68:2012–2021. doi: 10.4315/0362-028x-68.10.2012. [DOI] [PubMed] [Google Scholar]

PERMALINK

Dynamics of Salmonella transmission on a British pig grower-finisher farm: a stochastic model

A A HILL

E L SNARY

M E ARNOLD

L ALBAN

A J C COOK

SUMMARY

Introduction

METHODS

Farm characteristics

Table.

Initial conditions of model

Continuous production

Transmission of salmonella, and change in infection status, during finishing period

Fig. 1.

Susceptible→Excreting

Estimating pw and pb

Fig. 2.

Fig. 3.

Excreting→Carrier

Carrier→(Immune)→Susceptible

Modelling serological response

Construction and simulation of model

Model output

Modelling of control strategies

RESULTS

Epidemic curve

Fig. 4.

Validation

Sensitivity analysis: effect of immunity duration on prevalence of infection at slaughter age

Scenario analysis: effect of reducing pw and pb

Fig. 5.

Fig. 6.

Fig. 7.

DISCUSSION

ACKNOWLEDGEMENTS

DECLARATION OF INTEREST

REFERenceS

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Estimating p_w and p_b

Scenario analysis: effect of reducing p_w and p_b