SUMMARY
One of the areas most affected by SARS was Beijing with 2521 reported cases. We estimate the effective reproductive number Rt for the Beijing SARS epidemic, which represents the average number of secondary cases per primary case on each day of the epidemic and is therefore a measure of the underlying transmission dynamics. Our results provide a quantitative assessment of the effectiveness of public health control measures. More generally, our results illustrate how changes in Rt will reflect changes in the epidemic curve.
The first case of SARS in Beijing was reported on 5 March 2003, and via a series of imported index cases in the following weeks it became the largest outbreak of SARS in the world with a total of 2521 reported probable cases [1] of whom 193 (7·7%) died [2]. Here we assess the effectiveness of the various control measures that were implemented in Beijing by estimating the changes in the underlying degree of disease transmission during the epidemic.
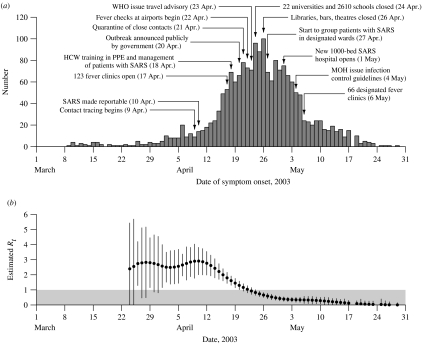
The only published epidemic curve describing dates of symptom onset of probable SARS cases in Beijing, rather than dates of hospital admission, is presented by Liang et al. [3]. The epidemic curve of symptom onset dates of 1896 patients (75% of the probable SARS cases in Beijing) is presented in the Figure, where dates of important control measures [1, 4] are superimposed. The epidemic curve reveals an exponential increase in early April, then a steady increase to a peak in late April, followed by a steady decline throughout May with the final cases occurring before the end of that month.
Fig.
(a) Number of cases of SARS by date of onset (n=1896) and dates of important control measures, Beijing, March–May 2003 [1, 3, 4]. (b) Daily estimates of the effective reproductive number Rt with 95% confidence intervals where the grey region indicates Rt⩽1. HCW, Health-care worker; PPE, personal protective equipment; WHO, World Health Organisation; MOH, China Ministry of Health.
Contact tracing and quarantine of close contacts of probable cases began on 9 April. SARS was made a notifiable disease and 3500 public health workers were mobilized on 10 April, while the mayor of Beijing set up the joint SARS leading group on 17 April. On the same day, some 123 fever clinics were set up in hospitals across Beijing, while near the end of the epidemic on 6 May these were reduced to 66 clinics separated from other patient areas [1]. From 18 April, health-care workers were given special training in the management of patients with SARS, infection control, and the use of personal protective equipment (PPE) including masks, goggles and gowns; detailed infection control guidelines were issued by the China Ministry of Health on 4 May [1]. The executive vice-minister of health announced the scope of the Beijing outbreak in a press conference on 20 April [1], and this was followed 3 days later by the WHO travel advisory [4]. After 21 April, there was a rapid increase in the number of quarantined close contacts of infected cases; these contacts were primarily quarantined at home while some were quarantined in hotels and university residences, and by the end of the epidemic a total of 30 000 individuals had been quarantined [1]. On 22 April, fever checks were set up at the Beijing international airport; screening was also conducted at major train stations and main roads into Beijing [1]. On 24 April all public elementary, middle and high schools were closed, and on 26 April major sites of public entertainment including libraries, bars and theatres were closed [1]. On 27 April SARS patients in hospitals began to be grouped together on designated wards, and on 1 May the new 1000-bed Xiao Tang Shan Hospital opened and began to receive SARS patients from other hospitals in Beijing, having been constructed in just 7 days [1].
To investigate the effectiveness of control measures in reducing the person-to-person transmission of SARS, we used the method of Wallinga & Teunis [5] to estimate Rt, the effective reproduction number on day t which is defined as the average number of secondary cases generated by one primary case with symptom onset on day t, and is a useful measure of the transmission dynamics of a disease [6]. If Rt exceeds 1, the epidemic will continue to spread, whereas Rt must be persistently reduced to below 1 to control an epidemic. Estimation of Rt requires the daily number of patients with onset of symptoms, and an estimate of the serial interval between onset of symptoms in a primary case and a secondary case. No data were available on the serial interval in Beijing, thus we used data from Singapore [7] to specify a Weibull distribution with mean 8·4 days, which was previously used to estimate Rt during the SARS epidemics in Hong Kong, Singapore, Toronto and Vietnam [5]. We estimated 95% confidence intervals for Rt on each day (see Appendix).
The resulting daily estimates of Rt are presented in the Figure. Prior to 23 March, the small number of cases resulted in unstable estimates of Rt with wide confidence intervals, thus we only present the estimates of Rt from 24 March onwards. The Figure shows that Rt initially remained at a constant level of about 3, before steadily declining after 11 April, falling to a level below 1 on 23 April, and then declining more slowly towards 0 throughout May.
The initial estimate of Rt≈3 early in the Beijing epidemic is very similar to estimates of the reproductive number early in the epidemics in Hong Kong, Vietnam, Singapore and Canada [5]. Our finding that the reproductive number only began to decline in mid-April, going below the threshold of 1 on 23 April, suggests that control measures in Beijing were fairly ineffective for 5 weeks after the first cases. However, once political attention was given to the outbreak, evidenced by the initiation of contact tracing on 9 April, and the order for SARS to be notifiable on 10 April, transmission (indicated by Rt) immediately began to decline. Shortly after the introduction of fever clinics, and training in use of PPE in hospitals in mid-April, Rt fell below the critical threshold of 1 (i.e. under control). Therefore, our results suggest that the most important factor in the control of SARS in Beijing as elsewhere was strong political commitment and a coordinated response. When the government finally announced on 20 April the scope of the ongoing SARS epidemic, the disease was already almost under control (Rt was just above 1).
Our estimates of Rt call into question the necessity and utility of closing schools, universities and other public places, with its disruptive effects on society. Furthermore, Rt had subsided to below 0·5 when the 1000-bed Xiao Tang Shan specialist SARS hospital was constructed, updated infection control guidelines were issued, and new fever clinics opened in early May. As our current analysis illustrates, the epidemic curve will typically continue to rise even after a disease has been controlled (with Rt<1), with the delay depending on the incubation period of the disease. In the Figure, case numbers continue to rise for 4 days after Rt falls below 1, whereas the mean incubation period of SARS was about 5 days [8]. We further observe that while Rt≈3 prior to 11 April, the epidemic curve continued to show exponential increase through March and early April until 16 April (i.e. a lag of 5 days).
This example, in addition to earlier examples from four other sites affected by SARS [5], highlights the connection between a unimodal epidemic curve and the underlying Rt; two properties are worth particular mention. First, while Rt is constant the curve will show an exponential increase which will continue for some time after Rt begins to fall. Second, the peak in the epidemic curve will occur some time after Rt falls below 1. In both cases the lag will approximately equal the mean incubation period. For outbreaks of infectious diseases with even longer mean incubation periods than SARS it is clear that it may not be reliable to assess the effect of control measures simply based on patterns in the epidemic curve, without considering the underlying transmission dynamics. We note that methods are now available to estimate Rt in real time [9, 10] and these may allow rapid assessment of the impact of control measures in future emerging infectious disease epidemics.
Previous assessments of the impact of public health interventions in Beijing have focused on the epidemic curve [1, 3], the number of individuals quarantined [1], attack rates [1], the onset to admission interval [1, 3], and the admission to notification interval [3]. For example, the onset to admission intervals averaged around 6 days while the epidemic was growing in early April, but these were reduced to a median of just 2 days by the end of May [1], whereas the interval between admission to hospital and notification of probable SARS cases declined rapidly at the beginning of April, and was below 1 day after 13 April [3]. Our analysis adds to these previous findings by demonstrating the changes in the underlying disease transmission during the epidemic, and aligning these changes with the temporal course of the various control measures.
A caveat of these analyses is that the available data on symptom onset dates only describe the epidemic curve for 75% of the SARS patients in Beijing [3]. However, further analysis using data for 2430 (96%) of the patients in Beijing [1] and imputing missing data on symptom onset dates showed a very similar pattern from April onwards (see Appendix and Appendix Fig.).
ACKNOWLEDGEMENTS
The authors are grateful to two anonymous referees for their helpful comments and suggestions. This work was supported in part through a commissioned research grant from the Research Fund for the Control of Infectious Diseases of the Health, Welfare, and Food Bureau of the Hong Kong Special Administrative Region Government; by the University of Hong Kong SARS Research Fund; and by the EU Sixth Framework Programme for research for policy support (contract SP22-CT-2004-511066).
APPENDIX
Estimation of confidence intervals for Rt
The methods used to estimate Rt are described in detail elsewhere in the literature [5]. Briefly, for an epidemic of n reported cases of which q contracted infection from outside the population, the relative likelihood that case k has been infected by case l is given by
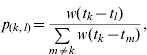 |
where w(·) is the generation interval (the average time between onset of symptoms in a primary case and onset of symptoms in a secondary case). The onset times of cases k and l are denoted tk and tl respectively. Note that p(k, l)=0 if tk⩽tl. Assuming that the probability of case l infecting case m is independent of the probability of case l infecting any other case, the distribution of the effective reproduction number for case l is denoted Rl and is distributed as follows
The average daily reproductive number Rt is calculated as the arithmetic mean over Rl for all cases l with symptom onset on day t [5].
When Rt is estimated in this way, it is straightforward to calculate the mean and variance as follows:
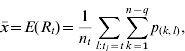 |
![\eqalign { s^{\setnum{2}} \equals {\rm Var}\lpar R_{t} \rpar \equals\tab {1 \over {n_{t}^{\setnum{2}} }}\hskip0\sum\limits_{k \equals \setnum{1}}^{n \minus q}\hskip-2 {\left[ \vskip-3pt{\sum\limits_{l\colon t_{l} \equals t} {p_{\lpar k\comma l\rpar } \lpar 1 \minus p_{\lpar k\comma l\rpar } \rpar }}\right.}\cr\tab\left.{\vskip-3\minus\hskip-2 \sum\limits_{l\comma m\colon t_{l} \equals t_{m} \equals t}\hskip-1 {p_{\lpar k\comma l\rpar } p_{\lpar k\comma m\rpar } } } } \right].}](https://cdn.ncbi.nlm.nih.gov/pmc/blobs/b50b/2870828/ac113b4d57b4/S0950268807008722_eqnU4.jpg) |
Then an approximate 95% confidence interval for Rt is given by 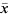 ±1·96s.
±1·96s.
Supplementary analysis – estimation of Rt by imputing missing data on onset dates
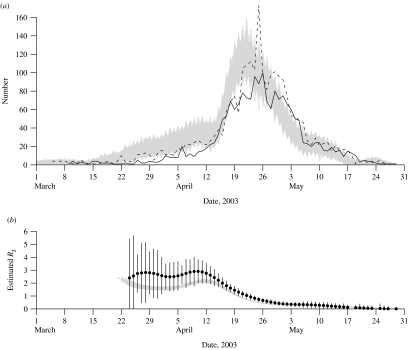
We conducted a simulation study to test the sensitivity of our results to missing data on the symptom onset dates of SARS patients in Beijing. Using data on admission dates [1] which were available for 2430 (96%) patients in Beijing, and data on the onset to admission intervals during various periods of the epidemic [3], we simulated the onset dates of those 2430 patients. We conducted 1000 simulations, each time drawing for each individual a random onset to admission time from a Poisson distribution with the mean between 1 and 7 days, depending on the period [3]. In particular, the mean onset to admission time was 3 days for patients admitted throughout March, 7 days from 1 to 15 April, 2 days from 15 April to 19 May, and 1 day from 20 May until the end of the epidemic [3]. The resulting 1000 epidemic curves are shown in the Appendix Figure [panel (a)], and show that the majority of missing data in the epidemic curve of Liang et al. [3] are most likely from the earlier stages of the epidemic. The Appendix Figure [panel (b)] also displays the available data on the epidemic curve by symptom onset dates [3] and by admission dates [1].
Appendix Fig.
(a) Number of cases of SARS by date of onset (n=1896;  ) [3] and by date of admission to hospital (n=2430; - - -) [1], with 1000 simulated epidemic curves for symptom onset (grey lines) based on the data on admission dates, Beijing, March–May 2003. (b) Daily estimates of the effective reproductive number Rt with 95% confidence intervals based on known symptom onset dates [3] as in the text Figure, and the daily estimates of the effective reproductive number Rt in each of the 1000 simulated epidemic curves (grey lines).
) [3] and by date of admission to hospital (n=2430; - - -) [1], with 1000 simulated epidemic curves for symptom onset (grey lines) based on the data on admission dates, Beijing, March–May 2003. (b) Daily estimates of the effective reproductive number Rt with 95% confidence intervals based on known symptom onset dates [3] as in the text Figure, and the daily estimates of the effective reproductive number Rt in each of the 1000 simulated epidemic curves (grey lines).
Next, we estimated the effective reproductive number Rt for each of the 1000 simulated datasets, and these estimates are presented in the Appendix Figure [panel (a)]. The estimates of Rt from the primary analysis are also superimposed for reference. The simulated curves suggest that Rt varied between 2 and 3 during the early stages of the epidemic, and as in the primary analysis Rt began to decline in the second week of April, falling below the threshold of 1 around 21 April (2 days earlier than in the main analysis). The estimated values of Rt in the simulated datasets are generally lower than in the main analysis, but the trends are very similar and therefore the conclusions of the primary analysis do not seem to be affected by the missing data on symptom onset dates.
DECLARATION OF INTEREST
None.
REFERENCES
- 1.Pang X et al. Evaluation of control measures implemented in the severe acute respiratory syndrome outbreak in Beijing, 2003. Journal of the American Medical Association. 2003;290:3215–3221. doi: 10.1001/jama.290.24.3215. [DOI] [PubMed] [Google Scholar]
- 2.Chen Q et al. Case fatality rate of severe acute respiratory syndromes in Beijing. Biomedical and Environmental Sciences. 2005;18:220–226. [PubMed] [Google Scholar]
- 3.Liang WN et al. Assessment of impacts of public health interventions on the SARS epidemic in Beijing in terms of the intervals between its symptom onset, hospital admission, and notification. Biomedical and Environmental Sciences. 2005;18:153–158. [PubMed] [Google Scholar]
- 4.World Health Organisation http://www.who.int/csr/sars/travel/en/index.html. 2006. http://www.who.int/csr/sars/travel/en/index.html . Severe Acute Respiratory Syndrome (SARS) travel advice ( ). Accessed 10 January .
- 5.Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. American Journal of Epidemiology. 2004;160:509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford University Press; 1991. [Google Scholar]
- 7.Lipsitch M et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300:1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cowling BJ et al. Alternative methods of estimating an incubation distribution: examples from Severe Acute Respiratory Syndrome. Epidemiology. 2007;18:253–259. doi: 10.1097/01.ede.0000254660.07942.fb. [DOI] [PubMed] [Google Scholar]
- 9.Cauchemez S et al. Real-time estimates in early detection of SARS. Emerging Infectious Diseases. 2006;12:110–113. doi: 10.3201/eid1201.050593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cauchemez S et al. Estimating in real time the efficacy of measures to control emerging communicable diseases. American Journal of Epidemiology. 2006;164:591–597. doi: 10.1093/aje/kwj274. [DOI] [PubMed] [Google Scholar]