The impact of a physical geographic barrier on the dynamics of measles

SUMMARY

Spatial–temporal patterns of measles incidence reflect the spatial distribution of human hosts. The heterogeneous spatial distribution of communities has been shown to introduce spatially dependent temporal lags in the timing of measles incidence. Incidence patterns reflect internal dynamics within a community and coupling of communities through the movement of infectious individuals. The central role of human movement in coupling dynamics in separate communities suggests that physical geographic barriers to movement should reduce spatial–temporal correlation. We examine measles dynamics in Maryland and Pennsylvania during the period of 1917–1938. The central feature of interest is the Chesapeake Bay, which separates Maryland into two distinct regions. We find that correlation of measles incidences in communities separated by the bay is reduced compared to communities not separated by the bay, suggesting the bay acted as a barrier to human movement during this time sufficient to decouple measles dynamics in Maryland counties.

INTRODUCTION

Studies of measles dynamics have been extremely important to the development of infectious disease dynamical theory and ecological theory in general. The availability of detailed, accurate spatial–temporal data on case rates have made possible many seminal investigations of the impact of seasonal forcing [1], population density [2], host demographic changes [3], and noise on disease dynamics [4, 5]. One outcome of this work is the finding that the spatial–temporal pattern of measles incidence reflects the underlying community structure [6]. Hierarchical waves of infections move from large cities to smaller towns due to the re-introduction of measles from large communities to smaller communities where measles transmission ceases in the troughs between seasonal epidemics. Theoretical models linking communities based upon the distance separating them and their relative population sizes successfully captures many of the features of the spatial–temporal pattern of measles in the United Kingdom.

Conversely, a lack of movement of people between two communities might decouple the dynamics in two communities. Physical geographic barriers, features such as rivers, mountains or bays, may by limiting travel decouple measles dynamics in communities separated by these features. Such features are important in the spread and dynamics of diseases of wildlife [6]. Here, we examine the impact of the Chesapeake Bay on the spatial–temporal correlation of measles incidence in Maryland, USA during the period 1917–1938. During the time of these data, no bridges or tunnels spanned the bay thus forcing travellers to either span the bay by boat or travel around the bay. At present the 4·3-mile-long Bay Bridge, built between 1949 and 1952, and the 23-mile Chesapeake Bay Bridge Tunnel, built between 1960 and 1964, traverse the bay. Although ships routinely crossed the bay during the time of these data (regular ferry services, begun in 1919, provided scheduled transportation services, with a 23-mile trip requiring 2 h) trips across the bay have dramatically increased since the construction of these two bridges.

We compared the spatial–temporal correlation in Maryland and one additional state, Pennsylvania, to previous results in the United Kingdom, and looked for evidence of spatial hierarchy in the data from the United States. Although temporal patterns in certain cities of the United States have been compared to incidence series in the United Kingdom and elsewhere [3, 7], and geographical coherence investigated with state-level data [8], a systematic review of the spatial–temporal correlation structure of county level measles data from the pre-vaccine era has not been performed. One factor that might produce different spatial–temporal dynamics in the United States compared to the United Kingdom is the difference in population density [9]. The population densities of the United Kingdom (166·47 persons/km²) and the United States (77 persons/km²) differs markedly and within Maryland, population density varies from 3672·21 persons/km² in Baltimore City and 627·03 persons/km² in Allegheny County in Pennsylvania where Pittsburgh is located to 23 persons/km² on the Eastern Shore and 36 persons/km² in the three most western counties.

In previous work, we described two distinct patterns of measles dynamics within one country, Cameroon. Before recent mass vaccination campaigns, one part of the country had annual epidemics while another had epidemics every third year [10]. Although we could not distinguish the respective role that differences in internal dynamics and spatial de-coupling of these populations played in creating the distinct patterns, we speculate that the very low level of travel between these regions allowed them to maintain different dynamics. Elimination campaigns in Africa and elsewhere must consider the coupling of populations within the targeted region and between the target region and other parts of the world. Coupling through migration of cases may link areas with heterogeneous rates of immunization and allow measles to persist even in areas with large vaccination coverage. Uncovering topographical features that are important in coupling or de-coupling regions may provide an advantage in moving successful elimination programmes forward.

METHODS

Data

Each of the US states has routinely reported cases of measles to the US Surgeon General since 1928. Unfortunately, these data do not appear in national publications for any reporting unit except the state level for any length of time. However, measles incidence and death data at the county level were available from some states of the United States. We obtained monthly case data from two states, Pennsylvania and Maryland. Monthly case data for 67 counties in Pennsylvania for the period between February 1928 and February 1934 were published in the Vital Statistics Bulletin of the State of Pennsylvania [11]. Monthly case data for the state of Maryland for a longer period (1917–1938) are available from the Annual Report of the State Board of Health of Maryland for the year ending December 31, 1917–1938 [12]. In both cases, dates were limited by the availability of data, as temporal gaps in reporting appeared in the Pennsylvania publication after 1934 and Maryland stopped routine publishing of monthly measles data by county after 1938. The total number of reported measles cases in these data is 486 424. The area covered in this dataset is ∼130 000 km². Over 10 million people lived in the two states at the time. We used contemporary county populations to calculate incidence in each county (datasets are available from corresponding author upon request).

The data were collected through passive surveillance and potentially suffer from under-reporting. Two studies during this period estimated that between 20% (as estimated through comparison with active case finding) [13, 14] and 33% (by comparing reported cases to the size of birth cohorts) of cases were actually reported to the passive surveillance system. We believe this proportion of cases gave us a sufficient sample to study the dynamics of cases in these areas during this time period.

Time-frequency decomposition

Measles incidence in this region during this time period, as in other areas of the world, exhibits multiple periodicities. Incidence is strongly seasonal, with peaks in incidence occurring during the winter months. In addition, multi-annual cycles in incidence occur with periods of between 2 and 4 years in these data. As in other measles datasets, we expect the seasonal variance to be fairly well synchronized over the region, but longer-term periodic components could exhibit phase relationships. We use wavelet decomposition to isolate the longer-term periodic model of temporal variance [9, 15], isolating normal seasonal variation of measles incidence and focusing instead on longer-term periodicity. Effectively, this technique smoothes variation at fast time-scales, so that we can examine characteristics of multi-annual cycles. A detailed description of our methods appears in the Appendix [15].

Phase and spatial synchrony

The term spatial synchrony has been used to describe the amount of correlation in incidence across a geographic region [9]. We estimate spatial synchrony be estimating the pair-wise correlation between counties in the dataset. Correlation gives a measure of the similarity of two series and depends both on the timing and relative amplitude of variance in the two series. We used wavelet reconstructed series to examine the correlation of the multi-annual variance in measles incidence rather than correlation of seasonal or shorter term variance.

We are also interested in whether the timing of peaks irrespective of their amplitude is similar across Maryland and Pennsylvania. To compare purely the timing of changes in incidence, we calculated wavelet phase angles for each reconstructed series. Details of the methodology appear in the Appendix [9].

The non-parametric covariance function was used to examine spatial and phase synchrony, the way in which correlation of either the reconstructed series or phase series varied as a function of the distance separating measurements [16]. Because we only had data for correlation at distinct distances, the set of distances between counties, we had to estimate the correlation at other distances using the non-parametric covariance function. The non-parametric covariance function provides a method for estimating correlation at continuous distances. Algorithms in the NCF library for R/S-plus were used (available at: http://asi23.ent.psu.edu/).

K-means clustering of time-series data

Clustering techniques have been used often as a tool in molecular and evolutionary genetics to determine homology and evolutionary relationships of individual genes as well as gene families [17]. We use clustering techniques as an exploratory technique to determine the geometry of spatial–temporal correlation in our disease data. Rather than clustering cases in space or time, an approach that has been used extensively in the past, we cluster time-series of incidence to obtain clusters of locales that have experienced similar patterns of incidence through time. Details of the method appear in the Appendix [18].

RESULTS

Across counties, measles incidence from both states during the years 1917–1934 (1938 for Maryland) were found to be positively correlated with a mean correlation of the shorter series of Pennsylvania and Maryland data of 0·25 (95% CI 0·22–0·28 using 1000 bootstrap samples). The temporally longer series of Maryland data has a mean correlation of 0·40 (95% CI 0·33–0·47). Correlation between the longer periodic mode of variance is on average lower for Pennsylvania and Maryland data combined with a mean of 0·15 of (95% CI 0·08–0·23). However, correlation in the temporally longer Maryland data remains high with a mean of 0·38 for the series (95% CI 0·27–0·51).

Reconstructions of the long-term periodic variance yielded series with fairly consistent periodicities across counties. In the Pennsylvania and Maryland data, the mean of the time-averaged period calculated for each county is 32·2 months (95% CI 31·5–32·9). The longer Maryland series has a mean time-averaged period of 33·7 months (95% CI 32·9–34·5).

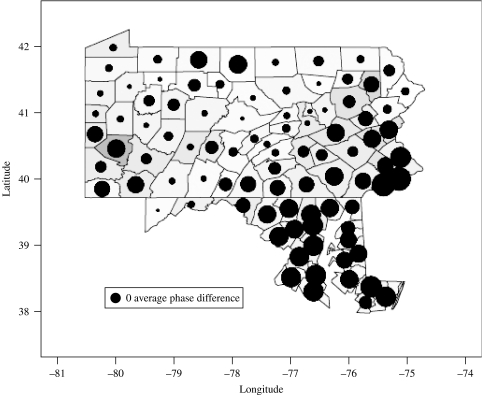
Figure 1 presents the average phase difference for each county in the Pennsylvania and Maryland set. The average phase difference for each county was calculated as the average of all time-averaged phase differences from each other county phase series in the dataset. Positive phase differences indicate that changes (peaks or troughs) in the incidence series precede peaks in other counties. Counties that are ahead of phase, on average, compared with other counties appear as larger circles on the map in Figure 1. Underlying the circular symbols indicating phase, the shading of counties indicates the population density (greyscale, square root-transformed population density used). Visually the map suggests that more densely populated areas are ahead in phase. We find that average phase difference is statistically significantly associated with population density (P<1×10⁻³, R²=0·23). Caution must be taken in interpreting results from this shorter series since phase relationships are calculated on the basis of just two cycles.

Fig. 1.

Map indicating the mean phase difference for the multi-annual variance of measles incidence in Pennsylvania. Large circles indicate counties that are on average ahead in phase of other counties in the dataset, meaning changes in incidence on average precede peaks in other counties by several months. The size of a circle indicating a zero average phase difference is shown in the bottom left-hand corner. Changes in incidence in a county with a zero average phase difference precede half of all counties and follow the remaining half. Underlying shading indicates population density with darker grey indicating counties of high population density. Coupled with population density, the map suggests that more densely populated areas are ahead in phase, suggesting epidemics originate in more populous areas.

Spatial and phase synchrony

To further understand the spatial pattern correlation structure of the Pennsylvania/Maryland series and for the longer Maryland series, we calculated the spatial synchrony of both series to determine how the long-term periodic components in each county are correlated as a function of distance. We found that adjacent counties had high correlation (mean correlation 76% in the shorter series and 80% in the longer series) and that correlation dropped quickly with distance, falling below 0·5 at 110 km (with 95% confidence). Although similar to each other, both datasets showed a smaller spatial extent (the distance for which correlation is statistically significantly different from 0) than data from the United Kingdom [9]. The Pennsylvania/Maryland data had a spatial extent of 240 km and the longer Maryland data a spatial extent of 200 km. The UK data had an extent of >600 km. The results from the Pennsylvania and Maryland datasets indicate that for counties separated by more than 200 km (or 240 km for the longer series) correlation is independent of spatial location.

Evidence of travelling waves

As the large urban centres in the United Kingdom were found to be the centres of travelling waves moving to surrounding areas, we examined the correlation of each county's measles series with Baltimore, the largest city in Maryland. Using the longer series, we calculated phase angles for each of the wavelet reconstructed series. We found a statistical significant relationship between phase difference and distance from Baltimore (beta=−2·2×10⁻³ per km, P<0·07). Excluding counties separated from Baltimore by the Chesapeake Bay from the linear regression increased the statistical significance dramatically (beta=−2·3×10⁻³, P<1×10⁻³).

We also analysed the structure of pair-wise cross-correlation in the Maryland data. We computed the cross-correlation of 24 counties relative to Baltimore City over a lag of ±36 months (73 total time periods). After calculating the interval in each county for which the lag value was at a maximum, an ordinary least squares linear regression of the maximum lag against the air distance from Baltimore revealed a strong positive relationship (P<0·001), indicating an increased lag time with increasing distance from Baltimore City. However, when using the overland distance, the correlation is not statistically significant (P<0·11), which implies that the Chesapeake Bay may play a role in disrupting distance-related dynamics.

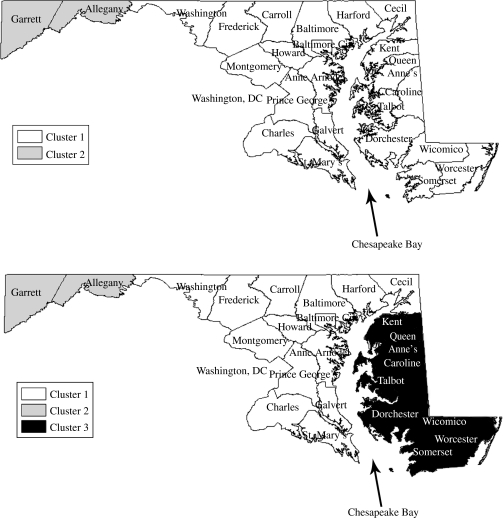
We use K-means clustering to divide the Maryland series into similar clusters (Fig. 2). Dividing Maryland into two clusters revealed a tight geographical relationship between the clusters, with one cluster primarily consisting of the counties in central Maryland and the other cluster containing the counties on the far eastern and western borders of the state (Fig. 2, top). This pattern may indicate a radial spread of measles from the centre of the state outward. Dividing Maryland into K=3 clusters indicated even more interesting geographical relationships (Fig. 2, bottom). The central Maryland counties remained essentially unchanged but the far eastern and western counties split into tighter clusters, separating themselves almost exclusively into geographical contiguous clusters.

Fig. 2.

K-mean cluster assignments for clustering log normalized measles incidence time-series for two (top map) and three (bottom map) clusters. Members of one cluster appear as the same colour (white, light grey, black). Membership in the same cluster indicates correlation in measles incidence.

Spatial synchrony in relation to the Chesapeake

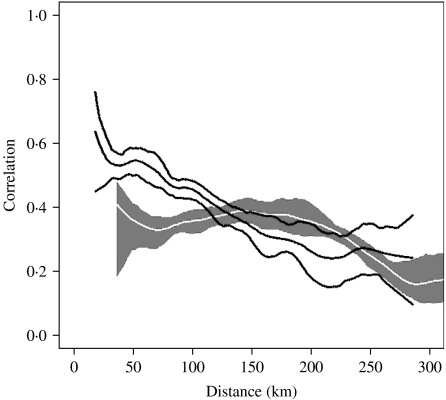
The results of the K-means analysis and the phase synchrony in relation to Baltimore suggested that the pattern of measles incidence on the eastern side of the Chesapeake Bay differed from the pattern on the western side. We hypothesized that correlation between counties that are separated by the Chesapeake Bay might be lower than correlation between counties not separated when controlling for distance separating pairs of counties. We explicitly investigated this by calculating the spatial synchrony individually for the set of county pairs separated by the bay (those for which the line connecting the centroid of each county intersects the bay) and for the set of county pairs that are not separated by the bay. Figure 3 shows the non-parametric covariance functions fit to these two sets of counties along with confidence intervals. At each value of the x-axis indicating the distance separating counties, Figure 3 shows the mean and confidence envelope for correlation of the multi-annual variance. The grey confidence intervals, and white mean curve, indicate the correlation as a function of distance for pairs of counties that are separated by the Chesapeake Bay. The black curves indicate correlation as a function of distance for the pairs of counties that are not separated by the Chesapeake Bay. For distances up to about 120 km, the correlation of pairs separated by the bay is significantly less than correlation of pairs not separated by the bay.

Fig. 3.

Spatial synchrony of the long-term mode of periodicity of measles incidence in Maryland as a function of distance. Spatial synchrony provides a measure of the correlation of series as a function of spatial distance separating them. The black curve surrounded by black 95% confidence intervals indicates the correlation of counties that are not separated by the Chesapeake Bay. The white curve surrounded by grey 95% confidence intervals indicates the correlation of counties that are separated by the Chesapeake Bay (meaning the line between the centroids of the counties intersects the Chesapeake Bay). The figure indicates that at a distance of ∼120 km the correlation of pairs separated by the bay is significantly less than the correlation of pairs not separated by the bay.

DISCUSSION

We found evidence of spatial–temporal correlation of measles incidence across Maryland and Pennsylvania and evidence that changes in incidence patterns in the more densely populated counties precede changes in less densely populated counties. We also found evidence of a travelling wave moving from Baltimore to the surrounding areas. However, we found on average less spatial synchrony in this region than has been documented in the United Kingdom [9]. One feature that acts to reduce spatial synchrony is the Chesapeake Bay.

The dynamics of measles in Maryland provides an additional example of how the correlation structure of measles dynamics is dictated not by purely physical spatial arrangements, but by the way in which space is navigated by human hosts. Gravity models incorporating both distance and the population of potential targets of travel as a proxy for the attractiveness of a community have captured many of the features of measles dynamics in the United Kingdom [19]. Our results indicate that distance in these models might benefit from incorporating some measure of the resources required to make a given journey.

There are several potential reasons why the data considered exhibit a smaller spatial extent than data from the United Kingdom. The spatial scale of the observations is different. Our data are reported at the county level as opposed to the city or town level in the United Kingdom data. Counties in the US dataset may include both large and small communities and thus reflect an aggregate behaviour from these communities. Another possible reason for the disparity is that the temporal scale of observations is coarser than the UK data (months as opposed to 2-week intervals). The UK analysis focused on a period when measles dynamics exhibited a strong biennial pattern. Our dataset covers a time when the dynamics were both biennial and triennial. These two behaviours may differ in their associated spatial synchrony. Finally, a difference in population density between the United Kingdom and the Maryland and Pennsylvania region (77 persons/km² as opposed to 166·47 persons/km² in 1930) may be responsible for the difference in spatial synchrony. Regions of low population density may act as barriers to coupling as insufficient hosts exist to maintain wave fronts. This may act to lower average spatial correlation.

The datasets considered here have limitations. In one we had a large spatial extent, but a limited length of time, in the other, a long temporal length but a smaller spatial extent. It is possible that detailed spatial temporal data exist from other regions of the United States. These datasets may be valuable resources for comparative studies of measles dynamics in regions with varying population density and demographic characteristics.

It is possible that the reduction in synchrony for pairs separated by the bay reflected the spatial geometry of population density. Our data spanned a historical time during which large-scale travel across the bay was not possible, but also considers two geographic areas that are of markedly different population densities both then and in the present day. If pairings of communities on opposite sides of the bay preferentially include pairs of significantly different population density, the reduction of synchrony would be expected purely due to the expected phase difference between large communities and small communities. However, we found no significant difference in the between-pair difference in population density for pairs separated by the bay than those not.

Regional de-coupling of measles dynamics may pose challenges to measles elimination campaigns as areas that have eliminated the disease may encounter cases from decoupled populations where transmission is ongoing. The more we can elucidate the network of spatial coupling across regions, the better we can target resources to isolate communities with on-going transmission, maintain low levels of transmission and potentially eliminate measles transmission from the globe. Analyses of historical patterns of measles have yielded large amounts of information on the dynamics of this pathogen and the general theory of contagion. Data from a variety of geographic settings may continue to inform our efforts to eliminate measles.

APPENDIX

Methods

Wavelet analysis

Wavelet analysis characterizes the distribution of power in a time-series across frequency modes [15]. The distribution of power across frequency is determined for each time-step of the data. The key feature of the technique is that, unlike the Fourier transform, it is appropriate for non-stationary data, data in which the cycle period changes over time. We use the Morlet wavelet to compute the continuous wavelet transform of each of the incidence series (time-series were log-transformed and normalized to zero mean and unit standard deviation). We then used wavelet reconstruction to isolate the variation of the original series contributed by periodicities between 18 months and 5 years. A full description of the approach appears elsewhere [15].

Phase and spatial synchrony

We calculated wavelet phases by comparing the imaginary and real parts of the wavelet transform. Wavelet phase angles vary from −π to π radians, spanning a complete cycle from peak to peak. As phases are circular, raw average phase differences were transformed using a mod function (mod(Θ+540, 360) – 180) to remove jumps in phase difference [9].

K-means clustering

We use the K-means algorithm to cluster time-series of length N into clusters according to their Euclidian distance in N dimensional space. The algorithm divides the points in N dimensions into a user-specified number of clusters in such away that it minimizes the sum of squared distance from any point to its assigned centre [18]. Cluster assignment yields information on the correlation structure of the dataset.

DECLARATION OF INTEREST

None.