Sero-epidemiology as a tool to study the incidence of Salmonella infections in humans

J SIMONSEN; M A STRID; K MØLBAK; K A KROGFELT; A LINNEBERG; P TEUNIS

doi:10.1017/S0950268807009314

. 2007 Aug 3;136(7):895–902. doi: 10.1017/S0950268807009314

Sero-epidemiology as a tool to study the incidence of Salmonella infections in humans

J SIMONSEN ^1,^*, M A STRID ², K MØLBAK ³, K A KROGFELT ², A LINNEBERG ⁴, P TEUNIS ⁵

PMCID: PMC2870874 PMID: 17678562

SUMMARY

Although most foodborne infections are undiagnosed, the incidence of these infections is usually calculated from reported cases. We present a novel population-based method to estimate the incidence of non-typhoid Salmonella infections. From 154 patients with confirmed Salmonella serotype Enteritidis infection, we determined the kinetics of the antibody response. The estimated mean responses for the three classes of serum antibodies were combined such that the time from infection could be estimated from antibody measurements. Next, serum samples collected in 1983, 1986, 1992, and 1999 from the general population were analysed for antibodies. We demonstrated how these measurements can be translated into an estimate of the general incidence. Based on serology markers there were 13 exposures leading to seroresponse of Salmonella Enteritidis/1000 person-years in 1983; the similar number in 1999 was 217. This trend confirms the increase in the number of culture-confirmed cases reported to the national surveillance system.

INTRODUCTION

Infections with non-typhoid Salmonella enterica continue to be an important cause of morbidity in industrialized countries. In many countries, the most common Salmonella type is Salmonella enterica serotype Enteritidis [1]. In Denmark, the reported incidence of this serotype increased from 220 laboratory-confirmed cases in 1983 (4·3/100 000 population) to 3674 in 1997 (69·6/100 000). From 1997, the numbers started to decrease and this decrease has been attributed to regulations and control programmes imposed on the agriculture industry [2, 3].

The true incidence and disease burden of Salmonella exposures as well as other foodborne bacteria cannot be estimated from the numbers of reported cases because of underreporting and underdiagnosis. Previous attempts to determine the degree of underreporting have been based on repeated cross-sectional interviews [4, 5] or large-scale prospective community-based studies [6, 7].

In the present study, we suggest that it is feasible to estimate the incidence of Salmonella exposures by analysing serological markers of infection measured in blood samples from the general population. The levels of the antibody isotypes can be used to classify a person as infected or not within a given period prior to sampling time. In order to accomplish this, it was essential to determine the expected levels of antibodies after infection and the kinetics of antibody decay. We determined antibody decay profiles in patients with culture-confirmed S. Enteritidis infection and developed a mathematical model for predicting antibody decay. The model accommodated a relatively rapid increase in antibody levels in the period just after infection. Following the acute phase of infection, antibody levels slowly decreased until reaching a steady-state level. The estimated curves enabled us to determine the mean decay of each class of antibodies (IgG, IgM and IgA) and thereby to estimate the time since infection for an individual with measurements of these antibodies [8–10].

This model was then used to analyse historical sera collected as a part of population studies in 1983, 1986, 1992, and 1999. Based on this, we determined time patterns in the incidence of S. Enteritidis infection from the incidence rates of seroresponses. These figures were compared with the numbers of reported cases from each of the four years in the national laboratory-based surveillance system by calculating the ratios between estimated numbers of infected individuals in the population and reported cases.

METHODS

Data material

An indirect ELISA was developed to determine antibodies against Salmonella lipopolysaccharide (LPS) in human sera. In connection with this a commercially available LPS (Sigma-Aldrich, Copenhagen, Denmark) from S. Enteritidis was used as the capture antigen [11]. In a longitudinal study, 154 patients with culture-confirmed S. Enteritidis were followed up and repeated blood samples taken. Samples were taken up to four times in the 18 months following infection. The sampling times were irregularly distributed throughout a period ranging from a few days after onset (date of first symptom) of infection up to the end of follow-up. At each sampling time the IgG, IgM and IgA levels were measured and expressed as optical density (OD) values (raw data are shown in ref. [11]).

The historical serum samples were obtained from the biobank of the Research Centre for Prevention and Health, Glostrup University Hospital, Denmark. Sera were collected as part of four population-based studies of age-stratified random samples of 30-, 40-, 50- and 60-year-olds from the general population of the western part of Copenhagen, Denmark, and included a random sample of the general population. The studies were carried out in 1983 [12], 1986 [13], 1992 [14] and 1999 [15]. Sampling area and methods were similar in all four surveys. From each of these studies a sex- and age-stratified random sample of about 150 persons from each stratum was drawn and subsequently analysed for Salmonella antibodies using the same methodology as in the longitudinal study.

Model

The first part of the analysis was aimed to determine the expected levels of antibodies in the period following infection. The three antibody classes were analysed separately. Measurements in persons with re-infection during the follow-up period would spoil the estimate of the decay rate of antibody levels. Hence we excluded measurements from persons who had a re-infection, which we defined as an increase in the antibody levels in one of the four samples to a level higher than three times the antibody level in the previous sample.

In response to infection, the antibody levels of each immunoglobulin class were assumed to rise in the acute phase. In the mathematical model, this was expressed as an increase in antibody production, driven by high pathogen levels presented to the immune system. The resulting high antibody levels then inactivated the pathogens, which decreased to a negligible state. Antibodies were assumed to be removed by a first-order decline towards a steady state. These interactions can be described by a set of differential equations:

$\left. \eqalign {x\prime \lpar t\rpar \equals \tab ax\lpar t\rpar y\lpar t\rpar \minus b\lpar x\lpar t\rpar \minus x\ast \rpar \cr y\prime \lpar t\rpar \equals \tab \minus cx\lpar t\rpar y\lpar t\rpar} \right\}\hfill$

(1)

where x(t) is the antibody level and y(t) is the pathogen level, both at time t after infection time. The parameters a and b respectively determine the rise in antibody level immediately after infection and the lengthy decline, x* is the antibody level in steady state; x(t) will decrease to x* as t tends to infinity; c determines the rate of pathogen inactivation per unit of circulating antibody.

Model fitting

Measurement errors were assumed to be log-normally distributed: the logarithm of measured antibody level (OD) at time t had a normal distribution with mean log [x(t)] and variance σ²_err.

A transformation of the parameters determining antibody decay was then chosen as $\lpar a\comma c\rpar \to \left[ {\surd \lpar a\sol c\rpar \comma \sqrt {ac} } \right]\colon \equals \lpar u_{\setnum{1}} \comma u_{\setnum{2}} \rpar$ . This was done partly in order to improve the stability of the estimates and partly to impose restrictions on the parameters: it was assumed that the initial values of antibody and pathogen levels [x(0), y(0)] and the parameters b, x* and u₂ could vary between individuals as independent samples from joint (log-normal) population distributions. The parameter u₁ was considered as a shared parameter, with an identical value for any individual in the infected population. With these assumptions individual response curves may vary in both amplitude of response, decay rate and steady-state level. However, this hierarchical structure of the parameters ensured that individual response curves could not deviate too much from each other.

Since there was no information on antibody levels prior to infection, it was impossible to evaluate the initial rise in antibody levels during the acute phase of infection. It was therefore assumed that the initial antibody level immediately before infection was equal to the steady-state level x(0)=x*. This left a set of parameters that were shared between individuals

$\rmTheta _{\setnum{1}} \equals \lcub u_{\setnum{1}} \comma \mu _{b} \comma \sigma _{b}^{\setnum{2}} \comma \mu _{u _{\setnum{2}}} \comma \sigma _{u _{\setnum{2}}}^{\setnum{2}} \comma \mu _{x\ast } \comma \sigma _{x\ast }^{\setnum{2}} \comma \mu _{y\lpar \setnum{0}\rpar } \comma \sigma _{y\lpar \setnum{0}\rpar }^{\setnum{2}} \comma \sigma _{{\rm err}}^{\setnum{2}} \rcub$

and a set describing all individually specified parameters

$\rmTheta _{\setnum{2}} \equals \lcub b_{i} \comma \, u_{\setnum{2}i} \comma \, x_{i}\hskip-2\ast \comma \, y\lpar 0\rpar _{i} \rcub _{i \in \lcub \setnum{1}..n\rcub}.$

With the above assumptions, the posterior function was a product of the likelihood function, which depended on the distribution of the measurements, and the prior function derived from the distribution of θ₂. Since we did not have any prior knowledge about θ₁ the above Bayesian structure on the parameters gave us the posterior function

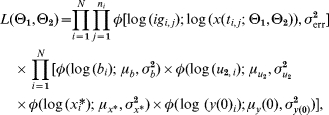$\eqalign{ \tab L\lpar \rmTheta _{\setnum{1}} \comma\hskip-1 \rmTheta _{\setnum{2}} \rpar \equals\hskip-3 \prod\limits_{i \equals \setnum{1}}^{N} {\prod\limits_{j \equals \setnum{1}}^{n_{i} } {\phi \lsqb {\rm log} \, \lpar ig_{i\comma j} \rpar \semi \,{\rm log} \, \lpar x\lpar t_{i\comma j} \semi\ \hskip-1\rmTheta _{\setnum{1}} \comma\hskip-1 \rmTheta _{\setnum{2}} \rpar \rpar \comma\sigma _{{\rm err}}^{\setnum{2}} \rsqb }} \cr \tab\quad \times \prod\limits_{i \equals \setnum{1}}^{N} \lsqb \phi \lpar {\rm log} \, \lpar b_{i} \rpar \semi \ \mu _{b} \comma \sigma _{b}^{\setnum{2}} \rpar \times \phi \lpar {\rm log} \, \lpar u_{\setnum{2}\comma i} \rpar \semi \ \mu _{u _{\setnum{2}}} \comma \sigma _{u_{\setnum{2}}}^{\setnum{2}} \cr \tab \quad\times \phi \lpar {\rm log} \, \lpar x_{i}\hskip-2\ast \rpar \semi \ \mu _{x\ast } \comma \sigma _{x\ast }^{\setnum{2}} \rpar \times \phi \lpar\hskip-1 \log \, \lpar y\lpar 0\rpar _{i} \rpar \semi \, \mu _{y} \lpar 0\rpar \comma \sigma _{y\lpar \setnum{0}\rpar }^{\setnum{2}} \rpar \rsqb \comma \cr}$

(2)

where φ(·; μ, σ²) is the density of a normal distribution with mean μ and variance σ², ig_i,j and t_i,j is respectively the antibody level and time corresponding to measurement j in subject i. N is the number of subjects and n_i is the number of samples from subject i.

A Markov chain Monte Carlo [16] method was then used to estimate the parameters. The chain was allowed to run for 50 000 iterations. By comparing the means of the posterior function between sections of the series it was verified that the chain was stationary. Estimates of the parameters were then obtained by choosing the set of parameter values from the iteration with highest value of the posterior function [equation (2)]. This procedure was done separately for each class of antibodies.

Estimated time since infection

The main objective of the present study was not only to describe antibody decay in infected subjects, but also to use this description of decay for translating an individual set of measurements of class-specific antibodies (IgG, IgM, and IgA) in the cross-sectional study against S. Enteritidis to the time since last infection. This was done in the following manner: a mean curve for each of the three antibody classes was obtained by using the estimated means (μ_b, μ_u₂, μ_x*, μ_y₀) and the estimate of the shared parameter u₁. For each sample time-point in an interval from 5 to 400 days following infection, the sum of squared distances from the (logarithm of) the mean predicted values at time t after infection to the (logarithm of) the observed values of antibody levels was computed. This produced a function dist(t) defined as

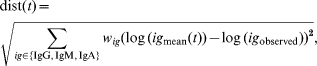$\eqalign{ \tab{\rm dist}\lpar t\rpar \equals \cr \tab \sqrt {\sum\limits_{ig \in \lcub {\rm IgG}\comma {\rm IgM}\comma {\rm IgA}\rcub } {w_{ig} \lpar {\rm log} \, \lpar ig_{{\rm mean}} \lpar t\rpar \rpar \minus {\rm log} \, \lpar ig_{{\rm observed}} \rpar \rpar ^{\setnum{2}} } }\comma$

where (w_IgG, w_IgM, w_IgA) are weights for each antibody class to adjust their contributions to the distance function dist(t), in order to increase the influence of antibodies that produce better predictions. The restriction w_IgG+w_IgM+w_IgA=1 is applied.

The time-point where this function obtained its minimum value can be interpreted as the time where the observed values of antibody levels of all three classes agree best with their expected values. Therefore, we considered this time-point as an estimate of the time elapsed since last infection. As the period of rising antibody levels is very short we ignored it and assumed that the estimated times since infection always exceeded the length of the increasing phase of the antibody response.

Based on earlier plots of antibody decay [11] we expected that the antibody levels would approach steady state values around 2–3 months after onset of illness. At this time, when antibody decay became very slow or stationary, it would be difficult to estimate the time since last infection with any degree of precision.

As a first test of the procedure, the method was applied to the same longitudinal data used for determining antibody decay, as the onset of infection was known in those subjects. All data were considered independent, ignoring the fact that each person was successively sampled up to four times. For a given choice of weights we could then estimate whether or not a subject would be predicted as having had an infection within a certain period before sampling time. Since the true number of days from infection to sampling time was known, we were able to investigate which set of weights (w_IgG, w_IgM, w_IgA) and which time window (period considered) produced the best combination of specificity and sensitivity.

Using these ‘optimum’ weights we then proceeded to the analysis of the historical cross-sectional data. For each of the four population surveys the proportion of individuals with a S. Enteritidis infection within the last 60 days prior to sampling was estimated.

The calculations of the incidence and confidence limits were based on the following assumptions: the false-positive rate is zero for individuals never infected or infected more than 120 days ago. The false-positive rate for individuals infected in the period 60–120 days ago equals Q_false. This rate could be estimated from the false-positive rate found on measurements from the longitudinal dataset restricted to measurements taken in this time window. It was also assumed that the incidence in the time-window 60–120 days ago equals the incidence in the time window 0–60 days ago. The true positive rate, Q_true, was estimated from the measurements taken in the first 60-day time window after infection onset. Therefore, the numbers of subjects classified as positive are distributed as

$x\hskip-1 \sim\hskip-1 {\rm binomial} \ \lpar n\comma pQ_{{\rm true}} \plus p\lpar 1 \minus p\rpar Q_{{\rm false}} \rpar \comma$

where n is number of persons in the cohort and p is the probability of getting infected in a 60-day window.

Estimates of p were obtained by maximizing the corresponding likelihood function. Confidence limits are calculated by using asymptotic likelihood theory [17].

The conversion to incidence (predicted number of cases/1000 person-years) was done by using the equation

$\hat{\lambda } \equals \minus \lpar 365 \sol 60\rpar \times 1000\times {\rm log} \, \lpar 1 \minus \hat{p}\rpar.$

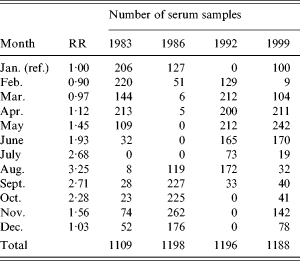
Since the blood samples were not taken at the same time each year, the calculated incidences were corrected to reflect the incidence in January. This correction was done in the following manner: from the national surveillance system of Denmark the relative rates between months were calculated (Table 1). These were smoothed by a 2-month backwards geometric average which reflects the time window with an increased antibody level. A weighted geometric mean of the smoothed relative risk was then calculated for each of the four years separately. The weights were taken from the distribution of sampling times on months for the specific year (Table 1). The serology-based incidence for that year was then scaled so as to reflect a January incidence.

Table 1.

Relative risk (RR) of Salmonella Enteritidis infection between months and the distribution of collected serum samples for the study

graphic file with name S0950268807009314_tab1.jpg

Open in a new tab

RESULTS

During the follow-up time, 29 out of 154 persons had an increase in antibody levels that satisfied our definition of a re-infection. After omitting the measurements from these persons 396 observations remained, distributed among 125 individuals.

A model check was performed in order to validate the performance of equation (1). This showed no contradiction with the assumption of log-normally distributed residuals, and further that the residuals were independent of time since infection.

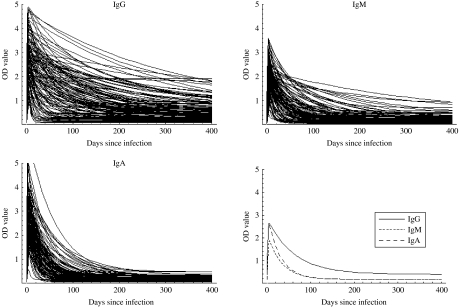
Table 2 summarizes some characteristics for the estimated response curves for each of the three antibody classes. The time to peak response was about 14 days for IgG while it was 5 days for IgM and IgA. Moreover, decay was considerably slower for IgG than for IgM and IgA. The Figure shows the mean curves determined from the estimates of Θ₁ together with the individual response curves for each antibody class. The estimated time for the antibodies to decrease to baseline was notably higher for IgG than for IgA and IgM.

Table 2.

Characteristics of the expected antibody levels in the period following an infection of Salmonella Enteritidis

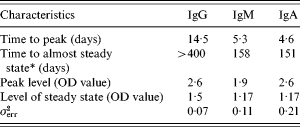
graphic file with name S0950268807009314_tab2.jpg

Open in a new tab

Almost steady level is defined as steady level+10%.

Fig — The individual response curves estimated from the model and the mean curves (determined from θ₁).

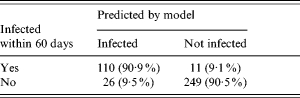
It was found that the set of weights (w_IgG=0·1, w_IgM=0·5, w_IgA=0·4) produced the best combination of sensitivity and specificity. With these chosen weights we calculated predicted numbers of observations with infection within the last 60 days prior to sampling (Table 3) and compared these predictions with the known times from infection. The true-positive rate (Q_true) was 90·9% and the false-positive rate was 9·5%. However, restricted to measurements in the time window 60–120 days from infection date, the false-positive rate (Q_false) was 20%.

Table 3.

Prediction of number of infected cases with Salmonella Enteritidis infection in a 60-day period when the true time since last infection is known

graphic file with name S0950268807009314_tab3.jpg

Open in a new tab

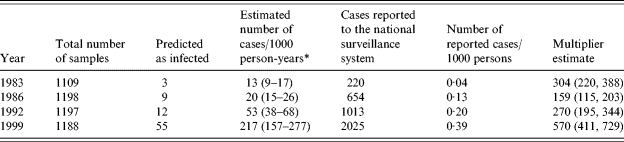
In the first sample of historical sera (from 1983), the median OD for IgG was 0·11, for IgA 0·10, and for IgM 0·08. These values increased over the years and were 0·22, 0·25, and 0·11 in 1999. Table 4 presents the results from the analyses of the historical sera. In a total of 4692 individual persons, 79 (1·7%) were predicted to have been infected within a 60-day time window. This proportion increased from 1983 (0·3%) to 1999 (4·6%). Converted into incidence, this corresponded to an increase in the incidence of seroresponses from 13 to 217/1000 person-years.

Table 4.

Comparison between serology-based incidence estimates and the number of reported cases with Salmonella Enteritidis infection in Denmark 1983 to 1999

graphic file with name S0950268807009314_tab4.jpg

Open in a new tab

Serology-based incidence. The incidence estimates are adjusted for season of blood collection.

There were some differences in the distribution of season of blood collection between the four different years (Table 1). These differences caused a change between the predicted number of infected persons and the incidence estimate following the adjustment for seasons. The ratio between these incidence estimates and the incidence estimates based on reported numbers of cases in the national surveillance system is also shown in Table 4. This ratio had a minimum level of 159 in 1986 and increased to about 570 in 1999.

DISCUSSION

Surveillance for Salmonella in humans is usually done by reporting episodes of culture-confirmed Salmonella infections to national public health institutes. Obviously, these figures will only represent a fraction of the total cases in the community. The sensitivity of laboratory-based Salmonella surveillance depends on the health-care-seeking behaviour of patients with gastroenteritis and the likelihood that the consulting physician will request a stool culture. Furthermore, ease of access to laboratories and the microbiological methods in place are of importance, as is the completeness in reporting positive findings to the public health authorities. Finally, public health jurisdictions with a tradition of active case-finding as part of outbreak investigations or extensive testing of contacts to known case-patients or food-handlers are likely to report higher numbers of infections than settings with only passive surveillance. Hence, the figures from the official reporting systems do not measure the burden of illness. Additionally, the sensitivity of the surveillance systems differs between countries and possibly also over time. The geographical variation in underreporting has been studied using Swedish travellers as ‘sentinels’ [18], but little information is available on the temporal sensitivity of Salmonella surveillance.

Community-based studies have applied questionnaire-based methods to determine ‘multiplier estimates’, i.e. the number of symptomatic infections in the community relative to each single case reported in the national surveillance registry. For non-typhoid Salmonella, a multiplier in the range of 3·8–38 has been estimated [4–7], However, such community-based studies are costly and difficult to conduct and may be subject to several types of information bias (e.g. recall) and selection bias. Moreover, such community-based studies do not account for asymptomatic cases, which is one reason why the estimates in the present study are much higher than in the studies quoted [4–7].

In veterinary medicine, surveillance based on routine testing of serological markers is a well-established methodology. In Denmark, the backbone of the Salmonella surveillance in poultry and pigs is a large-scale ongoing testing scheme of eggs and meat juice, respectively [3]. Whereas the test of a particular animal may not be sensitive and specific for an individual diagnosis, the analysis of grouped data is sufficient to characterize the Salmonella status of a herd of animals. The methods offer several advantages since they can be applied on unbiased samples of animals, can be automated, and are cost-effective compared with culture-based methods.

The purpose of the present study was to explore a similar use of serology to measure the incidence of S. Enteritidis seroresponses in human populations. To fulfil this objective, we had to develop a suitable serological assay to determine the decay of antibodies among infected patients, and to develop appropriate mathematical methods for performing back-calculations from cross-sectional serological data to the incidence of infections in humans. The results indicate that an increase in the reported incidence of S. Enteritidis from 4·4/100 000 in 1983 to 38·9/100 000 population in 1999, may mirror a rise in the infection rates in the community of 1300–21 700 per 100 000 population per year. During the late 1990s, large sections of Danish poultry were infected with Salmonella [3]. The present study indicates that during 1999 as many as one in five Danes may have been exposed to a sufficient level to give rise to a measurable seroresponse. The trend in Salmonella surveillance that we have witnessed over the past 20 years was reproducible, but the number of exposures in the community – as measured by a seroresponse – may be between 160 and 570 times higher than the reported culture-confirmed cases.

Under the assumption that there may be between 4 and 40 symptomatic Salmonella infections for each reported case [7], is it reasonable to assume that up to 500 exposures resulting in a seroresponse takes place? At present, we do not have the knowledge to answer this question, but given the high prevalence of Salmonella in many food products, the assumption may not be unreasonable [19]. Chalker & Blaser [20] estimated the incidence of Salmonella infections in the United States by using information of carriage rates and duration of excretion. They concluded that the estimated incidence was 16/1000 population prior to the S. Enteritidis pandemic. This is the same order of magnitude as our 1980s estimates. However, it seems important to explore how robust the estimates are to the choice of antigen in the test, e.g. by using a mixture of S. Enteritidis and S. Typhimurium as the capture antigen, and by comparing these results with the overall incidence of non-typhoid Salmonella infections.

The present study is subject to other limitations. First, the test was designed to determine the seroresponse to the most common Salmonella serotype, S. Enteritidis. Cross-reactions from infections with other serotypes may blur the picture, this is true in particular for group D Salmonella. Therefore, the multiplier estimates should be interpreted with a great deal of caution and may indeed be overestimated. Moreover, it is important to underscore that measurements based on serology encompass asymtomatic and mildly symptomatic cases; unlike reporting physicians, our serological approach makes no distinctions between these. Since the proportion of individuals who experience a symptomatic infection is reflected in our multiplier estimate, it will be an important issue to address in further studies. Finally, there is potential to improve the methodology by including age-dependent seroresponse and performing estimations that better take into account the heterogeneity of antibody response.

The modelling of the antibody response was based on information available from culture-confirmed cases between ages 10 and 76 years [11]. We have worked under the assumption that the antibody decay of all infected individuals follows the same kinetics; whether this is a plausible assumption needs to be addressed in future studies [9]. It may be natural to assume that asymptomatic cases in general only have a minor increase in antibody level, and the duration of that increase may be shorter compared with symptomatic cases. If this is true, this bias will lead to underestimation of the total number of cases.

Furthermore, the predicted antibody decay depended on the definition of re-infection. For example, if a person was considered as re-infected only if there had been a fourfold increase in immunoglobin level (IgG, IgM or IgA) from one measurement to the next, then more persons would have had high values at measurement long after infection, which would then result in a slower modelled decay rate. In contrast, a weaker re-infection criterion would result in a faster decay rate. Subjectively the threefold factor used in this study seems to be a good compromise.

In addition, the interaction between pathogen and antibody may be much more complex than suggested by equation (1). However, for the back-calculation, which was the main purpose of the model, it was important to have a sufficiently simple model that was able to describe the behaviour of antibody response in general.

As seen in the Figure, IgG remains at a high level longer than IgM and IgA. Therefore, if a longer time window was selected, a higher weight would have been given to IgG. However, the choice of a time window of 60 days together with the chosen weights gave the highest sensitivity and specificity. It is well known that IgA and IgM are associated with the acute response, and it was therefore unsurprising that the IgG value was relatively unimportant in a 60-day window.

In the present study the calculations of the confidence limits were based only on the estimated sensitivity and specificity. How much of the total variability in the predicted sera responses is due to uncertainty about the parameters in the model and how much is due to individual differences was not investigated. Further, we do not know how these variance components influence the false-positive/negative rates. Indeed, as some people who were not recently infected can have a high antibody level, one can argue that the inclusion of individual variation in the model may give a lower incidence estimate. Future studies will investigate these questions.

In summary, the present study was a first attempt to explore a novel approach in the surveillance of Salmonella and potentially measure its contribution to foodborne infections in human populations. Although the approach needs to be further validated and most probably refined, it shows promise as a potential tool to make unbiased comparisons between different national surveillance systems, and to determine geographical and temporal variation in the degrees of underreporting of specific pathogens.

ACKNOWLEDGEMENTS

This work was supported by The Danish Directorate for Food, Fisheries and Agri Business grant (FØSI00-7) and the EU network of Excellence for Zoonoses Research MED-VET-NET. The contribution of P.T. to this study was funded by POLYMOD, a European Commission project funded within the Sixth Framework Programme (contract number SSP22-CT-2004-502084).

DECLARATION OF INTEREST

None.

REFERENCES

1.Herikstad H, Motarjemi Y, Tauxe RV. Salmonella surveillance: a global survey of public health serotyping. Epidemiology and Infection. 2002;129:1–8. doi: 10.1017/s0950268802006842. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Mølbak K, Neimann J. Risk factors for sporadic infection with Salmonella enteritidis, Denmark, 1997–1999. American Journal of Epidemiology. 2002;156:654–661. doi: 10.1093/aje/kwf096. [DOI] [PubMed] [Google Scholar]
3.Wegener HC et al. Salmonella control programs in Denmark. Emerging Infectious Diseases. 2003;9:774–780. doi: 10.3201/eid0907.030024. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Voetsch AC et al. FoodNet estimate of the burden of illness caused by nontyphoidal Salmonella infections in the United States. Clinical Infectious Diseases. 2004;38:S127–S134. doi: 10.1086/381578. (Suppl. 3): [DOI] [PubMed] [Google Scholar]
5.Mead PS et al. Food-related illness and death in the United States. Emerging Infectious Diseases. 1999;5:607–625. doi: 10.3201/eid0505.990502. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Wheeler JG et al. Study of infectious intestinal disease in England: rates in the community, presenting to general practice, and reported to national surveillance. British Medical Journal. 1999;318:1046–1050. doi: 10.1136/bmj.318.7190.1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.de Wit MAS et al. A comparison of gastroenteritis in a general practice-based study and a community-based study. Epidemiology and Infection. 2001;127:389–397. doi: 10.1017/s0950268801006082. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Teunis PFM et al. Kinetics of IgG antibody response to pertussis toxin after infection with. B. pertussis. Epidemiology and Infection. 2002;129:479–489. doi: 10.1017/s0950268802007896. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Versteegh FGA et al. Age-specific long-term course of IgG antibodies to pertussis toxin after symptomatic infection with Bordetella pertussis. Epidemiology and Infection. 2005;133:737–748. doi: 10.1017/s0950268805003833. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.de Melker HE et al. The incidence of Bordetella pertussis infections estimated in the population from a combination of serological surveys. Journal of Infection. 2006;53:103–113. doi: 10.1016/j.jinf.2005.10.020. [DOI] [PubMed] [Google Scholar]
11.Strid M et al. Kinetics of the human antibody response against salmonella enterica serovars enteritidis and typhimurium determined by lipopolysaccharide enzyme-linked immunosorbent assay. Clinical vaccine immunology. 2007;14:741–747. doi: 10.1128/CVI.00192-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Jørgensen T. Prevalence of gallstones in a Danish population. American Journal of Epidemiology. 1987;126:912–921. doi: 10.1093/oxfordjournals.aje.a114728. [DOI] [PubMed] [Google Scholar]
13.Sjøl A, Schroll M. The cardiovascular risk profile in the Glostrup region Monica screening II, 1986/87. Ugeskrift for Lager. 1990;152:3449–3455. [PubMed] [Google Scholar]
14.Gerdes L et al. Trends in selected biological risk factors for cardiovascular diseases in the Danish MONICA population 1982–1992. Journal of Clinical Epidemiology. 2000;53:427–434. doi: 10.1016/s0895-4356(99)00193-6. [DOI] [PubMed] [Google Scholar]
15.Jørgensen T et al. A randomized non-pharmacological intervention study for prevention of ischaemic heart disease: baseline results inter99. European Journal of Cardiovascular Prevention and Rehabilitation. 2003;10:377–386. doi: 10.1097/01.hjr.0000096541.30533.82. [DOI] [PubMed] [Google Scholar]
16.Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. London: Chapman & Hall/CRC; 1995. pp. 45–56. , pp. [Google Scholar]
17.Armitage P, Colton T. Encyclopedia of Biostatistics. West Sussex, England: John Wiley & Sons Ltd; 2005. p. 2724. , p. [Google Scholar]
18.Ekdahl K et al. Travel-associated non-typhoidal salmonellosis: geographical and seasonal differences and serotype distribution. Clinical Microbiology and Infection. 2005;11:138–144. doi: 10.1111/j.1469-0691.2004.01045.x. [DOI] [PubMed] [Google Scholar]
19.Helwigh B 2004. Annual report on zoonoses in Denmark 2004. Technical report, Danish Institute for Food and Veterinary Research,
20.Chalker R, Blaser M. A review of human salmonellosis: III Magnitude of Salmonella infection in the United States. Reviews of Infectious Diseases. 1988;10:111–124. doi: 10.1093/clinids/10.1.111. [DOI] [PubMed] [Google Scholar]

[ref001] 1.Herikstad H, Motarjemi Y, Tauxe RV. Salmonella surveillance: a global survey of public health serotyping. Epidemiology and Infection. 2002;129:1–8. doi: 10.1017/s0950268802006842. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref002] 2.Mølbak K, Neimann J. Risk factors for sporadic infection with Salmonella enteritidis, Denmark, 1997–1999. American Journal of Epidemiology. 2002;156:654–661. doi: 10.1093/aje/kwf096. [DOI] [PubMed] [Google Scholar]

[ref003] 3.Wegener HC et al. Salmonella control programs in Denmark. Emerging Infectious Diseases. 2003;9:774–780. doi: 10.3201/eid0907.030024. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref004] 4.Voetsch AC et al. FoodNet estimate of the burden of illness caused by nontyphoidal Salmonella infections in the United States. Clinical Infectious Diseases. 2004;38:S127–S134. doi: 10.1086/381578. (Suppl. 3): [DOI] [PubMed] [Google Scholar]

[ref005] 5.Mead PS et al. Food-related illness and death in the United States. Emerging Infectious Diseases. 1999;5:607–625. doi: 10.3201/eid0505.990502. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref006] 6.Wheeler JG et al. Study of infectious intestinal disease in England: rates in the community, presenting to general practice, and reported to national surveillance. British Medical Journal. 1999;318:1046–1050. doi: 10.1136/bmj.318.7190.1046. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref007] 7.de Wit MAS et al. A comparison of gastroenteritis in a general practice-based study and a community-based study. Epidemiology and Infection. 2001;127:389–397. doi: 10.1017/s0950268801006082. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref008] 8.Teunis PFM et al. Kinetics of IgG antibody response to pertussis toxin after infection with. B. pertussis. Epidemiology and Infection. 2002;129:479–489. doi: 10.1017/s0950268802007896. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref009] 9.Versteegh FGA et al. Age-specific long-term course of IgG antibodies to pertussis toxin after symptomatic infection with Bordetella pertussis. Epidemiology and Infection. 2005;133:737–748. doi: 10.1017/s0950268805003833. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref010] 10.de Melker HE et al. The incidence of Bordetella pertussis infections estimated in the population from a combination of serological surveys. Journal of Infection. 2006;53:103–113. doi: 10.1016/j.jinf.2005.10.020. [DOI] [PubMed] [Google Scholar]

[ref011] 11.Strid M et al. Kinetics of the human antibody response against salmonella enterica serovars enteritidis and typhimurium determined by lipopolysaccharide enzyme-linked immunosorbent assay. Clinical vaccine immunology. 2007;14:741–747. doi: 10.1128/CVI.00192-06. [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref012] 12.Jørgensen T. Prevalence of gallstones in a Danish population. American Journal of Epidemiology. 1987;126:912–921. doi: 10.1093/oxfordjournals.aje.a114728. [DOI] [PubMed] [Google Scholar]

[ref013] 13.Sjøl A, Schroll M. The cardiovascular risk profile in the Glostrup region Monica screening II, 1986/87. Ugeskrift for Lager. 1990;152:3449–3455. [PubMed] [Google Scholar]

[ref014] 14.Gerdes L et al. Trends in selected biological risk factors for cardiovascular diseases in the Danish MONICA population 1982–1992. Journal of Clinical Epidemiology. 2000;53:427–434. doi: 10.1016/s0895-4356(99)00193-6. [DOI] [PubMed] [Google Scholar]

[ref015] 15.Jørgensen T et al. A randomized non-pharmacological intervention study for prevention of ischaemic heart disease: baseline results inter99. European Journal of Cardiovascular Prevention and Rehabilitation. 2003;10:377–386. doi: 10.1097/01.hjr.0000096541.30533.82. [DOI] [PubMed] [Google Scholar]

[ref016] 16.Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. London: Chapman & Hall/CRC; 1995. pp. 45–56. , pp. [Google Scholar]

[ref017] 17.Armitage P, Colton T. Encyclopedia of Biostatistics. West Sussex, England: John Wiley & Sons Ltd; 2005. p. 2724. , p. [Google Scholar]

[ref018] 18.Ekdahl K et al. Travel-associated non-typhoidal salmonellosis: geographical and seasonal differences and serotype distribution. Clinical Microbiology and Infection. 2005;11:138–144. doi: 10.1111/j.1469-0691.2004.01045.x. [DOI] [PubMed] [Google Scholar]

[ref019] 19.Helwigh B 2004. Annual report on zoonoses in Denmark 2004. Technical report, Danish Institute for Food and Veterinary Research,

[ref020] 20.Chalker R, Blaser M. A review of human salmonellosis: III Magnitude of Salmonella infection in the United States. Reviews of Infectious Diseases. 1988;10:111–124. doi: 10.1093/clinids/10.1.111. [DOI] [PubMed] [Google Scholar]

PERMALINK

Sero-epidemiology as a tool to study the incidence of Salmonella infections in humans

J SIMONSEN

M A STRID

K MØLBAK

K A KROGFELT

A LINNEBERG

P TEUNIS

SUMMARY

INTRODUCTION