Abstract
Since its formation about 1.75 million years ago, the Drosophila miranda neo-Y chromosome has undergone a rapid process of degeneration, having lost approximately half of the genes that it originally contained. Using estimates of mutation rates and selection coefficients for loss-of-function mutations, we show that the high rate of accumulation of these mutations can largely be explained by Muller's ratchet, the process of stochastic loss of the least-loaded mutational class from a finite, nonrecombining population. We show that selection at nonsynonymous coding sites can accelerate the process of gene loss and that this effect varies with the number of genes still present on the degenerating neo-Y chromosome.
IN the absence of recombination, different sites in the genome do not evolve independently of each other (Fisher 1930; Muller 1932; Felsenstein 1974). As has been shown by studies of Drosophila populations, for example, this leads to reduced levels of nucleotide diversity (Bachtrog and Charlesworth 2002; Bartolomé and Charlesworth 2006) and to signatures of reduced adaptation at the DNA and protein sequence levels, such as lower optimal codon usage and an elevated rate of amino acid substitutions (Betancourt and Presgraves 2002; Bachtrog 2003, 2005; Bartolomé and Charlesworth 2006; Betancourt et al. 2009). It is, however, still an open question how large-scale rearrangements and the loss of whole open reading frames can become fixed in nonrecombining regions of the genome, leading to the evolution of structures such as the small and degenerate Y chromosome of humans or the W chromosome of the chicken (Fridolfsson et al. 1998; Skaletsky et al. 2003).
The neo-Y chromosome of Drosophila miranda is an example of a large nonrecombining region that is relatively young and has only partially degenerated (Steinemann and Steinemann 1998; Bartolomé and Charlesworth 2006; Bachtrog et al. 2008), enabling us to study the time frame over which degeneration can occur, as well as its possible causes. The neo-Y arose when an autosome (corresponding to chromosome arm 2R in D. melanogaster) became fused to the Y chromosome. This originally contained about 3000 genes with a total of about 4.3 Mb of coding sequence, based on the relative sizes of the euchromatic portions of the chromosome arms in the D. melanogaster genome (Adams et al. 2000) and the data in Clark et al. (2007), Table 2. Since there is no recombinational exchange between homologs in Drosophila males (Gethmann 1988), recombination between the neo-X and neo-Y became immediately restricted; within a short evolutionary time frame of approximately 1.75 million years (Bartolomé and Charlesworth 2006), about half of the genes originally present on the neo-Y have lost their function (Bachtrog et al. 2008).
TABLE 2.
The expected rates (r/U) for simulations using scaled parameters for the D. miranda neo-Y
|
L (kb) |
||||||
|---|---|---|---|---|---|---|
| 32 | 192 | 320 | 640 | 1280 | ||
| U = 3.78, s = 0.63 | N0 | 0.27 | 0.10 | 0.06 | 0.05 | 0.03 |
| r/U (Gessler) | 0.00 | 0.17 | 0.17 | 0.50 | 0.33 | |
| r/U (Equations 2 with TA correction) | 0.11 | 0.15 | 0.17 | 0.18 | 0.19 | |
| U = 2.5, s = 0.63 | N0 | 2.04 | 0.76 | 0.49 | 0.40 | 0.26 |
| r/U (Gessler) | NA | 0.17 | 0.17 | 0.17 | 0.33 | |
| r/U (Equations 2 with TA correction) | 0.05 | 0.10 | 0.13 | 0.15 | 0.18 | |
| U = 1.89, s = 0.63 | N0 | 5.38 | 1.99 | 1.29 | 1.05 | 0.67 |
| r/U (Gessler) | NA | NA | NA | NA | 0.17 | |
| r/U (Equations 2 with TA correction) | 0.03 | 0.07 | 0.09 | 0.11 | 0.15 | |
Expected rates were calculated using both the method of Gessler (1995) and Equations 2 (with the addition of TA), including the effects of BGS on the value of Ne. The corresponding rates for the simulations are shown in Figure 2.
To quantify the rate of accumulation of loss-of-function mutations on the neo-Y chromosome, which we denote by r, it is convenient to estimate the base-line rate of fixation for neutral mutations (which is equal to the mutation rate) and compare this to the observed rate of fixation of “major” mutations. Bachtrog et al. (2008) showed that 55/118 genes present on the ancestral neo-Y contain at least one frameshift mutation, stop codon, or deletion, whereas these genes have remained intact in the neo-X lineage. Stop codons are reversible changes, which are therefore likely to behave like rather strongly selected nonsynonymous changes and hence fall into the class of mutations considered in our previous article (Kaiser and Charlesworth 2009). We have therefore excluded the seven genes with only a stop codon present from our count of loss-of-function mutations. Seventeen genes have both frameshifts and stop codons, and it is unclear which came first. It is reasonable to assume that a gene that has acquired a loss-of-function mutation will then evolve neutrally with respect to major mutational lesions, so that they should not be included in our count. The probability that a frameshift mutation preceded a stop codon can be estimated from the frequency of genes with stop codons among the genes with either a frameshift or a stop codon, 27/(27 + 7) = 0.79, giving an estimate of 31+ 17 × 0.79 = 44 for the number of genes with major lesions that are relevant to this analysis. With an average length of neo-Y linked coding sequence of 1188 bp in this data set (Bachtrog et al. 2008), the divergence per base pair with respect to loss-of-function mutations (KD) is given by KD = (44/118)/1188 = 3.1 × 10−4. These mutations all occurred along the neo-Y branch of the tree connecting the neo-Y and neo-X chromosomes to their common ancestor. The corresponding synonymous site divergence, KS, is about 1.2% for this lineage (Bartolomé and Charlesworth 2006). To estimate the neutral level of divergence along this branch with respect to indel mutations, we need to multiply the value of KS by 0.45, the estimated ratio of the number of new indel mutations in D. melanogaster to the number of new point mutations (Haag-Liautard et al. 2007). (This is probably an underestimate, since some indels in coding or regulatory sequences may been sufficiently deleterious to be selected against in these mutation accumulation experiments, where approximately 38% of the sequences characterized were coding.) If U is the rate of origination of major deleterious mutations on the neo-Y, the data thus suggest that r/U for the neo-Y, as given by KD/0.45KS), is about 5.8%.
We do not know what processes have driven this seemingly rapid accumulation of loss-of-function mutations. However, the selection coefficients against the heterozygous carriers of such mutations are likely to be rather large (Crow and Simmons 1983), and deleterious mutations for which Nes ≫ 1 (where Ne is the effective population size and s is the selection coefficient) have a very low probability of fixation (Kimura 1983). Accordingly, one or more forces must be acting to severely reduce the Ne of the neo-Y. Positive selection, causing selective sweeps (Maynard Smith and Haigh 1974; Kaplan et al. 1989), can drag deleterious, linked variants to fixation, provided that selection at the beneficial sites is strong enough to overcome the cumulative effect of selection against deleterious mutations in the background (Rice 1987; Johnson and Barton 2002; Hadany and Feldman 2005). While this possibility certainly cannot be ruled out, a high incidence of strong positive selection is probably necessary to explain the neo-Y data on this basis, and it is currently unclear whether this condition is satisfied (see discussion).
We have therefore examined an alternative “null” model that does not invoke selective sweeps. Assuming that deletions, frameshift mutations, and insertions of transposable elements are irreversible events, we have studied the process of Muller's ratchet as a means of fixing major mutational lesions (Muller 1964; Felsenstein 1974; Haigh 1978), as previously proposed for the evolution of Y chromosomes by Charlesworth (1978). Under this model, selection against deleterious mutations is sufficiently strong (Nes >1) that mutations in the freely recombining, ancestral population are close to mutation–selection equilibrium. With multiplicative fitness effects and a Poisson distribution of the number of mutations per haploid genome, the equilibrium size of the mutation-free class in a Wright–Fisher population is given by N0 = N exp(−U/s), where N is the population size in terms of number of haploid genomes, U is the haploid genomic mutation rate for deleterious mutations for the chromosome in question, and s is the selection coefficient against a deleterious mutation (Haigh 1978). If the population size is finite, genetic drift will eventually lead to the stochastic loss of this class of individuals; without recombination or backmutation, it cannot be restored (the ratchet has made one “click”). The process of repeated loss of the least-loaded class of individuals leads to the constant accumulation of deleterious mutations within the population, and with each click of the ratchet, one deleterious mutation becomes fixed (Charlesworth and Charlesworth 1997). The rate of fixation of irreversible deleterious mutations, r, is thus greatly increased over that for mutations with the same selection coefficients in a freely recombining population.
We can reasonably assume that major mutations are irreversible and that Nes for such mutations is much larger than one. However, we do not know a priori whether the ratchet can explain the neo-Y data, since it cannot operate if N0s is too large (Gordo and Charlesworth 2000a,b). One factor that might speed up the ratchet is the presence of deleterious mutations caused by base substitutions at amino acid sites in coding sequences. We call these sites “background selection” or BGS sites. As shown by Kaiser and Charlesworth (2009), selection at BGS sites can drastically reduce the Ne value for a nonrecombining genomic region because of Hill–Robertson interference (Hill and Robertson 1966), but the reduction in Ne levels off as the number of nonsynonymous sites under selection increases. For very long chromosomes such as the neo-Y, neutral diversity, which is directly proportional to Ne (Kimura 1983), asymptotes at a level of about 1.5% of the value with free recombination, with mutation and selection parameters that are plausible for Drosophila (Kaiser and Charlesworth (2009). We expect the reduction in Ne caused by the BGS sites to accelerate the rate of the ratchet, since Gordo and Charlesworth (2001) and Söderberg and Berg (2007) have shown that background selection can have such an effect, but the expected magnitude of the effect is unknown for realistic parameter values.
Here, we show that a high rate of fixation of strongly deleterious loss-of-function mutations on the neo-Y chromosome of D. miranda is compatible with a “null” model of selection acting against deleterious mutations alone. We also show that selection against amino acid mutations has a significant effect on the rate at which these major mutations can accumulate.
METHODS
Theoretical background:
Analytical and numerical results are available for the speed of the ratchet in a non-recombining, Wright–Fisher haploid population of size N, where the rate of origin of new deleterious mutations per generation is U, the selection coefficient against a single mutation is s, and fitness effects of different mutations combine multiplicatively (Haigh 1978; Pamilo et al. 1987; Stephan et al. 1993; Gessler 1995; Higgs and Woodcock 1995; Gordo and Charlesworth 2000a,b, 2001; Jain 2008; Rouzine et al. 2008).
We will make use of some of these results for interpreting the rate of movement of the ratchet. We first consider the case when N0 > 1, where N0 = N exp(−U/s)—see above. Following a click of the ratchet, the population will approach a new equilibrium after a time TA, with the number of individuals carrying just one mutation being equal to N exp(−U/s). TA has been estimated (Gordo and Charlesworth 2000a) as
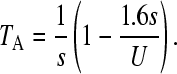 |
(1) |
Recently, Jain (2008) has derived analytical approximations for the average time, TC, between two clicks of the ratchet (disregarding TA), provided that N0 ≫ 1
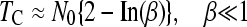 |
(2a) |
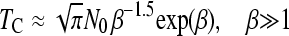 |
(2b) |
where β = 0.6N0s.
The net expected rate of fixation of deleterious mutations, r, is thus given by 1/(TA + TC). This can be compared with the value for a freely recombining haploid Wright-Fisher population of size N (Kimura 1962)
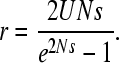 |
(3) |
The significance of N0 and N0s for driving the ratchet has been previously discussed (Haigh 1978; Bell 1988; Stephan et al. 1993; Gessler 1995; Gordo and Charlesworth 2000b). Equations 1 and 2 imply that the rate of the ratchet divided by N is constant if Ns is held constant. Similarly, r/U, (i.e., the rate relative to the neutral rate) is expected to be constant if the products Ns and NU are held constant, as would be expected from the fact that these results are derived from a diffusion equation approximation (Ewens 2004, p. 157).
In some cases that we studied, the condition N0 > 1 is violated. We then used numerical solutions of Equations 1 – 5 of Gessler (1995) to compute r.
The model:
To simulate the accumulation of irreversible major deleterious mutations by the ratchet in the presence of deleterious nonsynonymous mutations, we used forward simulations of sequence evolution, similar to those described in Kaiser and Charlesworth (2009). Briefly, we used a Wright-Fisher model consisting of a population of 1,000 haploid individuals, each of which carry a single non-recombining chromosome of length L, where L varies from 32kb to 1.28Mb. Two-thirds of all the sites on a chromosome are “background selection sites” (BGS sites), representing sites at which nonsynonymous mutations can occur. The selection coefficients for these sites are drawn from a log-normal distribution with a harmonic mean Ns = 10 in the corresponding diploid population of size 500, i.e., for which the coalescent effective population size N (Hudson 1990; Charlesworth 2009) is 500. At the remaining sites on the chromosome, major knock-out mutations can occur that have much larger fitness effects. These sites will be called “major” sites. Selection is multiplicative across all sites. Note that, because we do not allow recombination, the exact position of the “major” sites on our simulated chromosomes is irrelevant.
At the start of each run, all BGS sites are in mutation-selection equilibrium, whereas there are no mutations at the major sites. The rate of mutation at BGS sites is constant per site, i.e., adding more sites to the chromosome increases the chromosome-wide mutation rate for the BGS sites. In contrast, we keep the chromosome-wide mutation rate, U, at the major sites constant, i.e., we measure the effect of increasing or decreasing BGS, without changing the influx of major mutations. Mutations at major sites are irreversible and are thus expected to accumulate via a Muller's ratchet process; the BGS sites are reversible, and initially accumulate at a constant rate, until an equilibrium between forward and backward mutation is reached (Kaiser and Charlesworth 2009). The reduction in Ne for linked neutral sites, caused by the BGS sites, however, reaches a steady state very quickly (Kaiser and Charlesworth 2009).
10,000 generations of mutation, selection and reproduction were performed, and the rate, r, of fixation of major mutations was estimated by calculating the slope of the regression line for the number of sites fixed against time. Test runs were performed to check if the simulation results were compatible with the rates predicted by equations (1) and (2), using a range of parameters for U and s (see supporting information, Table S1).
Mutational parameters and scaling by population size:
To be able to compare our simulation results with the r/U value of 0.058 that we estimated for the D. miranda neo-Y chromosome, we used scaled values of mutation and selection parameters. According to diffusion theory, it is possible to infer the behavior of the system in a much larger population than assumed in the simulations by keeping the products of NeU and Nes constant (McVean and Charlesworth 2000; Ewens 2004, p.157), if time is measured in units of Ne generations. Without interference effects, the effective population size for the D. miranda neo-Y is likely to be one-quarter of the diploid Ne, which has been estimated to be about 840,000 (Loewe et al. 2006), although a more recent and larger study of synonymous diversity suggests a much lower value, of around 330,000 (P. Haddrill, L. Loewe and B. Charlesworth, unpublished data), so that 840,000 may be conservative as far as the speed of the ratchet is concerned. Mutation and selection parameters for use in our simulations with a haploid number of 1000 were obtained by multiplying the biologically realistic values by 2.1 × 105/500 = 420. The length of our runs therefore correspond to 4.2 million generations when rescaled, or 804,000 years assuming five generations per year for D. miranda.
We assume here that the main two causes of loss-of-function of a gene are indel mutations or TE insertions. Both types of mutations are likely to contribute equally to fitness loss and are hence treated as a single process from the point of view of the ratchet. The rate of origination of indel mutations in D. melanogaster is about 2.6 × 10−9/bp/generation (Haag-Liautard et al. 2007). With an estimated 4.3 million coding sequence sites on the neo-Y before degeneration (see the introduction), this gives a per-chromosome mutation rate of approximately 0.01. We further assume that the observed frequency of TE insertions into intronic sequences in the D. miranda neo-Y chromosome reflects the insertion rate into coding sequences, but without selective constraints. No TEs were found within coding sequences by Bachtrog et al. (2008), but 13 out of 118 genes that were present on the ancestral neo-Y carry new TE insertions in introns. The total length of intron sequence in the sample of genes studied by Bachtrog et al. (2008) is about 70.2 kb, so that the expected number of putatively neutral TE insertions per basepair is 13/(70.2 × 103), i.e., 1.85 × 10−4. The predicted level of accumulation of neutral indels per basepair on the neo-Y branch is about 45% of the value for base substitutions (Haag-Liautard et al. 2007), i.e., 0.0054, so that we estimate that the rate of insertion of new TEs into coding sequence relative to the rate for indels is 1.85 × 10−4/0.0054 = 0.034, which can be neglected.
We used a slightly conservative estimate of the rate of occurrence of “major” mutations on the neo-Y in D. miranda, before degeneration, of U = 0.009/generation. If we scale this value to a haploid population size of 1000, keeping NeU constant and using the above estimate of Ne for D. miranda, we obtain a U value of 3.78 for our simulations. Note that the scaled point mutation rate of Nu = 0.0052 at the BGS sites that we used in our simulations was obtained by combining the above estimate of the point mutation rate per basepair with the D. melanogaster estimate of Ne, which is about 1.3 million (Loewe et al. 2006; Loewe and Charlesworth 2007); this enabled us to estimate the reduction in Ne for neutral sites caused by the BGS sites alone, since data were available from previous simulations (Kaiser and Charlesworth 2009). A realistic value for D. miranda would be about 25% smaller than this, if the above estimate of Ne for D. miranda were used. It seems likely, however, that D. miranda has undergone a recent reduction in effective population size (Yi et al. 2003; Bachtrog and Andolfatto 2006; Bachtrog 2007), so that use of this larger value is probably realistic as far as the history of the neo-Y chromosome is concerned. In any case, having an increased u per BGS site is nearly equivalent to having more sites in the simulations and may actually give more realistic results, since we were unable to simulate as many selected sites as are present on the neo-Y.
Estimates of the selection coefficients against major mutations:
About one-quarter of loss-of-function mutations in Drosophila are lethal in the homozygous state, but lead to a mean reduction in fitness of only 1–2% when heterozygous (Crow and Simmons 1983; Charlesworth and Charlesworth 1998; Charlesworth and Hughes 2000). Since mutations on the neo-Y chromosome are nearly always masked by functional alleles on the neo-X (see discussion), we need here to consider only the heterozygous selection coefficients. Knock-out mutations are all not expected to have the same effects (i.e., losing a gene that is part of a gene family might be less deleterious than losing a single-copy gene). However, the mean selection coefficient against mutations that are segregating in a randomly mating population is close to the value for the harmonic mean s when there is a distribution of s values (Loewe et al. 2006), because segregating mutations tend to be less deleterious than the average of all new mutations. The mean heterozygous selection coefficient for segregating knock-out mutations for enzyme loci in D. melanogaster has been estimated to be about s = 0.0015 (Langley et al. 1981). For a haploid population of N = 1000, this corresponds to a scaled s value of 0.63 with our estimate of Ne for the D. miranda neo-Y chromosome.
To circumvent the problem of using a wide distribution of scaled s values, which can generate unrealistically large heterozygous selection coefficients (≫1), we tested whether simulations with a single selection coefficient for all major sites gave quantitatively similar results compared to using a distribution of s values, provided that the fixed selection coefficient is equal to the harmonic mean of the distribution of s values. Runs were performed for 10,000 generations, and r/U was calculated and compared between runs.
Tests of scaling:
Scaling of parameters of mutation and selection by the population size produces coherent results when the s values are relatively small (McVean and Charlesworth 2000), but the diffusion approximations might break down for stronger selection, such as the parameter space assumed for selection at the major sites. We therefore tested whether the scaling of s by the population size works, for both major and nonsynonymous sites; i.e., we tested whether r/U remains constant when the population size is changed, scaling mutation and parameters appropriately. Runs using a population size of N = 1000, 10,000, 20,000, or 40,000 individuals were performed. In these runs, all BGS sites were assigned a fixed selection coefficient that corresponds to a (diploid) Ns of 10, and the (diploid) Ns at the major sites was equal to 315. (This corresponds to a heterozygous s value of 0.63 for a haploid population size of N = 1000, the scaled neo-Y value). We measured r/U for the major mutations, using a chromosome length of 32 kb.
Testing how r/U behaves when the length of the chromosome increases:
Runs using scaled neo-Y parameters of mutation and selection were performed, with different lengths of chromosomes (32 kb to 1.28 Mb), and the average r/U was measured for each run.
To compare these results to the expected rates on the basis of Equations 1 and 2, we first calculated the reduction in Ne caused by the BGS sites alone, on the basis of levels of neutral diversity, π = 4Neu, as obtained from the previous BGS simulations (Kaiser and Charlesworth 2009). N in Equations 1 and 2 was then replaced by this value of Ne. In some cases, we cannot use Equation 2 because the equilibrium size of the least-loaded class, N0 = N exp (−U/s), < 1; as described above, we then used the approach of Gessler (1995) to calculate the expected rates.
RESULTS
The question that we explore is whether the estimated value for the D. miranda neo-Y chromosome of r/U, the rate of fixation of major mutations relative to their mutation rate, can be accounted for by Muller's ratchet, using the parameter values and simulation methods described above. We first discuss how well the rescaling by population size performs and then describe the major results of interest for interpreting the observations on D. miranda. The results shown in Figures 1 and 2 are the averages over four runs; those presented in Table 1 are from single simulation runs.
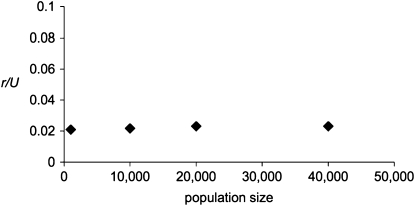
Figure 1.—
r/U scales with the diploid population size, N. At the “major” sites, Ns for the corresponding diploid population is 315, as estimated for “major” mutations. At the BGS sites, selection occurs with a constant selection coefficient, so that Ns = 10 for the diploid population. The mutation rates at all sites are also scaled by the population size. L = 32 kb in all cases; each data point is the average of four simulation runs.
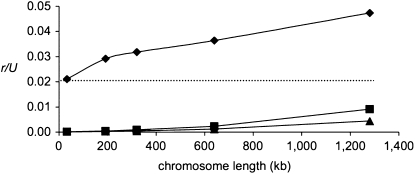
Figure 2.—
The effect of increasing the number of sites subject to BGS on the rate of fixation of “major” mutations (the values are the averages of four simulation runs). Diamonds: U = 3.78 and s = 0.63, which correspond to the scaled values of U = 0.009 and s = 0.0015 as estimated for the D. miranda neo-Y. Selection at the BGS sites is drawn from a log-normal distribution with Ns(harmonic mean) = 10. The dashed line indicates the simulated value of r/U when there is no BGS. Squares, U = 2.50, s = 0.63; triangles, U = 1.89, s = 0.63.
TABLE 1.
Simulation results for r/U for a range of s-values at the “major” sites
| s follows a log-normal distributiona | |||||||
|---|---|---|---|---|---|---|---|
| μ | −1.0 | −1.0 | −0.7 | −0.7 | −0.35 | −0.7 | −0.2 |
| σ | 0.4 | 0.1 | 0.4 | 0.1 | 0.2 | 0.1 | 0.1 |
| Fraction (lethal mutations) | 0.005 | 0.000 | 0.040 | 0.000 | 0.040 | 0.0002 | 0.022 |
| s (arithmetic) nonlethal | 0.394 | 0.370 | 0.511 | 0.499 | 0.704 | 0.708 | 0.818 |
| s (harmonic) nonlethal | 0.338 | 0.366 | 0.447 | 0.494 | 0.681 | 0.701 | 0.811 |
| s (arithmetic) total | 0.398 | 0.370 | 0.531 | 0.499 | 0.716 | 0.708 | 0.822 |
| s (harmonic) total | 0.339 | 0.366 | 0.457 | 0.494 | 0.689 | 0.701 | 0.814 |
| Fraction (0 ≤ s ≤ 0.2) | 0.064 | 0.000 | 0.011 | <0.001 | <0.001 | <0.001 | <0.001 |
| Fraction (0.2 < s ≤ 0.4) | 0.518 | 0.796 | 0.285 | 0.015 | 0.002 | <0.001 | <0.001 |
| Fraction (0.4 < s ≤ 0.6) | 0.306 | 0.204 | 0.385 | 0.956 | 0.211 | 0.054 | 0.001 |
| Fraction (0.6 < s ≤ 0.8) | 0.086 | 0.000 | 0.201 | 0.029 | 0.521 | 0.843 | 0.408 |
| Fraction (0.8 < s ≤ 1.0) | 0.026 | 0.000 | 0.118 | 0.000 | 0.265 | 0.103 | 0.591 |
| r/U | 0.144 | 0.135 | 0.089 | 0.077 | 0.018 | 0.015 | 0.001 |
| Fixed values of sb | |||||||
| s | 0.339 | 0.366 | 0.457 | 0.494 | 0.689 | 0.701 | 0.814 |
| r/U | 0.149 | 0.135 | 0.091 | 0.077 | 0.017 | 0.014 | 0.001 |
In all runs, BGS occurs at the first and second codon position, with a harmonic mean of Ns = 10 at the BGS sites (L = 320 kb; U = 3.78).
Distribution of s values at major sites. s is drawn from a log-normal distribution with mean μ and standard deviation σ on the log scale. The fraction of lethal mutations (s ≥ 1), as well as the arithmetic and harmonic mean of s is given, considering either only nonlethal mutations or all mutations at major sites. The fractions of major sites, where s takes values in the interval 0–0.2, 0.2–0.4, 0.4–0.6, 0.6–0.8, and 0.8–1.0 are indicated.
All major sites are assigned a fixed selection coefficient s, equal to the harmonic mean s of in the corresponding column at the top.
Tests of the scaling and selection parameters used in the simulations:
Using the approach described in methods, the procedure of scaling the mutation and selection parameters by the population size N produced very similar results for simulated values of r/U. Differences in N had almost no effect when the products of Ns and Nu were held constant for both the BGS sites and the major sites (Figure 1). Hence, we can be reasonably confident that our simulations of small populations can be used to predict the behavior of the ratchet in a much larger population, such as that of D. miranda.
We also found that r/U remains largely unchanged if a fixed s value is used for the major effect mutations, instead of a log-normal distribution of s values, provided that the fixed s value corresponds to the harmonic mean of the respective distribution (Table 1). This suggests that our simulations using scaled values with a fixed selection coefficient produce results comparable to those of a much larger population, where s values are drawn from a distribution.
The effects of BGS on the speed of the ratchet:
Our simulations show that selection at the BGS sites increases the rate of fixation at major sites. Figure 2 shows the effect of such selection on the rate of fixation of major mutations, with parameters estimated as being realistic for the neo-Y chromosome of D. miranda and scaled appropriately by the population size (N = 1000; s = 0.63; U = 3.78). As with the results shown in Figure S1 and Figure S2, for a much wider range of parameters, the value of r/U increases with the amount of background selection at nonsynonymous sites. Note, however, that for the parameter combinations estimated for the D. miranda neo-Y chromosome, the background selection effect is not very large: even when there is no selection at BGS sites (dotted line), r/U is about 2%. The ratio r/U increases to somewhat more than twice this value for the longest chromosomes simulated here (L = 1.28 Mb) and may be even higher for chromosomes of the size of the ancestral neo-Y chromosome (with over twice as much coding sequence), especially as we have only considered the BGS effects of nonsynonymous mutations.
Overall, the r/U obtained from the simulations for the largest set of BGS sites is 0.048, which is somewhat lower than the estimated value for the D. miranda neo-Y (0.058) given in the introduction, but the 95% confidence interval for this estimate is 0.045 to 0.071, ignoring the uncertainty in the estimate of the fraction of indel mutations. We can also ask if the simulated values correspond to those predicted using the equations presented in methods, using the effective population size for neutral sites in the presence of BGS at nonsynonymous sites when calculating N0. The results are shown in Table 2 and Table S2. The predicted rates are clearly higher than those observed in the simulations, so that the Ne driving the ratchet is much larger than is suggested by levels of neutral diversity.
DISCUSSION
Plausibility of the model:
The importance of Muller's ratchet in driving the degeneration of Y chromosomes has been questioned, mainly because the timescales involved were inferred to be too large to be biologically plausible (Charlesworth 1996). In addition, Engelstädter (2008) showed that, in some circumstances, the presence of low-frequency deleterious mutations on X-linked homologs of the Y chromosome can greatly slow down the ratchet, compared with what is found in haploid simulations of the type used here.
Here, we ignored the presence of these mutations, under the assumption that strongly deleterious mutations on the freely recombining X chromosome will be held at low frequencies under mutation–selection balance, as would be expected for mutations with selection coefficients of 0.0015 in populations with the effective size of D. miranda. We now consider whether this is justified. The selection coefficient used in our models of major mutations is the harmonic mean selection coefficient against major mutations on the evolving neo-Y chromosome, obtained from Langley et al. (1981). They used data on the frequencies of null alleles at autosomal loci in D. melanogaster populations, together with the rate of mutation to null alleles, and substituting these into the standard formula for mutation–selection equilibrium (Haldane 1927). Since the frequencies of null alleles are very low, their estimate can be equated to the harmonic mean of hs′+ q*s′, where h is the dominance coefficient, s′ is the homozygous selection coefficient, and q* is the equilibrium frequency of a null allele at a locus; the latter term takes into account the contribution of the occasional homozygote to the net fitness of a null allele. Under the assumptions of our model, this quantity should be the same as the net harmonic mean selection coefficient experienced by a major mutation on the neo-Y chromosome, incorporating its chance of encountering a mutation of the same type at the same locus on the neo-X chromosomes. It follows that our haploid model should accurately represent the early evolution of the D. miranda neo-Y chromosome.
Our simulation results show that a high rate of accumulation of strongly deleterious mutations on an evolving Y chromosome in a Drosophila population can be achieved with biologically reasonable parameters, due to Hill–Robertson interference effects among sites subject to purifying selection. Under free recombination, the expected rate of fixation of strongly deleterious loss-of-function mutations (Equation 3 in methods) is virtually zero when s = 0.63, U = 3.78, and N = 1000. When rescaled to the estimated effective population size for the D. miranda neo-Y chromosome, these parameter values correspond to a harmonic mean selection coefficient against major mutations of 0.0015, and a mutation rate to major mutations of 0.009, which we have argued to be plausible or even conservative. However, with no recombination, such mutations can become fixed in our simulations, at a rate that is not far from the rate observed for the neo-Y, especially when we take the effect of weak selection against amino acid mutations in the background (BGS sites) into account.
Given the exponential dependence of the rate of the ratchet, r, on U, a reduction in U has a large effect on r (Equations 1 and 2). As about half of the genes originally present on the D. miranda neo-Y have lost their function since the origin of the chromosome (Bachtrog et al. 2008), we can assume the maximum reduction in U to be 50%. Figure 2 shows that, when U is reduced to two-thirds or one-half of its original value, r/U is indeed reduced far below the observed value of 5.8%.
It is important to note in this context that the relative effect of selection at BGS sites on the speed of the ratchet is larger when U is smaller: for U = 2.5, r/U increases by a factor of about 160 when the number of BGS sites increases from 32 kb to 1.28 Mb, as opposed to a factor of only about 2 to 4 for U = 3.78. When U = 1.89, the ratchet was stalled for short chromosomes (L = 32 kb), but was going at a relative rate of 0.4% for L = 1.28 Mb. As previously suggested (Bachtrog 2008b; Engelstädter 2008), the speed of the ratchet is likely to vary over different stages of Y chromosome degeneration: when the overall occurrence of major mutations is still high, interference among very strongly selected mutations alone leads to their fast accumulation, and the process is accelerated (about two- to fourfold) by the presence of BGS sites. With the erosion of genes from the neo-Y, U decreases and the ratchet slows down, but the effect of mutations at nonsynonymous sites starts to increase, until U becomes so low that the BGS effect cannot greatly increase the ratchet any longer (eventually the BGS effect will disappear as well). This process might lead to a stable situation; i.e., once the Y chromosome contains few enough genes, selection will be able to purge the occasional loss-of-function mutations that hit it.
Most old nonrecombining chromosomes, such as the Y chromosome in humans or D. melanogaster, have a very low gene content (Skaletsky et al. 2003; Carvalho et al. 2009), and Muller's ratchet may no longer be driving the fixation of knock-out mutations. However, the process leading to this stage from a large nonrecombining region of the genome may well have been driven by a ratchet. The effects of the ratchet may also limit the size of nonrecombining regions of the genome, and, consistent with this, a large-scale expansion in the gene content of a nonrecombining region has not been reported, although small numbers of genes have been added to the highly degenerated Y chromosomes of Drosophila and mammals (Skaletsky et al. 2003; Carvalho et al. 2009). [The successive expansion of the nonrecombining regions of evolving Y chromosomes, resulting in “evolutionary strata” (Lahn and Page 1999), is a quite different process from this, since it involves a succession of events that create newly nonrecombining genomic regions from previously recombining ones.]
The effects of dosage compensation:
In an evolving sex chromosome system, gene loss from the Y chromosome is expected to lead to the evolution of dosage compensation (Charlesworth 1978), since there is a selective advantage to increasing the expression of functional alleles on the X relative to their inactivated counterparts on the Y. Even though the exact mechanisms are still unknown, there is evidence for partial dosage compensation in the D. miranda neo-X/neo-Y system (Bone and Kuroda 1996; Marin et al. 1996).
There is no clear relationship between the rate of amino acid evolution on the neo-Y and the relative expression levels of neo-Y vs. neo-X genes (Bachtrog 2006), which generally but not always have lower expression than their X-linked counterparts. It is not clear that this reduction in neo-Y gene expression reflects dosage compensation; the fact that a minority of neo-Y genes are more highly expressed than their counterparts on the neo-X suggests that mutations in regulatory sequences that disturb expression in either direction may well be accumulating (Bachtrog 2006). This would increase interference effects and hence speed up the ratchet. Similarly, genes that are recruited onto the Y chromosome (and hence not present on the X) will be under strong purifying selection and contribute to U. The overall impact of these factors seems, however, unlikely to change the parameter space to such an extent that the ratchet would come to a halt during the early stages of neo-Y evolution, although the ratchet may well not account for the full degeneration of Y chromosomes (Bachtrog 2008b).
The effect of BGS sites on the rate of the ratchet:
When the difference in mean s between the two types of selected sites (BGS sites and major sites) is very large, the model based on the reduction in Ne inferred from neutral sites subject to BGS performs poorly in predicting the rate of the ratchet; i.e., the ratchet clicks a lot more slowly than expected. In other words, the pool of individuals from which the population is ultimately derived, the “least-loaded class,” is larger than that predicted from the effective number of individuals that determines levels of nucleotide diversity in the BGS simulations (Kaiser and Charlesworth 2009) (see Figure 2, Table 2, and Figure S2). This makes intuitive sense, because the important factor determining transmission to the next generation is fitness relative to the population average. The relative fitness reduction due to “major” mutations is about 30 times larger than the mutations at BGS sites for the parameters used in Figure 2; hence, a few mutations at BGS sites in a chromosome will not make much of a difference for an individual that is otherwise free of “major” mutations—its overall fitness will still be high compared to the rest of the population.
However, when the s values at the two types of sites are similar (as in Figure S1), mutations at BGS sites can reduce the chance of reproduction considerably. In addition, the movement of a ratchet is associated with a substantial reduction in Ne at neutral or weakly selected sites (Gordo et al. 2002). This means that the Nes values at the BGS sites in our simulations will be greatly reduced relative to their values in the absence of the major mutations, thereby undermining their ability to cause Hill–Robertson interference. When U at the major sites is reduced, the relative effect of BGS mutations becomes larger, increasing the impact of BGS on the ratchet (Figure 2). The idea that that the extent of interference with other sites on the speed of the ratchet is affected by the relative magnitudes of the selection coefficients at the sites concerned has previously been discussed in a somewhat different context (Gordo and Charlesworth 2001; Söderberg and Berg 2007).
Can selective sweeps explain the neo-Y data?:
Selective sweeps can drag deleterious mutations to fixation, as long as the fitness benefit due to the advantageous mutation outweighs the cost of carrying deleterious mutations in the genomic background (Rice 1987; Johnson and Barton 2002; Hadany and Feldman 2005). Recent studies of DNA sequence evolution in D. melanogaster and D. simulans have suggested that around 50% of fixed differences between species in protein sequences and some types of noncoding sequences such as UTRs are the result of positive selection (Sella et al. 2009). If this applies to D. miranda and its relatives, as is suggested by recent data (Bachtrog 2008a), then there has been ample opportunity for numerous selective sweeps on the evolving neo-Y chromosome lineage, given the size of this chromosome (around 3000 genes) and its time of origin (1.75 million years ago, corresponding to KS = 0.012). For example, with KA/KS = 0.08 and assuming 1000 nonsynonymous nucleotide sites per gene, as is typical for Drosophila proteins (Clark et al. 2007), we would expect approximately 0.5 × 0.08 × 0.012 × 1000 × 3000 = 1440 sweeps to have occurred if the neo-Y protein sequences were evolving at the standard rate. With 10 generations a year, this would correspond to 1 sweep every 12,150 generations on the neo-Y lineage, a relatively modest rate.
Given this low rate, it is reasonable to assume that each sweep is followed by a period of recovery, after which mutation–selection balance for major mutations would be approximately reestablished (ignoring the ratchet). The estimates of the mutation and selection parameters for loss-of-function mutations on the neo-Y (see above) suggest that each ancestral neo-Y would have carried, on average, U/s = 6 major deleterious mutations. Hence, an advantageous mutation will, on average, arise on a genomic background that carries six such mutations. Assuming that there were originally about 3000 genes on the neo-Y, about half of which now carry “major” mutations, this suggests that the number of sweeps needed to explain the data is about 1500/6 = 250, much smaller than the above estimate.
This estimate is, however, likely to be conservative. First, even though an advantageous mutation will, on average hit a chromosome carrying six major deleterious mutations, the chance of fixation of the beneficial mutation will be higher when it happens to hit a chromosome with fewer mutations, decreasing the average number of major mutations fixed with each sweep. Second, with a decline in U over time, the number of major mutations segregating in the population will also decline, and with it the number of deleterious mutations fixed with each sweep. On the other hand, the chance of fixation of the beneficial mutation will increase when there are fewer deleterious mutations in the background, so these effects may counterbalance each other.
Third, Johnson and Barton (2002) showed that the fixation probabilities of beneficial mutations are considerably reduced by BGS if their selection coefficients are smaller in size than U. In this case, this result suggests that only beneficial mutations with selective advantages of the order of 1% would have a reasonable chance of fixation. The methods that have been used to estimate these selection coefficients in Drosophila yield very different values: the two extremes are 10−5 and 1% (Sella et al. 2009). The lower value would clearly not be compatible with the fixation of beneficial mutations in the presence of the major mutations we have been considering, while the higher value is compatible. Further research is needed to resolve this issue.
Selective sweeps may thus have contributed to some of the observed fixations, although patterns of neutral diversity on the neo-Y are consistent with the action of purifying selection alone (Kaiser and Charlesworth 2009). However, a recent analysis of the non-crossing-over dot chromosome of D. americana, which contains only 80 genes, found no evidence for adaptive fixations of amino acid mutations, in contrast to the large fraction of fixations on other chromosomes that appeared to have been driven by positive selection (Betancourt et al. 2009). This strongly suggests that the reduction in effective population size associated with reduced recombination greatly reduces the efficacy of positive selection, which would undermine the ability of selective sweeps to contribute to the degeneration of Y chromosomes. However, given the fact that our estimate of the contribution from the ratchet falls somewhat short of the observed rate of fixation of major effect mutations, both the ratchet and sweeps may contribute.
Acknowledgments
We thank members of the Charlesworth lab group for discussions of this work and two anonymous reviewers for their useful comments on the manuscript. V.B.K. was supported by a postgraduate studentship from the School of Biological Sciences, University of Edinburgh.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.109.112789/DC1.
References
- Adams, M. D., S. E. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne et al., 2000. The genome sequence of Drosophila melanogaster. Science 287 2185–2195. [DOI] [PubMed] [Google Scholar]
- Bachtrog, D., 2003. Protein evolution and codon usage bias on the neo-sex chromosomes of Drosophila miranda. Genetics 165 1221–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D., 2005. Sex chromosome evolution: molecular aspects of Y chromosome degeneration in Drosophila. Genome Res. 15 1393–1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D., 2006. Expression profile of a degenerating neo-Y chromosome in Drosophila. Curr. Biol. 16 1694–1699. [DOI] [PubMed] [Google Scholar]
- Bachtrog, D., 2007. Reduced selection for codon usage bias in Drosophila miranda. J. Mol. Evol. 64 586–590. [DOI] [PubMed] [Google Scholar]
- Bachtrog, D., 2008. a Similar rates of protein adaptation in Drosophila miranda and D. melanogaster, two species with different current effective population sizes. BMC Evol. Biol. 8 334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D., 2008. b The temporal dynamics of processes underlying Y chromosome degeneration. Genetics 179 1513–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D., and P. Andolfatto, 2006. Selection, recombination and demographic history in Drosophila miranda. Genetics 174 2045–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachtrog, D., and B. Charlesworth, 2002. Reduced adaptation of an evolving neo-Y chromosome. Nature 416 323–326. [DOI] [PubMed] [Google Scholar]
- Bachtrog, D., E. Hom, K. M. Wong, X. Maside and P. de Jong, 2008. Genomic degradation of a young Y chromosome in Drosophila miranda. Genome Biol. 9 R30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolomé, C., and B. Charlesworth, 2006. Evolution of amino-acid sequences and codon usage on the Drosophila miranda neo-sex chromosomes. Genetics 174 2033–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell, G., 1988. Recombination and the immortality of the germ line. J. Evol. Biol. 1 67–82. [Google Scholar]
- Betancourt, A. J., and D. C. Presgraves, 2002. Linkage limits the power of natural selection in Drosophila. Proc. Natl. Acad. Sci. USA 99 13616–13620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betancourt, A. J., J. J. Welch and B. Charlesworth, 2009. Reduced effectiveness of selection caused by a lack of recombination. Curr. Biol. 19 655–660. [DOI] [PubMed] [Google Scholar]
- Bone, J. R., and M. I. Kuroda, 1996. Dosage compensation regulatory proteins and the evolution of sex chromosomes in Drosophila. Genetics 144 705–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho, A. B., L. B. Koerich and A. G. Clark, 2009. Origin and evolution of Y chromosomes: Drosophila tales. Trends Genet. 25 270–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B., 1978. Model for evolution of Y chromosomes and dosage compensation. Proc. Natl. Acad. Sci. USA 75 5618–5622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B., 1996. The evolution of chromosomal sex determination and dosage compensation. Curr. Biol. 6 149–162. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 2009. Effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10 195–205. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., and D. Charlesworth, 1997. Rapid fixation of deleterious alleles can be caused by Muller's ratchet. Genet. Res. 70 63–73. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., and D. Charlesworth, 1998. Some evolutionary consequences of deleterious mutations. Genetica 103 3–19. [PubMed] [Google Scholar]
- Charlesworth, B., and K. A. Hughes, 2000. The maintenance of genetic variation in life-history traits, pp. 369–392 in Evolutionary Genetics: From Molecules to Morphology, edited by R. S. Singh and C. B. Krimbas. Cambridge University Press, Cambridge, UK.
- Clark, A. G., M. B. Eisen, D. R. Smith, C. M. Bergman, B. Oliver et al., 2007. Evolution of genes and genomes on the Drosophila phylogeny. Nature 450 203–218. [DOI] [PubMed] [Google Scholar]
- Crow, J. F., and M. J. Simmons, 1983. The mutation load in Drosophila, pp.1–35 in The Genetics and Biology of Drosophila, Vol. 3c, edited by M. Ashburner, H. L. Carson and J. N. Thompson. Academic Press, London.
- Engelstädter, J., 2008. Muller's ratchet and the degeneration of Y chromosomes: a simulation study. Genetics 180 957–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens, W. J., 2004. Mathematical Population Genetics. Springer-Verlag, Berlin.
- Felsenstein, J., 1974. Evolutionary advantage of recombination. Genetics 78 737–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, R. A., 1930. The Genetical Theory of Natural Selection. Clarendon Press, Oxford, UK.
- Fridolfsson, A. K., H. Cheng, N. G. Copeland, N. A. Jenkins, H. C. Liu et al., 1998. Evolution of the avian sex chromosomes from an ancestral pair of autosomes. Proc. Natl. Acad. Sci. USA 95 8147–8152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gessler, D. G., 1995. The constraints of finite size in asexual populations and the rate of the ratchet. Genet. Res. 66 241–253. [DOI] [PubMed] [Google Scholar]
- Gethmann, R. C., 1988. Crossing over in males of higher Diptera (Brachycera). J. Hered. 79 344–350. [DOI] [PubMed] [Google Scholar]
- Gordo, I., and B. Charlesworth, 2000. a On the speed of Muller's ratchet. Genetics 156 2137–2140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordo, I., and B. Charlesworth, 2000. b The degeneration of asexual haploid populations and the speed of Muller's ratchet. Genetics 154 1379–1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordo, I., and B. Charlesworth, 2001. The speed of Muller's ratchet with background selection, and the degeneration of Y chromosomes. Genet. Res. 78 149–161. [DOI] [PubMed] [Google Scholar]
- Gordo, I., A. Navarro and B. Charlesworth, 2002. Muller's ratchet and the pattern of variation at a neutral locus. Genetics 161 835–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag-Liautard, C., M. Dorris, X. Maside, S. Macaskill, D. L. Halligan et al., 2007. Direct estimation of per nucleotide and genomic deleterious mutation rates in Drosophila. Nature 445 82–85. [DOI] [PubMed] [Google Scholar]
- Hadany, L., and M. W. Feldman, 2005. Evolutionary traction: the cost of adaptation and the evolution of sex. J. Evol. Biol. 18 309–314. [DOI] [PubMed] [Google Scholar]
- Haigh, J., 1978. Accumulation of deleterious genes in a population: Muller's ratchet. Theor. Pop. Biol. 14 251–267. [DOI] [PubMed] [Google Scholar]
- Haldane, J. B. S., 1927. A mathematical theory of natural and artificial selection. V. Selection and mutation. Proc. Camb. Phil. Soc. 23 838–844. [Google Scholar]
- Higgs, P. G., and G. Woodcock, 1995. The accumulation of mutations in asexual populations and the structure of genealogical trees in the presence of selection. J. Math. Biol. 33 677–702. [Google Scholar]
- Hill, W. G., and A. Robertson, 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8 269–294. [PubMed] [Google Scholar]
- Hudson, R. R., 1990. Gene genealogies and the coalescent process. Oxf. Surv. Evol. Biol. 7 1–45. [Google Scholar]
- Jain, K., 2008. Loss of least-loaded class in asexual populations due to drift and epistasis. Genetics 179 2125–2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, T., and N. H. Barton, 2002. The effect of deleterious alleles on adaptation in asexual populations. Genetics 162 395–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser, V. B., and B. Charlesworth, 2009. The effects of deleterious mutations on evolution in non-recombining genomes. Trends Genet. 25 9–12. [DOI] [PubMed] [Google Scholar]
- Kaplan, N. L., R. R. Hudson and C. H. Langley, 1989. The hitchhiking effect revisited. Genetics 123 887–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M., 1962. On the probability of fixation of a mutant gene in a population. Genetics 47 713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M., 1983. The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge, UK.
- Lahn, B. T., and D. C. Page, 1999. Four evolutionary strata on the human X chromosome. Science 286 964–967. [DOI] [PubMed] [Google Scholar]
- Langley, C. H., R. A. Voelker, A. J. L. Brown, S. Ohnishi, B. Dickson et al., 1981. Null allele frequencies at allozyme loci in natural populations of Drosophila melanogaster. Genetics 99 151–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewe, L., and B. Charlesworth, 2007. Background selection in single genes may explain patterns of codon bias. Genetics 175 1381–1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewe, L., B. Charlesworth, C. Bartolomé and V. Noël, 2006. Estimating selection on nonsynonymous mutations. Genetics 172 1079–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marin, I., A. Franke, G. J. Bashaw and B. S. Baker, 1996. The dosage compensation system of Drosophila is co-opted by newly evolved X chromosomes. Nature 383 160–163. [DOI] [PubMed] [Google Scholar]
- Maynard Smith, J., and J. Haigh, 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23 23–35. [PubMed] [Google Scholar]
- McVean, G. A. T., and B. Charlesworth, 2000. The effects of Hill–Robertson interference between weakly selected mutations on patterns of molecular evolution and variation. Genetics 155 929–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller, H. J., 1932. Some genetic aspects of sex. Am. Nat. 66 118–138. [Google Scholar]
- Muller, H. J., 1964. The relation of recombination to mutational advance. Mutat. Res. 1 2–9. [DOI] [PubMed] [Google Scholar]
- Pamilo, P., M. Nei and W. H. Li, 1987. Accumulation of mutations in sexual and asexual Populations. Genet. Res. 49 135–146. [DOI] [PubMed] [Google Scholar]
- Rice, W. R., 1987. Genetic hitchhiking and the evolution of reduced genetic activity of the Y-sex chromosome. Genetics 116 161–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine, I. M., E. Brunet and C. O. Wilke, 2008. The traveling-wave approach to asexual evolution: Muller's ratchet and speed of adaptation. Theor. Pop. Biol. 73 24–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella, G., D. A. Petrov, M. Przeworski and P. Andolfatto, 2009. Pervasive natural selection in the Drosophila genome? PLoS Genet. 5: e1000495. [DOI] [PMC free article] [PubMed]
- Skaletsky, H., T. Kuroda-Kawaguchi, P. J. Minx, H. S. Cordum, L. Hillier et al., 2003. The male-specific region of the human Y chromosome is a mosaic of discrete sequence classes. Nature 423 825–837. [DOI] [PubMed] [Google Scholar]
- Söderberg, R. J., and O. G. Berg, 2007. Mutational interference and the progression of Muller's ratchet when mutations have a broad range of deleterious effects. Genetics 177 971–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinemann, M., and S. Steinemann, 1998. Enigma of Y chromosome degeneration: Neo-Y and neo-X chromosomes of Drosophila miranda a model for sex chromosome evolution. Genetica 102–3 409–420. [PubMed] [Google Scholar]
- Stephan, W., L. Chao and J. G. Smale, 1993. The advance of Muller's ratchet in a haploid asexual population: approximate solutions based on diffusion theory. Genet. Res. 61 225–231. [DOI] [PubMed] [Google Scholar]
- Yi, S., D. Bachtrog and B. Charlesworth, 2003. A survey of chromosomal and nucleotide sequence variation in Drosophila miranda. Genetics 164 1369–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]