Quantitative Trait Locus Mapping of Genes Under Selection Across Multiple Years and Sites in Avena barbata: Epistasis, Pleiotropy, and Genotype-by-Environment Interactions

Abstract

The genetic architecture of variation in evolutionary fitness determines the trajectory of adaptive change. We identified quantitative trait loci (QTL) affecting fitness in a mapping population of recombinant inbred lines (RILs) derived from a cross between moist- and dry- associated ecotypes of Avena barbata. We estimated fitness in 179 RILs in each of two natural environments in each of 4 years. Two loci account for over half of the variation in geometric mean fitness across environments. These loci are associated in repulsion phase in the wild ecotypes, suggesting the potential for strong transgressive segregation, but also show significant epistasis giving hybrid breakdown. This epistasis is the result of sharply lower fitness in only one of the recombinant genotypes, suggesting that the loci may contain synergistically acting mutations. Within each trial (year/site combination), we can explain less of the variation than for geometric mean fitness, but the two major loci are associated with variation in fitness in most environments. Tests for pleiotropic effects of QTL on fitness in different environments reveal that the same loci are under selection in all trials. Genotype-by-environment interactions are significant for some loci, but this reflects variation in the strength, not the direction of selection.

HERITABLE variation in lifetime reproductive success is the driving force of adaptation, and its genetic basis is an important determinant of the trajectory of evolution. Fisher (1930) showed that the short-term response to selection equals the additive variance in fitness (at least, in large panmictic populations). By extension then, additive variation in fitness is expected to be removed from the population by selection (Falconer 1989), and a number of studies have shown reduced heritabilities for traits under strong selection relative to more neutral traits (Roff and Mousseau 1987). By contrast, nonadditive genetic variation in fitness can remain in the population longer and is more likely to be present in traits related to fitness (Falconer 1989; Roff and Emerson 2006). Nonadditive gene effects can occur either between alleles within genes (dominance) or between separate loci (epistasis), and these two processes have different evolutionary consequences. Since most selectively favored alleles appear to be dominant to disadvantageous alleles (Roff 1997; Lynch and Walsh 1998; Forbes et al. 2004), dominance effects tend to increase the fitness of more heterozygous individuals and thereby (all else being equal) select against inbreeding (Charlesworth and Charlesworth 1987; Keller and Waller 2002). Epistasis, on the other hand, tends to disfavor distant crosses, because they disrupt beneficial epistatic interactions (Whitlock et al. 1995; Barton 2001) and introduce deleterious allelic combinations (Dobzhansky 1951; Turelli and Orr 2000).

Pleiotropy, the effects of genes on multiple traits, can also have important consequences for the trajectory of adaptive evolution, because it creates the potential for trade-offs among traits (Stearns 1989, 1992; Partridge and Sibly 1991; Roff 2002). Where selection acts to increase each of two or more traits in isolation, the negative covariance brought about by such pleiotropy presents an important limitation on evolution (Lande 1982; Charnov 1989). A special case of such trade-offs occurs when adaptation to geographically separate environments is negatively correlated, such that high fitness in one habitat is associated with low fitness in others (Levene 1953; Via and Lande 1987; Joshi and Thompson 1995). Where gene flow is limited, this situation can result in local adaptation, whereby each local deme is better adapted to its habitat than are immigrants arriving from other locations (Clausen et al. 1941; Charlesworth et al. 1997; Kawecki and Ebert 2004). Such trade-offs are usually described in an ANOVA framework using genotype-by-environment (G × E) interactions, but can easily be treated within a framework of pleiotropy and covariance (Falconer 1952; Via and Lande 1987). By treating fitness in two environments as separate, but potentially (negatively) correlated traits, local adaptation is a logical extension of theory on trade-offs.

Each of these aspects of fitness variation (additivity, dominance, epistasis, pleiotropy, and G × E interactions) is important in determining the evolutionary trajectory, but reliable information about them can be difficult to obtain in the field. Biometrical (i.e., quantitative genetic) approaches can be labor intensive, requiring large numbers of experimental crosses and estimates of fitness. By contrast, inferences from the patterns of molecular markers—although extremely popular—often depend upon many untestable assumptions, the failure of which can lead to serious error (Luikart et al. 2003 and Nielsen 2005 provide reviews).

Forty years ago in Genetics, Avena barbata (Pott ex Link), Poaceae, was one of the first species in which inferences about the genetic basis of fitness were drawn from molecular (allozyme) information (Marshall and Allard 1970). Clegg and Allard (1972) surveyed populations of this self-pollinating annual grass from throughout California for genotype frequencies at five polymorphic allozyme loci and made two striking observations. First, of 32 possible five-locus combinations, only two were observed with any frequency (Allard et al. 1972), and these contained the alternate alleles at each of the five loci (i.e., AABBCCDDEE and aabbccddee—because Avena is typically highly selfing, heterozygotes were not expected, and rarely observed). Second, these two multilocus genotypes were strongly associated with moist and dry habitats on both large [statewide (Clegg and Allard 1972)] and small spatial scales (Hamrick and Allard 1972; Hamrick and Holden 1979). This pattern led to the hypothesis that fitness in A. barbata was strongly influenced by coadapted gene complexes that showed local adaptation to moist and dry soil conditions, and the two genotypes became known as the “mesic” and “xeric” ecotypes (Allard et al. 1972).

A. barbata has been widely cited as an example of ecotypic divergence (e.g., Grant 1981; Avise 1994; Linhart and Grant 1996; Cox 2004), but this interpretation has not been without critics. For example, Lewontin (1974) questioned Marshall and Allard's (1970) contention that it was the allozymes per se that were under selection, while Hedrick and Holden (1979) questioned whether the multilocus combinations were maintained by selection rather than by the limited opportunities for recombination in a highly inbreeding species such as Avena. The inference of divergent selection was based almost entirely on the allozyme patterns, and early reciprocal transplant experiments either were limited in size (Jain and Rai 1980) or failed to reveal local adaptation (Hutchinson 1982).

A. barbata presents an excellent system in which to study the genetic basis of fitness variation directly. Its annual life cycle makes it possible to monitor individuals throughout their entire lifetime. A. barbata produces two single-seeded florets in each spikelet (Marshall and Jain 1969), and the glumes subtending the spikelet are retained on the plant after seeds drop, making it possible to assess lifetime reproductive success of each individual with a simple count. The high (≈98%) selfing rate means that this count includes male as well as female reproductive success, and the sedentary nature of plants makes it possible to expose numerous individuals to natural field conditions under which selection can occur.

Recently, we have undertaken extensive common garden studies of the fitness of A. barbata ecotypes and of recombinant inbred lines made from a cross between them (Latta et al. 2007). Latta (2009) analyzed 4 years of field data in each of mesic and xeric habitats for evidence of local adaptation [including a preliminary quantitative trait loci (QTL) analysis] and showed that the mesic ecotype consistently outperformed the xeric and that there was no evidence among recombinant inbred lines (RILs) of a negative relationship between performance in habitats native to the mesic and xeric ecotypes. In addition, Johansen-Morris and Latta (2006) documented pronounced hybrid breakdown in the field, which becomes less pronounced in more novel greenhouse environments (Johansen-Morris and Latta 2008), perhaps because the targets of selection differ markedly between greenhouse and field (Gardner and Latta 2006; Latta and McCain 2009). The present study provides a detailed analysis of QTL affecting fitness in the field to identify the specific loci underlying these patterns. We therefore extend here the earlier analyses (Gardner and Latta 2006; Latta 2009) to include epistatic effects, pleiotropic effects of loci across environments, and a Bayesian assessment of alternative models to explain the data.

MATERIALS AND METHODS

A. barbata is a selfing annual tetraploid grass, with disomic inheritance (Hutchinson et al. 1983). It therefore lends itself well to the creation and mapping of RILs. The crossing design was detailed in Gardner and Latta (2006). Briefly, a xeric maternal parent was pollinated from a mesic paternal parent. An F₁ individual was grown under abundant light, water, and nutrients, producing numerous F₂ seeds, 200 of which were used to found RILs, which were propagated by single-seed descent with self-fertilization to the F₆ stage, each homozygous for a unique random combination of the parental alleles. Although such homozygosity precludes our studying dominance interactions in the present study, RILs have the advantage that a given genotype can be replicated in multiple environments to test for G × E interactions. As the F₆ seed stocks began to run low, a further round of propagation gave F₇ seeds.

The genetic map was created from 180 of the RILs, each of which was screened for 129 polymorphic AFLPs (Gardner and Latta 2006). This yielded 19 linkage blocks spanning 640 cM. Since A. barbata has 14 chromosome pairs and likely 1600 cM (Jin et al. 2000; Wight et al. 2003), our map is clearly a partial map. However, additional AFLP and RAPD loci have so far failed to extend the map coverage (M. Morine, unpublished data). One region on LG 19 shows pronounced segregation distortion (Gardner and Latta 2006), which appears due to a locus affecting pollen viability (J. Pollack, unpublished data), such that pollen carrying the mesic allele is less likely to fertilize the F₂ offspring of the heterozygous F₁ than pollen with the xeric allele.

Fitness was estimated for each RIL and the parental ecotypes as described in Latta (2009). Common garden plots were established at Hopland and Sierra Foothills Research and Extension Centers, which are typical of the habitat in which the mesic and xeric ecotypes of Allard et al. (1972) occur naturally. At each site, we established a randomized block design, with three blocks. Each RIL was represented once in each block in a random location and was deliberately exposed to as much of the natural environment (both biotic and abiotic, above and below ground) as possible. At the onset of summer drought, and natural senescence, the above ground dry mass and the number of spikelets of each individual were recorded. This design was repeated [with minor modifications (Latta 2009)] in each of four growing seasons (2002–2003, 2003–2004, 2005–2006, and 2006–2007), which spanned the range of interannual climatic variation of the last two decades.

Analysis:

Individuals that failed to survive to flowering were assigned a fitness of zero (they produced no spikelets). Most of the nonsurvivors had also decomposed by the season's end and were assigned a mass of zero as well (see Latta and McCain 2009 for an analysis of selection on growth of seedlings). Because survivorship and fecundity were highly variable across the four growing seasons, relative fitness was calculated within each year/site combination by dividing through by the fitness of the midparent. Logarithms of (relative fitness + 0.05) gave more normal distributions for analysis. Mean fitness across years was calculated by averaging the logarithms of relative fitness—this is approximately (because of adding 0.05 to all values) equivalent to the logarithm of geometric mean fitness.

We began by mapping QTL for each trait [mean fitness as well as mass and fitness in each of the (2 × 4 =) eight year/site combinations] separately using composite interval mapping (Zeng 1993) as implemented in QTL Cartographer (Wang et al. 2007). Significance thresholds were estimated using the permutation method of Churchill and Doerge (1994), with 1000 permutations for mean fitness and 300 for each of the individual measures. Default settings of a 5-cM window and 5 cofactors were used.

Because composite interval mapping (CIM) returns a locus-by-locus test of significance, it is not automatically clear whether the model returned is substantially better fitting than other models. We therefore employed Bayesian interval mapping as implemented in R/qtlbim (Yi 2004; Yandell et al. 2007) to assess the posterior probability distribution of all possible QTL models that fit the data. We employed a Poisson prior distribution for the number of QTL with mean equal to the number of QTL returned by CIM. We also permitted epistatic interactions within the Bayesian interval mapping (BIM) models.

To test epistatic interactions among QTL, we employed multiple-interval mapping (Kao et al. 1999) in QTL Cartographer. Beginning with a model that pooled the QTL identified or suggested by CIM and BIM, we first optimized the chromosomal positions of these loci and then tested for any epistatic interactions among them. We then tested all effects for significance, retaining in the model only those for which the likelihood ratio exceeded the significance threshold.

We examined G × E interactions in two ways. Joint interval mapping (Jiang and Zeng 1995) in QTL Cartographer provides an explicit test for G × E interactions as well as a pooled test for significance of QTL for all traits (in this case, all year/site combinations). Significance testing in this approach is problematic for two reasons. First, most QTL mapping software treats the individuals from separate environments as independent genotypes (as when an F₂ or a backcross population is divided into subsets grown in different sites). Since individuals from a given RIL are not independent genotypes even though grown in different environments, this can inflate the significance. Second, randomization in permutation tests removes the main effect of the QTL, as well as its interaction with the environment, and so assumes that the probability distribution for G × E interactions is the same in the absence as in the presence of a QTL (cf. Nichols et al. 2007), which may not be the case.

Our second approach to G × E interactions involved a test for pleiotropy in multitrait multiple-interval mapping (MIM) (Zeng 1993) to determine whether the QTL affecting fitness in one trial was at a significantly different position from that affecting fitness in other trails. The test assesses the degree to which adaptation to different environments is independent (Via and Lande 1987) or constrained by a common set of underlying loci. We began with an overall test for pleiotropic effects in which a simple model based on QTL common to all trials was examined. QTL positions were optimized for their effects on all trials simultaneously. An additional QTL was introduced on the same linkage group as one of the existing QTL, positions were reoptimized, and then we determined whether the model with two linked QTL fit the data significantly better than a model with a single pleiotropic QTL.

We also examined each pair of trials separately, testing whether the QTL affecting fitness in the two trials were in significantly different positions. We used the same approach to determine whether QTL for mass and fitness within each environment were a single pleiotropic locus (as expected if selection were acting on plant size) or separate linked loci.

RESULTS

Mean fitness across environments:

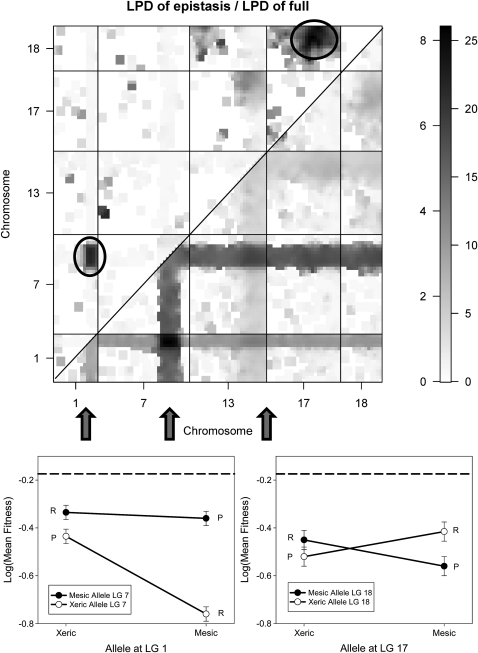
The permutation test suggested a 5% significance threshold of likelihood ratio (LR) = 12. Two loci exhibited highly significant associations with mean fitness and mean mass across years at both Hopland and Sierra Foothills (Figure 1). These same two loci (on LGs 1 and 7) showed an equally strong association with mean fitness and mass. These loci are associated in repulsion phase (AAbb and aaBB) in the parental ecotypes. The xeric allele at the QTL on LG 1 was consistently favored at both Hopland and Sierra Foothills, while the mesic allele at the QTL on LG 7 was consistently favored. Few other loci showed significant association with mean fitness, the only significant QTL being on LG 13, which had a weaker effect than that on either LG 1 or LG 7 and had no effect on mean fitness at Sierra Foothills. BIM confirms this finding of few loci affecting mean fitness. The posterior probability distribution (Figure 1, inset) suggests that as many as six loci may affect fitness; however, the strongly significant individual loci are those identified by CIM. These loci appeared in all the models of the posterior distribution, none of which contained fewer than two QTL.

Figure 1.—

Composite interval mapping results for mean mass and mean fitness across years and sites. Top, likelihood-ratio tests. Significance cutoff from 1000 permutations is given by the horizontal line. Bottom, allelic effects. A positive value indicates that the allele from the xeric parent increased the trait.

MIM reveals significant epistasis between the two QTL for fitness (Table 1). The likelihood ratio of this epistatic effect is 31 (d.f. = 1, P < 0.0001) and explains some 10% of the variation among RILs. The effect is positive—that is, the average fitness of the parental allelic combinations is greater than the average of the recombinants. The size of the effect is of the same order as the main effects of each locus, such that the beneficial effects of recombining the favored alleles at each QTL (in AABB recombinants) are only slightly greater than the loss of fitness through disrupting the positive epistatic effect in the parental combinations. Thus the main loss of fitness is in the recombinant with the disfavored (aabb) alleles at both QTL (Figure 2).

TABLE 1.

Final MIM model of mean fitness

Linkage group	Position	LR	Effecta	% variance explained
Additive effects
1	29	49.40	0.1024	16.5
7	45	77.93	−0.1320	24.6
13	49	19.08	−0.0681	5.6
17	16	1.11	0.0143	0.2
18	22	1.38	0.0195	0.7
Epistatic interactions
1 × 7		31.41	0.0792	9.9
17 × 18		11.45	−0.0604	3.2
Total variance explained				60.7

The dependent variable was Log[rel fitness + 0.05], averaged across all eight field trials.

^aA positive additive effect indicates that the allele inherited from the xeric parent increased the trait. A positive epistatic effect indicates that the parental combination of alleles increased the trait.

Figure 2.—

Results of Bayesian interval mapping of log mean fitness across all eight trials. Top, log posterior density (LPD) for the full model (below diagonal, right side of scale bar) and for epistatic interactions between pairs of loci (above diagonal, left side of scale bar). Results are shown only for linkage groups with a significant QTL or interaction. Bottom, interaction plots for the epistatic interactions between QTL on LG 1 and LG 7 (left) and between QTL on LG 17 and LG 18 (right). Labels “P” and “R” indicate the parental and recombinant genotypes, respectively, and the dashed horizontal line indicates log mean fitness of the midparent.

This interaction is present in all of the models included in the posterior distribution from BIM, but BIM suggests other possible interactions between loci that lack main effects (Figure 2). These interactions (between LGs 13 and 17 and between LGs 17 and 18) are far less significant than the interaction between the two main effect QTL. Only the interaction between LGs 17 and 18 remains marginally significant when included in a MIM model (LR = 11.4, P < 0.1; Table 1).

Overall, the loci account for over half of the variation in mean fitness among RILs, with most of this variance explained by the loci on LGs 1 and 7 (Table 1).

Individual environments and genotype-by-environment interactions:

In each of the eight year/site environments, analyzed separately, the QTL on LGs 1 and 7 are consistently associated with fitness, and these effects are consistently in the same direction. That is, the xeric allele at LG 1 and the mesic allele at LG 7 are consistently (though not always significantly) favored in all environments (Table 2; see also Latta 2009). The epistatic interaction between these QTL is only occasionally significant, notably in 2006.

TABLE 2.

Effects of QTL in the final multitrait MIM model of log relative fitness in each individual environment

	LG 1:	LG 7:	LG 13:		% variance explained
	29 cM	45 cM	47 cM	LG 1 × LG 7
Hopland 2003	0.1170	−0.1340	0.0288	0.1026	16.06
Hopland 2004	0.0690	−0.1120	−0.1744	0.2524	4.97
Hopland 2006	0.3012	−0.3665	0.0307	0.6908	41.27
Hopland 2007	0.2828	−0.2105	−0.4792	0.3874	19.26
Sierra 2003	0.1063	−0.1270	−0.0090	0.2825	31.30
Sierra 2004	0.1411	−0.3466	−0.1521	0.1171	15.30
Sierra 2006	0.3199	−0.3140	−0.0479	0.5407	30.54
Sierra 2007	0.2800	−0.4174	−0.1360	0.2353	29.92

A positive additive effect indicates that the allele inherited from the xeric parent increased the trait. A positive epistatic effect indicates that the parental combination of alleles increased the trait. Statistically significant effects are highlighted in boldface type. Percentage of variance explained is total across all QTL effects.

Other QTL affecting fitness exhibited significant effects on fitness within a particular year/site environment. QTL on LGs 3, 4, 13, and 17 have likelihood ratios that peaked above 9.5 in at least one year/site combination (CIM, not shown), and we used MIM to test whether these significantly improved the fit of the model over the QTL on LGs 1 and 7. LG 13 showed a significant association with fitness at Hopland in 2007. A QTL on LG 3 was marginally associated with fitness at Sierra that same year (Figure 3). In both cases the mesic allele is favored. The epistatic interaction between LGs 17 and 18 was marginally significant only for Sierra in 2007 and had no effect in any other environments. BIM was not applied to individual environments because the MCMC chains often failed to converge, but for those environments where the chain did converge, the results were largely consistent with the MIM model.

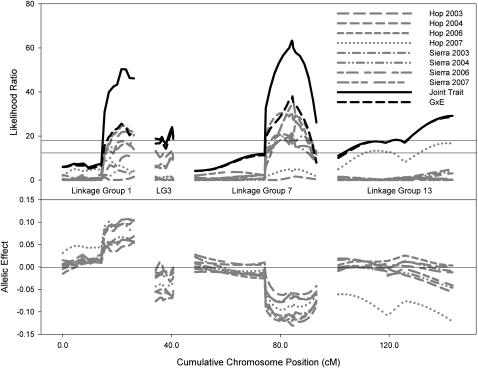
Figure 3.—

Joint interval mapping and test for genotype-by-environment interactions. Top, likelihood-ratio tests. (Note: where the LR trace for G × E interactions is not visible, this is because it is superimposed on the joint LR trace). Significance cutoff from 1000 permutations is given by the horizontal lines for single environments (bottom line) and the joint analysis (top line). Bottom, allelic effects as in Figure 1. Only those linkage groups with significant G × E interactions are shown.

Despite the additional power of joint interval mapping (through combining the “signal” across multiple correlated phenotypes), joint interval mapping (JIM) reveals little evidence for additional QTL affecting fitness. The G × E test in JIM revealed significant interactions at four loci (Figure 3). In three cases, this appears to be the result of variation in the strength of selection—the same allele is favored in each environment, but the effect on fitness varies. In the fourth case, LG 13, the QTL affects fitness in only a single environment (Hopland, 2007) and has no association with fitness in other environments.

Pleiotropy:

Our explicit tests of pleiotropy are restricted to only those loci with significant effects in multiple environments. The estimated position (peak of the LR plot) of QTL on LGs 1 and 7 varies among environments (Table 3). Beginning from a multitrait MIM model of all eight environments, with a single locus on each linkage group, introducing a second QTL on LG 1 increased the log-likelihood by 5, but the second QTL affected only Hopland 2004, and moreover, the two QTL had effects in repulsion phase in this environment. Introducing a second QTL on LG 7 increased the log-likelihood by 8, but again the two loci had effects in repulsion phase. Since multiple additional parameters (one position and eight allelic effects) are introduced by positing a second QTL, these likelihood ratios are not significant (d.f. = 9, P > 0.5).

TABLE 3.

Pairwise likelihood-ratio tests of pleiotropy vs. close linkage of QTL affecting relative fitness in different years/sites

In pairwise tests, the positions of the QTL affecting fitness in one environment were usually not significantly distinguishable from those of QTL affecting fitness in a different environment (Table 3), indicating that adaptation to the various environments is constrained by a common set of QTL. In all cases where linked loci gave a significantly better fit to the data than a single pleiotropic QTL, one of the traits was influenced in opposite ways by both loci (Table 4). For example, comparing results from 2003 and 2006 at Hopland, linked QTL on LG 1 provide a significantly better fit to the data, but the two linked loci have effects of +0.9 and −0.8 on fitness at Hopland in 2003. There is no evidence of such closely linked major loci in repulsion phase in the single-trait analyses. All such cases on LG 1 involved fitness at Hopland in 2003, while those on LG 7 all involved Sierra Foothills in 2006. Since very few recombinants are expected between such closely linked loci, these suggest a statistical artifact.

TABLE 4.

Allelic effects for the two-locus model in those cases where two linked loci fit the data significantly better than a single pleiotropic locus (see Table 3)

	Allelic effect
	Year/site 1:	Year/site 2:
QTL position	Hop 2003	Hop 2006
LG 1, 28 cM	0.9330	0.1799
LG 1, 29 cM	−0.8061	0.1288
	Allelic effect
	Year/site 1:	Year/site 2:
QTL position	Hop 2003	SF 2006
LG 1, 28 cM	0.9801	0.1894
LG 1, 29 cM	−0.8516	−0.0793
	Allelic effect
	Year/site 1:	Year/site 2:
QTL position	Hop 2003	SF 2007
LG 1, 26 cM	−0.7838	−0.0819
LG 1, 29 cM	0.9275	0.2070
	Allelic effect
	Year/site 1:	Year/site 2:
QTL position	SF 2004	SF 2006
LG 7 45 cM	−0.6423	0.3752
LG 7 46 cM	0.3148	−0.7155
	Allelic effect
	Year/site 1:	Year/site 2:
QTL position	SF 2006	SF 2007
LG 7 45 cM	0.3754	0.3636
LG 7 46 cM	0.1962	−0.5028

Most QTL affecting fitness showed parallel effects on mass (Figure 1). In all but one of these cases, the locations of the QTL affecting the two traits were not significantly different, suggesting pleiotropic effects of single QTL on both traits. As above, the only exception (Hopland, 2003) posited closely linked loci with large effects in repulsion phase.

DISCUSSION

The first, and in some ways most striking, result from this analysis is that two loci account for a large proportion of the variation in geometric mean fitness among the lines. These loci have pleiotropic effects on mass (Figure 1), implying that the mechanism of selection on the QTL is that they increase the size of the plants (cf. Latta and McCain 2009). Nearly one-quarter of the variation in mean fitness is accounted for by LG 7 with a further quarter attributable to LG 1 and the epistatic interaction (Table 1). This implies strong natural selection acting on specific genes in A. barbata. Effect sizes imply that LGs 1 and 7 experience selection coefficients of ∼10 and 13%, respectively. These effect sizes are at odds with the traditional assumption that many loci contribute to fitness. There are several reasons for this supposition. Analytical tractability (Fisher 1930; Lande 1975) mandated the assumption before computing power became readily available. Second, it is expected that loci under strong selection would be rapidly fixed by selection, removing variation at major loci (Roff and Mousseau 1987). Third, because fitness is a complex character, it is plausible that many different traits and loci would each contribute small amounts to variation in the overall lifetime reproductive success of an organism (Falconer 1989; Price and Schluter 1991).

A natural caveat to our result is the common observation that the effects of “major” QTL are prone to being overestimated, while QTL of small effect remain undetected. This occurs because of a combination of the significance threshold and error in the estimation of QTL effect sizes (Otto and Jones 2000; Xu 2003). In essence, loci for which the effect size is overestimated are more likely to exceed the significance threshold than those where the effect is underestimated. This effect is generally most pronounced when there are small sample sizes and low heritabilities (Roff 1997; Xu 2003). In A. barbata, heritability of fitness in the field is low (Gardner and Latta 2008), at least within any one environment. Thus within any one environment, a large portion of the variance in RIL means is likely due to sampling variation, especially since relatively few individuals per RIL were measured within each environment (error variance = σ²_e/n, where n = 3 for most RILs in most environments). However, the error variance of the mean fitness across all eight environments is proportional to 1/8n approximately, such that error variance likely plays a much smaller role in the mean fitness estimates. Moreover, the QTL on LGs 1 and 7 were consistently identified in multiple environments individually, despite the lower statistical power within each separate environment. Thus it would appear that their pronounced effects are not an artifact of low heritability.

Also of concern are artifacts caused by limited sampling of possible genotypes. Although we measured ∼6000 individuals across all environments, these represent only 179 different genotypes. In F₂ mapping designs, increasing the number of individuals increases the number of QTL found, while decreasing the estimated effect (Roff 1997; Otto and Jones 2000). It is not clear how this would apply to RIL mapping populations, but it seems that even with accurate estimates of RIL means, a small number of RILs would increase the possibility of spurious associations between particular chromosomal regions and fitness. Moreover, while we have included a moderately large number of RILs, our mapping population (like many such) contains the recombinant progeny of a single cross. Therefore an important follow-up to the present study would be to determine whether the same loci and interactions associate with fitness in independent crosses between the ecotypes.

Epistasis:

With these caveats in mind, if we accept the results reported here, we can ask what implications they have for the genetic basis of adaptation in A. barbata. A. barbata was originally discussed as an example both of coadapted gene complexes (epistasis) and of local adaptation (G × E) (Allard et al. 1972), of which the inference of local adaptation has been more widely cited (Avise 1994; Linhart and Grant 1996; Cox 2004). Ironically, the present results provide strong evidence for the presence of an epistatic interaction, with no evidence of local adaptation (cf. Latta 2009).

The nature of epistatic interactions in wild populations can be difficult to determine, in part because of the greater statistical power required (Lynch and Walsh 1998) and partly because there are more possible ways to be nonadditive (i.e., epistatic) than strictly additive. The present interaction is not the result of multiplicative fitness interactions [which are typically viewed as the standard mode of interaction at fitness loci (Charlesworth and Charlesworth 1987)], because these would have become additive following the logarithmic transformation. Genetic models traditionally fit the epistatic interaction as the departure from additivity between the loci. This is biologically relevant in highlighting the strong main effects (which can respond to short-term selection) that are often present even with strong epistasis.

However, the epistatic interaction between LG 1 and LG 7 is arguably the primary source of variation among the RILs. The interaction plot (Figure 2) makes clear that, rather than the parental allelic combinations having high fitness, one recombinant has particularly low fitness. Having the disfavored allele at one of the QTL produces relatively little loss in fitness, but having the disfavored allele at both QTL produces a pronounced fitness cost. This suggests that the nature of the interaction (at least for this locus pair) is more similar to synergistic deleterious mutations (Whitlock and Bourguet 2000; Kelly 2005) or a Dobzhansky–Muller incompatibility (Dobzhansky 1951; Turelli and Orr 2000) than to a coadapted gene complex as postulated by Allard et al. (1972). Since A. barbata is a tetraploid, one straightforward hypothesis would suggest that the interacting loci might be paralogs, with a mutation in one of the paralogs in each parental ecotype.

While the epistatic interaction is the primary source of variation for this specific locus pair, it does not fully explain the substantial hybrid breakdown seen in the RILs and that is particularly pronounced in the field (Johansen-Morris and Latta 2006, 2008). RILs with the two parental combinations at LG 1 and LG 7, and even RILs with the favored recombinant, are on average substantially less fit than the midparent (Figure 2). This implies that additional gene interactions are contributing to hybrid breakdown. Such interactions are either too weak to be detected in the present analysis or involve higher-order gene interactions that were not modeled here (and for which techniques are not well developed or widely implemented). These interactions may or may not show the same pattern of a single low-fitness recombinant as seen in LGs 1 and 7.

Interactions between loci without additive effects are relatively rare. The epistatic interaction between QTL on LGs 17 and 18 is therefore intriguing, but we approach the result with caution. This interaction is relatively weak, with wide error bars on the effects (Figure 2, bottom right), and enjoys only moderate support in the Bayesian analysis. Moreover, unlike LGs 1 and 7, the effect at LGs 17 and 18 is evident in only one of the individual environments (Sierra Foothills, 2007). However, it also has the unusual property of being an interaction in which the novel combinations are more fit than those in the parents. This is generally unexpected on theoretical grounds, since the parental genotypes have already experienced many generations of selection (though linkage disequilibrium could well prevent the most fit genotype from going to fixation—see below). It is also counter to our empirical observations that hybrid breakdown in the field is pronounced (Johansen-Morris and Latta 2006).

Genotype-by-environment interactions and evolutionary trajectory:

A careful search for evidence of local adaptation in A. barbata fails to support that hypothesis (Latta 2009). The mesic genotype appears to be consistently more fit than the xeric (Latta 2009), and the QTL results provide a straightforward explanation—the mesic allele is favored at more loci and by a larger amount than the xeric allele (Table 1). Although the same loci are under selection in each environment (Table 3) and we find significant G × E interactions for four QTL (Figure 3), in none of the cases does the interaction meet the criteria for local adaptation. In each case rather, the interaction involves variation in the size of the allelic effect, i.e., in the strength rather than the direction of selection on the locus. Selection acts consistently on LG 1 and LG 7, in most of the environments, but to differing degrees. LG 13 by contrast is under selection in only one environment (Hopland, 2007). Similarly, the epistatic interaction between LGs 17 and 18 affects fitness in only one of the environments. The QTL results show no evidence that alternate alleles are favored in different environments, and similar results have been reported in a number of species (e.g., Fry et al. 1998; Weinig et al. 2003; Verhoeven et al. 2004; Lowry et al. 2009; but see Hawthorne and Via 2001). These observations argue against the long-term maintenance of genetic variation at these loci because they imply that a single genotype can have high fitness across all environments. Instead, a single favored genotype is predicted to spread to fixation and Latta (2009) summarizes evidence that such evolutionary change may indeed be occurring in A. barbata.

The expectation that selection will have removed variation assumes that populations have come to equilibrium with their environments. This is less likely for recent colonists of new regions and there is considerable evidence that introduced species undergo a period of adaptation to novel habitats (Reznick and Ghalambor 2001; Cox 2004). While California and Spain are both Mediterranean climate regions, there may be many differences in other aspects of the habitat (e.g., soils, biotic interactions, etc.). Consequently, loci that were neutral in the ancestral range may well come under strong selection in California.

In addition, the elimination of genetic variation by natural selection can be substantially slowed by negative correlations between different targets of selection (Hill and Robertson 1966; Lande 1982; Roff and Fairbairn 2007). In the case of A. barbata our results show that such a correlation derives from linkage disequilibrium, with the favored allele at one QTL associated with the disfavored allele at others. This linkage disequilibrium is maintained by the highly inbred mating system typical of Avena and implies that the evolutionary trajectory is strongly constrained by opportunities for recombination (Hill and Robertson 1966). A recombinant can potentially be more fit than either of the parental ecotypes, if it combines the favored allele across loci. (Note, however, that the more loci must be recombined, the lower the probability that any one recombinant will inherit all of the favored alleles.) This potential is the likely mechanism underlying the pronounced transgressive segregation seen in A. barbata (Gardner and Latta 2006; Johansen-Morris and Latta 2006) as well as numerous other species (Rieseberg et al. 2003) and is hypothesized to be a driving mechanism underlying hybrid speciation and/or adaptation to novel habitats (e.g., Anderson and Stebbins 1954; Arnold 1997; Ellstrand and Schierenbeck 2000).

It can be argued that rare or unique selective effects (such as that acting on LG 13 at Hopland in 2007) can have important impacts on the adaptation of populations. Yet such cases are particularly frustrating. Being attributable to only a single year–site combination and neutral otherwise, they cannot be replicated, simply because particular years cannot be repeated. The effects are relatively weak within the single environments. This makes it plausible that they may be spurious, yet within individual environments most of the effects reported here are relatively weak, simply because the power to accurately estimate fitness in a single environment is so much less than for mean fitness.

What is clear, however, is that these effects have a relatively weak contribution to geometric mean fitness across sites and years. This measure is arguably the most relevant to adaptive evolution in the long term, because the genotype that maximizes geometric mean fitness will have the greatest overall evolutionary success. This is particularly true for temporal variation in the environment. Since A. barbata shows little dormancy in a seed bank (R. G. Latta, personal observations), a successful genotype must be able to survive and reproduce across the range of interannual environmental variation. Spatial variation shows a greater potential to maintain variation through local adaptation when migration between sites is limited (Levene 1953; Kawecki and Ebert 2004) as is likely in A. barbata. However, QTL for mean fitness within Hopland and Sierra Foothills closely mirror those for overall geometric mean fitness (Figure 1). QTL such as that on LG 13, which are under selection in only a single environment, will be neutral in the other. Consequently, the same genotype appears to be favored in both spatial environments, and the QTL results predict that such a genotype should increase in frequency.