Adaptive spatial calibration of a 3D ultrasound system

Abstract

Purpose: The authors present a method devised to calibrate the spatial relationship between a 3D ultrasound scanhead and its tracker completely automatically and reliably. The user interaction is limited to collecting ultrasound data on which the calibration is based.

Methods: The method of calibration is based on images of a fixed plane of unknown location with respect to the 3D tracking system. This approach has, for advantage, to eliminate the measurement of the plane location as a source of error. The devised method is sufficiently general and adaptable to calibrate scanheads for 2D images and 3D volume sets using the same approach. The basic algorithm for both types of scanheads is the same and can be run unattended fully automatically once the data are collected. The approach was devised by seeking the simplest and most robust solutions for each of the steps required. These are the identification of the plane intersection within the images or volumes and the optimization method used to compute a calibration transformation matrix. The authors use adaptive algorithms in these two steps to eliminate data that would otherwise prevent the convergence of the procedure, which contributes to the robustness of the method.

Results: The authors have run tests amounting to 57 runs of the calibration on two a scanhead that produce 3D imaging volumes, at all the available scales. The authors evaluated the system on two criteria: Robustness and accuracy. The program converged to useful values unattended for every one of the tests (100%). Its accuracy, based on the measured location of a reference plane, was estimated to be 0.7±0.6 mm for all tests combined.

Conclusions: The system presented is robust and allows unattended computations of the calibration parameters required for freehand tracked ultrasound based on either 2D or 3D imaging systems.

INTRODUCTION

The use of intraoperative imaging based navigation systems is becoming increasingly adopted in the operating room. One limitation that remains is the fact that they are typically based on preoperative imaging data. These data become increasingly less representative of the conditions in the operative field, due to tissue resection or deformation resulting from the surgery.^{1, 2} As a way to remedy the situation, intraoperative imaging has been explored by various groups in several forms. Intraoperative MRI, for one, has been installed in a number of centers, using dedicated scanners³ or specially designed less intrusive MR devices.⁴ Ultrasound imaging in neurosurgery is a useful alternative to intraoperative MRI or CT due to its much lower cost and smaller instrumentation footprint.^{5, 6, 7, 8, 9, 10, 11} It is even more attractive when spatially registered with preoperative MRI or CT studies and viewed side-by-side or merged as overlays.¹² Furthermore, ultrasound scanheads generating fully volumetric 3D data sets are now available and the data produced by these instruments can easily be merged with preoperative MRI or CT, provided that they can be appropriately calibrated. In order for this to be routinely realized, a calibration procedure is required which is the topic of this presentation. In this paper, we use the term voxel to designate image elements of both 2D and 3D data sets. More generally, we consider 2D images to be a special case, i.e., a subset, of the more general 3D volume in which the z coordinate is zero. We also will refer to coregistration only to MRI studies with the understanding that the discussion applies equally to both MR and CT.

General description of freehand tracked ultrasound

In the literature, the term “3D ultrasound” has often been used to describe systems based on conventional 2D ultrasound imaging in which the scanhead is rigidly coupled to a 3D tracker whose position in space can be monitored continuously.^{8, 12, 13, 14} The term has become ambiguous with the advent of fully 3D ultrasound imaging systems with which one can now collect volumetric imaging data without moving the scanhead. To clarify the terminology, we refer to freehand tracked ultrasound as the practice of using an ultrasound scanhead tracked spatially, whether it produces 2D or 3D data. We use the terms 2D and 3D to refer to the nature of the ultrasound data acquired, that is, 2D images or 3D volumes. In 2D ultrasound, also known as B-mode ultrasound, images are collected with linear arrays, whereas 3D ultrasound is collected with a two-dimensional array of piezoelectric elements phased to sweep a volume. There are also mechanically swept systems based on a single transducer (as used in a 3D TRUS by Envisioneering, St. Louis, MO) or mechanically swept linear arrays that can produce 3D data sets.

The process of coregistering imaging data produced from different sources requires it to be transformed into a common frame of reference or coordinate system. With two imaging modalities that are static, an example of which would be MRI and CT studies from the same patient, one can identify in both image stacks a few (at least three noncollinear but usually more) reference points designated fiducial markers and compute a single transformation matrix, which will express points from one data set in the coordinates of the other. A method for computing the transformation using singular values decomposition is described in detail in the book by Hajnal et al.¹⁵ This method has the precious advantage of ensuring an orthonormal transformation matrix compared to other published approaches.^{13, 16} Other techniques for coregistration of imaging modalities exist, based on mutual information, for example,17, 18 on outlined features using the iterative closest point procedure^{9, 19} or on a weighted combination of points and surfaces.²⁰

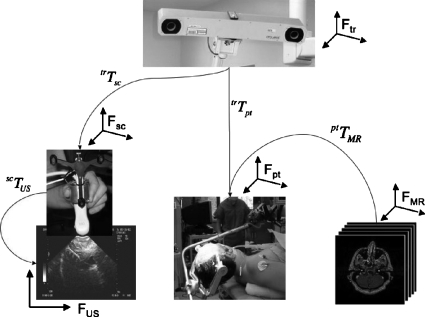
With freehand ultrasound, while the basic principles are the same, one must contend with multiple frames of reference, a potentially moving patient (e.g., an adjustable operating table) or tracking system, and a continuously changing position of the handheld scanhead which generates the imaging data to be coregistered. Figure 1 illustrates the various components of the coregistration problem involving tracked freehand ultrasound. In this illustration we identify five frames of reference: F_MR, the frame defined by the preoperative MRI imaging stack; F_pt, the frame of reference defined by a tracker that follows the patient’s movements; F_sc, the frame of reference defined by the tracker that follows the scanhead; F_US, the frame of reference defined by the ultrasound image data (2D or 3D); and F_tr, the frame of reference defined by the 3D tracking system. In this system, the 3D tracker produces continuously updated transformation matrices corresponding to the location of the ultrasound scanhead tracker ^trT_sc, expressed in F_tr, and the location of the patient ^trT_pt, also expressed in F_tr. The transformation matrix relating the MRI frame of reference F_MR to the patient ^ptT_MR is obtained at the beginning of a procedure using a fiducials-based patient registration process. The transformation matrix ^scT_US, which relates the voxels in the ultrasound data to the scanhead tracker, is obtained prior to surgery and constitutes the scanhead calibration which is the topic of this paper. Armed with all these transformations and data sets, it is possible to merge the ultrasound data with MRI in a common space. The chain of transformations required can be expressed as

$${\left(P_{\text{US}}\right)}_{\text{MR}}={\left({{}^{\text{pt}}T}_{\text{MR}}\right)}^{-1}\times {\left({{}^{\text{tr}}T}_{\text{pt}}\right)}^{-1}\times {{}^{\text{tr}}T}_{\text{sc}}\times {{}^{\text{sc}}T}_{\text{US}}\times P_{\text{US}},$$ (1)

where the subscripts for points (such as P_MR) designate the frame of reference in which they are expressed, and for transformation matrices (such as ^ptT_MR) the subscripts designate the originating frame of reference (“from”) while the prefixed superscripts indicate the destination frame of reference (“to”), using the customary notation.

Figure 1.

Overall view of the various components of image guidance involving freehand tracked ultrasound. At the top is the 3D tracker. The lower left image shows the ultrasound scanhead, its rigidly coupled tracker, and the image it produces. The lower middle image shows a patient and the tracker coupled to the head clamp in the OR. The lower right images show the preoperative MRI imaging study. The arrows indicate how the various frames of reference are related and the respective transformation matrices that are involved. The corresponding frames of reference are also shown (f) near each image.

In Eq. 1, the ultrasound data expressed in the MRI frame of reference (P_US)_MR need to be transformed to the scanhead space F_sc then to the tracker space F_tr successively using ^scT_US and ^trT_sc. Then it is transformed to the patient frame of reference F_pt using the reverse transformation relating the patient to the 3D tracker (^trT_pt)⁻¹ and from patient to MRI space using (^ptT_MR)⁻¹. The overall transformation is therefore the combination of these fixed and updated transformation matrices. Figure 2 shows an example of a 3D ultrasound data set merged with a preoperative MRI based on Eq. 1.

Figure 2.

3D ultrasound and MRI imaging data are merged. This image shows a patient’s head intersected by the three principal planes from the MRI and the overlapping 3D ultrasound planes visible as a triangular overlap in the saggital and coronal planes and a smaller rectangular image in the axial plane. Features that are visible in both imaging modalities align properly due to the correct spatial co-registration.

Existing scanhead calibration methods

The calibration of a US scanhead consists of computing the transformation matrix that relates the position of a voxel (we use voxel centers) in the ultrasound data reference frame and its position expressed in the frame of reference defined by a tracker coupled to the scanhead. This problem has been discussed in previous papers for use with 2D sequences of imaging data.^{13, 16, 18, 21, 22, 23, 24, 25, 26, 27, 28} Mercier²⁹ presented an extensive (at the time) review of the methods of calibration that have been proposed for 2D swept system, referred to as “freehand 3D ultrasound systems.” Referring to our strict definition of 2D and 3D ultrasound imaging, we do not know of anyone who presented a calibration method that applies for both 2D and fully 3D types of imaging systems. Broadly described, the methods of calibration involve imaging various types of objects in tanks. The types of objects ranged from a single point (the crossing of a few wires), an orthogonal set of wires, and “N-shaped” wire arrangements or surfaces (bottom of a tank). From these data, computation establishes the spatial relationship between the ultrasound imaging planes and the tracker. The objects’ position in several images and their position in absolute space produce sufficient data to solve for the unknowns in the system, three rotation angles (θ_x,θ_y,θ_z) and three translation distances (t_x,t_y,t_z). Some authors also propose to calibrate scaling along the three axes, thus adding three additional unknowns to the system of equation. We chose to use the dimensional information provided by the imaging data files (DICOM format headers) to scale all data to mm using the pixel∕voxel sizes given. The problem reduces to solving the following system of equations:

$$P_{W,i}={{}^{W}T}_{\text{tr},i}\times {{}^{\text{tr}}T}_{\text{US}}\times P_{\text{US},i}.$$ (2)

In Eq. 2, W indicates the world reference frame, while the i index indicates that multiple data points are recorded to produce the data needed to solve the system of equations. It is also important to observe that the transformation matrix ^trT_US is fixed, while the other elements of these equations will change with each image. The problem reduces to computing ^trT_US from the expanded system of equations:

$$\lfloor \begin{array}{llll}{x}_{W1}\hfill & x_{W2}\hfill & x_{W3}\hfill & \dots \hfill \\ y_{W1}\hfill & y_{W2}\hfill & y_{W3}\hfill & \dots \hfill \\ z_{W1}\hfill & z_{W2}\hfill & z_{W3}\hfill & \dots \hfill \\ 1\hfill & 1\hfill & 1\hfill & \dots \hfill \end{array}\rfloor ={{}^{W}T}_{\text{tr}}\times {{}^{\text{tr}}T}_{\text{US}}\times \lfloor \begin{array}{llll}{x}_{US1}\hfill & x_{US2}\hfill & x_{US3}\hfill & \dots \hfill \\ y_{US1}\hfill & y_{US2}\hfill & y_{US3}\hfill & \dots \hfill \\ z_{US1}\hfill & z_{US2}\hfill & z_{US3}\hfill & \dots \hfill \\ 1\hfill & 1\hfill & 1\hfill & \dots \hfill \end{array}\rfloor ,$$ (3)

keeping in mind that while the matrix ^trT_US is a 4×4 matrix, it only contains six independent variables which must be constrained to produce an orthonormal transformation matrix. It is also worth noting that z_USi in the right hand set of point vectors will be 0 for 2D images. ^trT_US can be expanded as four separate transformation matrices each representing the effect of the individual components angles and translations

$${{}^{\text{tr}}T}_{\text{US}}=\lfloor \begin{array}{llll}1\hfill & 0\hfill & 0\hfill & t_x\hfill \\ 0\hfill & 1\hfill & 0\hfill & t_y\hfill \\ 0\hfill & 0\hfill & 1\hfill & t_z\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\rfloor \times \lfloor \begin{array}{cccc}1& 0& 0& 0\\ 0& \text{cos}\left({\theta }_x\right)& \text{sin}\left({\theta }_x\right)& 0\\ 0& -\text{sin}\left({\theta }_x\right)& \text{cos}\left({\theta }_x\right)& 0\\ 0& 0& 0& 1\end{array}\rfloor \times \lfloor \begin{array}{cccc}\text{cos}\left({\theta }_y\right)& 0& -\text{sin}\left({\theta }_y\right)& 0\\ 0& 1& 0& 0\\ \text{sin}\left({\theta }_y\right)& 0& \text{cos}\left({\theta }_y\right)& 0\\ 0& 0& 0& 1\end{array}\rfloor \times \lfloor \begin{array}{cccc}\text{cos}\left({\theta }_z\right)& \text{sin}\left({\theta }_z\right)& 0& 0\\ -\text{sin}\left({\theta }_z\right)& \text{cos}\left({\theta }_z\right)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\rfloor .$$ (4)

Over the years, several methods have been proposed, involving the acquisition of images of objects in known positions (i.e., known world coordinates).^{16, 17} Several variations in this idea have been implemented, for example, using points defined by the intersection of wires arranged in an “N” (Ref. ³⁰) or objects with known shapes visible in ultrasound such as a planar surface at the bottom of a tank.¹³ Some of these techniques require knowledge of the position of the tanks in which the various objects are placed or the locations of the objects themselves while others do not. It is generally preferable, in our view, not to depend on measuring accurately the location of the calibration object since this will invariably be a source of error.

A formulation was proposed by Rousseau et al.,²¹ in which a plane with unknown but fixed position in absolute space is used. In this approach, the plane appears as easily identified strong echoes in the shape of a line intersecting the ultrasound images. The points on the images corresponding to the water∕plane (usually the bottom of a tank) boundary are collected in a series of images. Based on an initial assumption about the calibration matrix ^trT_US, their position in world coordinates is computed. Without spatially registering the plane of reference (the plane used for the calibration), it is not possible to express an objective function based on the distance of these points from the originating reference plane in world or tracker space. However, it is possible to compute the distances of this set of points from the plane that best fits them. Using this measure of “planarity” as an objective function, the matrix ^trT_US can be adjusted iteratively. It should be noted here that this method works for both 2D ultrasound, where the plane-image intersection reduces to a line, and for 3D ultrasound, where a portion of the plane is captured. Our formulation is based on the approach described by Rousseau et al.,²¹ with some significant departures in its implementation, which we present in Sec. 2, particularly its extension to 3D ultrasound.

CALIBRATION METHOD

In this section we present the details associated with the implementation of our calibration procedure. The data acquisition itself, i.e., the recording of ultrasound images or volumes is straightforward, involving the transfer of imaging data together with the corresponding spatial tracking coordinates, and is not discussed at length here, except when it affects the processes presented below. Our image guided surgery system is designed to acquire simultaneously an image (or volume) from the ultrasound system and the tracking data upon the user’s request either by clicking a button on the user interface, or by pressing a switch placed for this purpose on the tracking unit that is attached to the ultrasound scanhead. Corresponding images and tracking data are labeled with identical reference numbers so that the position of any image can be recovered. Another point of detail needs to be mentioned, pertaining to the difference in propagation velocities between plain water at room temperature and in vivo tissues. Others have made the observation that most clinical ultrasound are calibrated for a nominal sound speed of 1540 m∕s, while our tank experiment take place in water at room temperature, which has a sound speed closer to 1500 m∕s.³¹ We correct for this discrepancy in the simplest possible manner simply by scaling distance as measured in the ultrasound volumes by the ratio 1500∕1540. This correction, however, does not compensate the slight beam steering error introduced by the different speeds of propagation in water vs typical tissue. All computations were implemented using MATLAB (the Mathworks Inc., Needham MA) and, when possible, we made use of functions from its image processing toolbox. The method presented in this paper was initially developed for our Sonoline ultrasound system (Sonoline Sienna digital ultrasound, Siemens Medical Systems, Elmwood Park, NJ), which is a 2D scanner. The same algorithm was then adapted to work with our iU22 system (iU22 ultrasound system, Philips Medical Systems, Bothell, WA), which has both 2D and 3D imaging capabilities.

Plane identification

Our calibration procedure depends on producing sets of points from each image or volume which best describe the intersection of the image or volume with the plane of reference. Rousseau et al.²¹ used the Hough transform to identify the line representing the plane of intersection with each image. We experimented with the Hough transform and found that it was not reliable. While it worked well with the simulated images presented in Ref. 21, it failed on many of our images. In addition, the Hough transform, which was developed for 2D image processing does not have a natural extension to 3D.

We adopted a solution to this problem which is both simple and robust and readily implemented with either 2D or 3D imaging data. The method consists of tracing rays emanating from the transducer and extending to the distal end the image or volume, along which we compute the intensity profiles. Depending on the nature of the transducer, these rays could be parallel (linear array), or could converge to a point (phased arrays). We used every fifth column of voxels a way to accelerate the computations without incurring an unacceptable penalty in the accuracy or robustness of the algorithm. Image intensity along these rays was filtered using an eleven-point centered average so as not to introduce a spatial phase shift to the filtered data, and in order to reduce the effect of spurious ultrasound variations and∕or artifacts in the image. This is in effect a one-dimensional blur filter. We also normalized the intensity along this ray by the maximum value it contained and used this set of values to find the first point at which the relative filtered intensity exceeded a threshold value as a function of distance away from the US transducer scanhead. This normalization procedure allowed us to pick a single threshold for the detection of the transition between water and the object of interest. The value of the threshold was determined experimentally to result in a line that would follow the transition (maximum gradient) between water (dark pixels) and steel (very bright pixels). We found that by setting the threshold to 0.5, we obtained the best results. The first few voxels in a ray were set to zero to eliminate the high intensity values typically observed near the edge of the transducer. The identification of the threshold defined by the reflections from the steel plate was helped significantly by adjusting some of the ultrasound parameters, appropriately. In particular, we found that reducing the transmitted intensity improved the process by making the plane of interest appear as a bright single line on a dark background representing the water in the images. It also helped to reduce imaging artifacts caused by reflections from the sides of the tank, the water surface, and the transducer itself. By acquiring ultrasound images of a steel plate in a water tank we are able to control very carefully the quality of the images collected. This in turn allows us to use relatively simple algorithms to identify the calibration surface in our images.

With 2D images, the points collected in this fashion form a cluster along the hyperechoic plane of intersection. They are not necessarily exactly collinear, and there may be any number of distant outliers corresponding to artifacts or reflections which would significantly compromise the fit of a least-squares regression line. Instead, we have devised a modified implementation of the random sample consensus algorithm,³² where an adaptive method is used to determine the line of intersection by repeatedly computing the regression line and successively eliminating the farthest outliers until all of the points that remain are within a predetermined small distance of the resulting (and final) least-squares line. For each image, we save the two points corresponding to the intersections of the regression line and the image frame boundary.

This method extends naturally to 3D volumes by exploiting the fact that with our system (Philips iU22 with a X3–1 transducer), the image intensity data is organized in a 3D array indexed by (r,θ,ϕ), r being the distance from the transducer “center,” and θ and ϕ being angles along perpendicular directions representing a nonstandard spherical coordinate system that describes locations in a volume having the shape of a frustum. Step sizes in the radial and both angular coordinates are known so that a voxel’s location in space is easily computed. It should be noted here that the effective tangential resolution within the image volume decreases with distance away from the transducer. This indexing method is advantageous for identifying the intersection of the plane of interest with the frustum of ultrasound data because we can easily search along rays which represent one of the indexing directions in the matrix containing the volume of ultrasound intensity data. From the points (center of voxels) obtained by thresholding, we compute the best-fit by plane by minimizing the cumulative shortest absolute distances of the individual points from the plane based on the singular value decomposition solution of the least-squares problem.^{33, 34} Here, we use the same adaptive approach of computing multiple plane-fits and discarding the farthest outliers at each iteration until the remaining points are within a predefined narrow slice of space on either side of the final best-fit plane. This gradual elimination of distant outliers in either the linear (2D images) or planar (3D volumes) data fit algorithm is the first level of adaptability of our overall algorithm. The computations are outlined in more detail in the Appendix. The parameters defining the plane of reference, expressed in the coordinate system (F_US) of the 3D ultrasound image volume are used to compute the intersection points between this idealized plane and the four rays defining the edges of the frustum. Thus, four points are obtained from each 3D data set to be used in the optimization procedure described in Sec. 2B.

Objective function

The data in the left side matrix in Eq. 3 correspond to a set of points in F_W which represents a plane. When transforming the points obtained from the images or volumes, as described in the previous section, we make use of two transformations: ^trT_US which relates ultrasound coordinates to tracker coordinates and ^WT_tr which relates tracker coordinates to world coordinates. ^WT_tr is given by the tracking system and is assumed correct, while the parameters defining the matrix ^trT_US are unknown and need to be estimated. If all transformations leading from ultrasound image space to world coordinates are known accurately, then the points identified in the images or volumes will be coplanar once expressed in world coordinates, by definition, since they represent a fixed physical plane. Conversely, should ^trT_US be incorrect and all other transformations known, this would result in those points tending to diverge for different poses of the scanhead between data sets. While this is not a formal demonstration, it can easily be visualized or demonstrated with appropriate 3D representation tools. It is also de facto demonstrated in the fact that our calibration algorithm converges, provided the data is not corrupted.

This observation is used to compute the parameters of the ^trT_US transformation matrix by formulating a minimization problem in which the planarity of the points transformed into world coordinates is optimized. More specifically, we implement the following algorithm:

• (1)Initialize ^trT_US (arbitrary initial guess or last calibration).
• (2)Load US defined points P_US,i (see Sec. 2A).
• (3)Transform the points to world coordinates P_W,i per Eq. 2.
• (4)Compute the planarity of P_W,i (see Appendix).
• (5)If the data are sufficiently planar or if max number of iterations is reached, STOP.
• (6)Update ^trT_US (see Sec. 2C).
• (7)Go back to (3).

We refer the reader to the Appendix which describes how the measure of planarity is found as a byproduct of using the singular value decomposition solution to the least-squares problem of fitting a plane to a set of points. The remaining component of our calibration technique is the optimization, itself, which is discussed in Sec. II.C.

Optimization

We have six parameters to adjust [(t_x,t_y,t_z) and (θ_x,θ_y,θ_z)] in order to optimize the planarity of the points obtained from ultrasound data and transformed to world coordinates. We have programmed two algorithms to solve this problem, the first using a gradient descent (GD) and the second being an adaptation of simulated annealing (SA). Upon some preliminary experimentation, we have found that the GD algorithm, while much faster in its execution on occasion, would converge to a nonoptimal solution (compared to the SA algorithm) and decided not to use it for that reason. This was a deliberate choice we made, indicating a bias toward robustness (i.e., reliable unsupervised execution). Our tests did indicate that if a close initial guess was provided, the convergence of the GD algorithm occurred very close to 100% of the time. We must also add that while execution time may be a consideration for some, in our case the rigid coupling holding the tracker to the scanhead is semipermanent and very stiff, thus we can calibrate an assembly prior to use in the OR, overnight if necessary. Moreover, the completion of the computation for a given scale takes on the order of 15 min with the initial guess of all parameters being zero, and less than 5 min with a close initial guess (computations performed on a MacBook Pro, 2.16GHz Intel Core Duo).

Our implementation is a variation in the SA algorithm. The search variables, the translation, and rotation parameters are updated at every iteration by adding to the current parameters random values that are uniformly distributed in the range ±1 (mm or degrees) and scaled by a varying step size. This step size can be very large upon starting and thus the search space can be large initially. In accordance with the SA procedure, the step size is gradually decreased resulting in an increasingly small search neighborhood around the current position. Step sizes are different for angular and translation variables because of the different sensitivities of the objective function to these variables. The step size is increased by a large factor (∼1000) every time an improvement is obtained in the objective function, thus increasing the search space around the current optimum point. Conversely, any time a test computation results in no improvement, the step size is reduced by a small factor (0.6%). Thus, the search space is very gradually reduced to the neighborhood around the current optimum. Furthermore, the ratio of the adjustment factors regulates how long the algorithm dwells in the farther reaches of the search space, compared to the close neighborhood of the current optimum point. The search variable values are kept within reasonable ranges, by keeping the angles within ±180°, and the X and Z translation parameters within ±50 mm and the Y translation parameter to the range (0, 50) mm by successive subtractions, thus preserving the random element of the update step. This last value is based on our knowledge of the geometry of the physical coupling between the tracker and the ultrasound scanhead.

In addition, to the slow narrowing of the search toward the current optimum point in the search space, we also implemented a system in which we were able to detect and reject bad data sets. We designate as “bad data sets” points obtained from an individual ultrasound data set (or “3D image”) and which do not readily line up with the other planes. This poor alignment becomes apparent after the algorithm has run for some time and most of the other data sets form a very tight planar point cloud, while possibly a few do not. We discovered this simply by drawing the entire scene (reconstructed plane outlines in 3D space) using the 3D plotting facilities in MATLAB. Once we found this cause for occasional failures to properly converge, we were able to eliminate it. More precisely, it is possible to compute the distance of each point in the complete set (all the calibration ultrasound data sets) from the plane that best fits these points collectively (what we refer to as the planarity of the data sets). It is therefore possible to compute how well a given individual data set fits with that plane and eliminate it from the overall data pool if it exceeds a threshold. This is the second adaptive feature of our overall calibration procedure.

VALIDATION

We evaluated our calibration procedure based on two criteria separately: Robustness and accuracy. Since it was our goal to devise a program that would allow completely unattended computations, we evaluated it on that feature. Similarly, the accuracy of the resulting computations was critical in deciding if our code was useful and this aspect was evaluated separately as well. We describe our methodology for gauging both in the following paragraphs. We performed an extensive series of calibration tests with our ultrasound equipment, basing our evaluation on data obtained with the iU22 system. While we successfully and accurately used this technique to calibrate both 2D and 3D imaging data, we present here results of our 3D calibration with a X3–1 matrix transducer (Philips Medical Systems, Bothell, WA) since 2D calibration has been presented extensively by others. We calibrated several of the nominal scales available for this device, 15 in all, all of them in 3D mode. What we refer to as scale is the size of the volume spanned by the scanhead, expressed as the maximum radial distance from the top of the imaging volume frustum. For each scale we ran a few separate calibrations, between two and six separate runs based on approximately 20 images to test the overall procedure’s ability to converge. In all, we ran 57 tests using X3–1 scanhead.

Robustness

We define robustness as how reliably the procedure operates correctly while executing completely unsupervised, which was the goal. In a typical calibration session, the user acquires 20 images for a given setting at each of the 15 nominal scales. This number of images is most likely excessive, but the time needed to acquire it is not prohibitive, and it gave us sufficient redundancy to be able to safely discard a few images if necessary, as described above. In prior tests, we were able to successfully complete usable calibration with as few as three data sets. Volumes data sets are acquired in a tank in which a steel plate (12×10 in.², 1∕2 in. thick stock machine steel) is oriented in an oblique plane. The plate was clean and of even roughness, which was produced by sanding it with very fine sandpaper. The plane is clearly visible in the ultrasound images as a very bright reflection. We used an oblique plane because it provided an easy way to vary the distance between the intersected plane and the transducer, and it allowed us to accommodate all of the scales available, which range from 40 to 260 mm. We used a stand to hold the scanhead steady during image acquisition and 3D tracking. In addition to imaging data, we simultaneously acquired position data, recording the pose (location and angles) of the ultrasound scanhead using our Polaris Hybrid (Northern Digital Inc., Waterloo, Ontario) 3D tracking system. The tracking device attached to the ultrasound scanhead was of the active type, consisting of a Y shaped frame outfitted with three pods of seven infrared emitting diodes (IREDs) manufactured by Traxtal (Toronto, Ontario). In addition, we had a fixed tracker, simulating a patient tracker, attached to the tank in which the data acquisition was taking place. This precaution was used to avoid errors due to the tracking system itself, which is mounted on a cart, moving in relation to the experimental region of interest. In this fashion, we were able to compute the position of the ultrasound tracker in relation to that of the patient tracker regardless of any possible motion of the cart. During image acquisition, a deliberate effort was made to vary all degrees of freedom (rotation and translation about all three axes) by sliding the transducer over the plane in all directions (forward∕back, left∕right and up∕down) and by tilting it in all directions as well using a systematic pattern.

Following an image acquisition session, the calibration, consisting of the plane identification and optimization routines, proceeded automatically. Combining all the attempted calibration procedures, that is, every run performed for every scale, 57 runs in all for this evaluation of robustness, we found that every one succeeded, in that it converged to a result we considered accurate. We observed that in all the runs, one or more of the data sets recorded were discarded, indicating that the adaptive mechanism designed to reject “bad data” was working. Upon closer examination we determined that the cause for the rejection of data sets in almost all cases [56 out of 57 (98%)] was due incorrectly identified planes in the ultrasound data, due to reflections and other visible artifacts. We had one instance of bad 3D tracker data. In that particular case, one of the data sets was acquired while the patient tracker was not “seen” by the tracker (reported MISSING by the POLARIS software). This was most likely caused by the operator obstructing the line of sight between the camera and the target.

Accuracy

Groups of four points are produced for each ultrasound volume collected for a particular calibration and used to drive the optimization procedure to converge so that the points collectively form as good a fit to a global plane as possible. This plane does not necessarily match the location of the physical plane that was used to collect the ultrasound data. In order to gauge the accuracy of our procedure, we recorded the location of the steel plate defining our reference plane with a tracked stylus placed at its four corners in succession. We were able, therefore, to compute the distances of the calibration points obtained from the images or volumes to the digitized reference plane. Note that the reference plane location itself was not used to compute the calibration, and it would not be recorded under normal operation; it was recorded only for the purpose of this validation. We then defined our calibration accuracy as the distance between selected test points on the calibration volumes and the recorded position of the reference plane for that test. The test points in question were different from those used in the calibration. The points selected consisted of five points on the plane identified in the respective ultrasound volumes; one point corresponding to the intersection of the US beam axis (θ=0, ϕ=0) and four additional points on that same plane corresponding to (θ=0, ϕ=ϕ_min), (θ=0, ϕ=ϕ_max), (θ=θ_min, ϕ=0), and (θ=θ_max, ϕ=0). We performed our accuracy evaluation for each scale separately, basing it on the individual volume data sets collected for each, with 20 images per run (approximately) and two to six runs per scale, resulting in 40–120 tests per scale for our evaluation.

To gauge the accuracy of our calibration procedure, we used the overall mean distance of the test points from their respective reference planes which yielded an accuracy of 0.7±0.6 mm for all the tests at all the scales combined. Table 1 shows the breakdown of errors by scale.

Table 1.

Mean error by scales.

Scale (mm)	Mean (mm)	Stdev (mm)
40	0.83	0.90
50	0.36	0.32
70	0.23	0.19
80	0.39	0.32
100	0.96	0.87
120	0.68	0.49
130	0.59	0.46
141	0.63	0.47
161	0.60	0.47
170	0.71	0.56
180	0.82	0.74
200	1.08	0.77
221	0.83	0.57
242	0.79	0.78
261	1.03	0.71
All scales	0.70	0.61

While trends were visible between the mean and the nominal scales, as well as the standard deviation and the scales, the coefficient of determination were weak (r²=0.380 and 0.135, respectively).

DISCUSSION AND CONCLUSIONS

Our results are based on using an optical 3D tracking system. Such systems have well understood limitations, such as the need for an unobstructed line of sight between the tracking cameras and the objects of interest. Furthermore, the way of coupling the tracking device to the scanhead, with some distance separating the image field from the IREDs (for practical necessity) will likely have a multiplying effect on the measurement errors associated with the tracker in defining the image physical location. It should be noted, however, that these factors, while affecting our results, are not limitations of our algorithm, but those of the tracking system, and that our method could be applied to most freehand tracking technologies (e.g., trackers based on electromagnetic sensing). Errors, in the form of measurement inaccuracies, enter the calibration process we devised through several avenues. The first and most obvious is the error of the POLARIS 3D tracker system. The specification on its accuracy is given as 0.35 mm RMS for a single point.³⁵ Readings from multiple points are required to track an object and the error in defining its position and orientation (pose) is a complicated function of the contributions from the individual points used. Wiles³⁶ presents in some detail the complicated relationship between the reported point measurement accuracy and the reported tracker pose. This complicates significantly the task of establishing with what accuracy one can measure the location of an object consisting of several points in space, the accuracy of measuring individual points being a function of many parameters, including the position of the measurement volume inside the volume of operation of the 3D tracker. However, we can assume that the localization of a point in the center of a planar rectangle can be computed to a greater level of accuracy, given the positions of its corners with a given expected error, than for the corners themselves (inverse lever arm effect). Minimizing as much as possible this type of error was the reason for devising a calibration method which did not require knowing (e.g., measuring) the position of the reference plane. The present results estimate the error in tracked ultrasound to be 0.7±0.6 mm based on our calibration procedure and evaluation. These errors are approximately twice that specified for an individual point by the manufacturer of our tracking system. Another source of error in our procedure stems from the identification of the reference plane within the image or data volume. This error arises from the definition of the surface of the reference plane in terms of the voxel values in the resulting ultrasound data and from the result of our adaptive line or plane fit. We associated the surface of reference plane with the steepest gradient in image intensity. However, when dealing with actual images in water tanks, we have to contend with many features that have nothing to do with the plane of reference. For example, the spike in intensity that occurs at the transducer surface, multiple reflections from the water surface, the reference surface, the tank sides, and the transducer itself. In some cases, the formation of bubbles in nondegassed water produces additional artifacts in the images. For these reasons, we defined a 50% threshold in the normalized image intensity, along rays, as the surface detection criterion which provided us with a robust algorithm. Visually, the approach produced good results, although we do not know if the lines obtained correspond exactly to the plane of reference. Another factor that may introduce errors at this stage relates to our scaling of the speed of sound (1500 vs 1540 m∕s) amounting to approximately 2.6% in radial error and some unaccounted for amount of error in the lateral steering angle. It is well understood that the speed of sound in water in water is a function of temperature and that means that our single valued correction factor may be off by some amount simply on the basis of temperature fluctuations in the laboratory.

We have developed a semiautomatic calibration procedure, in which user intervention would be limited to the acquisition of ultrasound images or volumes consisting of the echo coming from a reflective plane in a tank. It is conceivable that even this part of the data collection could be automated with the use of a robotic arm. In our evaluation, the calibration algorithm converged to an acceptable solution in all cases. This is in large part due to two levels of adaptive features in our program, first in identifying the calibration plane in the collected ultrasound data, and second in rejecting data sets that do not follow the global trend of a given calibration set.

The only publication presenting a method similar to ours is from Rousseau et al.,²¹ where the Hough transform was used to identify the plane∕image intersection. Our program uses a different method which has the advantage of being more robust and extensible from 2D to 3D data sets. The algorithms we developed function effectively with both 2D and 3D ultrasound data, which has not been possible with previous approaches. We also established that the gradient descent method performs well with real data subject to the condition that a good starting point is selected. However, since in few cases the adoption of this algorithm resulted in failures to converge to a good solution, we decided to use a modified form of the simulated annealing algorithm instead. This has proved to be much more robust (100% convergence) and effective.

APPENDIX: COMPUTING PLANE PARAMETERS FROM A SET OF POINTS

Just as one can fit a line {y(x)=ax+b} through a set of points in a plane, one can also fit a plane {Ax+By+Cz+D=0} through a set of points in 3D space. In the case of a line fit, the solution consists of minimizing in a least-square sense some quantity which describes the goodness of fit. It should be noted that there are different ways to define the goodness of fit, one can aim to minimize the cumulative shortest distance to the line or one can minimize the distances along the ±y direction between the points and line.

We offer here a succinct presentation of our algorithm for fitting points to a plane. It is based on mathematical developments presented by Sharkarji.²² We also list a short MATLAB program that computes the parameters of a plane that best fits a set of points.

Given a set of points,

$$P=\lfloor \begin{array}{ccc}{x}_1& x_2& x_3\dots \\ y_1& y_2& y_3\dots \\ z_1& z_2& z_3\dots \end{array}\rfloor ,$$

there is a plane that best fits these points in the sense that it minimizes an objective function consisting of the cumulative shortest distances between these points and the plane they define collectively

$$J=\sum _{i=1}^N\frac{\left|A{x}_i+B{y}_i+C{z}_i+D\right|}{\sqrt{A^2+B^2+C^2}}.$$

For three points, the best-fit objective function will be zero (always a perfect fit); for fewer points there will be an infinite number of solutions (underdetermined problem); and for more points, the optimized objective function will be finite, if the points are not exactly coplanar. The least-square solution that minimizes the sum of distances is a plane that includes the centroid of the points (x₀,y₀,z₀). The optimization problem can be solved for the “de-meaned” data (i.e., the points are shifted such that their centroid is now at the origin) using the singular values decomposition. Conceptually this consists of finding a plane intersecting the origin whose normal direction will optimize the objective function. The singular values decomposition of P^′ (the de-meaned points) returns U×S×V^T=svd(P^′) in which the matrix V contains the plane parameters ABC, the normal vector. More precisely, the singular vector corresponding to the smallest singular value contains the parameters of the least-square fit plane solution to the optimization problem

$$V=\lfloor \begin{array}{ccc}{v}_{1,1}& v_{1,2}& A\\ v_{2,1}& v_{2,2}& B\\ v_{3,1}& v_{3,2}& C\end{array}\rfloor$$

(assuming the SVD computation routine returns the singular vectors sorted from greatest to least as is done in MATLAB). The remaining parameter can be computed from the one point that is known to be on the plane D=−(Ax₀+By₀+Cz₀).

It is useful to note that if we define the vector Q=[ABCD] and the matrix

$$P=\lfloor \begin{array}{cccc}{x}_1& x_2& x_3& \dots \\ y_1& y_2& y_3& \dots \\ z_1& z_2& z_3& \dots \\ 1& 1& 1& \dots \end{array}\rfloor ,$$

then the quantity $E=\sqrt{\left(Q\times P\right)\times {\left(Q\times P\right)}^T}$ is the root mean squared distance between the set of points in P and the plane expressed by Q.

Matlab code:

function [A B C D E]=points2plane(pts)
% This function computes the plane parameters that best fit
% a set of points.
%
% input: pts=[X…;Y…;Z…;1…] (one point per column)
% outputs: [A B C D E] plane parameters: Ax+By+Cz+D=0, and
% RMS error E.
%
% Alex Hartov, 9∕19∕07
% Compute the centroid of the points.
x=mean(pts(1,:));
y=mean(pts(2,:));
z=mean(pts(3,:));
% M contains the “de-meaned” points coordinates.
M=pts(1,:)′−x;
M=[M(pts(2,:)′−y)];
M=[M(pts(3,:)′−z)];
% Compute the plane parameters
[U,S,V]=svd(M); % V contains the normal vector (ABC)
A=V(1,3); % Reference plane normal components
B=V(2,3);
C=V(3,3);
D=−(A⋆x+B⋆y+C⋆z); % Last plane parameter
% Compute the error.
Q=[A B C D];
E=sqrt((Q⋆Pts)⋆(Q⋆Pts)′); % RMS fit error