The noise power spectrum in CT with direct fan beam reconstruction

Abstract

The noise power spectrum (NPS) is a useful metric for understanding the noise content in images. To examine some unique properties of the NPS of fan beam CT, the authors derived an analytical expression for the NPS of fan beam CT and validated it with computer simulations. The nonstationary noise behavior of fan beam CT was examined by analyzing local regions and the entire field-of-view (FOV). This was performed for cases with uniform as well as nonuniform noise across the detector cells and across views. The simulated NPS from the entire FOV and local regions showed good agreement with the analytically derived NPS. The analysis shows that whereas the NPS of a large FOV in parallel beam CT (using a ramp filter) is proportional to frequency, the NPS with direct fan beam FBP reconstruction shows a high frequency roll off. Even in small regions, the fan beam NPS can show a sharp transition (discontinuity) at high frequencies. These effects are due to the variable magnification and therefore are more pronounced as the fan angle increases. For cases with nonuniform noise, the NPS can show the directional dependence and additional effects.

INTRODUCTION

The noise in an image is an important factor in evaluating image quality and in determining system performance. In diagnostic CT imaging, noise is mainly caused by photon detection statistics¹ and cannot be avoided due to the desire to limit radiation dose. To quantify image noise, the pixel value variance is commonly used and much research has been done to study the image variance for parallel beam filtered backprojection (FBP)^{2, 3} and fan beam FBP reconstruction.^{4, 5, 6, 7, 8} However, while the image variance is relatively easy to calculate, it may not fully reflect the impact that the noise will have on a diagnostic task (e.g., lesion detection). For example, smoothing can lower the image variance while not changing the information content of the image. Compared to the variance, the noise power spectrum (NPS) can more fully describe the noise including correlation introduced by filtering and other processing steps. The NPS enables comparison of signal and noise at each spatial frequency, it can be used to predict detection performance,^{9, 10} and it is needed to compute the system DQE.^{11, 12} Since the pixel value variance can be estimated by integrating the NPS over all frequencies, the NPS is a more powerful metric for analyzing CT performance.

The NPS for parallel beam CT system has been studied and was shown to be dependent on the type of reconstruction filter.^{13, 14} An analytical formula for the NPS with a discrete reconstruction process was derived in Ref. 15, where the effects of sampling within the projection and angular sampling were considered. The effects of interpolation and noise aliasing caused by reconstruction pixel sampling were also studied in Ref. 16. All this work was for cases where the statistics are uniform across the raw data set, which in parallel beam CT produces stationary image noise. Note that in this work, we use the terms “uniform” and “nonuniform” to describe whether the noise properties in the raw data are the same across detector cells or views, and the terms “stationary” and “nonstationary” to describe the noise in two-dimensional (2D) or 3D images.

In contrast to parallel beam FBP reconstruction, direct fan beam and cone beam FBP (Ref. ¹⁷) multiply the projection data with a cosine weighting prior to filtering to compensate for the nonuniform ray density, and use weighted backprojection to compensate for the magnification (or convergence) in the backprojection step. As a result, the reconstructed images show a nonstationary noise behavior across the field-of-view (FOV).¹⁸ The impact of the nonstationary noise behavior on detectability was investigated in Refs. ^{19, 20} and several approaches to reduce the nonstationarity were proposed in Refs. ^{21, 22, 23}. The NPS of a cone beam CT system was studied in Refs. ^{24, 25}, where the analysis was performed in a region near isocenter.

In this paper, we investigate the NPS of the nonstationary noise for a fan beam CT system. While the NPS concept assumes the noise is stationary, the approach can be applied to images with nonstationary noise by calculating the spectrum in local regions that are small enough for the noise to be sufficiently stationary. With this approach, an analytical expression for the NPS of a fan beam CT system is derived and then verified using computer simulations. To investigate the nonstationary noise behavior, we analyze the NPS of several local regions and examine the effects of spatially varying magnification, cosine weighting, backprojection weighting, and nonuniform noise in the raw data. In addition, the effects of different fan angles on the NPS are investigated using both uniform and nonuniform noise in the raw data.

METHOD

Analytical derivation of the NPS

We assume the presence of quantum noise in the raw data that is additive and uncorrelated, and a 2D fan beam CT system using an equally spaced fan beam geometry, 360° rotation, and direct fan beam FBP reconstruction.¹⁷ When the noise is nonuniform across one view, the variance in the number of detected photons in the lth detector cell in the jth view σ_lj² is

$$\sigma _{lj}{}^2=\Delta r\times N_{lj}={\Psi }_{lj},$$ (1)

where N_lj is the mean number of the detected photons per unit distance (i.e., the fluence times the detector cell size in the slice direction) for the sample, Δr is the detector cell width, and Ψ_lj is the total number of detected photons for the ray.

After normalization and taking the negative logarithm of the raw data, projection data are computed, and as shown in Appendix A, the NPS of the jth view is

$$S_{p,j}\left(f\right)=\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{1}{N_{lj}},$$ (2)

where f is spatial frequency and k_j is the number of rays through the reconstruction region in the jth view. Since projection measurements are unitless, the NPS of a single view has units of inverse frequency (or distance).

During fan beam reconstruction, cosine weighting and reconstruction filtering are applied before backprojection. Filtering the projections multiplies the power spectrum by the squared magnitude of the filter frequency response.²⁶ Therefore, as shown in Appendix A, the NPS of one filtered projection is

$$S_{fp,j}\left(f\right)=\{\begin{array}{cc}\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{w_{lj}{}^2}{N_{lj}}{\left|f\right|}^2{\left|G\left(f\right)\right|}^2& \text{for}\left|f\right|\le f_c\\ 0& \text{elsewhere}\end{array}\phantom{\}},$$ (3)

where w_lj is the cosine weighting of the lth ray in the jth view, f_c is the Nyquist frequency of the projection data, and G(f) is the apodization window function used in the reconstruction. The 2D NPS has units of (image units)² per frequency squared. Our reconstructions produced images of the linear attenuation coefficient, so our 2D NPS are unitless.

Since the noise in direct fan beam FBP reconstruction is nonstationary across the image,¹⁸ we investigate the noise behavior by subdividing the full image I into n small subregions i_c

$$I=i_1+i_2+,\cdots ,i_n,$$ (4)

where each i_c is a masked image from the full image I and the mask is small enough to ensure the noise within it is stationary. We next derive the NPS for a small region.

Unlike parallel beam CT, during fan beam backprojection, any particular spatial frequency at the detector maps to a different frequency in different reconstruction regions because the samples of the filtered projection are effectively compressed with increasing distance from the detector, as shown in Fig. 1. As a result, the bandwidth of a single fan beam backprojection increases as we get closer to the source. For example, if we compare the bandwidth at three positions indicated by P1, P2, and P3 (f₁, f₂, and f₃) in Fig. 1, we have f₃>f₂>f₁. The effect of the sample compression on the NPS can be analyzed by using the scaling property of the Fourier transform²⁶

$$x\left(t\right)\leftrightarrow X\left(f\right),\text{then}x\left(\text{at}\right)\leftrightarrow \frac{1}{\left|a\right|}X\left(f∕a\right).$$ (5)

Figure 1.

Reconstruction positions in a single fan beam backprojection.

During backprojection, this scaling effect stretches the bandwidth of the NPS at the detector and reduces the amplitude as a function of position. This effect is shown in Fig. 2, where NPS at positions 1, 2, and 3 in Fig. 1 are depicted. In addition, the filtered projection is multiplied by the backprojection weighting (1∕u²) which amplifies the noise by an amount that depends on position. Therefore, the NPS at different positions can be expressed as

$$S_{p,j}\left(f\right)\to \frac{1}{a^2{u}^4}{S}_{p,j}\left(f∕a\right),$$ (6)

where a is 1 at the detector and increases toward the source. Again, we assume here that the region is small enough so that a and u are relatively constant over the region.

Figure 2.

NPS at positions 1, 2, and 3 in Fig. 1 after a single fan beam backprojection.

Within a small region, e.g., subregion i_c, fan beam rays can be approximated as parallel beam rays, and therefore the central slice theorem holds and each view in the CT data set contributes a spoke to the 2D NPS, S_ic(f_x,f_y). Consider a small rectangular region and the view direction in Fig. 3a. This view contributes a vertical line in the 2D NPS. When the gantry is rotated by 90° as shown in Fig. 3b, the contribution direction to the NPS is orthogonal to the (approximately parallel) rays passing through the small region. In each case, the bandwidth and the amplitude of the single view NPS are different because of view dependent scaling and backprojection weighting. As shown in Fig. 3c, by defining α_j and β_ic,j as a view angle and the angle of rays passing through the center of a small region in the jth view, the 2D NPS of a small region can be expressed as

$$S_{i_c}\left(f_x,f_y\right)={\left(\frac{\pi }{m}\right)}^2\sum _{j=1}^{m}R\left[\frac{S_{fp,j}\left(f∕a_{i_c,j}\right)}{a_{i_c,j}{}^{2}u_{i_c,j}{}^4}\delta \left(f_y\right),{\alpha }_j-{\beta }_{i_c,j}\right],$$ (7)

where R(h,θ) is a rotation of function h by an angle θ in the clockwise direction, a_ic,j and u_ic,j are the scaling factor and the backprojection weighting in the jth view, and m is the number of views. Note that a_ic,j and u_ic,j are constant over all views for the isocentered small region, but vary from view to view for off-centered small regions.

Figure 3.

A small rectangular region and view dependent contribution of NPS. [(a) and (b)] (Left) Source location and (right) corresponding contribution direction of NPS. (c) Fan beam data acquisition geometry.

In a full FOV image I [Eq. 4], the noise is likely to be nonstationary. Nonetheless, one may wish to compute (or measure) the NPS of the entire image. We recognize that the full FOV NPS may not accurately reflect the noise in any specific region. However, some investigators may wish to use it and it may represent the overall noise properties. By assuming that the cross correlation between small regions is negligible, the autocorrelation of I is

$${\text{AC}}_I=\sum _{c=1}^n{\text{AC}}_{i_c},$$ (8)

where AC_ic is the autocorrelation of i_c. Since the NPS is the Fourier transform of the autocorrelation, the NPS of the full noise image I is

$$S_I=\sum _{c=1}^n{S}_{i_c}.$$ (9)

Therefore, the NPS of the full noise image can be calculated by adding the NPS of small regions.

Often, especially when the NPS is roughly independent of angle, the NPS is characterized by its dependence on radial frequency. The radial NPS of the full image I can be calculated from Eq. 9, but as shown in Appendix B, a simpler expression can be used

$$S_{\text{radial}}\left(f\right)={\left(\frac{\pi }{m}\right)}^2\sum _{j=1}^m\left[\frac{1}{p_j}\sum _{i=1}^{p_j}\frac{S_{fp,j}\left(f∕a_{ij}\right)}{a_{ij}{}^{2}u_{ij}{}^4}\right]\frac{1}{\pi f},$$ (10)

where a_ij and u_ij are the scaling factor and the backprojection weighting at the ith position (as shown in Fig. 1) in the jth view and p_j is the number of positions in the source-detector direction for the jth view. As shown in Appendix B, when the source to detector distance is very large, Eq. 10 reduces to the expression for the radial NPS of a parallel beam system.

Computer simulations

The NPS expressions were tested using computer simulations of systems with a range of fan angles (and FOVs) and both uniform and nonuniform statistics in the raw data. The projections contained only noise from Poisson statistics (generated using “poissrnd” in MATLAB) with intensity distribution as described below. In each case, the “incident” intensity was the expected value (a noiseless version) of the detected intensity. That is, there was no object in the simulations; rather, the resulting images contain only noise whose properties are determined by the detected intensity distribution. For each case, unless otherwise indicated, 100 realizations were simulated, each comprised of 400 views and 64 rays per view. We recognize that these parameters do not match those of clinical systems. However, we verified that the properties demonstrated by the simulations apply to clinical system geometries. For example, for a fan angle of 33° and the same number of detected photons per unit distance and FOV, systems with 1 mm detector vs 1 cm detector have the same NPS (scaled for the different Nyquist frequency), but the one with fewer samples can be simulated much faster, allowing an increase in the number of noise realizations.

Images were reconstructed using direct fan beam FBP using an unweighted ramp filter. To avoid unwanted apodization or aliasing (see comments in Sec. 4), the projections were filtered using 20-fold Fourier interpolation and then pixel-driven backprojection with linear interpolation was performed onto a 128×128 array. 2D NPS images were calculated from the Fourier transform of noise only 2D images²⁷

$$S\left(f_x,f_y\right)=\frac{b_x{b}_y}{L_x{L}_y}⟨{\left|\text{DFT}\left\{I\left(x,y\right)\right\}\right|}^2⟩,$$ (11)

where b_x=b_y=reconstruction pixel size, L_x=L_y=128, the symbols < > indicate the ensemble average over 100 realizations, and I(x,y) is a noise only image. The radial NPS was calculated by circumferential averaging of 2D NPS, and the analytical radial NPS was calculated using Eq. 10 and p_j=128 for all views.

To investigate the effect of the fan angle on the NPS, uniform noise data (15 000 photons per detector cell over all views) were reconstructed with fan angles of 37.4°, 25.5°, and 12.9° (corresponding to FOVs of 300, 200, and 100 mm) at a source-to-isocenter distance of 450 mm. These examples with uniform noise can represent scans of air in a system with no bowtie filter²⁸ or scans of a circularly symmetric object with a bowtie filter that perfectly compensate for the object attenuation.

The effect of nonuniform noise in the raw data was studied using the intensity variations depicted in Fig. 5. For the case of Fig. 5a, the noise was view dependent but uniform across each single projection. This case is analogous to (but not exactly the same as) the noise that would be observed with an elliptical object or in an air scan with mA modulation. For the case of Fig. 5b, the noise was channel dependent but uniform for all views. This case is analogous to imaging a circularly symmetric object in a system without a bowtie filter. In each of these simulations, the fan angle was 37.4°.

Figure 5.

Simulated nonuniform noise profile. (a) Noise level from view to view. (b) Noise level across detector channels. View angle of zero corresponds to the horizontal direction as shown in Fig. 4.

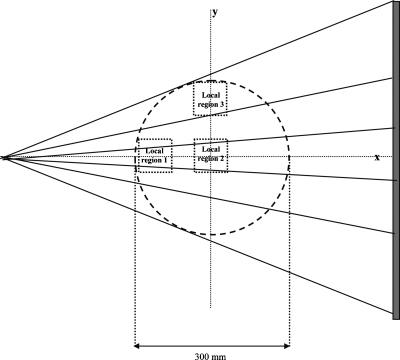
To examine the dependence of the NPS on spatial location, the NPS of local regions 1, 2, and 3 (10×10 mm²) in Fig. 4 centered at (−140 mm, 0), (0, 0), and (0, 140 mm), respectively, were calculated using the nonuniform noise profiles in Fig. 5. In each view, the variations in the backprojection weighting, scaling factor, and raw data noise within the local regions were less than ±5% from their mean values, so local regions were assumed to be small enough for the noise to be stationary. The noise images were generated from targeted reconstruction using 1890 rays per projection with 0.3 mm detector element spacing (corresponding to 37.4° fan angle), and then 2D NPS images were calculated. In local region 2, 64 rays out of 1890 rays passed through the region in each view, but the number of rays passing through regions 1 and 3 were different from view to view.

Figure 4.

Three local regions for the nonstationary noise study.

The simulated NPS from different FOVs and local regions were then compared to the analytical NPS. No additional or artificial scaling was used to match analytical and simulation results. Table 1 summarizes the parameters for the noise simulations.

Table 1.

Parameters for noise simulations.

	Full FOV			Local regions
Fan angle	37.4°	25.5°	12.9°	37.4°
Source-to-isocenter distance	450 mm
Source-to-center detector distance	850 mm
Detector array element spacing	9 mm	6 mm	3 mm	0.3 mm
Reconstruction pixel spacing	2.38 mm	1.59 mm	0.79 mm	0.079 mm
Reconstructed image size (128×128)	300×300 (mm2)	200×200 (mm2)	100×100 (mm2)	10×10 (mm2)
Number of views	400∕360°

RESULTS

Nonuniform noise with 37.4° fan angle

The NPS of local regions 1, 2, and 3 for the nonuniform noise cases are shown in Figs. 67. Figure 6 shows the simulated and analytical 2D NPS and corresponding sample noise images in the three regions (shown in Fig. 4) for the case when the noise was uniform across each view but varied from view to view according to Fig. 5a. Analytical 2D NPS were calculated by using Eq. 7. The 2D NPS images at local regions 1 and 3 show a sharp transition in directions in which the two 180° opposed views have very different bandwidth during backprojection onto each region. In region 1 [Fig. 6a], this happens in the horizontal view direction, so the sharp transition is in the vertical direction in the NPS. The central oblong region receives noise from both horizontal view directions while the outer region in the f_y direction only receives noise from one of the horizontal views (when the source is close to the local region). The contour of the nonzero region in frequency space is created by the view dependent bandwidth. This pattern rotates by 90° for region 3 [Fig. 6c]. Since there are no view dependent bandwidth variations in region 2, the 2D NPS of region 2 does not show any sharp transition. The NPS also shows angular dependent amplitude variation due to the different noise level from view to view, which produces the directionality of noise images (vertical noise structure in all noise images). Since the views in the horizontal direction have higher flux and therefore lower noise, the NPS is lower in the vertical (f_y) direction than in the horizontal (f_x) direction.

Figure 6.

NPS of local regions with view dependent nonuniform noise profile. (a)–(c) are simulated NPS (left), analytical NPS (center), and sample noise images (right) at local regions 1, 2, and 3, respectively.

Figure 7.

NPS of local regions with channel dependent nonuniform noise profile. (a)–(c) are simulated NPS (left), analytical NPS (center), and sample noise images (right) at local regions 1, 2, and 3, respectively.

The NPS of the three regions for the case of channel dependent noise profile [Fig. 5b] are shown in Figs. 7a, 7b, 7c. The effect of varying bandwidth (e.g., sharp transition) is again seen. However, the angular dependent amplitude variation in the 2D NPS is different than in the previous case. In the horizontal view directions, the number of photons through region 1 is smaller than that through region 3. Therefore, the 2D NPS in the vertical direction (f_y) has higher amplitude for region 1 than for region 3. When the gantry is rotated by 90°, the situation reverses. In region 2, the 2D NPS does not show the angular dependent amplitude variation because the number of photons through region 2 is the same over all views. The different amplitude variations in the NPS at local regions produce different directionality of noise images (horizontal, isotropic, and vertical noise structure in regions 1, 2, and 3), and therefore the detectability of anisotropic targets in these regions could be different. Note that regions 1 and 3 have the same variance. From Figs. 67, it can be observed that the noise behavior varies significantly across the full FOV.

Figures 8a, 8b show the entire FOV NPS results for the cases with nonuniform noise profiles. Figure 8a shows the results when the noise level varies from view to view as shown in Fig. 5a. The analytical 2D NPS was calculated by averaging analytical 2D NPS of 30×30 small regions (10×10 mm² each). Patterns of angularly dependent NPS amplitude variation and noise directionality similar to those of Fig. 6 are observed [Fig. 8a] although the sharp transitions are blurred by the averaging over many local regions.

Figure 8.

Full FOV NPS with nonuniform noise profiles. (a) Simulated NPS (left), analytical NPS (center), and sample noise image (right) with view dependent nonuniform noise profile. (b) Simulated NPS (left), radial NPS (center), and sample noise image (right) with channel dependent nonuniform noise profile.

When the noise level varies across the detector channels according to Fig. 5b, the NPS of the entire FOV does not show angular dependence. The angular dependence in local regions shown in Fig. 7 has been averaged out. The position and angle dependent bandwidth are instead reflected as a roll off in the spectrum at high frequencies. This is shown in Fig. 8b. Since the 2D NPS is symmetric, the analytical radial NPS was calculated using Eq. 10 and compared to the simulated radial NPS. They show excellent agreement.

Entire FOV, uniform noise, and varying fan angle

Figures 9a, 9b, 9c show full FOV 2D NPS images with different fan angles. Because uniform noise was used, the 2D NPS does not show angular dependence. Figures 9d, 9e, 9f show the corresponding radial NPS. High frequency roll off can be seen in the radial NPS and the starting frequency of the roll off decreases as the fan angle increases. The roll off results from the spatial variation in bandwidth during fan beam backprojection and is more pronounced at larger fan angles. Overall, we can observe excellent agreement between the analytical and simulated NPS.

Figure 9.

2D NPS and radial NPS images for different fan angles. (a)–(c) are the 2D NPS with fan angles of 37.4°, 25.5°, and 12.9°, and (d)–(f) are corresponding radial NPS.

DISCUSSION AND CONCLUSIONS

Studies of NPS provide a powerful tool for characterizing CT image noise. By using NPS, we can deduce such information as the amount of the noise in different view directions at each spatial frequency, the form of the reconstruction filter, the contrast resolution, and the variance at a pixel. In contrast to parallel beam CT, CT systems with direct fan beam FBP reconstruction have nonstationary noise across the FOV. In this paper, we derived analytical formulas for the NPS of fan beam FBP reconstruction and analyzed the nonstationary noise in cases with different fan angles and nonuniform noise using local regions.

NPS at different local regions showed symmetric and asymmetric shapes and different angular dependent amplitude variations. These phenomena occur because the bandwidth at local regions, backprojection weighting, and the number of photons through the local regions are different from view to view. Because of these effects, each local region showed different directional dependence, which can produce different detectability. In the NPS of the entire FOV, systems with a larger fan angle showed more high frequency roll off caused by more noise bandwidth variation across the FOV. In all cases, the analytical formulas showed excellent agreement with the simulated NPS.

In our simulations, we used an unweighted ramp filter and Fourier interpolation to retain the high frequency effects caused by direct fan beam FBP. The effect of window functions on the reconstruction filter is included in the derived expressions. The fact that window functions, such as Hanning window, are commonly used perhaps explains why the effects described here may not have been fully appreciated previously. Use of linear or nearest neighbor interpolation in backprojection with little or no Fourier interpolation would have several effects. First, as described in Refs. ^{16, 24, 25}, the interpolation step multiplies the NPS of the filtered projection with the squared magnitude of the frequency response of the interpolation filters [sinc²(Δrf) for linear and sinc(Δrf) for nearest neighbor interpolation]. In addition, interpolation can introduce erroneous high frequency energy from partially attenuated replicates of the spectrum. These could be included in the model in a straightforward manner. Finally, the finite pixel spacing is an additional sampling step that can introduce aliasing if the spacing is too coarse. We used a small pixel spacing to avoid this, as can be appreciated by the fact that our 2D NPS images have zero amplitude at high frequencies.

The proposed method to calculate the NPS can be used for any FBP reconstruction. For example, in parallel beam CT, the effect of noise that is not uniform across projections or from view to view is qualitatively the same as that presented here, and the method used in this paper can be adapted to derive the NPS in those cases. Some CT systems reconstruct fan beam data by rebinning to parallel ray projections. The resulting images will not have all the same properties as derived here for direct fan beam reconstruction. While the effects of nonuniform noise in the raw data will be similar, the parallel ray reconstruction will not produce the effects caused by variable magnification (e.g., the discontinuities in the NPS). At the same time, the rebinning step can introduce other effects, such as band limiting due to interpolations and possibly also noise aliasing. For direct short scan fan beam reconstruction, the present method could be adapted by incorporating the effect of the weighting function on the NPS of projection data. Future works will extend the work presented here to the 3D NPS of cone beam CT systems.

APPENDIX A: DERIVATION OF THE NPS FOR THE jth view projection

Since the noise in the samples in one view are uncorrelated (white), the NPS of the projection data S_p,j(f) is constant²⁶ and its noise power density S₀ is related to the variance across the detector cells σ² as

$${\int }_{-f_c}^{f_c}{S}_{p,j}\left(f\right)df=2f_c\times S_0=\frac{1}{\Delta r}\times S_0={\sigma }^2,$$ (A1)

where f_c is the Nyquist frequency of the projection data (f_c=1∕(2Δr)).

Let ε_lj be the error at the lth detector cell in the jth view. If the incident intensity is known exactly or is much larger than the detected intensity, the variance of each detector reading is¹³

$$\text{var}\left({\epsilon }_{lj}\right)\cong E\left[\epsilon ^2{}_{lj}\right]=\frac{1}{{\Psi }_{lj}}.$$ (A2)

Then the variance across the detector cells can also be expressed as²⁶, ²⁹

$${\sigma }^2=\frac{1}{k_j}\sum _{l=1}^{k_j}E\left[\epsilon ^2{}_{lj}\right].$$ (A3)

From Eqs. A1, A3, the NPS across the detector cells is

$$S_{p,j}\left(f\right)=\Delta r\times {\sigma }^2=\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{\Delta r}{{\Psi }_{lj}}=\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{1}{N_{lj}}.$$ (A4)

The next step in the reconstruction is multiplication with cosine weighting, after which the variance of each weighted sample is w_lj²∕Ψ_lj.

Following the same steps as above, the NPS of the cosine weighted projection is

$$S_{pw,j}\left(f\right)=\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{w_{lj}{}^2}{N_{lj}}.$$ (A5)

Since the filtering projections multiply the power spectrum by the squared magnitude of the filter frequency response,²⁶ the NPS for the filtered projection is

$$S_{fp,j}\left(f\right)=\{\begin{array}{cc}\frac{1}{k_j}\sum _{l=1}^{k_j}\frac{w_{lj}{}^2}{N_{lj}}{\left|f\right|}^2{\left|G\left(f\right)\right|}^2& \text{for}\left|f\right|\le f_c\\ 0& \text{elsewhere}\end{array}\phantom{\}},$$ (A6)

where G(f) is the apodization window function used in the reconstruction.

APPENDIX B: DERIVATION OF THE RADIAL NPS

Consider a single view first. As shown in Fig. 2, during the backprojection, the contribution to the NPS at different positions have different amplitude and bandwidth. We divide the FOV in the source-detector direction into p_j positions [the minimum p_j being comparable to the square root of the number of subregions in Eq. 4]. From Eq. 6, the NPS at the ith position for the jth view is

$$\frac{S_{fp,j}\left(f∕a_{ij}\right)}{a_{ij}{}^{2}u_{ij}{}^4}.$$ (B1)

Since the NPS at different positions contribute to the final 2D NPS, radial averaging of 2D NPS is equivalent to performing the radial averaging of NPS at different positions. Then, the contribution of the jth view to the radial NPS is

$$S_{\text{radial},j}\left(f\right)={\pi }^2\left[\frac{1}{p_j}\sum _{i=1}^{p_j}\frac{S_{fp,j}\left(f∕a_{ij}\right)}{a_{ij}{}^{2}u_{ij}{}^4}\right]\frac{1}{\pi f}.$$ (B2)

Since the noise is uncorrelated from view to view, the contributions from different views add. After including scaling of the image by the inverse of the number of views m, the radial NPS can be expressed as

$$S_{\text{radial}}\left(f\right)={\left(\frac{\pi }{m}\right)}^2\sum _{j=1}^m\left[\frac{1}{p_j}\sum _{i=1}^{p_j}\frac{S_{fp,j}\left(f∕a_{ij}\right)}{a_{ij}{}^{2}u_{ij}{}^4}\right]\frac{1}{\pi f}.$$ (B3)

In the special case when the noise is uniform over all views and detector cells, Eq. B3 reduces to

$$S_{\text{radial}}\left(f\right)={\left(\frac{\pi }{m}\right)}^2\left[\frac{1}{p_j}\sum _{i=1}^{p_j}\frac{S_{fp,j}\left(f∕a_{ij}\right)}{a_{ij}{}^{2}u_{ij}{}^4}\right]\frac{m}{\pi f}.$$ (B4)

When the source to detector distance is very large, a_ij and u_ij approach 1, and Eq. B4 reduces to the expression for the radial NPS of a parallel beam system.

$$S_{\text{radial}}\left(f\right)={\left(\frac{\pi }{m}\right)}^2\left[\frac{1}{p_j}\sum _{i=1}^{p_j}{S}_{fp,j}\right]\frac{m}{\pi f}=\frac{\pi }{m}\frac{S_{fp,j}}{f}=\frac{\pi }{m\overline{N}}\frac{{\left|f\right|}^2{\left|G\left(f\right)\right|}^2}{f}.$$ (B5)