Line-Walking Method for Predicting Inhibition of P450 Drug Metabolism

Abstract

A new method, called line-walking recursive partitioning (LWRP), for partitioning diverse structures based on chemical properties that uses only nine descriptors of the shape, polarizability, and charge of the molecule is described. We use a training set of over 600 compounds, and a validation set of 100 compounds for the cytochrome P450 enzymes 2C9, 2D6 and 3A4. The LWRP algorithm itself incorporates elements from support vector machines (SVM) and recursive partitioning, while circumventing the need for linear or quadratic programming methods required in SVM. We compare LWRP with a many-descriptor SVM model, using the same dataset as described in the literature¹. The line-walking method, using nine descriptors, predicted the validation set with about 84-90 % accuracy, a success rate comparable to the SVM method. Furthermore, line-walking was able to find errors in the assignment of inhibitor values within the validation set for the 2C9 inhibitors. When these errors are corrected, the model predicts with an even higher level of accuracy. While this method has been applied to P450 enzymes it should be of general use in partitioning molecules based on function.

Introduction

Drug design tools are becoming more important as the pharmacological targets for therapy become more complicated. While our abilities to develop a lead compound for a target have become much better, the toxicities and disposition of the chemical determines if the compound can be a drug. The better the drug-like properties of a series of compounds, the more likely a compound in the series is to survive clinical trials and become a successful drug. With the ever increasing cost of drug development, these properties become a make or break issue in the success of any given compound. It has been estimated that approximately 70% of new chemicals entering preclinical development are removed from the pipeline as a result of poor disposition or toxicities ².

For a drug to be successful it must meet a number of criteria which are outlined below. While a drug with less than ideal characteristics can be brought to the market, fast followers from other companies will erode profits, and hence new discovery funding. Early attention to making a good drug will lead to a better overall first generation drug with a better opportunity to recover development costs. To assure compliance, daily dosing is desirable. The compound also must be bioavailable, and get to the site of action. A drug must have low toxicity, which can be a result of target toxicity, or bioactivation to a reactive species. Drugs should have multiple metabolic pathways to lower the potential for drug-drug interactions and drug-xenobiotic interactions. High affinity for the target is important in decreasing toxicity, and drug-drug interactions. Of these criteria, often only high target specificity is used in early discovery. A potentially more successful approach is to balance target affinity, and the other characteristics that make a chemical a drug. Thus, tools for early screening of large numbers of molecules for drug-like properties as well as pharmacological activity are very important. An excellent example of this approach is the concurrent prediction of hERG K⁺ channels, a pharmacological target, and P450 2D6 inhibition properties by O’Brien and de Groot ³.

While design tools for pharmacological targets need to predict affinities for a single target site, predicting bioactivation, metabolic profiles, and bioavailability needs to take into account multiple active sites, and reactivities. A number of groups have developed local models for predicting affinities, or reactivities of the individual enzymes responsible for drug metabolism ^4-6, and bioavailability ⁷ that function very well. The metabolism models assume that a compound is a substrate for the enzyme, and that it is related to members of the training set. Thus, a rapid robust model for segregating chemicals into local space becomes important. One can imagine that compounds could be filtered to determine which drug metabolizing enzyme would interact with the compound, and than further segregated into groups with common structural features. Local models could then be used to predict affinity, and reactivity. Some efforts in filtering chemicals to predict the enzymes responsible for metabolism have recently been published ^1,8-11.

Recursive partitioning holds promise for filtering molecules to determine if a given molecule will be an inhibitor or substrate for a given metabolic enzyme. Recursive partitioning involves the construction of a decision tree, or forest of trees, based on a training set. Descriptors are used to partition molecules into sets which have a bias towards a given property, such as inhibition. The partitioning is continued to generate increasingly more pure groups of molecules (e.g., inhibitors or noninhibitors). One of the first applications of this method to metabolic enzymes was presented by Susnow and Dixon ⁹. A reportedly diverse training set of 100 compounds was used to train a recursive partitioning model to determine if a compound would bind to CYP2D6 with an affinity lower or higher than 10 μM. This model used 25 descriptors and was able to predict if a molecule from an external training set of 51 was an inhibitor with an impressive 80% accuracy. Around the same time Ekins and coworkers presented a recursive partitioning model for predicting if a compound was a substrate for CYP3A4 or CYP2D6 ¹¹. This model used a large training set of over 1759 CYP3A4 substrates and 1759 CYP2D6 substrates. The recursive partitioning models were built with 2500 descriptors, and a forest of 20 trees. These models did a reasonable job of predicting rank order affinities for an external validation set of 98 molecules. Sorich et al., have compared support vector machines to artificial neural networks, and partial least squares discrimination analysis ⁸ in their ability to determine if compound are substrates for 12 isoforms of UDP-glucuronosyltransferase. They concluded that the support vector machines gave the best results based on the percent predictability for each enzyme using an optimized subset of 67 descriptors and distinct training sets for each of the 12 isoforms of UDP-glucuronosyltransferase that ranged in size from 151 to 38 compounds. The support vector machines were able to predict substrates from an external validation set 30% the size of the training set with between 63 and 88 % accuracy, with the majority of predictions being over 75%.

One problem that appears when attempting to predict properties for new compounds is that newer drugs in general are more metabolically stable, or occupy a different chemical space than the training set of available drugs. Given this, a model for new drugs needs to be robust enough to predict outside of the chemical space of the training set. Most if not all methods developed for predicting drug metabolism make an attempt to optimize their ability to predict the training set. Often this leads to using a large set of descriptors to optimally define the model. The use of a large number of descriptors has a number of deleterious effects on the usefulness of the subsequent model. Two such problems are; 1) the more descriptors that are used, the less likely a model will be to be able to predict outside of the chemical space it is trained in, 2) models with a large number of descriptors are difficult to interpret, leading to a lower ability to visualize the changes required to re-design a chemical to have the desired properties.

Herein we present a new method which uses nine descriptors of the shape, polarizability, and charge of the molecule. These descriptors where chosen based on the common understanding of what is important in binding to drug metabolizing molecules, and on their ability to describe the differences in all the training sets. The small number of descriptors used means that the model should be more able to extrapolate from the training set to predict the properties of new chemical entities. Our method incorporates elements from SVM and recursive partitioning. Following each of these methods, we consider the training set as a collection of points in a high-dimensional space, each point with a label corresponding to some chemical property. Each dimension of the space corresponds to a chemical descriptor. In this geometric setting, we decide how to dissect the space into regions, each region containing points having a common label. In SVM, the number of dimensions is high enough to ensure that the dissection can be accomplished with a single decision, with few training errors, i.e. points with labels differing from the predominant label in the region. Also, the decision is in the form of a hyperplane that incorporates information from all of the descriptors simultaneously. Our method incorporates this latter feature into recursive partitioning; the space is dissected by a hyperplane into two regions, then each region is dissected into two regions, and so on until each of the resulting regions contains points having a common label. We employ a tactic called “line-walking” described in detail below in order to efficiently locate a hyperplane that minimizes the number of training errors at each step. We compare of line-walking with a many-descriptor SVM model, using the same dataset as Yap and Chen ¹. We choose to use this dataset since it allowed us to compare our model with an established model, and the Yap and Chen dataset is the only one readily available in the literature for comparison. Furthermore, Sorich et al., concluded that SVM were superior to artificial neural networks, and partial least squares discrimination analysis ⁸, placing this method as the gold standard for partitioning methods.

Methods

All computing and programming was done using the 2004.03 release of Chemical Computing Group’s Molecular Operating Environment (MOE) software. Descriptors were calculated using QuaSAR-descriptor using default MOE charges. SVM was done the SVMdark program available at http://www.cs.ucl.ac.uk/staff/M.Sewell/svmdark/SVMdark.exe

Database Selection

Yap and Chen’s database of compounds was selected as a ready-made collection of compounds already classified as inhibitors or noninhibitors ¹. This database is a collection of CYP 2C9, 3A4 and 2D6 substrates and a collection of non-P450 substrates. We used the same training set and external validation set as Yap and Chen as shown in Table 1.

Table 1.

The number of inhibitors and noninhibitors in training and validation set.

Enzyme	Training inhibitors	Training noninhibitors	Validation inhibitors	Validation noninhibitors
3A4	216	386	25	75
2D6	160	442	20	80
2C9	149	453	18	82

Descriptor Selection

In this manuscript the chemical property we are attempting to predict is inhibition (g) with g = 1 denoting an inhibitor and g = −1 denoting a non-inhibitor. Descriptors were selected from ~150 descriptors implemented in MOE; only the 2D descriptors were considered. Using MOE’s QSAR modeler, a least-squares fit to the g values of the training set was constructed. The descriptors that contributed the most to this fit and provided a rational explanation of size, polarizability, and charge were analyzed. A subset of similar descriptors was chosen based on the generality of the descriptor, and our ability to understand the chemical feature underlying the descriptor. Our goal was to describe the overall shape, flat versus round, and the overall surface charge of the molecule given only a two-dimensional representation of the compounds of interest. Table 2 lists the nine descriptors, and a short synopsis (as described in MOE helpfiles) of each chosen for model development. The same descriptor set is used for each dataset, since they are thought to be fundamental descriptors for binding to cytochrome P450 enzymes and also to provide comparisons of performance among the enzymes.

Table 2.

Descriptors used in Developing the Partitioning Models.

Descriptor	Synopsis
vsa_hyd	Approximation to the sum of VDW surface areas of hydrophobic atoms.
vdw_vol	van der Waals volume calculated using a connection table approximation.
apol	Sum of the atomic polarizabilities (including implicit hydrogens) with polarizabilities taken from [CRC 1994].
vdw_area	Area of van der Waals surface calculated using a connection table approximation.
weinerPol	Wiener polarity number: half the sum of all the distance matrix entries with a value of 3 as defined in [Balaban 1979].
PEOE_VSA_NEG	Total negative van der Waals surface area. This is the sum of the vi such that qi is negative1. The vi are calculated using a connection table approximation 2.
zagreb	Zagreb index: the sum of $d_i^2$ over all heavy atoms i.3
SlogP	Log of the octanol/water partition coefficient (including implicit hydrogens).
bpol	Sum of the absolute value of the difference between atomic polarizabilities of all bonded atoms in the molecule (including implicit hydrogens) with polarizabilities taken from [CRC 1994].

¹The variable q_i denotes the partial charge on atom i.

²V_i denotes the accessible van der Waals surface area of atom i calculated from a connection table.

³d_i is defined as the number of heavy atoms to which atom i is bonded.

Consensus Predictions

A single tree is rarely a good predictor of chemical properties, such as inhibition. Several authors have demonstrated the utility of consensus models whereupon a large number of different predictors are generated and then an overall prediction is based upon a simple majority of responses. The strategy is simple enough: An odd number of trees is generated and each is used to predict a chemical property. Whichever chemical property is predicted by the majority of the trees is returned as the consensus prediction.

Evaluation

The Matthews correlation coefficient λ, given by

$$\lambda =\frac{t_{+}{t}_{-}-f_{+}{f}_{-}}{\sqrt{(t_{+}+f_{+})(t_{+}+f_{-})(t_{-}+f_{+})\left(t_{-}+f_{-}\right)}},$$

was used to evaluate a predictor’s accuracy ¹². If the denominator is zero, then either all of the g values are the same or all of the predictions are identical. Neither case is interesting, so this case can be disregarded. In any other case, |λ|≤ 1. It is can be shown that if predictions are made completely by chance, then λ = 0. The case λ = 1 corresponds to a perfect predictor while λ = −1 corresponds to a perfect “anti-predictor”.

In this application, the true positives, t₊, were those g = 1 compounds correctly predicted, true negatives, t₋ were those g = −1 compounds correctly predicted, false positives, f₊, were g = −1 compounds incorrectly predicted, and false negatives, f₋, were g = 1 compounds incorrectly predicted

Theoretical Method Development

Suppose C = {c₁, c₂, …, c_n } is a set of n compounds in a training set and D = {d₁,…, d_m } is a set of m descriptors, thought of as real-valued functions. Define a_ij = d_j(c_i), i.e., the value of the j^th descriptor applied to the i^th compound. Furthermore, suppose there is some property we wish to predict, e.g. inhibition of cytochrome P450 2C9. For each compound c_i, we define g_i = 1 if it has the property and g_i = −1 otherwise.

Map Ranking Scheme

In similar studies, the descriptor values of the training set are often normalized to the interval [-1,1] by scaling and translation, i.e., compound c_i is mapped to the column vector r_i = [r_i1, r_i2,…r_im ]^t, where r_ij = 2(a_ij − a_mean,j) / (a_max,j − a_min,j). Here, a_mean,j represents the mean of a_max,j and a_min,j rather than the mean of all of the a_ij values. Since the distributions of the descriptors are likely to vary considerably, it can be asked whether this will distort the effects of linear algebraic computations to follow. Also, it is unlikely that the collection of compounds will be well-centered at the origin. The following “ranking” scheme is proposed to compensate for these shortcomings. For each descriptor d_j, the compounds are sorted in ascending order of their a_ij values. Rank 1 is assigned to the lowest, rank 2 to the next lowest, etc. until rank n is assigned to the compound with the highest a_ij value. If a group of compounds have the same a_ij value, each compound in the group is assigned the mean of the ranks of the group. For instance, if the four lowest compounds all have the same a_ij value, then each is assigned a rank of 2.5 (the mean of 1, 2, 3, and 4). Finally, the value r_ij is defined as the rank minus (n+ 1)/2; this centers the list of r_ij values at zero. Each compound c_i is then mapped into m-dimensional space as the column vector r_i = [r_i1, r_i2,…r_im ]^t. The origin of this space would represent a compound each of whose a_ij values is the median for the respective descriptor.

Predictions based both on traditional normalization and this ranking scheme are compared in the results section of this paper.

Splitting Planes and Decision Trees

The prediction strategy rests on the ability to separate the entire training set of vectors R = {r₁, r₂,…, r_n} into pieces, depending on their corresponding g_i values. A splitting hyperplane is determined by its normal vector n; the set R is split into two subsets R⁺ = {r_i: n · r_i > 1} and R⁻ = { r_i: n · r_i < 1}. If necessary, the components of n can be perturbed slightly so that R is in fact partitioned into R+ and R⁻, i.e., for no i, is n · r_i = 1. The aim is to choose n so that the sets of g values of the subsets are more “pure” than the set of g values of the original set. More formally, some objective function f is to be maximized over choices of n, where f (n) is determined by the g values of compounds in R⁺ and in R⁻. Suitable choices for f are discussed in the next section.

The same process is repeated on each set R⁺ and R⁻ if need be; a set whose g-values are either all 1’s or all −1’s need not be split further. The result is a “decision tree” whose internal vertices are labeled with the n vector and whose leaves are labeled “−1” and “1” depending on the common g value of the compounds in the corresponding set. To make a prediction of the g value of a test compound, one determines the ranking vector r for the compound in question. To determine each component of r, the following rules are used: If the descriptor value matches the value for a compound in the training set, then the r-value of the test compound is set to that of the training compound. If the descriptor value is between those of two training compounds, then the mean of the r-values of the training compounds is used. Finally, r-values of r_max + 1 or r_min − 1 are used for test compounds whose descriptor values lie above or below the entire set of test compounds’ descriptor values.

To make the actual prediction, beginning with the root node, the scalar product n · r is computed. If the result is less than 1, the left branch is followed. Otherwise, the right branch is followed. This process continues until a leaf is encountered. The label of the leaf is the predicted g value.

Measures of Purity and Success

There are many proposed measures of the “purity” function f. A naïve choice of f(n) would be

$$f\left(\mathbf{n}\right)=|\sum _{c_i\in R^{+}}{g}_i-\sum _{c_i\in R^{-}}{g}_i|.$$

This function measures the extent to which a splitting plane separates the positive g values from the negative g values. Among the drawbacks to this function is that there are situations where the maximum is achieved by not splitting R at all. For instance, this occurs if a single compound with g = −1 is surrounded by compounds with g = 1.

In this study, we use the Matthews coefficient as a measure of purity, where t₊, t₋, f₊, and f₋ are defined by

$$\begin{array}{r}{t}_{+}=\mathrm{the\; number\; of}g=1\mathrm{compounds\; in}{R}^{+},\\ t_{-}=\mathrm{the\; number\; of}g=-1\mathrm{compounds\; in}{R}^{-},\\ f_{+}=\mathrm{the\; number\; of}g=-1\mathrm{compounds\; in}{R}^{+},\mathrm{and}\\ f_{-}=\mathrm{the\; number\; of}g=1\mathrm{compounds\; in}{R}^{-}.\end{array}$$

The effort becomes to find a plane that maximizes |λ| since |λ| = 1 precisely when the plane perfectly splits the set.

The “Line-Walking” (LWRP) Tree-Building Algorithm

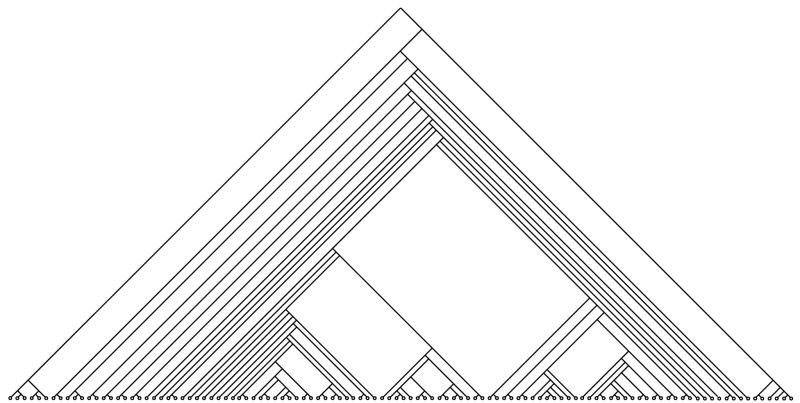
Constructing decision trees based on small (m ≈ 10) descriptor sets involves working in vector spaces of the same number of dimensions as there are descriptors. A strategy used early in this study was to select a large number of unit vectors u (chosen randomly from a uniform distribution over the unit m-sphere.) Then for each u, the value of s that maximized f(su) could be determined in linear time. The best of these su vectors was then set as n. To produce a “reasonable” tree by this method required generating a large number (≈ 10,000) of unit vectors even when m is small. Therefore, trees took a considerable length of time to generate. Even with a large number of vectors, the decision trees that resulted from this strategy tended to be unbalanced and have higher numbers of levels and leaves than desired – the number of potential decisions to make a prediction seemed excessive and many of the leaves corresponded to single compounds (see Figure 1) – and so a new algorithm, called “Line-Walking Recursive Partitioning”, or LWRP to combat these drawbacks was developed.

Figure 1.

2C9 Decision tree produced by random vector selection

Recalling that there are m descriptors being used, the first step in choosing a splitting plane for a set R is to choose vectors {r₁, r₂,…, r_m} from R, at random.

Given an m-element subset R’ = {r₁, r₂,…, r_m} of R, a single iteration of the LWRP algorithm consists of the following steps:

• Compute the vector p such that p · r_i = 1 for all r_i in R’ .

• Choose a value r_k at random from R’.

• Compute the vector q such that q · r_k = 2 and q · r_i = 1 for all i ≠ k.

• Defining L(t) = tq + (1 − t) p, determine for each r_s in R the value t_s such that L(t_s) · r_s = 1. L is the “line” mentioned in the name “line-walking algorithm.”

• Maximize f(L(t_s)) over s. If several values of s maximize f(L(t_s)), choose one at random.

• Replace r_k with r_s in R’. The new vector p is equal to L(t_s), so the next iteration begins at step 2.

There are several possibilities for conditions to halt the algorithm. The halting criterion chosen early in this research was if the maximized value of f remains unchanged for a pre-determined number of consecutive iterations. Later, it was decided to permute the vectors in R’, and adopt each in succession as r_k in step 2 if the maximum value of f remained unchanged. The algorithm halts if all of the vectors in R’ are exhausted in this manner. This condition results in locating a local maximum for f in the sense that no compound in R’ can be substituted resulting in raising the value of f(L(t_s)).

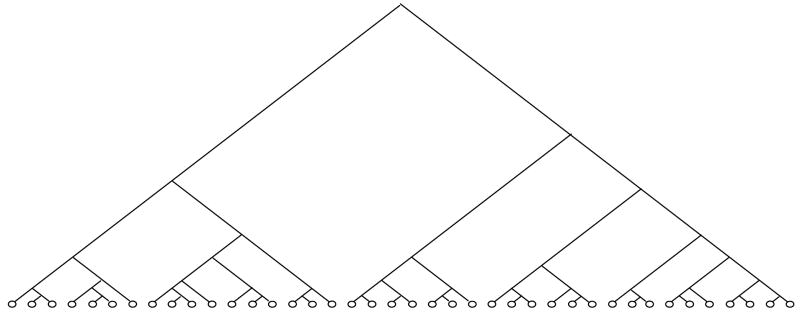
Steps 1 and 3 are the most computationally intensive in the LWRP algorithm as each involves row reducing an m × (m + 1) augmented matrix; standard techniques accomplish this in O(m³) time. Nonetheless, for m ≈ 10, this algorithm generates trees about as quickly as using 10,000 random vectors to generate hyperplanes. Also, the LWRP trees have far fewer leaves and levels than trees produced by random vectors. As illustration, the trees in Figures 1 and 2 were produced from the compounds in the 2C9 training set using the same nine descriptors in Table 2. Each interior node in the tree in Figure 1 represents a hyperplane selected from random vectors while each interior node in the tree in Figure 2 represents a hyperplane selected using LWRP. MOE generated each tree in about 30 seconds. The random-vector tree has 40 levels and 115 leaves while the LWRP tree has eight levels and 39 leaves.

Figure 2.

2C9 decision tree produced by LWRP algorithm

Results and Discussion

Comparison with Yap and Chen

Since of the manuscripts we are aware of, only Yap and Chen provide the data they used in the generation of their model, we decided to validate and compare line walking recursive partitioning with SVM using the Yap and Chen database of 702 compounds. Yap and Chen trained on a 602 molecules, with an external validation set of 100 molecules to predict if a compound would be a substrate for CYP3A4, 2C9 or 2D6. This SVM method used between 200, and 300 descriptors to build the model. Descriptor sets were different for each training set. For 3A4, true binders to the enzyme where predicted 77 % of the time, true noninhibitors 98% of the time, and the overall prediction had a Matthews coefficient of 0.83. For 2C9, true binders to the enzyme where predicted 82 % of the time, true noninhibitors 99% of the time, and the overall prediction had a Matthews coefficient of 0.85. For 2D6, true binders to the enzyme where predicted 79 % of the time, true noninhibitors 99% of the time, and the overall prediction had a Matthews coefficient of 0.83. In contrast, the LWRP method used nine descriptors predicted with about 85-90 % accuracy (concordance) as shown in Table 3.

Table 3.

Prediction of inhibitors and noninhibitors with LWRP method and 9 Descriptors.

	2C9		2D6		3A4
Scheme	Normed	Ranked	Normed	Ranked	Normed	Ranked
Concordance	90.60	90.10	89.20	89.60	85.00	84.80
Specificity	96.95	97.32	96.00	97.00	94.93	95.47
Sensitivity	61.67	57.22	62.00	60.00	55.20	52.80
λ	0.658526	0.633335	0.662455	0.660285	0.570278	0.561880

For each enzyme and scheme, ten forests each consisting of 101 trees were constructed. The data in Table 3 represent the means from these runs. In the table, “Scheme” denotes whether the descriptor values were normalized to the interval [-1,1] or ranked by the ranking scheme detailed above, “Concordance” denotes the percentage of compounds correctly predicted, “Specificity” denotes the percentage of g = −1 compounds correctly predicted, “Sensitivity” denotes the percentage of g = +1 compounds correctly predicted, and λ is the Matthews coefficient.

Overall the models do a good job of predicting inhibitors and non-inhibitors given the nature of the dataset, as described below. The models are very good at predicting noninhibitors with about a 94-97 % success rate. We note that the ranking scheme tends to favor the predominant g = −1 compounds, and the traditional normalizing scheme performs slightly better overall, using Matthews coefficients as a basis for overall comparison. The lowest success is with 3A4, which would be expected since it is very difficult to define what is an inhibitor as a results of the non-Michaelis-Menton nature of this enzyme ^13,14. The 2C9 and 2D6 enzymes have distinct pharmacophores ^{6,15 16} so predicting non-inhibitors might be expect to be more straight-forward. The lower ability to predict binders to each enzyme stems in large part from the training set which is likely to have a number of false negatives, since it is assumed that a compounds that are not reported as inhibitors are not inhibitors (see below for more details). Since Ki or IC50 values have only been reported for some compounds that are substrates, and all substrates are competive inhibitors most certainly this assumption is not 100% valid. Given the nature of the problem it is therefore difficult to know what is not an inhibitor of any of these enzymes.

Of the two different descriptor scaling schemes, map ranking and normalization, no clear-cut winner could be determined. However, we believe that normalization could lead to potential problems when considering unique compounds that have descriptors values outside the range of the training set. For example, if a new compound is evaluated and found to have a normalized value of 2, relative to the training set values, this has the potential to dominate the prediction. However, the map ranking method would still give this compound a descriptor value very close to the highest value in the training set. We hypothesize that when more diverse structures are encountered, that the map ranking scheme will provide a more robust model. Given that our goal is to move toward a more extensive method we plan on testing this hypothesis on new more diverse structures in the future.

The main difference between LWRP as implemented in this paper, and other reported methods such as simple recursive partitioning and SVM methods, is the LWRP can perform at a similar level with significantly fewer descriptors. All other reports in the literature that distinguish between inhibitors of different P450 enzymes use a large number of descriptors to develop a significant model. Most use between 20-60 descriptors per 100 molecules in the training set. The approach presented here provides a less perfect solution for the training set, but only uses about 1 descriptor per 100 molecules in the training set. Using a large number of descriptors, while providing a better description of the training set, means that only molecules related to those in the training set can be accurately predicted. In fact the training set, and external validation set of Yap and Chen were chosen such that they shared a common chemical space based on the descriptors that were used in the model such that “…compounds of similar structural and chemical features were evenly assigned into separate datasets” ¹. Arimoto et al., ¹⁷ came to the same conclusion when comparing models for 3A4 inhibition. They used molecular fingerprints to determine that their models only did well when predicting the affinity of compounds related to those in the training set. We believe that the minimum basis set LWRP implemented here should provide more extensible results, since it uses a small number of descriptors.

As additional support for the claim of extensibility, we used MOE to perform a principal component analysis of the 2C9 database using the 9 descriptors presented in Table 2. This analysis enabled us to visualize which compounds in the validation set were “distant” from other compounds and of these, which were correctly predicted to be inhibitors or non-inhibitors. Each of the principal components was scaled and translated to have mean 0 and variance 1. Of the validation compounds that were correctly predicted to be inhibitors, stiripentol is the most striking as the ten database compounds (taken from the training set) nearest to it in principal component space were all non-inhibitors. No other correctly predicted validation set inhibitor had more than six out of ten nearest neighbors that were non-inhibitors; carbamazepine and norfluoxetine were the only others to have six. Turning to correctly predicted non-inhibitors, aranidipine, nilutamide and pimobendan each had six inhibitors among the ten nearest neighbors while domperidone and trifluoperazine each had five. This indicates that the nearest neighbors are not dominant in the predictions.

Choice of descriptors/ independence of specific descriptors

The descriptors in Table 2 were chosen from the available MOE descriptors to provide information about the size, shape, and charge distribution of each molecule. In general it is believed that the three major P450 enzyme involved in drug metabolism cover the chemical space of drug-like-molecules in that both 2D6 and 2C9 metabolize medium sized, rounder molecules, while very large molecules are metabolized by 3A4. Most drug molecules exceed 200 Daltons for their molecular weight, while molecules smaller than that, such as inhalation anesthetics, are metabolized by CYP2E1. CYPs 2D6 and 2C9 further discriminate based on charge, with 2C9 binding negative charges, and 2D6 binding positive charges. Our descriptors selection is meant to encompass these features. Unlike others models which optimize the descriptors based on the training set for each enzyme we used the same descriptors for each of the three enzymes. This should be better for filtering a large dataset into each bin to classify a compound as a 3A4, 2C9, or 2D6 inhibitor.

Another advantage of the LWRP minimum basis set model is that it allows us to understand which features are important in determining binding for a given molecule. This has the obvious advantage of allowing the medicinal chemist the ability to rationally redesign a molecule to either bind, or not bind to a given P450. Models with many descriptors rely on an iterative approach, in which a structure is proposed and tested with the model, and the features that influence differential binding are not apparent. We can determine the major features important in placing a given molecule in a bin for inhibitor, or non-inhibitors. For example, the major determinants of a compound being a 2C9 substrate are vsa_hyd, and PEOE_VSA_NEG which describe hydrophobic surface area and negative charge on the surface of the molecule. This fits with the expectations based on a hydrophobic binding site, ¹⁸ and a site that interacts with a negative charge on the inhibitor¹⁵. We are exploring methods for labeling trees based on the major descriptors used in the decision. This should allow for us to understand why related molecules are either inhibitor or noninhibitors.

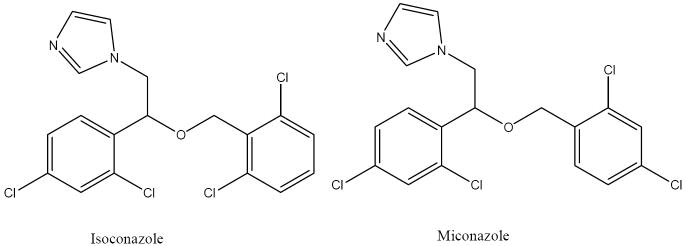
The nature of the Yap and Chen database needs to be considered when assessing the quality of the predictions. The dataset was constructed from literature data for inhibition. Any compound that exhibits inhibition, no matter how strong, is considered an inhibitor. Noninhibitors are compound taken from “…well-studied agents that are known inhibitors/substrates/agonists of proteins other than that enzyme..” and assumes that because an agent has been well-studied and not reported to be an inhibitor of a P450, it is not an inhibitor. These are reasonable assumptions but obviously some exceptions will exist. Thus, very high predictive capabilities for this dataset is not to be expected, and in fact the error in the training set of inhibitor and noninhibitors is likely to be over 20 %. One example is isoconazole, an antifungal agent closely related to a number of imidazole based inhibitors (such as miconazole shown in Scheme 1) of mammalian P450 enzymes which function by inhibiting fungal P450 enzymes. This compound has not been reported to be a 3A4, 2D6, or 2C9 inhibitor, but is always predicted by our models to be an inhibitor. In fact this molecule inhibits mammalian aromatase, a P450 ¹⁹, but has not been tested for 3A4, 2D6 or 2C9 inhibition since it is administered topically. Thus, predicting this to be a noninhibitor is almost certainly incorrect. If it is assumed to be an inhibitor our success rate is increased by 4 to 8 %.

Scheme 1.

Miconazole is a potent inhibitor of 2C9 while isoconazole is not reported to be an inhibitor.

Another obvious problem with the 3A4 dataset is that Yap and Chen report 312 compounds in the set to be substrates, and only 216 to be inhibitors. Since by definition all substrates for a given P450 are competitive inhibitors this indicates that at least 16 % of the noninhibitors are incorrectly labeled. This is most likely true for 2C9 and 2D6 as well. Thus, given the difficulties in defining what is or is not and inhibitor our success rates are very good. Obviously, a better goal is to predict potential tight binding compounds for each enzyme. In fact we have postulated in the past that only compounds that have Ki values lower than 10 uM are likely to be important physiological inhibitors ²⁰. Thus, we are working on constructed datasets that define inhibitors by this more restrictive methodology, and we will use these new training sets to develop models.

One indication of a robust model is when it tells you about incorrect data in the dataset. To see if we found any difficulties in the test set we looked at 2C9 inhibitor/noninhibitors that are predicted incorrectly by at least 5 out 7 of the forests. The compounds that gave false positive at least 5 out of 7 times were clonazepam and isoconazole. As described above isoconazole is a terminal imidazole compound structurally related to miconazole a potent 2C9 inhibitor (Scheme 1) ²¹ and is most likely an inhibitor of 2C9. It has not been tested as such, because this compound is used topically. The compounds that gave false negatives 5 out of 7 times were lopinavir, lornoxicam, pioglitazone, sulconazole, sulfadiazine, sulfatroxazole. Of these lopinavir has been reported to “…produce negligible inhibition of 2C9 ²², pioglitazone is a weak inhibitor of the *2 allylic variant not the native enzyme ²³, sulconazole was found to have an incorrect structure which when fixed put it in the correct inhibitor category, sulfadazine is only a weak inhibitor ²⁴, and we cannot find any reference to sulfatrazole being an inhibitor of 2C9 on Medline or the Web of Science. Given these observations two things become apparent; 1) that it is difficult to construct and accurate large dataset from the literature, and 2) that the LWRP model was able to find errors in the dataset. We reran the predictions making the corrections, and the results are shown in Table 4. Our predictive capacity was significantly increased by all measures. Given this “more correct” testing set we are able to match, using 9 descriptors, the predictive capacity of a method that use 20-30 times the number of descriptors.

Table 4.

Predictive Capacity with Repaired 2C9 Dataset

	2C9 With Compounds Reclassified
Scheme	Normed	Ranked
Concordance	95.60	95.10
Specificity	98.24	98.59
Sensitivity	80.67	75.33
λ	0.82	0.81

Terms are defined in Table 3.

However, if we repeat the same exercise for 2D6 we find that 5 compounds are predicted to be false negatives; benidipine, biperiden, manidipine, norfluoxetene, and propafenone but all of these compounds appear to be correctly reported in the database. We do not know if this reflects a problem with our 2D6 model, or that the dataset is better for 2D6 than for 2C9. Given the problems constructing a good dataset for 3A4, this exercise was not done for the 3A4 dataset.

As suggested by an anonymous reviewer we used the same descriptors and an SVM program (SVMdark), to see if a good choice of descriptors was responsible for our results. A number of different models were tried with representative results for 2C9 giving a Matthews coefficient of -0.17, a concordance value of 50%, a specificity of 56% and a sensitivity of 22%. While these poor results are not surprising results since SVM ideally would use many more descriptors for this problem, it does illustrate that LWRP is a more efficient method for partitioning these molecules, and that the choice of descriptors is not the major reason for the LWRP method’s success.

As another contrasting experiment, we used MOE’s prepackaged binary tree prediction software to generate binary prediction trees. Each decision node of these MOE trees represents a decision point based on a single variable, e.g., whether the value of the descriptor ‘SlogP’ is above 3.15. Using the same Yap and Chen 2C9 training set, the resulting single-variable prediction trees that were produced had significantly more nodes than trees produced by LWRP. Furthermore, consensus predictions based on LWRP trees consistently had higher Matthews coefficients than those based on single-variable trees. Table 5 summarizes results from these experiments.

Table 5.

Comparison of prediction results from various algorithms.

Algorithm	Mean # of Nodes	Mean Depth	Concordance	Specificity	Sensitivity	λ
LWRP	45.2	7.2	90.4	97.6	55.3	0.624572
Single-variable	144.3	9.5	81.2	87.0	54.4	0.393022
SVM	N/A	N/A	50.0	56.0	22.0	-0.17

In conclusion, we have developed a new method, line-walking-recursive-partitioning, which uses a minimum basis set to predict if a molecule is an inhibitor, or not, for a given P450 enzyme. Given the nature of the dataset used, the prediction are reasonable accurate. It compares favorably with the SVM models of Yap and Chen ¹, using 1/10 to 1/20 the number of descriptors while having the potential for guiding drug design efforts. This is a general method that should allow for the use of a small basis set for partitioning molecules of diverse structure.