Modeling motor connectivity using TMS/PET and structural equation modeling

Abstract

Structural equation modeling (SEM) was applied to positron emission tomographic (PET) images acquired during transcranial magnetic stimulation (TMS) of the primary motor cortex (M1_hand). TMS was applied across a range of intensities, and responses both at the stimulation site and remotely connected brain regions covaried with stimulus intensity. Regions of interest (ROIs) were identified through an activation likelihood estimation (ALE) meta-analysis of TMS studies. That these ROIs represented the network engaged by motor planning and execution was confirmed by an ALE meta-analysis of finger movement studies. Rather than postulate connections in the form of an a priori model (confirmatory approach), effective connectivity models were developed using a model-generating strategy based on improving tentatively specified models. This strategy exploited the experimentally-imposed causal relations: (1) that response variations were caused by stimulation variations, (2) that stimulation was unidirectionally applied to the M1_hand region, and (3) that remote effects must be caused, either directly or indirectly, by the M1_hand excitation. The path model thus derived exhibited an exceptional level of goodness (χ²=22.150, df = 38, P = 0.981, TLI=1.0). The regions and connections derived were in good agreement with the known anatomy of the human and primate motor system. The model-generating SEM strategy thus proved highly effective and successfully identified a complex set of causal relationships of motor connectivity.

INTRODUCTION

Structural equation modeling (SEM) is a powerful, general purpose tool for statistical analysis and modeling of interactions between observed and unobserved (latent) variables (Schumacker and Lomax, 2004), with the typical goal of testing causal relationships among variables. In the field of brain imaging, SEM can be used to model distributed neural systems composed of multiple regions, with these regions being modeled as observed variables and the neural pathways connecting them being modeled as causal relationships (i.e., inter-regional covariances) (McIntosh et al., 1994a; McIntosh et al., 1994b). Because covariance analyses result in bidirectional paths, a substantial challenge for SEM in neuroimaging is to reduce these to unidirectional paths. The most common strategy is hypothesis-based, in which optional paths are constrained with a priori information, typically from anatomical or functional connectivity studies in human or non-human species. However, it is often difficult to defend the assumptions made when constructing these hypothesis-based models. Moreover, the number and location of regions in the network needs to be established such that critical nodes are not omitted, while at the same time excluding regions of no relevance. This is critical given that SEM procedures mandate a limited number of regions of interest; thus, the selection of ROIs can be open to experimenter bias. A further challenge is that once the regions are selected, restrictions must be made on the paths connecting those regions. Testing a model in which every region is bidirectionally connected to every other region, known as the saturated model (Schumacher and Lomax, 2004), is not a viable option unless the model contains a very small number of regions. The goal of SEM in any context is to achieve a parsimonious model (i.e., one with few path tracings), yet one that also exhibits an increase in evaluating the adequacy (e.g., goodness) of the model. It must be determined which connections should be omitted in the saturated model, then if the remaining connections are bidirectional or unidirectional.

Recent studies have attempted to address these questions by developing methods to constrain starting models prior to SEM (Patel et al., 2006; Zheng et al., 2006). The purpose of these methods is to analyze the structure of the data in order to determine strong relationships that can later be modeled using SEM in a confirmatory approach. However, SEM theory provides an alternate way of analyzing covariance structure between variables, one that specifies tentative models that best fit the given data (Hershberger et al., 2003). Exploratory SEM methods have been utilized in previous studies investigating bimanual coordination (Zhuang et al., 2005), tactile shape perception (Peltier et al., 2007), and to some extent, semantic decision-making with covert articulation (Bullmore et al., 2000). These studies restricted their analyses to a very small number of brain regions and/or imposed initial constraints on various possible paths. Here, the goal was to investigate the applicability of exploratory structural equation modeling in positron emission tomography (PET) data during transcranial magnetic stimulation (TMS) with a large number of neural regions and no assumed constraints of the initial model.

TMS has been used in conjunction with imaging methods such as PET (Fox et al., 1997; Paus et al., 1997) and functional magnetic resonance imaging (fMRI) (Bohning et al., 1997), as well as event-related potentials (ERP) (Ilmoniemi et al., 1997). TMS can be applied to a discrete cortical site and propagates orthodromically from that site, resulting in detectable changes in cerebral blood flow of the entire network of connected regions (Fox et al., 1997). This basic principle can be applied to SEM to generate unidirectional starting paths from which to model, which is the strategy used in this study. This novel strategy is possible due to the ability to draw a known starting path based on the given experimental design, an exclusive property of applying SEM to TMS/PET data. By their nature, functional imaging tasks in which activations are derived from various perceptual, motor, or cognitive events do not fall into this same category of design. In these tasks, the entire neural network is activated as a whole and the starting point of stimulation of the network can only be derived hypothetically. Thus, TMS is unique since a discrete cortical area of interest is directly stimulated and the delivered signal propagates throughout the connected network of interest.

In this study, path analysis, a form of SEM involving only observed variables, was used to model the connectivity of the TMS-stimulated hand region of the left primary motor cortex (LMI_hand) in seven subjects. To reduce bias and minimize assumptions, regions in the LMI_hand TMS network of these subjects were restricted to those identified with activation likelihood estimation (ALE) meta-analysis of the TMS literature (Turkeltaub et al., 2002; Laird et al., 2005a). For each subject, TMS was delivered in a graded manner, resulting in graded responses both at the stimulation site and beyond. Thus, parametric intensity stimulation of the LMI_hand site occurred, ranging from above to below subjects’ individual motor thresholds. This experimental design allowed for an SEM analysis that included: (1) the stimuli itself as a quantitative variable and, (2) a known starting point for exploratory modeling of the system as a whole.

METHODS

Subjects

Seven healthy, right-handed volunteers were included in this study (4 women, 3 men; mean age = 35 years; standard deviation = 11.34 years; age range = 22-43 years). All subjects gave their written, informed consent in accordance with the Declaration of Helsinki and with approval from the Institutional Review Board and Radiation Safety Committee of the University of Texas Health Science Center at San Antonio. All subjects were healthy (no medical, neurological, or psychiatric illnesses) and taking no medications. The use of TMS at 3 Hz was approved by the United States Food and Drug Administration (IDE K905059D, held by Peter Fox). The data acquired in these 7 subjects were used in prior publications (Fox et al., 2004; Fox et al., 2006), and consisted of subjects representing the group of “cortical responders”. This designation indicated that significant PET activation during TMS was observed in these subjects. Four other subjects were omitted from the present analysis, as no significant PET activation was observed in this data, despite the presence of physiological evidence of stimulation.

TMS/PET Procedures

TMS was delivered at 3 Hz via a robotic, image-guided system (Lancaster et al., 2004) to LMI_hand. TMS was delivered with a water-cooled, B-shaped coil (Cadwell, Kennewick, WA). The coil was powered by a Cadwell HSMS unit, which delivers a triphasic electric pulse with a total duration of 240 μs and a peak E-field of 435 volts/meter at the coil surface at 100% of machine output. Motor thresholds were determined prior to imaging as described in Fox et al. (1997). During PET, each subject underwent two trials of TMS at 3 intensities relative to motor threshold (75% MT, 100% MT, and 125% MT), delivered in a pseudo-randomized order (6 stimulated scans per subject). TMS commenced 120 s prior to tracer injection and continued through the first 40 s of a 90-s image acquisition. In addition, subjects were also imaged during two trials of rest (0% MT).

PET image acquisition was performed using a General Electric (Milwaukee, WI) 4096 whole-body camera (pixel spacing = 2mm, spatial resolution = 6.5mm FWHM in the axial plane, inter-plane center-to-center distance = 6.5mm, scan planes = 15, z-axis FOV = 10.cm). Brain blood flow was measured using H₂¹⁵O, administered as an intravenous bolus of 8-10 ml saline containing 50-70 mCi per injection, tailored to obtain satisfactory coincidence detection rates. Ninety seconds of data were acquired, triggered by the tracer entering the brain. Throughout the PET session the subjects’ heads were immobilized with an individually fitted, thermoplastic facial mask (Fox et al., 1984). To minimize auditory activation due to the sound emitted by the TMS, foam earplugs were worn throughout the imaging study. Electromyographic (EMG) recordings were monitored throughout the period of TMS delivery to ensure effective stimulus delivery. Anatomical MRI was acquired in each subject and used to optimize spatial normalization. MR imaging was performed on a 1.9 T GE/Elscint Prestige (Haifa, Israel) at a voxel size of 1mm³.

Image Pre-Processing

Images were reconstructed into 60 slices (2mm thickness), with an image matrix size of 60×128×128, using a 5mm Hanning filter resulting in images with a spatial resolution of approximately 7mm (FWHM). PET images were value-normalized to a whole-brain mean of 1000. PET and MRI data were co-registered using the Convex Hull algorithm (Lancaster et al., 1999). MRI data were spatially normalized in series using both the Spatial Normalization (SN) (Lancaster et al., 1995) and Octree SN (OSN) algorithms (Kochunov et al., 1999). The SN algorithm performed “global” (nine-parameter) spatial normalization, which registered each subject to the target shape provided by the Talairach and Tournoux (1988) atlas. The OSN algorithm performed “local” spatial normalization, in which each subject's brain was anatomically deformed to match the median of the group in a high-resolution (1mm³), fully 3D-manner. OSN processing was used to optimize registration of anatomical features (and thereby functional areas) across subjects. OSN-derived deformation fields were applied to the PET data prior to computation of statistical parametric images (SPIs).

ALE Meta-Analysis

LMI_hand TMS Literature Search

An aim of this study was to develop more standardized, less user-dependent methods of ROI selection prior to SEM analyses. As an alternative to the highly variable methods currently observed in the neuroimaging literature, the ROI selection procedure was guided by a quantitative, voxel-based meta-analysis of TMS studies. A PubMed literature search was carried out to identify all studies published prior to June 2006 in which repetitive TMS (rTMS) was used to stimulate the left primary motor cortex during fMRI or PET (H₂¹⁵O or ¹⁸FDG) imaging. The search results were filtered to eliminate studies that lacked whole-brain results in the form of stereotactic (x,y,z) coordinates, which did not apply TMS concurrently with tracer uptake (PET) or with imaging (fMRI), and which had fewer than five subjects. Studies were also excluded if they reported only individual subject data, data from non-normal subjects, or decreases in signal due to TMS. This filtering of the PubMed search results yielded 6 contrasts and 53 foci from 5 rTMS papers in which LMI_hand was stimulated (Bestmann et al., 2004; Denslow et al., 2005; Siebner et al., 1999; Siebner et al., 2000; Speer et al., 2003). This final set of 5 papers varied by the intensity and frequency of TMS and the data analysis procedures (Table 1). Image acquisition and TMS were simultaneous in three studies (Bestmann et al., 2004; Denslow et al., 2005; Speer et al., 2003). This was not the case for two PET studies (Siebner et al., 1999; Siebner et al., 2000), but they were not excluded since TMS was simultaneous with uptake of the tracer. Generally, meta-analytic procedure dictates that ROI analyses be excluded; however, in the case of LMI_hand TMS studies, this limitation would restrict the total pool of studies to only two (Bestmann et al., 2004; Denslow et al., 2005). Thus, a heterogeneous mixture of whole-brain analyses (Bestmann et al., 2004; Denslow et al., 2005), ROI analyses (Siebner et al., 1999; Siebner et al., 2000), and correlation analyses (Speer et al., 2003) were included in the meta-analysis.

Table 1. Input Data for ALE Meta-Analysis of LMI_hand TMS Studies.

5 papers with 6 contrasts and 53 foci were included in the TMS meta-analysis (listed in alphabetical order by first author).

Author	n	Contrast	Intensity (% MT)	Frequency (Hz)	Modality
Bestmann	12	Suprathreshold rTMS – Rest	110%	3.125	3T MRI
Bestmann	12	Subthreshold rTMS – Rest	90%	3.125	3T MRI
Denslow	11	TMS vs. Rest, Increases	110%	1.0	1.5T MRI
Siebner, 1999	12	rTMS vs. Rest	140%	2.0	18FDG PET
Siebner, 2000	8	Post-rTMS vs. Rest	“just below” 100%	5.0	18FDG PET
Speer	10	Positive Correlations	80%-120%	1.0	H215O PET

n = number of subjects included in a given study; Intensity % MT = intensity at which TMS was delivered relative to each individual's relative percent of motor threshold.

Voluntary Movement Literature Search

To compare the LMI_hand TMS meta-analysis network to the network for overt, voluntary hand movement, an ALE meta-analysis of finger-tapping studies was performed. PubMed was searched for all studies in which right-handed finger tapping of simple sequences was imaged using fMRI or PET. Again, the pool of studies was restricted to include only those studies that published their results in the form of stereotactic (x,y,z) coordinates. Studies were additionally excluded in the usual fashion if they reported only individual subject data, data from non-normal subjects, deactivations, or ROI analyses. In contrast to the TMS meta-analysis, this last restriction was made possible by the fact that the finger-tapping task has frequently been employed in functional neuroimaging, thus yielding an extremely rich body of literature. Contrasts were isolated in which right-handed subjects performed simple tapping of either all of the fingers on the right hand, or the index or ring finger alone, was compared to rest (i.e., Tapping vs. Rest). The literature search and resultant filtering yielded 16 papers, 20 contrasts, and 204 foci (Table 2).

Table 2. Input Data for ALE Meta-Analysis of Finger Tapping Studies.

16 papers with 20 contrasts and 204 foci were included in the finger tapping (overt movement) meta-analysis (listed in alphabetical order by first author).

Author	n	Contrast	Modality
Aoki	10	Index Finger – Rest	PET
Aoki	10	Ring Finger – Rest	PET
Aoki	10	Double Finger Tapping – Rest	PET
Blinkenberg	8	Finger Tapping vs. Rest	PET
Calautti	7	Right Hand Tapping vs. Rest, Young Adults	PET
Catalan	13	Sequence 16 vs. Rest, Controls	PET
Denslow	11	Volitional Movement	fMRI
Gelnar	8	Motor vs. Rest	fMRI
Joliot, 1998	5	Finger Tapping – Rest	PET
Joliot, 1999	8	Finger Tapping, PET	PET
Joliot, 1999	8	Finger Tapping, fMRI (Average)	fMRI
Kawashima	6	Increased Movement, All Movements Compared to Rest	PET
Lehericy	12	Simple – Rest	fMRI
Lehericy	12	Scale – Rest	fMRI
Lerner	10	Tapping – Rest, Normals	PET
Mattay	8	Dominant Hand Simple Motor	fMRI
Riecker	10	Main Effects During Index Finger Movements, Young Adults	fMRI
Rounis	16	Main Effects of Movement	PET
Sadato	9	Right Unimanual vs. Rest	PET
Yoo	10	Group-Level Finger Tapping Activation	fMRI

n = number of subjects included in a given study.

ALE Meta-Analysis Procedure

ALE was performed in the BrainMap environment (Fox and Lancaster, 2002; Laird et al., 2005b). Upon insertion into the database, foci flagged as belonging to MNI space were automatically converted to Talairach space using the icbm2tal algorithm (Lancaster et al., 2007), which has shown to provide improved fit over the mni2tal transform (Brett, 1999). Each included foci was blurred with a FWHM of 12mm. The ALE statistic was computed for every voxel in the brain according to the algorithm developed by Turkeltaub et al. (2002). A permutation test that included 5000 permutations was performed to determine the statistical significance of the ALE results and those results were thresholded at P < 0.05, FDR-corrected (Laird et al., 2005a). ALE results were output to image format and overlaid onto a Talairach template (Kochunov et al., 2002).

Structural Equation Modeling

The locations of the regions of interest (ROIs) selected for inclusion in the structural equation model of TMS/PET data were taken directly from the results of the ALE meta-analysis of the TMS literature. Averaged normalized PET counts were extracted in each ROI from cubic volumes of 125 mm³ in the TMS/PET data. These data were input to Amos 7.0 (Arbuckle, 2006a) for SEM analysis. Each ROI was modeled as an observed variable, while TMS intensity was modeled as a separate observed variable directly modulating the stimulated site (Fox et al., 2006). The values of this intensity variable were 0 (representing the Rest condition), 3 (representing the condition in which TMS was applied at 75% of the motor threshold (MT)), 4 (representing the 100% MT condition), and 5 (representing the 125% MT condition). Error terms on each ROI were modeled as unknown, exogenous variables and the regression weights of these error terms were set to a value of 1.

Model Generating Specification Searches

The model-generating path analysis procedure began with a unidirectional input path (i.e., using an “instrumental variable” strategy as defined in Appendix A) that linked the TMS intensity variable to the left primary motor cortex (LMI_hand) variable (site of stimulation). From this single path, it was hypothesized that stimulation from LMI_hand would propagate to one or more of the other ROIs. Based on this reasoning, 10 unidirectional output paths were drawn from LMI_hand to all of the other brain regions. These paths were tested to identify the node or nodes of propagation using model-generating specification searches, allowing for multiple candidate models to be simultaneously tested using optional unidirectional path loadings to determine the most appropriate choice based on fit, parsimony, and interpretability (Arbuckle, 2006b). The path from the intensity variable to LMI_hand was set as a required path; all other paths originating from LMI_hand were set as optional. The optional paths were combined in various permutations to form the candidate models, thereby allowing for the assessment of which collection of path tracings produced the model exhibiting the highest degree of validity or goodness relative to the given data.

Two different types of specification searches were utilized: all subsets and stepwise. The preferred type of search was all subsets since this option tests all possible combinations of optional paths. In cases of large numbers of optional paths, a stepwise specification search was chosen to reduce computational time by using a combined forward and backward heuristic search strategy. During a forward specification search, the model with no optional paths is fitted first, then optional paths are added one at a time to determine which path provides the largest reduction in discrepancy between the candidate model and the given data. In a backward specification search, all optional paths are initially tested, then removed one by one. The stepwise search alternates these two search strategies (beginning with a forward search), and records the best one-optional-path model, two-optional-path model, etc. The search continues by adding or subtracting optional paths a forward and a backward search is completed with no improvement in model fit (Arbuckle, 2006b).

Model Fit Statistics

All specified models of signal output from LMI_hand were tested and compared. The model with the lowest Bayes information criterion (BIC) and Browne-Cudeck criterion (zero-scale) (BCC) values was selected as the model that represented the optimal model relative to the actual data. The BIC is defined as:

$$BIC=\widehat{C}+q\ln \left(N^{\left(1\right)}{p}^{\left(1\right)}\right),$$ [Equation 1]

where Ĉ is the minimum value of the discrepancy function, q is the number of parameters, N⁽¹⁾ is the number of observations in group 1, and p⁽¹⁾ is the number of observed variables in group 1. The BCC is defined as:

$$BCC=\widehat{C}+2q\frac{\sum _{g=1}^G{b}^{\left(g\right)}\frac{p^{\left(g\right)}(p^{\left(g\right)}+3)}{N^{\left(g\right)}-p^{\left(g\right)}-2}}{\sum _{g=1}^G{p}^{\left(g\right)}(p^{\left(g\right)}+3)},$$ [Equation 2]

where G is the number of groups, p^(g) is the number of observed variables in group g, and $b^{\left(g\right)}=n\frac{N^{\left(g\right)}}{N}$, where N^(g) equals the number of observations in group g and N equals the total number of observations in all groups combined. The BIC and BCC are predictive fit indices that are used to select among competing models that are fit to the same data, and provide information regarding comparative model fit and model complexity. That is, the BIC and BCC reflect a trade-off between the fit of a model and the effective number of parameters in the model. The BIC and BCC statistics were chosen as the ranking criteria over another possible relative-fit measure, the Akaike information criterion (AIC), since the AIC is not based on a strictly Bayesian approach and therefore is not viewed with as much reliability or accuracy as the BCC or BIC (Raftery, 1993; Arbuckle, 2006b). Selection of the model corresponding to the lowest BIC and BCC values identified the model that contained the next level of nodes in the network following LMI_hand stimulation. If the lowest BCC and BIC values specified different models, greater weight was given to the BCC criterion since the BIC imposes a greater penalty for model complexity than does the BIC. This reasoning is a conservative choice that was made when considering the large degree of complexity of the modeled system.

Selection of the model corresponding to the lowest BCC and BIC identified the model that contained the next level of nodes in the network following LMI_hand stimulation. From those second-level nodes, the next stage of the analysis proceeded and optional paths were drawn to all other regions in the network. This method of signal tracking and model testing to determine the path outputs from all subsequent nodes continued until no further paths were suggested via specification search.

While the BIC and BCC indices are appropriate when comparing candidate models during the model-generating procedure, once the final model was selected, it was necessary to evaluate the goodness of this model using appropriate measures of absolute and relative fit. Assessment of model fit is not a simple process, and there exists no definitive way to assess how well a model represents an actual data matrix (Bollen, 1989). In fact, there is no single statistical test that can be performed in order to identify that a given model is the correct model (Schumacker and Lomax, 2004). Therefore, a large number of descriptive statistics have been developed to aid researchers in evaluating the adequacy or goodness of model relative to a given data (covariance) matrix. In fact, multiple models can simultaneously fit the data equally well. Thus, the final model was evaluated using a number of descriptive fit statistics. To examine overall model adequacy, the likelihood ratio chi-square (χ²) statistic was used to test whether the discrepancy between the implied versus actual covariance matrix was for statistically different (Price, et al. 2002). Theoretical models that fit the given data perfectly have a chi-square value of zero. Thus, it is desirable to achieve a non-significant chi-square value, since a high P value indicates that the tested model cannot be refuted. Another global fit measure was computed, known as the root mean square error of approximation (RMSEA) and its associated 90^th percentile confidence interval (90% CI_RMSEA). Obtaining an RMSEA value of less than 0.05 indicates a good model fit. Lastly, the comparative fit index (CFI) and Tucker-Lewis index (TLI) (relative fit indices) were computed, both of which range from values of 0 (no fit) to 1 (perfect fit), with values of 0.95 or greater indicating a good model fit (Schumacker and Lomax, 2004).

RESULTS

ALE Meta-Analysis

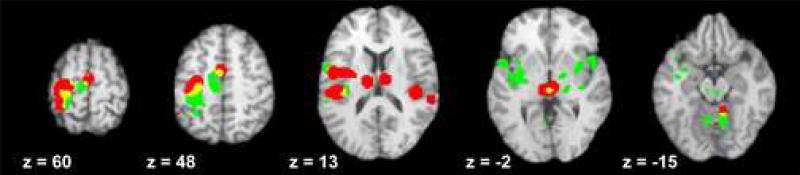
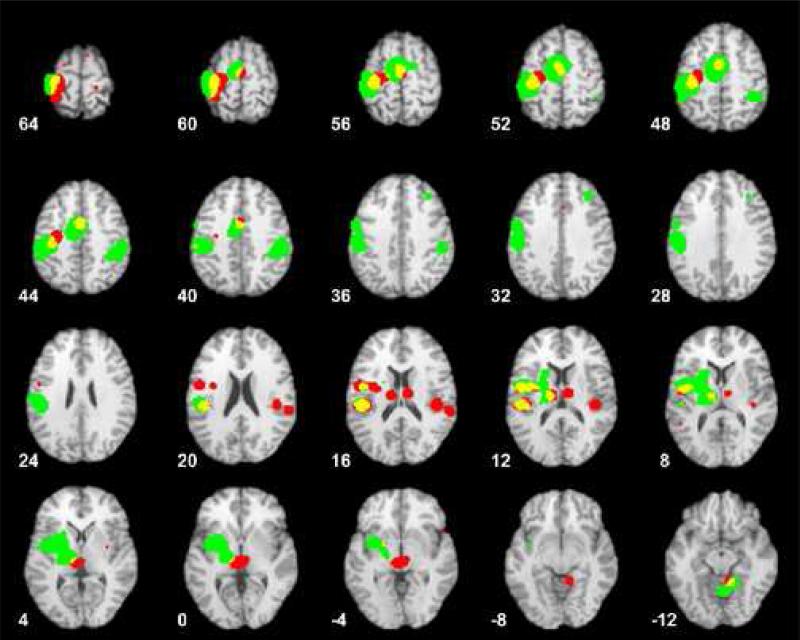
ALE meta-analysis of the TMS literature yielded 11 ROIs: the hand region of the left primary sensorimotor cortex (LMI_hand), left posterior parietal cortex (LPPC), left ventral premotor cortex (LPMv), left and right secondary somatosensory cortex (LSII and RSII), left and right ventral lateral nucleus of the thalamus (LTHvl and RTHvl), left ventral posterolateral nucleus of the thalamus (LTHvpl), bilateral supplementary motor area (SMA), bilateral cingulate (Cing), and right cerebellum (RCer) (Table 3). To confirm that the TMS meta-analysis yielded reasonable results, the TMS ALE maps were compared to two images: (1) the activation map for the 125% MT – Rest contrast in the TMS/PET data and (2) the ALE results of the overt movement (finger tapping) meta-analysis. Figure 1 shows the agreement between the TMS meta-analysis of the literature and the suprathreshold activation results in the experimental TMS data. Overlap of the TMS meta-analysis and activation in the 7 TMS subjects was observed in 8 of the 11 meta-analysis ROIs: LMI_hand, LPPC, SMA, Cing, LPMv, LSII, LTHvpl, and RCer. No overlap was observed between bilateral thalamus (RTHvl and LTHvl) and right secondary somatosensory cortex (RSII). Figure 2 shows the agreement between the TMS and finger tapping meta-analyses (Table 4). Overlap between the two meta-analyses was seen in 8 of the 11 TMS ROIs: LMI_hand, LPPC, SMA, Cing, LPMv, LSII, LTHvl, and RCer. No overlap was observed in the right ventral lateral nucleus of the thalamus (RTHvl), right secondary somatosensory cortex (RSII), and left ventral posterolateral nucleus of the thalamus (LTHvpl). We judge these overlap data as reasonable confirmation of the ROI selection method presented here.

Table 3. Results of the TMS Meta-Analysis.

11 ROIs were returned by the ALE meta-analysis of published studies that investigated TMS of left primary motor cortex in normal subjects.

Region of Interest (ROI)	BA	x	y	z	ALE	mm3
Left primary sensorimotor cortex (LMIhand)	4,3	-30	-22	50	0.0100	9208
Left posterior parietal cortex (LPPC)	5	-30	-42	62	0.0061	s.c.
Left ventral posterolateral nucleus of the thalamus (LTHvpl)	–	-4	-26	0	0.0085	3944
Left ventral lateral nucleus of the thalamus (LTHvl)	–	-11	-16	14	0.0075	s.c.
Left ventral premotor area (LPMv)	6	-50	-4	18	0.0074	3576
Cingulate gyrus (Cing)	24	0	-2	44	0.0067	3024
Supplementary motor area (SMA)	6	0	-14	58	0.0065	s.c.
Right secondary somatosensory cortex (RSII)	40	42	-28	14	0.0071	2672
Left secondary somatosensory cortex (LSII)	40	-42	-28	16	0.0091	2552
Right ventrolateral thalamus (RTHvl)	–	8	-14	14	0.0074	1104
Right cerebellum (RCer)	–	10	-46	-10	0.0059	800

s.c. = same cluster as listed on previous line; ALE = maximum activation likelihood estimation value for the given cluster; mm³ = cluster volume.

Figure 1. Overlap Between TMS Meta-Analysis and Activation Results of the TMS/PET Data.

These axial slices show the overall agreement between the results of the ALE meta-analysis of 7 TMS studies (P<0.05) (red) and the activation data from 7 subjects acquired at the Research Imaging Center in the contrast of 125% MT TMS – Rest (P<0.05) (green). Areas of overlap between these two maps (yellow) were found in the left primary motor cortex (LMI_hand), left posterior parietal cortex (LPPC), supplementary motor area (SMA), cingulate gyrus (Cing), left ventral premotor area (LPMv), left secondary somatosensory cortex (LSII), left ventral posterolateral nucleus of the thalamus (LTHvpl), and right cerebellum (RCer).

Figure 2. Overlap Between TMS Meta-Analysis and Finger Tapping Meta-Analysis.

Shown here are the results of the ALE meta-analysis of 7 TMS studies (P<0.05) (red), the results of the ALE meta-analysis of 16 finger tapping studies (P<0.05) (green) and the overlap between them (yellow). Overlap between these two ALE maps exists in the left motor cortex (LMI_hand), left posterior parietal cortex (LPPC), supplementary motor area (SMA), cingulate gyrus (Cing), left ventral premotor area (LPMv), left secondary somatosensory cortex (LSII), left ventral lateral nucleus of the thalamus (LTHvl), and right cerebellum (RCer).

Table 4. Results of the Finger Tapping Meta-Analysis.

9 ROIs were returned by the ALE meta-analysis of published studies that investigated simple finger tapping of the dominant hand by right-handed, normal subjects.

Region of Interest (ROI)	BA	x	y	z	ALE	mm3
Left primary sensorimotor cortex (LMIhand)	4,3	-38	-28	52	0.0345	25288
Left secondary somatosensory cortex (LSII)	40	-48	-26	22	0.0145	s.c.
Left ventral premotor area (LPMv)	6	-34	-4	4	0.0178	15504
Left ventral lateral nucleus of the thalamus (LTHvl)	–	-14	-18	6	0.0169	s.c.
Supplementary motor area (SMA)	6	-6	-10	50	0.0326	13104
Right cerebellum (RCer)	–	18	-50	-20	0.0216	6544
Right primary motor cortex (RMIhand)	4,3	50	-28	42	0.0106	4872
Left cerebellum (LCer)	–	-22	-56	-24	0.0101	1072
Right middle frontal gyrus (RMiFG)	9	34	32	32	0.0088	656

Structural Equation Modeling

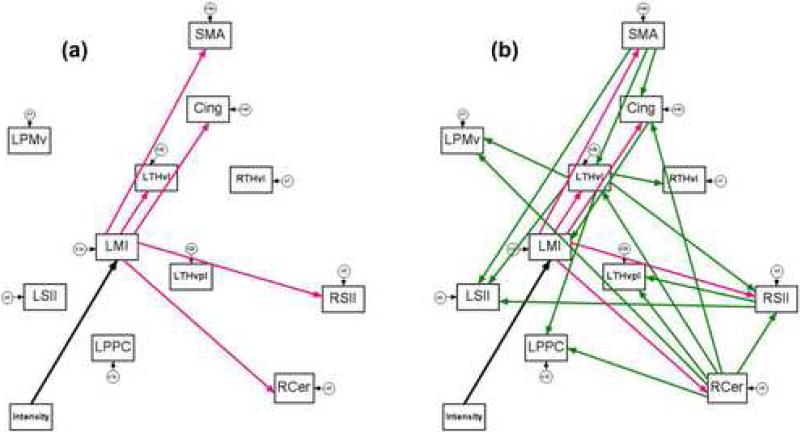
The sample size of the TMS/PET data was 56 (7 subjects × 4 conditions × 2 trials) with 23 variables: 11 observed, endogenous variables for each ROI; 11 unobserved, exogenous variables representing the error terms loaded onto those ROIs; and 1 observed, exogenous variable for TMS intensity. Given the required path of intensity loaded upon LMI_hand, the possible loadings from LMI_hand to all other nodes in the network (10 optional paths) were investigated. Specification search (all subsets) revealed that from the LMI_hand stimulation site, activation propagated to five regions: supplementary motor area (SMA), cingulate gyrus (Cing), left ventral lateral nucleus of the thalamus (LTHvl), right secondary somatosensory cortex (RSII), and right cerebellum (RCer). We termed these loadings “first-level paths” or the “first-level cascade” to indicate that they were the first nodes to receive input from LMI_hand following stimulation; they can be viewed in Figure 3a (red paths).

Figure 3. First-Level and Second-Level Paths in the LMI TMS Model.

(a) Following stimulation with TMS, exploratory SEM revealed that the signal propagated from LMI_hand to five nodes, designated by the five red paths to supplementary motor area (SMA), cingulate gyrus (Cing), left ventral lateral nucleus of the thalamus (LTHvl), right secondary somatosensory cortex (RSII), and right cerebellum. We termed these “first-level paths”. (b) Propagation of the TMS signal from those five nodes to all other nodes was determined next, generating the second-level paths in the model (green paths). Error terms are represented by the circular variables.

To determine the second level of paths, optional loadings were added from each of the five first-level ROIs to all other nodes available (5 ROIs × 10 possible nodes = 50 optional loadings). The five previous paths from LMI_hand were relabeled as required, not optional. Due to the large number of possible paths in this level of the analysis, a stepwise specification search was performed, which returned a best-fit model with 17 additional loadings as seen in Figure 3b (green paths). There were 9 ROIs that received input due to the second-level paths: LMI_hand, LSII, LTHvl, Cing, RTHvl, RSII, LPPC, LTHvpl, and LPMv (only the SMA and RCer received no input at the secondary level).

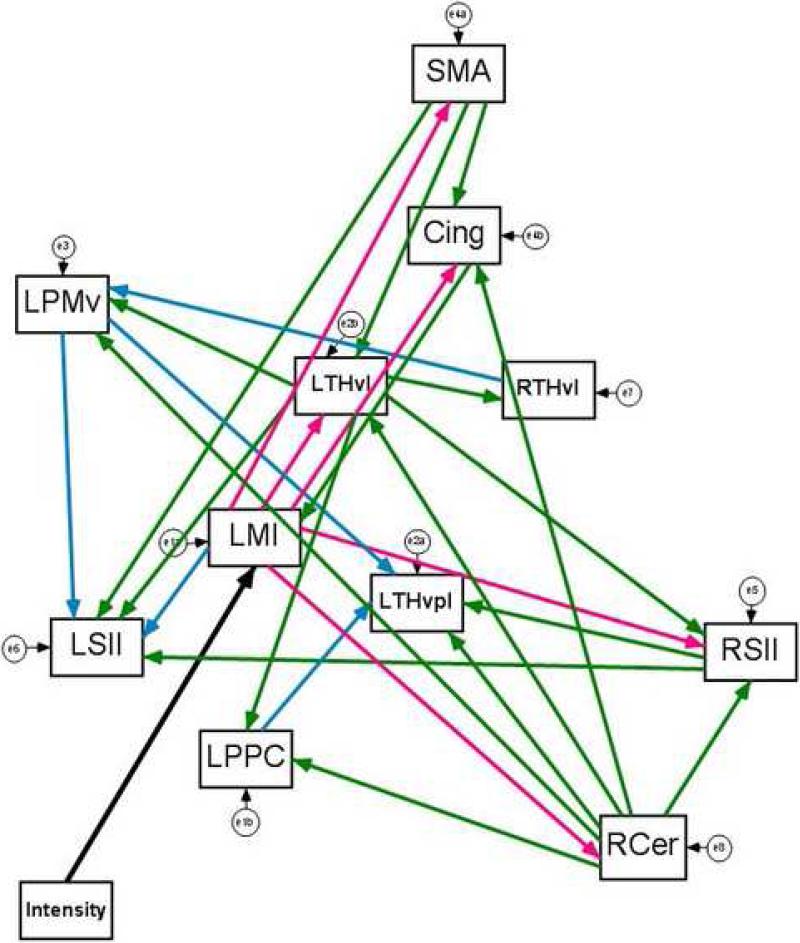
To determine the third-level paths, optional loadings were drawn for the 9 nodes listed above; both first-level and secondary-level paths were set as required. Stepwise specification search revealed only five additional loadings in the model: RTHvl to LPMv, LPMv to LTHvpl and LSII, LMI_hand to LSII, and LPPC to LTHvpl (Figure 4, blue paths). A fourth-level specification search with optional loadings originating from these three additional nodes (LPMv, LTHvpl, and LSII) revealed no other paths should be added to the model.

Figure 4. Final Model of LMI_hand Connectivity.

Exploratory analysis of 11 TMS ROIs using SEM revealed a complex network of LMI_hand connectivity that fit the data extremely well (χ² = 22.150, df = 38, P = 0.981, CFI = 1.0, TLI = 1.0, RMSEA = 0.000, 90% CI_RMSEA = 0.000-0.000). Red paths = first-level paths from LM1; green paths = second-level paths; blue paths = third-level paths. Error terms are represented by the circular variables.

Model Fit Statistics

Measures of model goodness and fit for all three levels of specification searches (Table 5) show that while the initial model of only 6 loadings did not fit the data well, additional levels of analysis improved the fit of the model dramatically. Specifically, the last round of specification searches generated an extremely large increase in the P value, resulting in the non-significance of the model (P = 0.004 for second-level paths to P = 0.981 for third-level paths; Table 5). This large transition possibly indicates the introduction of critical paths during that stage of the analysis. After the last round of specification searches, the estimates were calculated and it was determined that the overall final model fit was outstanding (χ² = 22.150, df = 38, P = 0.981, CFI = 1.0, TLI = 1.0, RMSEA = 0.000, 90% CI_RMSEA = 0.000-0.000). These statistics indicate little difference between the sample variance-covariance matrix and the reproduced variance-covariance matrix implied by this model (Schumacker and Lomax, 2004). Regression weights for these paths can be seen in Table 6. A non-recursive (i.e., interdependent systems) loop is present in the final model, involving the nodes of left motor cortex (LMI_hand), right cerebellum (RCer), supplementary motor area (SMA), and cingulate gyrus (Cing). Non-recursive relations pose a unique challenge during simultaneous estimation of the model structural coefficients due an infinite sequence of linear dependencies among nodes. For some regression weights, these dependencies will converge to a set of well-defined relations thereby exhibiting system stability. To ensure that an adequate level of stability for the network system was achieved (i.e., within the range of -1.0 to +1.0; Bentler and Freeman, 1983; Fox, 1980), we used an instrumental variable design strategy (Heise, 1975). Once implemented, the stability of the recursive loops and the entire system was estimated using the full information maximum likelihood (FIML) estimation algorithm (to allow for a sparse variance-covariance matrix) with the ridge regression option invoked. The statistical basis for evaluating the stability of the non-recursive path model is provided by Bentler and Freeman (1983) and is described in Appendix B. The stability index was observed as + 0.78, indicating a mathematically stable solution.

Table 5. Fit Statistics of the Models in Each Level of Analysis.

Overall model goodness improved as more paths were added via specification search. The first-level cascade contained only the intensity to LMI_hand loading and the 5 loadings originating from LMI_hand (6 total paths; Figure 4a, red paths). The second-level paths added 17 additional loadings to the model (23 total paths; Figure 4b, green paths). Lastly, 5 loadings were added in the third-level of specification searches (28 total paths; Figure 5, blue paths).

	C	C – df	BCC (0)	BIC (0)	C/df	P
First-Level Paths	410.998	350.998	0.000	1.090	6.850	0.000
Second-Level Paths	71.232	28.232	0.000	1.533	1.657	0.004
Third-Level Paths	22.150	-15.850	0.000	0.000	0.583	0.981

C = minimum value of the discrepancy (chi-square value); df = degrees of freedom; BCC(0) = Browne-Cudeck criterion, scaled such that the lowest BCC is zero, with all other values being positive; BIC(0) = Bayes information criterion, also scaled such that the minimum value for the tested models equals zero; P = probability of getting as large a discrepancy as occurred with the present sample (P value for testing that the model fits perfectly in the given population). For both BCC and BIC, smaller values indicate a higher degree of goodness than larger values. For P, larger values indicate a better fit of the model.

Table 6. Maximum Likelihood Estimates of the Final Model.

After the model-generating procedure SEM, the estimates for the final model were calculated as seen in Figure 4.

Path	Estimate	Std. Estimate	S.E.	C.R.	P
LMI ← Intensity	36.228	0.562	19.921	1.819	0.069
LTHvl ← LMI	-0.419	-0.192	0.234	-1.792	0.073
LTHvl ← SMA	1.336	0.416	0.333	4.013	***
LTHvl ← RCer	1.079	0.536	0.210	5.151	***
RTHvl ← LTHvl	0.766	0.921	0.044	17.564	***
RSII ← LMI	0.550	0.500	0.108	5.112	***
RSII ← LTHvl	0.177	0.351	0.056	3.167	0.002
RSII ← RCer	0.439	0.432	0.115	3.831	***
LPPC ← RCer	0.426	0.481	0.114	3.727	***
LPPC ← LTHvl	-0.302	-0.687	0.057	-5.340	***
LPMv ← RTHvl	0.355	1.000	0.084	4.227	***
LPMv ← LTHvl	-0.215	-0.738	0.075	-2.870	0.004
LPMv ← RCer	0.289	0.493	0.065	4.439	***
LTHvpl ← RSII	0.369	0.296	0.114	3.234	0.001
LSII ← RSII	1.289	0.624	0.185	6.975	***
LSII ← LMI	-0.505	-0.222	0.197	-2.567	0.010
LSII ← LPMv	0.787	0.220	0.296	2.662	0.008
LTHvpl ← LPPC	0.378	0.265	0.117	3.236	0.001
LTHvpl ← RCer	0.312	0.246	0.131	2.373	0.018
LTHvpl ← LPMv	0.925	0.429	0.208	4.450	***
LSII ← SMA	-0.686	-0.205	0.264	-2.594	0.009
LSII ← LTHvl	0.221	0.212	0.105	2.097	0.036
Cing ← SMA	0.379	0.429	0.143	2.659	0.008
LMI ← Cing	-1.578	-0.946	1.340	-1.178	0.239
Cing ← LMI	0.460	0.767	0.144	3.186	0.001
SMA ← LMI	0.319	0.469	0.125	2.550	0.011
RCer ← LMI	0.010	0.009	0.247	0.042	0.967
Cing ← RCer	0.322	0.581	0.103	3.113	0.002

Estimate = estimate of the regression weight (e.g., when Intensity goes up by 1, LMI_hand goes up by 36.228); Std. Estimate = estimate of the standardized regression weight (e.g., when Intensity goes up by 1 standard deviation, LMI_hand goes up by 0.562 standard deviations); S.E. = standard error of the regression weight; C.R. = critical ratio for regression weight, which is computed by dividing the regression weight estimate by the estimate of its standard error (e.g., for the path from Intensity to LMI_hand, the regression weight estimate is 1.819 standard errors above zero); P = level of significance for regression weight

^***P < 0.001 (Arbuckle, 2006b).

In Table 5, all three values of the Brown-Cudeck criterion (BCC) are zero. Since Amos only uses BCC values in a comparative sense, zero-scaled BCC values are used in which the lowest BCC is set to 0, and the other values are scaled accordingly. Thus, the BCC values of zero in Table 5 indicate that the three models listed were the lowest of their respective stage of the analysis. The BIC values for the first- and second-level analyses are non-zero, indicating that these were not the models specified by the lowest BIC values. In the two cases of conflict between the BCC and BIC, the BIC specified models with two fewer paths (due to its increased penalty for model complexity), thus returning alternate models that were extremely similar to those generated when using the BCC as a selection criterion. In the last stage of analysis (third-level paths), the BCC and BIC returned the same model.

DISCUSSION

The main aim of this study was to use TMS/PET as a novel approach to quantifying effective connectivity during stimulation of the LMI_hand region. ALE meta-analysis of the TMS literature was used to identify regions of interest (ROIs) that were subsequently analyzed in a TMS/PET data set of 7 subjects using a model-generating SEM procedure. Eleven ROIs and TMS intensity were modeled as observed variables in the path model. Exploratory SEM analysis revealed that after TMS of LMI_hand, activation propagated to five regions: the supplementary motor area (SMA), cingulate gyrus (Cing), left ventral lateral nucleus of the thalamus (LTHvl), right secondary somatosensory cortex (RSII), and right cerebellum (RCer). Further signal propagation was determined, resulting in the model observed in Figure 4. This final model fit the data extremely well, indicating little difference between the actual and model-implied covariance matrices (χ² = 22.150, df = 38, P = 0.981, CFI = 1.0, TLI = 1.0, RMSEA = 0.000, 90% CI_RMSEA = 0.000-0.000). The validity of this method was established through both quantitative and qualitative measures. Quantitatively, an outstanding fit was observed, and a comparison of fit statistics in previous SEM studies suggested that the exploratory nature of this analysis is responsible for the fit of the model. Qualitatively, the utility of the ROI selection method (via meta-analysis) presented here was confirmed by a comparison with both an analysis of the TMS/PET data and a meta-analysis of overt movement. Consistent findings between the final model presented here and SEM motor studies in humans and motor connectivity studies in the macaque literature were observed. In addition, various features of the final path model were explored, including connections to secondary somatosensory cortex and model criticisms.

Fit Statistics of the Final Path Model

As stated previously, the final model seen in Figure 4 fit the experimental data extraordinarily well. There are three plausible reasons that might explain why such a good fit was obtained. First, the parametric manner in which TMS was utilized over a wide range of intensities possibly contributed to a greater degree in which the system was probed, leading to the robustness of the results. Second, it is conceivable that the task-independent nature of stimulation with TMS is more conducive in general to the analysis of network interactions. Finally, the exploratory nature of this analysis might have been a critical factor in the strength of the overall results. A brief inspection of the SEM literature in neuroimaging isolated a sub-sample of studies in which the global fit measures of a single model or models were published, rather than the more prevalent chi-square difference values between two models. These studies presented SEM analyses that were either exploratory (Zhuang et al., 2005; Peltier et al., 2007) or confirmatory (Goncalves et al., 2001; Honey et al., 2002; Glabus et al., 2003; Erickson et al., 2005; Au Duong et al., 2005; de Marco et al., 2006), and examined a mixture of paradigms and subject groups. After comparing the reported model fit indices and experimental design factors for each paper, the first two possible explanations of the excellent degree of the results presented above were refuted. However, no hypothesis-driven models in the examined studies obtained fit statistics as good as those observed in the exploratory analyses. A reasonable interpretation is then that taking a data-driven approach to generate an optimal model is a more precise way to investigate effective connectivity. While this may seem a trivial conclusion, it is still a point that must be made, given the overwhelming preference in favor of testing a priori SEM models in neuroimaging data. More research is needed to determine if this is an accurate assessment of the data and the analysis method.

Plausibility of LMI_hand Regions

Overall, excellent agreement was found between the TMS meta-analysis results and (1) the activation map for the 125% MT – Rest contrast in the TMS/PET data of 7 subjects, and (2) the meta-analysis results of voluntary right-finger tapping. In comparison to the 125% MT – Rest activation map, overlap was found in the LMI_hand, LPPC, SMA, Cing, LPMv, LSII, LTHvpl, and RCer (Figure 1). While the ROIs for SEM analysis could have been selected from the activation map alone, the meta-analysis approach provided a more defensible means of isolating nodes common to a larger group of subjects, thereby reducing variability due to imaging and analysis methods. In general, ROI selection is highly variable among SEM studies. Using meta-analysis as a technique for ROI selection provides a more standardized, less user-dependent strategy. Overlap between the meta-analysis results and the activation results indicates that the present TMS/PET data agree well with other reports in the literature, and gives greater confidence in the selection of motor regions.

Second, in the comparison between the TMS and finger tapping meta-analyses, overlap was seen in the LMI, LPPC, SMA, Cing, LPMv, LSII, LTHvl, and RCer (Figure 2). Regions present in the TMS meta-analysis that were not observed in the finger tapping meta-analysis are arguably more strongly related to the somatosensory system (LTHvpl), and their omission can be attributed to laterality issues associated with right-handed finger tapping (RTHvl and RSII). Thus, with a few exceptions, the TMS network identified via meta-analysis agrees well with the network of voluntary motor function. These results confirm that the meta-analysis method of ROI selection was successful both in identifying the nodes stimulated with TMS and that these nodes are representative of general motor function.

Plausibility of LMI_hand Connections

The final model generated through exploratory path modeling includes a large number of both ROIs and loadings, which implies a level of complexity appropriate for a neural systems model. The presence of many of the observed paths in the final model have been confirmed in previous SEM studies of self-initiated and externally-cued finger movements (Taniwaki et al., 2006) and visually-guided motor grasping (Grafton et al., 1994), including various paths connecting left primary motor cortex (LMI), supplementary motor area (SMA), left ventral lateral nucleus of the thalamus (LTHvl), left ventral premotor cortex (LPMv), left ventral posterolateral nucleus of the thalamus (LTHvpl), and right cerebellum (RCer).

In addition to finding agreement between the final model presented here and other published SEM results of human neuroimaging data, agreement was also found between these results and the macaque literature. The connections in the final model were compared to the connectivity map of the FI_arm region (the homologue of MI_hand) (Karol and Pandya, 1971; Schmahmann and Pandya, 2006). In the present model, direct LMI_hand connections were observed to the cingulate cortex, supplementary motor area, secondary somatosensory cortex (SII), thalamus, and cerebellum. Convergence exists between these connections and the connectivity of FI in the macaque (Schmahmann and Pandya, 2006), giving further support to the validity of these results. The complexity of the presented model of LMI connectivity is well supported by the macaque literature and likely provides a realistic model of motor system connectivity.

LMI_hand Path Model Features

In the present model, five regions are directly modulated by LMI_hand following TMS: SMA, Cing, LTHvl, RSII, and RCer (Figure 3a, red paths). Thus, there were five nodes that did not receive immediate input from LMI_hand and were thus not introduced into the model until later in the analysis. For example, left premotor cortex (LPMv) was introduced only after receiving input from the left ventral lateral nucleus of the thalamus (LTHvl) and right cerebellum (RCer). In addition, the left ventral posterolateral nucleus of the thalamus (LTHvpl) was introduced after receiving input from right secondary somatosensory cortex (RSII) and right cerebellum (RCer) (Figure 3b, green paths). It is interesting to note that all possible nodes were introduced into the model during either the first- or second-level analyses, leaving no new nodes to be introduced in the third-level analysis.

At this point, it is unclear what functional significance can be attributed to the first-, second-, and third-level cascades. The hierarchical nature of the present method adds paths to the model in an iterative fashion, and this model progression is data-driven and guided by the search for the model yielding the best indices of model goodness and fit. It can be seen that the order in which some of these paths were added was merely based on the fact that a region cannot directly load onto another region until the first region receives a loading itself (e.g., LPPC → LTHvpl isn't added to the model until after the incoming paths to the LPPC are considered). However, one loading (LMI → LSII) does not show up until the third-level paths are tested, despite the fact that this particular path was tested in the first-level cascade following LMI_hand stimulation. It is unknown if the level of analysis ascribed to a loading is a function of the distance traveled from the site of stimulation, the strength of the connection, or the loading's relative influence in the entire network. For now, this issue remains open for exploration in future studies.

The loading of LMI_hand onto RCer was small (standardized path coefficient = 0.009), but this path had a critical effect on the model as seen in the large number of second-level outgoing paths from cerebellum to RSII, Cing, LTHvl, LTHvpl, LPMv, and LPPC. Investigation of the total effects that each variable had on all the other variables in the model (McIntosh et al., 1994b) revealed that the average total effects of the right cerebellum on all other variables was the largest in the entire model (average total effects = 0.308). Thus, in this model of LMI_hand connectivity, it is evident that the right cerebellum is a major relay station for information from LMI_hand to cortical and subcortical nodes in the network. This finding of the importance of the LMI_hand to RCer connection, despite its small path coefficient, casts doubt on the practice of filtering out paths with small regression weights.

Table 6 shows the standardized path coefficients for the loadings in the final model (Figure 4). Note that several of these coefficients are not significant. Once the model-generating analysis was complete and no more additional loadings were suggested, the lower or insignificant regression weights (e.g., LMI to RCer) were not additionally filtered. To do so would have rendered the exploratory signal tracking procedure unsound. That is, since the goal was to track the TMS signal, once a connection was created it was necessary for future specification searches (e.g., the LMI to RCer loading was introduced during the first-level cascade and therefore was relevant to all five outgoing paths from the RCer determined in the second-level model).

In particular, Table 6 shows that the path from Intensity to LMI_hand is not significant (P=0.069), yet is clear that the data supports the inclusion of this path. To illustrate this, in the final model we labeled the Intensity → LMI connection as optional and tested the two candidate models. The model that included the connection obtained much lower BCC and BIC values (0.000 for both criteria) as compared to the model that omitted this path (BCC=4.646 and BIC=3.239). In terms of the absolute and relative fit statistics, excluding this path resulted in a decrease in the fit of the data to the given model (P<0.981 with the path, as compared to P<0.867 without the path). Thus the data does support this path.

The regression weights (unstandardized=36.22, standardized=0.562) were observed as being not statistically significant, but they are classified as being “large” (Cohen, 1988). Mathematically, the test of statistical significance is equal to the product of the effect size and the size of the study (sample size). Although the regression of LMI on Intensity was not statistically significant, the magnitude of the regression weight is practically important. For correlations, the effect size is the coefficient of determination (R-square) and indicates the variability in the model that can be predicted from the relationship between the two variables. The importance of the effect size in this case is evidenced by the regression path exhibiting a coefficient of determination of 0.3158. That is, 32% of the variability in the overall model was accounted for or explained by this single path. From a practical perspective, this effect is reasonable, considering the large physiological effect delivered to the site of stimulation (i.e., LMI) by the TMS coil. Thus, while the regression weights were found to be not statistically significant, this is a result of the small sample size, and not due to any weakness in the final model.

Path Connections to Secondary Somatosensory Cortex (SII)

In the final TMS connectivity model (Figure 4), LMI_hand is found to act directly upon both left and right secondary somatosensory cortex (SII). However, these two loadings are very different. LMI to RSII was added as a first-level path, right after LMI received input from TMS. During this stage of the analysis, the data did not support a connection from LMI to LSII. As mentioned previously, this path was not added until the third-level analysis. Between the first-level and third-level analyses, only one variable acted upon LMI: the cingulate gyrus. Thus, the LMI to LSII connection was only made possible after LMI received input from the cingulate cortex. This was also accompanied by a loading of RSII onto LSII. We hypothesize that the nodes in these interactions (LMI, RSII, LSII, and Cing) are particularly important in the LMI_hand connectivity network. The LMI → Cing → LMI non-recursive loop seems especially significant since the cingulate gyrus was found to have a direct effect only on LMI, and conversely, the only node to directly input LMI was the cingulate gyrus. Our interpretation of these observations is that the LMI/Cing feedback loop is of critical influence in the present network.

Model Criticisms and Limitations

There are three major criticisms of the final model. The first criticism is that this model does not include a variable for primary somatosensory cortex (SI). The aim here was to remain very strict in only extracting data from ROIs explicitly returned by the meta-analysis. The largest ALE cluster returned centered on left primary motor cortex (LMI), which was connected to a secondary cluster in BA 5 in posterior parietal cortex (LPPC). The results did reveal that activation of left SI was included in this large frontal-parietal cluster, contained in the zone bridging the primary motor cortex to PPC. However, since SI was not represented as a well-defined sub-cluster in the ALE results, it was not possible to include this region as a node in the path model. Hence, the coupled interaction between MI and SI was not dissociated using the current methodology.

The second major criticism of the model is that a second-level path was found from the left to the right ventral lateral nucleus of the thalamus, despite the fact that there is no known connection between these nuclei (Carpenter, 1985). There are two possible reasons why this path was generated: (1) these regions are located very close to each other in space, resulting in the acquisition of highly-correlated data that is not representative of functionally connected regions, or (2) the LTHvl to RTHvl connection in the model is an indirect one, possibly modulated by an unknown variable not included in the existing network. Analysis of the total effects of each variable in the model initially suggested the former cause. That is, the effects of all other variables on both the LTHvl and RTHvl were nearly identical to each other, indicating that the two nodes received input more as a single entity rather than two distinct variables. However, close examination revealed that this occurred since RTHvl only received direct input from LTHvl. At this point, neither of the above reasons may be ruled out.

Thirdly, a similar criticism lies in the fact that the literature does not support a direct connection between LMI_hand and contralateral secondary somatosensory area (RSII). This first-level path in the final model may also represent an indirect path modulated by an unknown ROI. A related explanation for the presence of this loading may be due to the fact that the effects of primary motor (MI) and primary sensory (SI) regions could not be dissociated. As the SII area receives both contralateral SI and SII input (Jones and Powell, 1969), the first-level path from LMI_hand to RSII could simply be due to somatosensory input distributed to both hemispheres following stimulation with TMS. Typically, the connection from MI to ipsilateral SII has been discussed in primate literature, with no mention of a connection from MI to contralateral SII (Stepniewska et al., 1993; Schmahmann and Pandya, 2006). It has not been shown that RSII is physically connected to LMI_hand.

Lastly, a potential limitation of this study lies in the selection of subject data. Data were analyzed in seven subjects who showed measurable PET response during TMS (i.e., the “cortical responder” group) (Fox et al., 2004; 2006). Data were omitted from the group of “cortical non-responders” (n=4), who exhibited no significant PET activations during TMS at the site of stimulation (LMI) or any other regions. When comparing the responders and non-responders, the same average EMG response was observed in terms of the magnitude and latency of response. Further analysis of these subjects indicate that the absence of a cortical response to TMS was a real effect, not an artifact of statistical thresholding (Fox et al., 2004), and it has been hypothesized that this effect was due to direct stimulation of the exiting corticospinal axons, rather than MI gray matter (Fox et al., 2004; 2006). Thus, the non-responders remain a perplexing group of subjects, particularly so since strong PET responses were observed during overt finger movement in this group. Inclusion of these subjects into the SEM analysis of responders would have confounded the results and rendered them difficult to interpret, since no difference in signal was detected between rest and TMS in the pre-specified ROIs. With this in mind, we chose to only analyze the responders as they revealed consistent, measurable responses during the given conditions. While it is clear that the lack of a PET-detected response during corticospinal excitation as shown by EMG is intriguing and would likely reveal connectivity differences between the responders and non-responders, this comparison was not possible due to lack of power (n=4). In conclusion, the dichotomy of subject responses to TMS led to an overall bias in data selection. This selection, in turn, may possibly limit the conclusions drawn in this study, contributing to findings that cannot be extrapolated to the general population.

Future Work

Applying SEM to TMS/PET data yielded insightful information on the effective connectivity of LMI_hand. We feel that this technique holds great promise for further studies of effective connectivity. However, at this point, it is unclear how generalizable the results are. For example, it is unknown if any of the network connections determined in the path model are similar to the connections at work during the performance of a functional task. Future studies will involve testing the model presented in Figure 4 in task-dependent data, such as right-handed finger tapping. Alternatively, while the model generated here included contributions from TMS data acquired over a range of intensities, this analysis could be pursued on the individual conditions, either above or below motor threshold (i.e., with and without overt movement). This type of analysis might prove valuable in dissociating the relative roles of proprioception and efference copy within the sensorimotor system. Lastly, it would be interesting to apply this exploratory analysis technique to data in which other nodes in the network were stimulated, such as the supplementary motor area, secondary somatosensory cortex, or premotor regions.

CONCLUSIONS

In this study, H₂¹⁵O PET data were acquired during stimulation of the hand region of the primary motor cortex (LMI_hand) using transcranial magnetic stimulation (TMS). The data were analyzed using structural equation modeling (SEM) in order to study the effective connectivity of the human motor system during task-independent stimulation. It was determined that meta-analysis of the existing literature using activation likelihood estimation (Turkeltaub et al., 2002; Laird et al., 2005a) yielded plausible regions of the motor system in an unbiased fashion. These regions were modeled in TMS/PET data using a model-generating path analysis procedure. The resulting hierarchical model fit the data extremely well, which, based on an inspection of similar studies, may be due to the exploratory nature of the analysis. Overall, the plausibility of the brain ROIs and path connections was substantiated in the human and macaque literature. In the final path model, it was determined that the LMI_hand to right cerebellum (RCer) loading was critically important to the network interactions, despite the small path coefficient for this loading. This finding casts doubt on the practice of filtering out paths with small regression weights. Lastly, a strongly influential feedback loop was observed between LMI_hand and the cingulate gyrus (Cing).

Appendix A

Instrumental Variables

To address the challenge of estimating stable and reliable structural coefficients within the context of non-recursive or interdependent systems path analytic modeling, the guidelines for using an instrumental variable (e.g., TMS intensity) were followed as offered by Heise (1975, pp. 160 - 161).

1. A variable, X (e.g., TMS intensity), is an instrument for Y (e.g., LMI_hand) in the non-recursive relationship Y (e.g., LMI _hand) → Z (e.g., Cing) if

   1. X has no direct effect on Z;
   2. X does affect Y, either directly or through an intervening variable that has no direct effect on Z;
   3. neither Y or Z has a direct or indirect effect on X;
   4. no unspecified factor jointly affects X and Z and, in general, X is uncoordinated with the disturbances (i.e., errors) of Z.

2. A variable, X’, that is only correlated with Y also is an instrument for the Y → Z relationship providing it fulfills conditions (a), (c), and (d) above.

Appendix B

The application of linear structural equations to our data consisted of equations in random vectors of the form attributed to Bentler and Freeman (1983):

$$\eta =B\eta +\Gamma \xi +\varsigma$$ (B1)

where, B is the square of the coefficient matrix for the structural “direct” effects of endogenous variables, η, on each other, Γ is the coefficient matrix for the direct effects of exogenous variables, ξ, on endogenous variables, and ς is a residual error vector (Joreskog and Sorbom, 1981).

Using algebraic manipulation and substituting the right hand side of equation (B1) for η we have:

$$\eta =B^2\eta +(I+B)(\mathrm{T}\xi +\varsigma )$$ (B2)

Substituting (B1) into (B2), yields

$$\eta =B^3\eta +(\mathrm{I}+B+B^2)(\Gamma \xi +\varsigma )$$ (B3)

Performing this operation k times yields

$$\eta =B^k\eta +(\mathrm{I}+B+B^2+\cdots +B^{k-1})(\Gamma \xi +\varsigma )$$ (B4)

In (B4) the coefficient matrix B^k represents the “indirect” effects of length k for endogenous variables on each other. Since k is arbitrary, the ultimate effect of endogenous variables on endogenous variables is given by B^k as k gets arbitrarily large. The ultimate effect of exogenous variables on endogenous variables is given by (I + B ... +B^k−1)Γ, as k gets arbitrarily large. In the case of the effects of endogenous variables on each other, the total effect is defined by the sum B + B² + B³ ... B^k [from (B1), (B2), (B3), and (B4)] as k gets arbitrarily large. In the case of the effects of exogenous variables on endogenous variables, the total effect is defined as the ultimate effect. If these effect matrices “converge” to specific matrices, the system is termed “stable”. Further, a square matrix B is called convergent (Ben-Israel and Greville, 1974) if

$$B^k\to 0\text{as}k\to \infty$$ (B5)

And, a matrix is “convergent” if and only if the absolute value of the largest eigenvalue is less than one, i.e.,

$$\rho \left(B\right)<1$$ (B6)