Detection of event‐related modulations of oscillatory brain activity with multivariate statistical analysis of MEG data

Abstract

We describe a method to detect brain activation in cortically constrained maps of current density computed from magnetoencephalography (MEG) data using multivariate statistical inference. We apply time–frequency (wavelet) analysis to individual epochs to produce dynamic images of brain signal power on the cerebral cortex in multiple time–frequency bands. We form vector observations by concatenating the power in each frequency band, and fit them into separate multivariate linear models for each time band and cortical location with experimental conditions as predictor variables. The resulting Roy's maximum root statistic maps are thresholded for significance using permutation tests and the maximum statistic approach. A source is considered significant if it exceeds a statistical threshold, which is chosen to control the familywise error rate, or the probability of at least one false positive, across the cortical surface. We compare and evaluate the multivariate approach with existing univariate approaches to time–frequency MEG signal analysis, both on simulated data and experimental data from an MEG visuomotor task study. Our results indicate that the multivariate method is more powerful than the univariate approach in detecting experimental effects when correlations exist between power across frequency bands. We further describe protected F‐tests and linear discriminant analysis to identify individual frequencies that contribute significantly to experimental effects. Hum Brain Mapp, 2009. © 2009 Wiley‐Liss, Inc.

INTRODUCTION

Statistical inference in magnetoencephalography (MEG) distributed activation maps typically uses the general linear modeling (GLM) framework [Kiebel, 2003], which is considered a standard in functional magnetic resonance imaging (fMRI) [Friston et al., 1995] and positron‐emission tomography (PET) [Worsley et al., 1992] neuroimaging studies. However, there are important differences between MEG and the other neuroimaging modalities related to how observations are fitted in general linear models, as well as how subsequent statistical inference is performed. The investigation of stimulus‐locked event‐related components typically involves a mass univariate approach where separate analysis of variance (ANOVA) models are fitted at each spatial location [Barnes and Hillebrand, 2003; Brookes et al., 2004; Park et al., 2002], or each spatial–temporal location [Pantazis et al., 2003, 2005a; Sekihara et al., 2005]. Recently, there has also been a great deal of interest in the analysis of the induced response, which corresponds to stimulus‐related variations in power in different oscillatory bands as a function of time. This allows us to detect experimental oscillatory effects corresponding to modulations in power in specific frequency bands, even though the oscillations themselves are not phase‐locked to the stimulus or response. Induced effects are typically investigated using a time–frequency decomposition such as the Morlet wavelet transform [Tallon‐Baudry and Bertrand, 1999; Teolis, 1998]. Examples of the use of ANOVA models to analyze the induced response include Durka et al. [ 2004]; Kiebel et al. [ 2005]; Pantazis et al. [ 2005b, 2009]; and Singh et al. [ 2003].

This paper presents a method for the detection of task‐based changes in brain activity from MEG data, which analyzes signals in the time–frequency domain based on a multivariate statistical approach. The statistic used to measure group separation is Roy's maximum root, which can be thought of as a generalization of the conventional F‐statistic for higher‐dimensional problems. The significance of each source is estimated based on the familywise error rate (FWER), or the probability of at least one false positive under the null hypothesis of no changes in brain activation. The FWER is related to the probability distribution of the maximum statistic across all sources and resampling methods are used to estimate this distribution [Nichols and Hayasaka, 2003]. The performance of our method is compared with that achieved with univariate approaches, using simulations and real data obtained from a visuomotor MEG study [Jerbi et al., 2007]. Although the emphasis here is on MEG, our method readily applies to EEG signal analysis, and even to combined EEG/MEG acquisitions.

Our motivation for the application of multivariate analysis of variance (MANOVA) to MEG comes from findings both in neuroscience and in statistical inference: studies in which changes in brain activity were found across several frequency bands [Başar et al., 2001; Kilner et al., 2005; Pantazis et al., 2005b] have been reported; in such cases, dealing simultaneously with all frequency bands of interest in a multivariate model might be advantageous over applying univariate approaches to each frequency band separately, especially because the improved detection of event‐related modulations provided by the former in the presence of correlated variables has been shown [Cole et al., 1994; Field, 2005]. MANOVA has been applied successfully to medical imaging studies, such as the analysis of deformation‐based morphometry using structural MRI [Worsley et al., 2004; Taylor and Worsley, 2008]; in EEG/MEG, applications include the creation of multivariate observations in the spatial dimension [Carbonell et al., 2004] or in the spatial–temporal dimension where entire trials were used to form observations [Friston et al., 1996]. However, in contrast to these studies, here we use the time–frequency information in the MEG signals, after inverse mapping to the cortical surface, as the observations for our multivariate model.

Methods

In this section, we describe the use of MANOVA models to detect task‐based changes in oscillatory brain activity. Observations for several frequency bands are constructed using complex Morlet wavelet time–frequency decomposition and are fitted to separate MANOVA models at each source location. The resulting Roy's maximum root maps are tested for significance using permutation tests, and follow‐up protected F‐tests and linear discriminant analysis allow us to identify individual frequencies that contribute significantly to experimental effects.

Model

Our MEG data set consists of J stimulus‐locked event‐related trials, one per stimulus repetition. Each trial is an array of data M (n _sensors × n _timepoints) representing the measured magnetic field at each sensor and each time instant. Brain activation Z (n _sources × n _timepoints) is modeled as being linearly related to the measurements, according to the expression:

(1)

where G (n _channels × n _sources) is the forward operator, also called lead field matrix, and N represents noise in the measurements. G depends on the shape and conductivity of the head and can be estimated with simplified spherical head models or, more precisely, with boundary or finite element methods, accounting for the true head shape and conductivity [Baillet et al., 2001, 2004; Huang et al., 1999; Mosher et al., 1999]. An estimate of the spatiotemporal activity Z can be produced by applying a Tikhonov regularized minimum‐norm inverse method [Okada, 2003; Tikhonov and Arsenin, 1977]:

(2)

The reconstructed time series at each source location s are then given by Z^st, where t is the time index. Even though we use cortically constrained regularized minimum‐norm, our method can be used with any inverse solution, surface or volume based.

Our goal is to detect event‐related modulations of brain activity over time, space, and frequency, and for that we need an estimate of neural activation energy at specific time–frequency instances [Pantazis et al., 2009]. This estimate is given by:

(3)

where C ^stf = Z ^st * w ^tf are the complex wavelet coefficients obtained from convolving each source time series Z ^st with a continuous‐time Morlet wavelet kernel w ^tf [Teolis, 1998]. To improve the signal‐to‐noise ratio and increase the statistical power by minimizing the total number of statistics that need to be tested for significance, we may choose to summarize the observations over spatial regions of interest S, time bands T = [t ₁,t ₂], and frequency bands F = [f ₁,f ₂]:

(4)

Multivariate Analysis of Variance

Each trial provides us energy observations y^STF in several spatial–temporal‐spectral bands STF. We introduce new indices to identify the observations: i∈{1,2,…} denotes the condition (e.g., 1 for the main task of interest and 2 for the baseline or rest condition), and j denotes the trials acquired from each condition i. With these indices, the observations can be arranged into general linear models. The methodology used here expands the statistical parametric mapping approach [Friston, 1996] to include in the analysis the multivariate data now available at each source location [Worsley et al., 2004].

Consider the ANOVA model:

(5)

where β${}_{\mathit{\text{i}}}^{\mathit{\text{STF}}}$ are the activation parameters for each condition and u ${}_{\mathit{\text{ij}}}^{\mathit{\text{STF}}}$ is the model error term, assumed to be zero‐mean Gaussian. ANOVA is used in situations in which there is one dependent variable (or observation) and so it is known as a univariate test. The superscripts STF indicate that we fit the same model at all spatial–temporal spectral bands. Since a separate but identical GLM is fitted at each band, this approach is typically referred to as mass univariate analysis.

MANOVA is designed to look at several dependent variables (observations) simultaneously and so it is a multivariate test. We convert the univariate model described above to a MANOVA model by reorganizing all the variables into row vectors, whose elements consist of observations over different frequency bands F. For example, row vector y ${}_{\mathit{\text{ij}}}^{\mathit{\text{ST}}}$ contains the values of the scalars y ${}_{\mathit{\text{ij}}}^{\mathit{\text{STF}}}$ for all F. Thus, the MANOVA model becomes:

(6)

Since we fit a separate but identical MANOVA at each spatial–temporal band, it is appropriate to call this approach mass multivariate analysis, with mass referring to the spatial and temporal dimensions, and multivariate to the frequency dimension. Note that we could have equivalently formed multivariate observations over other dimensions, provided that the multivariate dimension is small enough to allow for stable estimation of the covariance matrices involved in the calculation of test statistics, as described in the next section. We chose the frequency dimension because multiple studies have reported simultaneous changes in brain activity across several frequency bands [Başar et al., 2001; Kilner et al., 2005; Pantazis et al., 2005b].

The main reason for preferring MANOVA over ANOVA design is the increased sensitivity offered by the former when an experimental effect appears in multiple frequencies. If separate ANOVAs are conducted on each frequency variable, then any relationship between frequencies is ignored. As such, we lose information about any correlations that might exist between frequencies. MANOVA, by including all frequency observations in the same model, takes into account the relationship between different frequencies. Consequently, MANOVA has greater power to detect an effect, because it can detect whether experimental conditions differ along a combination of variables (frequencies), whereas ANOVA can detect only if they differ along a single variable.

GLM theory assumes normal distributions, which is reasonable for averaged evoked responses due to the central limit theorem. However, power time–frequency decompositions y ${}_{\mathit{\text{ij}}}^{\mathit{\text{STF}}}$ of single trial data have a chi‐square distribution. Fortunately, Kiebel et al. [ 2005] have shown that, under most circumstances, one can appeal to the central limit theorem or apply a log or square‐root transform on the MEG power estimates to make the error terms normal, and thus GLM theory is still appropriate. Furthermore, when nonparametric thresholding schemes are used, as in this paper, parametric assumptions are not necessary and any deviations from Gaussianity will affect the sensitivity of detecting an experimental effect, but not error control.

We can equivalently write the MANOVA model in matrix form, where we “stack” all row vectors described above to form matrices:

(7)

where Y ^ST (n _observations × n _variables) is the matrix of all observations, B ^ST (n _conditions × n _variables) is the parameter matrix with the parameter activation vectors for all conditions, U ^ST (n _observations × n _variables) is the error matrix, and X ^ST (n _observations × n _conditions) is the design matrix relating each observation to one of the conditions and whose elements are either 0 or 1.

Test Statistics

Even though Y 1 gives us information about the dynamics of brain activity for a given task, it is necessary to verify the statistical significance of the observed effects. Based on the linear model shown in Eq. (7) [Seber, 1984], we write in matrix form the null hypothesis we are interested in testing:

(8)

where the dimension of A is n _contrasts × n _conditions and the dimension of C is n _contrasts × n _variables. For instance, if there are two conditions in our study and we want to test for differences in brain activity between them (a single‐contrast case), we use A = [1 − 1] and C = 0 in Eq. (8), so that the null hypothesis of no activation changes becomes H ₀ : β₁ = β₂.

The statistic used in our hypothesis testing is a multivariate equivalent of the F‐statistic, which is the ratio of the between‐group to the within‐group variances. Here, this ratio is represented by the multivariate F matrix E ⁻¹ H, where H (n _variables × n _variables) and E (n _variables × n _variables) are the between‐group and within‐group variance matrices, respectively, and are given by:

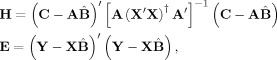(9)

where 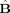is the least‐squares estimate of the parameter matrix, and (X′X)^† indicates the pseudo‐inverse of (X′X). Again, in the case where we test the difference between two conditions, the matrices of Eq. (9) become:

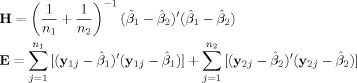(10)

where n ₁ and n ₂ are the number of trials for condition 1 and 2, respectively, and each 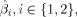is given by the mean of all trials that belong to condition i, such that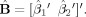

A number of statistics reduce the matrices described above into scalar values to test for statistical significance, including Roy's maximum root, Wilks' likelihood ratio, Lawley‐Hotelling trace, and Pillai's V [Seber, 1984]. They are all functions of the eigenvalues of E ⁻¹ H, and differ in terms of power and robustness to violations of multivariate normality, homogeneity of the covariance matrix, and unequal sample sizes. In this work, we use Roy's maximum root R, which is given by the maximum eigenvalue of E ⁻¹ H, because it is most powerful when the conditions are mainly separated by one discriminant function [Bray and Maxwell, 1985; Field, 2005]. Furthermore, an analytical solution exists to threshold Roy's maximum root statistical maps with random field theory [Worsley et al., 2004], even though we use a permutation approach in this study. In the single‐contrast case shown in Eq. (10) there is only one nonzero eigenvalue and all the above statistics, including R, are equivalent to the Hotelling's T ² [Taylor and Worsley, 2008; Worsley et al., 2004].

For each spatial and temporal location where we fit a MANOVA model, the null hypothesis is rejected with level of confidence (1−α) if the statistic R exceeds a threshold R _α; this threshold is based on a measure that provides control of the number of false positives. The standard approach [Nichols and Hayasaka, 2003] is to control the FWER, or the probability of at least one false positive under the null hypothesis. For MANOVA, this measure can be controlled over space; for ANOVA computed at different frequency bands, it can be controlled over space (therefore, allowing multiple comparison errors over frequencies), or alternatively, simultaneously over space and frequency.

The FWER is directly related to the global maximum distribution of the statistic: one or more voxels will exceed the threshold R _α under H ₀ only if the maximum statistic exceeds R _α. The distribution of the maximum statistic can be estimated empirically with nonparametric permutation methods [Nichols and Holmes, 2001; Pantazis et al., 2005a], since they are exact, computationally feasible, and require very few assumptions about the data (most importantly, exchangeability under H ₀). The permutation samples are created by randomly exchanging the 0's and 1's at the rows of the design matrix X, recomputing the R‐statistic map for the permuted data, and getting its maximum. Repeating this procedure several times and building a histogram from the resulting samples gives us the empirical distribution. To preserve the spatial correlation of the data in the permutation samples, the same randomization of X is applied to each spatial location when computing the permuted R‐map. The same is true for the ANOVA case, with the exception that when controlling FWER over space and frequency, the same randomization scheme is used over space and frequency.

Post‐hoc Analysis

After detecting significant sources in the brain using the method described above, one might be interested in finding which variable, or set of variables, is responsible for the significance of that source. In the present work, we use two approaches: protected F‐tests and linear discriminant analysis [Rencher and Scott, 1990].

Protected F‐tests

This technique consists of fitting a univariate ANOVA model at each of the variables individually, with FWER correction over space and frequency, but only on those sources that were previously considered significant according to the MANOVA method; in other words, the map of significant activity points is used as a “mask”, on whose sources each variable is tested for significance. The use of this “mask” is what makes the protected tests different from the “unprotected” ones, which are simply F‐tests computed at every spatial location and every frequency band of interest, with FWER corrected over space and frequency.

Linear discriminant analysis

Discriminant analysis is a popular technique in pattern classification, with a wide range of applications that also includes MEG [Besserve et al., 2007]. Here, we are more interested in its use as a descriptive tool.

Discriminant functions are linear combinations of variables that best separate groups. Given our observations y _ij, a linear combination transforms them into scalars:

(11)

The vector a that provides the best group separation is the one that maximizes the differences between the mean values of the z _ij's for each group 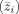, divided by their covariances. In the two‐condition case, this standardized difference is given by [Rencher, 1995]:

(12)

where S is the sample covariance. Using the relationships between S and E, and between 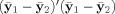and H, shown in Eq. (10), we get:

(13)

Thus the a that maximizes λ = a′Ha/a′Ea is the discriminant function coefficient vector. The solution to Eq. (13) is given by the eigenvector corresponding to the maximum eigenvalue λ of the generalized eigenvalue problem:

(14)

or equivalently the eigenvector a corresponding to the largest eigenvalue of E ⁻¹ H. Since the highest λ is, by definition, Roy's maximum root, finding R gives us a automatically.

If discriminant functions will be used to estimate the relative contribution of each variable to overall group separation, their coefficients must be standardized, because of differences in their magnitudes and in their variances. One way of doing this is by means of discriminant ratio coefficients (DRCs) [Thomas, 1992; Thomas and Zumbo, 1996], which are given by the expression:

(15)

where (.)_k is the k‐th row of (.), and T = E + H is the total variance matrix. The value of d _k is always positive, and therefore indicates how much each variable contributes to the experimental effect, but not whether that variable increases or decreases for a given experimental condition. This information can be retrieved from the estimated parameter matrix 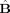of the MANOVA model.

Results

To assess the utility of the proposed MANOVA approach, we compared its performance to that of the ANOVA methods that we previously used in MEG analysis [Pantazis et al., 2009], using both simulated and real MEG data. In MANOVA, the FWER is controlled over space, whereas in ANOVA, unless stated otherwise, the FWER is controlled over space and frequency; the confidence level in all tests is (1−α) = 95%.

In this study, we configured the Morlet wavelet such that at 10 Hz the temporal resolution is 300 msec and the frequency resolution is 2.12 Hz. Furthermore, we used a single time interval T, which covers the entire duration of the experiment (1 sec for both simulated and real data), and the following six frequency bands F: delta (2–4 Hz), theta (5–8 Hz), alpha (8–12 Hz), beta (15–30 Hz), low‐gamma (30–60 Hz), and high‐gamma (60–90 Hz). The choice of these frequency bands is based on previous findings that suggested distinct functional roles for these frequencies in the sensorimotor cortex [Jerbi et al., 2004; Crone et al., 1998; Salmelin et al., 1995; Waldert et al., 2008]. Also, no integration over space was performed on the wavelet coefficients, i.e., S = s for every s.

Simulations

The simulated brain activation Z has the spatial profile shown in Figure 1a, consisting of two active sources, one in each hemisphere. The source in the left hemisphere is a cosine signal with frequency 10 Hz (within the alpha frequency band); the energy of this signal for each trial is sampled from a normal distribution, depending on the trial condition:

(16)

where 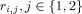are the signal energies for each trial and condition, 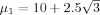, , 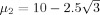and σ = 1. The source in the right hemisphere is a summation of three cosine signals with frequencies 10, 22.5, and 45 Hz (within the alpha, beta, and low‐gamma frequency bands, respectively); the energies of these signals are sampled from a multivariate normal distribution:

(17)

where 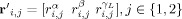are the signal energies for each trial, condition and frequency, and the parameters of the multivariate distribution are:

(18)

Figure 1.

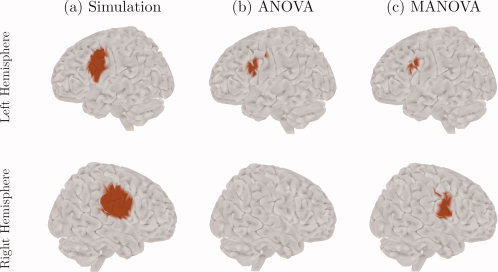
Simulation results. (a) The spatial profile of the two sources simulated on the brain surface; the signal on the left hemisphere lies in the alpha band, whereas the signal on the right hemisphere lies in the alpha, beta and low‐gamma bands; (b) the significant activation regions obtained from the univariate approach (ANOVA), with FWER controlled over space and frequency; (c) the significant activation regions obtained from the multivariate approach (MANOVA), with FWER controlled over space.

The time profile of our simulated sources was inspired by an activation pattern estimated with EEG during a hand movement task [Pfurtscheller and Lopes da Silva, 1999].

Our simulated sources are then projected onto the sensor space according to Eq. (1); zero‐mean Gaussian noise is added thereafter, such that the SNR is 1/200. We simulated a total of 100 trials, or 50 trials per condition. Power observations for the frequency bands mentioned above were fitted to MANOVA models and R‐maps were created for the simulated data. We further performed separate ANOVA tests for each frequency band. The threshold for both cases was set to control 5% FWER, only in space for the MANOVA model, and in space and frequency for the ANOVA model.

Figures 1b,c show the significant sources obtained with both ANOVA and MANOVA approaches, respectively. MANOVA was able to detect both single‐ and multiple‐frequency sources, as we see two activation regions, one on each hemisphere, that reflect the spatial location of the simulated signals. On the other hand, ANOVA was completely insensitive to the multiple‐frequency source, since only the activation region on the left hemisphere is present, although this region is larger than its MANOVA counterpart.

In Figure 2, the results of our post‐hoc analysis methods are presented. Here, we see the significant sources according to the protected F‐tests, and also the sources where the value of DRC was greater than or equal to 1/6, a rule for assessing the contribution of a variable suggested by Thomas [ 1992]. These results are in agreement with the simulated sources, i.e., they indicate that the detected activity on the left hemisphere comes only from the alpha frequency band, whereas that on the right hemisphere comes from the alpha, beta and low‐gamma bands.

Figure 2.

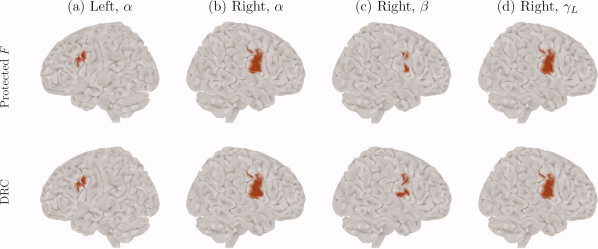
Post‐hoc analysis results on the simulated data, at the α, β, and γ_L frequency bands. Top row: significant sources obtained from the protected F‐test. Bottom row: sources where the discriminant ratio coefficient (DRC) was greater than or equal to 1/6. For the other frequency bands, none of the methods found any active source.

In summary, we find that when compared with ANOVA, MANOVA is able to detect induced activity with higher sensitivity in cases where effects involving signals with multiple, correlated frequencies are present. We also find evidence that our post‐hoc analysis methods are reliable tools for finding the frequency bands that cause the separation among conditions.

Experimental Data

The data used in our work was acquired from a visuomotor task study [Jerbi et al., 2004, 2007]. Two conditions for a single subject were tested: sustained visuomotor control (VM), in which the subject watched a randomly rotating cube in a screen in front of him and manipulated a trackball to prevent the cube from rotating by minimizing its angular deviation, and rest (R), in which the subject looked at a still cube without performing any activity.

Figure 3a shows cortical maps with the values of the R‐statistic at each source, after thresholding for significance. These maps indicate that the differences in brain activity between the VM and R conditions appear in wide regions across the cortical surface, mostly in the parietal lobes, with highest values around the left sensorimotor cortex. Also, as expected, the highest values of R predominantly lie in the left hemisphere, which is in line with the fact that the subject used his right hand to move the trackball.

Figure 3.

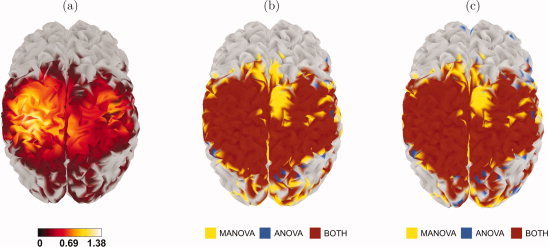
Results of the analysis with data from a visuomotor study. (a) Brain map of the R‐statistic, after thresholding for significance; (b) comparison between ANOVA (FWER corrected over space and frequency) and MANOVA; (c) comparison between ANOVA (FWER corrected over space) and MANOVA. In the last two maps, sources in red were detected by both methods, sources in yellow were detected by MANOVA only, and sources in blue were detected by ANOVA only.

A comparison of the performance of our MANOVA method with that of ANOVA can be found in Figure 3b. Besides the considerable amount of overlap between the sources detected by both methods, an interesting feature of these maps is that the extent of the cortical regions showing experimental effects detected only by ANOVA is smaller than of those detected only by MANOVA. We may take a less conservative approach and perform the ANOVA test with FWER correction only over space. Here, in the worst case where the frequency bands are independent, the achieved confidence level is not (1−α) = 95%, but (1 − α)⁶ = 73.51%. Even in this case, MANOVA is still able to detect sources that ANOVA is not, as Figure 3c shows. (In fact, these images show that, in this study, the difference between correction over space and frequency and correction only over space is very small in ANOVA.)

Given the difference between the MANOVA and ANOVA methods, it is important to find the frequency band (or bands) responsible for the significance in the R maps. As discussed above, protected F‐tests and linear discriminants are suitable methods for finding this information, and the resulting cortical maps are shown in Figures 4 and 5, respectively. There are some differences between these maps, for instance the active sources for the high‐gamma band have very different spatial patterns, which should be expected since each method performs a different kind of analysis: protected F‐tests look at each frequency band without taking into account the other bands, whereas linear discriminants look at all variables simultaneously. However, it is clear from both maps that the beta frequency band brings the greatest contribution to the overall group separation, followed by the low‐gamma band but with considerably less influence in the activation changes.

Figure 4.

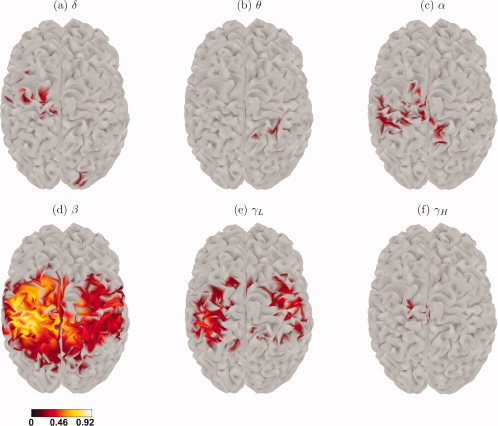
Thresholded protected F brain maps for each frequency band of interest.

Figure 5.

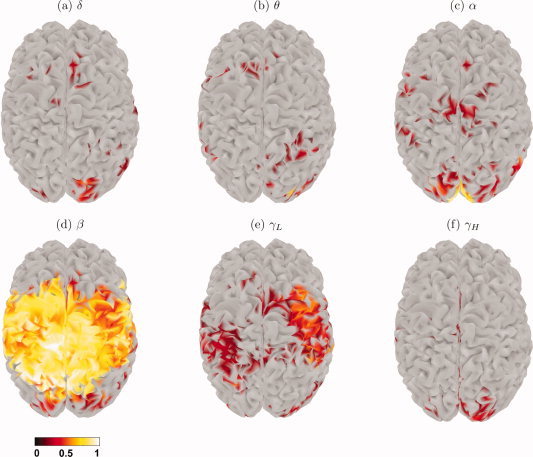
Brain maps of the DRCs greater than or equal to 1/6 for each frequency band of interest.

A closer look at the behavior of a few selected voxels is provided by Figure 6. It shows the DRC values and the mean power for each condition, normalized by the standard deviation, for the voxel with the highest value of the R‐statistic (Fig. 6a), a voxel detected by MANOVA but not by ANOVA nor by any of the protected F‐tests (Fig. 6b), and a voxel not detected by MANOVA (Fig. 6c). In the first case, the changes in activation are mostly caused by the beta, low‐, and high‐gamma frequency bands. In the second case, a combination of the delta, alpha, beta, and high‐gamma bands causes a significant discrimination, but none of these frequencies is significant by itself. Finally, in the third case, the changes between conditions are very small for every band; even though some DRCs have large values, this reflects the fact that they are standardized to sum to 1, and should not be considered evidence of significant overall separation.

Figure 6.

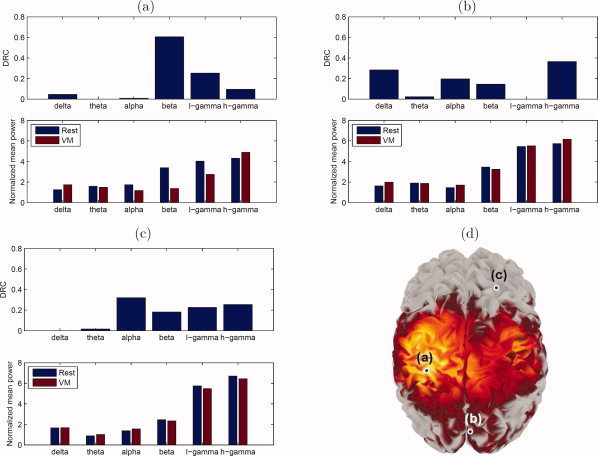
DRC and normalized mean power for both conditions at specific voxels. (a) Voxel with the highest value of the R‐statistic; (b) voxel detected by MANOVA, but not by ANOVA nor by any of the protected F‐tests; (c) voxel not detected by MANOVA; (d) spatial location on the cortical surface of each of the selected voxels.

Discussion

In this study, we have developed a multivariate method for the detection of significant task‐related modulations of oscillatory activity in MEG data. By combining time–frequency decomposition of the MEG signals and multivariate statistical inference, we were able to reliably detect task‐related cortical activations where univariate approaches were previously insensitive. The advantages of the multivariate technique were shown with both simulated data and MEG visuomotor recordings.

In both simulated and real data, despite the considerable overlap between both MANOVA and ANOVA methods, the number of statistically significant surface elements obtained from MANOVA was higher than the number of significant sources obtained from ANOVA. Also, MANOVA was more sensitive to the activity of a number of sources even if less conservative ANOVA tests were performed. The difference in performance between the two methods is more evident in the simulation results, where MANOVA was sensitive to both single‐frequency and multiple‐frequency sources (i.e., to changes in a single variable as well as to changes in multiple variables, respectively), whereas ANOVA found sources only in the former.

A number of factors may have influenced our results, such as the choice of a specific inverse operator to reconstruct current density maps, or the selection of a volumetric source space rather than cortical imaging. We could have also used alternative ways to control false positives, for example multivariate random field methods [Carbonell et al., 2008; Taylor and Worsley, 2008] instead of permutations to estimate the maximum distribution, or even the use of false discovery rate [Benjamini and Hochberg, 1995; Genovese et al., 2002] instead of the FWER.

Our findings are better understood if we look at the basic concepts behind Roy's maximum root, and the operations this statistic performs on the multivariate data. The key concept behind it is the union–intersection principle [Roy, 1953; Seber, 1984; Worsley et al., 2004]: a multivariate null hypothesis is the intersection of simpler univariate null hypotheses, or conversely, the multivariate alternative hypothesis is the union of univariate alternative hypotheses. Based on this principle, R can be computed by creating a univariate model from the original multivariate model through a linear combination on the observations, computing the F‐statistic for the new model, repeating this procedure for all linear combinations, and taking the maximum F. Thus, Roy's maximum root is a statistical test that simultaneously considers all possible simpler hypothesis F‐tests derived by linearly combining the multivariate observations (infinite in number). The combined null hypothesis is the intersection of the simpler null hypotheses, and therefore, to control the error rate among them, we need to apply a higher threshold than the one we would apply to control only a single univariate test. However, if a correlation pattern causes a linear combination of the observations to have a high F‐statistic, then only MANOVA will detect it because ANOVA does not test for arbitrary linear combinations of observations. ANOVA only tests for the trivial linear combinations of observations that assign 1 to the variable of interest, and 0 to all other frequency bands.

Given the relationship between Roy's maximum root and the union–intersection principle, the work of Carbonell et al. [ 2004] is in a sense a direct precursor of our MANOVA method. In this paper, a one‐dimensional statistical map was formed over time by using a multivariate statistic over space. The statistical map was thresholded by means of random field theory, and once significant time instances were identified, the union–intersection principle allowed further localization of the effect in space. In our work, we form the statistical map in space–time instead of just time, and threshold it using permutation tests instead of random field theory. Furthermore, the union–intersection principle of Roy's maximum root would have allowed us to further localize the effect in frequency, similarly to Carbonell et al. [ 2004] in space. However, we implemented an alternative method based on protected F‐tests, whose significance was evaluated with an additional permutation analysis to exactly control the FWER on the locations in space–time where the null hypothesis had already been rejected. We further evaluated the contribution of each frequency to the experimental effect with discriminant analysis, an approach not included in Carbonell et al. [ 2004].

Going back to our results, it is reasonable to expect sources sensitive only to ANOVA because, when a single variable shows differences between conditions, MANOVA is more conservative than ANOVA, since here the former is equivalent to a univariate test at a level higher than (1−α). On the other hand, it is also reasonable to expect sources that can only be detected by MANOVA because this might relate to variables that do not show an effect when considered individually, but that contribute to group separation when combined, especially if they are somewhat correlated.

As a follow‐up method to our MANOVA technique, we found that both protected F‐tests and linear discriminants are reliable ways to identify individual frequency bands that contribute significantly to changes in brain activation. This is demonstrated by our simulation results, since either method was able to detect accurately the bands that form the simulated time series on each source.

When applied to real data, our post‐hoc analysis points towards interesting results. One noteworthy finding is how the sources detected by each technique differ; as mentioned before, this is evident for the high‐gamma band (among other cases), as the activation found by the protected F‐test lies entirely on the left hemisphere, whereas most of the sources with sufficiently high DRCs are on the right hemisphere. If we assume that all the significant results of our statistical tests faithfully describe the experimental effects of the real data, then these seemingly contradictory findings are in fact evidence of different activation patterns in the brain, to which each of the methods here is sensitive. In particular, the significant F values in the left hemisphere in Figure 4f indicate sources with a high between‐condition variation in high‐gamma power. However, these sources have small DRCs in the high‐gamma band, as seen in Figure 5f, because the beta frequency contributes much more to the condition separation than high‐gamma. On the contrary, high DRCs on the right hemisphere of Figure 5f denote sources where high‐gamma changes contribute strongly to the separation between conditions, together with other bands, but high‐gamma itself is insufficient to separate the two conditions with an F‐test.

Figure 6b refers to a voxel in the right visual cortex that is sensitive to MANOVA but not to ANOVA. In this voxel, no frequency band is significantly active, according to the protected F‐tests, but the DRC values and the differences in the normalized mean power between conditions indicate that the activity variation there comes mostly from the high‐gamma, alpha, delta, and beta bands. Thus, it is a situation in which separation is caused not by a single variable but by a combination of variables, and it demonstrates not only the advantages of multivariate over univariate analysis, but also the potential of MANOVA as a tool for studying frequency interactions in the brain. An increasing number of studies suggest that investigating the relationship between power and phase modulations in multiple frequency bands in various cortical structures might provide fundamental insights into the network dynamics underlying various aspects of neural processing [Canolty et al., 2006; Darvas et al., 2009; Jensen and Colgin, 2007]. The multivariate framework proposed here and its possible extensions may provide a novel procedure to address the question of cross‐frequency coupling in the human brain.

Finally, even though we demonstrated the MANOVA approach on a single‐subject study, it can be similarly applied to multi‐subject studies. The easiest way would be to use the summary statistics approach [Beckmann et al., 2003; Holmes and Friston, 1998; Mumford and Nichols, 2006], where a first or lower level model fits the data for each subject separately, and a second level combines the different subjects. In this case, the first stage model could estimate a multivariate contrast of interest, such as the difference in power between two conditions for each frequency. The second stage model could then use the multivariate contrasts from each subject as multivariate observations in a MANOVA model.