Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2010 Feb 3;277(1688):1743–1749. doi: 10.1098/rspb.2009.2191

An experimental test of a fundamental food web motif

Jason M K Rip 1, Kevin S McCann 1,*, Denis H Lynn 1, Sonia Fawcett 1
PMCID: PMC2871856  PMID: 20129988

Abstract

Large-scale changes to the world's ecosystem are resulting in the deterioration of biostructure—the complex web of species interactions that make up ecological communities. A difficult, yet crucial task is to identify food web structures, or food web motifs, that are the building blocks of this baroque network of interactions. Once identified, these food web motifs can then be examined through experiments and theory to provide mechanistic explanations for how structure governs ecosystem stability. Here, we synthesize recent ecological research to show that generalist consumers coupling resources with different interaction strengths, is one such motif. This motif amazingly occurs across an enormous range of spatial scales, and so acts to distribute coupled weak and strong interactions throughout food webs. We then perform an experiment that illustrates the importance of this motif to ecological stability. We find that weak interactions coupled to strong interactions by generalist consumers dampen strong interaction strengths and increase community stability. This study takes a critical step by isolating a common food web motif and through clear, experimental manipulation, identifies the fundamental stabilizing consequences of this structure for ecological communities.

Keywords: motif, module, interaction strength, stability, weak interactions

1. Introduction

Knowledge of the interaction strength between species has proven crucial to understanding the role of food web structure in governing stability (May 1973; Yodzis 1981; McCann 2000). Although a daunting task, there is a relatively long history of assessing patterns in the structure and strength of real food webs (e.g. Cohen et al. 1990; Pimm et al. 1991) with a recent extension of these early results to include modern network theory (e.g. Milo et al. 2002; Williams et al. 2002). From this modern network research several empirical trends have emerged. First, researchers have identified certain network motifs (i.e. an i species sub-system) that are ubiquitous in food webs regardless of ecosystem type (Milo et al. 2002; Bascompte & Melian 2005; Stouffer et al. 2007). Second, these complex food web networks are known to have a hierarchical structure with some motifs repeated at a variety of hierarchical scales (Clauset et al. 2008). Third, estimates of interaction strength within communities repeatedly show a distribution of many weak interactions with only a few strong interactions (Berlow et al. 1999; Neutel et al. 2002; Berlow et al. 2004). Finally, these motifs have been shown to effect the stability of networks (Kondoh 2008; Stouffer & Bascompte 2009).

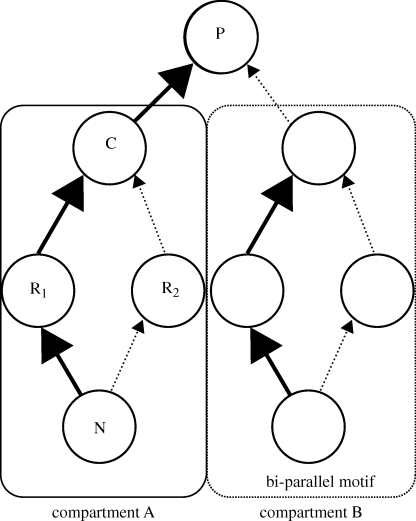
The bi-parallel food web motif, in particular, integrates across all these findings (figure 1). It has been repeatedly shown to be over-represented in the existing food web data (Milo et al. 2002; Bascompte & Melian 2005; Stouffer et al. 2007), occurs across enormous spatial scales, and commonly displays differential interaction strengths (McCann & Rooney 2009). For clarity, it is worth pointing out that a motif with interaction strengths is also commonly referred to as a food web or community module in the ecological literature (sensu Holt 1997). Hereafter, in order to integrate with the more general use of the term in network theory, we refer to these low number sub-systems as a food web motif.

Figure 1.

Figure 1.

Open in a new tab

Representative food web showing the fundamental food web module of a generalist consumer coupling resources with different interaction strengths. Compartment A shows the module tested in the current experiment, a consumer (C) with two resources (R). Compartment B shows an example of the bi-parallel motif, a common structural arrangement within food webs. The top predator (P) couples both compartments together.

One explanation for the common existence of differential interaction strength in this motif arises from a basic ecological trade-off between growth and edibility. In general, resources that tend to grow fast remain less defended than those resources that allocate significant resources to defence (Agrawal et al. 1999). This translates into consumers having high attack rates on fast growing resources and low attack rates on well-defended resources.

At the smallest scale of a consumer with one resource species, individual variability (e.g. arising either from phenotypic plasticity or genetic variation) can set up a gradient in resource defensibility and thus interaction strength (Spitze 1992). In addition, within a given habitat, individuals consume different resource species embodying the general growth-defence trade-off, and so also produce a range of interaction strengths (Agrawal et al. 1999; Kneitel & Chase 2004; figure 1 compartment A: sub-motif occurs when consumer C consumes R1 strongly and R2 weakly). Finally, at the largest spatial scale, consumers capable of moving across major habitat types differentially couple compartments occurring within and across ecosystems—in this latter case often large size differences between prey species from very different habitats drive different interaction strength pathways (Wootton 1997; Krause et al. 2003; Rooney et al. 2006; figure 1: motif occurs when higher order predator P consumes species in two compartments, A and B). The recurrence of differential interaction strengths between a generalist consumer and its prey at a variety of ecological scales sets up a powerful hierarchical structure that distributes coupled strong and weak interactions throughout food webs. This fascinating repetition across scales highlights the fundamental and repeated nature of this food web motif.

It remains to examine the implications of this structure. An interesting property of the bi-parallel motif is that it has been shown theoretically to impact the stability of communities in two important ways: by dampening strong species interactions and generating negative covariance between the abundances of resource species (McCann 2000). A classic theoretical observation in ecology is that strong consumer–resource interactions tend to be destabilizing (Rosenzweig 1971). Given that increased interaction strengths destabilize dynamics then it is also true that any biological mechanism capable of reducing the strength of a potentially strong consumer–resource interaction should play a critical role in stabilizing a community by dampening or eliminating complex and oscillatory population dynamics (McCann et al. 1998). One way of reducing the strength of potentially destabilizing interactions is to couple strong interactions within a community to weaker interactions through generalist consumption (McCann et al. 1998). Again, the bi-parallel motif and its accompanying trade-offs readily produce this coupling of strong and weak interactions.

In addition to reducing the strength of strong interactions, generalist consumers are also capable of generating negative covariance in the abundances of competing resource species (McCann 2000). Negative covariance between species can be important, as increasing the number of negatively covarying species within a community reduces total community variability, thus increasing stability (Tilman 1996). By reducing potentially destabilizing interaction strengths throughout the web and driving negative covariance, the ubiquitous bi-parallel motif may therefore play a critical role in the maintenance and functioning of diverse food webs.

To experimentally examine the stabilizing role of the bi-parallel motif we isolated a naturally occurring generalist consumer and two of its common resources. To our knowledge this is the first experiment to directly test this motif. This naturally occurring motif importantly readily produces differential interaction strengths. We sought to test three predictions: (i) coupling a weak interaction to a strong one should dampen the interaction strength between the consumer and its resources relative to a community where only the strong interaction is present; (ii) consumers should generate negative covariance between resources; and (iii) coupling a weak interaction to a strong one should increase community stability relative to a community where only the strong interaction is present.

2. Material and methods

Our manipulation was accomplished by setting up replicate aquatic microcosms in three treatments, each with a different community composition. Our aquatic microcosms were created from natural planktonic food webs and contained combinations of the rotifer consumer (Brachionus calyciflorus) and two algal resources, Chlorella vulgaris and Scenedesmus obliquus. Our first treatment contained the consumer (B. calyciflorus) and a resource (S. obliquus) for which it has a strong consumer–resource interaction. Our second treatment contained the consumer (B. calyciflorus) and a resource (C. vulgaris) for which it has a weak consumer–resource interaction. Our third treatment contained the consumer (B. calyciflorus) and both resources (S. obliquus and C. vulgaris), where the consumer couples through consumption of both a strong and a weak interaction. Interaction strength treatments were established from research showing that B. calyciflorus has higher growth rates and consumption rates on larger algal species, such as S. obliquus (mean ± s.e.m. of longest linear dimension (LLD) = 11.62 ± 0.34 µm, n = 25), compared with smaller species, such as C. vulgaris (Rothhaupt 1990; Pagano 2008; LLD = 5.56 ± 0.39 µm, n = 25).

Aquatic microcosms were composed of 500 ml of autoclaved, artificial COMBO medium (Kilham et al. 1998) maintained in an incubator at 20°C with a 12 h light : 12 h dark cycle. Each microcosm was randomly assigned to one of the three different treatments, each with five replicates. Treatments were: (i) B. calyciflorus (Florida Aqua Farms Inc., Dade City, USA) and S. obliquus (University of Toronto Culture Collection (UTCC), Toronto, Canada, number 157); (ii) B. calyciflorus and C. vulgaris (UTCC number 90); (iii) B. calyciflorus and both S. obliquus and C. vulgaris. On day 0, each microcosm was inoculated with an equivalent biovolume density of algae (1.4 × 107 µl ml−1). In communities with both algal species, each species made up 50 per cent of the total biovolume. In addition, on day 0, 20 B. calyciflorus, previously cultured on the same alga as to be used in their treatment, were added to each microcosm. In communities with both algal species, half of the B. calyciflorus added were grown on S. obliquus and half were grown on C. vulgaris. On day 36 of the experiment, an additional treatment was started to assess algal dynamics in the absence of B. calyciflorus. These microcosms were set up exactly as above with the exception that no rotifers were added to the treatment.

Population dynamics were estimated every second day for 56 days. Prior to sampling, microcosms were stirred gently. Brachionus calyciflorus populations were estimated by withdrawing 2 ml of microcosm fluid and counting the number of individuals under a dissecting microscope. This was repeated until either 50 rotifers or 10 ml of fluid had been examined. Samples were returned to their appropriate microcosm following sampling. Density was then converted to biovolume by multiplying density by the mean volume (mean ± s.e.m. of biovolume of ellipsoid = 3.4e6 ± 2.6e6 µm3 (using standard geometric formula (Wetzel & Likens 1991)). In single algal treatments, algal populations were estimated by withdrawing 3 ml of microcosm fluid and measuring chlorophyll a (Chl a) using an in vivo fluorometer (AquafluorTM handheld fluorometer, Turner Designs, Sunnyvale, USA). Chl a was then converted to biovolume using empirically determined regressions (C. vulgaris: biovolume (µm3) = 1.76e6 × Chl a, S. obliquus: biovolume (µm3) = 3.99e6 × Chl a). In treatments with both algal species, algal populations were estimated by counting the number of each species in an 8-µl sample using a haemocytometer under a compound microscope. This was repeated until either 100 cells or 4 mm2 of the haemocytometer were counted. Algal cell density was then converted to biovolume by multiplying density with the mean volume of each species (C. vulgaris: mean ± s.e.m. of biovolume of sphere = 109.8 ± 16.1 µm3; S. obliquus: mean ± s.e.m. of biovolume of ellipsoid = 63.3 ± 5.3 µm3 (using standard geometric formula; Wetzel & Likens 1991)).

Interaction strength was estimated as the exponential growth rate of B. calyciflorus over the first 10 days of the experiment. The following formula was used: ln(N10/N2)/t10 − t2, where N is the biovolume density of B. calyciflorus and t time in days. Day 2 was used for the initial measurement as it was the first sampling date. This is a metric of per capita interaction strength at high resource densities, estimating the strength of the coupling term between the consumers and the resource as proposed by McCann et al. (1998). While this is not equivalent to the interaction strength employed in removal experiments (Wootton 1997), it is consistent with the numerous dynamic energetics-based interaction strength definitions of recent theory (McCann 2000). Interaction strength was measured independently for each treatment (e.g. for the coupled treatment, interaction strength was measured as the rotifer growth rate on both resources). Analysis of variance (ANOVA) with Tukey's HSD was used to test for differences between experimental treatments.

Stability was measured in several ways. Temporal variability was measured as the coefficient of variation of each time series (for both algal species and B. calyciflorus) following an initial transient. The transient period was determined using a Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test for stationarity (l = 0) and confirmed through analysis of model fits (Kwiatkowski et al. 1992). ANOVA with Tukey's HSD was used to test for differences in coefficient of variation between groups. Boundedness from zero was measured as the minimum algal density or B. calyciflorus density over the 56 days of sampling following an initial period of growth. ANOVA with Tukey's HSD was used to test for differences between groups for boundedness from zero. Periodicity was tested using an auto-correlation function for each B. calyciflorus time series. Mathematical stability was estimated as the maximum eigenvalue for the best-fit model to each replicate community. The best model fit was based on the maximum log-likelihood fit of a basic multispecies model to the time series. The model was the following system of three equations:

2. 2.5
2. 2.5

and

2. 2.5

We assumed basic logistic growth for both resources—C. vulgaris (RA) and S. obliquus (RS), where rR was the growth rate and kR the carrying capacity. We further assumed a multispecies functional response between the consumer B. calyciflorus (C) and both resources, where aR was the attack rate, hR the handling time and e the conversion efficiency of resource to consumer. Finally, we assumed a linear mortality term m for the consumer.

Negative covariance between algal species was calculated as the correlation between C. vulgaris and S. obliquus in treatments where both species were present. A two-tailed, t-test was used to compare the mean correlation in jars with and without B. calyciflorus.

3. Results

(a). Interaction strength

Estimates of interaction strength from our experimental data matched those of previous experiments (Rothhaupt 1990; Pagano 2008). Rotifers growing on S. obliquus showed the highest interaction strength (i.e. growth rate; table 1). This was significantly higher than that of the rotifer growing on C. vulgaris. As predicted by theory, the rotifer consuming both species of resource had an intermediate interaction strength on both species. This shows that weak interactions when coupled to strong ones are capable of dampening the strong interaction.

Table 1.

Estimates of interaction strength and resulting measures of stability for each experimental treatment. Here, n is the number of replicate microcosms. Numbers presented are means ± s.e. Letters (A, B, C) represent significant differences from ANOVA (d.f. = 2, 13) with Tukey's HSD analysis (p ≤ 0.05). ACF, autocorrelation function.

stability metric units strong interaction (B. calyciflorus with S. obliquus) weak interaction (B. calyciflorus with C. vulgaris) coupled interactions (B. calyciflorus with S. obliquus and C. vulgaris)
interaction strength (ln(Δ B. calyciflorus) day−1) 0.50 ± 0.04A 0.34 ± 0.04B 0.43 ± 0.03A,B
temporal variability (CV algal biovolume ml−1 × 106) 0.74 ± 0.03A 0.23 ± 0.01B 0.55 ± 0.07C
(CV B. calyciflorus biovolume ml−1 × 106) 1.00 ± 0.06A 0.80 ± 0.10A 0.49 ± 0.07B
boundedness from zero (min. algal biovolume ml−1 × 106) 10.02 ± 1.09A 84.34 ± 10.29B 17.54 ± 3.84A
(min. B. calyciflorus biovolume ml−1 × 106) 0.82 ± 0.17A 5.67 ± 1.97B 5.80 ± 1.04B
periodicity max. ACF for algae where p < 0.05 14 day-ACF (n = 4) 20 day-ACF (n = 4) 23 day-ACF (n = 2)
max. ACF for B. calyciflorus where p < 0.05 10 day-ACF (n = 5) 20 day +ACF (n = 4) 17 day-ACF (n = 3) 16 day-ACF (n = 1)
mathematical stability (average model eigenvalue) −0.066 ± 0.011 −1.49 ± 0.17 −0.19 ± 0.047
dynamical behaviour damped oscillations (n = 5) damped oscillations (n = 1) stable equilibrium (n = 4) damped oscillations (n = 3) stable equilibrium (n = 2)
Open in a new tab

(b). Negative covariance

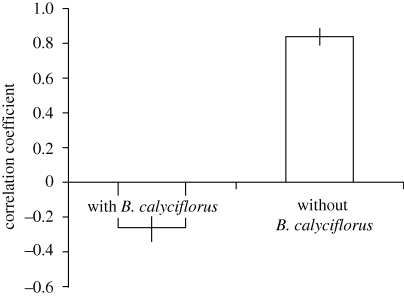
As predicted, rotifers generated negative covariance between resources. In communities where the consumer was absent, resources were positively correlated (figure 2). When the consumer was present, resources were significantly more negatively correlated (figure 2).

Figure 2.

Figure 2.

Open in a new tab

Correlation coefficients between the density of C. vulgaris and S. obliquus in communities with and without B. calyciflorus. Here we show mean ± s.e. Communities with B. calyciflorus are significantly more negatively correlated than communities without B. calyciflorus (two-tailed t-test, d.f. = 8, p < 0.001).

(c). Stability

Our results on community stability were consistent with theory on weak interactions. We adopt the approach of using a variety of stability metrics (Grimm & Wissel 1997; Ives & Carpenter 2007), and examine consistency across our results. For all four of our empirical estimates of stability (see below), the observed trends show that communities with only a strong interaction were less stable than those with only a weak interaction, and that coupling a weak interaction to a strong interaction increased the stability of the community (figure 3 and table 1).

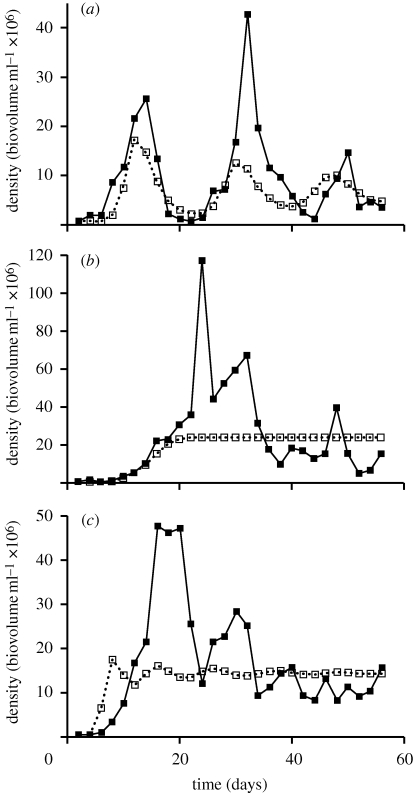
Figure 3.

Figure 3.

Open in a new tab

Sample population dynamics of B. calyciflorus for each experimental treatment. Presented are population dynamics (solid line) and model dynamics (dotted line) for each of the three treatments: (a) the strong consumer–resource interaction; (b) the weak consumer–resource interaction and (c) the weak and strong consumer–resource interaction.

Our first estimate of stability was temporal variability calculated using the coefficient of variation of both rotifer and algal time series. Temporal variability of algal populations was significantly greater in the community with only the strong interaction than in the community with both interactions coupled together, which in turn was significantly greater than the community with only the weak interaction (table 1). Temporal variability of the rotifer populations with only the strong interaction was highest but not significantly different than the community with only the weak interaction (table 1). The rotifer populations with both interactions coupled together were significantly more stable than both of the single interaction communities (table 1).

A second estimate of stability was boundedness from zero. This is an important metric, common to theoretical studies, as populations near zero have an increased risk of extinction owing to random perturbations. Algal populations in the community with only the strong interaction were closest to zero, but not significantly different than communities with both interactions (table 1). The community with only the weak interaction was the most well-bounded from zero, being significantly higher than the other treatments (table 1). Rotifer populations were significantly closer to zero in the community with only the strong interaction compared to the communities with the weak interaction, and with both interactions (table 1).

A third estimate of stability was periodicity observed in an autocorrelation function of the time series. For the communities composed of only the strong interaction, there was evidence of cyclic population dynamics since in the majority of replicates, there was significant positive autocorrelation at 20 days for the rotifers and a significant negative autocorrelation of 10 days for the rotifers and 14 days for the algae (table 1). For the communities with only the weak interaction there was no evidence of positive autocorrelation suggesting non-cyclic population dynamics (table 1). In some replicates of this treatment there was significant negative autocorrelation at 17 days for the rotifer and 20 days for the algae (table 1). This suggests some evidence for half a cycle in these time series, as these populations show an overshoot before reaching equilibrium (figure 3). The communities with coupled interactions showed the least evidence of periodicity with no positive and rare negative autocorrelations. Two algal replicates showed a 23-day negative autocorrelation, while one rotifer population had a 16-day negative autocorrelation (table 1).

Finally, we examined the mathematical stability of each community by fitting time series data to a simple consumer–resource model. We chose a well-known model with realistic assumptions capable of generating a range of dynamical behaviour (Murdoch et al. 2003). This allowed us to compare the eigenvalue and qualitative dynamical behaviour across treatments. Here, model-fits are used to describe the qualitative dynamics (e.g. estimate eigenvalues) produced by the best model fits. In communities with only the strong interaction, mathematical model fits were the least stable with communities possessing eigenvalues close to 0 (table 1). Model behaviour consistently showed oscillations dampening to equilibrium (figure 3a). In communities with only the weak interaction, model fits were most stable with negative eigenvalues farthest from 0 (table 1). Here, model behaviour was characterized by monotonic or, in one case, dampening oscillations to a stable equilibrium (figure 3b). Communities where both weak and strong interactions were coupled together were more stable than communities with only the strong interaction and less stable than communities with only the weak interaction (table 1). Model behaviour was also intermediate to the single species communities, whereby dynamics showed dampening oscillations to a stable equilibrium in three cases, and monotonic approach to equilibrium in two cases (figure 3c).

4. Discussion

Major goals of ecological research are to identify and understand the importance of biological structure. Here we have identified a fundamental food web motif, a generalist consumer coupling resource together with different interaction strengths, and taken the first critical step in empirically isolating and testing the importance of this structure for community stability. We showed that in direct correspondence with ecological theory, weak interactions serve to mute strong interactions, generate negative covariance, and increase community stability. Our results are consistent across a variety of stability metrics. In addition, our results highlight the power of small-scale experimental manipulations. While ultimately it is of importance to experimentally test the hierarchical implications of such nested structures, it remains that the fundamental unit underlying this hierarchical structure must be clearly tested. Here, we do this by extracting a small-scale unit from a natural aquatic food web, and show that this motif plays a potent stabilizing role in food webs.

In our microcosms, generalist consumers drove asynchrony in their resources. Increased negative covariance between species has been important in explaining why increased biodiversity can increase stability. Increasing the number of species in a community that vary asynchronously with each other reduces the overall variability of a community (Tilman 1996; McCann 2000). Any structure that increases the negative covariance between species further serves to increase overall community stability (Tilman 1996). Here, we have demonstrated that generalist consumption can act as a mechanism capable of generating negative covariance between species, which further reinforces the relevance of both generalist consumers and this food web motif to natural ecological communities. This result has also been seen in natural pelagic plankton communities where crustacean consumption generates negative covariance between edible and non-edible algae (Vasseur et al. 2005). A recent experimental study (Jiang et al. 2009), which focused on the role of prey diversity in a microbial food chain, has found that weak interactions may play a role in stabilizing food chains with multiple resources. Although this is not an exact example of the motif we studied here, it does importantly suggest that our results may scale up to include prey diversity and more complex pathways.

Our experimental community, drawn from a real natural food web, shows the importance of this structure at the small scale of a single consumer with two resources. However, given the prevalence of this motif across a broad range of spatial scales—from within-habitats to across whole ecosystems (Milo et al. 2002; Rooney et al. 2006)—our results may extend beyond microcosms to wherever this motif is observed. In addition, these motifs have been shown to comprise the building blocks of complex empirical food webs, with important consequences for stability (Bascompte et al. 2005; Kondoh 2008). It becomes critical to identify other such biostructures and address whether human modification is deteriorating these natural building blocks or not.

Acknowledgements

J.M.K.R., K.S.M. and D.H.L. contributed to the design of the experiment, discussion of the results, and writing of the manuscript. J.M.K.R. and S.F. conducted the experiment. We thank N. Rooney and J. Fryxell for their comments on the manuscript. Research funded by a NSERC discovery grants to K.S.M. and D.H.L. We also thank two anonymous reviewers as their suggestions improved the manuscript.

References

  1. Agrawal A. A., Laforsch C., Tollrian R.1999Transgenerational induction of defences in animals and plants. Nature 401, 60–63 (doi:10.1038/43425) [Google Scholar]
  2. Bascompte J., Melian C. J.2005Simple trophic modules for complex food webs. Ecology 86, 2868–2873 (doi:10.1890/05-0101) [Google Scholar]
  3. Bascompte J., Melian C. J., Sala E.2005Interaction strength combinations and the overfishing of a marine food web. Proc. Natl Acad. Sci. 102, 5443–5447 (doi:10.1073/pnas.0501562102) [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berlow E. L., Navarrete S. A., Briggs C. J., Power M. E., Menge B. A.1999Quantifying variation in the strengths of species interactions. Ecology 80, 2206–2224 [Google Scholar]
  5. Berlow E. L., et al. 2004Petchey interaction strengths in food webs: issues and opportunities. J. Anim. Ecol. 73, 585–598 (doi:10.1111/j.0021-8790.2004.00833.x) [Google Scholar]
  6. Cohen J. E., Briand F., Newman C.1990Community food webs: data and theory, 308 pp..New York, NY: Springer [Google Scholar]
  7. Clauset A., Moore C., Newman M. E. J.2008Hierarchical structure and the prediction of missing links in networks. Nature 453, 98–101 (doi:10.1038/nature06830) [DOI] [PubMed] [Google Scholar]
  8. Grimm V., Wissel C.1997Babel, or the ecological stability discussions: an inventory and analysis of terminology and a guide for avoiding confusion. Oecologia 109, 323–334 (doi:10.1007/s004420050090) [DOI] [PubMed] [Google Scholar]
  9. Holt R. D.1997Community modules. In Multitrophic interactions in terrestrial ecosystems, 36th Symposium of the British Ecological Society (eds Gange A. C., Brown V. K.). London, UK: Blackwell Science Ltd [Google Scholar]
  10. Ives A. R., Carpenter S. R.2007Stability and diversity of ecosystems. Science 317, 58–62 (doi:10.1126/science.1133258) [DOI] [PubMed] [Google Scholar]
  11. Jiang L., Joshi H., Patel S. N.2009Predation alters relationship between biodiversity and temporal stability. Am. Nat. 173, 389–399 (doi:10.1086/596540) [DOI] [PubMed] [Google Scholar]
  12. Kilham S. S., Kreeger D. A., Lynn S. G., Goulden C. E., Herrera L.1998COMBO: a defined freshwater culture medium for algae and zooplankton. Hydrobiologia 377, 147–159 (doi:10.1023/A:1003231628456) [Google Scholar]
  13. Kneitel J. M., Chase J. M.2004Trade-offs in community ecology: linking spatial scales and species coexistence. Ecol. Lett. 7, 69–80 (doi:10.1046/j.1461-0248.2003.00551.x) [Google Scholar]
  14. Kondoh M.2008Building trophic modules into a persistent food web. Proc. Natl Acad. Sci. 152, 16 631–16 635 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Krause A. E., Frank K. A., Mason D. M., Ulanowicz R. E., Taylor W. W.2003Compartments revealed in food-web structure. Nature 426, 282–285 (doi:10.1038/nature02115) [DOI] [PubMed] [Google Scholar]
  16. Kwiatkowski D., Phillips P. C. B., Schmidt P., Shin Y. C.1992Testing the null hypothesis of stationarity against the alternative of a unit-root—how sure are we that economic time-series have a unit-root. J. Econ. 54, 159–178 (doi:10.1016/0304-4076(92)90104-Y) [Google Scholar]
  17. May R.1973Stability and complexity in model ecosystems Princeton, NJ: Princeton University Press [Google Scholar]
  18. McCann K. S.2000The diversity-stability debate. Nature 405, 228–233 (doi:10.1038/35012234) [DOI] [PubMed] [Google Scholar]
  19. McCann K., Hastings A., Huxel G. R.1998Weak trophic interactions and the balance of nature. Nature 395, 794–798 (doi:10.1038/27427) [Google Scholar]
  20. McCann K. S., Rooney N.2009The more food webs change the more they stay the same. Phil. Trans. R. Soc. B 364, 1789–1801 (doi:10.1098/rstb.2008.0273) [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Milo R., Shen-Orr S., Itzkovitz S., Kashtan N., Chklovskii D., Alon U.2002Network motifs: simple building blocks of complex networks. Science 298, 824–827 (doi:10.1126/science.298.5594.824) [DOI] [PubMed] [Google Scholar]
  22. Murdoch W. W., Briggs C. J., Nisbet R. M.2003Consumer-resource dynamics Princeton, NJ: Princeton University Press [Google Scholar]
  23. Neutel A. M., Heesterbeek J. A. P., de Ruiter P. C.2002Stability in real food webs: weak links in long loops. Science 296, 1120–1123 (doi:10.1126/science.1068326) [DOI] [PubMed] [Google Scholar]
  24. Pagano M.2008Feeding of tropical cladocerans (Moina micrura, Diaphanosoma excisum) and rotifer (Brachionus calyciflorus) on natural phytoplankton: effect of phytoplankton size-structure. J. Plankton Res. 30, 401–414 (doi:10.1093/plankt/fbn014) [Google Scholar]
  25. Pimm S. L., Lawton J. H., Cohen J. E.1991Food web patterns and their consequences. Nature 350, 669–674 (doi:10.1038/350669a0) [Google Scholar]
  26. Rooney N., McCann K., Gellner G., Moore J. C.2006Structural asymmetry and the stability of diverse food webs. Nature 442, 265–269 (doi:10.1038/nature04887) [DOI] [PubMed] [Google Scholar]
  27. Rosenzweig M. L.1971Paradox of enrichment: destabilization of exploitation ecosystems in ecological time. Science 171, 385–387 (doi:10.1126/science.171.3969.385) [DOI] [PubMed] [Google Scholar]
  28. Rothhaupt K. O.1990Population-growth rates of 2 closely related rotifer species: effects of food quantity, particle-size, and nutritional quality. Freshw. Biol. 23, 561–570 (doi:10.1111/j.1365-2427.1990.tb00295.x) [Google Scholar]
  29. Spitze K.1992Predator-mediated plasticity of prey life history and morphology: Chaoborus americanus predation on Dapnia pulex. Am. Nat. 139, 229–247 (doi:10.1086/285325) [Google Scholar]
  30. Stouffer D. B., Bascompte J.2009Understanding food-web persistence from local to global scales. Ecol. Lett. 13, 154–161 (doi:10.1111/j.1461-0248.2009.01407.x) [DOI] [PubMed] [Google Scholar]
  31. Stouffer D. B., Camacho J., Jiang W., Amaral L. A. N.2007Evidence for the existence of a robust pattern of prey selection in food webs. Proc. R. Soc. B 274, 1931–1940 (doi:10.1098/rspb.2007.0571) [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Tilman D.1996Biodiversity: population versus ecosystem stability. Ecology 77, 350–363 (doi:10.2307/2265614) [Google Scholar]
  33. Vasseur D. A., Gaedke U., McCann K. S.2005A seasonal alternation of coherent and compensatory dynamics occurs in phytoplankton. Oikos 110, 507–514 (doi:10.1111/j.0030-1299.2005.14006.x) [Google Scholar]
  34. Wetzel R. G., Likens G. E.1991Limnological analyses, 2nd ed.New York, NY: Springer [Google Scholar]
  35. Williams R., Berlow E., Dunne J., Barabasi A., Martinez N.2002Two degrees of separation in complex food webs. Proc. Natl Acad. Sci. 99, 12 913–12 916 (doi:10.1073/pnas.192448799) [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wootton J. T.1997Estimates and tests of per capita interaction strength: diet, abundance, and impact of intertidally foraging birds. Ecol. Monogr. 67, 45–46 [Google Scholar]
  37. Yodzis P.1981The stability of real ecosystems. Nature 289, 674–676 (doi:10.1038/289674a0) [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES