Trends in entropy production during ecosystem development in the Amazon Basin

Abstract

Understanding successional trends in energy and matter exchange across the ecosystem–atmosphere boundary layer is an essential focus in ecological research; however, a general theory describing the observed pattern remains elusive. This paper examines whether the principle of maximum entropy production could provide the solution. A general framework is developed for calculating entropy production using data from terrestrial eddy covariance and micrometeorological studies. We apply this framework to data from eight tropical forest and pasture flux sites in the Amazon Basin and show that forest sites had consistently higher entropy production rates than pasture sites (0.461 versus 0.422 W m⁻² K⁻¹, respectively). It is suggested that during development, changes in canopy structure minimize surface albedo, and development of deeper root systems optimizes access to soil water and thus potential transpiration, resulting in lower surface temperatures and increased entropy production. We discuss our results in the context of a theoretical model of entropy production versus ecosystem developmental stage. We conclude that, although further work is required, entropy production could potentially provide a much-needed theoretical basis for understanding the effects of deforestation and land-use change on the land-surface energy balance.

1. Introduction

There is at present no general theory that adequately explains the observed variation in terrestrial energy fluxes during ecosystem growth and development (e.g. Odum 1969; Fath et al. 2004; Amiro et al. 2006). However, the principle of maximum entropy production (MEP) has potential to provide a theoretical framework for understanding the relationships between surface energy fluxes and ecosystem dynamics (Ozawa et al. 2003; Kleidon & Fraedrich 2005; Martyushev & Seleznev 2006). The MEP theory states that open, energetically forced, non-equilibrium systems with many degrees of freedom, such as ecosystems, tend to self-organize to states of MEP (Ozawa et al. 2003; Kleidon 2009). To date, most entropy-related studies have focused on the global earth system, atmospheric dynamics (Ozawa et al. 2003) or aquatic systems (Aoki 1995; Meysman & Bruers 2007). The few, primarily theoretical, attempts at applying entropy-related ideas to terrestrial ecosystems suggest that the land-surface ecosystem entropy production is closely related to its surface temperature and to the magnitude and partitioning of the energy fluxes (Ulanowicz & Hannon 1987; Schneider & Kay 1994; Kleidon & Fraedrich 2005; Kleidon et al. 2008). These predictions, however, remain to be properly investigated using empirical data.

The Amazon Basin is among the most studied geographical regions in terms of energy budget and micrometeorology studies because of its importance for carbon storage and climate–vegetation feedbacks (e.g. Betts et al. 2008; Bonan 2008). The development of a correct understanding of the effects of dynamic land-surface vegetation on the fluxes of energy and water is a research priority given the ongoing and rapid deforestation and land-use change that is occurring in this area (Nepstad et al. 2008). Results arising from the Anglo-Brazilian Amazonian Climate Observational Study (ABRACOS) and the Large-Scale Biosphere–Atmosphere Experiment in Amazonia (LBA) indicate that forests generally have lower albedo, lower outgoing long-wave radiation (i.e. lower surface temperatures) and thus larger net radiation flux than pastures (Culf et al. 1995; Gash & Nobre 1997; Giambelluca et al. 1997; Berbert & Costa 2003; von Randow et al. 2004). Furthermore, a greater proportion of the net radiation appears to be dissipated via latent heat flux associated with transpiration, resulting in forests having generally lower ratios of sensible to latent heat flux (i.e. lower Bowen ratios) than pasture sites (von Randow et al. 2004). A mechanistic explanation of these results is emerging based on forests having increased surface roughness (Ogunjemiyo et al. 2005) that allow them to absorb more energy and deeper roots that provide greater access to soil moisture for transpiration, especially during the dry season when water is limiting (von Randow et al. 2004). MEP may provide a suitable theoretical framework to underpin this mechanistic explanation and, by corollary, the Amazonian tropical forest–pasture comparison may provide a sufficiently data-rich case study in which to investigate patterns of entropy production in terrestrial ecosystems.

In this paper, we introduce a framework for conducting an entropy analysis of terrestrial ecosystems using eddy covariance and micrometeorology data. We then apply this to data from tropical forest and pasture flux sites in the Amazon Basin and relate variation in rates of entropy production back to the observed trends in albedo, Bowen ratio and surface temperature. We hypothesize that if ecosystem development follows the path of increasing entropy production (Ulanowicz & Hannon 1987; Schneider & Kay 1994; Aoki 1995), then forests should have a higher rate of entropy production than pasture in the Amazon owing to their later successional status. We discuss our results in relation to the principle of MEP and present a general model describing changes in ecosystem entropy production during ecosystem succession. Our results suggest that entropy production theory has the potential to provide a much-needed framework to explain the observed variation in surface energy balance parameters.

2. Theoretical framework

(a). System boundaries and energy balance equation

Our ‘ecosystem’ refers to the land-surface system commonly used in eddy-flux and micrometeorology studies (Noilhan & Planton 1989; Sellers et al. 1997). To include the below-ground component of the ecosystem, we set the lower boundary at the zero flux point into the soil, which is typically lower than the maximum rooting depth (Kleidon et al. 2008). The general energy balance equation for our system is

2.1

where K_n is the net (incoming) short-wave radiation, L_n is the net (outgoing) long-wave radiation, H is the net sensible heat flux (outgoing) and LE is the net (outgoing) latent heat flux associated with the mass flux of water vapour. The change in energy stored within the system itself, dG, can be broken down into different storage terms representing the changes in internal energy of air, water, soil and biomass components within the system. In most studies, these storage terms (with the exception of soil heat flux) are regarded as negligible or assumed to be in a steady state (e.g. Gholz & Clark 2002, but see Gu et al. 2007).

(b). Second law of entropy equation

The land-surface system is an open system with both heat and matter flows across its boundaries, and therefore it can be analysed within the framework of an engineering control volume (i.e. open system). The general entropy equation for a control volume is given by the following equation (Moran & Shapiro 2006):

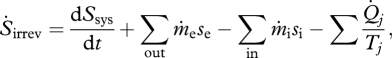2.2

where 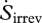is the entropy production due to irreversible reactions occurring inside the system, dS_sys/dt is the rate of change in entropy content inside the system, 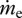and 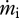are the mass flows into and out of the system, respectively, s_e and s_i are the specific entropies of those flows, 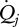is the heat flux across the system boundaries of component j, expressed here as positive when coming into the system, and T_j is the temperature of that heat flux at the position it crosses the system's boundary. The second law of thermodynamics states that the entropy production resulting from irreversible processes inside the system (i.e. S_irrev) is always greater than zero. When applied to our terrestrial land-surface system, the general control volume entropy equation becomes

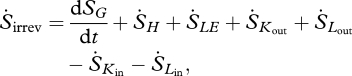2.3

where dS_G/dt is the entropy flux associated with storage an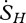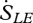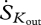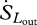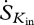d , , , , and 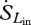are entropy fluxes associated with the net sensible heat flux, the net latent heat flux, outgoing short-wave radiation, outgoing long-wave radiation, incoming short-wave radiation and incoming long-wave radiation, respectively. We now explain how each of these fluxes can be estimated from measurements taken by instruments mounted on eddy covariance towers.

(c). Entropy of radiation

The entropy content of radiation emitted into a vacuum is equal to its radiation heat content (W m⁻²) divided by the black body temperature of the surface that emitted the radiation (Wildt 1956; Ozawa et al. 2003). Thus, the entropy of pure short-wave radiation before it enters the Earth's atmosphere is

2.4

where T_br is the brightness temperature, which in Earth's case is equal to the surface temperature of the Sun (about 5760 K). A major limitation of this approach is that incoming short-wave radiation at the land surface has been modified by the Earth's atmosphere. Some wavelengths are absorbed by atmospheric particles to a greater extent than others, and short wavelengths are scattered and polarized in the atmosphere (Kabelac 2005). As a consequence, radiation reaching the land surface has a lower brightness temperature and higher entropy content than given in equation (2.4). Kabelac (2005) has developed empirical models to estimate the entropy content of diffuse and direct beam radiation using the radiation energy intensity and the degree of polarization. The entropy content of short-wave radiation at the Earth's surface (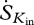) was closely related to the following empirical relationship:

2.5

where K_in is the incoming short-wave radiation (W m⁻²), p_dir is the direct-beam proportion of K_in, (1−p_dir) is the diffuse component, and C_dir and C_diff are empirically derived correlation coefficients of 0.000462 and 0.0014, respectively. Because C_diff ≫ C_dir, the entropy content of the incoming radiation increases as the proportion of incoming diffuse light increases. Although these equations are empirically determined, and thus potentially subject to changes in empirically derived coefficients, they provide a more accurate estimate of the entropy content of the incoming radiation than other methods used to date (Kabelac 2005, cf. Ozawa et al. 2003; Kleidon et al. 2008).

Terrestrial long-wave radiation fluxes from the atmosphere and the land surface are not as affected by atmospheric absorption or scattering. Therefore, the entropy content of the incoming and outgoing long-wave radiation fluxes (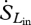, 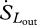) can be accurately estimated as

2.6

and

2.7

where L_in and L_out are the incoming and outgoing long-wave radiation fluxes, respectively, T_sky is the effective thermodynamic sky temperature and T_surf is the surface temperature. Both of these temperatures can be estimated using the Stefan–Boltzmann law, which relates the energy content of radiation (L) to the black body temperature (T) of the object emitting such that L = σɛT⁴, where σ is the Stefan–Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴) and ɛ is the emissivity of the object, which is one for a true black body. The emissivity of plant tissues approximates that of a true black body, with ɛ ≈ 0.98 (Humes et al. 1994).

(d). Entropy of sensible and latent heat flows

The entropy flux of sensible heat flow (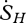) is simply the heat flux (H) divided by the air temperature at the system boundary (T_air), which is typically at a height of 2 m for the pasture sites and approximately 60 m for the forest sites:

2.8

The entropy flux associated with the change of state from liquid to vapour has two components. The larger component is associated with the latent heat content of the water vapour ():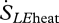

2.9

The smaller component is associated with mixing of saturated air with air that has a relative humidity less than one. The entropy of mixing (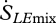) is given by

2.10

where E is the evaporation rate (kg m⁻² s⁻¹), R_V is the gas constant of water vapour (461 J kg⁻¹ K⁻¹ for moist air) and RH_amb is the ambient relative humidity at the point at which the flux is occurring (Kleidon et al. 2008). The overall entropy flux associated with the mass flow of water is therefore the sum of the two terms, 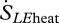and .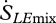

(e). Storage terms and steady-state assumptions

The entropy change for each storage component G_i, at temperature T_i, which receives a net flux of energy of dG_i/dt is given by

2.11

If steady state is assumed for the system for all storage components (i.e. dS_Gi/dt = 0), this would remove the need to quantify the entropy change for the system. However, the assumption of steady state is dependent on time scales of the data and the comparisons one wishes to make. For daily patterns (and average daily patterns), the heat storage terms will play a large role (Gu et al. 2007), but the biomass chemical storage term will be negligible. For monthly or yearly patterns, the net heat storage terms can be considered in a steady state, and the biomass change is also in approximately steady state. For longer time periods (i.e. multi-year succession), increases in canopy height and total biomass are likely to result in increased canopy heat storage; however, the magnitude of this effect would be very small compared with the other entropy production terms.

(f). Study sites and data

Four pairs of tropical forest and pasture sites were analysed, the data being sourced online from the LBA and ABRACOS projects (Gash & Nobre 1997; Keller et al. 2004). Sites were paired on the basis of geographical region and climate, as well as (where possible) measurements conducted at the same time (table 1; electronic supplementary material, table S1). For a detailed description of the sites, instruments and measurement details see the references given in table 1. When the paired sites had different levels of data resolution and length of data coverage, the analysis was restricted to the level of detail available at the more poorly replicated of the two sites.

Table 1.

Site details, data sources and references for the eight Amazonian eddy-flux sites used in the forest–pasture comparison.

district	tower ID	vegetation	data source	data period used	season	references
Maraba	Reserva Vale	forest	ABRACOS	October 1993	dry	Gash et al. (1996)
Maraba	Fazenda Boa Sorte	pasture	ABRACOS	October 1993	dry	Gash et al. (1996)
Manaus	K34	forest	LBA	July–October 1999–2006	dry	Malhi et al. (1998, 2002); Araújo et al. (2002)
Manaus	Fazenda Dimona	pasture	ABRACOS	July–October 1990–1991	dry	Gash et al. (1996)
Santarem	K83	forest	LBA	January–December 2000–2004	all year	Goulden et al. (2004); da Rocha et al. (2004); Miller et al. (2004)
Santarem	K77	pasture/crop	LBA	January–December 2000–2004	all year	Sakai et al. (2004)
Rondonia	Reserva Jaru	forest	LBA	January–December 2001–2002	all year	von Randow et al. (2004); Kruijt et al. (2004)
Rondonia	Fazenda Nossa Senhora	pasture	LBA	January–December 2001–2002	all year	von Randow et al. (2004)

The most important variables that we required in order to estimate entropy production were: incoming and outgoing short-wave radiation (K_in and K_out), net radiation (R_n), sensible heat flux (H), latent heat flux (LE), ambient temperature (T_air) and relative humidity (RH). Net long-wave radiation (L_n) was estimated from the residual of the net radiation after subtracting the net short-wave radiation component. We used mean hourly incoming long-wave radiation from forest and pasture sites in Rondonia (the only location where such data were available) to estimate L_in at the other sites and then calculated the outgoing long-wave radiation as L_out = L_n −L_in. Relevant temperatures for L_in and L_out were then calculated using the Stefan–Boltzmann law, as described earlier, using an emissivity of 0.98 (Humes et al. 1994). A ratio of 50 per cent diffuse and 50 per cent direct light was used for the incoming solar radiation across all sites. Although this ratio is highly variable from day to day, a 50 per cent average is comparable to published values (Roderick et al. 2001).

In most cases, data on energy storage components were unavailable, and energy balance closure was not achieved (Wilson et al. 2002; Jacobs et al. 2008). In these instances, a bulk storage term dG/dt was estimated from the hourly energy balance residual, and its associated entropy change was calculated by dividing dG by the ambient air temperature. Storage of chemical energy in biomass (i.e. net primary productivity; NPP) was assumed to be in steady state and the associated entropy change was not included in our analysis. This was a reasonable assumption, as the energy converted into biomass is only a tiny fraction (less than 1%) of the total energy flux (Malhi et al. 2002).

All calculations were made at hourly time intervals and then averaged over the entire period to get the average entropy production rate for each site. Integrated daily means over the observation period were used when calculating mean values of the Bowen ratio (ratio of sensible to latent heat flux) and albedo for each site. All statistical analysis was done in R (R Development Core Team 2006).

3. Results

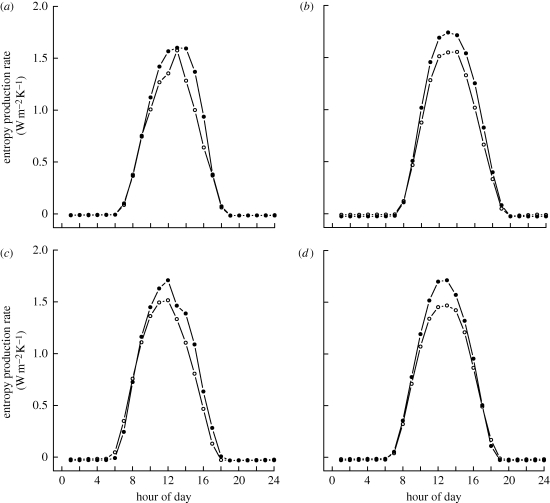
The mean entropy production rate was 0.461 W m⁻² K⁻¹ for the forest sites, which was 9.2 per cent higher than the mean entropy production rate of pasture of 0.422 W m⁻² K⁻¹ (95% confidence intervals: forest, 0.443–0.478; pasture, 0.400–0.443; paired t-test: t = 6.7, d.f. = 3, p = 0.074). Mean hourly entropy production rates showed strong diurnal variation related to the pattern of incoming solar energy (figure 1). The diurnal pattern was similar for forests and pasture. The exception was a period of about 6 h around midday, during which forests had consistently higher rates of entropy production than pasture across all sites (figure 1).

Figure 1.

Mean hourly rates of entropy production for each pair of forest (closed circles) and pasture sites (open circles) in Southwest Amazonia: (a) Maraba, (b) Manaus, (c) Santarem and (d) Rondonia. Note that during the middle of the day across all locations forests have consistently higher rates of entropy production than pasture.

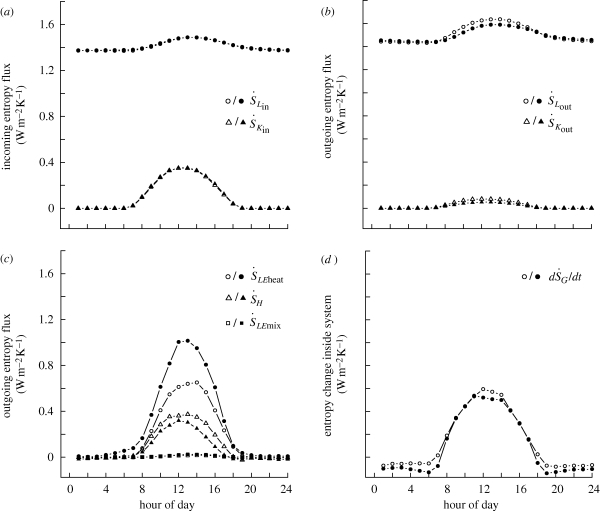
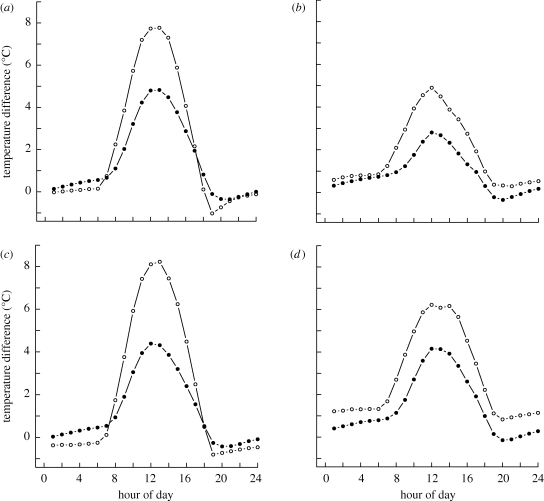
Incoming entropy flux was dominated by downward long-wave radiation (figure 2a) and showed little variation with vegetation type. Observed differences in entropy production rates were therefore due to an increase in net outgoing entropy fluxes at the forest sites. Although pasture sites generally had higher outgoing entropy flux associated with outgoing long-wave radiation and sensible heat flux, forests had much larger entropy flux associated with the mass flow of water vapour (figure 2b,c). The increased latent heat flux resulted in forests having a cooler surface temperature than pasture during the middle of the day (figure 3, forest mean midday surface temperature = 305.2 K, pasture = 308.1 K), with temperature differences being more pronounced on sunny days (figure 3a,b) and during the dry season (figure 3c,d).

Figure 2.

Mean hourly rates of entropy flux associated with each component of the entropy production calculations (equation (2.3)). Data are from forest (closed symbols) and pasture sites (open symbols) in Rondonia, Southwest Amazonia. Panels are divided into entropy fluxes associated with (a) incoming radiation, (b) outgoing radiation, (c) sensible heat, latent heat and entropy of mixing and (d) entropy change within the system.

Figure 3.

Mean hourly difference between black body surface temperature and air temperatures for forest (closed circles) and pasture sites (open circles) in Rondonia, Southwest Amazonia, showing differences between (a) sunny and (b) cloudy days and between (c) dry and (d) wet seasons. Sunny days are defined as having a total incoming short-wave radiation flux of greater than 30 MJ d⁻¹, whereas cloudy days have less than 30 MJ d⁻¹. Wet season is from January to March, and the dry season is July–September, inclusive.

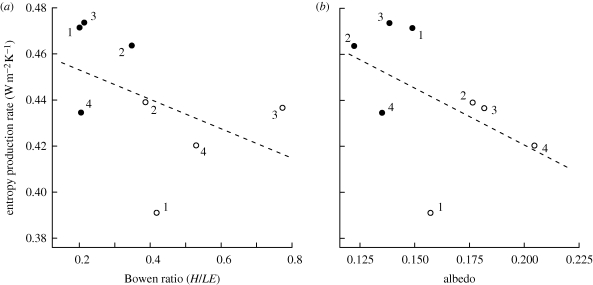
Compared with pasture, forests tended to have lower albedos (forest: mean = 0.136; 95% confidence interval: 0.12–0.15; pasture: mean = 0.18; 95% confidence interval: 0.16–0.20; paired t-test: t = −3.37, d.f. = 3, p = 0.044) and lower Bowen ratios (forest mean = 0.24 (0.17 − 0.31); pasture: mean = 0.53 (0.36 − 0.70); t = −2.62, d.f. = 3, p = 0.079). In all four site pairings, an increase in entropy production was associated with a decline in both the Bowen ratio and surface albedo (figure 4); however, this relationship was insufficiently replicated to be statistically significant across all sites.

Figure 4.

Relationship between mean entropy production rates (W m⁻² K⁻¹) and (a) the mean Bowen ratio and (b) albedo for sites from the Brazilian Amazon. Forest sites are shown as closed circles, pasture sites as open circles. Numbers indicate paired locations: (1) Maraba, (2) Manaus, (3) Santarem and (4) Rondonia. Dotted line shows correlation across all sites (a) Pearson's correlation = −0.45, p = 0.26 and (b) Pearson's correlation = −0.49, p = 0.22. For more details of sites see table 1 and electronic supplementary material, table S1.

4. Discussion

Our results represent the first attempt at calculating ecosystem entropy production from eddy-flux data for terrestrial systems and suggest that forest has higher entropy production rates than pasture ecosystems in the Amazon Basin. Although the flux sites that were compared in this study involved different instruments, measurement intervals, data manipulation techniques and different levels of assumptions regarding energy balance closure, we still obtained a consistent effect of vegetation type across all sites. This suggests that these results are robust. Tropical grasslands in the study areas would readily revert back to forest if abandoned as a classic ‘old field succession’ process (Uhl et al. 1988), and therefore our results provide support for the hypothesis that ecosystem development proceeds in a direction of increasing entropy production (Ulanowicz & Hannon 1987; Schneider & Kay 1994).

(a). Energy balance trade-offs

Although not statistically significant, our results suggest that ecosystem entropy production rates are related to the surface albedo and Bowen ratio (figure 4). This may provide direct insights into the energy balance tradeoffs that result in increased entropy production. A lower surface albedo increases the flux of energy through the system, and according to the energy balance equation (equation (2.1)), the increased incoming short-wave radiation associated with low albedo must be balanced by an increase in one or more of the outgoing dissipative fluxes. Increased energy flux through the ecosystem (i.e. low albedo), combined with bias towards dissipative pathways that result in a cooler surface temperature, will tend to result in an increased rate of entropy production given the constraints imposed by equation (2.1).

In the land-surface system, there are three possible routes for energy dissipation; long-wave radiation, sensible heat and latent heat. Long-wave radiation has the lowest entropy production per watt of energy released. This is due to its flux being dependent on surface temperature, and thus an increase in flux requires a relatively large increase in surface temperature such that the entropy per unit long-wave radiation emitted decreases. Sensible heat flux requires the air temperature to be less than surface temperature in order for the heat to flow and is therefore ineffective at cooling the surface temperature below ambient. Latent heat flux, however, offers a means to cool the surface below ambient temperature via evaporative cooling and is very effective at dissipating excess heat in environments where water is not limiting (Bonan 2008). Compared with pasture sites, the observed cooler surface temperatures (figure 3) and shift towards evaporative fluxes (figure 2) in forest sites are therefore both consistent with the hypothesis that as ecosystems develop they increase their rates of entropy production.

When compared with earlier stages of succession, lower albedos have been observed for mature forests throughout the world, including boreal (Amiro et al. 2006), temperate (Roberts et al. 2004; Ogunjemiyo et al. 2005) and tropical forests (Culf et al. 1995; Giambelluca et al. 1997). High rates of evaporative fluxes (i.e. lower Bowen ratios) are also known to occur over forested surfaces (e.g. Hayden 1998; Bonan 2008). We hypothesize that the general reductions in surface albedo and increased shift towards increased evaporative fluxes observed during succession in other systems similarly correspond to increasing rates of entropy production, but this remains to be confirmed.

(b). Biotic feedback mechanisms

There are a variety of positive feedback mechanisms between biotic activity and land-surface fluxes that could potentially lead to increased entropy production rates (Kleidon & Fraedrich 2005; Bonan 2008). Storage of chemical energy by photosynthesis results in increased canopy size and a deeper root system. Deeper roots allow forests to access more soil water, especially during the dry season, enhancing transpiration (von Randow et al. 2004) and increasing evaporative cooling which results in lower surface temperatures and the maintenance of a ‘wet’ surface albedo (Idso et al. 1975). Increased canopy size also facilitates increased heat storage in the canopy without necessarily increasing the canopy temperature (i.e. the same amount of heat spread over a much larger volume results in a smaller increase in temperature). This would tend to decrease the diurnal variation in surface temperature by delaying some of the peak heat flux out of the system until later in the day or at night when temperatures are considerably cooler (Gu et al. 2007), resulting in increased entropy production rates.

Increases in forest biomass and structural complexity during succession also have strong feedbacks on surface albedo (and thus on entropy production). As the canopy grows taller, increased vertical structuring of the canopy increases surface roughness, leading to a decrease in surface albedo (Ogunjemiyo et al. 2005). This is because a rough surface allows the short-wave radiation to penetrate deeper into the canopy before being absorbed or reflected. Then, the portion that gets reflected from the first point of interception has a much greater chance of being absorbed by another surface before it exits the land-surface system, resulting in a lower overall surface albedo. Leaf area index may also increase in taller forests owing to increased vertical stratification within the canopy (Holdaway et al. 2008), and this increase in functional surface area would potentially increase both total light interception and canopy-level evaporative fluxes.

(c). Bare soil as a null model

How much of the land-surface entropy production is directly attributable to the living components, and how much is purely due to abiotic factors? Such a question could be quantified within the framework presented by the inclusion of a null model of a basic abiotic land surface. We suggest that bare soil of similar composition to the study sites, with similar annual rainfall, would provide an excellent null model, although detailed energy balance data for such surfaces are noticeably lacking. What data are available suggest that bare soil, when at field water holding capacity, behaves very similar to mature forest vegetation, with low albedo and a high Bowen ratio (Idso et al. 1975; Giambelluca et al. 1997). However, under even slightly dry conditions, the soil surface dries quickly owing to the generally poor water conductance of soil. This results in the formation of a dry layer that inhibits further evaporation, heats up quickly and has a much higher albedo of between 0.3 and 0.6 depending on the soil type (Idso et al. 1975; Oguntunde et al. 2006). Integrated over the course of a year, this would most probably result in a lower entropy production rate than vegetated surfaces, but exactly how much lower requires quantification.

(d). MEP theory of ecological succession

Given that increased energy flux leads to increased entropy production, the principle of MEP appears to be consistent with the concept first proposed by Lotka nearly a century ago that natural selection selects for maximum energy throughput (i.e. maximum power) (Lotka 1922; Odum & Pinkerton 1955; Fath et al. 2001; Delong 2008). We therefore suggest that MEP may be interpreted as an emergent characteristic that is the result of natural selection pressures for maximizing the flux (and dissipation) of energy and propose that MEP provides the explicit criteria linking selection at the individual level to emergent and directional properties at higher levels of organization such as communities and ecosystems (Wicken 1989; Hoelzer et al. 2006).

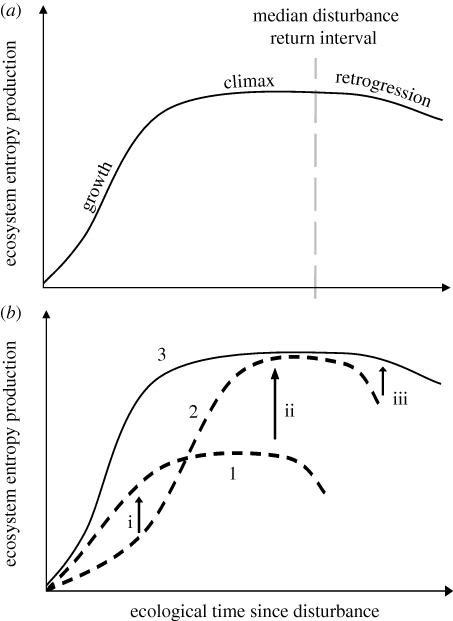
Integrating this causal framework based around MEP with current understanding of ecological succession, we hypothesize that entropy production should increase during the initial growth stage before obtaining a maximum at the mature or ‘climax’ stage of ecosystem development (Odum 1969; figure 5a). Entropy production rates are then predicted to decline during the retrogression phase in the absence of major disturbance, as the build-up of constraints such as nutrient shortage becomes limiting (Wardle et al. 2004). The predicted relationship in figure 5a is similar to that proposed by Aoki (1995, 1998) for lake ecosystems and is generally consistent with the ideas of Ulanowicz & Hannon (1987) and Schneider & Kay (1994).

Figure 5.

General model of changes in ecosystem entropy production during succession. Entropy production increases during the growth phase to a maximum at maturity, which is maintained for a relatively long period of time (a). If disturbance does not reset the succession then retrogression may occur. Three directional selection pressures (1–3) leading to increased entropy production at all stages of succession are shown in (b). The curves illustrate changes in entropy production during development of hypothetical communities consisting of (1) r-selected species only, (2) K-selected species only, and (3) the MEP trajectory that combines both r and K strategies, simultaneously maximizing both (i) the rate at which entropy production increases through successional time (dEP/dt), and (ii) maximum sustained entropy production at maturity (EP_mature). The additional selective force (iii) is for stress-tolerating species extending the effective mature phase and postponing retrogression.

We also speculate that there are three different MEP selection pressures at work during ecosystem development (figure 5b). The first maximizes the rate at which entropy production increases through successional time (dEP/dt), which, initially at least, is achieved via rapid colonization and increases in leaf area and biomass (i.e. r-selected species with fast individual/population growth rates). The second selection component of MEP is for maximum sustained entropy production during maturity (EP_mature). This is achieved via maximizing biomass and structural complexity and necessarily involves longer-lived, larger, slower-growing organisms (i.e. K-selected species). The third selection component is for stress-tolerating species extending the effective mature phase and postponing retrogression. Thus, given the existence of ecological disturbance in the landscape, the MEP theory leads to the prediction that there should be long-term co-existence of r- and K-selected species, a directional transition from r- to K-selected species during the course of succession and increasing predominance of K-selected species in ecosystems with longer disturbance return times.

The framework presented in figure 5 could be tested by combining experimental manipulation of known constraints (e.g. time since last disturbance, site fertility, water and light regimes and dispersing propagule availability), with precise measurements of parameters required to calculate entropy production. For example, using a mature ecosystem, a maximum in EP_mature could be tested for by making conditions more or less favourable (e.g. through experimental water stress, reduction in incoming solar energy or removal of taxa) and looking for the expected increase or decrease in ecosystem entropy production. In long-term studies of succession, taxa could be experimentally limited to only r- or K-selected species to test for changes in dEP/dt. In order to make such detailed investigations, the accuracy, comparability and closure of the energy balance measurements need to be improved to ensure detection of relatively small variations in entropy production. Such work calls for direct collaboration between the eco-physiology, ecology and thermodynamic research communities and has great potential to be a very productive and important area of future study.

(e). Concluding remarks

Using micrometeorology and eddy covariance data, we applied a novel framework for conducting ecosystem entropy analysis on terrestrial systems to a tropical forest versus pasture comparison in the Amazon. Our results indicated that forests had a higher rate of entropy production than pastures (0.461 and 0.422 W m⁻² K⁻¹, respectively). The higher rate of entropy production for the forest was linked to its lower albedo, increased latent heat flux and lower radiative surface temperature, especially in the period around midday. These results are consistent with the hypothesis that ecosystems develop towards states of increasing entropy production. Further application of the MEP theory to succession gives the prediction that there should be selection for both maximizing the rate at which entropy production increases during succession (dEP/dt) and maximizing entropy production at the mature or ‘climax’ stage of succession (EP_mature), resulting in a dynamic change from r- to K-dominated communities through time. Future collaborative investigation, including the use of appropriate null models, is required to test these predictions. Our results suggest that the principle of MEP has considerable potential to explain the directional trends in land-surface fluxes of energy and water that occur during ecosystem development and to provide an underlying framework for understanding ecological succession. Future work in this area will add to our understanding of the effects of deforestation and land-use change on the land-surface energy balance and is likely to strengthen the theoretical basis of ecology in general.