Optimality approaches to describe characteristic fluvial patterns on landscapes

Abstract

Mother Nature has left amazingly regular geomorphic patterns on the Earth's surface. These patterns are often explained as having arisen as a result of some optimal behaviour of natural processes. However, there is little agreement on what is being optimized. As a result, a number of alternatives have been proposed, often with little a priori justification with the argument that successful predictions will lend a posteriori support to the hypothesized optimality principle. Given that maximum entropy production is an optimality principle attempting to predict the microscopic behaviour from a macroscopic characterization, this paper provides a review of similar approaches with the goal of providing a comparison and contrast between them to enable synthesis. While assumptions of optimal behaviour approach a system from a macroscopic viewpoint, process-based formulations attempt to resolve the mechanistic details whose interactions lead to the system level functions. Using observed optimality trends may help simplify problem formulation at appropriate levels of scale of interest. However, for such an approach to be successful, we suggest that optimality approaches should be formulated at a broader level of environmental systems' viewpoint, i.e. incorporating the dynamic nature of environmental variables and complex feedback mechanisms between fluvial and non-fluvial processes.

1. Introduction

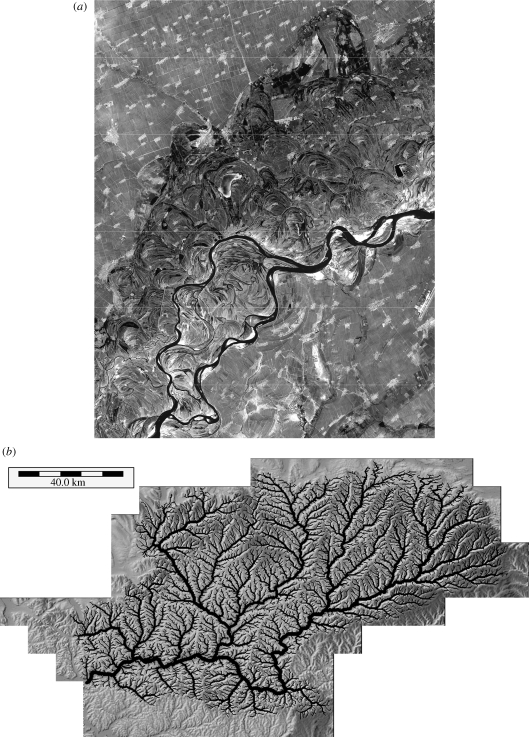
Over a range of time scales, the flow of water has left characteristic patterns on Earth's terrestrial surface, such as self-similar binary tree organization of river networks (e.g. Peckham 1995), meandering streams (e.g. Tal & Paola 2007), regular stream bed profiles (e.g. Leopold 1953), systematic downstream grain-size sorting (e.g. Yatsu 1955) and power-law hydraulic geometry relationships (Leopold & Maddock 1953) (figure 1). These self-organized patterns are signatures of past hydrological processes over a number of scales. Many interesting statistical relationships have been reported on the regularity of geomorphic patterns. For example, the number of streams and average length of streams, of given stream order, exhibit log-linear relationships with the stream order (Horton 1945). As another example, relationships between upstream area and main channel length ubiquitously exhibit a power law, indicating self-similarity of river network organization, with their scaling exponents in a narrow range (Hack 1957).

Figure 1.

Some patterns on Earth's surface. (a) Meandering patterns of Songhua River (Image courtesy of NASA/GSFC/METI/ERSDAC/JAROS, and US/Japan ASTER Science Team). (b) Self-similar tree network of Upper Susquehanna River basin (Image modified from Saco (2003)).

Identifying and quantifying the signatures of geomorphic patterns and attributing them to the causative mechanism is of significant interest in a variety of contexts ranging from enabling a better understanding of complex feedback mechanisms on Earth's surface processes to predicting the impact of disturbance on future landform as well as its influence on broader environmental systems. Understanding mechanisms underlying the formation of these patterns also helps investigate the existence of water on other planets, such as Mars. Characteristic geomorphic patterns, similar to what we observe on Earth, such as self-similar tree network and meandering, have been found on Mars’ surface (e.g. Stepinski et al. 2002; Wood 2006), indicating the possibility that a substantial flow of water existed in the past and has carved such patterns on the Mars’ surface.

One viewpoint for the formation of these regular patterns is that there is a certain principle that dictates the landform evolution, and observed regular patterns can be explained by this principle as the destination of landform evolution. Significant efforts have been made to identify this principle. Since Leopold & Langbein (1962) introduced the concept of entropy in landform evolution, a number of metrics have been proposed to represent entropy production in landscape formation. This has given birth to several alternative hypotheses.

A contrasting viewpoint holds that the observed regularity of patterns arises as emergent characteristics from local interactions of physical, biological and chemical processes occurring at a number of scales. For example, we have shown (Paik & Kumar 2008) that inherent randomness is a sufficient condition for the generation of self-similar tree organization driven by the erosion—deposition process under a gravitational gradient, and demonstrated that the decrease in total energy expenditure, the optimality condition such as that used in the optimal channel network theory (Rodríguez-Iturbe et al. 1992), is not the cause but a consequent signature.

Both these differing perspectives are valuable and can contribute to improving our predictive capability. Prediction of Earth's surface processes is vital for a variety of environmental studies. There are emerging social issues as consequences of artificially modified environments, such as channelization, dams, mining, urbanization and their restoration or removal, as well as complex environmental changes over longer time scales such as climate change. However, our ability to predict the dynamics of systems that evolve in time, such as Earth's surface processes, is limited (Kumar 2007). Better prediction of their dynamics demands the integration of a greater number of processes and feedback mechanisms. When using process-based models, this means increasingly complicated formulation and generation of numerous parameters that are subject to uncertainty. However, identification of macroscopic governing laws, such as optimality principles, can provide a simpler approach for reproducing the observed patterns. The value of many existing optimality hypotheses including the maximum entropy production principle has to be recognized in this context.

The purpose of this review paper is to reconcile a number of different notions that are prevalent in this context. We provide a comprehensive overview of existing optimality hypotheses, a detailed comparison of these, i.e. the scale issues and philosophical background, and synthesis of their implication towards a better understanding of characteristic patterns in landform dynamics. In §2, we define fluvial landscape evolution and discuss issues on its modelling. Then, existing optimality hypotheses are reviewed in §3. In §4, an insightful discussion is given for these hypotheses. Conclusions are provided in §5.

2. Nature of fluvial landscape evolution

Land surfaces, including both channels and hillslopes, serve as corridors for transporting a variety of constituents such as biomass, carbon, nutrient, pollutant, sediment, water, etc. Spatial and temporal variability in these components continuously reshapes the flow path by lifting materials that form the land surface and depositing them at other places. Fluvial landscape evolution refers to the continuous variation of landform as a result of the relocation of land-forming materials powered by water flow. While surface water flow is at the core of landscape evolution, landscape evolution is also driven by complex feedback mechanisms among ecological, geomorphological and hydrological functions where different climatic, geographical and geological conditions play key roles.

Fluvial landscape evolution has been studied by either fieldwork-based observations, laboratory experiments or mathematical modelling. Observations provide key references for modelling studies, but are available only for limited time spans, simply because nobody can watch landscape evolution over its vast scales (spatially ranging from a definable minimum grain size to the entire Earth's surface; and temporally from an instance to geological time scale and beyond).

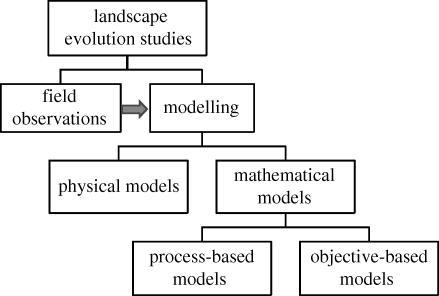
Models for fluvial landscape evolution can be largely divided into two types: (i) physical models, i.e. models physically built at scales usually smaller than the prototype, where physical experiments can be conducted under controlled flow characteristics (e.g. Schumm & Khan 1972) and (ii) mathematical models, which enable simulations based on specified formulations. Based on the model formulation, we classify the mathematical models into process-based models, where a set of physically based equations is used (e.g. Willgoose et al. 1991), and objective-based models, which use hypothesized governing principles, where each hypothesis defines an objective or a goal that the evolutionary process attempts to achieve (e.g. Leopold & Langbein 1962) (figure 2). A number of optimality hypotheses have been proposed as the governing principle for objective-based models. The subject of this paper is the mathematical models with a focus on optimality hypotheses used for objective-based models.

Figure 2.

Classification of different approaches in investigating landscape evolution problems. The arrow indicates that field observations provide references for all modelling approaches.

Process-based models simulate landscape evolution using physically formulated governing equations, such as conservation of mass and momentum (for both sediment and water), under various scenarios of atmospheric and tectonic activities over a range of time scales. They are targeted towards engineering goals, e.g. to estimate variation of stream bed profiles under given conditions (Wu et al. 2004) or scientific explorations, e.g. to reproduce the observed tree network patterns on the Earth's surface (Paik & Kumar 2008). For detailed reviews on existing process-based landscape evolution models for the scale of the whole landscape, readers may refer to Willgoose (2005) and Codilean et al. (2006).

Although process-based models are rooted in first principles, albeit with a variety of approximations and parametrizations, their practical implementations are rife with challenges. For example, current models have large uncertainty in their predictions of sediment transport through natural streams. Sediment flux is influenced by not only the distribution of the size but also the shape of each grain and their interaction, such as hiding effect (e.g. Egiazaroff 1965). Particle detachment mechanism for cohesive soils differs from that for non-cohesive soils, which adds uncertainty in the estimation of sediment transport.

Vegetation also plays a significant role by increasing the resistance to water and sediment flux with its leaves and stems. Further, existence of roots substantially affects particles' aggregate stability. Evaluating the effect of vegetation is also crucial in estimating the water balance of a catchment system since transpiration constitutes a significant portion (as high as 90% in certain regions) of a catchment's water budget. Surface–subsurface interaction is also an important element in that this governs water balance that directly regulates surface flow. Infiltration losses reduce stream power in overland flow. Therefore, an appropriate estimate of infiltration is important as well. However, existing models for whole landscape evolution have very unrealistic settings, i.e. bare soil with zero infiltration capacity and no groundwater flow. This assumption definitely limits models' capability to capture complex feedbacks. Other limitations include accommodating stream bank failure and sensitive processes at channel confluences. Besides these physical processes, existing models have limited implementation of biological and chemical processes. However, as we increase model complexity, we increase the number of model parameters. As each model parameter value is subject to uncertainty, complicated model structure does not necessarily help obtain better scientific insights.

Objective-based models can often provide a closure condition for the solution of process-based models. For example, finding hydraulic geometry exponents has been treated as a problem that has more unknowns than known relationships (deterministic conditions), and optimality hypotheses have been used as the additional constraint to solve the problem (e.g. Leopold & Langbein 1962; Yang 1976). In objective-based models, the prediction of landform evolution is considered as an optimization problem where the proposed optimality principles become objective functions (or cost functions) while the deterministic conditions (either biological, chemical or physical) serve as constraints. In §3, we discuss details of existing optimality hypotheses.

3. Optimality hypotheses

Optimality approaches proclaim that landscapes evolve towards a state that is characterized by an optimal condition. The exact nature of this optimality remains moot and several alternative hypotheses, often involving statistical measures such as entropy, have been proposed. They were called ‘stochastic’ approaches (e.g. Yang 1971a). However, the term stochastic is misleading since many process-based models also have stochastic properties in their model parameters, boundary or initial conditions. Alternatively, optimality hypotheses were often called extremal hypotheses (Davies & Sutherland 1983) since proposed objective functions of most hypotheses pursue extremal states, i.e. minimization or maximization of a defined metric. However, hypotheses in non-extremal form do exist, such as the hypotheses of ‘constant Froude number’ (Lacey 1958) and ‘equal energy expenditure per unit area of channel’ (Rodríguez-Iturbe et al. 1992). Here, we use the term optimality hypotheses to group such approaches. This terminology is general enough to encompass hypotheses in non-extremal form and clear enough to be distinct from process-based approaches. In this section, we provide a review on existing optimality hypotheses. Through this review, it will be shown that most existing hypotheses focus on flow efficiency.

The attempt to describe landform patterns as pre-determined by an optimality principle dates back to the study on channel geometry by British engineers in India. Kennedy (1895) proposed the empirical regime theory motivated by stable irrigation canals in India. The regime theory proposed that there is a regime, or optimal range, of flow and channel geometry that enables the irrigation canals to be stable. The regime theory, developed for artificial waterways, i.e. irrigation canals, was later expanded to similar empirical relationships, called hydraulic geometry relationships (Leopold & Maddock 1953), applicable to natural rivers that cover a wider range of flow discharge and channel slope. The basic principle that guides landform evolution towards the stable regime has been an elusive question.

Leopold & Langbein (1962) were the first to use the concept of entropy in landscape evolution. This work was restated, using a statistical term, as the ‘minimum variance’ hypothesis (Langbein 1964) since it assumes that naturally evolved channels follow the ‘most probable’ geometry. Here, the definition of the most probable state depends on the choice of variables under consideration. Hence, the minimum variance hypothesis yields multiple solutions depending on the constraints used and the choice of dependent variables whose variance would be minimized (e.g. see cases shown in Williams (1978)). Since the minimum variance hypothesis explains the evolution only through a probabilistic perspective, it could be applied regardless of physical attributes (e.g. cohesiveness of channel boundaries) (Williams 1978). However, this implies a lack of physical basis to support the minimum variance hypothesis (e.g. Kennedy et al. 1964).

Most hypotheses proposed after the minimum variance hypothesis have therefore emphasized physical interpretation by adopting physical terms such as energy, stream power, Froude number, sediment transport and friction factor, instead of the statistical measure ‘variance’. Brebner & Wilson (1967) applied the principle of ‘minimum energy degradation rate’ (von Helmholtz 1868) to the channel geometry problem and showed that this principle yields channel geometry equations close to the empirical regime theory. This early optimality hypothesis on energy dissipation rate was tested for pressurized conduits in a laboratory (Brebner & Wilson 1967). This test has brought an argument that the comparison of the results obtained from the pressurized conduits with the observed regime equations for open channels that have free water surface exposed to atmospheric pressure is inappropriate (e.g. Barr & Herbertson 1967; Lacey 1967).

Yang (1971a) proposed two hypotheses of ‘average stream fall’ and ‘least rate of energy expenditure’ to explain meandering (Yang 1971a,b) and the formation of riffles and pools (Yang 1971c). Then, Yang (1972) found that the rate of energy expenditure can be expressed using the term ‘stream power’ originally proposed by Bagnold (1960). Yang (1972) proposed a sediment transport equation where the sediment transport is expressed as a function of the unit stream power. In his successive work, Yang (1973, 1976) proposed the hypothesis of ‘minimum unit stream power’ (MUSP) stating that ‘an alluvial channel with subcritical flow in the lower flow regime tends to adjust its velocity, depth, slope, and channel roughness in such a manner that given water discharge and sediment concentration can be transported with the minimum amount of unit stream power under given geologic and climatic constraints’ (Yang 1976). However, it should be noted that the formulation of the ‘MUSP’ is identical to that of an earlier hypothesis of minimum energy degradation rate (Brebner & Wilson 1967), which was derived from a different approach (table 1).

Table 1.

List of selected existing optimality hypotheses. V is the mean flow velocity, S is the channel slope, ρ is the density of water, g is the gravitational acceleration constant, Q is the flow discharge, L is the reach length, ρ_s is the density of sediment, Q_s is the sediment transport rate, W is the channel width, H is the hydraulic depth, and η is a constant. Q_j and L_j are the discharge and the length of link j (channel between two confluences), respectively. In application of these hypotheses, Q and Q_s are treated as given constants, and channel or network geometry is adjusted to obtain the optimal combination of variables such as V, S, H, W and L to satisfy a given objective function.

hypotheses	mathematical form	references
MUSP	min VS	Brebner & Wilson (1967); Yang (1973, 1976)
MSP =MSTC	min ρgQS	Chang & Hill (1977); Chang (1979a); White et al. (1982)
MEDR	min (ρgQ + ρsgQs)LS	Yang et al. (1981)
MFF	max W2H3S/Q2	Davies & Sutherland (1980, 1983)
minimum Froude number	min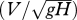	Jia (1990)
minimum total energy expenditure	min	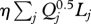Rodríguez-Iturbe et al. (1992)

Stimulated by the MUSP hypothesis, Chang & Hill (1977) proposed a similar ‘minimum stream power’ (MSP) hypothesis. This hypothesis was used to provide a boundary condition for numerical calculation for delta streams (Chang & Hill 1977) and to explain hydraulic geometry (Chang 1979a, 1980) as well as meandering (Chang 1979b). The measure minimized in this hypothesis is ρgQS, where ρ, g, Q and S are the density of water, the gravitational acceleration constant, the flow discharge (volume/time) and the channel slope, respectively. This measure was called the cross-sectional stream power by Rhoads (1987).

Later, Yang & Song (1979) proposed the ‘minimum energy dissipation rate’ (MEDR) hypothesis stating that ‘it appears that all natural rivers have a tendency to adjust whatever possible under the given constraints to achieve an objective of transporting water and sediment with a minimum rate of energy dissipation’. Because of the general nature of this principle, the formulation of this principle can be derived in various ways. For example, MEDR can be achieved by adjusting channel geometry (the formulation derived for this case is shown in the table 1). If channel boundary is fixed, MEDR can be still accomplished by adjusting the flow depth, the velocity distribution and other turbulent characteristics. Song & Yang (1980) showed that the total rate of energy loss is equal to the total stream power when the river boundary is fixed, and claimed MEDR as a general hypothesis for this thread of reasoning that has the previous hypotheses of MUSP and MSP as its special cases. Differences among MUSP, MSP and MEDR are shown in table 1 and further described by Griffiths (1984). Based on a similar idea, Rodríguez-Iturbe et al. (1992) proposed principles of ‘minimum energy expenditure in any link of the network’ and ‘minimum total energy expenditure’ in a river network, and applied them for the river network organization problem. These two, later unified as the ‘global optimal energy expenditure’ hypothesis by Molnár & Ramírez (1998), can also be grouped with the MEDR hypothesis.

The Froude number has also been popularly used for building optimality hypotheses. Through an analytical study on the regime relationships, Lacey (1958) showed that the Froude number should be constant for the constant slope and sediment load. However, Barr & Herbertson (1968) argued whether insights gained from two-dimensional formulation, which Lacey's hypothesis is based on, can be extended to real three-dimensional relationships. This constant Froude number hypothesis seems to be connected with the concept of minimum energy degradation rate according to Brebner & Wilson (1967) who stated ‘For the minimization of energy degradation rate, the hydraulic radius of the waterway will have been adjusted so that a certain value of the Froude number is obtained. This value is a function of the particle properties and concentration but is completely independent of the discharge.’ Jia (1990) further argued that the maximum channel stability is achieved when the Froude number is not only a constant but also a minimum value. This ‘minimum Froude number’ hypothesis is related to the earlier MUSP hypothesis since Yang (1978) already found that the prediction accuracy of the MUSP hypothesis improves as the sediment concentration and the Froude number decreases. Later, Grant (1997) proposed that mobile-bed channels adapt to prevent supercritical flow (the state defined as its Froude number is greater than the unity).

Another approach has focused on the sediment transport capacity (Pickup 1976; Kirkby 1977; Ramette 1980; White et al. 1982). White et al. (1982) proposed the hypothesis of ‘maximum sediment transporting capacity’ (MSTC). This hypothesis was recognized as being equivalent to the MSP hypothesis (White et al. 1982; Griffiths 1984). This can be conceptually explained as follows: under a fixed discharge, if the flow can reduce energy loss, stream has more ability to transport sediments from upstream, which helps prevent deposition. This concept, in turn, agrees with the ‘maximum flow efficiency’ (MFE) hypothesis (Huang & Nanson 2000), proposed as a more general principle of former MEDR and MSTC. Here, the flow efficiency is defined as the MSTC per unit available stream power. The MFE hypothesis was derived for a straight single-thread channel. Later, Huang et al. (2004) proposed the ‘maximum energy’ as the principle to illustrate the condition of MFE for a more general open channel flow, not limited to straight channels. All optimality hypotheses discussed by far have a common tenet: geomorphological features adjust towards the state that enables the most efficient flow or least energy loss, in turn the maximum capacity to transport sediment particles. This state is also understood as the state of greatest stability where net deformation is the least (e.g. Jia 1990; Eaton et al. 2004).

These hypotheses have shown a wide range of applications. Many early optimality hypotheses were applied to estimate the scaling exponents of hydraulic geometry relationships (e.g. Leopold & Langbein 1962; Langbein 1964, 1965; Williams 1978; Chang 1980; Yang et al. 1981; Huang & Nanson 2000). Many of them were also used to explain the meandering (Yang 1971a,b; Chang 1979b; Huang et al. 2004), the formation of riffles and pools (Yang 1971c) and self-similar river network formation (Rodríguez-Iturbe et al. 1992). Although existing optimality hypotheses have achieved insightful results in several applications, there have been criticisms as explained in the next section.

4. Debates over existing optimality hypotheses

There have been continuous debates over existing optimality hypotheses, mostly pertaining to their physical justification (e.g. Griffiths 1984). It has been argued that they mimic entropy production of linear thermodynamics with highly nonlinear energy transformations in river flows (Davy & Davies 1979), and use assumptions only applicable to laminar flows for river flows that are turbulent in nature (e.g. Davies & Sutherland 1983). To fortify their physical justification, additional components have been incorporated in the formulation of optimality hypotheses. For example, bank stability relationship was added to White et al.'s (1982) formulation for non-cohesive (Millar & Quick 1993; Eaton et al. 2004; Millar 2005) and cohesive (Millar & Quick 1998) banks. Nevertheless, existing optimality hypotheses still suffer from significant limitations, such as (i) they have little consideration on the dynamic nature of environmental systems and (ii) feedbacks from closely related non-fluvial components such as tectonic activities and ecosystem functions are rarely incorporated.

First, the dynamic nature of environmental variables is rarely accounted for in the formulation of existing optimality hypotheses. For example, existing hypotheses predict the channel formation under a constant flow discharge (mostly dominant discharge). However, stream discharge is directly dependent on hydrological variation and consequently time-variant in nature. If discharge is not a fixed constant but a variable quantity, MSP would be satisfied for discharge Q = 0 while MSTC would be satisfied as Q diverges to infinity. Based on this argument, under varying Q, MSP and MSTC may no longer be equivalent, conflicting with earlier studies on these hypotheses (White et al. 1982). Consequently, existing hypotheses are only applicable to the ideal steady flow conditions (e.g. Yang 1978; Jia 1990). Existing hypotheses also adopt the constant sediment load condition. Since sediment load continuously varies along with flow discharge, this assumption is also problematic.

Existing hypotheses have little consideration on feedbacks between fluvial and non-fluvial processes. Landscape evolution cannot be isolated from atmospheric processes, geological activities and ecosystem functions (e.g. Dietrich & Perron 2006). For example, vegetation coevolves with landform, and this coevolution is found to be critical in forming meandering patterns (Tal & Paola 2007). However, no existing optimality hypothesis integrates coevolutionary processes.

These two points, i.e. the dynamic nature of environmental systems and feedbacks between fluvial and non-fluvial processes, are related to each other. As a result of this complexity, landform evolution may never reach a stable state but is always subject to dynamic changes. Phillips (1990) demonstrated that at-a-station hydraulic geometry is inevitably unstable, questioning the validity of equilibrium constraints. Simon & Thorne (1996) observed rapid adjustment of the Toutle River to the debris avalanche accompanied by the eruption of Mount St Helens and showed that existing optimality hypotheses are only partially applicable.

Sometimes, conflicts between existing optimality hypotheses have been reported in a general context. Howard (1972, p. 477) stated:

Since plane Couette flow has the least energy dissipation among all solenoidal fields satisfying the boundary conditions and is in fact the motion that will occur when R (Reynold's number) is small, one might be tempted to consider as a sort of metaphysical principle the statement that ‘nature chooses that motion which minimizes energy dissipation.’ Such a statement, while true for R < Rc (critical Reynolds number), could not always be true since plane Couette flow does not in fact occur if R is large. But even for small R such a statement is misleading, for one should not compare the flow that occurs with all solenoidal vector fields, but only with those motions that are possible, i.e. the real question is: ‘Among all solutions (with steady averages) of the Navier–Stokes equations, which one (or ones) actually occur under the given boundary conditions?’ Since when R ≤ Rc there is actually only one competitor, the exactly opposite metaphysical principle ‘Nature chooses (from among the possibilities available) that motion which maximizes the energy dissipation’ is equally true. Any selection principle at all will be ‘correct’ when there is no choice.

Motivated by Howard (1972), Davies & Sutherland (1980, 1983) investigated the case that the evolution proceeds towards the state of ‘maximum friction factor’ (MFF), which is conceptually opposite to the minimum energy dissipation. Ironically, Davies & Sutherland (1983) found that the MFF hypothesis pursues the same extrema as the MEDR group hypotheses depending on circumstances. The MFF hypothesis was refined as the hypothesis of ‘maximum resistance to flow in the fluvial system as a whole’, which considers the friction factor as well as other resistance terms (Eaton et al. 2004). The MFF hypothesis was also criticized in that no MFF is available when channel width, depth and slope are dependent variables (Griffiths 1984).

There have been insufficient field observations to support existing optimality hypotheses. To make matters worse, field observations are often inconsistent with the formulation of these hypotheses. For several major rivers in the USA, Leopold & Maddock (1953) reported that the rate of flow velocity increase downstream is very little. Based on this, the formulation of the optimal channel network theory was made assuming no velocity increase downstream (Rodríguez-Iturbe et al. 1992). However, observations made later in New Zealand showed that the flow velocity increases downstream at a rate much greater than was widely accepted, putting in question the validity of the formulation of the optimal channel network theory (Ibbitt 1997).

5. Conclusions

This paper provides a review on the mathematical formulation of landscape evolution that has left characteristic patterns, with a focus on optimality approaches. There have been a number of optimality hypotheses proposed and large efforts to find their backgrounds from a physical basis. Although existing optimality hypotheses have achieved insightful results in several applications, there have been continuous criticisms on their physical basis. This indicates the difficulty of interpreting the entropy production of the thermodynamics principle for the complex and dynamic geomorphological system.

While the early study of Leopold & Langbein (1962) used the entropy concept, most hypotheses proposed thereafter have chosen different approaches in formulating their optimality principles as described in this review paper. This contrasts to other disciplines where thermodynamics-based optimality approaches such as the maximum entropy production hypothesis have been established based on theoretical grounds (e.g. Lorenz 1960; Dewar 2003). Treating landscape evolution with entropy aspects is difficult in that it is the mechanical energy that plays the main role in driving landform evolution while the main theme of the classical thermodynamics is heat energy. As a result, the maximum entropy production principle has not been used in landform evolution problems. While the formulation of landscape evolution into the context of maximum entropy production is challenging, it is worth investigating the maximum entropy production principle in this research context.

We suggest that the formulation of optimality principles should accommodate the dynamic nature of the system, such as hydrological variability and complex feedbacks from non-fluvial processes, e.g. atmospheric processes, geological activities and ecosystem functions. Future interpretation of the thermodynamics principle for landscape evolution problems should be made in this context of coevolution with a broader environmental system. It would be also worth considering different dissipation regimes in a natural river system in relation to the necessity of structural patterns.

Nevertheless, it should be noted that the scope of optimality approaches is to find the final or optimal state of evolution. In other words, a well-formulated optimality hypothesis can give an acceptable prediction of geomorphological variables for an instantaneous snapshot of a continuous movie of landscape evolution, i.e. the final state expected under given ideal conditions, but basically may not be a good tool for predicting time-dependent evolution. If carefully used with a good understanding on these limitations, optimality principles can contribute to simplifying the formulation of process-based models. Optimality approaches can also provide insightful findings on the macroscopic behaviour of environmental systems.