The principle of ‘maximum energy dissipation’: a novel thermodynamic perspective on rapid water flow in connected soil structures

Abstract

Preferential flow in biological soil structures is of key importance for infiltration and soil water flow at a range of scales. In the present study, we treat soil water flow as a dissipative process in an open non-equilibrium thermodynamic system, to better understand this key process. We define the chemical potential and Helmholtz free energy based on soil physical quantities, parametrize a physically based hydrological model based on field data and simulate the evolution of Helmholtz free energy in a cohesive soil with different populations of worm burrows for a range of rainfall scenarios. The simulations suggest that flow in connected worm burrows allows a more efficient redistribution of water within the soil, which implies a more efficient dissipation of free energy/higher production of entropy. There is additional evidence that the spatial pattern of worm burrow density at the hillslope scale is a major control of energy dissipation. The pattern typically found in the study is more efficient in dissipating energy/producing entropy than other patterns. This is because upslope run-off accumulates and infiltrates via the worm burrows into the dry soil in the lower part of the hillslope, which results in an overall more efficient dissipation of free energy.

1. Introduction

‘There is preferential flow at all scales!’ This was a key message of a talk on ‘Idle thoughts on a unifying theory of catchment hydrology’ given by Günter Blöschl at the 2006 EGU General Assembly (Blöschl 2006) in a session on ‘Catchment hydrology—scale-integrated monitoring, process heterogeneity and steps towards a unifying catchment theory’. In this context, ‘preferential flow’ was used to address rapid water flow along spatially connected—often biologically mediated—flow paths of minimum flow resistance. Preferential flow, in fact, seems to be the rule rather than the exception as pointed out by Blöschl (2006) and later summarized by Uhlenbrook (2006). It occurs locally in ‘non-capillary’ macropores (Beven & Germann 1982; Simunek et al. 2003), at the hillslope scale in surface rills or through subsurface pipes (Western & Grayson 1998; Weiler & McDonnell 2007; Stefanovic & Bryan 2009) and in river networks (Rodriguez-Iturbe & Rinaldo 2001). Originally, the term preferential flow was introduced after realizing that water flow in non-capillary soil structures—often worm burrows or root channels—was much faster than would be expected from the classical theory of flow and transport in porous media (Beven & Germann 1982; Flury et al. 1994; Zehe & Fluehler 2001a,b). Today, rapid flow in connected biopores or sometimes shrinkage cracks is widely acknowledged to play a key role in the transport of agrochemicals in cohesive soils (Flury 1996). The spatial distribution of worm burrows in the landscape may, furthermore, exert a crucial control on rainfall run-off response and sediment yield at the hillslope and catchment scales (Niehoff et al. 2002; Zehe & Blöschl 2004; Zehe et al. 2005).

However, even if the population of connected biopores/macropores in soil is known, we struggle in predicting onset, timing and strength of preferential flow events (Weiler & Fluehler 2004; Blöschl & Zehe 2005; Zehe et al. 2007). Preferential flow is an intermittent threshold phenomenon; onset and intensity are determined by the strength of the rainfall forcing and the wetness state of the soil (Zehe & Fluehler 2001b; Weiler 2006; McGrath et al. 2007). Furthermore, burrows of deep-digging anecic earthworms (such as Lumbricus terrestris or Aporectodea longa) can—even when being abandoned—persist over decades as suggested by accumulation of clay particles in worm burrows (Lavelle et al. 1997; Hedde et al. 2005; Milcu et al. 2006). Thus, these structures ‘survive’ severe rainfall and subsurface flow events and still retain their hydrological function. Why is it sometimes ‘favourable’ for soil water to flow along paths of minimum flow resistance, but sometimes not? Why do these structures persist such a long time? The present study suggests—as far as we know—for the first time that a thermodynamic perspective may help in unravelling these questions and thus to better understand preferential flow phenomena. The thermodynamic perspective looks at soil water flow as a dissipative process in an open non-equilibrium thermodynamic system.

Rodriguez-Iturbe et al. (1998) and Rodriguez-Iturbe & Rinaldo (2001) as well as Rinaldo et al. (1996) employed thermodynamics to explain the organization of river networks as ‘least energy structures’. Leopold & Langbein (1962) used a thermodynamic analogy—heat flow from higher to lower temperatures—to explain water flow along topographic gradients. Recently, Kleidon & Schymanski (2008) proposed that most processes in the hydrological cycle, including soil wetting, are irreversible and produce entropy. They treat the subsurface as an open thermodynamic system far from thermodynamic equilibrium (TE) and suggest that an optimal/steady-state ‘configuration’ ensures that exchange fluxes of mass and energy maximize entropy production. The maximum entropy production (MEP) hypothesis emerges from the trade-off between thermodynamic ‘forces’ and fluxes, because the latter depletes the driving gradient/thermodynamic force (Kleidon & Schymanski 2008). It had been previously used to predict properties of planetary atmospheres (Lorenz et al. 2001) or to identify parameters of general circulation models (Kleidon et al. 2006).

In the present study, we follow Kleidon & Schymanski (2008) when treating the unsaturated zone of the soil as an open thermodynamic system far from equilibrium. However, in this study, we take a complementary but equivalent perspective on soil water flow, focusing on dissipation of Helmholtz free energy. Helmholtz free energy is at minimum at TE (Kondepudi & Prigogine 1998), whereas entropy is at maximum. We hypothesize that water flow in soils in general organizes in such a way that dissipation of Helmholtz free energy becomes maximum for a given rainfall input (disturbance) and for a given soil type and given soil structures. We hypothesize furthermore that biopores and other connective structures allow a faster relaxation towards TE, because they allow a faster infiltration of ‘excess water’ and a faster redistribution of capillary water within the soil. Through simulations with a physically based hydrological model, we will show that the latter is of prime importance in the case of cohesive soils where the pore-size distribution is dominated by medium and small pores that exert strong capillary forces on soil water. We provide additional evidence that the spatial patterns of worm burrow density at the hillslope scale are a major control on energy dissipation and relaxation to TE because they control the lateral redistribution of water as overland flow. The hypotheses of maximum energy dissipation (MED) or of maximizing entropy production (MEP) are equivalent from a thermodynamic view. However, we consider the former to be a little more intuitive than the latter.

2. Theoretical background

This section provides a novel interpretation of standard soil physics in terms of thermodynamic variables and principles. Second, we provide evidence for the importance of earthworm burrows for water flows and transport from numerous hydrological and soil ecological studies. Section 2c discusses how to define Helmholtz free energy in the soil and how to use hydrological process models to shed light on soil water flows as dissipative processes.

(a). Soil water dynamics, run-off generation and related thermodynamic concepts

From a physical point of view, a soil is a mixture of several phases, namely the water, air and solid phases. The solid phase is arranged into a (rigid) matrix that contains partly interconnected voids termed the pore space. The pore space may be partly or totally filled with water, and the volumetric soil water content at saturation, θ_s, is then equal to the volumetric fraction of the pore space, which is termed soil porosity. Soil water is influenced by various forces. The most important forces are gravity and capillarity. The latter occurs because water acts as a wetting fluid in the soil. Capillarity increases nonlinearly with decreasing pore size and is zero at local saturation. The pore-size distribution of a soil is thus characteristic of its capability to store water against losses such as drainage, evaporation and root extraction. At the macroscale, gravity and capillarity are characterized by gradients in the heads of gravity potential z (m) and matric potential ψ (m). The latter is zero at saturation and can be interpreted as being proportional to the work release when a small water mass is added to the water phase. The hydraulic head ψ_H equals the sum of gravity and matric potential heads:

2.1

Steady state in soils—usually termed hydraulic equilibrium (HE)—is reached at a zero gradient of ψ_H, i.e. when ψ decreases linearly from the groundwater table to the soil surface, where the hydraulic head and thus z is usually set to zero.

So far, this has been standard soil physics (Jury & Horton 2004). The new perspective comes into play when regarding the hydraulic head as the analogue to the chemical potential that represents the ‘binding energy per water mass’ (Kleidon & Schymanski 2008),

2.2

and HE as equivalent to TE, where g (m s⁻²) is the gravitational acceleration and θ (m³ m⁻³) is the volumetric water content. The soil water retention curve ψ(θ) describes essentially the strength of the capillary binding of water as a function of the volumetric soil water content. It is highly nonlinear and a characteristic fingerprint of the pore-size distribution, which is in turn characteristic of the biological and chemical weathering processes that have formed the soil from the parent material in a landscape and the distinct climate. The soil moisture profile at TE is therefore nonlinear too and a characteristic fingerprint of the soil type as well as depth to groundwater. The soil water flux q is usually described by Darcy's law, where k denotes the soil hydraulic conductivity.

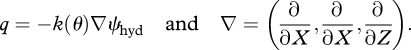2.3

Combining equation (2.3) with the continuity equation yields the Richards equation for soil water dynamics.

2.4

Soil hydraulic conductivity is also a characteristic fingerprint of the pore-size distribution and connectivity of the pore space (Vogel 2000; Vogel & Roth 2001) and decreases strongly and nonlinearly with decreasing soil water content (Mualem 1976; Jury & Horton 2004). Physically based hydrological models may simulate the development of soil water content and matric potential based on the Richards equation for given boundary conditions (rainfall, evaporation) and when the soil hydraulic functions k(θ) and ψ(θ) are known. The latter are often characterized by means of the van Genuchten (1980) approach to relate ψ and θ:

2.5

as well as the Mualem (1976) approach to characterize k as a function of the effective water saturation Se:

2.6

This approach is based on six parameters, namely the saturated hydraulic conductivity k_s (m s⁻¹), the saturated soil water content θ_s (m³ m⁻³), the residual soil water content θ_r (m³ m⁻³) and the air entry value α (1 m⁻¹) that characterizes the maximum radius of the soil pores. The parameters m and n determine the spread of the different pores sizes that compile the pore space. The pore space of a sandy soil consists, for instance, mainly of coarse pores with n values around 12–14, and the pore space of loamy soil contains on the contrary fine, middle and coarse pores, with corresponding n values between 2 and 4. These van Genuchten–Mualem parameters are usually determined based on multi-step outflow experiments with undisturbed soil cores (see, for instance, Iden & Durner 2008).

(b). Biological soil structures as accelerators of infiltration and redistribution processes

Connective soil structures such as channels, shrinkage cracks and worm burrows allow locally up to 100–1000 times faster water fluxes especially in fine-grained soils (Beven & Germann 1982). This is because capillarity may be neglected in those structures and flow resistances in the direction of the driving potential gradient are rather small. Earthworms play a pivotal role in building long-lasting soil structures that exert significant influence on water flows (Edwards et al. 1990; Shipitalo & Butt 1999; Shipitalo et al. 2000), solute transport (Edwards et al. 1993; Domínguez et al. 2004; Alekseeva et al. 2006; Le Bayon & Binet 2006), organic matter dynamics, pedogenetic processes and plant growth (Lavelle et al. 1997; Hedde et al. 2005; Milcu et al. 2006).

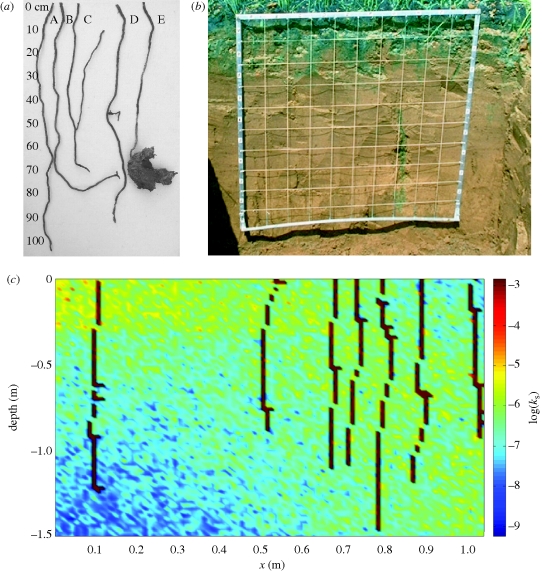
The density per area, depth and tortuosity of the burrow system depends strongly on the abundant earthworms species, and this in turn depends on spatio-temporal patterns of organic matter content (Rossi et al. 1997), soil hydrological properties and soil water content (Cannavacciuolo et al. 1998; Nuutinen et al. 1998, 2001), biotic interactions (Nuutinen 1997; Rossi 2004) and disturbance regimes related to agricultural practice (Joschko et al. 2006; Whalen & Fox 2007). In the present study we focus on structures formed by deep-digging anecic earthworms (L. terrestris, A. longa). They build mainly vertically oriented, weakly tortuous burrows up to 2 m depth (figure 1a) that may substantially accelerate infiltration at the plot and field scale (Shipitalo & Butt 1999; Zehe & Fluehler 2001a; Bastardie et al. 2003; figure 1b) and even decrease overland flow response at the catchment scales (Zehe et al. 2005). We will show that ecosystem engineering of these earthworms is also most interesting from a thermodynamic perspective on soil water flows.

Figure 1.

(a) Structure of anecic earthworm burrows as reported in Shipitalo & Butt (1999, fig. 3); (b) preferential flow in a worm burrow observed during a dye tracer experiment in the Weiherbach catchment; (c) exemplary generation of earthworm channels of high conductivity for 1.5 m× 1 m model domain for case n_b = 10, l_b = 1.1 ± 0.1 m and p_lat = 0.1.

(c). A novel thermodynamic perspective on soil water flows and preferential flow

In the following, we assume that the soil is an open thermodynamic system of a given volume that exchanges energy and mass with the atmosphere and the groundwater system. Thus, Helmholtz free energy, F (J), is the appropriate thermodynamic potential for characterizing this system, and TE is a state of minimum free energy (Kondepudi & Prigogine 1998). The differential change of F is defined as

2.7

where S is the entropy (J K⁻¹), T is the absolute temperature (K), p is the pressure (N m⁻²), V is the soil volume (m³) and μ is the chemical potential (J kg⁻¹). M is the water mass (kg) calculated as

2.8

where ρ (kg m⁻³) is the density of water. Following Milly (1982), we assume that soil water fluxes and infiltration are isotherm processes and that the soil neither shrinks nor swells. Thus, the terms ‘S dT’ and ‘p dV’ in equation (2.7) are zero. The Helmholtz free energy of the unsaturated soil zone is thus

2.9

where c is an integration constant (note that V and ρ are constant). When inserting equation (2.2) into equation (2.9), we finally obtain

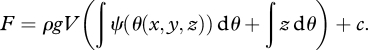2.10

This expression for Helmholtz free energy is valid as long as the matric potential is well defined and the gravity and matric potential are additive. It may be used in combination with Darcy's law (as done here) or with a more general law for water flow in soils.

In general, there is always a trade-off between driving forces for soil water fluxes that increase with soil moisture gradients and try to establish TE and decreasing hydraulic conductivity (owing to low water contents) that impedes flow from wet to dry parts of the soil. Especially in fine-grained soils with a high amount of medium and small pores, such as loam and clay soils, soil water redistribution from wet to dry regions is rather inefficient owing to this ‘bottleneck’ effect of low hydraulic conductivities. This bottleneck effect is also crucial for infiltration and overland flow formation in landscapes with fine textured cohesive soils. The actual infiltration capacity of the soil matrix continuum—also described by Darcy's law—is rather low during dry conditions. Rainfall intensity may quickly exceed infiltration capacity and most of the water runs off as Hortonian overland flow. Infiltration and redistribution of water in the matrix of fine-grained soils are rather inefficient during summer conditions, and the dissipation of free energy and relaxation towards TE is thus strongly impeded. The soil system remains in an awkward state of high free energies where strong thermodynamic gradients persist. We suggest that apparent preferential pathways allow on the contrary a much higher infiltration and faster redistribution of water in soil. Energy dissipation becomes strongly enlarged, relaxation of the system towards TE is accelerated and thermodynamic gradients are efficiently depleted.

3. Application for a rural landscape

(a). Study area and database

The Weiherbach catchment is an intensely monitored research catchment located in southwestern Germany. Geologically, it consists of Keuper and Loess layers of up to 15 m thickness. The climate is semihumid with an average annual precipitation of 750–800 mm yr⁻¹, average annual run-off of 150 mm yr⁻¹ and annual potential evapo-transpiration of 775 mm yr⁻¹. More than 95 per cent of the total catchment area is used for cultivation of agricultural crops or pasture, 4 per cent is forested and 1 per cent is paved area. Crop rotation is usually once a year. This landscape is characterized by gentle slopes with typical loess soil catenas formed by erosion with moist but drained colluvisols at the foot of the hillslopes and valley floors and drier Calcarig Regosol soil in the upper hillslope sectors. A mapping of anecic earthworm burrows (L. terrestris and A. Longa) showed a higher spatial density of larger and deeper worm burrows within the downslope Colluvisol soils. One likely reason for this spatial organization is that earthworms find better habitat conditions owing to the more even moisture regime and the higher amount of soil organic material within the Colluvisols. This typical spatial pattern of soils and macroporosity has, in turn, led to a spatially organized pattern of flow and transport at the slope scale (Zehe & Fluehler 2001b), and exerts a key influence on the catchment scale run-off response to extreme rainfall events (Zehe et al. 2005).

The present study focuses on a very intensely investigated gentle hillslope where flow and transport in worm burrows was observed during several sprinkling experiments (Zehe & Fluehler 2001a). The database includes the density, width and depth of worm burrows mapped on two 4 × 4 m plots and soil hydraulic properties, derived from undisturbed soil samples from two depths (20 replicas per depth and plot). We found an average density of anecic worm burrows (diameter larger than 6 mm) of n_b = 10 worm burrows per m², with an average length l_b = 0.8 ± 0.1 m. Furthermore, we measured maximum flow rates in worm burrows using undisturbed soil columns extracted such that the worm burrow was concentric in the middle of the core cutter (five replicas for diameters ranging from 2 to 9 mm). Flow rates, Q_b, in worm burrows larger than 6 mm were on average 2.2 × 10⁻⁶ m³ s⁻¹.

(b). Soil hydrological model

As numerical model we used CATFLOW (Zehe et al. 2001). CATFLOW represents a hillslope along the steepest descent line as a two-dimensional cross section that is discretized by two-dimensional curvilinear orthogonal coordinates. The hillslope is thus assumed to be homogeneous perpendicular to the slope line. Soil water dynamics are described by the Richards equation in the potential form that is numerically solved by an implicit mass conservative Picard iteration (Celia & Bouloutas 1990). Soil hydraulic functions are described after van Genuchten (1980) and Mualem (1976). Evapo-transpiration is represented by an advanced SVAT approach based on the Penman–Monteith equation. Surface run-off routing down the hillslopes is based on the diffusion wave approximation to the one-dimensional Saint-Venant equations. It is numerically solved by an explicit upstream finite-difference scheme.

(c). Set-up of the simulation domain and simulation variants

As we wanted to represent the worm burrows explicitly as connected flow paths of high hydraulic conductivity and low retention properties, we discretized the 30 m long study hillslope down to a depth of 2 m at a very high resolution of 2 × 2 cm. In a first step, we assigned the soil hydraulic parameters listed in table 1 to each model node. Next, we accounted for the observed small-scale stochastic heterogeneity of k_s and porosity by generating heterogeneous fields with observed variance and correlation length of 2 m by means of the turning-bands method (Brooker 1985; Zehe et al. 2005). As the averages k_s and porosity observed at the two plots were identical within the confidence limits, the assumption of a correlation length smaller than 4 m is justified. We then generated a population of earthworm burrows with a three-step procedure. First we simulated the number of worm burrows in a surface grid cell by a Poisson process as suggested by Beven & Clarke (1986). In case the number of macropores exceeded one, we simulated the length of the burrow according to a normal distribution and then extended the worm burrow into the model soil by non-isotropic random walk. The probability for the digging direction to deviate from the vertical was either p_lat = 0.1 or p_lat = 0.15 to allow for different degrees of tortuosity. The hydraulic conductivity of the worm burrows was computed by dividing Q_b by the horizontal cross-sectional area of the grid cell. In the last step, we replaced the soil type in the worm burrow by a sand of porosity 0.9 and low retention properties to minimize the effect of capillary forces during simulation. Such a double porosity approach (Simunek et al. 2003) to treat macropore flow and matrix flow in one domain is feasible in the case of a high spatial resolution as used in the present study. The big drawback of this approach is the high computational cost, and the advantage is the spatially explicit nature and that it may be parametrized on field data. Figure 1c shows exemplarily generated worm burrows to highlight their similarity to worm burrows observed by Shipitalo & Butt (1999).

Table 1.

Average soil hydraulic parameters after van Genuchten (1980) and Mualem (1976) defined in equations (2.5) and (2.6), derived from multi-step outflow experiments (Zehe et al. 2001); k_s (m s⁻¹) is the soil hydraulic conductivity, θ_s (m³ m⁻³) the saturated soil water content, θ_r (m³ m⁻³) the residual soil water content and α (1 m⁻¹) the air entry value that characterizes the maximum radius of the soil pores. The parameter n determines whether the spread of pore sizes in the pore space is wide.

depth	ks (m s−1)	θs (m3 m−3)	θr (m3 m−3)	α (m−1)	n (−)
0–30	4.7 × 10−6	0.43	0.11	3.80	1.20
30–200	1.7 × 10−6	0.40	0.04	1.90	1.25

At first, we compared different populations with n_b = 0, 5, 10, 15, 20 and 25 worm burrows per m². The case n_b = 10 and l_b = 0.8 m corresponds to the observed population. For each n_b, we compared two degrees of tortuosity with p_lat = 0.1 and 0.15, respectively. For simplicity, we simulated the response of each of these set-ups to constant intensity block rainfall of 5 mm h⁻¹ and different rainfall totals of 10, 25 and 40 mm. The start date of the stimulation was 27 June 1994 and simulated time was one day. The initial state was a linear profile in matric potential head with −5 m at the surface and −3 m at the lower boundary of the model domain in all cases. This corresponds to a relative saturation of 0.45 in the top soil and 0.55 in the deeper soil. Climate input data, i.e. global radiation, wind speed and direction, air temperature and air humidity, were taken from the nearby climate station (Zehe et al. 2001).

As explained above, the variability of anecic worm burrows along a typical hillslope is spatially organized, with a higher spatial density of larger and deeper burrows at the downslope locations. We thus compared two set-ups with the same overall average density of 10 worm burrows per m². In case A, the worm burrows were assumed to be clustered in the lower half of the hillslope, while in case B they were assumed to be clustered in the upper half. The underlying hypothesis is that a high amount of worm burrows located at the downslope region will trap more surface run-off and thus allow a faster relaxation to TE as case B.

4. Results

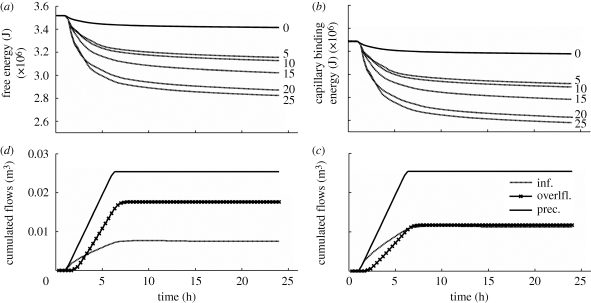
As shown in figure 2a exemplarily for the 10 mm rainfall event, the soil without worm burrows/connected preferential pathways remains in a state of rather high free energy throughout the entire simulation. Increasing the density of worm burrows results in a faster relaxation towards states of smaller free energy and thus towards TE where gradients are zero (figure 2a). This may be explained by the reduced overland flow response and enhanced infiltration, as shown for the case of n_b = 25 burrows per m² and 25 mm rainfall where infiltration is enhanced by almost 100 per cent (figure 2c,d). Figure 2b highlights that capillary binding energy makes up approximately 80 per cent of the total free energy in this fine-grained Loess-Colluvisol. Thus, during these dry summer states, infiltration and redistribution of water are the more efficient processes to dissipate free energy when compared with surface run-off production and run-off concentration in the stream. The latter reduces mainly the potential energy, but capillary binding energy is the dominating term in fine-grained soils.

Figure 2.

(a) Free energy and (b) capillary binding energy plotted against simulation time for increasing density of worm burrows (given by the integers) during the 10 mm rainfall event. The solid line belongs to a zero burrow density; average worm burrow depth is 0.8 m. (d) Water balances namely accumulated rainfall, infiltration and overland flow for the rainfall event with 25 mm for the case of no worm burrows and (c) the case of n_b = 25 m⁻².

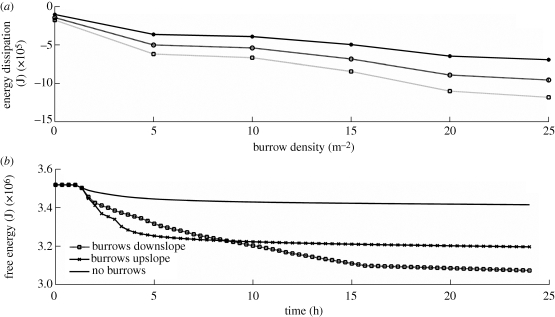
Figure 3a shows the total energy dissipation, defined as the difference of initial and final free energy, plotted as a function of worm burrow density and rainfall totals. As infiltration and wetting are isothermal and isochoric processes, total dissipation of free energy is directly proportional to the entropy production in this case (compare equation (2.7)). For a given rainfall total, the absolute value of total energy dissipation and thus entropy production increases by almost a factor of five when increasing the burrow density from zero to the observed value of n_b = 10 m^−2,. The total amount of dissipated energy increases by a factor of 10 when n_b reaches 25 m⁻². It is interesting to note that energy dissipation and thus entropy production increases with increasing rainfall totals, but this increase is much stronger when macropores/worm burrows are present than in the case of zero macropores. This suggests that a population of worm burrows that can act as preferential pathways is even more favourable for an efficient dissipation of energy in the case of strong mass inflows owing to extreme rainfall events.

Figure 3.

(a) Total dissipation of free energy calculated as difference of free energies at the initial minus the final state as a function of increasing burrow density per m² and different rainfall totals. (b) Free energy and plotted against simulation time for the case of no burrows, burrows clustered at the downslope half (case A) and burrows clustered in the upslope half (case B).

Figure 3b gives further evidence that not only the average density of worm burrows but also their spatial distribution along the hillslope has a strong influence on the dissipation of energy during rainfall events. In the early phase, energy dissipation is more efficient in case B where the worm burrows are clustered in the upper part of the slope because total free energy drops faster with time. However, water that runs off to the lower almost flat parts of the hillslope cannot infiltrate owing to the bottleneck effect of the dry soil. Thus, the slope of the free energy curve flattens after 4 h. In case A, energy dissipation is slower in the early phase, but remains efficient in later stages because run-off accumulates in the downslope half and infiltrates via the worm burrows/connected preferential pathways into the dry soil. Overall, the total amount of dissipated energy and thus produced entropy is approximately 1.5 times higher than for case B.

5. Discussion and conclusions

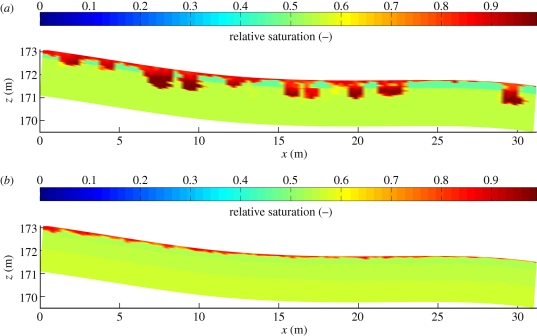
In the present study, we postulated that water flow in soils in general organizes in such a way that dissipation of Helmholtz free energy becomes maximum for a given rainfall input (disturbance) and for a given soil type and with given soil structures. The presented results suggest that during summer conditions the dry topsoil matrix of fine-textured soils strongly inhibits infiltration owing to the bottleneck effect of low hydraulic conductivities, as underpinned by the final pattern of relative water saturation shown in figure 4b. Relaxation towards TE is thus strongly impeded. Connected worm burrows act as ‘shortcuts’ through this topsoil bottleneck. Water may rapidly infiltrate, which implies a much more efficient redistribution of water against the thermodynamic gradient, as highlighted by the pattern of relative water saturation in figure 4a. A higher density of worm burrows/connected preferential pathways thus enhances the capability of the unsaturated zone to efficiently redistribute water against thermodynamic gradients. This implies a more efficient dissipation of free energy and thus a higher production of entropy during rainfall events. We thus may conclude that earthworm burrows or connected preferential pathways in general offer additional degrees of freedom to water flow. They allow a faster infiltration and faster redistribution of water during dry conditions and thus a faster relaxation of the soil system towards TE. Apparent connected preferential flow paths thus enlarge the system's capacity to dissipate free energy and thus improve ‘the functioning’ of the soil system from a thermodynamic perspective.

Figure 4.

(a) Relative saturation after 24 h for 25 mm rainfall in the case of 25 and (b) 0 worm burrows per m².

It is furthermore a striking coincidence that a spatial pattern of worm burrows similar to the typical spatially organized pattern of worm burrows that was observed at the Weiherbach hillslopes and has been shown to crucially determine the overland flow response of this catchment (Zehe et al. 2006) is favourable for an efficient dissipation of free energy during rainfall events. Lateral redistribution owing to overland flow causes a downslope accumulation of surface water, where water infiltrates via the worm burrows and is redistributed against thermodynamic gradients in the soil. This combined effect causes a very efficient dissipation of free energy and thus production of entropy.

It is now of interest to ask, why the bio-geomorphic flow system indeed seems to maximize energy dissipation. Earthworms build their burrows because of their biological needs and specific niche, rather than to optimize the efficiency of flow at the hillslope scale. The higher spatial density of deeper worm burrows in the downslope regions is, therefore, a result of ecological optimality as it reflects the earthworms’ preference for a more even and wetter soil moisture regime and higher contents of organic matter. Nevertheless, worm burrows do act as dissipative structures and their presence and the typical distribution at the hillslope scale imply a more favourable configuration in the light of ‘maximum energy dissipation’ as an emerging principle. Probably, this is a result of coevolution and self organization as suggested by Paik & Kumar (2008). Water acts as a geomorphic agent and determines soil formation and redistribution of soil material, resulting in a Loess catena that is typical for this landscape. Water is furthermore a primary resource for organisms and redistributes resources at the hillslope scale, which affects the distribution of earthworm species along the hillslope. A high density of connected preferential pathways in the lower reaches is, as shown, favourable from a thermodynamic perspective. The latter implies a higher geomorphic resilience of the hillslope, as excess water during severe events is redistributed more efficiently with less surface run-off and the system approaches TE more efficiently. Let us assume the ecological optimal pattern of worm burrows at slope scale was strongly different from the one that is favourable from a thermodynamic perspective. This would imply that the worms worked against the geomorphic resilience of their own habitat. This fact could in turn act as a selection criterion against those species that reduce the geomorphic resilience of their habitat during coevolution of species and landscape and explain ‘long-term convergence’ of ecological optimality and thermodynamic optimality. In this light, also the long-term stability of worm burrows appears rather logical because they are favourable for the geomorphic resilience/stability of the hillslope during extreme events.

We conclude that the nature of preferential flow in soils may be much better understood from the suggested thermodynamic perspective and the MED hypothesis. Preferential pathways offer additional degrees of freedom to water flows in landscapes with cohesive soils, especially during dry summer conditions. ‘Switching on’ preferential flow means to switch to a more efficient mode of dissipating energy during rainfall events, similar to the switch from laminar to turbulent heat transport when a tea kettle is heated or in the Raleigh Bernard cell when the inflow of energy into the system exceeds a certain threshold. Thus, the threshold nature of preferential flow is not a big surprise when looking at soil water flow as a dissipative process. Many dissipative processes exhibit threshold behaviour and switching between intermittent regimes as recently discussed by Zehe & Sivapalan (2009). The fact that preferential flow seems to occur at all scales (Blöschl 2006; Uhlenbrook 2006), either in connective surface/subsurface structures or along flow fingers, suggests indeed that water flow in the environment organizes according to similar or even the same optimality principle. Paik & Kumar (2010) discussed several possible alternatives to the MED or MEP principles such as the minimum energy expenditure, minimum unit stream power or minimum energy dissipation that are employed to explain the organization of river nets in fluvial geomorphology. At first sight, they seem to contradict the hypotheses of MED and MEP. However, a closer look shows that the principles of minimum energy expenditure and maximum entropy production are not contradicting at all. The first one applies locally and is necessary for stability of the river cross section. The second one applies globally i.e. looks at the river from its source to its mouth. Most of the energy dissipation during steady state conditions happens at the mouth when the river enters the sea.

Similar to Paik & Kumar (2010) we overall conclude that future research on the organization of flow processes and related structures must become much more systematic. For instance, evapo-transpiration is the most efficient process of dissipating energy owing the high specific heat of vaporization (Holdaway et al. 2010). However, during rainfall conditions, this process is blocked, as air is saturated with water vapour and short-wave radiation is close to zero. Optimal structures that maximize energy dissipation during non-rainfall conditions when energy inputs are large and during rainfall conditions when mass inputs to the system are large will thus be probably different. Future research should hence focus on better understanding which vegetation structures and soil structures optimize dissipation in these different dissipation regimes and how they interact across scales.