A basic introduction to the thermodynamics of the Earth system far from equilibrium and maximum entropy production

Abstract

The Earth system is remarkably different from its planetary neighbours in that it shows pronounced, strong global cycling of matter. These global cycles result in the maintenance of a unique thermodynamic state of the Earth's atmosphere which is far from thermodynamic equilibrium (TE). Here, I provide a simple introduction of the thermodynamic basis to understand why Earth system processes operate so far away from TE. I use a simple toy model to illustrate the application of non-equilibrium thermodynamics and to classify applications of the proposed principle of maximum entropy production (MEP) to such processes into three different cases of contrasting flexibility in the boundary conditions. I then provide a brief overview of the different processes within the Earth system that produce entropy, review actual examples of MEP in environmental and ecological systems, and discuss the role of interactions among dissipative processes in making boundary conditions more flexible. I close with a brief summary and conclusion.

1. Introduction

Matter mixes, water flows downhill and wood burns into ashes. If nothing else were to take place, sooner or later all matter would end up in a uniform mix of everything, water would collect in the world's oceans and all biomass would be burnt to ashes. All processes would lead to a ‘dead’ Earth state with no gradients present to drive fluxes and no free energy available to run life. What seem like trivial observations, these examples highlight an underlying general direction into which any process in the Earth system evolves in time. The three examples are processes that are undoable, or technically speaking, they are irreversible. They happen spontaneously. This direction can be understood and quantified in general terms of thermodynamics. Specifically, this is what the second law of thermodynamics tells us. The common form of this law formulates this direction in quantifiable terms, using entropy as a measure for the lack of gradients and free energy. By depleting gradients and sources of free energy, these processes are directed towards the state of thermodynamic equilibrium (TE) at which the entropy of the system and its surroundings is maximized. In this state, matter is well mixed and no free energy is available to perform physical work or run chemical reactions.

That the Earth system is not in a ‘dead’ state seems like a violation to this general trend and thus to the second law of thermodynamics. What is it about the system Earth that allows it to be maintained far away from the final ‘dead’ state of TE? To prevent such a ‘dead’ state of Earth, some processes need to take place that create gradients and sources of free energy in a setting that does not violate the second law. These processes need to perform physical and chemical work in order to separate matter, to move water up the hill, or to produce wood out of ashes or, in general terms, create gradients to keep global cycling of matter going. In such a ‘living’ state of the Earth system, processes can be viewed and separated into those that continuously perform work and create free energy, and others (the irreversible ones) that dissipate it and continuously produce entropy.

(a). Equilibrium thermodynamics

Most common is the application of thermodynamics to isolated systems in equilibrium (‘equilibrium thermodynamics’). The textbook example for such a system is the ideal gas: a large number of interacting molecules are confined to a certain volume. The ideal gas is treated as an isolated system. It does not exchange energy or mass with the surroundings.

For the ideal gas, we can distinguish properties that describe the state at the microscopic scale of individual molecules from those that describe the gas as a whole. Microscopic properties describe the position and velocity of every molecule in the volume. Macroscopic properties are ones that we are more familiar with and usually measure: the temperature of the gas refers to the mean kinetic energy of the molecules, pressure describes the average intensity by which the molecules collide with the walls of the volume, and density measures the average number of molecules per unit volume. These average properties are defined at the scale of the gas, but are ill-defined at the level of individual molecules. Statistical mechanics tells us that the predictability of the macroscopic variables in thermodynamics, as for instance reflected in the ideal gas equation, originates from (i) the constraints that the microscopic dynamics are subjected to; and (ii) the assumption that the macroscopic state is by far the most probable state given these constraints. The conservation of energy and mass restricts the interactions at the microscopic level to processes that are almost, but not completely random. The most probable macroscopic state by definition is the state of maximum entropy, as stated by Boltzmann's famous equation S = k log W, with S being the entropy and W the statistical weight of a macrostate, i.e. the number of ways it can be realized microscopically. This macroscopic state represents the vast majority of microscopic states. Hence, energy and mass balance constraints in conjunction with the assumption of maximum entropy yields the predictability of the gas as a whole as reflected in equilibrium thermodynamics. Furthermore, this leads to a general direction of an isolated system evolving towards a state of maximum entropy, as formalized by the second law of thermodynamics, which states that entropy changes can only be positive.

The distinction between macroscopic and microscopic dynamics applies to understanding the large-scale behaviour of environmental systems and ecosystems. Just as the example of the ideal gas represents the scaling of microscopic dynamics of molecules to the macroscopic behaviour of a gas, we deal with the scaling of a range of turbulent eddies to planetary-scale motion in the atmosphere and oceans, and with the scaling of plant physiological processes of diverse communities to large-scale land atmosphere exchange fluxes.

(b). Thermodynamics of the Earth system

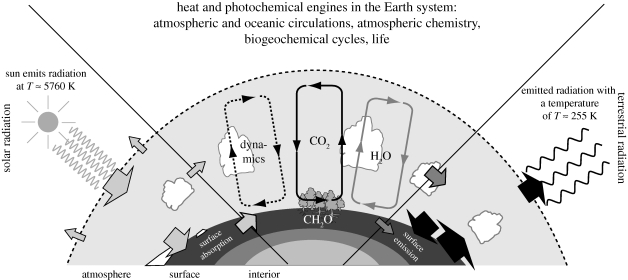
One critical aspect that distinguishes Earth systems from the ideal gas example is that Earth systems are anything but isolated systems, and strongly interact. While at the planetary level we can safely neglect mass exchange with space (although there may be some climatic effects of, e.g. cosmic rays on clouds), the various types of energy exchange with space is critical in keeping these systems running (figure 1): spatial and temporal differences in the absorption of solar radiation provide the radiative forcing gradients that drive the atmospheric heat engine, which provides the means to transport geochemical elements within the Earth system. The atmospheric circulation acts to dehumidify the atmosphere and drive the global water cycle away from TE. That is, the atmospheric circulation continuously performs work, and the dissipated heat is rejected to space in the form of longwave radiation. Hence, in total, the absorption of solar radiation and the subsequent emission of terrestrial radiation to space provides the ultimate driving force to operate Earth systems far away from TE.

Figure 1.

The thermodynamic context of environmental and ecological systems. The cycling of matter at the planetary scale—as manifested by a strong atmospheric circulation and the global cycles of water and carbon—require engines to continuously operate to keep these cycles running. These engines ultimately run on gradients of radiative fluxes, which result from the vastly different radiative temperatures of the Sun (with T_sun ≈5760 K) and Earth (with T_earth ≈ 255 K). Gradients in radiative fluxes can result in gradients of heating, which drive heat engines such as the atmospheric circulation, or photochemical engines that make use of low entropy solar radiation directly.

Solar radiation also provides the photochemical energy to drive photosynthesis, which in turn provides the major source of free energy to drive geochemical cycles within the Earth system. The heat generated by the consumption of free energy is again ultimately rejected to space in the form of longwave radiation. This state far from TE is then reflected into an atmospheric composition with 21 per cent reactive oxygen and an atmosphere that is mostly non-saturated with vapour. This notion of an atmospheric composition far from TE in turn has been interpreted as a sign of widespread life on Earth (Lovelock 1965) and resulted in the formulation of the controversial Gaia hypothesis (Lovelock 1972a,b; Lovelock & Margulis 1974).

But why, and how far, are systems driven away from states of TE? The possibility to sustain a state away from TE can be resolved when considering that the Earth system exchanges entropy with space. The trend away from TE can be related to the proposed thermodynamic principle of maximum entropy production (MEP) (Dewar 2003, 2005a,b; Kleidon & Lorenz 2005), which states that thermodynamic processes in non-equilibirum systems assume steady states at which their rates of entropy production are maximized. Roughly speaking, this would imply that the resulting thermodynamic state is, to the maximum extent possible, away from TE. It would thus seem that non-equilibrium thermodynamics and the related MEP principle would provide a holistic basis for understanding the emergent state of environmental and ecological systems far from TE. We can take this perspective further and ask: what is the role of life in maintaining states away from TE at the planetary level? Is life the thermodynamic implementation, in the form of biogeochemical processes, that maintain a planetary state so far from TE?

(c). Scope of this paper

The purpose of this paper is to provide a simple introduction to non-equilibrium thermodynamics and the MEP principle as it applies to Earth systems. The emphasis is on a simple toy model to illustrate why and to what extent systems are driven out of TE and to demonstrate how this applies to processes within the Earth system. The thermodynamics away from equilibrium is briefly described in §2. The application of MEP is classified into three cases that differ in the flexibility of the boundary conditions. In the following section, the entropy budget of the Earth is then reviewed to provide a perspective on how dissipative Earth system processes are in comparison with each other. Examples of the application of MEP are then given, and the flexibility in boundary conditions is described in terms of interactions among dissipative processes within the Earth system. The paper closes with a brief summary and conclusions.

2. Thermodynamics away from equilibrium

In the following I will use a simple model to demonstrate the evolution of TE, describe the conditions under which a system evolves away from TE, and how the proposed principle of MEP relates to these conditions. In the description I will provide the explanations with minimal use of equations. For a more detailed treatment, the reader is referred to the general background covered in excellent textbooks in the area of non-equilibrium thermodynamics (e.g. Kondepudi & Prigogine 1998). The details of the model used here are given in appendix A.

(a). Evolution towards TE

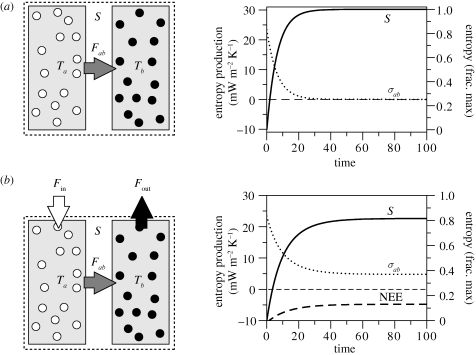
I first illustrate the evolution of an isolated system to the state of TE and relate this to the second law of thermodynamics. To do so, I use a simple example shown in figure 2a. Two boxes of equal mass initially have different initial temperatures T_a and T_b, respectively, and we arbitrarily set the temperatures such that T_a > T_b. We connect the two boxes, which allows for a heat flux F_ab to exchange heat between the two boxes.

Figure 2.

Illustration of the evolution towards (a) a state of thermodynamic equilibrium (TE) for an isolated system, and (b) a state that is maintained away from TE for a non-isolated system that exchanges entropy with the surroundings. The symbols represent: S, the entropy of the system; F_ab, the heat flux from box a to b; T_a and T_b, the temperatures of the respective boxes; F_in, the heat flux into the system; F_out, the heat export from the system to the surroundings. NEE, net entropy exchange. (Adapted from Kleidon (2009b).)

Intuitively, we know that the heat flux would be directed such that it removes heat from the warmer box and adds it to the colder box. To understand how this direction results from the second law of thermodynamics and how this is quantified by entropy production, let us go through the following considerations. The heat flux F_ab removes a certain amount of heat dQ from the warm box, dQ = F_ab dt, during a time interval dt at a certain temperature T_a. This heat is then added to the other box at temperature T_b. The heat flux removes entropy from the first box, and adds and mixes it in the second box. Using the standard thermodynamic definition of entropy change, dS = dQ/T, entropy of the first box is removed in the amount of dS = dQ/T_a. When the heat dQ is added to the other box, entropy is being increased in this box by the same amount dS = dQ/T_a. By mixing the added heat dQ with the heat already present in the box b of temperature T_b, entropy is further increased (or produced) by mixing of dQ. This extra increase in entropy of dS = dQ(1/T_b − 1/T_a) results in an overall increase of the entropy of the whole system as stated by the second law (dS > 0):

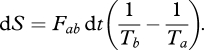2.1

This somewhat more detailed explanation to arrive at equation (2.1) emphasizes that heat advection by itself is a reversible process. The irreversible process that produces entropy is the mixing of the advected heat with its new surroundings.

In the following I will use the term ‘entropy production’ with the symbol σ to refer to the increase of entropy of the system because of a certain, irreversible process (mixing by heat exchange in this example). For our simple example we can write the entropy balance using this terminology in the form of:

2.2

with the entropy production σ_ab given by:

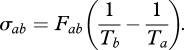2.3

Figure 2a also shows the time evolution of our example. The initial conditions, reflected in differing temperatures of the two boxes T_a and T_b, are depleted rapidly with time through the flux F_ab. As the initial temperature difference is depleted with time, the entropy of the system increases towards its maximum value, while entropy production diminishes to zero.

(b). Evolution away from TE

Our local system can evolve away from TE and still conform to the second law of thermodynamics. For this to take place, we require an exchange of energy or mass with the surroundings of the system (as illustrated in figure 2b). The second law then states that the total entropy increase, that is, the entropy increase of our system dS/dt plus the increase in entropy in the surroundings, dS_surr/dt, can only increase:

2.4

In other words, while the local system can evolve away from TE, the system plus its surroundings evolve closer (and faster) to TE. The entropy increase of the surroundings is equivalent to the net entropy exchange, NEE, between our system and the surroundings, so that we extend our entropy balance to:

2.5

In steady state (dS/dt = 0), entropy production σ_ab is equal to the NEE, so that entropy fluxes across the boundary can be used to compute entropy production in steady state (see also appendix A for an example).

The time evolution of this modified example is shown in figure 2b. For the same initial condition as above, we essentially find a very similar time evolution in which the entropy of the system increases because of the mixing, but entropy saturates at a value below the maximum entropy state found in the case of F_in = F_out = 0. The maintenance of this state away from TE is because of the energy exchange across the system boundary and the resulting NEE. The greater this entropy exchange, the lower the entropy in steady state (see also below).

Hence, it is the entropy exchange across the system boundary that maintains steady states away from TE. The extent to which the boundary is flexible in exporting entropy is a critical factor in calculating how far the system can evolve away from TE. This aspect is investigated next.

(c). Sensitivity of the entropy budget and MEP

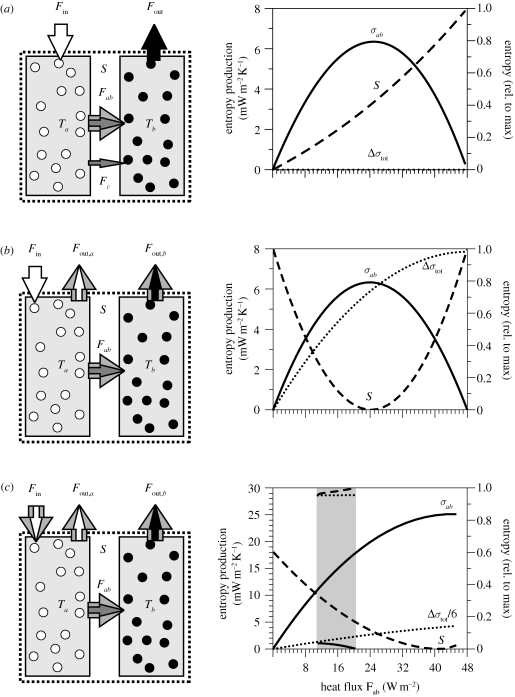
In order to understand how systems can evolve away from TE by changing the internal processing of energy and mass, we now add flexibility to the transfer process from box a to box b, and to boundary conditions of our simple system. We then investigate how the entropy budget of our system reacts to the flux, F_ab. Three different cases of MEP considered here with varying degrees of flexibility are illustrated in figure 3.

Figure 3.

Illustration of three different cases in which an internal process alters the entropy budget of the system (left diagrams) and the entropy production σ_ab owing to the heat flux F_ab, the increase of total entropy production Δσ_tot, and the entropy of the system S, as functions of the heat flux F_ab. (a) Case (i) allows for two types of heat transfer between boxes a and b. Flux F_c operates with a fixed conductivity and the flux F_ab is taken to have degrees of freedom so that its magnitude can vary. The fluxes across the system boundary are fixed in terms of their energy and entropy. Since F_out is proportional to T_b but fixed in steady state to F_in, T_b is fixed to a value of F_in/k_b. (b) Case (ii) extends case (i) in which it allows flexibility in the entropy export by flux F_out from the system. The flux F_c is neglected in this set-up. (c) Case (iii) extends case (ii) in which it allows flexibility in the influx F_in as well. The graphs on the right show the resulting sensitivities of the system's entropy budget to the heat flux F_ab of entropy production σ_ab owing to the heat flux F_ab, the increase in total entropy production by the system Δσ_tot compared with the total entropy production with F_ab = 0, and the entropy of the system S. The grey area in the lowest graph indicates a region in which a particular value of heat flux F_ab can result from a higher value of F_in and a comparatively lower temperature gradient or a lower value of F_in and a higher temperature gradient.

(i). Case (i): no flexibility in the boundary conditions

We first consider the simplest case (figure 3a), in which the boundary fluxes are prescribed, but two ways of transporting heat from box a to b are considered. This is, for instance, the case for mantle convection, where the heat generation within the interior is independent of the prevailing temperature, and heat is lost to the planetary surface at a temperature that is mostly determined by climate system processes and not by processes in the interior. Hence, we deal with a system with fixed ‘influx’ of heat, and heat export at a fixed temperature.

The two processes of transporting heat are implemented as follows. We take conduction as our first process, and represent the heat flux as F_c = k_c(T_a − T_b) with a fixed conductivity k_c. The alternative way to transport heat uses an effective conductivity k_ab, which may vary as is the case for convection, for which heat transport results from the generated motion within the system.

The sensitivity of the entropy budget of the system is also shown in figure 3a. With increased flux, F_ab, the entropy production σ_ab first increases because the increase in flux outweighs the depleted temperature gradient in the entropy production. However, this imbalance decreases with increasing flux, so that at one point a maximum in entropy production at an intermediate value of heat flux, F_ab is reached. Beyond the MEP state the increase in flux no longer compensates the decline in temperature gradient so that entropy production decreases. Hence, a clear maximum is found in the sensitivity of σ_ab to the flux, F_ab. In addition to entropy production by flux F_ab, entropy is also produced by the flux F_c, and by the mixing of the influx of heat F_in at temperature T_a. These components of the entropy budget are not shown here for simplicity.

The total entropy production of the system is fixed because of the boundary conditions that we impose. This can easily be understood as follows: we consider a fixed influx F_in of heat and entropy. When we express the outflux as F_out = k_bT_b, the steady state results in a fixed outflux F_out = F_in at a fixed temperature T_b = F_in/k_b, hence also resulting in a fixed entropy export from the system. Hence, the total entropy production of the system is fixed in steady state as well and insensitive to the partitioning among F_c and F_ab.

Since the entropy exchange to the surroundings is fixed, enhanced entropy production within the system has to result in a higher entropy S of the system. Hence, S increases with increasing heat flux F_ab.

(ii). Case (ii): flexibility in the outflux F_out

We now introduce flexibility in the boundary conditions by allowing heat loss from both boxes (fluxes F_out,a and F_out,b as indicated in figure 3b). For a given influx F_in, the outflux F_out = F_out,a + F_out,b is still constrained by the steady state condition (F_in = F_out), but the heat loss can occur under different proportions and of different entropy, depending on flux F_ab. This is, for instance, the case for pole-ward heat transport in the climate system, where absorbed solar radiation is redistributed to regions of colder temperatures, resulting in higher entropy export (see also below). What this set-up essentially implements is that the internal configuration of the system, in terms of temperatures T_a and T_b, is able to alter the entropy export of the system. The conductive flux F_c is assumed to be negligible and is omitted in the following considerations.

Figure 3b shows the sensitivity of the entropy budget to flux F_ab for this altered system. A maximum in entropy production in σ_ab exists as in the case above, resulting from a similar trade-off in which an increased flux depletes the temperature gradient. Overall entropy export to the surroundings is, however, at a maximum at maximum heat flux, which corresponds to equal temperatures of both boxes. The difference between total entropy production σ_tot and σ_ab is caused by the mixing of the added heat by F_in within box a at the temperature T_a, which increases with lower values of T_a.

The MEP state also corresponds to a state of minimum entropy S of the system. This minimum results from the competing effects of increased entropy export to the surroundings (which would lower S) and increased mixing (which would increase S) with increased flux, F_ab (Kleidon 2009b).

(iii). Case (iii): flexibility in the influx F_in

Even more flexibility exists in the boundary conditions if internal properties can also affect the influx, F_in. This is, for instance, the case if the influx F_in depends on the temperature of the system. To illustrate such an effect on the entropy budget of our system, we introduce a simple, linear temperature dependency of the flux F_in on the temperature of box T_b.

The sensitivity of the model for this case is shown in figure 3c. The sensitivity is similar to case (ii), except that the magnitude of entropy production is considerably enhanced and the sensitivity shows a more complex behaviour (as indicated by the grey area in the graph). This complexity results from the ambiguity of F_ab and σ_ab: the same flux F_ab can result from a higher value of F_in and a comparatively lower temperature gradient and a lower value of F_in and a higher temperature gradient.

The MEP state also corresponds to a state of minimum entropy as in case (ii).

(iv). Summary

The example set up in this section provides a simple illustration of how a system can evolve away from a state of TE by altering the configuration of fluxes within the system without violating the second law. A necessary condition for it to be able to evolve to a state of lower entropy are flexible boundary conditions. These allow the system to maintain states of higher entropy production (i.e. being more dissipative) and lower its entropy.

Three different examples were given for possible states of MEP, which differ in the flexibility of the boundary conditions. When the flux maintains a state of MEP, this roughly corresponds to the strongest dissipative activity and maintenance of a state furthest away from TE. When the entropy change of the system is considered together with the entropy increase of the surroundings, this state implies fastest evolution to a state of global TE.

3. Entropy production in the Earth system

To extend the simple example above to the broader context of the functioning of Earth systems and the role that biotic processes play in these, we need to understand the dissipative nature of various Earth system processes. Essentially, all processes within the Earth system are associated with irreversibility and entropy production and their entropy production can be represented as the product of a thermodynamic force and flux. In the example of entropy production given above (equation (2.3)), the thermodynamic flux is the heat flux, and the thermodynamic force is the gradient of 1/T. For mass fluxes, entropy production is expressed as the product of a mass flux and the gradient in chemical potential, divided by temperature. Other pairs of conjugated variables that can perform work are wind stress and velocity, pressure and volume, electromotive force and charge, surface tension and surface area, and so on. Since in steady state the rate at which work is performed equals dissipation, changes in these conjugated variables result in entropy production.

(a). Irreversibility by the Earth system processes

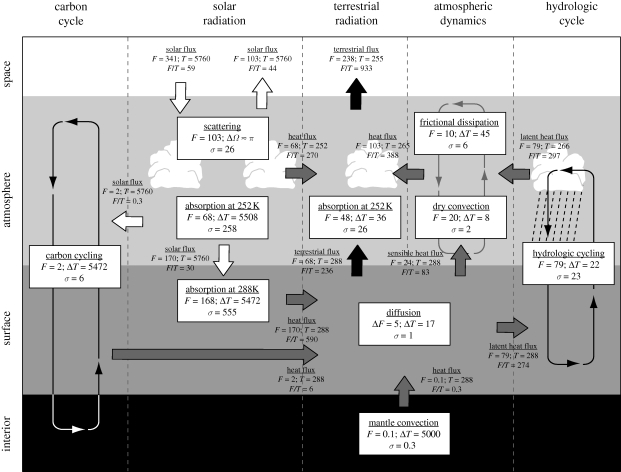
The Earth's entropy budget, as shown in figure 4, provides a quantification of entropy production and allows us to compare the relative contribution of irreversible processes to the overall entropy production by the Earth system as a whole. The following list provides a brief explanation of the irreversibility of the processes shown in figure 4:

• — Absorption. Absorption of radiation is irreversible when the radiative flux representative of a higher emission temperature is absorbed at a lower temperature. This is the case when solar radiation is absorbed at the Earth's surface at temperatures much lower than the emission temperature of the Sun. Because of the very large temperature difference between the Sun's surface and the Earth's surface and a comparatively large flux, absorption of solar radiation contributes the largest component to the entropy budget. The irreversibility of absorption is reflected by the fact that radiation is emitted from the Earth at much longer wavelengths than the wavelengths of the absorbed, solar radiation. Or, expressed in other words, the absorbed solar radiation is distributed over more and less energetic photons when leaving the Earth system in the form of terrestrial radiation.

• — Scattering. Scattering distributes a radiative flux into a wider solid angle. In the Earth system, the incoming flux of solar radiation covers a small solid angle and is then scattered, e.g. by molecules, aerosols, water droplets and by the surface into practically all directions. This process can be viewed as the free expansion of a photon gas, so that it is irreversible but does not perform physical work within the Earth system. The irreversibility is manifested in the directionality of the scattering process: a direct beam of radiation can be scattered into a diffuse flux of radiation, but this process cannot be reversed.

• — Diffusion. Diffusion reflects the natural tendency of gradients to be depleted in time, as illustrated by the example shown in figure 2. This is for instance the case for changes in heat storage of the ground. The diurnal and seasonal variations in solar radiation create variable heating and cooling sources at the surface, resulting in a temperature gradient near the surface. This gradient drives the heat exchange with the ground, which in turn depletes the gradient. Irreversibility results from the dampening of the initial variable forcing in time.

• — Dry convection and frictional dissipation. Temperature gradients cause gradients in density and pressure that create kinetic energy and motion. Vertical convection in the atmosphere is created by the net absorption of radiation at the surface and the net emission in the atmosphere aloft. The large-scale pole-ward transport of heat results from the greater absorption of radiation in the tropics compared with the polar regions. Motion is inevitably connected to frictional dissipation, which converts kinetic energy into heat. The irreversibility results from the conversion of temperature gradients into heat that can no longer be used to generate kinetic energy.

• — Hydrologic cycling. In the absence of motion, air over an open water surface would eventually reach saturation by evaporation, which is the corresponding state of TE. The atmospheric circulation acts to dehumidify the atmosphere (Pauluis & Held 2002a,b) by lifting air to supersaturation, which allows for condensation and precipitation of water droplets. Once the lifted air descends, it quickly reaches a vapour content below saturation, which can then drive evaporation at the surface. Hence, the atmospheric circulation brings the water cycle out of equilibrium, and the strength of the atmospheric circulation is related to the extent to which the water cycle operates away from TE. The irreversibility originates from the fact that evaporated water cannot be removed from the unsaturated air, and that condensed vapour cannot be evaporated into supersatured air.

• — Carbon cycling and biotic activity. In the absence of biotic activity, the concentration of atmospheric carbon dioxide (CO₂) would increase from the present-day levels to possibly much higher levels until the atmospheric partial pressure is in equilibrium with the corresponding partial pressure of CO₂ of the mantle. The present-day imbalance between atmospheric CO₂ and the mantle results in volcanic outgassing of CO₂, which is eventually deposited at the sea floor in the form of carbonates, forming the geologic carbon cycle. Irreversibility originates from the depletion of gradients in CO₂.

Biotic activity strongly shapes atmospheric CO₂ concentrations and contributes the most entropy production in the budget shown in figure 4. Photosynthesis uses the low entropy of sunlight to drive chemical reactions that remove CO₂ from the atmosphere and build up free energy in the form of carbohydrates. When these carbohydrates are respired, e.g. by building or maintaining biomass, or by the activity of heterotrophs, the chemical energy is converted into heat. The irreversibility is associated with the conversion of solar radiation into heat, which can no longer be used to drive photosynthesis.

Figure 4.

The Earth's entropy budget. White arrows denote fluxes of solar radiation, black arrows terrestrial radiation, grey arrows fluxes of heat, and thin lines material cycling. The boxes describe irreversible processes. The symbols are: F, flux of energy or heat (in W m⁻²); Ω, solid angle (in radians); T, temperature (in K); and σ, entropy production (in W m⁻² s⁻¹). (Adapted from Kleidon (2009b).)

For a more quantitative treatment of these processes and estimates of entropy production, the reader is referred to Nicolis & Nicolis (1980), Aoki (1983), Peixoto et al. (1991), Goody (2000), Kleidon & Lorenz (2005) and Kleidon (2009b).

(b). Examples of MEP

The existence of MEP states and the associated, realistic properties has been demonstrated for a range of examples relevant to the Earth systems. Here, I will focus on a few examples only and relate them to the three cases as discussed above. The examples are summarized in table 1. For more comprehensive reviews on applications of MEP, see Ozawa et al. (2003), Martyushev & Seleznev (2006), and Kleidon (2009b).

Table 1.

Examples of environmental and ecological systems for the three different cases of MEP given in figure 3.

case	system	Fin	Fout	Fab
(i)	mantle	heat generation in the interior	heat flux to surface	heat transport by mantle convection
	ecosystems	productivity	heat	ecosystem metabolism
(ii)	atmosphere	difference in radiative heating between tropics and poles	radiative cooling	pole-ward heat transport
	ocean sediment	detrital flux	heat and inorganic matter	ecosystem metabolism
(iii)	atmosphere and surface	difference in radiative heating between tropics and poles	radiative cooling	pole-ward heat transport
	biosphere	solar radiation	heat released	biospheric metabolism

An example for case (i) in an environmental system is the application of MEP to mantle convection (Vanyo & Paltridge 1981; Lorenz 2002). The generation of heat in the interior is independent of the prevailing temperatures. Hence, the influx of heat into the system ‘mantle’ is fixed. The heat export to the surface takes place at the temperature of the surface, which is largely determined by climate system processes, in particular the strength of the atmospheric greenhouse effect. Hence, the entropy export from the system is also taking place at a fixed temperature, so that the overall entropy exchange is fixed as well (at least to the extent discussed here). The application of MEP to mantle convection is justified in that convection adds an alternative pathway of heat transfer to conduction with many degrees of freedom. In this application, MEP yields estimates for interior temperatures and a temperature profile within the mantle that compares well to best estimates (Lorenz 2002).

Another example for case (i) can be found in the application of MEP to ecosystems. For these it has been hypothesized that these evolve to a state at which maximum dissipation occurs, which is equivalent to MEP at a given, fixed temperature. This hypothesis has received continuous attention (Ulanowicz & Hannon 1987; Odum 1988; Lotka 1922a,b; Schneider & Kay 1994; Loreau 1995; Jorgensen & Svirezhev 2004; Schneider & Sagan 2005). Commonly, these examples do not consider the effects of ecosystem dissipation on the environmental boundary conditions. For instance, Lotka (1922a) discusses the maximization of dissipation as a consequence of natural selection since ‘advantage must go to those organisms whose energy-capturing devices are most efficient in directing available energy into channels favourable to the preservation of the species’. However, the effect of the dissipation of species on the environmental conditions is not considered.

A common example for case (ii) is the application of MEP to pole-ward heat transport (Paltridge 1975, 1978, 1979; Lorenz et al. 2001). Absorption of solar radiation creates a heating gradient between the tropics and poles because of the orientation of the Earth's surface to the incoming radiation. For absorption, the radiative temperature of solar radiation does not affect the system, so that the influx of heat to the system ‘atmosphere’ is fixed. MEP is applied to pole-ward heat transport, which acts to level out the imbalance in heating. The outflux in this case is the emission of terrestrial radiation to space. Since the pole-ward heat flux results in a more equal distribution of temperatures, the outflux of the system is lowered, hence resulting in flexible boundary conditions in the outflux. Paltridge's work showed that it was possible to derive the observed latitudinal temperature gradient from MEP, while Lorenz and co-workers (2001) showed the same for different planetary bodies.

Another example for case (ii) is the metabolic activity of decomposers of detritus in ocean sediments (Meysman & Bruers 2007). Here, the influx corresponds to the import of free energy associated with detritus, which, after decomposition, is exported in the form of heat and matter of high entropy. The flexible boundary condition comes from the fact that the turnover of decomposer biomass adds to the detritus flux, so that the influx is flexible and the outflux is fixed. The study of Meysman & Bruers (2007) shows that decomposition rates of different sediment ecosystems can be adequately explained by using MEP applied to ecosystem metabolism.

Examples for case (iii) MEP can be found in applications of MEP to pole-ward heat transport that include the sea-ice albedo effect (Nicolis & Nicolis 1980; Gerard et al. 1990). In these examples, the magnitude of pole-ward heat transport affects polar temperatures, which in turn affects the presence of ice and snow. Since ice and snow are highly reflective, their presence alters the radiative forcing gradient between the tropics and the poles. With more polar ice cover, more solar radiation is reflected in the high latitudes, thereby amplifying the radiative forcing gradient and thereby affecting the ‘influx’ as discussed above.

Another example for case (iii) is the application of MEP to the planetary level. Kleidon (2004) argued that a planetary state of MEP should exist on the Earth resulting from the trade-off between less ice cover but increased cloud cover with increased global mean surface temperature. This state of MEP could be achieved by the biospheric effects on carbon cycling, which would affect the atmospheric concentration of CO₂, the atmospheric greenhouse effect and hence surface temperature. The influx here would be the solar radiation absorbed by the biosphere through photosynthesis, and the outflux being the heat released by the biospheric metabolism.

(c). Potential applications of MEP

In the following, I discuss two examples of how MEP should help us in a more applied context to yield better descriptions of the Earth system processes and in terms of getting a better theoretical understanding of the Earth system change and evolution.

(i). MEP and scaling of small-scale processes

MEP may be useful for improving the representation of small-scale, unresolved processes in numerical simulation models, where the effects of sub-grid scale heterogeneity are often treated empirically. Examples of such heterogeneities in the Earth system include the conditions in which water vapour condenses to form cloud droplets in the atmosphere, spatial and temporal variability in the infiltration and movement of water in soils, and the clumping and pattern formation of vegetation (e.g. in semiarid regions). Numerical models—which represent clouds, soils and vegetation with a minimum spatial resolution or grid cell size—typically characterize the state of each cell by a set of macroscopic variables (e.g. liquid water content, soil moisture, biomass) and ignore hetereogeneity on smaller scales. These models also implicitly assume local TE and empirically relate the cell state to thermodynamic properties such as gravitational and chemical potentials. As explained in the introduction, recent progress (Dewar 2003, 2005a,b) suggests that the theoretical basis of MEP may reside in the principle of maximum entropy (MaxEnt). In equilibrium statistical mechanics where it is well-established, MaxEnt yields the least-biased probability distribution of the microscopic state of an equilibrium system given certain macrosopic information (usually in the form of constraints on mean energy, particle number, etc.). Applied to non-equilibrium systems, MaxEnt—and hence MEP (if indeed it can be rigorously derived from MaxEnt)—would yield the least-biased parameterization of unresolved, sub-grid scale heterogeneity for a given set of resolved modelled constraints. Some work in this direction is reported by Kazantsev et al. (1998) and Frederiksen & O'Kane (2008).

(ii). MEP as the basis of a holistic theory of the Earth system

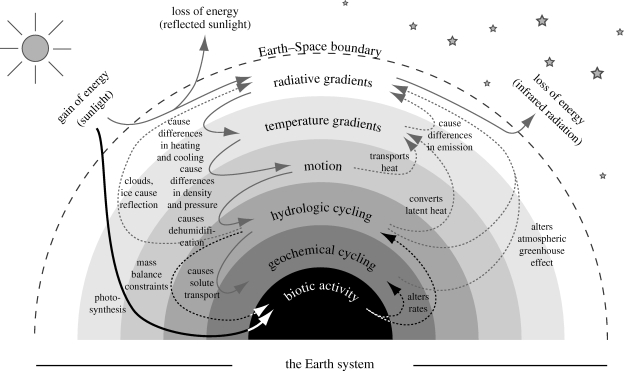
One aspect that is not explored in the above examples of MEP is that in most cases the dissipative activity of one process strongly interacts with the intensity by which other processes dissipate. These interactions, as summarized in a simplified way in figure 5, can be formulated solely in terms of thermodynamic fluxes, and hence MEP should provide us with a holistic theory of the Earth system which presently does not exist. The processes and interactions are described in a hierarchy, where the emphasis is on how the dissipative activity of one process causes gradients for another process at another level of the hierarchy.

Figure 5.

Simplified diagram to illustrate the main interactions of different irreversible processes within the Earth system and the place of biotic activity in these interactions. (Adapted from Kleidon (2009b).)

Radiative gradients in space and time, shown as the outer shell in figure 5, cause temperature gradients to develop that in turn result in density and pressure gradients. These density and pressure gradients are converted into kinetic energy that is associated with motion in the atmosphere and oceans. The atmospheric circulation in turn acts to dehumidify the atmosphere, thereby creating gradients in relative humidity that drive net fluxes of evaporation and precipitation, hence the hydrologic cycle. The hydrologic cycle wets the land, where it provides the means to transport weathered material to the ocean, thereby enabling stronger geochemical cycling.

The processes further down in the hierarchy affect the boundary conditions further up in the hierarchy, as shown by the dashed lines in figure 5. Starting from the top, temperature gradients cause differences in emission, thereby affecting radiative gradients. Motion and hydrologic cycling transport heat (the latter in the form of latent heat), thereby depleting temperature gradients. Water vapour concentrations, clouds and ice also affect radiative gradients in terms of albedo differences and in terms of the atmospheric greenhouse effect. Geochemical cycling shapes the atmospheric composition, which affects the atmospheric greenhouse effect.

Embedded in this nested hierarchy of the Earth system processes is biotic activity. It skips the hierarchy of energy conversions by directly using solar radiation to drive photosynthesis. The generated chemical energy is used to sustain life, but also to provide additional free energy to geochemical reactions, thereby altering their rates. This additional energy has been suggested to have profound effects: Rosing et al. (2006) link this additional energy to the rise of continents, and Schwartzman & Volk (1989) showed that biotic activity has substantially altered the weathering rates of silicate rocks on land, thereby affecting the habitability of the planet.

What is not shown in figure 5 is that these interactions can occur at very different time scales. Convective activity associated with atmospheric motion can take place on time scales of minutes and hours, while some geochemical cycles operate on time scales of hundreds of thousands of years. Despite these vastly different time scales, these processes interact quite strongly: convection and atmospheric motion drive the hydrologic cycle, which brings moisture to land. Moisture transport to land is the necessary means to efficiently bring the weathered material from the land to the oceans in the form of river basin discharge and thereby drives geochemical cycling on long time scales. Thus, atmospheric motion indirectly drives the geologic carbon cycle, which slowly shapes the concentration of atmospheric CO₂ and the strength of the atmospheric greenhouse effect. This, in turn, affects the gradients in radiative forcing that set the atmosphere into motion in the first place. Ultimately, it is the longest time scale that dominates the emergent state of MEP for the interacting system. Hence, when we explore the applicability of MEP to the Earth system at the planetary level, this would most likely be reflected in a slow evolution towards states of higher planetary entropy production. Such a trend, in turn, could be used to reconstruct Earth's environmental conditions of the deep past (Kleidon 2009a, 2010).

4. Summary and conclusions

This article started with the simple question why the Earth system is maintained in a state so far away from TE despite the natural direction towards mixing matter and depleting sources of free energy. A simple toy model was used to demonstrate that the exchange of energy and/or mass with the surroundings is a critical component that allows systems to evolve away from TE without violating the second law of thermodynamics. The application of the proposed principle of MEP was classified into three cases with contrasting levels of flexibility in the boundary conditions. As the flexibility of the boundary conditions increases, the state of MEP also typically corresponds to the state of lowest entropy of the system that is furthest away from TE. The evolutionary direction of the Earth systems away from TE can thus be understood as a consequence of the MEP principle.

I then explained the irreversibility of a range of the Earth system processes, provided a brief overview of the Earth's entropy budget, and discussed how the dissipative activities of processes interact and affect the boundary conditions of other processes. This mostly qualitative discussion hopefully provides a perspective for the future that demonstrates that non-equilibrium thermodynamics and MEP provide a theoretical framework for understanding the vast range of the Earth system processes.

Two examples were discussed for which the MEP principle should be highly relevant. First, MEP should provide us with a holistic, quantitative theory of Earth system functioning that should allow us to better understand the functioning of different Earth systems, reconstruct their past evolution, and to better formulate the impacts of human modifications for the future evolution of the Earth system. Second, MEP ought to be the recipe to get better parameterizations of unresolved details for large- to planetary scale descriptions of Earth system processes. In fact, it should give us the best parameterizations possible given the constraints that are explicitly resolved in such descriptions. In this sense, MEP is not just an interesting idea, but should be highly relevant for a better understanding and prediction of the Earth system dynamics.

Appendix A

The simple model used in §2 is based on Kleidon (2009b). The governing equations are the energy balances of the two boxes:

A1

and

A2

where c is the heat capacity, T_a and T_b are the respective temperatures of the boxes, F_in the influx into box a, F_c a conductive flux from box a to box b, F_ab the flux by an alternative process, and F_out,a and F_out,b the heat losses from the two boxes to the environment.

The net entropy exchanges NEE_a and NEE_b of boxes a and b are given by the exchange fluxes of heat and the respective temperatures at which heat is exchanged:

A3

and

A4

For the whole system, the NEE is:

A5

The corresponding entropy balances for the two boxes with entropies S_a and S_b are:

A6

and

A7

and for the whole system with entropy S:

A8

The entropy production σ_in results from the mixing of the influx F_in at temperature T_a, and the entropy productions σ_c and σ_ab owing to the mixing of fluxes F_c and F_ab at temperature T_b, respectively. These are expressed as:

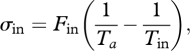A9

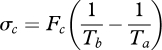A10

and

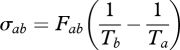A11

and the total entropy production given by:

A12

The fluxes F_c, F_ab, F_out,a, and F_out,b are parameterized as:

A13

A14

A15

and

A16

where k_c is a fixed conductivity, k_ab is an eddy conductivity that captures heat transport by motion and is varied to demonstrate MEP and k_b is a cooling rate.

Values are chosen such that these are similar to applications in the climate system. The value of F_in has been chosen to be similar to the difference of absorbed radiation between the tropics and the poles of about 0.4 × 240 = 96 W m⁻². The entropy of the influx is chosen to correspond to a temperature similar to the emission temperature of the Sun of T_in = 5760 K. The value of k_b is derived from the commonly used, linearized parameterization of net longwave loss from the surface in the form a + b T, with a = 204 W m⁻² and b = 2.17 W m⁻² °C⁻¹, so that k_b = b is used. The heat capacity c = 2 × 10⁸ J K⁻¹ m⁻² is chosen to reflect a water surface of 50 m depth.

To represent the three different cases, the following modifications were made: case (i): flux F_out,a = 0; case (ii): F_c = 0; case (iii): F_c = 0 and F_in = 96 + 35 × f(T_b) W m⁻² with f(T_b) = (15°C − T_b)/30 K and constrained to 0 ≤ f(T_b) ≤ 1. The parameterization of F_in was derived using common values of sea and ice albedo.