The two-box model of climate: limitations and applications to planetary habitability and maximum entropy production studies

Abstract

The ‘two-box model’ of planetary climate is discussed. This model has been used to demonstrate consistency of the equator–pole temperature gradient on Earth, Mars and Titan with what would be predicted from a principle of maximum entropy production (MEP). While useful for exposition and for generating first-order estimates of planetary heat transports, it has too low a resolution to investigate climate systems with strong feedbacks. A two-box MEP model agrees well with the observed day : night temperature contrast observed on the extrasolar planet HD 189733b.

1. Introduction

The hypothesis that climate systems may adjust themselves to steady states that maximize the production of entropy (‘maximum entropy production (MEP)’) by turbulent heat flows (e.g. Paltridge 1975) attracted much discussion in the literature at the time, and has experienced something of a revival and generalization to other systems (e.g. Ozawa et al. 2003; Kleidon & Lorenz 2005 for recent reviews). A popular motif in the discussion of this concept has been the ‘two-box’ model of climate (Lorenz et al. 2001), wherein two climate zones are considered, usually representing the low and high latitude halves of a spherical planet. When the solar heat flux into each zone, and the function of outgoing radiative heat flux versus temperature, is specified, one unknown remains, namely the heat flux between the two zones. It was argued (Lorenz et al. 2001) that when MEP is used to choose that heat flux, the resultant temperature contrast between the boxes was in useful agreement with the observed equator-to-pole surface temperature gradients on Earth, Mars and Titan.

The simplicity of the model has led to its wide citation and adaptation to other systems. In this paper, I review the history of the model, discuss its limitations and applicability to planetary climate and offer some remarks on experimental investigation of the model at the laboratory scale.

2. Background

Although some ideas related to MEP were discussed by the late E. N. Lorenz many years before (Lorenz 1960), the notion that heat flows across a planetary surface might be controlled by an entropy production extremization was first expressed in those terms by Paltridge (1975), who used a zonal energy balance model with 10 ‘boxes’ or latitude zones and found that the present-day terrestrial climate could be reasonably predicted if the heat fluxes between boxes were optimized to a minimum in external entropy production. As pointed out promptly and succinctly by Rodgers (1976), this corresponds to a maximum in internal entropy production. Rodgers also notes ‘the method is in principle much simpler than would appear from Paltridge's paper’.

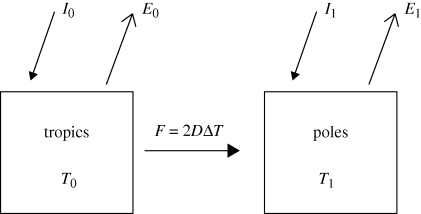
Most subsequent studies were variants of Paltridge's approach to the present, or greenhouse-enhanced, terrestrial climate, with varying (and usually higher) complexity. However, in considering a situation for which much less data was available, namely the climate of Saturn's moon Titan, Lorenz et al. (2001) collapsed the model into only two zones (figure 1).

Figure 1.

The ‘two-box’ model.

I₀ and I₁ represent the absorbed shortwave fluxes from the Sun, with I₀ > I₁. The outgoing fluxes E₀ and E₁ are functions of the respective temperatures T₀ and T₁ (often expressed in linear form, i.e. E(T) = A + BT, with A, B constants.) The flux between the two boxes is F, and is assumed to be proportional to (T₀ − T₁): following the formalism in energy balance models of Budyko (1969) and Sellers (1969), the proportionality reflects a ‘diffusion-like’ heat transport and accordingly is often represented by D. Energy balance for each box requires that I₀ − E₀ − F = 0 and I₁ − E₁ + F = 0. Model closure requires either the specification of D, which for the present Earth has a value of the order of 1 Wm⁻² K⁻¹. In energy balance model studies of the climate of Mars (e.g. Hoffert et al. 1981; James & North 1982; Francois et al. 1990) and extrasolar planets (Williams & Kasting 1997), D is usually assumed to be proportional to atmospheric pressure, with possible additional factors including planetary radius and rotation rate. Lorenz et al. (2001) noted that these parameterizations of D applied to Titan's small-radius, high-density, slowly rotating environment gave values of D that would be higher than Earth's, yet the temperature gradient indicated by Voyager data required D ∼ 0.02 Wm⁻² K⁻¹, a value that happens to correspond to a maximum in entropy production dS/dt = (F/T₁ − F/T₀). Although not expressed as succinctly in Lorenz et al. (2001), it has been subsequently noticed that the heat transport coefficient D that results is essentially equal in dimension and magnitude to the overall planetary entropy production dS/dt = I/T, where I and T are simply representative values (e.g. I ∼ (I₀ + I₁)/2 and T ∼ (T₀ + T₁)/2)—for Earth, these quantities are roughly 240 Wm⁻² and 290 K, respectively, yielding D ∼ dS/dt ∼ 0.8 Wm⁻² K⁻¹.

While the ‘two-box model’ is often attributed to Lorenz et al. (2001), it should be noted that, in fact, a sketch of a two-box model is given by Paltridge (1981) for the purpose of exposition in a paper attempting to understand why a system should attain MEP. However, that graphic showed only net fluxes rather than calling out explicitly the ingoing shortwave and outgoing thermal fluxes, and therefore fails to draw a direct link between the derivative of outgoing flux with temperature (dE/dT) and the optimum transport coefficient T (note that one can optimize the flux F directly in such a model without invoking a diffusive-type heat transfer coefficient D). Further, the paper itself attracted rather little attention, unlike Paltridge's original 1975 paper. Another formative paper is that by Wyant et al. (1988) which shows simple plots of entropy production as a function of D, with an evident extremum, although this paper uses a Fourier series representation of temperature with latitude, and therefore lacks the conceptual simplicity of the discretized ‘box’ model. Thus, the virtues of the Lorenz et al. (2001) two-box model are clarity and simplicity, rather than originality. The paper's application of MEP to climates other than that of Earth was, however, entirely novel.

The Lorenz et al. (2001) paper suggests without proof (by inspection of numerical trials) that the optimum value for D, i.e. that which maximizes the entropy production dS/dt, is given by D ∼ B/4. A formal solution can be derived via the calculus of variations (e.g. Rodgers 1976; Withers 2003; Goody 2007) and can be expressed as (E₀/E₁) = (I₀/I₁)^0.5: as observed by Withers (2003), the result D ∼ B/4 only holds strictly when (I₀ − I₁) ≪ I₀, i.e. when the two hemispheres have somewhat similar insolation. It may be noted that if B is obtained by simply differentiating the Stefan–Boltzmann law E = σT⁴ (with σ the Stefan–Boltzmann constant), then B ∼ dE/dT ∼ 4σT³ ∼ 4I/T, and thus the value of D for MEP (approx. B/4) corresponds to (I/T).

(a). Criticisms of the model

The model was published in Geophysical Research Letters in early 2001: in fact, the paper was accepted for publication in Nature in summer of 2000 after peer review, but acceptance was subsequently withdrawn, a circumstance that occurs ‘a few times a year’ (L. Sage 2006, personal communication). The story of the model's development is documented by Lorenz (2001).

Among referees’ feedback was the criticism that the equator-to-pole temperature gradient on Titan, estimated to be approximately 3 K from thermal infrared spectral measurements by the Voyager 1 spacecraft (Flasar et al. 1981; Samuelson et al. 1997), might not accurately represent the surface temperatures but rather might reflect an unknown contribution from the stratospheric haze. In fact, the Samuelson et al. (1997) analysis explicitly included the stratospheric emission. Further, more recent observations by the Cassini spacecraft have included thermal infrared measurements (with higher spectral resolution and much wider geographical coverage than Voyager) which return essentially the same result, a 2–3 K latitudinal temperature gradient (Jennings et al. 2009). Measurements of the microwave thermal emission using the radiometer capability of the receiver of the Cassini RADAR experiment (Janssen et al. 2009) support this result, as do results from the radio-occultation experiment by Cassini.

Much other criticism was that which had been applied to the MEP hypothesis generally (indeed, within months of Paltridge's 1975 paper—e.g. Rodgers 1976), namely that it apparently disregards planetary parameters known to be of importance in meteorology, such as surface pressure and planetary rotation rate. These criticisms are discussed in the next section, although we may note here that it is now understood that the issue is one of formulation: in this context, MEP serves as a selection principle that chooses among states that are physically permitted by these physical constraints, and if these constraints do not permit the optimal state then the system cannot choose it.

Another major criticism, and one which Paltridge (1979, 1981) struggled with in subsequent papers, was that there was no convincing argument why a system would want to seek an MEP state. Paltridge attempted to argue with electrical analogues that a system with fluctuating properties would progressively ‘ratchet’ itself into states of progressively higher entropy production. However, the analogy was—by the author's own admission—not entirely satisfactory (see also discussion of this problem by Ozawa et al. 2003). A further distraction is the well-known result by Prigogine that non-equilibrium systems may attain a state of minimum entropy production, although the qualification that this result applies only to systems that have restricted degrees of freedom and that are only weakly forced away from equilibrium is often forgotten.

Major progress on this question was achieved by Dewar (2003)—see also Lorenz (2003) who applied statistical mechanics principles to show that a non-equilibrium system with adequate degrees of freedom would see more of its available steady states at or near the MEP configuration. In other words, like the attainment of maximum entropy via the second law, the MEP state in systems held away from equilibrium is a statistical likelihood. He further showed that self-organized criticality is a feature of such systems. It should be noted, however, that Dewar's arguments (the application of Jaynes’ MaxEnt approach to paths rather than states) have received some criticism (e.g. Bruers 2007).

More recently, Goody (2007) discusses the MEP principle, and the two-box model of planetary climate in particular. He argues that observations of solar and thermal fluxes at Earth, Mars and Titan (and Venus) do not agree with MEP predictions. He suggests that these observations do not support the MEP hypothesis. However, he discusses the total fluxes observed from space, rather than those incident on the planetary surface which was the subject of Lorenz et al. (2001). Further, it has been suggested (F. Taylor 2009, personal communication) that the shortwave flux values he assumes for Mars may not be correct.

Consider a planetary body, for which estimates of I and E(T) exist. The two-box model will suggest how the two temperatures will depend on the heat transport between them, and one value of the possible heat transports will yield a maximum in entropy production. In reality, the planet may have a heat transport that is equal to this optimum value, or it may be lower, or it may be higher. What do these scenarios mean?

In the case that the heat transport is equal to that predicted by MEP, the theory may claim some success, as has been argued to be the case for Earth (Paltridge 1975) and for Mars and Titan. However, it could be argued—as indeed, it used to be argued (Rodgers 1976)—that such agreement is mere coincidence, a ‘lucky guess’.

If the heat transport is less than the MEP value, there are several interpretations. A first possibility is that physical or dynamical constraints exist to prevent the system attaining the (unconstrained) MEP value. Two obvious examples are a planet that spins very fast (wherein Coriolis forces shear out large, efficient eddy structures, thereby inhibiting latitudinal heat transport) or a planet with a very thin atmosphere (wherein the number of atoms available simply cannot transport the required heat flux). Put another way, the MEP principle can only select among permitted flow configurations: if no physically permitted configuration can yield the flux required for MEP, then the system cannot attain MEP. Thus, to be useful, MEP must be subject to constraints. The corollary is that a system observed to have lower flux than that for MEP may imply that the system is somehow constrained in ways that were not incorporated into the MEP model.

If the observed heat transport is more than MEP would suggest, it may be that other effects are at work. This, for example, is the case for naive application of the two-box model to Jupiter, wherein the small obliquity means a substantial difference in annual average insolation at high and low latitudes, which should thereby yield a substantial equator-to-pole temperature gradient, which is not observed. However, there is also an internal heat flux from Jupiter's core—if this were to distribute itself to compensate for the uneven insolation, then the temperature contrasts would be small (Ingersoll & Porco 1978). In this sense, the difficult point with the application of MEP to planetary climate may be knowing to which part of the climate system (if any) MEP applies—this is particularly true where vertical and horizontal transports both play a role. Results may depend on which of these dominates, and how the other is parameterized.

(b). Application to planetary habitability

The model's development was stimulated by the author's interest in planetary climate and climate stability, specifically, feedbacks in several planetary environments wherein a major climate variable is controlled by the temperature of the coldest region of a planet. The earliest example is of course the ice-albedo feedback in the terrestrial climate system, as studied, for example, in the one-dimensional zonal energy balance models of Budyko (1969) and Sellers (1969)—see also North (1975). If polar temperatures drop sufficiently, ice forms, increasing the local albedo. If this reflective ice cover is sufficiently extensive, the resultant cooling can lead to runaway expansion of the ice region to cover the planet completely (‘snowball Earth’). The transport of heat from low to high latitudes is instrumental in controlling this feedback.

Gerard et al. (1990) explored the implications of heat transport being determined by MEP for a zonal energy balance model of the Earth with a reduced solar luminosity, as is believed to have pertained earlier in solar system history. They found that lower insolation resulted in less efficient equator-to-pole heat transport (which can be readily understood given our assertion above that D ∼ I/T) and thus makes the system less likely to runaway to a complete glaciations (see also Endal & Schatten 1982). (In passing, we note that Ou (2001) has considered the faint early sun problem from a global mean climate perspective, with radiative balance controlled by the relative amounts of low- and high-altitude clouds: the cloud amounts are determined by vertical heat transports, and he adopts MEP for those transports to achieve model closure. He too finds the habitability of the terrestrial climate—i.e. its maintenance above the freezing point—robust with respect to insolation variations of 30%.)

Another example of feedback is in the Martian climate, wherein the greenhouse effect depends on the total pressure of CO₂ in the atmosphere, which in turn depends on the surface temperature at the coldest point, namely the pole (Gierasch & Toon 1973). If the equator-to-pole heat transport is too weak, the pole can be cold and thus the atmosphere freezes out: as conventional parameterizations set the transport coefficient D as proportional to pressure, this freezout reduces D, cooling the pole further and accelerating the collapse of the atmosphere.

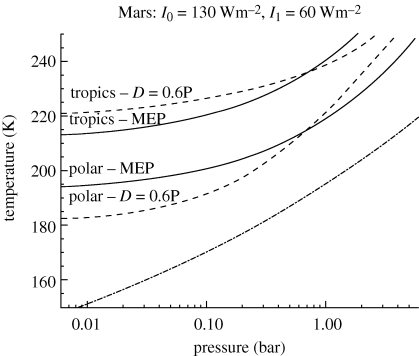
Figure 2 shows the result of a two-box model applied to Mars, with the greenhouse opacity τ related to pressure and D specified either as proportional to pressure or specified by MEP. Above about 0.7 bar, MEP indicates lower heat transport than the pressure-dependent value (consistent with the terrestrial situation discussed above, where the pole and equator are somewhat decoupled). At low pressures, however, MEP predicts a higher heat transport than the pressure-dependent case. However, the lack of seasonal resolution and the limited spatial resolution means that condensation never occurs (i.e. the temperature curves never cross the vapour pressure equilibrium curve), whereas in fact it is known that seasonal CO₂ condensation occurs on Mars. In fact, as Lorenz et al. (2001) point out, this seasonal condensation at one pole implies a substantial latent heat transport, whose amount is rather consistent with the amount implied by MEP.

Figure 2.

Results of a two-box model applied to the Martian climate. If the heat transfer coefficient D is specified as a function of pressure, the temperature contrast is larger than if it is instead specified by MEP. In neither case, however, does collapse occur, suggesting that the two boxes do not provide adequate resolution to detect the controlling local temperature minimum. τ = 0.9P^0.56; dashed–dotted line, CO₂ vapour pressure.

A similar pressure–temperature feedback exists for Titan, wherein substantial greenhouse warming occurs owing to methane, nitrogen and hydrogen (e.g. McKay et al. 1991). The first two of these gases can exist in condensed form on the surface, and thus surface temperature increases can raise the partial pressure of these gases in the atmosphere. This climate feedback was noted in a grey radiative equilibrium model by Lunine & Rizk (1989) and in a one-dimensional radiative–convective model by McKay et al. (1993), and explored further by Lorenz et al. (1997, 1999). All of these studies, however, were one-dimensional (the vertical dimension), and did not consider the variation of temperature with latitude, although Lorenz et al. (1997) pointed out that such variation would be important.

While the two-box model can give insight into these problems (e.g. qualitatively predicting that equator-to-pole heat transports will be lower under an enhanced-greenhouse climate), its application to habitability questions is limited by its low resolution. Specifically, as the cold regions controlling the greenhouse and/or albedo feedbacks can be quite small the hemispheric scale of the two boxes is likely to be too coarse to adequately describe the temperature. It might be that analytic continuous expressions (Legendre polynomials or similar functions) of temperature with latitude (e.g. Sellers 1969; North 1975) can give a reasonable estimate of the lowest temperatures: however, such approaches lack the conceptual simplicity of the discrete two-box model.

(c). Application to extrasolar planets

Over the last approximately 15 years, the number of known planets around other stars has increased from zero (ignoring a system of planets previously detected around a pulsar) to over 200. Detection methods favour massive planets in short period orbits around their stars, and indeed many of the known planets were found to be surprisingly close to their parent stars. One result of these close orbits is that the planets are likely to be tidally locked, always presenting the same face to the star (as the moon does to Earth).

If we make the assumption that the heating by starlight is deposited at the same pressure level from which the planet then re-radiates it, we can apply the MEP formalism used for zonal climate studies. In this instance, the two boxes correspond to the dayside and nightside of the planet, and I₁ = 0. Lunine & Lorenz (2002) noted that applying the two-box model approach with MEP leads to the expectation of a day : night contrast equal to one-third of the effective temperature of the planet (because (I₀ − I₁) ∼ I₀, the ‘classic’ MEP result of D = B/4 does not hold).

Only one extrasolar planet so far has had a reliable estimate of day- and nightside temperatures (Knutson et al. 2007), namely the 1.13 Jupiter-mass planet HD 189733b in a 2.2-day period. The 8 µm emission from the planet and its star was observed by the Spitzer space telescope: by studying the variation in the combined flux as the planet goes into eclipse, the contribution from the planet can be isolated. That work suggests that the minimum brightness temperature is 973 K, and the maximum is 1212 K—a contrast in fair agreement with the MEP prediction by Lunine & Lorenz (2002).

Although the extrasolar planets discovered so far are gas giants, many undetected terrestrial-like planets probably exist. Many of these may lie in the ‘habitable zone’ wherein the planetary average temperature can accommodate liquid water. However, some 75 per cent of the stellar population consists of M-dwarf stars, which are of low luminosity. This means that a planet in the habitable zone may be close enough to be tidally locked, which presents an atmospheric collapse problem analogous to that for the Martian zonal climate—the atmosphere itself, the water or both may freeze out on the nightside of the planet. Some global circulation model (GCM) studies have been conducted (e.g. Joshi et al. 1997). As one entire hemisphere is in continuous and complete darkness, it may be that such situations are more accurately treated than the Martian polar collapse problem.

3. Conclusions

As argued by Goody (2007), the applicability domain of the MEP hypothesis needs to be properly defined before the principle can be used with confidence. Within the possible domain of MEP, the smaller realm of problems to which a simple two-box model using MEP can be usefully devoted for predictive purposes is rather narrow. The two-box model's original purpose was to expose in an algebraically simple way the relationship between equator–pole temperature contrast, meridional heat transports and the resultant entropy production, and to investigate these relationships for planetary climates about which there was minimal information (specifically Titan). For that purpose, and for the day : night contrast on tidally locked extrasolar planets, the two-box model serves reasonably well, and as a pedagogical tool it has useful simplicity. However, the horizontal resolution of a two-box model appears to be too small to adequately represent condensable greenhouse effects that may be controlled by the cold poles of a planet, and in thicker atmospheres the complications introduced by the vertical heat transports required to move heat from the deposition altitude to that where emission occurs require separate treatment. General circulation models for Titan and for extrasolar planets are becoming available, and can offer results of desired complexity and will probably be the tools of choice in studying these climates. Whatever the merits or limitations of the MEP hypothesis itself, there appears growing recognition of the importance of thermodynamics in controlling—subject to dynamical constraints—large-scale heat transport such as the poleward heat transport on Earth (e.g. Barry et al. 2002) and the day–night transport on giant planets (e.g. Goodman 2009). Thus, entropy budget considerations may serve as useful checks on the results of GCMs, and on the formulation of sub-grid-scale parameterizations put into them (e.g. Kleidon et al. 2006).

A worthwhile question for future work is whether a laboratory-scale system that resembles (and thus can be simulated with) the two-box model can be constructed. Malkus (1954) constructed an experiment with two brass blocks separated by a fluid layer and noted the onset of various modes, suggesting that even this simple system shows remarkable complexity, although he was not exploring MEP as such. For the statistical mechanics perspective of MEP to hold, a system must have many modes of internal heat transport, such that a multitude of combinations is available and thus the relative abundance of combinations near MEP can emerge: turbulent fluids should have adequate degrees of freedom. Dewar (2003) and Ozawa et al. (2003) have argued that the Rayleigh–Benard system is MEP optimum, in the sense that the temperature difference is fixed and the flux is maximized (thereby maximizing the flux-force product, or entropy production). However, this end-member case is not very persuasive.

Perhaps an appropriate analogue to the two-box climate model is similar to Malkus’ experiment, with two heated reservoirs connected by a fluid, but with two additional conductive heat leaks to some low temperature heat sink which correspond to the radiative heat losses to space in the climate model. It is the existence of these leak paths that give the system the opportunity to ‘choose’ an optimum. Such an experiment should not, in principle, be difficult to construct.