Maximum entropy production in environmental and ecological systems

Abstract

The coupled biosphere–atmosphere system entails a vast range of processes at different scales, from ecosystem exchange fluxes of energy, water and carbon to the processes that drive global biogeochemical cycles, atmospheric composition and, ultimately, the planetary energy balance. These processes are generally complex with numerous interactions and feedbacks, and they are irreversible in their nature, thereby producing entropy. The proposed principle of maximum entropy production (MEP), based on statistical mechanics and information theory, states that thermodynamic processes far from thermodynamic equilibrium will adapt to steady states at which they dissipate energy and produce entropy at the maximum possible rate. This issue focuses on the latest development of applications of MEP to the biosphere–atmosphere system including aspects of the atmospheric circulation, the role of clouds, hydrology, vegetation effects, ecosystem exchange of energy and mass, biogeochemical interactions and the Gaia hypothesis. The examples shown in this special issue demonstrate the potential of MEP to contribute to improved understanding and modelling of the biosphere and the wider Earth system, and also explore limitations and constraints to the application of the MEP principle.

1. Thermodynamics and environmental and ecological systems

Thermodynamics has long been recognized as critical for understanding complex systems ranging from the living cell to planet Earth (Boltzmann 1886; Schrödinger 1944; Lovelock 1965). Boltzmann already noted in 1886 that:

… the general struggle for existence of animate beings is not a struggle for raw materials—these, for organisms, are air, water and soil, all abundantly available, nor for energy which exists in plenty in any body in the form of heat, but a struggle for entropy, which becomes available through the transition of energy from the hot sun to the cold Earth.

Schrödinger (1944) extended this perspective in his seminal book What is life? in which he suggested that the living cell maintains its organized structure in a state of thermodynamic disequilibrium by depleting sources of free energy and exporting high entropy waste. At the planetary scale, Lovelock (1965) recognized that the Earth's atmospheric composition is maintained in a state far from thermodynamic equilibrium, and he attributed this unique thermodynamic state to the profound effect that life has on its environment.

Taken together, these examples suggest that in order to better understand Earth's environmental and ecological systems and their couplings, we need to view these as coupled thermodynamic systems that are organized in a state far from thermodynamic equilibrium. Central to thermodynamics is the concept of ‘entropy’ as a measure of ‘disorder’ or ‘randomness’. While the use of ‘entropy’ is often surrounded with ambiguity, it can nevertheless be used in purely quantitative terms to measure the distance of a given state from thermodynamic equilibrium. Hence, it would seem that entropy can serve as an important concept to characterize the organization of the unique thermodynamic states of life and Earth's habitable environments and to understand the driving processes that result in these unique states.

The most prominent use of entropy is in the context of the second law of thermodynamics. The second law states that for isolated systems that do not exchange energy or mass with their surroundings, the entropy of that system can only increase. Over time, this law translates into an evolutionary direction by which a system evolves to a state of thermodynamic equilibrium, which is characterized by the absence of gradients in temperature or chemical species. Many extensions related to the second law of thermodynamics and new thermodynamic laws have been proposed to explain systems far from a state of thermodynamic equilibrium. Among these, for instance, are Prigogine's principle of minimum entropy production (Prigogine 1955; Bejan 1996), maximum entropy production (MEP)—as a separate ‘law’ (Swenson 1997) or as an extension of the second law to non-equilibrium systems (Dewar 2003)—maximum power (Lotka 1922a,b; Odum 1988) or exergy (Jorgensen & Svirezhev 2004), depletion of gradients (Schneider & Sagan 2005) and a proposed constructal law (Bejan & Lorente 2006). Many of these hypotheses have in common that at least in part they have been motivated by thermodynamics, specifically the second law of thermodynamics. However, these hypotheses have mostly been proposed at a highly qualitative level with many ambiguities that hinder their quantitative verification. Consequently, these hypotheses have received little acceptance in the mainstream field of what is now called Earth system science.

This issue deals with one of the proposed principles, the principle of MEP. The MEP principle states that non-equilibrium thermodynamic systems are organized in steady state such that the rate of entropy production is maximized. We focus on MEP among these optimality principles since its theoretical foundation has been strengthened by recent work (Dewar 2003, 2005a,b) moving it beyond a descriptive law to something beginning to approximate (or with at least the potential to be) a fundamental principle grounded in the statistical mechanics of non-equilibrium systems. The MEP principle has also received increased attention over the last 10 years (e.g. recent reviews by Ozawa et al. 2003; Kleidon & Lorenz 2005; Whitfield 2005; Martyushev & Seleznev 2006; Kleidon 2009) and indications for its general validity in simple energy balance models of heat transport (Lorenz et al. 2001) as well as complex climate models (Kleidon et al. 2003, 2006).

This special issue resulted from a workshop on the topic of ‘Maximum Entropy Production in the Earth system’, held in May 2008 at the Max-Planck-Institute for Biogeochemistry in Jena, Germany. The contributions aim to shed light on how Earth systems are maintained and organized far from thermodynamic equilibrium, with special emphasis on how these system states can be described by using the proposed MEP principle.

Before we provide an overview of the contributions, we will briefly elaborate on the nature of the MEP principle, and the ambiguities that surround its applications and interpretation. We first note that at a fundamental level, the dynamics of all natural processes, no matter whether environmental or ecological, are constrained by the conservation of energy, mass, momentum and other properties. Often some form of stationarity can be assumed so that statistical properties such as annual mean temperature, heat content or annual mean heat and mass fluxes (such as the sensible and latent heat flux, precipitation or carbon exchange fluxes) do not change in time. While the conservation laws constrain the dynamics of these processes, they are nevertheless insufficient to fully describe the dynamics. For instance, an atmosphere at rest conserves energy, mass and momentum, as does an atmosphere with strongly turbulent flow. Likewise, a bare desert surface conserves the water and carbon balance as does a surface covered by a tropical rainforest (but the latter only if sufficient water and light is available). What the proposed MEP principle states is that if there are sufficient degrees of freedom, that is, sufficient choice among steady states that all meet the fundamental conservation laws, the system would be characterized by a maximization of entropy production. Roughly speaking, this MEP state would correspond to a state at which maximum physical power is generated, gradients are dissipated at the fastest possible rate and hence the associated entropy production is maximized.

This sounds relatively straightforward, but in practice many questions come up. Before we can test the application of MEP, how do we describe environmental and ecological processes in purely thermodynamic terms? Which are the relevant constraints? What are the degrees of freedom? How do these degrees of freedom develop and how are they maintained? Which flux should be optimized, and why this flux and not another? The contributions in this special issue aim to resolve some of these questions.

2. Contents of this issue

This issue starts with a basic introduction to the far from equilibrium thermodynamics of the Earth system by Kleidon (2010). This paper reviews the basics of thermodynamics to demonstrate that thermodynamics provides the means of describing practically all Earth system processes in purely thermodynamic terms. Entropy production is not just defined for heat fluxes and temperature gradients, but rather for a very broad range of conjugated variables, demonstrating that MEP has potentially wide-ranging applications within Earth and environmental systems.

This introduction is followed by a critical outside view by Volk & Pauluis (2010) on the contributions of this special issue. Rather than discussing every contribution of this issue in detail, they focus on a few key questions that summarize the challenges of applying MEP and that should guide future developments. Using the example of dry versus moist convection, they show that systems can produce the same amount of entropy but by very different means. They also point out the somewhat arbitrary selection of which entropy production should be maximized. Until these issues are resolved, natural evolution of biotic systems are difficult to understand in terms of more general thermodynamic trends. They conclude that future studies should spend more attention on the details of how the entropy is being produced.

The next few papers of this issue deal with theoretical issues. Niven (2010) examines a new formulation of non-equilibrium thermodynamics using a generalized free energy concept. He provides an alternative derivation of MEP and shows that the state inferred from MEP shows high variability in its instantaneous fluxes and rates, as found for instance in turbulent fluid flow, heat convection and ecological systems. Martyushev (2010) provides a brief account on the reasonability of MEP within the context of non-equilibrium thermodynamics. Bejan & Lorente (2010) provide an overview of the so-called constructal law, as a possibly complementary approach to understand how optimized structures develop, such as the organization of river systems or blood vessels in living organisms. This approach may supplement the developments of MEP in that it provides a possible mechanism by which MEP states might be realized. It is as yet unclear how the term ‘access’ in the definition of the constructal theory can be quantified, but its original roots are undoubtedly in thermodynamics.

The next three papers deal with physical processes within the atmosphere. Lorenz (2010) reviews simple climate models within the context of planetary systems, extending the application of MEP to the temperature gradient between day and night temperature contrast on a tidally locked exoplanet. Jupp & Cox (2010) extend the two-box energy balance model of poleward heat transport that is commonly used to demonstrate MEP and include simple atmospheric dynamics to account for the effects of atmospheric thickness, rotation rate and advective capacity. With this they are able to identify the conditions for which dynamic constraints do or do not affect the MEP state. Wu & Liu (2010) set up a one-dimensional radiative transfer model to evaluate the radiative entropy flux of the Earth's atmosphere. They evaluate the effect of greenhouse gases on the vertical structure of entropy fluxes and suggest that there is an intrinsic connection between net radiative entropy fluxes and overall long-wave optical depth. Their results indicate that radiative entropy fluxes are closely related to the concentration of greenhouse gases in the atmosphere.

The following two papers deal with hydrological processes on land. Zehe et al. (2010) evaluate the effect of preferential flow associated with biogenic soil structures on hydrological fluxes using non-equilibrium thermodynamics. They show that these structures act to maximize dissipation of chemical potential gradients within the soil. Paik & Kumar (2010) provide a review of optimality approaches that have been proposed to characterize fluvial patterns in hydrology and geomorphology. Several of these are related to energetic properties, such as minimum stream power, minimum energy dissipation, maximum friction and minimum energy expenditure. In order to evaluate the validity of these apparently contrasting optimality approaches, they suggest that these approaches should accommodate for the dynamic nature of the system (such as hydrologic variability) and take a broader view that accounts for complex feedback processes with atmospherical, biological and geological processes.

The last six papers deal with various aspects of biotic organisms, ranging from the scale of bacteria (Županović et al. 2010) to plants (Dewar 2010) to food webs (Meysman & Bruers 2010; Vallino 2010) and ecosystems (Holdaway et al. 2010; Schymanski et al. 2010). Županović et al. (2010) take a thermodynamic view of bacterial chemotaxis—the ability of some bacteria to direct their movement towards certain chemicals such as glucose. They conclude that the migrating band associated with bacterial chemotaxis results from positive feedbacks, resulting in the maximization of the flux of nutrients. Meysman & Bruers (2010) evaluate biotic effects on entropy production in the context of conventional food web models. They set up three hypotheses: (i) that biotic effects enhance entropy production compared with abiotic processes, (ii) that among multiple steady states, the state with the highest entropy production is selected, and (iii) that when the thermodynamic gradient is enhanced, the food web should enhance its entropy production. While they found that hypothesis (i) was valid in all cases they tested, they found that hypotheses (ii) and (iii) do not always hold within the context of their model. Vallino (2010) uses a distributed metabolic network to test the applicability of MEP to biogeochemical transformations. He points out that biological structures cannot occur if entropy production is maximized instantaneously and argues that it is the spatio-temporal averaging (maximizing long-term entropy production rather than instantaneous entropy production) that allows biological systems to outperform abiotic processes in entropy production. Vallino argues that ecosystems should be viewed as self-organizing molecular machines that function to maximize long-term entropy production at the levels of ecosystem. Dewar (2010) reviews different optimization theories in plant physiology and shows how MEP can unify these different theories. By setting the system boundary at different scales (leaf, plant and ecosystem), he shows that MEP associated with the dissipation of the chemical energy created by photosynthesis can result in the maximization of different plant fluxes, such as net primary productivity, net growth rate and canopy photosynthesis, respectively. He suggests that the statistical interpretation of MEP offers a new paradigm for biological evolution of the ‘survival of the likeliest’, which applies to groups of cells and ecosystems, not just individuals. Holdaway et al. (2010) develop a general framework to calculate entropy production from eddy covariance and micrometeorological observations. Using field data from Amazonian forests and pastures, they find that, during forest development, the changes in vegetation properties, such as a lower canopy albedo and deeper rooting depths, result in cooler surface temperatures and higher rates of entropy production. They suggest that entropy production could potentially serve as the theoretical basis to better understand the effects of land cover change on the land surface energy balance. Schymanski et al. (2010) examine the application of MEP to a simple model of pattern formation in vegetation in semiarid regions. They show that the patterned state can be adequately represented by a simple two-box model if the vegetated fraction is optimized to yield MEP. They conclude that MEP could be used to better aggregate subgrid scale heterogeneity in numerical simulation models of the land–atmosphere system.

3. A note of caution

At the end of this introduction, we wish to sound a note of caution. In terms of terminologies, we first need to clearly distinguish between a state of maximum entropy (where entropy is a thermodynamic property of a system and a maximum entropy state corresponding to thermodynamic equilibrium of an isolated system), the maximum entropy approach of information theory (an inference method in information theory, abbreviated MaxEnt) and the proposed principle of MEP. Whether MEP should be interpreted thermodynamically or from an inference point of view, or whether these contrasting viewpoints are in the end equivalent, is still subject to discussion (see also special issue on ‘What is Maximum Entropy Production and how should it be used?’ in the journal Entropy, in progress).

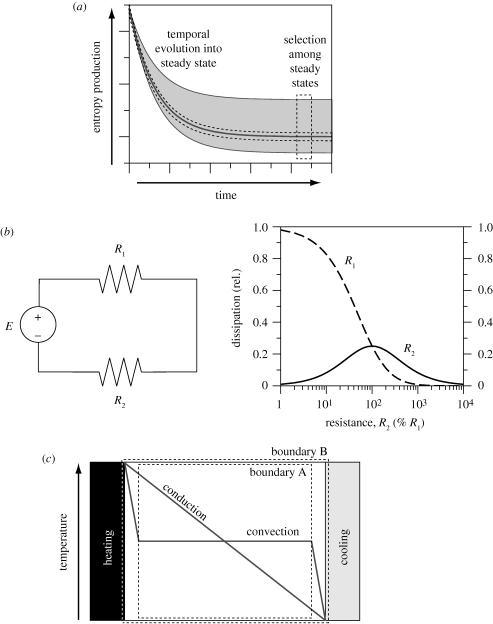
Also, the use of different optimization functions, and whether these are minimized or maximized, can result in a great deal of confusion and apparent contradictions that can be resolved on closer inspection. Some examples are illustrated in figure 1.

Figure 1.

Three different examples that can lead to confusion regarding maximization of entropy production: (a) confusion 1, originating from a difference in focus on understanding transient behaviour versus the selection among steady states of a system; (b) confusion 2, originating from the maximization of one flux that can simultaneously result in a decrease or even minimization of another flux, here illustrated with a simple electric circuit diagram with a fixed resistance R₁ and the sensitivity of dissipation of the resistances R₁ and R₂ to the value of R₂ and (c) confusion 3, originating from the drawing of the system's boundary (see text for further explanations).

One source of confusion arises from the distinction between the behaviour of a system in a steady state and the instantaneous response of a system undergoing a temporal evolution (figure 1a). While Prigogine's principle of minimum entropy production applies near thermodynamic equilibrium and to transient effects, MEP is the selection principle that decides among the possible steady states—hence, there is no contradiction between minimization or maximization since we deal with optimization under different conditions.

Also, the minimization of one function (or flux) can be associated with the maximization of another flux. In the context of engineering, a minimization of (waste) entropy production, e.g. in the design of a power plant, is applied to maximize the useful work output. Such a situation is illustrated in figure 1b, which shows that the variation of a resistance R₂ in a simple electric circuit can maximize the dissipation associated with that resistance, but substantially reduce the dissipation associated with another resistance R₁.

Finally, a third example is given in figure 1c, illustrating the importance of where the boundaries defining a system are drawn. Two temperature profiles are shown in figure 1c for the case of conductive heat transport only, which results in a uniform temperature gradient, and the case of convective heat transport, for which sharp gradients form at the boundary of the fluid. If one uses boundary A to define the system under consideration, then it would seem that conduction results in much more entropy production than convection because of the presence of temperature gradients. However, when using the boundary B, which includes the steep gradients at the system boundary, it becomes clear that overall convection results in higher entropy production than conduction.

Hopefully, these examples help to prepare the reader for some of the contrasting interpretations in this special issue.

4. Conclusions and outlook

The wide range of topics dealt within this special issue illustrates the great potential for MEP-like principles to apply to aspects of ecosystems and the environment. This is a field of active research that still faces the challenges of resolving the theoretical foundations of MEP and understanding the conditions and constraints under which MEP principles are applicable.

If MEP is indeed valid and its range of applicability is understood in more detail, it would be of tremendous help. It would allow us to formulate fundamental evolutionary directions for both environmental as well as ecological systems. Given that natural processes operate and interact at vastly different time scales (e.g. weather versus plate tectonics, leaf gas exchange versus speciation), the tendency of slow processes to evolve to an MEP state should manifest itself in an evolutionary trend towards higher rates of entropy production at shorter time scales. At a practical level, the MEP principle could pave the way for better and more theoretically grounded parameterizations in Earth system models of different complexities. Here, MEP would play a critical role in scaling spatial heterogeneities and temporal variabilities to the inevitable coarser grid and time steps that are unavoidable in numerical representations of environmental and ecological systems.

We hope that this special issue conveys the excitement of this emerging field and hints at the potential of MEP approaches to improve our understanding of complex biological and planetary systems.