Abstract
Midsagittal cerebral morphology provides a homologous geometrical reference for brain shape and cortical vs. subcortical spatial relationships. In this study, midsagittal brain shape variation is investigated in a sample of 102 humans, in order to describe and quantify the major patterns of correlation between morphological features, the effect of size and sex on general anatomy, and the degree of integration between different cortical and subcortical areas. The only evident pattern of covariation was associated with fronto-parietal cortical bulging. The allometric component was weak for the cortical profile, but more robust for the posterior subcortical areas. Apparent sex differences were evidenced in size but not in brain shape. Cortical and subcortical elements displayed scarcely integrated changes, suggesting a modular separation between these two areas. However, a certain correlation was found between posterior subcortical and parietal cortical variations. These results should be directly integrated with information ranging from functional craniology to wiring organization, and with hypotheses linking brain shape and the mechanical properties of neurons during morphogenesis.
Keywords: brain modularity, brain morphology, geometric morphometrics, multivariate analysis
Introduction
Studies focusing on brain morphology have generally dealt with quantitative differences in overall brain dimensions or volumetric analyses of specific brain portions. However, many factors in brain biology may depend upon the spatial organization of the neural elements, more than upon their absolute size. In terms of morphometrics, spatial organization refers to shape analysis, or the quantification and description of the geometrical relationships within a given anatomical system. Brain and braincase are part of a single structural and functional unit, and their final morphology is the result of structural and functional interactions between soft and hard tissues (Richtsmeier et al. 2006; Bruner, 2007). Such relationships are more linear in the vault, where changes in size (growth) and shape (development) during ontogenesis are directly related to brain pressure and connective tensions, respectively (Moss & Young, 1960). On the other hand, at the cranial base the relationships between bones and neural structures are far more complex, involving many non-neural factors (from mastication to speech) leading to non-linear and multimodal responses, both at ontogenetic and evolutionary levels (Enlow, 1990; Lieberman et al. 2000; Jeffery & Spoor, 2002; Bookstein et al. 2003; Bastir et al. 2006; Bastir, 2008; Bruner & Ripani, 2008; Bastir & Rosas, 2009; Neubauer et al. 2009). Hence, brain morphology is the result of neural adaptations as well as structural consequences correlated with the network of the cranial functional matrix. Multivariate morphometrics is a fundamental tool to understand the processes regulating the integration between these two components.
Despite the many studies in brain biology, little information is currently available on the patterns of variation of brain shape, especially with large samples. Morphological variation is the result of an underlying system of relationships (physiological, embryological, mechanical, and genetic) that represents the true biological bauplan produced by the phylogenetic processes, sensitive to selection and evolution. Hence, the recognition and quantification of the normal patterns of shape changes is the basic preliminary step to approach a posteriori the functional analysis of any anatomical organization.
Recently, much attention has been paid to the biomechanical factors probably associated with brain organization and with the physical properties of neurons, possibly influencing the general spatial structure (Van Essen, 1997), or with localized features related to the organization of gyri and sulci (Hilgetag & Barbas, 2005, 2006; Toro & Burnod, 2005). Similarly, tensions and strains related to the mechanical composition of the endocranial soft tissues (neural connections and meningeal connectives) may have a relevant role in shaping brain structure, and these levels of organization should be recognizable in the covariance patterns, possibly with large-scale variations.
Within this framework, the boundary between causes and consequences is rather spurious, and a system-based perspective is more useful when approaching the integration between anatomical components. As a matter of fact, if the degree and patterns of covariation are actual properties of the biological model, the networks of relationships generating such structure are, in contrast, a posteriori speculative hypotheses needing direct evidence. A given variation can be either the primary result of natural selection in evolutionary terms or, instead, a secondary consequence related to other changes, with no direct relationship to specific biological functions. In the case of brain variation we can synthesize two types of influence: primary functional variations associated with neural evolution and organization (intrinsic variations), and secondary structural variations associated with cranial arrangement and architecture (extrinsic variations). For example, connectivity (Sporns et al. 2004) is a topic partially related to brain shape, being the wiring pathways influenced by spatial organization factors such as the flexion of the cranial base (McCarthy, 2001). Hence, changes in the geometrical organization of the nervous networks may represent primary responses to neural selection or secondary adjustments related to architectural cranial variations. In both cases, neural wiring must be interpreted as a part of the neural integrated system formed by brain and braincase.
As morphological integration has become a crucial topic in morphometrics (Chernoff & Magwene, 1999), it has become apparent that the degree of covariation may vary more or less discontinuously, revealing in some cases the existence of semi-independent units, called modules (Cheverud, 1996; Wagner, 1996; Klingenberg, 2002; Schlosser & Wagner, 2004; Mitteroecker & Bookstein, 2007). Together with the information on the general structure of shape variation, the recognition of modular components supplies necessary clues to focus investigations on given groups of traits.
The midsagittal profile has been largely used in morphometrics since the earliest anthropometric approaches, and it is currently employed to investigate primate brain evolution (e.g. Jeffery, 2002; Bruner & Jeffery, 2007), as well as neurocranial and endocranial variation in paleoanthropology (e.g. Lieberman, 1995; Lieberman et al. 2002; Bookstein et al. 2003; Bruner, 2004; Bruner et al. 2004). Midsagittal brain morphology can be analyzed with current MRI tools, providing at the same time reliable and homologous anatomical indications. This plane is a reference for both cortical and subcortical morphology, supplying also information on the cranial base.
The present paper is aimed at introducing these issues analyzing the shape variation in the midsagittal cortical and subcortical elements of the human brain, according to two main goals. The first target is an explorative and heuristic approach to the patterns of covariation. Multivariate statistics is used to describe and quantify the spatial organization of the midsagittal brain morphology, including the adult normal variation, sex differences, and the allometric component. The associated multivariate vectors are supposed to be the numerical models of the underlying endocranial functional matrix, resulting from the interactions between brain and braincase and showing the patterns of correlations channelling the phenotype along preferred axes of variation (Polly, 2004).
The second target is to investigate the modular organization of the midsagittal brain morphology. Morphological integration refers to the degree and extent to which variations of the anatomical elements are correlated through functional, structural, or developmental processes. Such levels of organization are particularly relevant when dealing with cranial anatomy because of the many subtle relationships among the cranial bones and between bones and soft tissues (Bastir, 2008). As mentioned, groups of elements more correlated with each others than with other groups can be defined ‘modules’. Hence, we investigated the midsagittal brain shape through landmarks variation to localize possible morphological modules, assuming that spatial correlation may be the result of shared functional or structural influences between anatomical components. In particular, we tested the degree of dependence of the cortical and subcortical elements. Because of their physical contiguity, it must be expected that cortical and subcortical morphology may exert reciprocal morphological influence. In particular, taking into account that the cortical areas develop later than the subcortical ones and that they occupy a larger volume, it may be assumed that the cortical shape changes may influence subcortical geometry, mostly because of the pressures exerted by the cortical elements undergoing growth and maturation. Here, we check the covariation between these two components, following a null hypothesis of no relationship.
Material and methods
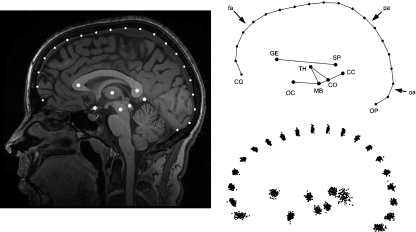
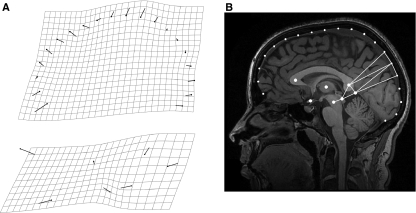
The sample included 102 subjects (44% males, age range 18–27 years). None of the participants had any history of neurological complaints or other health problems preventing their exposure to a magnetic field. All participants gave written informed consent prior to the study. A 3.0-T GE scanner (HDx, 14.x with 16 channels; amplitude 50 mT m–1; slew rate 150 mT m–1 × ms), equipped with a standard birdcage head coil, was used for magnetic resonance imaging. High-resolution images of the whole brain were acquired from each participant using a T1-weighted three-dimensional 3DSPGR sequence (30 axial adjacent slices, 512 × 512 pixel matrix per slice, TR = 11.2 ms, TE = 2.21 ms). Images were rotated and aligned to attain the same orientation as the ICBM template using the display function from SPM 5 (Wellcome Trust Centre for Neuroimaging, 2008). After orientating the specimen along the midsagittal axis, the most midsagittal slice was selected by using anatomical references as the falx cerebri and the thalamic structures. The midsagittal axis passes through the interhemispheric scissure and crosses the superior venous sinus. However, the endocranial outline does not present major discontinuities either along its profile and or compared with the parasagittal contiguous outlines, following the actual brain shape without relevant differences. Therefore, the midsagittal endocranial outline was taken as proxy for the cortical profile, this association being not only geometric but also morphogenetic (Moss & Young, 1960). The shape of the midsagittal brain section was investigated by using a two-dimensional configuration including 20 cortical and seven subcortical landmarks (Fig. 1). The cortical profile has been sampled from the junction between the crista galli and the frontal bone to the internal occipital protuberance, with equally spaced landmarks. Crista galli represents the anterior border of the anterior fossa and the main insertion of the falx cerebri. Hence, although it does not correspond to a given homologous brain reference, it represents a relevant cranial structural element. On the other hand, the internal occipital protuberance represents both a functional and structural reference, being at the same time the posterior attachment of the falx cerebri and the posterior boundary between the cerebral (occipital) and cerebellar areas. The subcortical landmarks included the midbrain and thalamic areas (centre of the thalamus, midbrain colliculi, and centre of the midbrain), the corpus callosum (centres of the genu and splenium), the optic chiasm, and the midpoint between cerebral, cerebellar, and subcortical structures.
Fig. 1.
The configuration is based onto seven subcortical landmarks and 20 cortical landmarks (fronto-parieto-occipital profile). The coordinates were superimposed using a Procrustes approach. The scatterplot (lower right) shows the variation of the whole sample after superimposition. CC, cerebro-cerebellar inner boundary; CG, crista galli; CO, colliculi; GE, genu; MB, midbrain; OC, optic chiasm; OP, internal occipital protuberance; SP, splenium; TH, centre of the thalamus. Arrows: frontal areas (fa), occipital areas (oa), parietal areas (pa).
Centroid size was used as size index, computed as the square root of the sum of squared distances of all the landmarks from their centroid. Coordinates were superimposed through Procrustes superimposition, by translation to a common centroid, scaling to unitary centroid size, and rotation to minimize the squared differences between corresponding landmarks (Bookstein, 1991). The residual variation was investigated by using the tools from geometric morphometrics (Zelditch et al. 2004). Principal component analysis, multivariate regression onto centroid size, discriminant analysis between sexes, partial least-squares analysis, and modularity tests were computed with MorphoJ (Klingenberg, 2008). Basic statistics was performed using PAST 1.91 (Hammer et al. 2001). The analyses were computed on the whole configuration and on the cortical and subcortical sub-configurations separately. Partial least-squares analysis (PLS) was used to quantify the degree of covariation between the two subsets following an eigenvector approach to the two multivariate datasets (Rohlf & Corti, 2000). Modularity was tested using a 2-block model, one including the cortical landmarks and one including the subcortical ones. The correlation between these two blocks was compared with the correlation between the whole set of possible partitions, including contiguous and non-contiguous groups of landmarks (see Klingenberg, 2009 for technical details). The covariation between blocks is measured as RV coefficient (Escoufier, 1973), by using Procrustes coordinates. A distribution of RV coefficients is provided from a large set of random partitions, and compared with the RV value of the partition investigated in the modularity hypothesis. Hence, the result is not an absolute value of integration, but shows the goodness of the hypothesis within the variation of the available alternatives. Consequently, this approach does not offer a clear-cut method for accepting or rejecting a given hypothesis of modularity, but provides a measure of correlation between the two blocks relative to the correlation of all the other possible associations. Such a ‘smooth’ approach is definitely recommendable in studying modularity and integration because of the peculiar nature of these principles. Modularity and integration are the results of hierarchical processes, being the relationships between elements organized in a hierarchical structure. At the same time, there is no reason to think that ‘modules’ are tightly closed entities, showing in general major or minor relationships with other modules of the same rank. This is even more evident when thinking about the relationships between different ‘kinds’ of modules (anatomical, histological, biochemical, genetic). Hence, modularity must not be interpreted as a strictly closed partition of independent blocks, but as a fuzzy organization of partially independent elements. This ‘partial independence’ therefore cannot be investigated with statistical tools based onto accepting/rejecting hypothesis, but can be analyzed through numerical approaches aimed at furnishing a general ‘goodness’ of the hypothesis. RV coefficients are a continuous measure of the integration between parts, and we can know if our investigated partition shows a stronger or weaker integration level when compared with all the possible subdivisions of that specific case-study. If two blocks are relatively independent, most of the alternative partitions will show higher correlation coefficients. High modularity is supposed to show small correlations, whereas high morphological integration is supposed to show large correlations when compared with the distribution of the correlation coefficients computed on the whole set of random partitions. The partition showing the lowest coefficient of covariation merits attention, as it shows the highest modularity level. As final note, these explorative approaches are useful only to detect possible modular organization of the anatomical elements. Such numerical evidence must then be biologically based using other sources of information (embryology, physiology, morphogenesis, histology).
Results
Full configuration
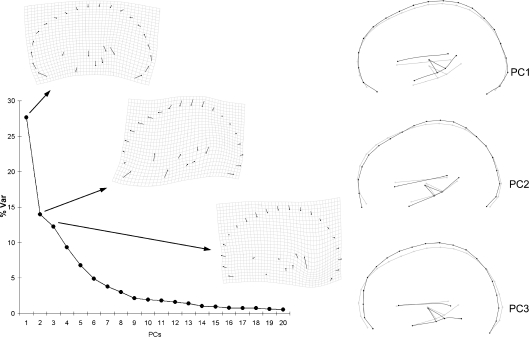
After Procrustes superimposition the resulting multivariate shape space based on the covariance matrix of the Procrustes coordinates is characterized by a largely dominant component explaining 27.7% of the variance (Fig. 2). The second and third components display comparable values, accumulating 53.9% of the variance. Components after the sixth axis explain less that 5% of the total variance each, a threshold often associated with noisy vectors. Ninety-five percent of the variance is accumulated at the 18th component. Hence, whereas the first vector stands out in terms of variance explained, suggesting a reliable statistical stability, the following axes show a gradient which is generally associated with less stable components. This distribution of the variance suggests that apart from the first axis of covariation, the morphospace is not structured according to strong biological patterns of shape change, the general morphology being largely influenced by several non-dependent factors.
Fig. 2.
Principal component analysis of the full configuration. The scree plot shows the distribution of the variance along the principal components, and the covariation patterns (thin plate spline deformation grids and wireframes) for the first three principal components.
The first component involves globularization of the whole configuration through cortical bulging at the fronto-parietal profile and inclusion of the subcortical areas within the cortical volumes. The same vector in the opposite direction involves bending of the fronto-occipital axis. The geometry of the subcortical block is not strongly affected by these changes, influencing just its vertical position relatively to the cortical volume. The second component involves lengthening of the frontal chord, from the anterior fossa to the fronto-parietal boundary. The third component involves globularization (brachycephalization) by means of vertical stretching at the upper frontal profile, associated with a marked lowering of the cerebellar junction. The following components are associated with the antero-posterior position of the posterior subcortical landmarks (PC4), parieto-occipital flattening (PC5), and lengthening/shortening of the occipito-cerebellar space.
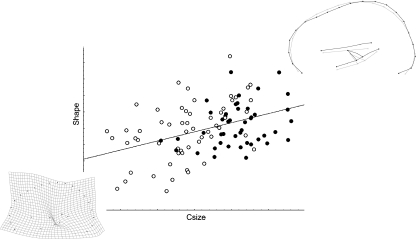
Males are larger in size than females (t-Test, P < 0.001), showing also lower variance (Levene test, P < 0.04). Shape changes are only slightly related to size changes, centroid size accounting for only 2.9% of the whole shape variation (P = 0.005) in the pooled sample. The allometric vector involves (from smaller to larger configurations) frontal vertical flattening and parietal bulging, with elevation of the subcortical structures (Fig. 3). The reverse pattern (that is, from larger to smaller brain sections) when magnified beyond the natural range of covariation localizes a crease at the centre of the thalamic region, mostly because of the splenium approaching this area. Centroid size variation is not related to any specific principal axis of covariation, being correlated to a limited extent to PC1 (r = −0.23; P = 0.02) and PC4 (r = −0.27; P = 0.006). Because of this limited allometric component, although size is statistically different between males and females, discriminant analysis on Procrustes coordinates failed to reveal shape differences between the sexes (T2 = 0.18; P = 0.21). Analysing males and females separately, the covariance matrices are highly correlated (r = 0.84; P < 0.000). A multivariate regression on centroid size computed on the pooled-within variation of each sex (that is, computed by using the residual of each individual value from its group mean) does not show peculiar differences from the overall allometric analysis. However, when computing the allometric vector separately for each sex, some differences emerge: males show a smaller allometric component (2.9%), which is not even significant (P = 0.23) and is associated with frontal flattening, whereas females show a larger allometric component (6.1%; P = 0.004) associated with parietal bulging.
Fig. 3.
Multivariate regression of shape (Procrustes coordinates) onto centroid size (males: black dots; females: white dots). The wireframe shows the pattern of covariation along the allometric vector. The deformation grid shows the reverse pattern (from larger to smaller size) after magnification, showing a crease at thalamic area.
Subcortical and cortical configurations
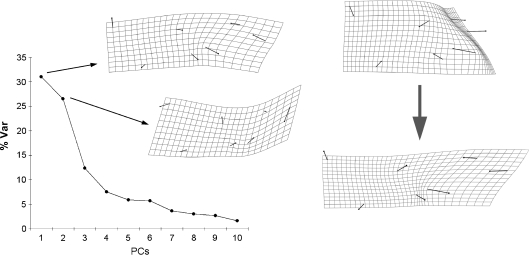
The shape space of the subcortical configuration is largely characterized by the first two principal components, explaining 31.0% and 26.5% of the variance, respectively (Fig. 4). After the second component, the amount of covariance explained shows a marked decrease, suggesting a minor role of the following axes. PC1 is not related to the first component of the preceding analysis, and involves bending of the anterior areas (thalamus) against the posterior ones (splenium and cerebellar boundary). The second component (slightly correlated to the third component of the preceding analysis; r = −0.43) is largely associated with vertical movement of the cerebellar boundary relatively to the thalamus position.
Fig. 4.
Left: principal component analysis of the subcortical configuration. The scree plot shows the distribution of the variance along the principal components, and the covariation patterns (thin plate spline deformation grids) for the first two principal components. Right: allometric vector, from small (above, magnified) to large (below) size.
Shape is more correlated to size variation than in the former analysis and this factor accounts for 12.1% of the whole variance (P < 0.001). The allometric component is correlated to both PC1 (r = 0.58; P < 0.001) and PC2 (r = 0.21; P < 0.03). It involves stretching at the posterior areas (splenium, cerebellar boundary) and geometric compression at the thalamic region. The inverse pattern (from larger to smaller configurations) localizes a crease at the posterior thalamic boundary. Centroid size is again larger in males (P = 0.001), but mean differences are more modest than in the former analysis, and variance homogeneity is not rejected (P = 0.37). However, no shape differences can be shown after discriminant analysis (T2 = 0.15; P = 0.15).
The analysis of the cortical profile alone displays a morphospace largely polarized by the first component, explaining 40.2% of the variance. This component involves globularization by means of fronto-parietal bulging, and it is strongly correlated to the first component of the full configuration analysis (r = 0.87). Size variation explains 4.0% of the total shape variation (P = 0.003), the allometric vector being associated with parietal bulging and correlated with PC1 (r = −0.22; P = 0.03) and PC3 (r = −0.32; P = 0.001). Males have a larger mean size (P < 0.001) and females a larger size variance (P < 0.015). Shape differences between the sexes are not supported by discriminant analysis (T2 = 0.42; P = 0.43).
Integration between cortical and subcortical variation
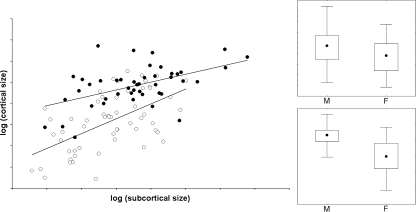
Subcortical and cortical centroid sizes show a moderate correlation (r = 0.59; P < 0.0001). Males and females appear to display minor differences in slopes (P = 0.05), but definitely different mean values after correction through analysis of covariance (P = 1.58E-08). Although analysis of covariance is better performed on distributions with similar slopes, the difference is rather patent: at the same subcortical size, males show larger cortical size than females (Fig. 5).
Fig. 5.
Left: log-log least-squares regression between subcortical and cortical size (males: black dots; females: white dots). Right: non-parametric distributions (median, interquartile, range) of the subcortical (above) and cortical (below) centroid size for males (M) and females (F).
Partial least-squares analysis between cortical and subcortical configurations provides evidence of a certain correlation, which, however, is very low (Rv = 0.07; P = 0.05). The first latent vector between the two blocks associates the frontal stretching described by the global PC2 with dilation of the posterior subcortical areas and vertical compression of the anterior ones (Fig. 6A). It explains 59% of the covariation between the two blocks, without reaching full statistical relevance (P = 0.09).
Fig. 6.
(A) First latent vector from PLS regression between cortical (above) and subcortical (below) areas. (B) The partitions with lower correlation isolates posterior subcortical and parietal cortical landmarks from the rest of the configuration.
The 2-block modularity analysis generated 888030 different partitions, of which only 688 showed a correlation lower than the one separating the cortical and subcortical landmarks. Hence, the hypothesis of modularity between these two blocks is supported (P = 0.0008), suggesting a larger independence between these two components than that observed among other groups of anatomical elements. However, the partition showing the smaller correlation (that is, the partition separating the most independent blocks) is the one grouping the posterior subcortical landmarks with the parietal cortical profile (Fig. 6B).
Discussion
The covariation between anatomical elements is the result of the underlying biological network, linking traits through spatial interactions (biomechanics) or functional relationships (physiology, biochemistry). At the same time, the covariance matrix of the phenotype is proportionally related to the covariance matrix of the genotype, representing a link between evolutionary and intra-specific variations (Ackermann & Cheverud, 2004; Hlusko, 2004). Hence, heuristic techniques such as principal component analysis provide a numerical model of the true biological bauplan, influenced and shaped by selection and drift during evolution (Polly, 2004). Although between-species morphological patterns are not necessarily based on common biological processes, within-species variation can be assumed to be more related to actual biological signals, when correlations between elements are considered (Martin & Barbour, 1989). When a given shape component can be patently distinguished from the other components along the scree plot because of the variance explained, its stability may support the presence of a true biological correlation between the elements involved (Wagner, 1984). In this sense, the levels of morphological integration (or, conversely, the independence between components when the organization is based on different modules) therefore can be investigated through multivariate shape analysis, assuming that marked polarized spaces are the result of integrated systems (Bruner & Ripani, 2008).
Following these principles, the aim of this study was to reveal the patterns of covariation between cortical and subcortical geometry in the midsagittal plane, demonstrating the major factors shaping gross brain morphology. Principal component analysis showed that there is only one dominant pattern of variation, the rest of the variance being explained gradually within the rest of the morphospace. As mentioned, this structure of the multivariate space suggests that these secondary components must be interpreted more carefully, as they may be simply numerical ordinations of the eigenvector analysis and have no strict biological meaning (see Jolliffe, 2002). On the other hand, in the present analysis the first principal component may represent a true biological vector, the result of the underlying biological correlations which polarize the morphospace constraining the phenotype by generating a preferred axis of variability, and channeling variation in a non-random way (Polly, 2004). In the current sample the first axis accounts for almost 30% of the variance and is related to the degree of globularity of the cortical profile. Bulging is particularly evidenced at the fronto-parietal boundary. Interestingly, this pattern is definitely similar to the principal axis of variation described for the evolutionary changes within the human genus, mostly distinguishing modern from non-modern species (Bookstein et al. 2003; Bruner et al. 2004). It is also worth noting that in more spherical brains the subcortical elements are shifted superiorly but without changes in their general geometrical arrangement. Thus, this change in the cortical profile influences the relative position of the subcortical elements but not their intrinsic spatial relationships. Brain globularization in primates may be associated with the flexion of the cranial base, which in turn is related to an increase in relative brain size (see Lieberman et al. 2000). However, this does not seem to be the case here, as the correlation between this pattern and size was very limited and, most importantly, the cranial base flexion was associated with correspondent changes in the contiguous subcortical elements (flexion of the trunk, compression at thalamus, rotation of the corpus callosum; Bruner & Jeffery, 2007). Hence, although the influence of the cranial base and of the cranial architecture in general cannot be completely ruled out, a direct relationship between this shape vector and the relative development of the fronto-parietal cortex must be carefully considered. Whatever the primary source of this variation, it represents a major contribution to the midsagittal cortical variability in a large adult human sample.
Apart from this first shape component, there may be no dominant integration patterns accounting for the variation of the brain midsagittal geometry, and variability is rather scattered through the shape space in a quite homogeneous distribution. The following principal components described in this study (mostly the second and the third vectors, as relative enlargement of the frontal areas and brachycephalization through relative lengthening of the vertex-cerebellar axis) might worth further attention, but as shown, their respective loadings were not as distinctive as for the first component.
In addition, the allometric component (which is often a relevant source of morphological integration) is definitely weak. Although larger brains display a relative enlargement of the posterior areas (from the thalamus to the parietal profile) such a pattern accounts for just 3% of the shape variation. The crease at the posterior subcortical region merits further attention, suggesting possible morphogenetic variation associated with brain size in that specific area. Creases are only numerical results of the interpolation function associated with the model of variation of a given sample (Bookstein, 2000), and their possible biological meaning is debated. Nonetheless, if the numerical model correctly represents the structure of the biological organization, it may be assumed that along an allometric vector creases represent a source of geometrical dilation. Actually, in some cases creasing of the thin plate spline deformation grids has been found in association with morphogenetic elements such as sutures (Bruner & Costantini, 2007). As a matter of fact, we can state that cortex is scarcely sensitive to allometric constraints, whereas the same allometric component described in the full configuration (relative dilation at the posterior subcortical elements) is more relevant in shaping the subcortical geometry alone, strongly characterizing the structure of subcortical shape covariation in its vertical and longitudinal displacements.
Apart from the inferences based on the structure of the morphospace, the relative independence between cortical and subcortical variations is further supported by partial least-squares and modularity analyses. PLS showed a certain association between relative lengthening of the frontal area and bending of the subcortical configuration. However, this correlation was very small, accounting for a minor percentage of variation, and the resulting first latent vector is not fully significant. At the same time, the hypothesis of modularity (independence as lack of correlation or correlation smaller than all the possible partitions using the current set of landmarks) between cortical and subcortical shape variation is strongly supported. As already mentioned, a modularity test must not be interpreted as black-or-white evidence on which to accept or reject a specific hypothesis, but as an explorative tool to quantify the degree of association/independence between groups of anatomical elements. Integration and modularity are the results of continuous processes, their degree of expression being relevant to evolution. Morphometrics only investigates the actual degree of dependence between anatomical components, whereas proper modularity hypotheses must be provided on specific biological grounds (histological, embryological). In this framework, the current analysis shows that the cortical and subcortical profiles are much more independent than most of the other possible groups of midsagittal brain elements. However, the most independent module according to the covariation pattern of the present sample is a block formed by the posterior subcortical landmarks and the parietal profile. Whether this is the result of spatial contiguity and reciprocal physical interaction or, conversely, the result of some joint biological factor (e.g. wiring organization, embryological processes, etc.) is an issue for further investigation. It is worth noting, nevertheless, that the posterior subcortical area coincides with the inner meeting point between falx cerebri and tentorium cerebelli. At the same time, the parietal profile has been hypothesized to be influenced potentially by allometric variation because of its intermediate position along the brain axis and the size-related constraints of the falx cerebri and its tension (Bruner, 2004). Hence, the degree of integration between posterior subcortical areas and parietal profile might be another result of the cranial functional matrix and of the biomechanical effects of the connective dura layers. Of course, other hypotheses must be taken into consideration, most of them attending to the structural and functional role of the splenium and of its organized bundles of transversal fibres (Wakana et al. 2003).
The present configuration of landmarks has not been able to detect any shape differences between the sexes, either in the cortical or in the subcortical areas. In contrast, size differences deserve attention. Sizes in males were larger than in females, particularly for the subcortical areas. More interesting, cortical and subcortical size scaled differently between the sexes, with males showing larger cortical values at the same subcortical size. Volumetric sexual differences in subcortical structures such as the corpus callosum have long been discussed and evidenced (Dubb et al. 2003), and they may account for the different trajectories described in this analysis. These size variations must be carefully considered in future investigations, particularly when dealing not with absolute volumes but with allometric trends, as evidenced in the present study. Some shape differences were detected when computing allometric vectors by sex independently. However, these differences are absent in the pooled and in the pooled-within allometric regressions. Also, considering that the supposed different patterns are ‘complementary’ (frontal flattening and parietal bulging represent the same shape changes in terms of relative differences), we suspect that this could be a bias associated with the different degree of size variation and accordingly with the different degree of allometric effect (larger in females). Of course, this point must be further considered.
These results on the patterns of covariance should be interpreted in terms of morphogenesis and structural organization of the brain. If the physical properties of neurons do influence the anatomical organization at low or medium morphological scale (lobes and circumvolutions; Van Essen, 1997; Hilgetag & Barbas, 2005, 2006; Toro & Burnod, 2005), large-scale biomechanical effects can be hypothesized, particularly when dealing with large tracts of fibres or high densities of connections. This also represents a link associating brain geometry with connectivity and neural wiring (Sporns et al. 2002, 2004; Hilgetag & Barbas, 2006). In this regard, it is worth noting that brain globularity has long been related to evolutionary dynamics associated with the cranial base, also through possible influences on the wiring efficiency (see McCarthy, 2001). Hence, it could be expected that large structural influences would exert a certain canalization of the resulting phenotypical output, recognizable as a correlation between traits and clear shape vectors. As mentioned, according to the present analysis the only clearly recognizable pattern of covariation is represented by a cortical bulging associated with fronto-parietal relative enlargement. It is worth noting that the frontal and parietal areas are strongly associated through cortico-cortical connections which, apart from representing physical tensors, provide strong functional relationships through re-entrant signalling based on ipsilateral projections and intrinsic connectivity (Battaglia-Mayer & Caminiti, 2002; Battaglia-Mayer et al. 2006). At the same time, the fronto-parietal network is supposed to play a pivotal role in the management of high-level cognitive functions (Lee et al. 2006; Jung & Haier, 2007; Colom et al. 2009). It is also worth noting that in human evolution, species displaying widening of the parietal areas (modern humans and Neandertals) also display a relative widening of frontal areas (Bruner & Holloway, 2010). Hence, the fact that the only patent pattern of covariation is related to fronto-parietal geometrical dilation merits further attention.
Apart from these specific signals associated with the fronto-parietal bulging and with the correlation between parietal profile and posterior subcortical shape, the scarce integration detected in this analysis may also suggest that biomechanical constraints and wiring patterns influence the gross brain shape only to a limited extent, or only at localized regional areas, rather than the overall geometrical structure of the brain. As usually stated, absence of evidence is not evidence of absence, and the limits of this exploratory analysis must be considered. First, these results are related strictly to the landmarks used in the current configuration, which may not properly represent all the cortical and subcortical brain spatial relationships. Secondly, this analysis is limited to the midsagittal profile, and three-dimensional approaches to whole brain volumes are needed to provide a more complete perspective. Thirdly, we must take into consideration that we have investigated static adult variation. Even if such variation is supposed to be the result of the underlying biological relationships, ontogenetic data are needed to provide a link between structural models and morphogenetic patterns. During morphogenesis the upper endocranial areas (frontal and parietal) show a linear and integrated development, whereas the lower areas show curvilinear and polyphasic stages, with shape changes continuing even after the brain has reached its full size because of the interaction between these areas and the system composed by the facial and basal structures (Bastir et al. 2006; Neubauer et al. 2009). Such dissociation between shape and size changes has been interpreted as being a result of the modular nature of the neurocranial/basicranial elements (Bastir & Rosas, 2009). This information might account, at least in part, for the patterns observed in the present analysis: a certain integration of the fronto-parietal profile together with a very limited integration of the lower cortical and subcortical elements.
Concluding remarks
The present survey on the human variation at the midsagittal brain section suggests a scarce integration within the neural elements. Relative independence of the lower areas, as well as their limited association with actual neural changes, has been frequently hypothesized on the basis of the analysis of the endocranial fossae, accounting for the non-neural functional and structural factors involved in cranial base morphogenesis (Enlow, 1990; Lieberman et al. 2000; Bastir, 2008; Bruner & Ripani, 2008; Neubauer et al. 2009). On the other hand, the variation at the upper areas (frontal and parietal) is supposed to be related more to actual neural changes (Moss & Young, 1960). Actually, in the present study the only dominant shape vector is associated with bulging of the fronto-parietal profile, leading to globularization. Size-related changes in shape are detected mostly at the posterior subcortical areas, whereas the cortical profile is scarcely sensitive to allometric constraints. Although there are notable size differences between males and females, no shape differences have been shown. Finally, the current analyses also support the hypothesis of relative independence between cortical and subcortical geometry, although there is evidence of some degree of correlation between the posterior subcortical areas and the parietal profile. Apart from possible integration with information on wiring and morphogenesis, the present results must also be considered when the endocranial shape variations are investigated in extinct human species, in the attempt to interpret the fossil evidence of endocranial changes through modern patterns of brain organization.
Acknowledgments
Manuel Martín-Loeches and Roberto Colom are funded by grant SEJ-2006-07890, Ministerio de Ciencia e Innovacion (MICINN). Roberto Colom is also funded by grant PR2008-0038, MICINN. Manuel Martín-Loeches is also funded by the grant SEJ-2007-60485, MICINN. Emiliano Bruner is funded by the Program GR. 249, Junta de Castilla y Leon, Spain. We are grateful to two anonymous referees for their effective and constructive comments, which have definitely improved this paper.
References
- Ackermann RR, Cheverud JM. Detecting genetic drift versus selection in human evolution. Proc Natl Acad Sci U S A. 2004;101:17946–17951. doi: 10.1073/pnas.0405919102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastir M. A systems-model for the morphological analysis of integration and modularity in human craniofacial evolution. J Anthropol Sci. 2008;86:37–58. [PubMed] [Google Scholar]
- Bastir M, Rosas A. Mosaic evolution of the basicranium in Homo and its relation to modular development. Evol Biol. 2009;36:57–70. [Google Scholar]
- Bastir M, Rosas A, O’Higgins P. Craniofacial levels and the morphological maturation of the human skull. J Anat. 2006;209:637–654. doi: 10.1111/j.1469-7580.2006.00644.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battaglia-Mayer A, Caminiti R. Optic ataxia as a result of the breakdown of the global tuning fields of parietal neurons. Brain. 2002;125:225–237. doi: 10.1093/brain/awf034. [DOI] [PubMed] [Google Scholar]
- Battaglia-Mayer A, Archambault PS, Caminiti R. The cortical network for eye–hand coordination and its relevance to understanding motor disorders of parietal patients. Neuropsychologia. 2006;44:2607–2620. doi: 10.1016/j.neuropsychologia.2005.11.021. [DOI] [PubMed] [Google Scholar]
- Bookstein FL. Morphometric Tools for Landmark Data. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Bookstein FL. Creases as local features of deformation grids. Med Image Anal. 2000;4:93–110. doi: 10.1016/s1361-8415(00)00015-3. [DOI] [PubMed] [Google Scholar]
- Bookstein FL, Gunz P, Mitteroecker P, et al. Cranial integration in Homo: singular warps analysis of the midsagittal plane in ontogeny and evolution. J Hum Evol. 2003;44:167–187. doi: 10.1016/s0047-2484(02)00201-4. [DOI] [PubMed] [Google Scholar]
- Bruner E. Geometric morphometrics and paleoneurology: brain shape evolution in the genus Homo. J Hum Evol. 2004;47:279–303. doi: 10.1016/j.jhevol.2004.03.009. [DOI] [PubMed] [Google Scholar]
- Bruner E. Cranial shape and size variation in human evolution: structural and functional perspectives. Child’s Nerv Sys. 2007;23:1357–1365. doi: 10.1007/s00381-007-0434-2. [DOI] [PubMed] [Google Scholar]
- Bruner E, Costantini D. Head morphological variation in Podarcis muralis and Podarcis sicula: a landmark-based approach. Amphibia-Reptil. 2007;28:566–573. [Google Scholar]
- Bruner E, Holloway RL. A bivariate approach to the widening of the frontal lobes in the genus Homo. J Hum Evol. 2010;58:138–146. doi: 10.1016/j.jhevol.2009.10.005. [DOI] [PubMed] [Google Scholar]
- Bruner E, Jeffery N. Extracting functional, phylogenetic and structural data from the subcortical brain: an exploratory geometric morphometric survey. J Anthropol Sci. 2007;85:125–138. [Google Scholar]
- Bruner E, Ripani M. A quantitative and descriptive approach to morphological variation of the endocranial base in modern humans. Am J Phys Anthropol. 2008;137:30–40. doi: 10.1002/ajpa.20837. [DOI] [PubMed] [Google Scholar]
- Bruner E, Saracino B, Passarello P, et al. Midsagittal cranial shape variation in the genus Homo by geometric morphometrics. Coll Antropol. 2004;28:99–112. [PubMed] [Google Scholar]
- Chernoff B, Magwene PM. Afterword. In: Olson EC, Miller PL, editors. Morphological Integration. Chicago: University of Chicago; 1999. pp. 319–353. [Google Scholar]
- Cheverud JM. Developmental integration and the evolution of pleiotropy. Am Zool. 1996;36:44–50. [Google Scholar]
- Colom R, Haier RJ, Head K, et al. Gray matter correlates of fluid, crystallized, and spatial intelligence: testing the P-FIT model. Intelligence. 2009;37:124–135. [Google Scholar]
- Dubb A, Gur R, Avants B, et al. Characterization of sexual dimorphism in the human corpus callosum. Neuroimage. 2003;20:512–519. doi: 10.1016/s1053-8119(03)00313-6. [DOI] [PubMed] [Google Scholar]
- Enlow DH. Facial Growth. Philadelphia: WB Saunders Company; 1990. [Google Scholar]
- Escoufier Y. Le traitement des variables vectorielles. Biometrics. 1973;29:751–760. [Google Scholar]
- Hammer Ø, Harper DAT, Ryan PD. PAST: paleontological statistics software package for education and data analysis. Palaentol Electronica. 2001;4:1–9. [Google Scholar]
- Hilgetag CC, Barbas H. Developmental mechanics of the primate cerebral cortex. Anat Embryol. 2005;210:411–417. doi: 10.1007/s00429-005-0041-5. [DOI] [PubMed] [Google Scholar]
- Hilgetag CC, Barbas H. Role of mechanical factors in the morphology of the primate cerebral cortex. PLoS Comput Biol. 2006;2:e22. doi: 10.1371/journal.pcbi.0020022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hlusko LJ. Integrating the genotype and phenotype in hominid paleontology. Proc Natl Acad Sci U S A. 2004;101:2653–2657. doi: 10.1073/pnas.0307678101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery N. Differential regional brain growth and rotation of the prenatal human tentorium cerebelli. J Anat. 2002;200:135–144. doi: 10.1046/j.0021-8782.2001.00017.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery N, Spoor F. Brain size and the human cranial base: a prenatal perspective. Am J Phys Anthropol. 2002;118:324–330. doi: 10.1002/ajpa.10040. [DOI] [PubMed] [Google Scholar]
- Jolliffe IT. Principal Component Analysis. New York: Springer; 2002. [Google Scholar]
- Jung RE, Haier RJ. The Parieto-Frontal Integration Theory (P-FIT) of Intelligence: converging neuroimaging evidence. Behav Brain Sci. 2007;30:135–187. doi: 10.1017/S0140525X07001185. [DOI] [PubMed] [Google Scholar]
- Klingenberg CP. Morphometrics and the role of the phenotype in studies of the evolution of developmental mechanisms. Gene. 2002;287:3–10. doi: 10.1016/s0378-1119(01)00867-8. [DOI] [PubMed] [Google Scholar]
- Klingenberg CP. MorphoJ. UK: Faculty of Life Sciences, University of Manchester; 2008. http://www.flywings.org.uk/MorphoJ_page.htm. [Google Scholar]
- Klingenberg CP. Morphometric integration and modularity in configurations of landmarks: Tools for evaluating a-priori hypotheses. Evol Dev. 2009;11:405–421. doi: 10.1111/j.1525-142X.2009.00347.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KH, Choi YY, Gray JR, et al. Neural correlates of superior intelligence: stronger recruitment of posterior parietal cortex. Neuroimage. 2006;29:578–586. doi: 10.1016/j.neuroimage.2005.07.036. [DOI] [PubMed] [Google Scholar]
- Lieberman DE. Testing hypotheses about recent human evolution from skulls. Curr Anthropol. 1995;36:159–197. [Google Scholar]
- Lieberman DE, Ross C, Ravosa M. The primate cranial base: ontogeny function and integration. Yearb Phys Anthropol. 2000;43:117–169. doi: 10.1002/1096-8644(2000)43:31+<117::aid-ajpa5>3.3.co;2-9. [DOI] [PubMed] [Google Scholar]
- Lieberman DE, McBratney BM, Krovitz G. The evolution and development of cranial form in Homo sapiens. Proc Natl Acad Sci U S A. 2002;99:1134–1139. doi: 10.1073/pnas.022440799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin RD, Barbour AD. Aspects of line-fitting in bivariate allometric analyses. Folia Primatol. 1989;53:65–81. doi: 10.1159/000156409. [DOI] [PubMed] [Google Scholar]
- McCarthy RC. Anthropoid cranial base architecture and scaling relationships. J Hum Evol. 2001;40:41–66. doi: 10.1006/jhev.2000.0446. [DOI] [PubMed] [Google Scholar]
- Mitteroecker P, Bookstein FL. The conceptual and statistical relationship between modularity and morphological integration. Syst Biol. 2007;56:818–836. doi: 10.1080/10635150701648029. [DOI] [PubMed] [Google Scholar]
- Moss ML, Young RW. A functional approach to craniology. Am J Phys Anthropol. 1960;18:281–292. doi: 10.1002/ajpa.1330180406. [DOI] [PubMed] [Google Scholar]
- Neubauer S, Gunz P, Hublin JJ. The pattern of endocranial ontogenetic shape changes in humans. J Anat. 2009;215:240–255. doi: 10.1111/j.1469-7580.2009.01106.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polly PD. On the simulation of the evolution of morphological shape: multivariate shape under selection and drift. Palaentol Electronica. 2004;7:1–28. [Google Scholar]
- Richtsmeier JT, Aldridge K, de Leon VB, et al. Phenotypic integration of neurocranium and brain. J Exp Zool B Mol Dev Evol. 2006;306B:360–378. doi: 10.1002/jez.b.21092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohlf FJ, Corti M. Use of two-block partial least-squares to study covariation in shape. Syst Biol. 2000;49:740–753. doi: 10.1080/106351500750049806. [DOI] [PubMed] [Google Scholar]
- Schlosser G, Wagner GP. Modularity in Development and Evolution. Chicago: The University of Chicago Press; 2004. [Google Scholar]
- Sporns O, Tononi G, Edelman GM. Theoretical neuroanatomy and the connectivity of the cerebral cortex. Behav Brain Res. 2002;135:69–74. doi: 10.1016/s0166-4328(02)00157-2. [DOI] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, et al. Organization, development and function of complex brain networks. Trends Cogn Sci. 2004;8:418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Toro R, Burnod Y. A morphogenetic model for the development of cortical convolutions. Cereb Cortex. 2005;15:1900–1913. doi: 10.1093/cercor/bhi068. [DOI] [PubMed] [Google Scholar]
- Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- Wagner GP. On the eigenvalue distribution of genetic and phenotypic dispersion matrices: evidence for a nonrandom organization of quantitative character variation. J Math Biol. 1984;21:77–95. [Google Scholar]
- Wagner G. Homologues, natural kinds and the evolution of modularity. Am Zool. 1996;36:36–43. [Google Scholar]
- Wakana S, Jlang H, Nagae-Poestcher LM, et al. Fiber tract-based atlas of human white matter anatomy. Radiology. 2003;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Zelditch ML, Swidersky DL, Sheets HD, et al. Geometric Morphometrics for Biologists. San Diego: Elsevier; 2004. [Google Scholar]