Abstract
The spontaneous loss of coherence catastrophe (SLCC) is a frequently observed, yet poorly studied, space-charge related effect in Fourier-transform ion cyclotron resonance mass spectrometry (FTICR-MS). This manuscript presents an application of the filter diagonalization method (FDM) in the analysis of this phenomenon. The temporal frequency behavior reproduced by frequency shift analysis using the FDM shows the complex nature of the SLCC, which can be explained by a combination of factors occurring concurrently, governed by electrostatics and ion packet trajectories inside the ICR cell.
Since the introduction of the soft ionization methods [1-3], mass spectrometry has been steadily gaining prominence, and is currently one of the most important experimental techniques in the biosciences. It is impossible to imagine contemporary proteomics, genomics, or glycobiology without mass spectrometric analytical methods. There is an increasing number of different types of mass spectrometers and hybrid instruments being developed and deployed every year, starting from simple quadrupole [4] instruments up to hybrid Fourier transform mass spectrometers (FTICR MS) [5-8].
In general, requirements for higher mass accuracy and resolving power of the contemporary mass spectrometers are becoming more and more pronounced [9]. As studies have shown [10, 11], proteomic experiments require sub-ppm mass accuracy for unique determination of peptide amino acid composition. Currently FTICR MS [12, 13] instruments are established leaders in mass accuracy and resolving power, capable of achieving ∼1 ppm accuracy internally calibrated [14-17] and ∼5 ppm externally calibrated [18, 19] under normal conditions, yet routine measurements in the sub 0.1 ppm region have not yet been reported. It is a substantial challenge for instrumentation, theorists, and experimental scientists to break through this 100 ppb “barrier”.
The major contributor to mass error in FTICR MS is space-charge—a phenomenon rising from the coulombic interaction between and within ion clouds in the ion cyclotron resonance (ICR) cells [65]. Frequency shifts due to space-charge were reported to be greater than ±400 ppm within an isotopic beat [20], which affects both position and width of the peaks, although these periodic shifts tend to mostly average out over a long transient. Substantial effort has been invested and there have been previous attempts to study it in situ [21, 22], yet the phenomenon remains poorly studied due to its rather fast nature, which requires frequency shift analysis on very short segments of transient signals. Most of the widely used signal processing techniques are not applicable to the task. For Fourier transform (FT) based techniques such as the FFT [23], wavelet and chirplet transforms [24], and the shifted basis technique [25], the limiting factor is the FT uncertainty principle [26]. For such high-resolution techniques as linear prediction [27, 28] and Prony method-based techniques [29, 30], the limiting factors are the time complexity of the calculations and poor tolerance for noise, which generate false positives (hence rendering these techniques impractical for experimental data).
The filter diagonalization method (FDM) [31-39] is a recent addition [20] to the repertoire of computational techniques in mass spectrometry, which addresses these issues. Like the FFT, it finds a solution for the generic harmonic inversion problem [37] (HIP) eq 1,
| (1) |
where the dk’s and ωk’s are complex amplitudes and complex frequencies respectively, and C(tn) is a time signal defined on an equidistant time grid tn = nτ, n = 0,1, . . . ,N - 1, where N is the number of data points, τ is the time step, and complex frequencies ωk = 2πfk - iγk include damping γk.
Because FDM’s resolution depends not on the length of the transient signal, but rather on the local peak density [38], it bypasses the FT uncertainty principle [32] and is thus capable of operating on very short transients. Even 1000 data points (1 ms with a 1 MHz acquisition rate) can provide sufficient information for the FDM to produce resolution defined only by the damping constant γk (eq 1) in frequency, and consequently, in mass domains [20], while having the similar time complexity in computation to the FFT. It is reliable under noisy conditions [39], and it reproduces complete information about a peak, namely position, amplitude, width, decay parameter, and phase. All of these factors make it an ideal technique for studying rapid spacecharge induced frequency modulations in FTICR MS.
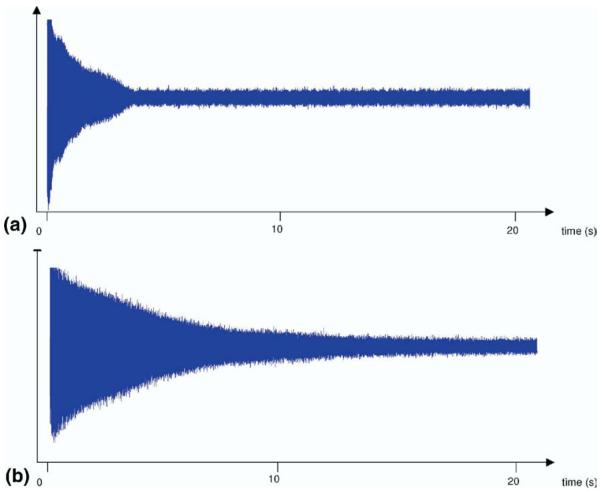
This manuscript presents application of the FDM to the study of a space-charge related frequency behavior of ion clouds in ICR called the spontaneous loss of coherence catastrophe (SLCC), colloquially known as the “nipple effect”. Unlike the theoretical behavior of a transient signal that decays exponentially (Figure 1a) or that acquired under near ideal conditions (Figure 1b), during the SLCC, a transient starts off with exponential decay, but at some point, which can be somewhat controlled by changing the number of ions in the cell, the transient collapses and dies out rather quickly (Figure 1c), forming a nipple-like shape. This is a space-charge related phenomenon, which directly depends on the number of charges in the ICR cell, an observation which was also reproduced by computer simulations [40]. When the number of charges is relatively low, the nipple effect is not observed in the experimental lifetime (Figure 1b). On the other hand, it is easy to reproduce this particular behavior (Figure 1c) by overloading the cell. Understanding of the ion cloud’s behavior during the SLCC should give insight into its behavior under high space-charge conditions in general, which potentially can be used in modeling, deconvolution, and data reduction in FTICR MS, improving mass accuracy and resolution.
Figure 1.
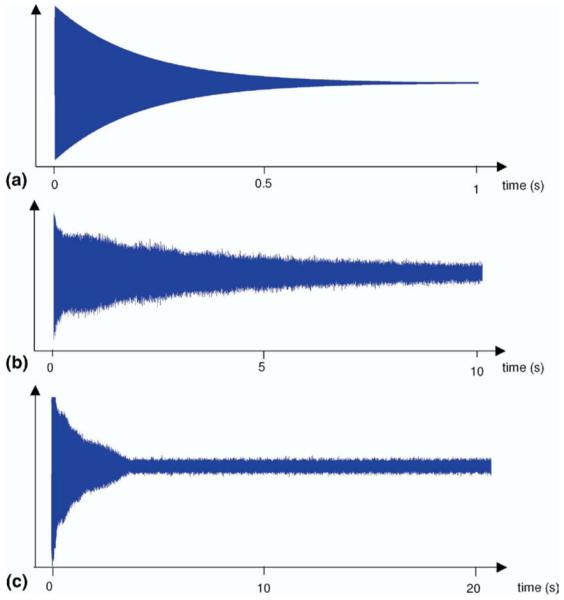
Examples of the transient signals: (a) hypothetical exponentially decaying sinusoidal signal; (b) transient of a high-resolution substance-P spectrum; (c) an example of SLCC where a period of exponential decay is followed by a rapid noncorrelated decay.
Methods
The experiments were conducted on custom MALDI-FTICRMS [41] and ESI-qQq-FTICRMS [6, 8] instruments, both based on 7 T actively shielded superconducting magnets (Cryomagnetics, Oak Ridge, TN), and each equipped with capacitively coupled cylindrical cell [42] with additional external trapping plates. All the experiments were conducted in the positive ion mode. The ions were trapped with +15 V during the excite event, but the potential was lowered to +1 V during detection. The MALDI instrument is equipped with 355 nm Nd:YAG laser, a novel modular data system [43], a low noise amplifier [44], and a 16 bit ADC, with ion optics consisting of a pair of hexapoles driven by RF oscillators [45, 46], and separated by a thin gate valve [47]. The analytes and matrices used in the experiments, substance P (MW 1347), renin substrate (MW 1759), angiotensinogen (1-13) (MW 1645.9), cesium iodide, 2,5-dihydroxy benzoic acid (DHB), and sinapinic acid (SA) were purchased from Sigma Chemical Co. (St. Louis, MO).
For all the MALDI experiments, DHB and SA were dissolved in methanol:acetonitrile:water (2:2:1) to make saturated solutions. For each sample, 0.5 uL of the 10 μM standard aqueous solution was applied on a target on top of the matrix crystals using the dried droplet method [48]. The acquisition rate was set at 1 MHz, and up to 4 s transients were stored.
Electrospray solutions of Substance-P were prepared in 49:49:2 methanol:water:formic acid solvents and that of cesium iodide in 70:30 water:methanol. The isolation of the species of interest was done in Q1. The ions were axially cooled by pulsing Nitrogen gas twice (2 ms pulse, 2 mbar backing pressure, pulsing to 1.4 × 10-5 mbar in the cell) into the cell during a 2 min cool down period after ion injection into the cell and before the excitation event. Substance-P 25 s transients were acquired in heterodyne mode at 10 kHz sampling rate and those of cesium iodide at 4 MHz (direct detection mode) using IonSpec electronics.
The ESI-FTICR mass spectrometer [6, 8] used in this study is a hybrid instrument with a triple quad front end, consisting of mass resolving quadrupole, ion accumulation, and collision cell linear trap, and a transmission quadrupole coupled with a set of ion guide hexapoles via the thin gate valve [47]. The instrument is equipped with the electron gun for ECD [49-52] experiments, which was used in all the electron promoted ion coherence (EPIC) [53-55] experiments. The electron beam was turned on during the detection event only. The current on the electron gun heater was set at 1.2 A, 4.7 V, and the voltage on the reflector was set at -1.0 V to propel electrons into the cell, while kept at +7.0 V otherwise.
Data analysis was performed on the latest release of the Boston University Data Analysis (BUDA) [56] system (soon to be available online). All frequency chasing experiments were performed using an FFTW-based [57], in-house C++ implementation of the FFT square window FDM [20] integrated into BUDA.
To produce the frequency behavior picture, frequency shift calculations [20] were conducted on the acquired spectra. For the angiotensinogen transients, the monoisotopic peak at ∼65 kHz was monitored. The parameters for FDM used were: Kwin of 7, 5 ms (5000 data points) of the time domain window, stepping 5 ms (5 data points) into the transient. For the frequency shift analysis, the cesium iodide (Cs1I2+) 272.7 kHz peak was studied, with Kwin of 5, 0.75 ms (3000 data points) of the time domain window, stepping 1 μs (4 data points) into the transient.
Results
An illustration of different time domain signals is presented in Figure 1. A transient of a hypothetical exponentially decaying harmonic signal is shown in Figure 1a. Figure 1b shows a nearly ideal experimental transient of Substance-P, and 1c is an example of the SLCC transient of Substance-P with its characteristic concave shape.
The application of EPIC can eliminate the SLCC altogether. Figure 2a shows the example of the nipple effect in the course of ESI-FTICRMS experiment. By turning the electron beam on during the detection, yet keeping all the other experimental conditions the same, it was possible to achieve a nearly ideal exponentially decaying signal (Figure 2b), which looks almost identical to that in Figure 1a.
Figure 2.
An illustration of an effect EPIC has on SLCC: (a) a SLCC during substance-P signal acquisition; (b) complete elimination of SLCC by applying EPIC (all other experimental parameters are kept the same).
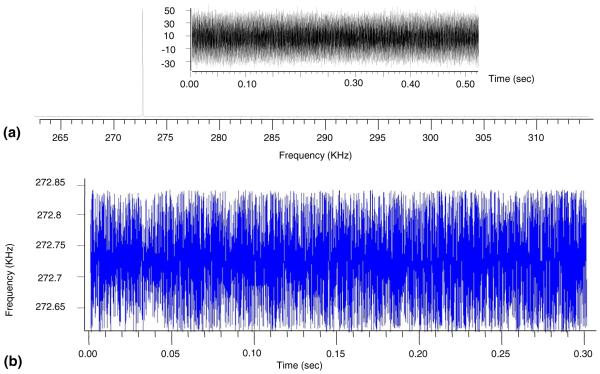
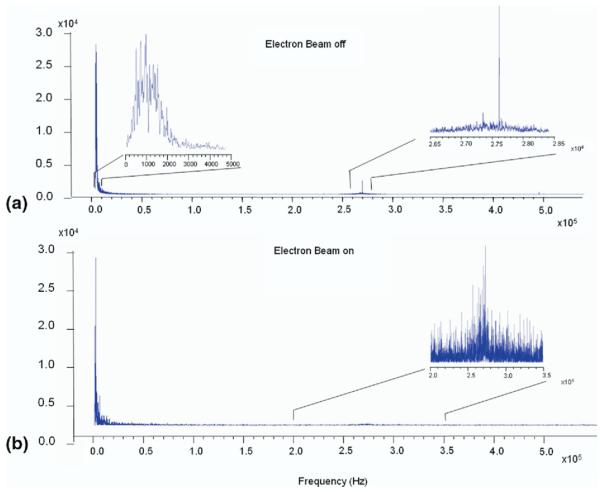
Figure 3a shows the ESI-FTICR frequency spectrum of an isolated Cs2I1+ cluster and its time domain signal (see the insert). An FDM frequency shift calculation is shown in Figure 3b. To detect periodic frequency modulations, the FFT was performed on the frequency shift calculation results. Figure 4 presents Fourier transforms of the frequency shift calculations conducted on the cesium iodide signals without (Figure 4a) and with (Figure 4b) the electron beam. There are two general regions in the frequency domain where modulations were stable and systematic. The major peak is at double that of axial frequency (the factor of two is due to the cell’s symmetry in Z direction), which should be in the vicinity of 700 Hz [58]. The minor peak is centered at the native ICR frequency in the standard Cs2I1+ spectrum, but is conspicuously absent in the Cs2I1+ EPIC signal.
Figure 3.
(a) A frequency domain spectrum and the transient of an isolated cesium iodide cluster and (b) the frequency shift modulation calculations of the ICR peak at 272.75 kHz.
Figure 4.
A Fourier Transform of the frequency shift calculations (see Figure 3b) conducted on the cesium iodide signals acquired without (a) and with (b) application of EPIC.
Frequency shift analysis calculations using FDM of the SLCC angiotensinogen signals (Figure 5a) are shown in Figure 5 reproduce the evolution of the amplitude (I, II) and frequency (III) parameters of the induced harmonic signal (damping constant and phase are also produced by FDM but are omitted due to the clutter produced by isotopic beat pattern [59, 60] and noise). The temporal behavior of the amplitude, dk from eq 1 follows exactly the outline of the transient signal in pre as well as post-nipple stages).
Figure 5.
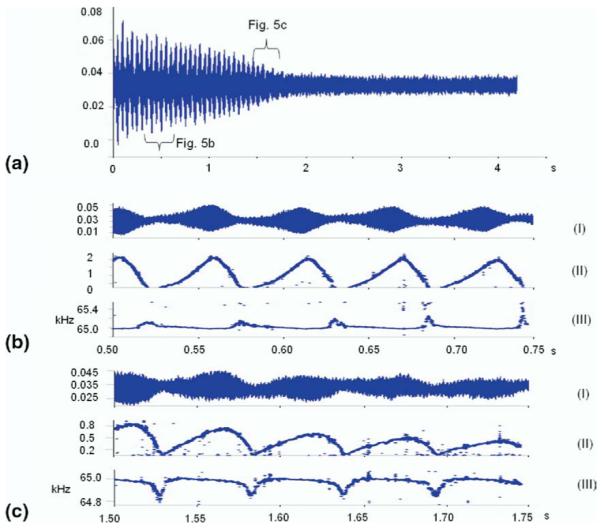
The results of the frequency shift calculations conducted on (a) the experimental SLCC of angiotensinogen. (I) is the magnification of the region of the time domain transient signal under investigation, (II) its amplitude dk, and (III) frequency fk temporal behaviors calculated using FDM (b) before, and (c) after the nipple.
The frequency behavior of the ions (Figure 5b, c III) through the SLCC has several signature features. Initially, frequency spikes are observed, which correspond in time with minima in the time domain transient isotopic beat pattern. These frequency spikes increase in magnitude with time (Figure 5b III), whereas the baseline stays relatively constant. Later, during the SLCC, these spikes “flip” becoming negative dips (Figure 5c III). The dips also coincide with the amplitude minima. This behavior is consistent, and a second set of data is available in the supplementary materials, which can be found in the electronic version of this article.
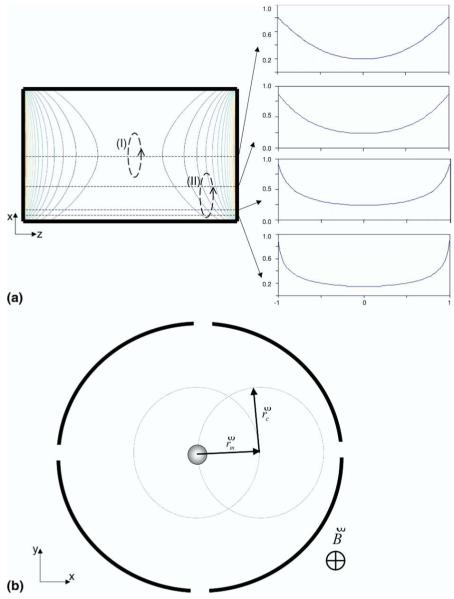
Figure 6a presents a simple plot of the inhomogeneities of the electric field inside the ICR cell experienced by a coherently excited ion cloud. As long as the contributions of magnetron and axial motions are small (orbit I), an ion packet does not experience much deviation from the largely hyperbolic electric field as it progresses through its cyclotron orbit. On the other hand, when both magnetron and ion axial contributions become significant (illustrated in extremis in orbit II), ion packets travel through highly inhomogeneous regions of the ICR cell. Figure 6b presents a schematic representation of an ion packet being temporarily positioned in the center of the cell as a result of superimposition of the cyclotron and magnetron motions (see the Discussion section below).
Figure 6.
(a) An illustration of the inhomogeneities in the electric field experienced by a trapped ion packet in a closed, cylindrical ICR cell. When the ions follow the cyclotron orbit close to the middle of the cell (trajectory I), they are subjected to nearly hyperbolic electric potential. As the axial and magnetron components start to contribute ions travel through highly inhomogeneous electric field (for example, trajectory II), which perturbs the motion further increasing the magnetron component. The orbits are not drawn to scale. (b) A schematic representation of the ions being temporally positioned in the center of the cell as consequence of the superimposition the cyclotron and magnetron orbits. The figure is not drawn to scale.
Discussion
Kaiser et al., who pioneered EPIC, showed that application of the technique, substantially increases the lifetime of the ICR experiment [55]. These experiments were reproduced on SLCC spectra (Figure 2a) demonstrating that the alteration to the electric field within the cell caused by the electron beam can not only prolong the duration of the signal, but eliminate the nipple effect altogether (Figure 2b). To analyze its effects on the temporal behavior of the ICR frequency and to minimize all other space-charge related frequency perturbations (except for “self space-charge” of the ions of the same m/z) [61, 62], as was described in the Methods and Results sections, a single cesium iodide cluster (Figure 3a) was isolated for ICR experiments under normal and EPIC conditions. The resulting signals were subjected to the FDM frequency shift calculations (Figure 3b) followed by Fourier transform to find stable harmonic modulations.
The major difference between the two modulation spectra is a much larger peak at the native ICR frequency (Figure 4a) under non-EPIC conditions—a clear indication that the center of the cyclotron orbit is substantially off-center in the XY-plane (a non-zero magnetron component), and the modulations are due to the radial inhomogeneity of the trapping field within its diameter. A virtual elimination of this peak in Figure 4b suggests that EPIC prevents or delays magnetron expansion so that the cyclotron orbit remains centered at the center of the cell for the duration of the experiment, which strongly supports earlier findings [54].
This evidence of the relationship between magnetron motion and the nipple effect will be instrumental in investigation of another tell-tale observation—temporal frequency fluctuations within an isotopic envelope going through the SLCC. An isotopic beat pattern [59, 60] in the observed ICR signal is not simply a result of superimposition of multiple sinusoids. Had it been, the observed frequencies would not vary in time. It has been shown previously [20] and can be observed in the pre-nipple stage of the experiments (Figure 5b) that frequencies “spike” up at the points when the amplitude of the transient is the smallest. This phenomenon can be described as a straight forward manifestation of the fundamentals of the classical principles of ion motion [63] in a Penning trap [64] including the spacecharge correction [65]:
| (2) |
| (3) |
| (4) |
| (5) |
where ωc, ωm, are fundamental cyclotron, magnetron, and reduced cyclotron frequencies, q is the charge, B magnetic field, V0 trapping potential, m particle’s mass, d is the distance between the trapping plates, GT is the geometry factor of a specific ICR cell, Gi is the geometry factor of an ion cloud, ε0 permittivity of a vacuum, and ρ, is the ion density.
Under the high space-charge conditions, when the ion density ρ is maximum, the space-charge correction term in eq 2 is maximized and the observed frequency is minimized. These conditions occur when the ion packets of different isotopes are in-phase (the beats of the beat pattern) therefore the minima of the frequency beat pattern in the pre-nipple part of the transient of the experimental SLCC (Figure 5b) coincide with amplitude maxima. On the other hand, when the packets are in anti-phase, the space-charge effect is minimized and the is the largest, which explains the frequency spikes at the amplitude minima.
A steady increase in the magnitude of frequency “spikes” is the manifestation of the positive frequency “drift” [66]. This behavior can be explained by the isotope beat pattern (ion clouds coming into phase with each other), which scatters and dephases the ion packets reducing ion density. Furthermore, image charge [67, 68], being oppositely charged, is reflected as attraction of the ions to the ICR cell walls, which slows down the cyclotron motion. Consequently, the detected frequency is reduced by Δω according to
| (6) |
where rtrap and rion are cylindrical cell and cyclotron motion radii respectively. Over time, dephasing and expansion of the ion clouds decreases ρ (more rapidly under high space-charge conditions); therefore the detected average frequency shows positive drift.
On the other hand, a simple electrostatics explanation for the nipple and post-nipple behavior fails at the SLCC. For instance, rapid negative frequency shifts (”dips”) (Figure 2c) corresponding to the “out-of-phase” ion position (abundance minima) violate eq 2 if one neglects consideration of the magnetron/cyclotron orbital geometries. Moreover, neither loss of ions nor the expansion of the ion clouds can explain the deviation from the exponential decay in the time domain data and beating in the frequency domain post-SLCC.
As was previously mentioned, a simple coulombic explanation of the post-nipple frequency behavior fails. Indeed, initially the ions are tightly bundled into a packet, and the frequency minima correspond to the isotopic ion packets coming into phase. At such a point, as discussed above, the space-charge is maximum, which causes the observed frequency to minimize (Figure 5b). The reverse happens later on (Figure 5c) in the course of the SLCC, when the frequency minimizes (”dips”) at the minimum of the amplitude. Since frequency minima correspond to the positions of the highest ion density (eq 2), and since amplitude corresponds to net ion cloud distance from the cell detection plates, the maximum space-charge condition must be occurring with the center of mass of the ion cloud at, or near, the center of the cell.
This seeming contradiction disappears in the light of evidence of substantial magnetron expansion obtained in the EPIC experiments. Indeed, since the transient amplitude minima correspond to the center of masses being in the center of the ICR cell (or rather, the furthest away from the detection plates, hence minimum signal intensities), the only feasible explanation to the observed (Figure 5) post-nipple “dips” is a shift in the ion trajectories via a significant increase in average magnetron radius. As the magnetron trajectory expands and its radius becomes sufficiently large, ions, when in phase, find themselves periodically positioned (without loss of momentum) very close the center of the cell as a consequence of the superposition of the cyclotron and magnetron motions as schematically shown in the Figure 6b.
Thus, the SLCC can be explained by uncorrelated magnetron expansion. Magnetron motion in a Penning trap always expands [63, 69] under normal conditions. Moreover, the magnetron expansion rate tends to increase as the magnetron orbit increases due to the increased gradient in the potential hill [70]. Indeed, in the center of the ICR cell, the trapping potential is nearly hyperbolic, but closer to the edges it squares off (Figure 6a). So, as ion packets move away from the center of the cell along the magnetron orbit, they are exposed to increasingly inhomogeneous electric fields in both axial and cyclotron motions (Figure 6a I). While some of the ions will experience substantial magnetron expansion, collide with the ICR cell walls, and be neutralized, all ions will experience rapid fluctuations in their instantaneous electric fields over their axial and cyclotron oscillations before collision with the cell wall becomes a possibility. These fluctuations in electric field will modulate (from eqs 2 and 3) as well as the axial frequency which will contribute strongly to the dephasing of the ion cloud. In other words, space- and image-charge induced (diocotron) drift shifts ions into the regions of the ICR cell where electric field inhomogeneities cause dephasing, and the rate of expansion governs the SLCC position in time, which is itself governed by ion density (eq 6).
Rapid, uncorrelated magnetron expansion thus yields an intuitive and plausible explanation for the SLCC “nipple effect” phenomenon. While this model nicely explains the unexpected observations of frequency decreases that correlate with amplitude minima, it is hardly a tested theory. A more thorough investigation, which uses these same frequency shift analysis methods and explores the behavior of these frequency shifts with varying excitation radius, ion population, trapping potentials, electric/magnetic field homogeneity, as well as global and local space-charge should yield a better understanding of the SLCC and space-charge phenomena in general.
Summary and Conclusions
This work presented an application of the filter diagonalization method (FDM) in the study of the space-charge in the form of the spontaneous loss of coherence catastrophe (SLCC). Due to its high-resolution on short transients and tolerance to noise, the FDM made possible detailed frequency chasing experiments, which provide some insight into ion cloud behavior in the ICR cell. The temporal frequency and abundance behavior thus revealed the cause of such a mysterious phenomenon as the SLCC. Specifically, the fact that frequency spikes are observed pre-SLCC that correlate with amplitude minima agrees with the known observation that frequency increases are correlated with low space-charge conditions. The fact that this correlation flips over at the SLCC suggests that the isotope ion packets are temporarily coming back into phase (high space-charge) at the amplitude minima, which is only possible geometrically if the magnetron orbit diameter is similar to that of the cyclotron orbit. This claim is supported by the EPIC experiments, which show that the SLCC is observed only when there is a strong magnetron component. Thus, the SLCC occurs when (1) the image charge drift, the space-charge related scattering, and scattering of ions off neutral molecules result in substantial magnetron expansion, which moves the ion clouds radially into the regions of the cell with large electric field inhomogeneities, and (2) when the magnetron orbit expands to approximately the same diameter as the cyclotron orbit diameter.
These findings yet again reinforce the need for reduction of magnetron drift and space-charge induced frequency modulation when pursuing the higher mass accuracy and resolving power capabilities of the FTICR MS. A number of experimental techniques and cell designs have been proposed in the literature to deal with this issue [71-81]. Clearly, EPIC [53-55] has proven to be a good countermeasure for magnetron expansion and a capable tool to counteract image charge drift and stabilize the transient. Quadrupolar axialization methods should also be revisited [82-91]. This area of research remains active, and such combined methods should help address these issues.
Acknowledgments
The authors acknowledge support for this work by NIH/NCRR P41-RR10888, NIH/NHLBI NO1 HV28178, and R01GM078293. The authors acknowledge Christian Carl, Jason Cournoyer, Weidong Cui, Vera B. Ivleva, Parminder Kaur, Xiaojuan Li, Cheng Lin, Tzu-Yung Lin, Mark E. McComb, David H. Perlman, Nadezhda Sargaeva, James West, Xiang Yu, Cheng Zhao, and Eugene Nikolaev for experimental assistance and helpful discussions.
References
- 1.Fenn JB, Mann M, Meng CK, Wong SF, Whitehouse CM. Electrospray ionization for mass-spectrometry of large biomolecules. Science. 1989;246:64–71. doi: 10.1126/science.2675315. [DOI] [PubMed] [Google Scholar]
- 2.Karas M, Bachmann D, Bahr U, Hillenkamp F. Matrix-assisted ultraviolet-laser desorption of nonvolatile compounds. Int. J. Mass Spectrom. Ion Processes. 1987;78:53–68. [Google Scholar]
- 3.Tanaka K, Waki H, Ido Yutaka, Akita Y, Yoshida Y, Yoshida T, Matsuo T. Protein and polymer analyses up to m/z. 100 000 by laser ionization time-of-flight mass spectrometry. Rapid Commun. Mass Spectrom. 1988;2:151–153. [Google Scholar]
- 4.Paul W. Electromagnetic traps for charged and neutral particles. Angew. Chem. Int. Ed. Engl. 1990;29:739–748. [Google Scholar]
- 5.Senko MW, Hendrickson CL, Emmett MR, Shi SDH, Marshall AG. External accumulation of ions for enhanced electrospray ionization Fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 1997;8:970–976. [Google Scholar]
- 6.O’Connor PB, Pittman JL, Thomson BA, Budnik BA, Cournoyer JC, Jebanathirajah J, Lin C, Moyer S, Zhao C. A new hybrid electrospray Fourier transform mass spectrometer: Design and performance characteristics. Rapid Commun. Mass Spectrom. 2006;20:259–266. doi: 10.1002/rcm.2307. [DOI] [PubMed] [Google Scholar]
- 7.Belov ME, Anderson GA, Wingerd MA, Udseth HR, Tang K, Prior DC, Swanson KR, Buschbach MA, Strittmatter EF, Moore RJ, Smith RD. An automated high performance capillary liquid chromatography-Fourier transform ion cyclotron resonance mass spectrometer for high-throughput proteomics. J. Am. Soc. Mass Spectrom. 2004;15:212–232. doi: 10.1016/j.jasms.2003.09.008. [DOI] [PubMed] [Google Scholar]
- 8.Jebanathirajah JA, Pittman JL, Thomson BA, Budnik BA, Kaur P, Rape M, Kirschner M, Costello CE, O’Connor PB. Characterization of a new qQq-FTICR mass spectrometer for post-translational. modification analysis and top-down tandem mass spectrometry of whole proteins. J. Am. Soc. Mass Spectrom. 2005;16:1985–1999. doi: 10.1016/j.jasms.2005.08.008. [DOI] [PubMed] [Google Scholar]
- 9.Zubarev R, Mann M. On the proper use of mass accuracy in proteomics. Mol. Cell. Proteom. 2007;6:377–381. doi: 10.1074/mcp.M600380-MCP200. [DOI] [PubMed] [Google Scholar]
- 10.Norbeck AD, Monroe ME, Adkins JN, Anderson KK, Daly DS, Smith RD. The utility of accurate mass and LC elution time information in the analysis of complex proteomes. J. Am. Soc. Mass Spectrom. 2005;16:1239–1249. doi: 10.1016/j.jasms.2005.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Spengler B. De novo sequencing, peptide composition analysis, and composition-based sequencing: A new strategy employing accurate mass determination by Fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 2004;15:703–714. doi: 10.1016/j.jasms.2004.01.007. [DOI] [PubMed] [Google Scholar]
- 12.Comisarow MB, Marshall AG. Fourier-transform ion cyclotron resonance spectroscopy. Chem. Phys. Lett. 1974;25:282–283. [Google Scholar]
- 13.Marshall AG. Milestones in Fourier-transform ion cyclotron resonance mass spectrometry technique development. Int. J. Mass Spectrom. 2000;200:331–356. [Google Scholar]
- 14.Belov ME, Zhang R, Strittmatter EF, Prior DC, Tang K, Smith RD. Automated gain control and internal calibration with external ion accumulation capillary liquid chromatography-electrospray ionization Fourier-transform ion cyclotron resonance. Anal. Chem. 2003;75:4195–4205. doi: 10.1021/ac0206770. [DOI] [PubMed] [Google Scholar]
- 15.Lorenz SA, Moy MA, Dolan AR, Wood TD. Electrospray ionization Fourier-transform mass spectrometry quantification of enkephalin using an internal standard. Rapid Commun. Mass Spectrom. 1999;13:2098–2102. doi: 10.1002/(SICI)1097-0231(19991115)13:21<2098::AID-RCM759>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 16.O’Connor PB, Costello CE. Internal calibration on adjacent samples (InCAS) with Fourier-transform mass spectrometry. Anal. Chem. 2000;72:5881–5885. doi: 10.1021/ac000770t. [DOI] [PubMed] [Google Scholar]
- 17.Flora JW, Hannis JC, Muddiman DC. High-mass accuracy of product ions produced by SORI-CID using a dual electrospray ionization source coupled with FTICR mass spectrometry. Anal. Chem. 2001;73:1247–1251. doi: 10.1021/ac0011282. [DOI] [PubMed] [Google Scholar]
- 18.Easterling ML, Mize TH, Amster IJ. MALDI FTMS analysis of polymers: Improved performance using an open ended cylindrical analyzer cell. Int. J. Mass Spectrom. 1997;169:387–400. [Google Scholar]
- 19.Hannis JC, Muddiman DC. A dual electrospray ionization source combined with hexapole accumulation to achieve high mass accuracy of biopolymers in Fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 2000;11:876–883. doi: 10.1016/S1044-0305(00)00160-4. [DOI] [PubMed] [Google Scholar]
- 20.Aizikov K, O’Connor PB. Use of the filter diagonalization method in the study of space charge related frequency modulation in Fourier transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 2006;17:836–843. doi: 10.1016/j.jasms.2006.02.018. [DOI] [PubMed] [Google Scholar]
- 21.Guan S, Wahl MC, Marshall AG. Elimination of frequency drift from Fourier-transform ion cyclotron resonance mass spectra by digital quadrature heterodyning: Ultrahigh mass resolving power for laser-desorbed molecules. Anal. Chem. 1993;65:3647–3653. doi: 10.1021/ac00072a019. [DOI] [PubMed] [Google Scholar]
- 22.Nikolaev EN, Miluchihin NV, Inoue M. Evolution of an ion cloud in a Fourier-transform ion-cyclotron resonance mass-spectrometer during signal-detection—its influence on spectral-line shape and position. Int. J. Mass Spectrom. Ion Processes. 1995;148:145–157. [Google Scholar]
- 23.Cooley JW, Tukey JW. An algorithm for the machine calculation of complex Fourier series. Math. Comp. 1965;19:297–301. [Google Scholar]
- 24.Mann S, Haykin S. Adaptive chirplet-transform—an adaptive generalization of the wavelet transform. Opt. Eng. 1992;31:1243–1256. [Google Scholar]
- 25.Savitski MM, Ivonin IA, Nielsen ML, Zubarev RA, Tsybin YO, Hakansson P. Shifted-basis technique improves accuracy of peak position determination in Fourier transform mass spectrometry. J. Am. Soc. Mass Spectrom. 2004;15:457–461. doi: 10.1016/j.jasms.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 26.Smith JO. Mathematics of the Discrete Fourier Transform (DFT) 2003 http://www-ccrma.stanford.edu/~jos/mdft/ ISBN 0-9745607-0-7.
- 27.Guan SH, Marshall AG. Linear prediction Cholesky decomposition versus Fourier transform spectral analysis for ion cyclotron resonance mass spectrometry. Anal. Chem. 1997;69:1156–1162. doi: 10.1021/ac960755h. [DOI] [PubMed] [Google Scholar]
- 28.Farrar TC, Elling JW, Krahling MD. Application of linear prediction to Fourier-transform ion-cyclotron resonance signals for accurate relative ion abundance measurements. Anal. Chem. 1992;64:2770–2774. [Google Scholar]
- 29.Marple SL., Jr. Digital spectral analysis with applications. Prentice-Hall, Inc.; Englewood Cliffs, NJ: 1987. pp. 303–349. [Google Scholar]
- 30.Roy R, Sumpter BG, Pfeffer GA, Gray SK, Noid DW. Novel methods for spectral analysis. Phys. Rep. 1991;205:109–152. [Google Scholar]
- 31.Neuhauser D. Bound state Eigen functions from wave packets: Time→energy resolution. J. Chem. Phys. 1990;93:2611–2616. [Google Scholar]
- 32.Neuhauser D. Circumventing the Heisenberg principle: A rigorous demonstration of filter-diagonalization on a LiCN model. J. Chem. Phys. 1994;100:5076–5079. [Google Scholar]
- 33.Wall MR, Neuhauser D. Extraction, through filter-diagonalization, of general quantum Eigenvalues or classical normal mode frequencies from a small number of residues or a short-time segment of a signal. I. Theory and application to a quantum-dynamics model. J. Chem. Phys. 1995;102:8011–9022. [Google Scholar]
- 34.Hu HT, Van QN, Mandelshtam VA, Shaka AJ. Reference deconvolution, phase correction, and line listing of NMR spectra by the 1D filter diagonalization method. J. Magn. Reson. 1998;134:76–87. doi: 10.1006/jmre.1998.1516. [DOI] [PubMed] [Google Scholar]
- 35.Mandelshtam VA. On harmonic inversion of cross-correlation functions by the filter diagonalization method. J. Theor. Comp. Chem. 2003;2:1–9. [Google Scholar]
- 36.Mandelshtam VAT, Howard S. Spectral analysis of time correlation function for a dissipative dynamical system using filter diagonalization: Application to calculation of unimolecular decay rates. Phys. Rev. Lett. 1997;78:3274–3277. [Google Scholar]
- 37.Mandelshtam VA, Taylor HS. Harmonic inversion of time signals and its applications. J. Chem. Phys. 1997;107:6756. [Google Scholar]; (b) J. Chem. Phys. 1998;109:4128–4128. [Google Scholar]
- 38.Mandelshtam VA. FDM: The filter diagonalization method for data processing in NMR experiments. Prog. Nucl. Magn. Res. Spectrosc. 2001;38:159–196. [Google Scholar]
- 39.Chen JH, Mandelshtam VA. Multiscale filter diagonalization method for spectral analysis of noisy data with nonlocalized features. J. Chem. Phys. 2000;112:4429–4437. [Google Scholar]
- 40.Nikolaev EN, Heeren RM, Popov AM, Pozdneev AV, Chingin KS. Realistic modeling of ion cloud motion in a Fourier transform ion cyclotron resonance cell by use of a particle-in-cell approach. Rapid Commun. Mass Spectrom. 2007;21:3527–3546. doi: 10.1002/rcm.3234. [DOI] [PubMed] [Google Scholar]
- 41.O’Connor PB, Budnik BA, Ivleva VB, Kaur P, Moyer SC, Pittman JL, Costello CE. A high pressure matrix-assisted laser desorption ion source for Fourier transform mass spectrometry designed to accommodate large targets with diverse surfaces. J. Am. Soc. Mass Spectrom. 2004;15:128–132. doi: 10.1016/j.jasms.2003.10.005. [DOI] [PubMed] [Google Scholar]
- 42.Beu SC, Laude DA. Open trapped ion cell geometries for Fourier-transform ion cyclotron resonance mass-spectrometry. Int. J. Mass Spectrom. Ion Processes. 1992;112:215–230. [Google Scholar]
- 43.Mize TH, Taban I, Duursma M, Seynen M, Konijnenburg M, Vijftigschild A, Doornik CV, Rooij GV, Heeren RMA. A modular data and control system to improve sensitivity, selectivity, speed of analysis, ease of use, and transient duration in an external source FTICR-MS. Int. J. Mass Spectrom. 2004;235:243–253. [Google Scholar]
- 44.Mathur R, Knepper RW, O’Connor PB. A low-noise, wideband preamplifier for a Fourier-transform ion cyclotron resonance mass spectrometer. J. Am. Soc. Mass Spectrom. 2007;18:2233–2241. doi: 10.1016/j.jasms.2007.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mathur R, O’Connor PB. Design and implementation of a high power RF oscillator on a printed circuit board for multipole ion guides. Rev. Sci. Instrum. 2006;77:114101-1–114101-7. [Google Scholar]
- 46.O’Connor PB, Costello CE, Earle WE. A high voltage rf oscillator for driving multipole ion guides. J. Am. Soc. Mass Spectrom. 2002;13:1370–1375. doi: 10.1016/S1044-0305(02)00700-6. [DOI] [PubMed] [Google Scholar]
- 47.Pittman JL, O’Connor PB. A minimum thickness gate valve with integrated ion optics for mass spectrometry. J. Am. Soc. Mass Spectrom. 2005;16:441–445. doi: 10.1016/j.jasms.2004.12.010. [DOI] [PubMed] [Google Scholar]
- 48.Kussmann M, Nordhoff E, Rahbeknielsen H, Haebel S, Rossel-larsen M, Jakobsen L, Gobom J, Mirgorodskaya E, Krollkristensen A, Palm L, Roepstorff P. Matrix-assisted laser desorption/ionization mass spectrometry sample preparation techniques designed for various peptide and protein analytes. J. Mass Spectrom. 1997;32:593–601. [Google Scholar]
- 49.Zubarev RA, Kelleher NL, McLafferty FW. Electron capture dissociation of multiply charged protein cations. A nonergodic process. J. Am. Chem. Soc. 1998;120:3265–3266. [Google Scholar]
- 50.Adamson JT, Hakansson K. Electron capture dissociation of oligosaccharides ionized with alkali, alkaline earth, and transition metals. Anal. Chem. 2007;79:2901–2910. doi: 10.1021/ac0621423. [DOI] [PubMed] [Google Scholar]
- 51.Zubarev RA, Kruger NA, Fridriksson EK, Lewis MA, Horn DM, Carpenter BK, McLafferty FW. Electron capture dissociation of gaseous multiply-charged proteins is favored at disulfide bonds and other sites of high hydrogen atom affinity. J. Am. Chem. Soc. 1999;121:2857–2862. [Google Scholar]
- 52.Leymarie N, Costello CE, O’Connor PB. Electron capture dissociation initiates a free radical reaction cascade. J. Am. Chem. Soc. 2003;125:8949–8958. doi: 10.1021/ja028831n. [DOI] [PubMed] [Google Scholar]
- 53.Kaiser NK, Weisbrod CR, Webb BN, Bruce JE. Reduction of axial kinetic energy induced perturbations on observed cyclotron frequency. J. Am. Soc. Mass Spectrom. 2008;19:467–478. doi: 10.1016/j.jasms.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kaiser NK, Bruce JE. Reduction of ion magnetron motion and space charge using radial electric field modulation. Int. J. Mass Spectrom. 2007;265:271–280. [Google Scholar]
- 55.Kaiser NK, Bruce JE. Observation of increased ion cyclotron resonance signal duration through electric field perturbations. Anal. Chem. 2005;77:5973–5981. doi: 10.1021/ac050606b. [DOI] [PubMed] [Google Scholar]
- 56.O’Connor PB, Boston University Data Analysis (BUDA) 2002 http://www.bumc.bu.edu/ftms/buda. [Google Scholar]
- 57.Frigo M, Johnson SG. The design and implementation of FFTW3. Proc. IEEE. 2005;93:216–231. [Google Scholar]
- 58.Marshall AG, Hendrickson CL, Jackson GS. Fourier-transform ion cyclotron resonance mass spectrometry: A primer. Mass Spectrom. Rev. 1998;17:1–35. doi: 10.1002/(SICI)1098-2787(1998)17:1<1::AID-MAS1>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 59.Easterling ML, Amster IJ, van Rooij GJ, Heeren RMA. Isotope beating effects in the analysis of polymer distributions by Fourier transform Mass spectrometry. J. Am. Soc. Mass Spectrom. 1999;10:1074–1082. [Google Scholar]
- 60.Hofstadler SA, Bruce JE, Rockwood AL, Anderson GA, Winger BE, Smith RD. Isotopic beat patterns in Fourier-transform ion-cyclotron resonance mass-spectrometry—implications for high-resolution mass measurements of large biopolymers. Int. J. Mass Spectrom. 1994;132:109–127. [Google Scholar]
- 61.Wineland D, Dehmelt H. Line shifts and widths of axial, cyclotron, and G-2 resonances in tailored, stored electron (ion) cloud. Int. J. Mass Spectrom. Ion. Phys. 1975;16:338–342. [Google Scholar]
- 62.Wong RL, Amster IJ. Experimental evidence for space-charge effects between ions of the same mass-to-charge in Fourier-transform ion cyclotron resonance mass spectrometry. Int. J. Mass Spectrom. 2007;265:99–105. doi: 10.1016/j.ijms.2007.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Brown LS, Gabrielse G. Geonium theory: Physics of a single electron or ion in a Penning trap. Rev. Mod. Phys. 1986;58:233–311. [Google Scholar]
- 64.Penning FM. Die Glimmentladung bei niedrigem Druck zwischen koaxialen Zylindern in einem axialen Magnetfeld. Phys. Rev. Lett. 1936;3:873–894. [Google Scholar]
- 65.Jeffries JB, Barlow SE, Dunn GH. Theory of space-charge shift of ion-cyclotron resonance frequencies. Int. J. Mass Spectrom. Ion Processes. 1983;54:169–187. [Google Scholar]
- 66.Bruce JE, Anderson GA, Hofstadler SA, Winger BE, Smith RD. Time-base modulation for the correction of cyclotron frequency shifts observed in long-lived transients from Fourier-transform ion-cyclotron-resonance mass spectrometry of electrosprayed biopolymers. Rapid Commun. Mass Spectrom. 1993;7:700–703. [Google Scholar]
- 67.Xiang XZ, Grosshans PB, Marshall AG. Image charge-induced ion-cyclotron orbital frequency-shift for orthorhombic and cylindrical FT-ICR ion traps. Int. J. Mass Spectrom. Ion Processes. 1993;125:33–43. [Google Scholar]
- 68.Gorshkov MV, Marshall AG, Nikolaev EN. Analysis and elimination of Systematic-Errors Originating from Coulomb Mutual Interaction and Image Charge in Fourier-Transform Ion-Cyclotron Resonance Precise Mass Difference Measurements. J. Am. Soc. Mass Spectrom. 1993;4:855–868. doi: 10.1016/1044-0305(93)87003-U. [DOI] [PubMed] [Google Scholar]
- 69.Hendrickson CL, Hofstadler SA, Beu SC, Laude DA. Initiation of coherent magnetron motion following ion injection into a Fourier-transform ion-cyclotron resonance trapped ion cell. Int. J. Mass Spectrom. Ion Processes. 1993;123:49–58. [Google Scholar]
- 70.Honovich JP, Markey SP. Magnetron motion and the transfer of ions in a dual cell ion-cyclotron resonance mass-spectrometer. Int. J. Mass Spectrom. Ion Processes. 1990;101:21–34. [Google Scholar]
- 71.Gooden JK, Rempel DL, Gross ML. Evaluation of different combinations of gated trapping, rf-only mode and trap compensation for in-field MALDI Fourier transform mass spectrometry. J. Am. Soc. Mass Spectrom. 2004;15:1109–1115. doi: 10.1016/j.jasms.2004.05.006. [DOI] [PubMed] [Google Scholar]
- 72.Guan SH, Marshall AG. Ion traps for Fourier-transform ion-cyclotron resonance mass-spectrometry—principles and design of geometric and electric configurations. Int. J. Mass Spectrom. Ion Processes. 1995;146:261–296. [Google Scholar]
- 73.Pan Y, Ridge DP, Rockwood AL. Harmonic signal enhancement in ion-cyclotron resonance mass-spectrometry using multiple electrode detection. Int. J. Mass Spectrom. Ion Processes. 1988;84:293–304. [Google Scholar]
- 74.Gillig KJ, Bluhm BK, Russell DH. Ion motion in a Fourier transform ion cyclotron resonance wire ion guide cell. Int. J. Mass Spectrom. Ion Processes. 1996;158:129–147. [Google Scholar]
- 75.Gabrielse G, Mackintosh FC. Cylindrical penning traps with orthogonalized anharmonicity compensation. Int. J. Mass Spectrom. Ion Processes. 1984;57:1–17. [Google Scholar]
- 76.Vartanian VH, Laude DA. Optimization of a fixed-volume open geometry trapped ion cell for Fourier-transform ion cyclotron mass spectrometry. Int. J. Mass Spectrom. Ion Processes. 1995;141:189–200. [Google Scholar]
- 77.Jackson GS, White FM, Guan SH, Marshall AG. Matrix-shimmed ion cyclotron resonance ion trap simultaneously optimized for excitation, detection, quadrupolar axialization, and trapping. J. Am. Soc. Mass Spectrom. 1999;10:759–769. [Google Scholar]
- 78.Bruce JE, Anderson GA, Lin CY, Gorshkov M, Rockwood AL, Smith RD. A novel high-performance Fourier transform ion cyclotron resonance cell for improved biopolymer characterization. J. Mass Spectrom. 2000;35:85–94. doi: 10.1002/(SICI)1096-9888(200001)35:1<85::AID-JMS910>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- 79.Brustkern AM, Rempel DL, Gross ML. An electrically compensated trap designed to eighth order for FT-ICR mass spectrometry. J. Am. Soc. Mass Spectrom. 2008;19:1281–1285. doi: 10.1016/j.jasms.2008.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Tolmachev AV, Robinson EW, Wu S, Kang H, Lourette NM, Pasa-Tolic L, Smith RD. Trapped-ion cell with improved DC potential harmonicity for FT-ICR MS. J. Am. Soc. Mass Spectrom. 2008;19:586–597. doi: 10.1016/j.jasms.2008.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Weisbrod CR, Kaiser NK, Skulason GE, Bruce JE. Series, Trapping Ring Electrode Cell (TREC): A novel ICR cell for ultra-high sensitivity, resolution, and mass measurement accuracy; Proceedings of the 56th ASMS Conference on Mass Spectrometry and Allied Topics; Denver, CO. 2008. [Google Scholar]
- 82.Savard G, Becker S, Bollen G, Kluge H-J, Moore RB, Schweikhard L, Stolzenberg H, Wiess U. A new cooling technique for heavy ions in a Penning trap. Phys. Lett. A. 1991;158:247–252. [Google Scholar]
- 83.Schweikhard L, Guan SH, Marshall AG. Quadrupolar excitation and collisional cooling for axialization and high-pressure trapping of ions in Fourier-transform ion cyclotron resonance mass spectrometry. Int. J. Mass Spectrom. Ion Processes. 1992;120:71–83. [Google Scholar]
- 84.Speir JP, Gorman GS, Pitsenberger CC, Turner CA, Wang PP, Amster IJ. Remeasurement of ions using quadrupolar excitation Fourier-transform ion cyclotron resonance spectrometry. Anal. Chem. 1993;65:1746–1752. doi: 10.1021/ac00061a018. [DOI] [PubMed] [Google Scholar]
- 85.Pastor SJ, Castoro JA, Wilkins CL. High-mass analysis using quadrupolar excitation ion cooling in a Fourier-transform mass spectrometry. Anal. Chem. 1995;67:379–384. doi: 10.1021/ac00098a024. [DOI] [PubMed] [Google Scholar]
- 86.Bruce JE, Anderson GA, Hofstadler SA, Vanorden SL, Sherman MS, Rockwood AL, Smith RD. Selected-ion accumulation from an external electrospray ionization source with a Fourier-transform ion cyclotron resonance mass spectrometer. Rapid Commun. Mass Spectrom. 1993;7:914–919. [Google Scholar]
- 87.Hendrickson CL, Laude DA., Jr. Quadrupolar axialization for improved control of electrosprayed proteins in FTICR mass spectrometry. Anal. Chem. 1995;67:1717–1721. [Google Scholar]
- 88.Hendrickson CL, Drader JJ, Laude DA. Simplified application of quadrupolar excitation in Fourier-transform ion cyclotron resonance mass spectrometry. J. Am. Soc. Mass Spectrom. 1995;6:448–452. doi: 10.1016/1044-0305(95)00054-H. [DOI] [PubMed] [Google Scholar]
- 89.Bruce JE, Vanorden SL, Anderson GA, Hofstadler SA, Sherman MG, Rockwood AL, Smith RD. Selected ion accumulation of noncovalent complexes in a Fourier-transform ion cyclotron resonance mass spectrometer. J. Mass Spectrom. 1995;30:124–133. [Google Scholar]
- 90.O’Connor PB, Speir JP, Wood TD, Chorush RA, Guan Z, McLafferty FW. Quadrupolar axialization of large multiply charged ions. J. Mass Spectrom. 1996;31:555–559. doi: 10.1002/(SICI)1096-9888(199605)31:5<555::AID-JMS324>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 91.Hasse HU, Becker S, Dietrich G, Klisch N, Kluge HJ, Lindinger M, Lutzendirchen K, Schweikhard L, Ziegler J. External ion accumulation in a Penning trap with quadrupole excitation assisted buffer gas cooling. Int. J. Mass Spectrom. Ion Processes. 1994;132:181–191. [Google Scholar]