Age-dependent Fourier model of the shape of the isolated ex vivo human crystalline lens

Abstract

Purpose

To develop an age-dependent mathematical model of the zero-order shape of the isolated ex vivo human crystalline lens, using one mathematical function, that can be subsequently used to facilitate the development of other models for specific purposes such as optical modeling and analytical and numerical modeling of the lens.

Methods

Profiles of whole isolated human lenses (n=30) aged 20 to 69, were measured from shadow-photogrammetric images. The profiles were fit to a 10^th-order Fourier series consisting of cosine functions in polar-coordinate system that included terms for tilt and decentration. The profiles were corrected using these terms and processed in two ways. In the first, each lens was fit to a 10^th-order Fourier series to obtain thickness and diameter, while in the second, all lenses were simultaneously fit to a Fourier series equation that explicitly include linear terms for age to develop an age-dependent mathematical model for the whole lens shape.

Results

Thickness and diameter obtained from Fourier series fits exhibited high correlation with manual measurements made from shadow-photogrammetric images. The root-mean-squared-error of the age-dependent fit was 205 μm. The age-dependent equations provide a reliable lens model for ages 20 to 60 years.

Conclusion

The contour of the whole human crystalline lens can be modeled with a Fourier series. Shape obtained from the age-dependent model described in this paper can be used to facilitate the development of other models for specific purposes such as optical modeling and analytical and numerical modeling of the lens.

1. Introduction

There is much interest in computational modeling for the analysis of accommodative functions of the human crystalline lens. For such modeling to be valid, the geometrical, optical and mechanical parameters of the accommodative system need to be established. In the first instance, as it sets the initial conditions, a reliable geometric model of the lens will, to a large extent, impact the validity of data obtainable from computational models. Geometrically, the crystalline lens is a solid in three-dimensional space that approximately possesses one axis of rotational symmetry. The presence of rotational symmetry provides for simplification by modeling in axi-symmetric two-dimensions. However, the presence of anterior and posterior surfaces, as well as regions of vertical surfaces at the equator, invokes certain geometric conditions in modeling.

Chien, Huang and Schachar (2003) listed five compulsory requirements for any analytical function that seeks to represents the shape of the crystalline lens to meet geometric conditions. The five compulsory requirements are (1) the lens profile should be continuous and smooth (2) the derivative at the pole should be zero (3) the lens profile should be zero at the equator (4) the slope at the equator should be vertical and (5) the surface slope should decrease monotonically as distance from the axis increases so that the generated surface has a positive Gaussian curvature everywhere.

They also listed four desirable conditions, for the surface to have appropriate optical qualities, which are (1) the model should follow the original lens profile closely (2) the radii of curvature should be continuous (3) the rate of change of the radii of curvature should be zero at the poles and (4) The rate of change of the radius of curvature with respect to distance from the axis should be gentle at least in the pole regions.

Against the foregoing geometric conditions, the majority of existing lens models describe the lens with two mathematical functions, one each for the two surfaces of the lens (Howcroft and Parker 1977; Koretz, Handelman and Brown 1984; Dubbelman and van der Heijde 2001; Chien et al., 2003; Manns, Fernandez, Zipper, Sandadi, Hamaoui, Ho and Parel 2004; Strenk, Strenk, Semmlow and DeMarco 2004; Rosen, Denham, Fernandez, Borja, Ho, Manns, Parel and Augusteyn 2006; Borja, Manns, Ho, Ziebarth, Rosen, Jain, Amelinckx, Arrieta, Augusteyn and Parel 2008). These models were mostly developed for supporting optical modeling and therefore focus on the central 4 to 5 mm region, bypassing the need for accurate portrayal of the lens equator. As an alternative to using two functions to describe anterior and posterior lens surfaces, Kasprzak (2000) and Smith, Atchison, Iskander, Jones and Pope (2009) approximated the whole profile of the human lens using hyperbolic cosine functions and a generalized conic function.

It would be ideal to develop one mathematical model for the lens shape that can be applied for various purposes such as optical and mechanical modeling. But this would involve imposing various constraints to the lens shape and its subsequent derivatives, which would prohibit the model from being faithful to the true lens shape. A faithful age-dependent mathematical model of the zero-order shape of the lens contour would be beneficial to scientists who wish to develop their own models with constraints for specific purposes. This model would serve as a substitute for actual lens measurements.

We recently developed two age-dependent polynomial models (Urs, Manns, Ho, Borja, Amelinckx, Smith, Jain Augusteyn and Parel 2009). The Two Curves Model (TCM) used two 10^th-order even polynomials to describe the two lens surfaces from equator to equator and the One Curve Model (OCM) described one meridional half of the lens using one 10^th-order polynomial equation from pole to pole. While both models were age-dependent and attempted to model the whole lens profile including the equatorial regions, they did not represent the whole lens profile with a single mathematical expression. This limitation caused, in the TCM model, the lens surfaces and their derivates to be discontinuous at the equator and in the OCM model, the derivative of the profile to be non-zero at the poles. Constraints can be set to fitting functions to overcome this problem. However, these conditions may cause the fitting functions to not closely model the lens.

The purpose of the current study is to develop an age-dependent mathematical model of the whole lens profile, using one mathematical function. This model should address the shortcomings of the previous models and ideally satisfy as many as possible of the geometrical conditions defined above. This age-dependent model should provide reliable lens contour shapes to facilitate development of new mathematical functions for various purposes such as optical modeling and analytical and numerical modeling of the lens.

2. Materials and Methods

Lens Preparation

All human eyes were obtained and used in compliance with the guidelines of the Declaration of Helsinki for research involving the use of human tissue. Crystalline lenses (n=30) from donors in the age range of 20 to 69 were used in this study. They were extracted from whole, intact cadaver eyes, obtained from various US eye banks. The post-mortem time ranged from 1 to 5 days. The lens extraction procedure consisted of first removing the globe's posterior pole, the cornea and the iris. Then the adherent vitreous was carefully removed, the zonules were cut and the lens was extracted and placed in the imaging cell containing DMEM (Augusteyn, Rosen, Borja, Ziebarth and Parel, 2006). Of the 105 lenses available for this study, 75 lenses were excluded either because of capsular tear or separation. This proportion is similar to that reported by Augusteyn et al., (2006)

Lens Imaging and Image Analysis

Lenses were imaged using the technique of shadow-photogrammetry (Denham, Holland, Mandelbaum, Pflugfelder and Parel, 1989; Pflugfelder, Roussel, Denham, Feuer, Mandelbaum and Parel, 1992; Rosen et al., 2006; Augusteyn et al., 2006, Urs et al., 2009). The shadow-photogrammetric system consists of a modified optical comparator (BP-30S, Topcon, Tokyo, Japan) with two light sources to enable photography of the crystalline lens in the coronal and sagittal planes. A 20× magnified shadow of the excised lens is projected onto a viewing screen and images are captured by a 4.0 Mp Nikon Coolpix 4500 digital camera (Tokyo, Japan) positioned at a fixed distance from the screen. For scaling purposes a ruler (1376T-25, Keuffel and Esser Co., Hoboken, New Jersey) was concurrently photographed on each image.

Lens contour detection has been described in a previous publication (Urs et al, 2009). Binary images of the lens contours were loaded into MATLAB. An approximate center for the lens was determined by examining the outermost pixels along the equatorial axis and the optical axis. The initially centered lens contour was positioned such that, the anterior surface of the lens was in the second and third quadrants of the Cartesian coordinate system and the posterior surface in the first and fourth quadrants (Figure 1). This coordinate system was converted to polar domain and the lens contour was fit to a 10^th-order cosine series function (Equation 1) using MATLAB's curve-fitting toolbox.

Figure 1.

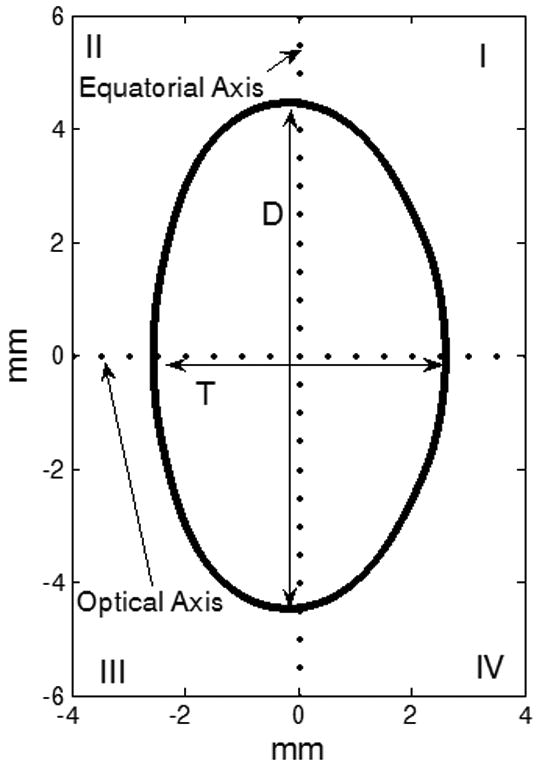
The co-ordinate system for the Fourier model. The lens anterior surface was placed in quadrants II and III and the posterior surface was placed in the quadrants I and IV. T and D represent the thickness and diameter of the lens.

$${\rho }_c(\theta )=a_0+\sum _{n=1}^{10}{a}_{n}cos\left(n\times \left({tan}^{-1}\left(\frac{y-y_c}{x-x_c}\right)-{\theta }_c\right)\right)$$ Equation 1

The curve fit provided values for x_c and y_c (the center displacement terms), and θ_c (the angle displacement term), to correct for decentration and tilt, and scaling coefficients a₀ to a_n (for the cosine series). The center and angle displacements of the lens contour were first corrected with the values x_c, y_c and θ_c obtained from the curve fit. In the Cartesian coordinate system the corrected profile was then translated to place the equator on the y-axis (i.e. x = 0), where the equator is defined as the largest linear dimension of the lens parallel to the equatorial axis. The original lens profile, the curve fit and corrected profile are shown in Figure 2, for a 28 year-old lens, in both the Cartesian and polar coordinate systems. The translated, corrected profiles were processed in two ways: one for individual lens biometry and the other for obtaining an age-dependent model.

Figure 2.

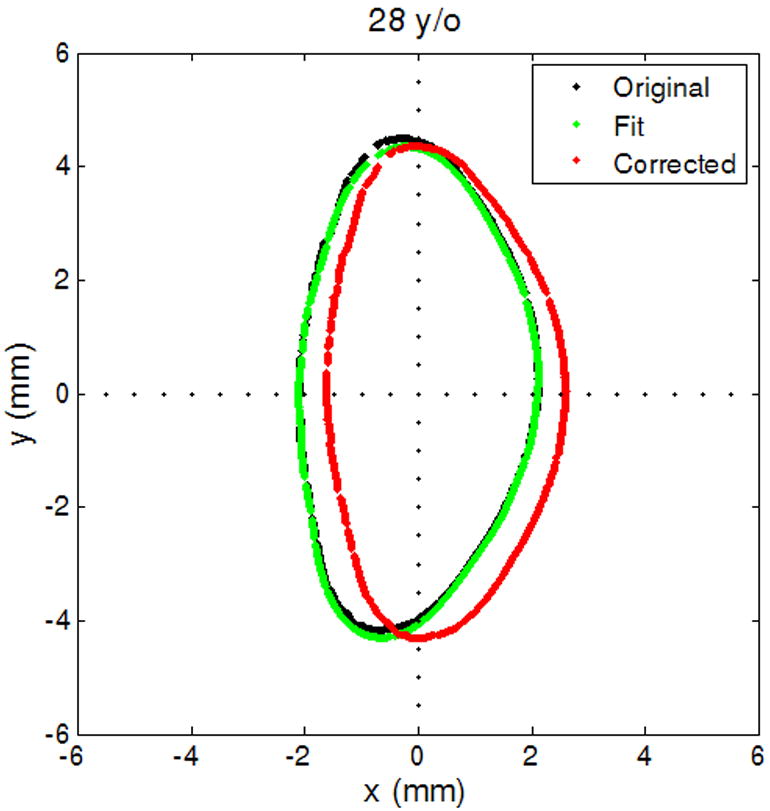
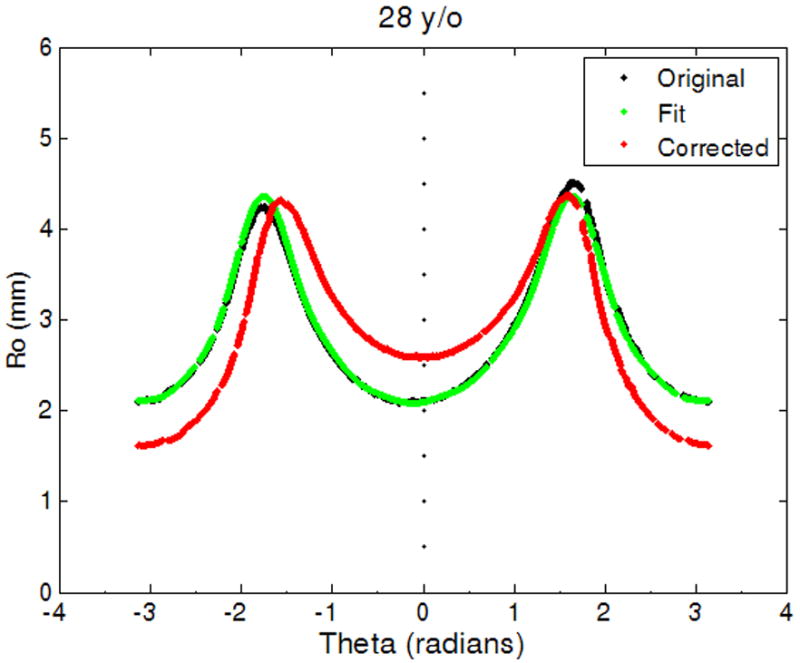
The original lens contour (black), lens contour fit to Equation 1 (green) and the adjusted lens contour (red). (2a) Shows lens contour in Cartesian coordinates and (2b) in polar coordinates for contour extracted from shadow-photogrammetric images of a 28 year-old human crystalline lens that was 3 days post mortem.

First, each lens contour was fit to a 10^th-order Fourier series of cosine functions (Equation 2).

$${\rho }_r(\theta )=\sum _{n=0}^{10}(b_n)cos(n\theta )$$ Equation 2

The Fourier series of Equation 2 assumes a period π and mirror symmetry since the lens is assumed to be rotationally symmetric. The equatorial diameter (D) was calculated as twice the radial distance at θ=π/2. The anterior sagittal thickness and the posterior sagittal thickness were calculated as the radial distances at θ=π and θ=0 respectively. Total sagittal thickness was calculated as the sum of the two thicknesses. Thickness and diameter were also measured directly from the shadow-photogrammetric images using Canvas (version 9.0, ACD Systems of America, Miami, FL).

In a second, separate process, the translated, corrected profiles of all 30 lenses were re-sampled with a sampling step-size of 10^-4 radians and fit simultaneously to an age-dependent Fourier series model (Equation 3) using MATLAB's least-square curve-fit method to develop an age-dependent model for the lens.

$$\rho (\theta )=\sum _{n=0}^{10}(A_{n1}+A_{n2}\times \mathit{\text{age}})\text{cos}(n\theta )$$ Equation 3

The coefficients obtained from the fits were used to plot lens shapes for 20, 40 and 60 year-old lenses.

3. Results

The root-mean-squared-error (rmse) of the Fourier fits of the individual lenses ranged from 11 to 137 μm with a mean of 37 ±24 μm for the 30 lenses.

Figure 3 shows the linear regression graphs of thickness and diameter versus age. Both dimensions increased significantly with age (p<0.05). Pearson correlation of thickness and diameter calculated by the Fourier function fits and measured from the shadow-photogrammetric images, revealed that the two methods were highly correlated for measurement of both dimensions (R > 0.98; p<.0001). Regression analysis of both dimensions yielded comparable slopes (0.01±0.004mm/year for thickness from Fourier fits and 0.01±0.01 mm/year for thickness from shadow-photogrammetric images and 0.02±0.01 mm/year for diameter from both methods). Bland-Altman analysis (Figure 4) demonstrated that the mean measurement error was 0.02±0.04 mm for the thickness and 0.01±0.1 mm for the diameter. Most of the measurements were within 2 standard deviations of the mean measurement error.

Figure 3.

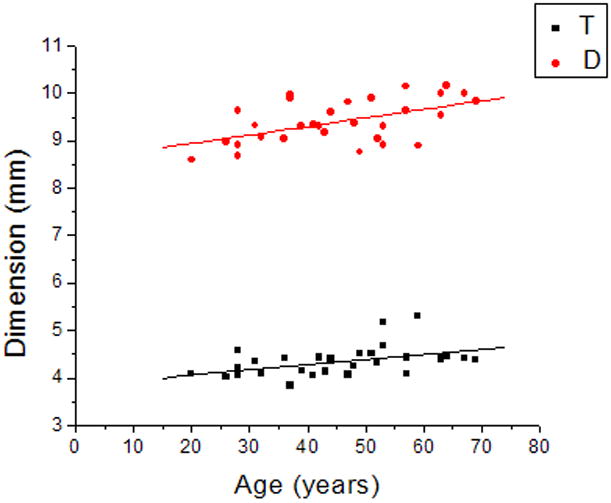
Linear regression of thickness (T) and diameter (D) of the human crystalline lens with age yielded T = 3.8 (±0.9) + 0.01(±0.004) × Age (R=0.45, p=0.01) and D = 8.6 (±0.3) + 0.02(±0.01) × Age (R=0.53, p=0.002).

Figure 4.

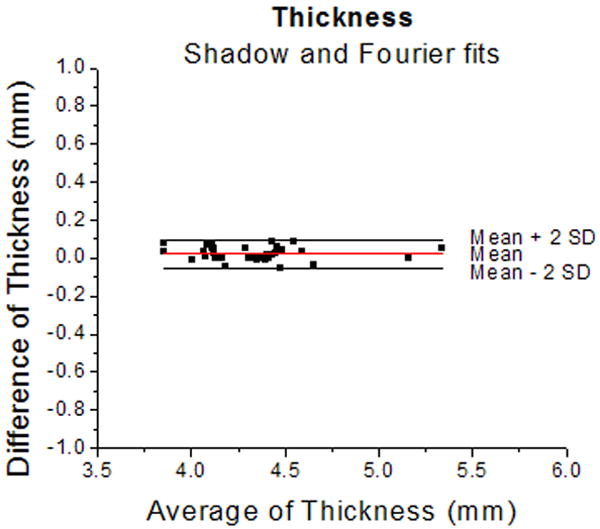
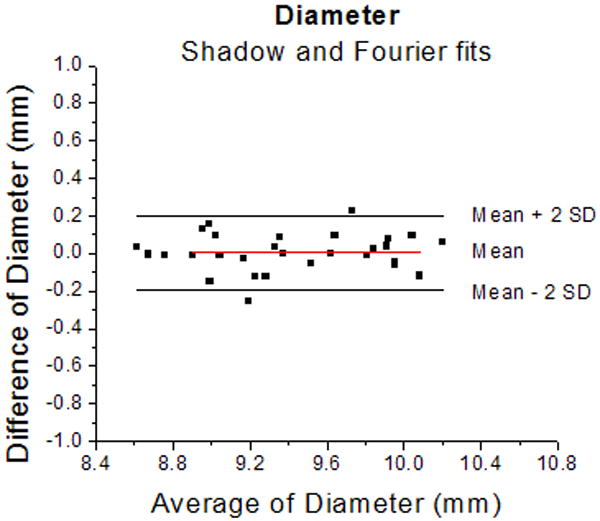
Bland-Altman plots for thickness (4a) and diameter (4b) of the lens measured from shadow-photogrammetric images and from Fourier function fits. Most measurements were within 2 standard deviations of the mean measurement error. The mean measurement error was 0.02±0.04 mm for the thickness and 0.01±0.1 mm for the diameter. These results indicate that measurements from both methods are the same.

Table 1 lists the age-dependent Fourier coefficients. The root-mean-squared-error (rmse) of the age-dependent fit for the 30 lenses was 205 μm. Figure 5 shows the Fourier model for lenses aged 20, 40 and 60 years. Figure 6 shows the model superimposed on lenses of various ages.

Table 1.

Fourier coefficients of the age-dependent Fourier model, where A_n = A_n1 + A_n2 × Age.

Fourier Coefficient	An1	An2
A0	2.6466	812.11E-5
A1	0.2246	170.62E-5
A2	-0.97938	-297.37E-5
A3	0.010573	-34.901E-5
A4	0.37993	-26.276E-5
A5	-0.032321	1.6647E-5
A6	-0.16846	69.192E-5
A7	0.027934	-9.5571E-5
A8	0.066522	-42.251E-5
A9	-0.014232	1.7295E-5
A10	-0.021375	18.638E-5

Figure 5.

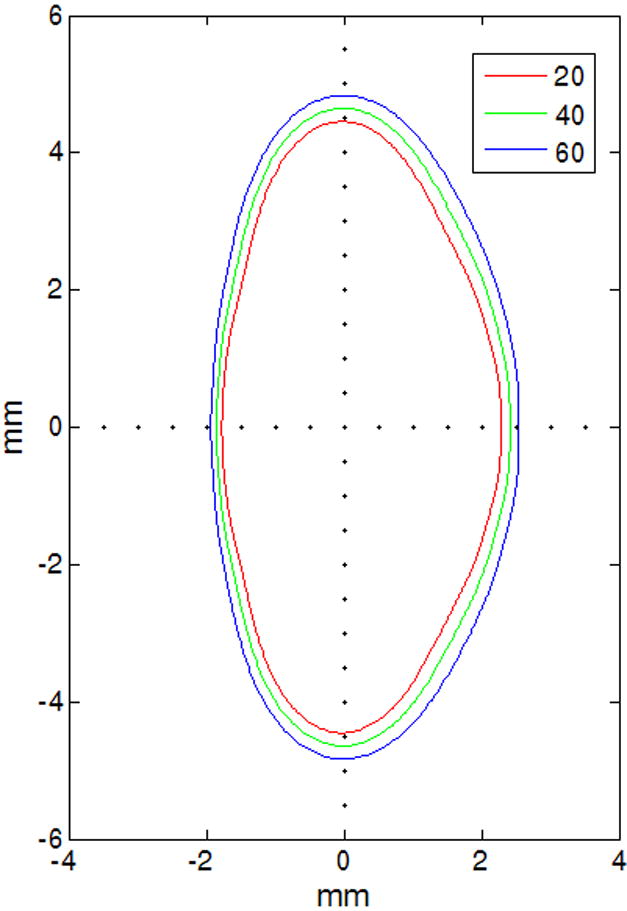
Age-dependent Fourier model of 20 (red), 40 (green) and 60 (blue) year-old lenses

Figure 6.

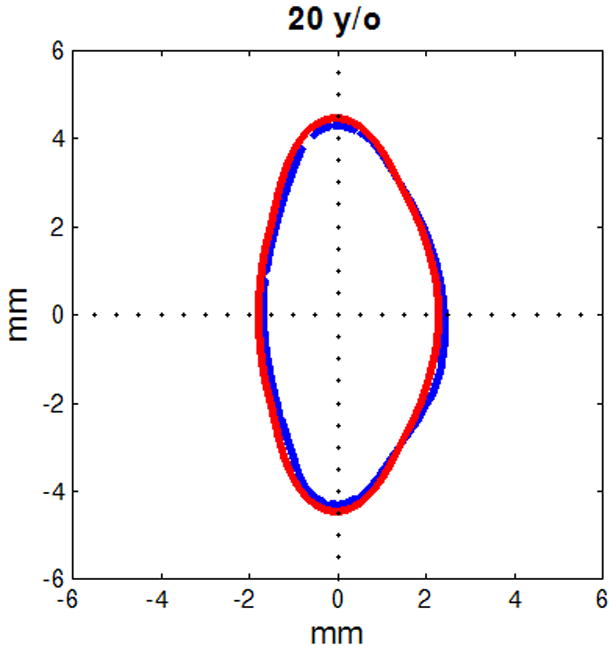
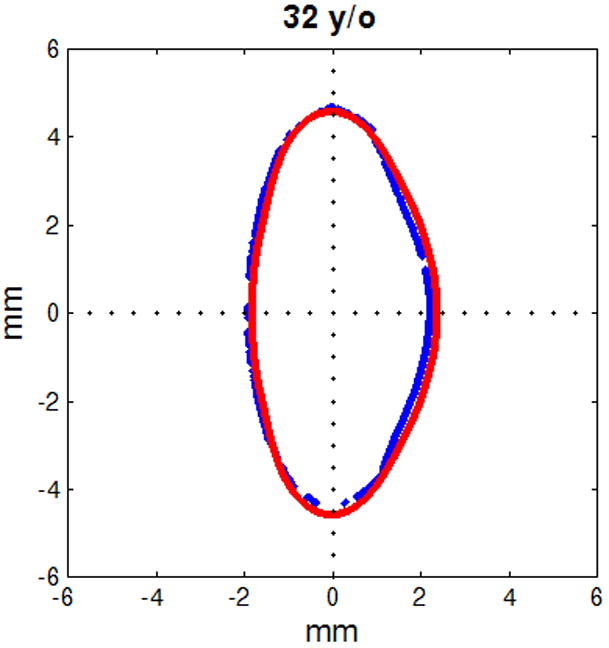
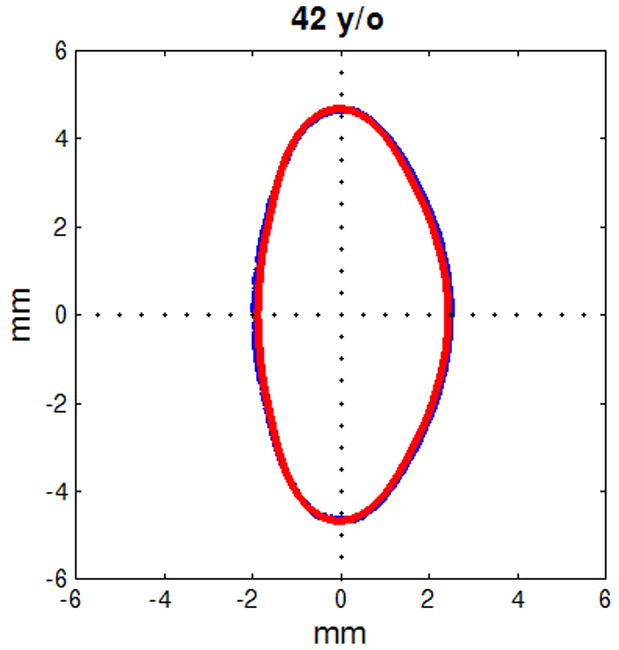
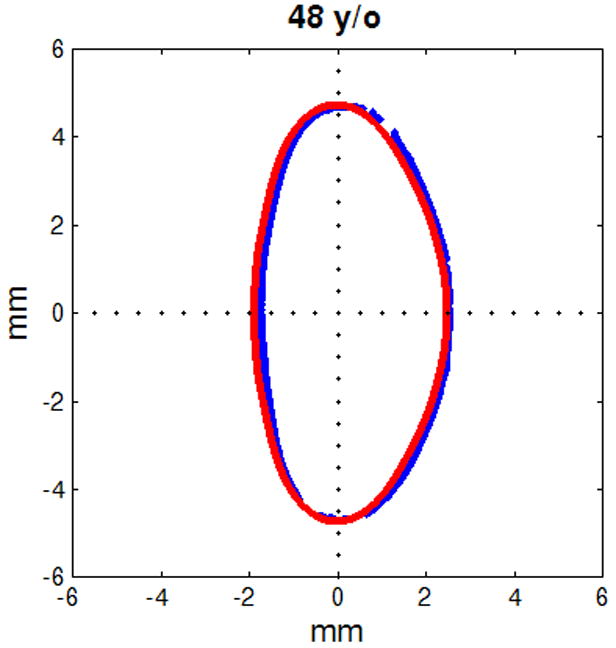
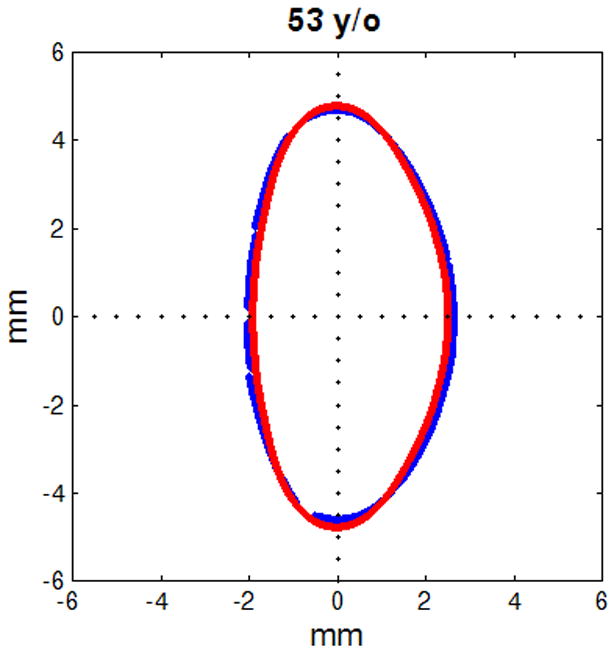
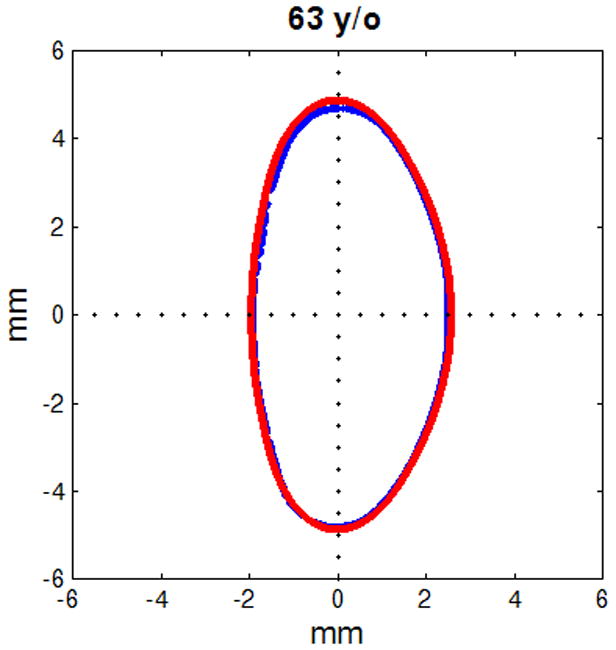
Figure shows raw lens contours (blue) of ages 20 (a), 32 (b), 42 (c), 48 (d), 53 (e) and 63 (f) years on which the corresponding shape obtained from the age-dependent Fourier lens model is superimposed (red).

4. Discussion

In this study, shapes of 30 explanted human crystalline lenses were recorded using a shadow-photogrammetric system. These lenses were from cadaver eyes, where the vertical and horizontal meridians were unknown and therefore the lens was assumed to be rotationally symmetric. Profiles of these lenses were extracted from the images and corrected for angular and centration misalignments. The corrected profiles were individually fit to a 10^th-order Fourier series of cosine functions for lens biometry. The corrected profiles were also re-sampled and simultaneously fit to a 10^th-order age-dependent Fourier series model to obtain the age-dependent Fourier amplitudes. Lens shapes for lenses aged 20, 40 and 60 were plotted using this age-dependent model (Figure 5). The Fourier series chosen did not include phase terms (i.e. shifts in θ) because the lens was assumed to be symmetric around the optical axis. We chose to use a 10^th-order Fourier series as our preliminary evaluations suggested that the rmse of the fits converged at order 10 and did not decrease significantly for higher orders (Figure 7). At 10^th-order, the average rmse for the 30 profiles was 37 ± 24 μm indicating a very good fit to actual data.

Figure 7.

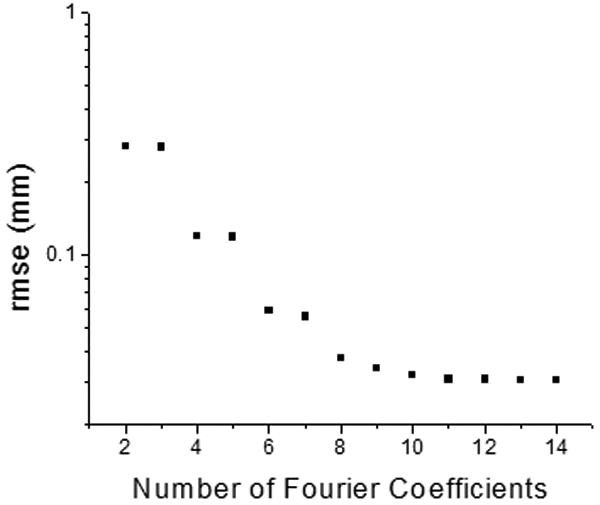
Graph shows effect of the number of coefficients included in the Fourier series on the RMSE fit of a lens surface. Overall RMSE values converged at order 10 and did not decrease significantly for orders higher than 10.

Thickness and diameter calculated from the fits displayed an age-dependent trend similar to that reported by Rosen, et al., (2006). Unlike the typical approach of statistically fitting coefficients to age values post model-fitting, our age-dependent model explicitly included age within the function (Equation 3). Thus, the model is a true age-dependent model of lens shape. This age-dependent model is applicable for lenses aged 20-60, being limited by the age-range of lenses available for this study. While it is known that certain geometrical parameters of the lens follow curvilinear relationships with age especially at the younger age ranges (Zadnik, Mutti, Fusaro & Adams 1995; Mutti, Zadnik, Fusaro, Friedman, Sholtz, & Adams 1998; Augusteyn 2007, Augusteyn 2008), due to the few number of samples available, linear age-dependence was assumed for the lens shape in the development of this model. A more sophisticated model (e.g. in which the Fourier amplitude coefficients have curvilinear or power relationship with age) can be developed when greater number of lenses and especially younger lenses become available.

The cosine function-based model has some advantages over the polynomial models published earlier (Urs et al., 2009). In particular, the whole lens shape can be modeled with one mathematical function. In addition the lens profile, as well as the derivative of the whole lens profile is continuous, with zero slopes at the poles.

Therefore, of the five compulsory requirements listed by Chien et al., (2003) the age-dependent Fourier model of the present study satisfies the first two compulsory requirements.

The third and fourth requirements which state that the equator should coincide with the X-axis and that the slope should be vertical at the equator is not precisely satisfied by this model. However, this requirement is not strictly compulsory for numerical modeling such as finite element or optical modeling as these techniques are invariant with translation. Further, since the function is based on cosine functions on a polar coordinate system, analytically, it can be shown that there are two points on the curve where the slope is vertical when converted back to Cartesian coordinates. In the present models, these points are very close to the X-axis. Since by most definitions, the line passing through these two points is the equator, if required, the curve can be translated (very slightly) to place the equator on the X-axis. This minor translation will render the model's compliance with the third and fourth requirements.

The fifth requirement, which states that the surface slope should decrease monotonically as distance from the axis increases, is only satisfied for lenses aged 43 to 59. However, there is evidence that the lens profile may not always obey the positive Gaussian curvature condition. For example Zeeman (1908) showed that the lens profile may be locally concave in the mid-periphery of the posterior surface. While the preparation method might account for some of these observations, forcing positive Gaussian curvature on models that intend to fit all possible lens profiles may render it less general and valid. Therefore, depending on the lens sample, the ‘compulsory’ fifth requirement of Chien et al., (2003) may not necessarily be considered compulsory.

This model also does not meet one desirable condition for optical modeling which is that the rate of change of the radius of curvature with respect to distance from the axis should be gentle at least in the pole regions. The relatively erratic behavior of local radii of curvature (which can be calculated using the first and second derivatives) might be anticipated from this model as it included higher-order (i.e. frequency) series.

The primary purpose of this model is to provide an age-dependent contour of the zero-order lens shape. This model could then be used to facilitate the development of other mathematical models for specific purposes. To illustrate this application, the central 6 mm of the raw lens contour obtained from shadow-photogrammetric images and that of the contour obtained from the age-dependent Fourier model were fit to conic functions. The radii of curvature obtained from the fits were analyzed with a two-sample t-test, which revealed that the datasets acquired from the two methods were not significantly different at the 0.05 significance level (p=0.96 for posterior radius of curvature and p=0.58 for anterior radius of curvature). The age-dependency of the radii of curvature was also analyzed (Figure 8). Linear regression yielded similar results for age-dependency for both posterior radius of curvature (0.05±0.1 mm/year for conic fits of raw lens shape and 0.04±7E-5 mm/year for conic fits of age-dependent Fourier lens model) and anterior radius of curvature (0.08±0.03 mm/year for conic fits of raw lens shape and 0.11±0.002 mm/year for conic fits of age-dependent Fourier lens model). Furthermore an F-test revealed that the linear regressions were not significantly different at the 0.05 significance level. (F=0.001, p=0.99 for posterior radius of curvature and F=0.02, p=0.98 for anterior radius of curvature). From this analysis it can be deduced that the lens shape as described by the age-dependent Fourier model is close to the actual lens shape, and as such, can be used to develop models for other specific purposes such as optical modeling.

Figure 8.

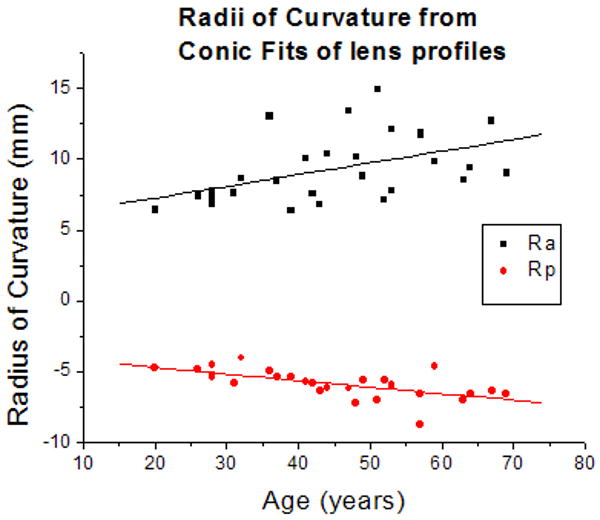
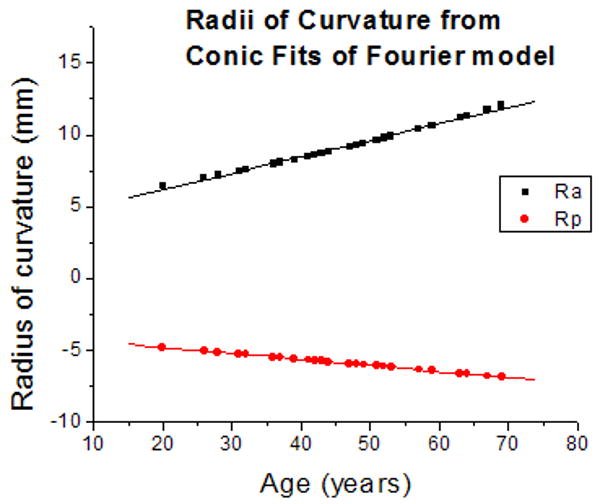
(8a) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of raw lens contours. Linear regression of curvatures as a function of age yielded Ra = 5.6 (±1.4) + 0.08 (±0.03) × Age (R = 0.47; p=0.009) and Rp = -3.81 (±0.51) - 0.05 (±0.01) × Age (R = -0.62; p=0.0002). (8b) Anterior (Ra) and Posterior (Rp) radii of curvature obtained from conic function fits of the age-dependent Fourier lens model. Linear regression of curvatures as a function of age yielded Ra = 3.9 (±0.1) + 0.11 (±0.002) × Age (R = 0.99; p<.0001) and Rp = -3.96 (±0.004) - 0.04 (±7E-5) × Age (R = -0.99; p<.0001).

One feature of this model is that it allows determination of the equatorial plane, the point at which the derivative is zero. This enables prediction of the aspect ratio (ratio of anterior to posterior thickness) of the lens. The model predicts a mean aspect ratio of 0.78 (±0.01) which is comparable to experimental data of 0.7 (±0.013) (Rosen, et al., 2006). This provides further evidence for the efficacy of the age-dependent Fourier model.

In this study we have presented an age-dependent mathematical model for the whole shape of the ex vivo human crystalline lens, using a single mathematical function. The method described can be used for individual lens biometry as it provides a mathematical method for correction of tilt and decentration. While only human lens shapes were tested, the approach should be applicable to all lenses that follow similar geometrical conditions. We believe that the shape obtained from the age-dependent Fourier model can be used to develop new models for other purposes such as mechanical modeling, to obtain reliable information about the accommodative mechanism of the human eye with particular advantage in the modeling of the equatorial region, or optical modeling.