Evolutionary tabu search strategies for the simultaneous registration of multiple atomic structures in cryo-EM reconstructions

Abstract

A structural characterization of multi-component cellular assemblies is essential to explain the mechanisms governing biological function. Macromolecular architectures may be revealed by integrating information collected from various biophysical sources - for instance, by intepreting low-resolution electron cryomicroscopy reconstructions in relation to the crystal structures of the constituent fragments. A simultaneous registration of multiple components is beneficial when building atomic models as it introduces additional spatial constraints to facilitate the native placement inside the map. The high-dimensional nature of such a search problem prevents the exhaustive exploration of all possible solutions. Here we introduce a novel method based on genetic algorithms, for the effcient exploration of the multi-body registration search space. The classic scheme of a genetic algorithm was enhanced with new genetic operations, tabu search and parallel computing strategies and validated on a benchmark of synthetic and experimental cryo-EM datasets. Even at a low level of detail, for example 35–40Å, the technique successfully registered multiple component biomolecules, measuring accuracies within one order of magnitude of the nominal resolutions of the maps. The algorithm was implemented using the Sculptor molecular modeling framework, which also provides a user-friendly graphical interface and enables an instantaneous, visual exploration of intermediate solutions.

1. Introduction

Fundamental biological processes such as DNA transcription, protein translation or cellular transport are efficiently carried out by macromolecular assemblies through the coordinated interaction of their constituent biomolecules [1]. Thousands of different macromolecules coexist at a given time inside a cell, but only few have a well-characterized molecular mechanism [2]. The structural description of such assemblies is crucial to explain their functional behaviors. X-ray crystallography, a main source of high-resolution information, solved structures of cellular assemblies such as the ribosome [3, 4] or RNA polymerase II [5]. However, multicomponent complexes are refractory to structural determination by crystallography due to their large size and intrinsic flexibility. Therefore, crystal structures are often available only for individual fragments.

Alternatively, electron cryomicroscopy (cryo-EM) is an imaging technique suitable for the structural characterization of large systems in near-native environments. Two-dimensional projections are collected from the sample in solution and used for the reconstruction of a 3D volumetric map [6]. Although the number of cryo-EM maps determined at high-resolutions (3–5Å) has considerably increased over the last decade, low-resolution maps are still commonly obtained for asymmetric or/and dynamic assemblies. Such cryo-EM reconstructions provide information about the overall shape of macromolecules, but their reduced level of detail prevents a direct atomic characterization. Yet, such low-resolution cryo-EM maps may be interpreted in relation to the crystal structure of component fragments through the application of multi-resolution modeling techniques.

Hybrid approaches are employed to integrate information from various biophysical sources, including, but not restricted to, X-ray crystallography and cryo-EM [7]. Atomic models of low-resolution cryo-EM maps may be generated by docking the atomic structure of the constituent biomolecules. Such models are often obtained by independently placing each fragment either using interactive molecular graphics software [8, 9] or by employing automatic techniques to optimize a goodness-of-fit measure. The optimization may be constrained to rigid-body transformations - translations and rotations [10, 11, 12, 13, 14, 15, 16] but can also include flexible deformations [17, 18].

Simultaneous registration of multiple subunits is beneficial to identify their native spatial organization inside the assembly. The additional information thus introduced provides spatial constraints that facilitate proper docking and prevent steric clashing. At low resolutions, independently fitted fragments may measure maximal correlations at the interior of the maps, where densities are high, but far from their correct docking position. Such spurious solutions are caused by the reduced interior detail of the reconstruction and/or due to the resolution heterogeneities [19]. By simultaneously registering all constituents, major steric clashes are limited as the correlation scores would be reduced for such cases.

Although valuable, such a simultaneous registration has a prohibitive computational cost. Identifying the optimal docking of one probe involves the exploration of six degrees of freedom. As the number of fragments increases, the dimensionality of the search space grows exponentially with a complexity of O(n^6N), where N is the number of registered pieces. Albeit an exhaustive exploration of all possible rotations and translations can be achieved for one component [10], such investigation is unfeasible as additional constituents are taken into account.

A possible approach to solve the multi-body registration problem, while overcoming the computational complexity of an exhaustive exploration, involves limiting the search to a portion of the space. Computational techniques were proposed following this strategy. Some iteratively refine one component at the time while either masking the others [11] or removing the occupied volumes of already docked fragments [13]. Other methods are inspired from crystallographic refinement, and assume that an overall correct placement is already known before performing a local simultaneous refinement in real [20, 21] or reciprocal [22] space. Recently, Lasker et. al. proposed a simultaneous global docking technique that discretizes the search space around centroid points [23].

Here we introduce a novel optimization technique for the simultaneous registration of multiple atomic structures into cryo-EM envelopes. Based on a genetic algorithm, MOSAEC (Multi-Object Simultaneous Alignment by Evolutionary Computing) makes no assumption about the scoring landscape and enables the multi-body global registration without restricting the search to a particular region. Genetic algorithms (GA) are heuristics inspired by evolutionary biology, commonly employed to solve high-dimensional optimization problems [24, 25, 26]. Darwin's concepts of natural selection and survival of the fittest [27] are introduced in an iterative scheme to enable the optimization of a scoring function. An abstract representation of the solution is generated by converting the variable to be optimized - here the rotation and translation of the constituents - into a linear form known as a chromosome. A population of such individuals adapts towards an optimal score following a process that mimics biological evolution. In MOSAEC, we adapted the classic scheme of a genetic algorithm to enhance the exploration of the search space. New genetic operators were introduced to preserve the genetic diversity of the population and were used in combination with parallel evolution of subpopulations. Moreover, the exploration of the complex search space was improved by including tabu regions - areas of the search space which are marked as local optima and thereby should not be further sampled.

In the following section, we will describe MOSAEC by first giving an overview of the method followed by the details of the implementation. Then, in the `Results' section, we present the testing and validation of the algorithm on a series of synthetic and experimental datasets. We conclude with a discussion of the results.

2. Material and methods

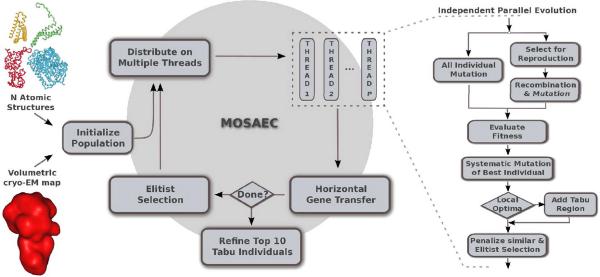
MOSAEC is an optimization technique derived from genetic algorithms (GAs) that explores and identifies optima in the highly dimensional search space of the multi-body registration problem. An overview of the procedure is given next (also summarized in figure 1) followed by a more detailed description of MOSAEC's implementation.

Figure 1.

Schematic rendering of MOSAEC. (Left) The atomic structure of the constituent fragments and the volumetric map of the entire assembly are used as input for the algorithm. (Center) Parallel computing strategies are implemented to exploit both the multi-core architecture of current computers and the ability of GAs to explore different paths in the search space. (Right) In each independent thread, MOSAEC follows the classic GA scheme which was enhanced with new genetic operators and tabu-search strategies

2.1. Genetic algorithms

GAs are computational methods that mimic biological evolution to optimize a scoring function. These algorithms integrate the concept of natural selection and survival of the fittest, in an iterative scheme that progressively improves the solution while exploring the parameter search space [24, 25, 26]. Evolutionary algorithms such as GAs can be distinguished from the other optimization techniques as they consider a population of solutions instead of just a single one at a given point in time. The individuals in this population are a linear representation of the parameters to be optimized (see section `Encoding of a candidate solution' on how the multi-body registration problem is represented). Each such individidual has a fitness value that indicates the optimality of the solution, i.e. the scoring evaluated for the encoded parameters. The algorithm starts with a set of individuals initialized through a random sampling of the search space. This population iteratively evolves under the influence of genetic operators while maximizing the fitness function, here the cross-correlation coefficient of the encoded atomic model and the target map. At each generation, a reproduction pool is selected with probabilities proportional to the fitness of the individuals. Recombination and mutation are applied to these solutions (sections `Recombination' and `Mutation'), as well as novel genetic operators (see description in the section `Other genetic operators'). Following mating, an improved population is selected based on an elitist reinsertion scheme detailed in section `Reinsertion', which ensures that better scoring individuals have higher chances to reproduce. Following this scheme that mimics mating, the scoring function is optimized progressively as better individuals are selected for the future generations. Also, tabu regions are introduced during reinsertion to prevent unnecessary explorations of regions marked as local optima (see section `Tabu search'). Moreover, MOSAEC exploits the stochastic nature of evolutionary strategies by allowing subpopulations to evolve in parallel (see description in section `Parallel evolution').

2.1.1. Encoding of a candidate solution

Each individual in the population represents an atomic model of the entire assembly, encoded as a linear string of real-valued genes representing translations and rotations of the constituent fragments. Individuals are composed of 4N genes […, x_i, y_i, z_i, r_i, …], i = 1..N where N is the number of components, x_i,|y_i, z_i represent the translation (in the space defined by the cryo-EM map) and r_i corresponds to an index in a list of rotational angles. This list provides a complete and uniform coverage of the 3D rotational space, reducing the search dimensionality (from 3 to 1) while at the same time avoiding gimbal lock problems. Each individual has associated a fitness value that quantifies the optimality of the solution they represent, i.e. the overlap between the multicomponent model and the cryo-EM map (see detailed description below).

The evolution starts with a population of n individuals randomly sampling the search space. In MOSAEC, this initial group of individuals is distributed over P threads that evolve independently in parallel. Without loss of generality, we consider in the following that P = 1 and treat the case P > 1 in a later section. For each generation, the first step consists in selecting the individuals that are allowed to reproduce following a linear ranking scheme [28] in which higher mating probabilities are given to fittest individuals. The selected solutions undergo a process that simulates mating in which genetic operators such as recombination and mutation are applied to generate a population of offspring.

2.1.2. Recombination

The crossover operator enables the recombination of two “parent” individuals to create one or two offspring. The new individual(s) inherit(s) genes from the parents following a stochastic process that swaps/alters them following different schemes. For instance, the one-point crossover generates two offspring by swapping parental genes at only one location:

$$\begin{array}{cc}\hfill \mathit{Parent}1:& \left[\dots x_i{y}_i{z}_i{r}_i\dots \right]\hfill \\ \hfill \mathit{Parent}2:& \left[\dots X_i{Y}_i{Z}_i{R}_i\dots \right]\hfill \\ \hfill \mathrm{Off}\mathrm{spring}1:& \left[\dots x_i{y}_i{Z}_i{R}_i\dots \right]\hfill \\ \hfill \mathrm{Off}\mathrm{spring}2:& \left[\dots X_i{Y}_i{z}_i{r}_i\dots \right]\hfill \end{array}$$

while other schemes use multiple crossover locations, e.g. two-point or uniform crossover. Schemes may also generate only one offspring by applying arithmetic operations such as averaging. The recombination through crossover is based on the building block hypothesis which considers that better individuals may be generated from the best partial solutions of previous generations. This process enables a guided and effcient exploration of the search space.

MOSAEC stochastically applies each of these schemes.

2.1.3. Mutation

This operator takes a single individual and alters its genes creating a contiguous individual. Similar to the crossover, different schemes have been defined and used in MOSAEC, some randomly modifying the genes while other schemes only introduce small variations. Although such adjustments often model a bell curve, in MOSAEC they follow a Cauchy distribution:

$$C(\alpha ,\beta ,x)=\beta ∕(\pi \cdot ({\beta }^2+{(x-\alpha )}^2))$$ (1)

where α is the statistical median and β > 0 corresponds to the half-width at half-maximum. Similar to the normal distributions, Cauchy distributions have high probabilities to create small variations, however it also introduces larger changes which help the algorithm to escape from local optima.

2.1.4. New genetic operators in MOSAEC

In addition to the recombination and mutation, MOSAEC also introduces two new genetic operators to enhance the exploration and exploitation of the search space. A systematic operator applies stochastic mutations to all individuals in the population. Although computationally expensive, this operator was shown in our tests to be helpful for the identification of a global optima. The second novel operator introduced in MOSAEC applies ten Cauchy mutations to each gene of the fittest individual, thereby accelerating the local refinement.

2.1.5. Reinsertion

Following mating, 2 * n + 1 new individuals are created: n from the reproduction pool via crossover and mutation, another n from the systematic mutation operator and eventually one from local search around the fittest individual. After evaluating their fitness, these individuals are merged with the n solutions of the original population, creating a pool of 3 * n + 1 individuals, from which only the best n will be selected for the next generation.

MOSAEC applies a reinsertion scheme based on the elitist selection with fitness penalties for highly similar individuals. Classic elitist schemes conserve the fittest individuals typically without enforcing preservation of the genetic diversity. Maintaining a heterogeneous population is essential when solving optimization problems, in particular for complex cases that show multiple local optima. In MOSAEC, highly similar individuals are penalized if their gene distance (square root mean deviation of the gene values) is below a threshold inducing a decrease in fitness value (default by 10%).

2.1.6. Tabu Search

The exploration of the search space was enhanced in MOSAEC by introducing a tabu search strategy to prevent premature convergence to local optima. Such strategies are heuristics that combine local searches with adaptive memory to store the solutions [29]. MOSAEC considers a region as tabu, if the fittest individual has essentially not improved over the past (T = 30) generations. When a tabu region is introduced, the fittest individual is preserved in the list of optima and the region around it is considered prohibited and not allowed further exploration. MOSAEC introduces by default small tabu regions to prevent that they contain more than one local optima. At the end of the run, the list of optima is examined and the top ten fittest individuals are refined.

2.2. Parallel evolution

Due to the stochastic nature of GAs, independent executions of the algorithm with the same initial population may result in the exploration of different regions of the search space. To take advantage of such a behavior, we modified the classic scheme of a GA to allow an independent evolution of subpopulations followed by a horizontal gene transfer. Identical subpopulations are distributed on different threads and are permitted to evolve for a small number of generations (100 generations by default). If our implementation is executed on a multi-core machine, such independent evolutions can run in parallel on different processing units. The user can choose the number of independent threads that will run in parallel, which typically should be the same as the number of cores available in the system. At the end of each cycle, the resulting subpopulations are merged and only the top individuals are selected (same number as in the initial subpopulation). This cycle is repeated until the total number of generations is achieved (Figure 1).

2.3. Fitness evaluation

Each individual in the population has a fitness value that quantifies the optimality of the solution it encodes. In MOSAEC, the fitness is assessed using the standard cross-correlation coefficient between the multicomponent atomic model and the volumetric map of the assembly as defined in eq. 2. ρ_calc and ρ_em are the direct space density distributions of the model and of the cryo-EM map, $\stackrel{‒}{\rho }$ and σ(ρ) are the average and, respectively, the standard deviation of a distribution ρ while T_i represent the transformation applied to the i^th, i = 1..N component (both rotation and translation included). The density distribution ρ_calc has identical dimensions as ρ_em and was obtained by projecting the atoms of the model onto a 3D lattice followed by a Gaussian blurring. Similar cross-correlation coefficients are employed by others, see [19] for a review.

$$CCC(\dots ,T_i,\dots )=\frac{\int ({\rho }_{\mathit{em}}\left(\mathbf{r}\right)-\overline{{\rho }_{\mathit{em}}})\cdot \left({\rho }_{\mathit{calc}}(\dots ,T_i,\dots ,\mathbf{r})-\overline{{\rho }_{\mathit{calc}}(\dots ,T_i,\dots )}\right)d^3\mathbf{r}}{\sigma \left({\rho }_{\mathit{em}}\right)\cdot \sigma \left({\rho }_{\mathit{calc}}(\dots ,T_i,\dots )\right)}$$ (2)

A coarse version of the cross-correlation coefficient was also implemented in MOSAEC to accelerate the execution. This score is computed following eq. 2 using coarse representations for ρ_calc and ρ_em. Topology-representing networks (TRN) were applied on the model to generate a simplified representation using feature points [30]. Such clustering techniques have been frequently employed in multi-resolution modeling of cryo-EM data [31, 17, 32, 9, 18]. These feature points were then projected onto the 3D lattice and low-pass filtered with a Gaussian kernel. Moreover, tri-linear interpolation can optionally be applied in MOSAEC to reduce the dimensions of the map ρ_em, for a further decrease in computational cost.

Fitness values in MOSAEC can be computed following the before mentioned forms of cross-correlation coefficients, whereby, according to our tests, even the coarse version is sufficient to identify global optima up to resolutions of 35–40Å. Note that contour enhancing filters, such as the Laplacian, were not applied in our validations, nor additional terms to penalize overlap between fragments.

3. Results

The performance of the method was assessed on multiple synthetic and experimental datasets. In this section, we present the results of this evaluation along with a study of the cross-correlation coefficient landscape in a simultaneous versus an independent registration.

3.1. Synthetic datasets

The benchmark for the validation of MOSAEC included simulated datasets of several biomolecular systems (Table 1). The component domains of these complexes were simultaneously docked into the volumetric map of the entire assembly, generated by Gaussian low-pass filtering to different resolutions. The best atomic model generated (measuring the highest cross-correlation coefficient during the run) was then compared with the native configuration of the assembly, as defined by the crystal structure.

Table 1.

Biomolecular systems used for the validation of MOSAEC

Systems	PDB ID	# Atoms	# Parts	Refs
Oxido-reductase	1NIC	7908	3	[34]
Catalase	1QQW	16048	4	[35]
IκBα/NF-κB Complex	1IKN	4767	4	[36]
Helicase	1XMV	13338	6	[37]
GroEL	1OEL	26929	7	[38]

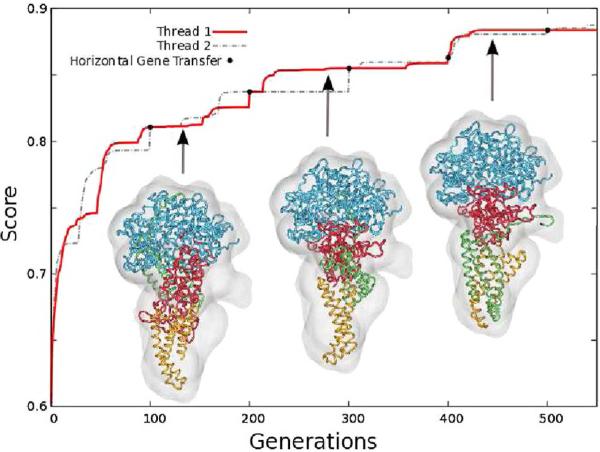
First, we present the progress of the best atomic model during a run for the pentamer Succinate Dehydrogenase (PDB ID 1NEK, [33]). This system was chosen to demonstrate the ability of the algorithm to explore a complex search space and to identify the global optima. Four fragments, of different size and shape, were registered into a 10Å-resolution synthetic map. Figure 2 shows the evolution of the best score over multiple iterations. Starting with a random distribution of the fragments, MOSAEC increases the scoring function within the first generations by placing all components inside the molecular envelope, but this placement is not optimal yet. As the evolution progresses further, the algorithm identifies the correct translation and rotation of each fragment, where often the large domains are found first, followed later by the smaller ones (see thumbnails in Figure 2). Identification of a native configuration is facilitated by the insertion of tabu regions as they enhance the investigation of unexplored areas within the search space.

Figure 2.

The evolution of the best score during a MOSAEC run in which four fragments were simultaneously docked into a 10Å resolution map of Succinate Dehydrogenase (PDB ID 1NEK).

Moreover, the independent parallel evolution of subpopulations, followed by horizontal gene transfer, also enhances the sampling as different paths are explored at the same time. Indeed, we can observe in Figure 2 that different scores and local optima are reached in the parallel evolution, for example between generations 100 and 200. However, the horizontal gene transfer ensures that the best optima are conserved and that the diversity of the population is maintained.

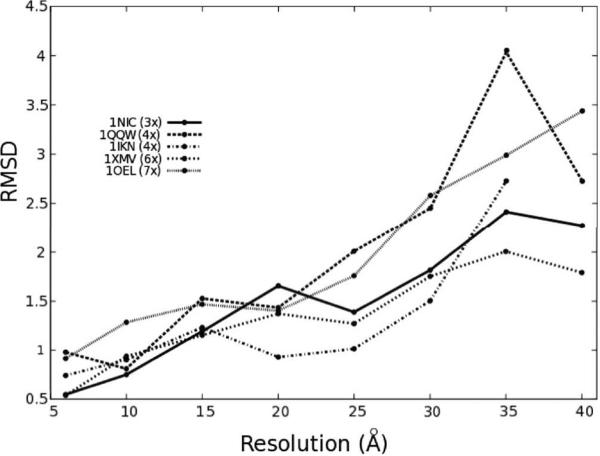
In a second step, we put MOSAEC to a stringent test to assess the performance of the algorithm at different resolutions. The biomolecular systems presented in Table 1 were used for validation at resolutions ranging between 6ÅA and 40Å. These systems have different complexities, some only require the registration of three fragments while others have up to seven components. At each run, the root mean squared deviation (RMSD), measured in Ångström (Å), between the best atomic model and the native configuration was measured and plotted in Figure 3. These tests indicated that MOSAEC was successful in simultaneously docking multiple fragments up to 40Å resolution, with accuracies within one order of magnitude of the nominal resolution of maps.

Figure 3.

The accuracy of MOSAEC estimated in synthetic test cases at different resolutions. Root mean squared deviations (RMSD) were measured between the model generated and the known solution (Values computed for all atoms and shown in Ångström (Å)).

3.2. Experimental datasets

The performance of the method was also assessed using experimental datasets. We performed a simultaneous registration of the bacterial ribosome and of the chaperonin GroEL.

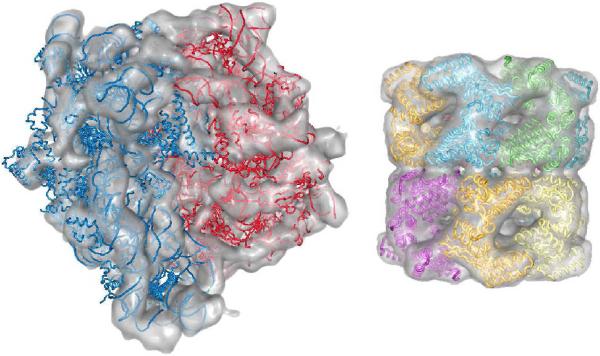
The ribosome is the macromolecular assembly responsible for the protein translation, that enables the synthesis of polypeptide chains using the genetic information of the messenger RNA [39, 40]. Ribosomes are complexes of RNAs and proteins, and are organized into two subunits [41]. We carried out the simultaneous docking of these two fragments (PDB IDs 1GIX, 1GIY, [41]) into the cryo-EM map of the assembly solved at 14 Å resolution (ID: emd-1005, [42]). MOSAEC successfully identified a native configuration (Figure 4), although only trace atoms were available for the crystal structures of the subunits. The model thus generated measures a 7.0Å RMSD from the one proposed by the authors of the map, but it improved the cross-correlation coefficient from 0.286 to 0.321 (measurement on alpha carbons and phosphates).

Figure 4.

Experimental benchmark: (Left) ribosome - two subunits docked into a 14Å-resolution map (emd-1005); (Right) chaperonin GroEL - 14 monomers fitted into the 11.5Å resolution map (emd-1080)

GroEL is a bacterial chaperonin that in association with co-chaperonin GroES is involved in the folding of proteins [43, 44, 45]. Our validation includes the cryo-EM map of GroEL alone as a double heptameric ring which displays a barrel-shape architecture. Fourteen monomers were simultaneously docked (PDB ID 1OEL [38]) into the 11.5Å resolution map (emd-1080,[46]). MOSAEC properly placed all these components, displaying a correlation coefficient of 0.947 with the experimental map (Figure 4).

3.3. Scoring landscape in simultaneous versus independent registration

Although MOSAEC introduces a novel optimization technique, the scoring function used to assess the model is the classic density-based cross-correlation coefficient (used in similar forms by other programs [47, 31, 11, 12, 13]). This goodness-of-fit measure is computed in MOSAEC using all component fragments in the model (see eq. 2). Yet, one can independently dock each fragment at a time using readily available techniques [31, 11, 12, 13] and assemble a complete model from the top scoring solutions. This model will not necessarily maximize eq. 2, but the additive measure:

$$CC{C}_{\Sigma }(T_1,\dots ,T_N)=\sum _{i=1}^{N}CCC\left(T_i\right)$$ (3)

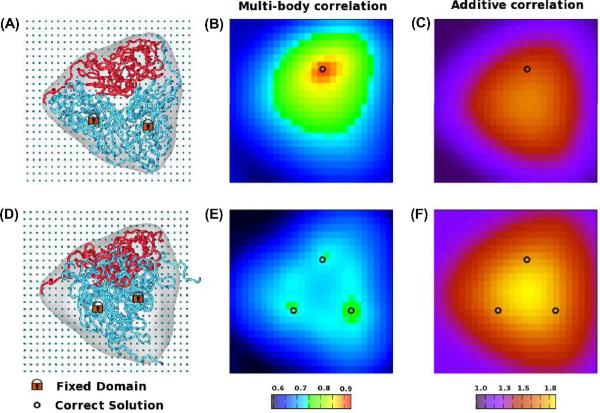
where T_i is the transformation that includes both translation and rotation of the i^th, i = 1..N fragment, and CCC(T_i) corresponds to the cross-correlation coefficient as defined in eq. 2. In the following, we investigate such a strategy and compare it with the simultaneous registration procedure proposed in MOSAEC. The discrepancies between the two approaches are shown by plotting the score landscape of eq. 2 and eq. 3 when fitting the three domains of homo-trimer oxido-reductase (PDB ID 1NIC) into a 15Å-resolution map. The high dimensionality of such a tri-body registration problem prevents the exhaustive exploration of all (18) degrees of freedom and, moreover, renders it difficult to visualize the results. Hence, here we show the landscape obtained when the position of only one fragment is variable within the plane known to contain the solution (rotations are all scanned), while the other two components are held fix at predefined locations inside the map. These locked components either occupy the configuration of the crystal structure (Figure 5A) or are placed at the center of the map (Figure 5C).

Figure 5.

Scoring landscape of the multi-body correlation CCC and of the additive measure CCC_Σ for the homo-trimer oxido-reductase (PDB ID 1NIC). The landscape shows, for each grid position, the best score measured over all rotations (9° angular step size) in a scenario in which one fragment (red tube in A and D) is mobile on the grid and the other units are held fixed (blue tube) either in the crystallographic configuration (A) or at the center of the map (D).

The first scenario, depicted in Figure 5A, represent a simple optimization problem in which only the configuration of one fragment must be identified given that the remaining domains are already properly docked inside the assembly. The multi-body correlation CCC (eq. 2) shows a prominent peak at the correct docking position (Figure 5B), yet the maxima of the additive correlation is observed far from this location (Figure 5C). These results indicate that optimization techniques may promptly identify the native placement of the fragment using the multi-body correlation, but will provide spurious solutions when scoring models with the additive measure CCC_∑.

Figure 5D shows a more difficult test in which the two fixed fragments occupy non-optimal docking positions, at the interior of the map. The multi-body correlation displays three peaks - one for each of the identical monomers in the crystal structure (Figure 5E). Due to the placement of the fixed components, the mobile fragment has three optimal scores instead of only one, as it can occupy either one of the three correct positions. When using this multi-body correlation score, optimization techniques are able to identify the placement of the monomer at one of the correct docking positions even if the rest of the components are arbitrarily placed inside the envelope.

On the other hand, CCC_∑ shows one global optima at the center of the map, far from the correct docking locations (Figure 5F). Moreover, this global optima scores higher than the best model in Figure 5C. Such landscape prevents the additive sum CCC_∑ from identifying the proper docking position of the fragments, creating models that show considerable overlap between constituents. To prevent such incorrect models, additive measures can be paired with terms that penalize the overlap between fragments [23]. Such multi-term scoring functions typically require an extra parametrization step to identify the weights of each element in the equation.

4. Discussion

In this paper, we described a method for the simultaneous registration of multiple component atomic structures into cryo-EM volumetric maps of biomolecular assemblies. MOSAEC is a population-based optimization technique designed to explore the intricate and high-dimensional search space of the multi-body docking problem. This approach is derived from genetic algorithms and enhanced with parallel computing and tabu search strategies to enable a better exploration of the scoring landscape.

MOSAEC successfully identified the spatial organization of constituent fragments within the cryo-EM envelope of the assembly. Our benchmark indicated that the algorithm is able to simultaneously register multiple component structures, identifying their placement and orientation with accuracies within one order of magnitude of the nominal resolution of the cryo-EM maps. Using the classic cross-correlation coefficient as a scoring function, such performance was observed for resolutions as low as 40Å. Maps with such low level of detail are typically beyond the reach of traditional docking methods that employ similar scores, but independently fit each component [48].

The successful registration was facilitated by the simultaneous docking of the constituent domains. The concurrent fitting of multiple structures indirectly introduces spatial constraints that guide the optimization towards identifying the correct configuration inside the complex. This additional information is especially beneficial at low-resolutions, where the volumetric maps have reduced interior detail and the boundaries between domains are ambiguous [19]. As opposed to other registration methods [11, 13, 23], these constraints are incorporated here solely by the shape of the scoring landscape and not by restraining the placement of the fragments to subregions of the search space.

Although the simultaneous registration favors the building of native atomic models, such an optimization procedure is computationally expensive. The calculation of the cross-correlation coefficient represents the most complex step of the approach, in particular for assemblies composed of a larger number of fragments, which require a more intensive sampling of the search space. To enable an efficient optimization, we employed a coarse scoring function (see Material and Methods section). This score allowed MOSAEC to successfully register the biomolecular systems included in the benchmark (see Results section) with runtimes ranging from minutes to a few hours. For example, the seven monomers of GroEL were simultaneously fitted into a 20Å-resolution volumetric map in 139 min² with an accuracy of 1.52Å RMSD from the known solution (700 individuals, 2000 generations and 4 parallel threads). These runtimes were obtained using the conservative default parameters of our software. However, tests indicated that smaller population sizes, a coarser representation of the data or of the score may still successfully identify the native configuration of the system, with up to a 36 fold speed up (3.8 min) and at the same time achieving an acceptable accuracy of 3.31Å RMSD (for a population size 100, 3.3 fold less feature vectors and no Gaussian blurring). Moreover, the deviations mentioned in this paragraph were computed before any optional refinement, which is available as a final step during a MOSAEC run in our software Sculptor.

Also, the optimization procedure was enhanced with parallel computing strategies accompanied by horizontal gene transfer. Such techniques were implemented both to exploit the multi-core architecture of current computers and to take advantage of the stochastic nature of genetic algorithms. Independent parallel evolutions are distributed on the available CPU cores to enable a more efficient exploration of the scoring landscape while investigating different pathways in the search space. The periodic horizontal gene transfer that follows each parallel evolution cycle ensures the conservation of the best individuals from each independent thread and the preservation of gene diversity in the population.

The previously mentioned outcomes were obtained using a default set of parameters that were estimated through empirical testing. The population size is the sole parameter that should be modified for each system to reflect the complexity of the assembly by setting its value proportional to the number of components to be registered (suggested scaling factor 100). All other parameters should otherwise be held constant as tests indicated that the algorithm is robust under changes in these values. Some parameters, such as the population size or the number of parallel threads, affect the sampling rate while others control the tabu search strategy influencing the amount of local optimization versus global search. The default values were selected to create a balance between sampling rate and runtime of the optimization, on one hand, and exploration and exploitation on the other.

The implementation of MOSAEC uses the C++ framework of our molecular modeling and visualization software Sculptor [9]. Sculptor provides a user-friendly graphical interface to set up the registration, to inspect intermediate results and to pause/restart/stop the optimization process when desired results were achieved. The interactive exploration of the intermediate results is possible in Sculptor due to the GA's characteristic to provide partial solutions to the problem during the optimization. Sculptor is freely available at http://sculptor.biomachina.org. In addition, we plan to develop a command-line version of the algorithm, to be distributed with the Situs program package.

To our knowledge MOSAEC is the first method to enable the simultaneous registration of multiple components on an essentially continuous search space. Without restricting the translations to a grid and with a rotational step size of just one degree, MOSAEC samples the scoring landscape in a continuous fashion making no assumptions about the shape of the system. The exploration of this search space is solely guided by the scoring function, a well established cross-correlation coefficient.