Sequential Learning Models for the Wisconsin Card Sort Task: Assessing Processes in Substance Dependent Individuals

Abstract

The Wisconsin Card Sort Task (WCST) is a commonly used neuropsychological test of executive or frontal lobe functioning. Traditional behavioral measures from the task (e.g., perseverative errors) distinguish healthy controls from clinical populations, but such measures can be difficult to interpret. In an attempt to supplement traditional measures, we developed and tested a family of sequential learning models that allowed for estimation of processes at the individual subject level in the WCST. Testing the model with substance dependent individuals and healthy controls, the model parameters significantly predicted group membership even when controlling for traditional behavioral measures from the task. Substance dependence was associated with a) slower attention shifting following punished trials and b) reduced decision consistency. Results suggest that model parameters may offer both incremental content validity and incremental predictive validity.

The Wisconsin Card Sort Task (WCST) is perhaps the most famous task used to measure inflexible persistence (Berg, 1948; Grant & Berg, 1948). The task involves sorting cards based on rules that periodically change. Patients with frontal lobe damage often make errors on this task, persistently using an old rule even when it is no longer valid (Demakis, 2003; Milner, 1963). Unfortunately, such errors occur in a variety of populations, including individuals with substance dependence (Bechara & Damasio, 2002), schizophrenia (Braff, Heaton, Kuck, & Cullum, 1991), Huntington’s disease (Zakzanis, 1998), and Alzheimer’s disease (Bondi, Monsch, Butters, & Salmon, 1993) to name a few. Although these errors are sometimes interpreted as the result of “frontal function” or “executive control” deficits, these errors may have multiple psychological bases, bases that vary across clinical populations. That is, rather than measuring a single, unitary construct, the WCST may measure multiple processes. The goal of the current research is to disentangle these processes through cognitive modeling, and furthermore, to identify the processes associated with substance dependence.

The idea that the WCST depends on multiple processes is certainly not new. The WCST has roots back to the University of Wisconsin Laboratory in the 1940’s, where monkeys were trained to make discriminations among abstract dimensions. It was speculated that the monkeys’ performance depended on such factors as the “rate of habit formation, rate of habit extinction, and response variability” (Zable & Harlow, 1946, p. 23). We propose a formal family of models that are related to Zable and Harlow’s speculation. A key difference, though, is that the current work allows for these multiple processes to be systematically measured. Such measurement has the potential to improve the diagnosticity and interpretation of the WCST.

There has been a recent surge of interest in modeling the WCST (Amos, 2000; Carter, 2000; Dahaene & Changeux, 1991; Kimberg & Farah, 1993; Levine & Prueitt, 1989; Monchi, Taylor, & Dagher, 2000; Rougier & O’Reilly, 2002). The goal in most cases has been to develop a model that is biologically inspired. Such models have been tested by attempting to simulate general qualitative patterns of data, for example, simulating more errors in one condition than another. The downside to these models, though, is that they have been too elaborate for precise parameter estimation at the individual subject level.

In contrast, the primary goal here is to use modeling to measure processes at the individual level, and so parameter estimation at that level is of paramount importance. This general approach, using cognitive modeling for measurement of underlying processes of individuals, is sometimes referred to as cognitive psychometrics (Batchelder, 1998). The family of models presented here were designed to improve parameter estimation in three ways. First, the models were designed to be simple enough for maximum likelihood estimation of parameters. Second, models were tractable enough to allow for fitting of individual subject data rather than just group data. Third, these models allowed for the fitting of complete, trial-by-trial choice data rather than just summary data (e.g., total perseverative errors). An additional benefit of the models considered here was that, because they were tractable enough for maximum likelihood estimation, they allowed for formal quantitative comparisons of model performance.

There are encouraging precedents for using these kinds of tractable cognitive models to better understand individual differences. For example, such models have been used to estimate individual performance in the Iowa Gambling Task (Busemeyer & Stout, 2002), the Balloon Analog Risk Task (Wallsten, Pleskac, & Lejuez, 2005), and the Go-No-Go Task (Yechiam et al., 2006; also see Neufeld, 2007). However, there is no currently published research using cognitive modeling in this way for the WCST. The WCST has been used in clinical psychology and neuropsychology for several decades and it continues to be popular (Butler, Retzlaff, & Vanderploeg, 1991; Rabin, Barr, & Burton, 2005). Thus, a tractable cognitive model of the WCST would be a novel and potentially powerful tool.

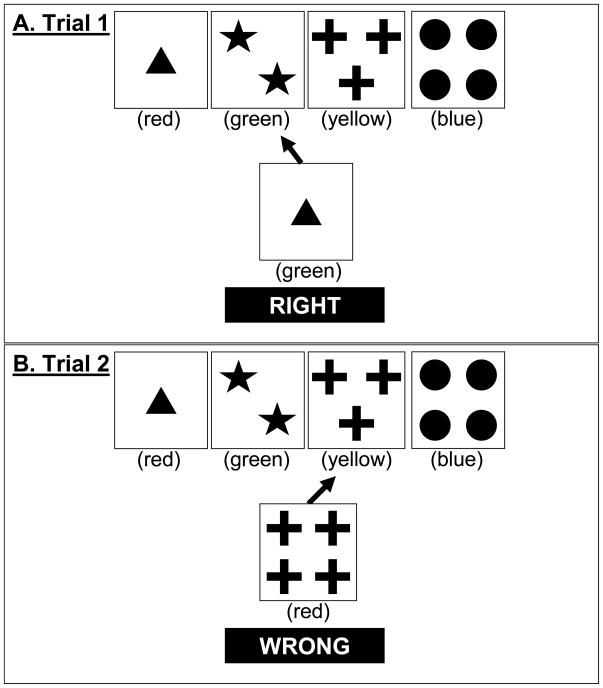
We developed a family of models for one of the most common versions of the WCST, the Heaton version (Heaton, Chelune, Talley, Kay, & Curtiss, 1993), though these models could conceivably be adapted to other versions as well (e.g., Nelson, 1976). In the Heaton version, participants sort cards that vary in terms of the color, form, and number of objects on them. Each card can be sorted into one of 4 key cards (shown at the top of Figure 1A). For example, as shown in Figure 1A, a participant is given a single green triangle and decides to sort it with the key card that has two green stars.

Figure 1.

Examples of trials in the Wisconsin Card Sort Task. Arrows represent choices made by a hypothetical participant.

The instructions are deliberately vague. Participants are told to match the cards but not how. They are only told “right” or “wrong” after each choice. The correct sorting rule is either color, form, or number on any given trial. The rule starts out as color, but importantly, after 10 consecutive matches by color, the rule changes without warning. Participants sometimes persist on the old rule after this happens, and this is referred to as a perseverative error. The task ends after completing six rules (getting 10 consecutive correct within a rule) or 128 trials, whichever comes first. In addition to perseverative errors, other common scoring measures include nonperseverative errors, categories completed, and failure to maintain set. A nonperseverative error is any error that does not appear perseverative (there are complex rules for scoring perseverative and nonperseverative errors; see Heaton et al., 1993). Categories completed are the number of rules completed, with a maximum of 6. Failure to maintain set is scored as the total number of errors that occur within a rule after at least 5 consecutive correct responses.

Such standard scoring measures can be useful. For example, in patient populations, the measures predict functioning in everyday life, such as occupational status (Kibby, Schmitter-Edgecombe, & Long, 1998) and independent living (Little, Templer, Persel, & Ashley, 1996). Standard scoring measures also predict abnormal behavior, such as confabulation (Burgess, Alderman, Evans, Emslie, & Wilson, 1998).

However, the standard scoring measures are sometimes difficult to interpret because it is unclear what kinds of processes they represent. For example, Categories Completed has no clear process interpretation. Even the interpretation of perseverative errors is ambiguous; what is scored as a perseverative error can result from a failure to shift attention after an error, a failure to preserve attention after correct feedback, or occasionally even a random response. Next, we present a family of sequential learning models that encourage process oriented interpretations of the WCST. Then, we consider how substance dependence might be related to model parameters.

The Family of Models Considered

Common Characteristics of the Models

Overview

In the WCST, participants must shift attention across various possible sorting rules. Though participants may occasionally use complicated conjunctive rules or exceptions, simple categorization strategies appear to be more common (Martin & Caramazza, 1980). Because of this, all models considered here involve shifting attention weights across simple rules, rules for matching on the basis of color, form, or number.

Various candidate mechanisms were considered across a family of 12 models. The performance of these models was compared so as to allow the data to inform the selection of the most important mechanisms. For each model, the set of free parameters was estimated separately for each subject. Free parameters varied across subjects, not across trials within subjects.

All models included a free parameter r, which represents how quickly attention weights change in response to rewarding feedback (i.e., “RIGHT”). Some models also included up to 3 additional free parameters. The p parameter represents how quickly attention weights change in response to punishing feedback (i.e., “WRONG”). The d parameter represents decision or choice consistency. Finally, the f parameter represents attentional focusing, which matters for trials with ambiguous feedback. ¹

Attention Weight Vector

The behavior of all models depends on the relative attention devoted to color, form, and number on any given trial. An attention weight vector, a_t, represents the weight given to each of these dimensions on trial t. A simplifying assumption is that attention weights start evenly divided among the dimensions on the first trial (t=1):

$${\mathbf{a}}_1=\left[\begin{array}{c}.33\\ .33\\ .33\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (1)

The elements of vector a_t always sum to 1, so that as attention to one dimension increases, attention to other dimensions tends to decrease. The value of a changes across trials, with the rate of change being determined by the free parameters in the model.

Attention Change

To implement changes of attention, the attention weight vector on the next trial, a_t+1, is a weighted average of the attention weight vector of the current trial, a_t, and a feedback signal vector from the current trial, s_t. Consider the example displayed in Figure 1A for Trial 1. The participant chooses the 2^nd pile and is told “right” (i.e., correct). This feedback implies that color is the current correct dimension to sort by because only the color of the sorted card matches any dimension of the key card. Therefore, the signal s_t indicates that attention should move toward 1 for color and toward 0 for the other dimensions. For this particular example:

$${\mathbf{s}}_t=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (2)

To define s_t more generally, let us first define another vector m_t,k, which is a 3 × 1 matching vector whose values depend on the match between the card that must be sorted on trial t and the pile k in which it is eventually placed. The i-th element of m_t,k, denoted m_t,k,i, has a value of 1 if the card that must be sorted matches the pile in which it is eventually placed on dimension i, and a value of 0 otherwise. Whenever the feedback is “right” and unambiguous (consistent with one and only one dimension being the correct dimension to sort by), the feedback signal is defined as:

$${\mathbf{s}}_t\mid \begin{array}{c}\text{unambiguously}\\ \text{rewarded}\end{array}={\mathbf{m}}_{t,k}$$ (3)

Whenever feedback is wrong and unambiguous:

$${\mathbf{s}}_t\mid \begin{array}{c}\text{unambiguously}\\ \text{punished}\end{array}=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]-{\mathbf{m}}_{t,k}$$ (4)

For example, if pile 1 were selected on trial 1, the feedback would be “wrong,” and based on Equation 4:

$$\mathbf{s}=\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (5)

Equations for ambiguous feedback signals are described later.

How rapidly attention changes toward feedback signals is determined by a free parameter r for rewarded trials. When trial t is rewarded (i.e., “right” feedback), attention on the next trial is:

$${\mathbf{a}}_{t+1}\mid {\text{rewarded}}_t=(1-r){\mathbf{a}}_t+r\mathbf{s}$$ (6)

Parameter r ranges from 0 to 1. When r = 0, there is no attention shifting, and when r = 1, there is complete attention shifting toward the feedback signal. In the example in Figure 1, if r = .1, attention would shift only slightly toward color from trial 1 to trial 2. Using Equation 6, attention weights on trial 2 would be as follows:

$${\mathbf{a}}_2=(1-.1)\left[\begin{array}{c}.33\\ .33\\ .33\end{array}\right]+.1\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}.40\\ .30\\ .30\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (7)

Mechanisms That Differ Across Models

Differential Attention Shifting for Reward and Punishment

Attention updating may occur at different rates for rewarded and punished trials due to different updating mechanisms. Distinct updating mechanisms would be consistent with neuroimaging studies that have found distinct neural correlates of rewarded and punished choices in the WCST (Monchi, Petrides, Petre, Worsley, & Dagher, 2001; Monchi, Petrides, Doyon, Postuma, Worsley, & Dagher, 2004). Neural regions specifically correlated with wrong choices include the anterior cingulate, as well as a cortical basal ganglia loop originating in the ventrolateral prefrontal cortex. In contrast, the dorsolateral prefrontal cortex has been associated with both right and wrong feedback (also see Mansouri, Matsumoto, & Tanaka, 2006).

Attention shifting may also be distinctive following punishment because such shifting may be more closely related to inhibitory functioning. After attention has built up toward a particular dimension, and then new feedback suggests that this dimension is wrong, attention to this dimension may need to be inhibited to support switching attention to a new dimension. For these reasons, attention shifting following punishment may occur at a different rate than attention shifting following reward.

In the family of models considered, attention change after punishment works in the same manner as that after reward (see Equation 6), but with a separate parameter p to allow for the possibility of different shifting rates. When trial t is punished, attention on the next trial is:

$${\mathbf{a}}_{t+1}\mid {\text{punished}}_t=(1-p){\mathbf{a}}_t+p\mathbf{s}$$ (8)

Like the r parameter, the p parameter ranges from 0 to 1, with higher values tending to lead to better task performance. To examine the possibility that there are different attention shifting rates for reward and punishment, models where r and p were allowed to vary freely were compared with models that constrained r and p to be equal.

Individual differences in decision-consistency

Individuals may vary in how much their decisions are consistent with their attention weights. That is, some individuals may be more deterministic while others may be more random or haphazard in terms of how their decisions are aligned with attention weights. This “consistency” mechanism is typical in models of decision-making tasks, such as the Iowa Gambling Task and the Balloon Analog Risk Task (Busemeyer & Stout, 2002; Wallsten et al., respectively). However, it is unclear whether decision-consistency will play a major role in the WCST, a task usually thought to measure executive function rather than decision-making.

To formalize decision-consistency, the predicted probability of choosing a particular pile is influenced by a decision-consistency parameter, d. Specifically, the predicted probability (P) of choosing pile k on trial t was defined as:

$${\text{P}}_{t,k}=\frac{{\mathbf{m}}_{t,k}^{\prime }{\mathbf{a}}_t^d}{{\displaystyle \sum _{j=1}^4}\left({\mathbf{m}}_{t,j}^{\prime }{\mathbf{a}}_t^d\right)},$$ (9)

where m_t,k denotes the match between the card that must be sorted on trial t and the pile k in which it could be placed (m′ simply denotes the transpose of m), and ${\mathbf{a}}_t^d$ is a column vector with the element for each dimension i raised to the d power ( $a_{t,i}^d$). In the denominator of Equation 9, j ranges from 1 to 4 for the summation across all 4 piles. Dividing by the summation of piles forces P_t,k to add up to 1 across piles.

When d=1, the probability of choosing each pile is simply the sum of the elements of the attention vector that match that pile. For example, when d=1, the predicted probability of sorting to the far left pile in Figure 1A would be 2/3 because the card to be sorted matches that pile both in form (triangle) and number (one), and attention is currently 1/3 to form and 1/3 to number. As d becomes higher than 1, choices become more deterministic and constrained by attention. For example, when d=2, the predicted probability of sorting to the far left pile in Figure 1A would be .89. As d becomes lower, choices become more random and less consistent with attention. For example, when d=0.5, the predicted probability of sorting to the far left pile would be .59.

To assess the importance of the decision-consistency mechanism for explaining individual differences, models where d was free to vary were compared with models where d was constrained to equal 1. For parameter estimation purposes, when d was allowed to vary, it was constrained such that .01 ≤ d ≤ 5.

Attentional Focus

To illustrate the relevance of attentional focus, consider the example of Trial 2 in Figure 1B where the participant sorts on the basis of matching form but is told “wrong.” The feedback is ambiguous because either color or number could be the proper dimension to sort by. In ambiguous cases like this, the feedback signal s depends on a free parameter f that represents how focused or narrow attention is. As f approaches 0, representing no focus, the feedback signal is split evenly among all possible correct dimensions. In this example:

$$asf\to 0,\mathbf{s}\to \left[\begin{array}{c}.5\\ 0\\ .5\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (10)

In this particular example, the ambiguity is not a drastic deterrent to learning, but in other situations, ambiguity could lead to increased error rates. Consider a case where a participant has correctly matched on the basis of color for several trials, and so attention to color has increased up to .9. Then, color is correctly chosen again, but this time the match is ambiguous, being consistent with both color and number. A low value of f will yield a feedback signal indicating that attention should be split between color and number. This signal would reduce attention to color for the next trial even though color is the correct dimension. Thus, a low f can increase the likelihood of errors after ambiguous feedback.

Higher values of f can avoid this problem. If f=1, s is split proportionally to current attention weights. For example, consider a case where current attention is weighted .60 to color, .20 to form, and .20 to number, and as in Figure 1B, the feedback is consistent with either color or number being the correct rule. In this particular example:

$$iff=1,\mathbf{s}=\left[\begin{array}{c}.75\\ 0\\ .25\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (11)

As f approaches infinity, the feedback signals the maximum attention element that is consistent with the feedback. Considering this same example:

$$asf\to \infty ,\mathbf{s}\to \left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\begin{array}{c}\mathit{color}\\ \mathit{form}\\ \mathit{number}\end{array}$$ (12)

More generally, the feedback signal for correct trial t on dimension i is:

$$s_{t,i}\mid \text{rewarded}=\frac{m_{t,k,i}{a}_{t,i}^f}{{\displaystyle \sum _{h=1}^3}\left(m_{t,k,h}{a}_{t,h}^f\right)}$$ (13)

For incorrect trials, the signal is:

$$s_{t,i}\mid \text{punished}=\frac{\left(1-m_{t,k,i}\right)a_{t,i}^f}{{\displaystyle \sum _{h=1}^3}\left[\left(1-m_{t,k,h}\right)a_{t,h}^f\right]}$$ (14)

where k is the chosen pile, m_t,k,i is the element of the match vector m_t,k at dimension i, and likewise, a_t,i is the element of attention vector a_t at dimension i. In the denominators of Equations 13 and 14, h ranges from 1 to 3 for the summation of all 3 dimensions. Dividing by the summation of dimensions forces the feedback signal to add up to 1 across dimensions. Note that Equations 13 and 14 simplify to Equations 3 and 4 when the feedback is unambiguous, and so the value of f is only relevant for trials with ambiguous feedback. For estimation purposes, the f parameter was constrained such that 0.01 ≤ f ≤ 5.

Attentional focusing mechanisms have been used in other models of the WCST (e.g., Amos, 2000). The potential value of this attentional focus mechanism is that, in addition to having feedback influence shifts of attention, the mechanism allows attention to influence the interpretation of feedback. To examine the importance of attentional focus in the WCST, three types of models were compared: Models where f⃗0 (no attentional focusing), where f=1 (focusing proportional to the attentional vector a; fixed across individuals), and where f was free to vary (attentional focusing differs across individuals).²

Model Comparison

The three model mechanisms (differential attention shifting for reward and punishment, different decision-consistencies across individuals, and attentional focus) were examined by considering different model constraints. These model constraints led to a factorial design of 12 models: p free vs. p=r crossed with d free vs. d=1 crossed with f free vs. f⃗0vs. f=1. In addition to the family of 12 models, a baseline model with zero free parameters was considered as a point of comparison. The baseline model assumed no attention shifting, just simple proportional matching. It predicted that the probability of choosing a particular pile was simply the number of dimensions matching between the pile and the current card, divided by 3. The baseline model was equivalent to having constraints r=0, p=0, and d=1, with f being irrelevant.

Modeling Substance Dependent Individuals

There are many possible reasons that substance dependent individuals (SDI) may have different estimated model parameters than healthy controls. We consider two prominent possibilities: first, that SDI will show a lower p parameter due to inattention to error signals and/or inhibitory failures, and second, that SDI will show a lower d parameter due to more haphazard decision-making.

Substance users often show decreased neural activity in regions specifically associated with errors. Anterior cingulate activation has been associated with the monitoring and prediction of errors in several tasks (e.g., Carter et al., 1998; 2000), including the WCST (Monchi et al., 2001, 2004). In attention shifting tasks, hypoactive anterior cingulate activation has been observed in substance users following errors (Kübler, Murphy, & Garavan, 2005; for a review, see Garavan & Stout, 2005). In addition to anterior cingulate activation, error responses (but not correct responses) on the WCST have been associated with a ventral lateral prefrontal cortex/striatal loop (Monchi et al., 2001, 2004). Loops between the frontal cortex and basal-ganglia structures are altered through substance use (Volkow et al., 1993; Willuhn, Sun, & Steiner, 2003).

A related finding is that substance users often fail to inhibit irrelevant information. In the WCST, inhibition would be most important in cases where a person had built up attention to a particular dimension (e.g., color), but then the feedback started to indicate that that dimension was wrong. Failure to inhibit this no longer relevant dimension would be associated with slower attention shifting following punished trials. A deficit in inhibiting irrelevant information has been observed in substance users, and specifically when performing switching tasks (Salo et al., 2005). Interestingly, an inhibitory deficit may be a precursor to drug use rather than the result of it, with poor inhibitory control at age 10–12 predicting substance use at age 19 (Tarter et al., 2003). Whatever the causal mechanism, though, the association between substance use and poor inhibitory control suggests that substance users may be slow to shift attention in response to punishing feedback.

These various findings can be summarized as two general patterns: substance use is associated with failures to fully use negative feedback and failures to inhibit previously relevant information. Both patterns would suggest that SDI will have a low p parameter relative to healthy controls.

Substance use is sometimes associated with random, inconsistent decisions on decision-making tasks. In the Iowa Gambling Task, substance users’ choices are less consistent with what they have learned on the task compared to the choices of healthy controls (Bishara et al., under review; Stout, Busemeyer, Lin, Grant, & Bonson, 2004). More generally, substance users’ behavior is often described as “impulsive” (see Jentsch & Taylor, 1999), though that word has several meanings (Evenden, 1999). Here, the interest is in the kind of impulsivity related to a lack of forethought that can lead to haphazard decisions. For example, substance users sometimes perform poorly due to rushed choices. This can occur even in tests of cognition not specifically intended to measure decision-making (Ersche, Clark, London, Robbins, & Sahakian, 2005). Therefore, substance users may make inconsistent decisions on the WCST, and thus display a lower d parameter.

Primary Questions

In this study, there were five questions of interest. First, in the family of models considered, which model would show the best quantitative fit to the data? This question was addressed primarily with the Bayesian Information Criterion, but also via nested comparisons with G². Second, how well can the quantitatively best fitting model reproduce qualitative patterns in the data? This question was addressed by using estimated model parameters to simulate WCST performance, and then compare simulated performance to actual performance of SDI and controls. Third, would the model parameters relate to substance dependence even when controlling for traditional behavioral measures, such as perseverative errors (i.e., would the model parameters have incremental predictive validity)? This question was addressed by using logistic regression to predict group membership, with behavioral measures entered as predictors first, and model parameters entered second. Fourth, how would substance dependence be related to individual model parameters? This question was addressed via separate logistic regressions for each model parameter. Finally, would different types of drug users show different patterns of parameter values? This exploratory question was addressed by comparing SDI whose drug of choice was alcohol to SDI whose drug of choice was a stimulant (e.g., cocaine, crack, and methamphetamine).

Method

Participants

Table 1 shows demographic and other information about participants. Substance Dependent Individuals (SDIs) were recruited while undergoing or after having completed inpatient treatment at the Mid-Eastern Council on Chemical Abuse in Iowa City (see Bechara et al., 2001; Bechara & Damasio, 2002; Bechara, Dolan, & Hinders, 2002). Among SDI, the drug of choice was alcohol for 16 participants, stimulants for 22 participants, and unclear for 1 participant.

Table 1.

Participant demographics

	N	% Female	Age	Education
Control	49	49.0	33.6 (10.9)	14.4 (2.2)
Substance Dependent	39	56.4	34.1 (10.3)	12.5 (1.8)
Stimulant	22	68.2	30.3 (7.2)	12.3 (1.5)
Alcohol	16	37.5	39.9 (11.6)	12.9 (2.2)

Note. For Age and Education, the mean is shown with standard deviation in parentheses. “Stimulant” and “Alcohol” are drug preference subsets of the Substance Dependent group. Note that one individual did not report drug preference.

The selection criteria for SDIs were: (1) meeting the DSM-IV criteria for substance dependence; (2) absence of psychosis; and (3) no documented head injury or seizure disorder. Normal control subjects had no history of mental retardation, learning disability, psychiatric disorder, substance abuse, or any systemic disease capable of affecting the central nervous system. The Structured Clinical Interview for DSM-IV (First, Spitzer, Gibbon, & Williams, 1997) was used to determine a diagnosis of substance dependence. The interview was administered by a trained PhD candidate in clinical psychology.

For 3 subjects in the SDI group, the WCST was ended prematurely, which would bias the standard behavioral measures to be low. Accordingly, those 3 subjects were excluded from all analyses that involved standard behavioral measures.

Procedure and Materials

Participants were given the manual administration of the WCST using the Heaton et al. (1993) version. SDIs were tested after a minimum period of 15 days of abstinence from any substance use. SDIs were paid for their participation in the study with gift certificates with an hourly rate identical to that earned by normal controls.

Model Fitting and Analyses

Maximum Likelihood Estimation was used to estimate parameters separately for each model and each participant (see Appendix for further details). There were 12 models in the family of models of interest, and they consisted of every combination of the mechanisms tested: two p constraints (free p & p=r) by two d constraints (free d & d=1) by three f constraints (free f, f⃗0, & f=1). To adjust for differences in the number of parameters used for each model, the Bayesian Information Criterion (BIC) was used (Schwarz, 1978; see Appendix for further details). The BIC is based on asymptotic principles from Bayesian model comparison. Smaller BICs indicate better model performance. BIC allows all models to be put on a comparable metric of model performance. This is important, because many pairs of models considered here are non-nested. BIC was also chosen because, compared to other complexity corrections (e.g., Akaike Information Criterion), BIC tends to favor models with fewer free parameters. Using only a small number of free parameters encourages more independence among parameters and more precise estimation of those parameters.

G² was also used to examine nested relationships, comparing all models to the baseline model. Additionally, to further test the model that had the smallest BIC, we compared that model to similar models via nested tests. The percentage of subjects where a parameter constraint led to a significant worsening of model fit was examined.

The best performing model was then used to simulate performance and compare it to actually observed performance. First, for each subject, the maximum likelihood parameter values were estimated from the observed data. Then, for each subject, the subjects’ parameter estimates and a₁ were used to generate choice probabilities for trial 1, then simulate a choice in accord with those probabilities, then update a₂ based on the simulated choice, and then start the process again using a₂ and parameter estimates to generate choice probabilities for the trial 2. This process was repeated until the simulated sequence of choices produced 6 categories completed or 128 trials. Note that these simulations relied on one-step-ahead predictions using simulated choices, not actually observed choices, from the previous step.

Each subject’s simulated sequence of choices was analyzed with four standard behavioral measures. Categories Completed and Perseverative Errors were examined because these two measures are commonly reported in the literature. However, these two measures tend to be strongly correlated, and so two other scores were included: Nonperseverative Errors and Set Failures. These latter two scores were chosen because they sometimes load on two distinct factors in factor analysis, and these two factors are distinct from a more dominant factor that includes both Categories Completed and Perseverative Errors (Greve, Ingram, & Bianchini, 1998). To reduce within-subject noise, simulations were repeated 1000 times for each subject, and the standard behavioral measures were averaged across these 1000 repetitions.

Using the best fitting model, maximum likelihood estimates of parameters for each individual participant were analyzed. Logistic regression was used to analyze the relationship between estimated model parameters and groups so as to allow for other variables to be controlled for. Because of extremely non-normal parameter distributions, the Goodman-Kruskal γ correlation was used to indicate effect size for the relationships between subject groups and parameters. Like the Pearson correlation, γ ranges from −1 to 1, and 0 indicates no association.

Results

Quantitative Model Fit

The family of 12 attention shifting models generally fit the data better than the baseline model did. Table 2 displays the mean BIC across subjects for each model. All 12 models of interest had a significantly smaller mean BIC than the baseline model, as shown by pairwise t-tests, all ps < .001. Because all 12 models of interest were nested within the baseline model, comparisons to the baseline model were also analyzed with G². G² was computed separately for each subject and each model of interest. Significant improvement of the model of interest over the baseline model was assessed using the chi-squared distribution and df equal to the number of free parameters in the model of interest (because the baseline model had 0 free parameters). These analyses confirmed that the models of interest generally outperformed the baseline model. All models of interest fit significantly better than the baseline model for 86 out of the 88 subjects. The two remaining subjects were outliers in that they were the only two subjects to complete 0 categories.

Table 2.

Mean BIC as a function of model constraints.

Model Constraints					Baseline Model
		f free	f = 0	f = 1
p free	d free	83.69	88.54	81.99	150.72
	d = 1	83.94	97.58	86.51
p = r	d free	84.39	88.95	82.79
	d = 1	82.83	95.66	86.10

Comparing the BICs of the models of interest, two patterns were particularly noticeable in Table 2. First, BIC was higher when f was constrained to be 0 than when it was constrained to be 1 or was free to vary. Second, BIC was higher when both f and d were constrained to 1, or when both were free to vary. However, when only one was free to vary, BIC tended to be smaller. Thus, constraining f to 0 tended to hurt model performance, but constraining f to 1 was benign so long as d was free to vary.

Overall, the model with the lowest mean BIC had f constrained to 1 but allowed r, p, and d to vary freely. This model fit significantly better than 9 out of the 11 other models of interest, ps < .01. This model was not significantly different from the two remaining models, ps > .20. For additional analyses, we focus on this best fitting model, and denote it as rpd1 to indicate that r, p, and d are free to vary, whereas f is fixed at 1.

Nested comparisons and G² were used at the subject level to further examine the performance of the rpd1 model. Using rpd1 as a point of reference, allowing f to vary freely failed to significantly improve the fit for 75% of the subjects (i.e., G² < 3.84, the critical value for a chi-squared distribution with 1 df). In contrast, constraining d to equal 1 significantly worsened the fit for 53% of the subjects. Constraining p to equal r significantly worsened the fit for 34% of the subjects. Overall, the nested comparisons supported constraining f to equal 1 and allowing d to vary freely for the majority of subjects, but the usefulness of allowing p to vary freely was less clear.

Finally, we considered a variant of the rpd1 model where the assumption of equal attention weights on trial 1 was relaxed. Two additional free parameters were used for the initial attention weight to color and form (with the weight to number being determined by 1 minus the sum of the other weights). This variant of the rpd1 model was not well supported by the fit statistics. This variant had a worse BIC than the original rpd1 model for 94% of subjects. Furthermore, in nested comparisons, the variant’s improvement in fit relative to the original model was nonsignificant (G²(2) < 5.99) for 87% of subjects. The simplifying assumption of equal attention weights on trial 1 may work well enough because the attention weight vector often changes rapidly after the first trial.

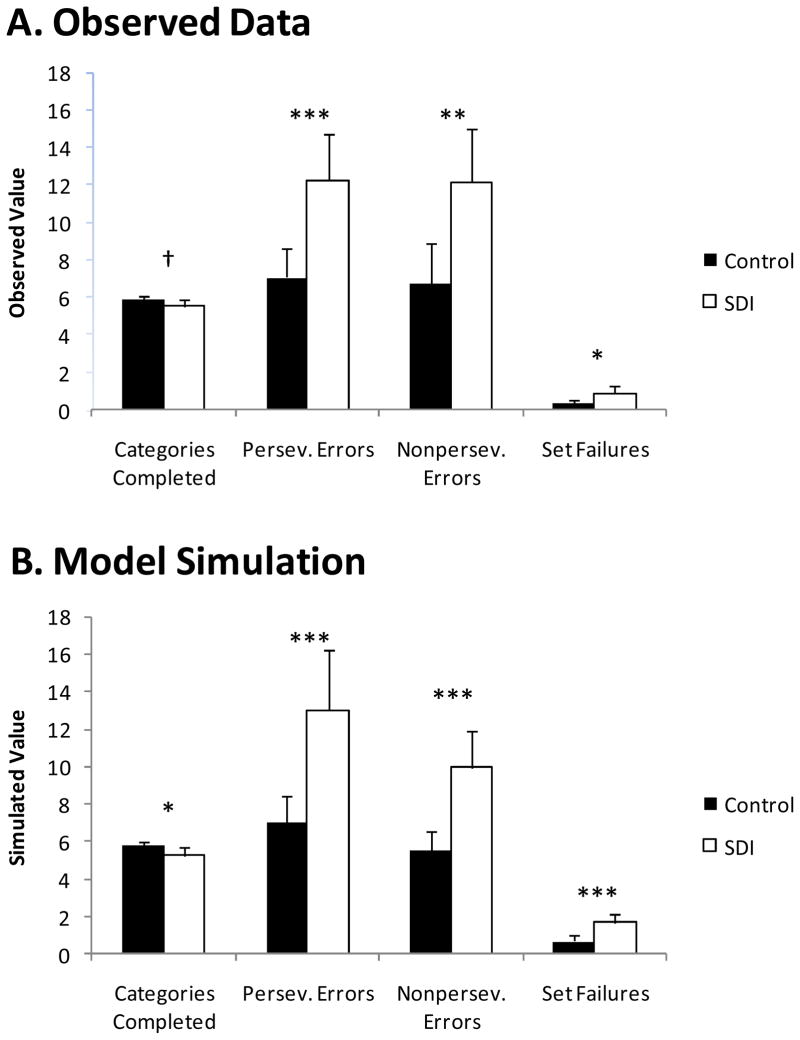
Model Simulations of Standard Scores

Figure 2A shows the observed standard behavioral scores for healthy controls and substance dependent individuals (SDI). As compared to healthy controls, SDI showed marginally fewer categories completed, t(83) = 1.87, p <.07, η²=.04, and significantly more perseverative errors, t(83) = 3.78, p < .001, η²=.15, nonperseverative errors, t(83) = 3.16, p < .01, η²=.11, and set failures, t(83) = 2.37, p < .05, η²=.06.

Figure 2.

Observed scores (A) and model simulated scores (B) for standard behavioral measures. Error bars show 95% confidence intervals of the mean. †p<.10, *p<.05, **p<.01, ***p<.001.

As shown in Figure 2B, model simulations generally reproduced the actual pattern of behavioral results. SDI had significantly fewer categories completed, t(83) = 2.58, p < .05, η² = .07, and significantly more perseverative errors, t(83) = 3.81, p < .001, η² = .15, nonperseverative errors, t(83) = 4.42, p < .001, η² = .19, and set failures, t(83) = 3.86, p < .001, η² = .15. Overall, the model could simulate the qualitative pattern of significant findings and directions of effects in the standard behavioral measures, however, the model did tend to underestimate nonperseverative errors and overestimate set failures. It should be noted that the model was not fit directly to the standard behavioral measures, for instance, by minimizing squared error between observed and simulated perseverative errors. Rather, the model’s maximum likelihood parameter estimates were used to re-simulate data.

Predicting Substance Dependence with Model Parameters

In order to determine whether the model provided predictive validity beyond the standard behavioral measures, a series of logistic regressions were performed with group (Control vs. SDI) as the dependent variable. In the initial analysis, in the first step, the behavioral measures (shown in Figure 2A) were entered as predictors, and in the second step, the model parameters r, p, and d were entered as predictors. Not surprisingly, the behavioral measures were significant, χ²(4) = 17.37, p < .01, sensitivity (to SDI) = 52.8%, specificity = 83.7%. However, even controlling for behavioral measures, the model parameters significantly improved prediction of group, χ²(3) = 15.05, p < .01, sensitivity = 63.9%, specificity= 77.6%. When the order of entry was reversed, with model parameters entered first and behavioral measures entered second, the model parameters were significant, χ²(3) = 30.28, p < .001, sensitivity = 58.3%, specificity = 79.6%, but the behavioral measures were not, χ²(4) = 2.14, p = .71. Thus, the model parameters were related to group even when controlling for standard behavioral measures, but not vice versa.

This general pattern of results was robust to several variations in the logistic regression analysis. In one analysis, demographic variables (gender, age, and education) were controlled for by being entered as predictors of group membership prior to entry of behavioral measures and model parameters. In another analysis, the rpd1 model parameters were replaced with the rd1 model parameters (constraining p to equal r). This was done because rd1 fit the data almost as well as rpd1. In yet another analysis, Categories Completed and Nonperseverative Errors were omitted from the behavioral measures step because those two scores were strongly correlated with Perseverative Errors in this study. Categories Completed and Nonperseverative errors might thereby cost the behavioral measures step two degrees of freedom in the logistic regression without providing much benefit. In every analysis, though, the pattern of results was the same. Model parameters significantly improved prediction beyond behavioral measures, but behavioral measures did not significantly improve prediction beyond model parameters.

In order to consider which parameter(s) contributed to the incremental predictive validity of the model, additional logistic regression analyses were performed again using the behavioral measures as predictors in the first step, but adding only a single parameter as a predictor in the second step. Adding r or p as a predictor for the second step did not significantly improve prediction of group membership, χ²(1) = 0.51, p > .10, and, χ²(1) = 0.22, p > .10, respectively. However, adding d lead to a significant improvement, χ²(1) = 9.22, p = <.01, sensitivity = 61.1%, specificity = 75.5%. Thus, although the set of all three model parameters provided incremental predictive validity over the traditional measures of WCST, this pattern was driven mainly by the decision consistency parameter.

Individual Parameter Analyses

As shown in Table 3, SDI was associated with declines in the p and d parameters, but not the r parameter, and this was true in both the means in medians. Compared to healthy controls, SDI had a significantly lower p parameter, χ²(1) = 16.20, odds-ratio = 8.7, p < .001, γ = −.44, and d parameter, χ²(1)=22.20, odds-ratio = 5.2, p <.001, γ = −.45. The r parameter was not significantly associated with substance dependence, χ²(1) = .26, p = .61.

Table 3.

Mean, median, and standard deviation of model parameter estimates.

Group	Parameters
	r	p	d
Mean
Control	.82	.78 ***	1.70 ***
SDI	.85	.42	.25
Stimulant	.92 *	.42	.27
Alcohol	.74	.45	.24
Median
Control	.989	.98	.34
SDI	.998	.30	.18
Stimulant	.999	.31	.19
Alcohol	.922	.29	.18
Standard Deviation
Control	.25	.35	2.11
SDI	.27	.42	.20
Stimulant	.20	.41	.22
Alcohol	.32	.44	.18

Notes. SDI=Substance Dependent Individuals. Asterisks indicate significant differences between the Control and SDI groups, or between the Stimulant and Alcohol groups.

^*p<.05,

^***p<.001.

Comparing Stimulant and Alcohol groups in Table 3, the r parameter was higher in the stimulant group, but the p and d parameters were remarkably similar. Stimulant preference was associated with a significantly higher r parameter than alcohol preference, χ²(1) = 4.28, p < .05, odds-ratio = 15.0, γ = .35. Even when compared to the control group, the stimulant group’s r was marginally higher, χ²(1) = 3.03, odds-ratio = 8.9, p < .09, γ = .21. However, the alcohol and the control groups’ r parameters were not significantly different from one another, p > .30. There were no significant differences between the stimulant and alcohol groups in the p and d parameters, ps > .60.

General Discussion

Quantitative and qualitative analyses suggest that a three parameter sequential learning model can provide a reasonable fit to WCST data. Interestingly, the three processes implicated here are reminiscent of the processes that were speculated about six decades ago. Zable and Harlow speculated that WCST performance depended on the “rate of habit formation, rate of habit extinction, and response variability” (1946, p. 23), which are notably similar to attention shifting following reward, attention shifting following punishment, and decision-consistency. We arrived at our model independently of Zable and Harlow’s ideas, and so there are some differences in conceptualization. Most importantly, our formalization and model fitting provides psychometric precision to assessing such processes in the WCST.³

The model parameters suggest a nuanced interpretation of WCST performance in substance dependence, an interpretation that can be connected to a broader literature on cognition and decision-making. Compared to healthy controls, SDI showed slower attention shifting following punishment. This pattern is consistent with previous evidence of insensitivity to negative feedback and inhibitory failures in substance users (Garavan & Stout, 2005; Hester, Simões-Franklin, & Garavan, 2007; Salo et al., 2005). SDI also showed a lower decision-consistency parameter. This pattern is consistent with the haphazard decision-making observed in substance users on other tasks (e.g., Ersche et al., 2005).

Whereas the p and d parameters differed between SDI and controls, there was some evidence that the r parameter distinguished different kinds of SDI. Compared to the alcohol group, the stimulant group showed faster attention shifting following rewarded trials. It is possible that stimulant users are more sensitized to rewards because stimulants act more directly on the dopamine system than alcohol does (Grace, 2000).

The finding of lower decision-consistency in substance users on the WCST converges with findings from a cognitive model of the Iowa Gambling Task (IGT). Substance users often show lower consistency on that task when performance is analyzed via the Expectancy Valence Learning (EVL) model (Busemeyer & Stout, 2002; for discussion of decision-consistency and substance use, see Bishara et al., under review; Stout et al., 2004). Though the mathematics behind the d parameter here and the consistency parameter in the EVL model are similar, they are not identical. In the EVL model, consistency represents not just how decisions match learning, but how that changes over time. That is, the construct of decision-consistency may overlap only slightly across tasks and models (Bishara et al., under review).

Other parameters may overlap even less. There is a superficial similarity between the attention to losses parameter of the IGT and the r and p parameters of the WCST. However, the bases of these parameters most likely differ across the two tasks. The WCST involves an extradimensional shift of attention, whereas the IGT involves shifting valences within each deck, a process more akin to reversal learning (Fellows & Farah, 2005). Extradimensional and reversal shifts have been modeled via distinct mechanisms (Kruschke, 1996). Perhaps because of this distinction, the WCST tends to involve lateral areas of prefrontal cortex (Monchi et al., 2001) whereas the IGT tends to involve medial areas of prefrontal cortex (Bechara, Damasio, Damasio, & Anderson, 1994; also see Dias, Robbins, & Roberts, 1996). Thus, the EVL model and the WCST model used here might overlap in their assessment of decision consistency, but less so in their assessment of other parameters. Of course, more research is needed to directly compare the two models and tasks.

We have suggested that cognitive modeling is valuable because it allows for a nuanced theoretical analysis of WCST performance. That is, cognitive modeling provides incremental content validity to the WCST (see Haynes & Lench, 2003). However, perhaps an even greater contribution of the modeling is that it improves discrimination between SDI and healthy controls, i.e., the modeling provides incremental predictive validity. The model parameters here were able to significantly predict group membership even when controlling for traditional measures of the WCST, measures that had become popular in part because of their ability to distinguish clinical populations from controls. Of course, our logistic regression results should be interpreted with some caution. In order to provide stronger evidence of the incremental predictive validity of our model, larger samples would be desirable in future research, as well as separate calibration and validation samples.

Conclusion

The WCST is enormously popular in clinical neuropsychology. In one survey of neuropsychologists, 71% reported using the WCST with most of their patients, and the WCST was the most commonly used task to measure executive function (Butler et al., 1991). However, WCST interpretation is complicated because task performance can reflect multiple processes. Modeling approaches hold the promise of moving beyond simplistic “one task equals one process” interpretations, thereby improving the analytical and diagnostic capabilities of the WCST.

Appendix: Modeling Methods

All of the model evaluations are based on “one step ahead” predictions generated by each model for each individual participant. The accuracy of these predictions is measured using the log likelihood criterion. To be more specific, for a given subject, let y_t be a t x 1 vector representing the sequence of choices up to and including trial t, and let x_t be the corresponding sequence of “right” and “wrong” feedback. Let P_t+1,k|y_t,x_t be a model’s predicted choice probability for the next trial (t +1) and pile k given information about choices and feedback only up to trial t. Finally, let δ_t,k be the observed choice made by a decision maker on trial t for pile k, such that δ_t,k = 1 if k was chosen on trial t; else δ_t,k = 0. The log likelihood of the model (LL_model) is determined by predictions for one trial ahead, summed across trials and piles:

$${LL}_{\text{model}}=\sum _{t=1}^v\sum _{k=1}^4\left[ln({\text{P}}_{t+1,k}\mid {\mathbf{y}}_t,{\mathbf{x}}_t)·{\delta }_{t+1,k}\right]$$ (A1)

where v is the number of trials administered minus 1.

Because LL measures goodness of fit, −LL measures badness of fit. Parameters were estimated by minimizing −LL separately for each participant and each model. Estimation was implemented with the programming language “R” (R Development Core Team, 2006) using the robust combination of a simplex method (Nelder & Mead, 1965) and multiple quasi-random starting points.

BIC was also used to measure model performance:

$$\text{BIC}=-2\ast L{L}_{\text{model}}+\mathit{u}lnv$$ (A2)

In the right side of Equation A2, the first expression represents badness of model fit. The second expression represents a penalty for model complexity, where u is the number of free parameters in the model, and v is the number of observations modeled for the participant (number of trials administered minus 1).