Abstract
The Wisconsin Card Sort Task (WCST) is a commonly used neuropsychological test of executive or frontal lobe functioning. Traditional behavioral measures from the task (e.g., perseverative errors) distinguish healthy controls from clinical populations, but such measures can be difficult to interpret. In an attempt to supplement traditional measures, we developed and tested a family of sequential learning models that allowed for estimation of processes at the individual subject level in the WCST. Testing the model with substance dependent individuals and healthy controls, the model parameters significantly predicted group membership even when controlling for traditional behavioral measures from the task. Substance dependence was associated with a) slower attention shifting following punished trials and b) reduced decision consistency. Results suggest that model parameters may offer both incremental content validity and incremental predictive validity.
Keywords: Wisconsin Card Sort, Cognitive Model, Substance Dependence, Decision-making, Executive Function
The Wisconsin Card Sort Task (WCST) is perhaps the most famous task used to measure inflexible persistence (Berg, 1948; Grant & Berg, 1948). The task involves sorting cards based on rules that periodically change. Patients with frontal lobe damage often make errors on this task, persistently using an old rule even when it is no longer valid (Demakis, 2003; Milner, 1963). Unfortunately, such errors occur in a variety of populations, including individuals with substance dependence (Bechara & Damasio, 2002), schizophrenia (Braff, Heaton, Kuck, & Cullum, 1991), Huntington’s disease (Zakzanis, 1998), and Alzheimer’s disease (Bondi, Monsch, Butters, & Salmon, 1993) to name a few. Although these errors are sometimes interpreted as the result of “frontal function” or “executive control” deficits, these errors may have multiple psychological bases, bases that vary across clinical populations. That is, rather than measuring a single, unitary construct, the WCST may measure multiple processes. The goal of the current research is to disentangle these processes through cognitive modeling, and furthermore, to identify the processes associated with substance dependence.
The idea that the WCST depends on multiple processes is certainly not new. The WCST has roots back to the University of Wisconsin Laboratory in the 1940’s, where monkeys were trained to make discriminations among abstract dimensions. It was speculated that the monkeys’ performance depended on such factors as the “rate of habit formation, rate of habit extinction, and response variability” (Zable & Harlow, 1946, p. 23). We propose a formal family of models that are related to Zable and Harlow’s speculation. A key difference, though, is that the current work allows for these multiple processes to be systematically measured. Such measurement has the potential to improve the diagnosticity and interpretation of the WCST.
There has been a recent surge of interest in modeling the WCST (Amos, 2000; Carter, 2000; Dahaene & Changeux, 1991; Kimberg & Farah, 1993; Levine & Prueitt, 1989; Monchi, Taylor, & Dagher, 2000; Rougier & O’Reilly, 2002). The goal in most cases has been to develop a model that is biologically inspired. Such models have been tested by attempting to simulate general qualitative patterns of data, for example, simulating more errors in one condition than another. The downside to these models, though, is that they have been too elaborate for precise parameter estimation at the individual subject level.
In contrast, the primary goal here is to use modeling to measure processes at the individual level, and so parameter estimation at that level is of paramount importance. This general approach, using cognitive modeling for measurement of underlying processes of individuals, is sometimes referred to as cognitive psychometrics (Batchelder, 1998). The family of models presented here were designed to improve parameter estimation in three ways. First, the models were designed to be simple enough for maximum likelihood estimation of parameters. Second, models were tractable enough to allow for fitting of individual subject data rather than just group data. Third, these models allowed for the fitting of complete, trial-by-trial choice data rather than just summary data (e.g., total perseverative errors). An additional benefit of the models considered here was that, because they were tractable enough for maximum likelihood estimation, they allowed for formal quantitative comparisons of model performance.
There are encouraging precedents for using these kinds of tractable cognitive models to better understand individual differences. For example, such models have been used to estimate individual performance in the Iowa Gambling Task (Busemeyer & Stout, 2002), the Balloon Analog Risk Task (Wallsten, Pleskac, & Lejuez, 2005), and the Go-No-Go Task (Yechiam et al., 2006; also see Neufeld, 2007). However, there is no currently published research using cognitive modeling in this way for the WCST. The WCST has been used in clinical psychology and neuropsychology for several decades and it continues to be popular (Butler, Retzlaff, & Vanderploeg, 1991; Rabin, Barr, & Burton, 2005). Thus, a tractable cognitive model of the WCST would be a novel and potentially powerful tool.
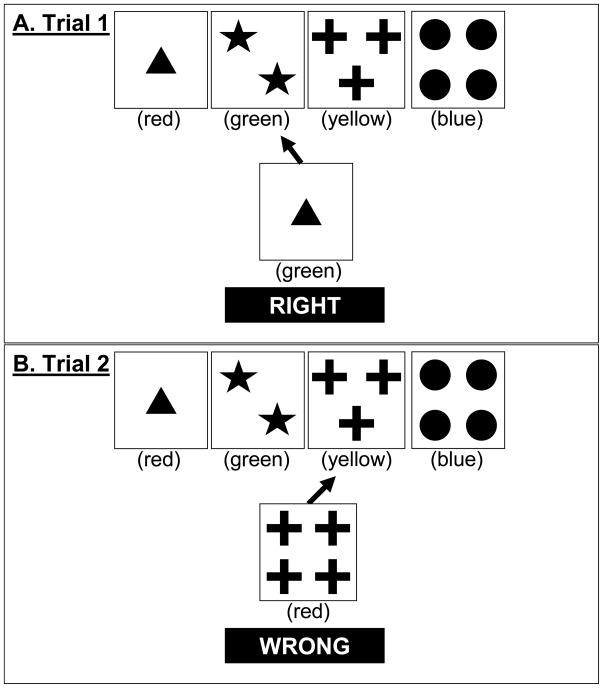
We developed a family of models for one of the most common versions of the WCST, the Heaton version (Heaton, Chelune, Talley, Kay, & Curtiss, 1993), though these models could conceivably be adapted to other versions as well (e.g., Nelson, 1976). In the Heaton version, participants sort cards that vary in terms of the color, form, and number of objects on them. Each card can be sorted into one of 4 key cards (shown at the top of Figure 1A). For example, as shown in Figure 1A, a participant is given a single green triangle and decides to sort it with the key card that has two green stars.
Figure 1.
Examples of trials in the Wisconsin Card Sort Task. Arrows represent choices made by a hypothetical participant.
The instructions are deliberately vague. Participants are told to match the cards but not how. They are only told “right” or “wrong” after each choice. The correct sorting rule is either color, form, or number on any given trial. The rule starts out as color, but importantly, after 10 consecutive matches by color, the rule changes without warning. Participants sometimes persist on the old rule after this happens, and this is referred to as a perseverative error. The task ends after completing six rules (getting 10 consecutive correct within a rule) or 128 trials, whichever comes first. In addition to perseverative errors, other common scoring measures include nonperseverative errors, categories completed, and failure to maintain set. A nonperseverative error is any error that does not appear perseverative (there are complex rules for scoring perseverative and nonperseverative errors; see Heaton et al., 1993). Categories completed are the number of rules completed, with a maximum of 6. Failure to maintain set is scored as the total number of errors that occur within a rule after at least 5 consecutive correct responses.
Such standard scoring measures can be useful. For example, in patient populations, the measures predict functioning in everyday life, such as occupational status (Kibby, Schmitter-Edgecombe, & Long, 1998) and independent living (Little, Templer, Persel, & Ashley, 1996). Standard scoring measures also predict abnormal behavior, such as confabulation (Burgess, Alderman, Evans, Emslie, & Wilson, 1998).
However, the standard scoring measures are sometimes difficult to interpret because it is unclear what kinds of processes they represent. For example, Categories Completed has no clear process interpretation. Even the interpretation of perseverative errors is ambiguous; what is scored as a perseverative error can result from a failure to shift attention after an error, a failure to preserve attention after correct feedback, or occasionally even a random response. Next, we present a family of sequential learning models that encourage process oriented interpretations of the WCST. Then, we consider how substance dependence might be related to model parameters.
The Family of Models Considered
Common Characteristics of the Models
Overview
In the WCST, participants must shift attention across various possible sorting rules. Though participants may occasionally use complicated conjunctive rules or exceptions, simple categorization strategies appear to be more common (Martin & Caramazza, 1980). Because of this, all models considered here involve shifting attention weights across simple rules, rules for matching on the basis of color, form, or number.
Various candidate mechanisms were considered across a family of 12 models. The performance of these models was compared so as to allow the data to inform the selection of the most important mechanisms. For each model, the set of free parameters was estimated separately for each subject. Free parameters varied across subjects, not across trials within subjects.
All models included a free parameter r, which represents how quickly attention weights change in response to rewarding feedback (i.e., “RIGHT”). Some models also included up to 3 additional free parameters. The p parameter represents how quickly attention weights change in response to punishing feedback (i.e., “WRONG”). The d parameter represents decision or choice consistency. Finally, the f parameter represents attentional focusing, which matters for trials with ambiguous feedback. 1
Attention Weight Vector
The behavior of all models depends on the relative attention devoted to color, form, and number on any given trial. An attention weight vector, at, represents the weight given to each of these dimensions on trial t. A simplifying assumption is that attention weights start evenly divided among the dimensions on the first trial (t=1):
| (1) |
The elements of vector at always sum to 1, so that as attention to one dimension increases, attention to other dimensions tends to decrease. The value of a changes across trials, with the rate of change being determined by the free parameters in the model.
Attention Change
To implement changes of attention, the attention weight vector on the next trial, at+1, is a weighted average of the attention weight vector of the current trial, at, and a feedback signal vector from the current trial, st. Consider the example displayed in Figure 1A for Trial 1. The participant chooses the 2nd pile and is told “right” (i.e., correct). This feedback implies that color is the current correct dimension to sort by because only the color of the sorted card matches any dimension of the key card. Therefore, the signal st indicates that attention should move toward 1 for color and toward 0 for the other dimensions. For this particular example:
| (2) |
To define st more generally, let us first define another vector mt,k, which is a 3 × 1 matching vector whose values depend on the match between the card that must be sorted on trial t and the pile k in which it is eventually placed. The i-th element of mt,k, denoted mt,k,i, has a value of 1 if the card that must be sorted matches the pile in which it is eventually placed on dimension i, and a value of 0 otherwise. Whenever the feedback is “right” and unambiguous (consistent with one and only one dimension being the correct dimension to sort by), the feedback signal is defined as:
| (3) |
Whenever feedback is wrong and unambiguous:
| (4) |
For example, if pile 1 were selected on trial 1, the feedback would be “wrong,” and based on Equation 4:
| (5) |
Equations for ambiguous feedback signals are described later.
How rapidly attention changes toward feedback signals is determined by a free parameter r for rewarded trials. When trial t is rewarded (i.e., “right” feedback), attention on the next trial is:
| (6) |
Parameter r ranges from 0 to 1. When r = 0, there is no attention shifting, and when r = 1, there is complete attention shifting toward the feedback signal. In the example in Figure 1, if r = .1, attention would shift only slightly toward color from trial 1 to trial 2. Using Equation 6, attention weights on trial 2 would be as follows:
| (7) |
Mechanisms That Differ Across Models
Differential Attention Shifting for Reward and Punishment
Attention updating may occur at different rates for rewarded and punished trials due to different updating mechanisms. Distinct updating mechanisms would be consistent with neuroimaging studies that have found distinct neural correlates of rewarded and punished choices in the WCST (Monchi, Petrides, Petre, Worsley, & Dagher, 2001; Monchi, Petrides, Doyon, Postuma, Worsley, & Dagher, 2004). Neural regions specifically correlated with wrong choices include the anterior cingulate, as well as a cortical basal ganglia loop originating in the ventrolateral prefrontal cortex. In contrast, the dorsolateral prefrontal cortex has been associated with both right and wrong feedback (also see Mansouri, Matsumoto, & Tanaka, 2006).
Attention shifting may also be distinctive following punishment because such shifting may be more closely related to inhibitory functioning. After attention has built up toward a particular dimension, and then new feedback suggests that this dimension is wrong, attention to this dimension may need to be inhibited to support switching attention to a new dimension. For these reasons, attention shifting following punishment may occur at a different rate than attention shifting following reward.
In the family of models considered, attention change after punishment works in the same manner as that after reward (see Equation 6), but with a separate parameter p to allow for the possibility of different shifting rates. When trial t is punished, attention on the next trial is:
| (8) |
Like the r parameter, the p parameter ranges from 0 to 1, with higher values tending to lead to better task performance. To examine the possibility that there are different attention shifting rates for reward and punishment, models where r and p were allowed to vary freely were compared with models that constrained r and p to be equal.
Individual differences in decision-consistency
Individuals may vary in how much their decisions are consistent with their attention weights. That is, some individuals may be more deterministic while others may be more random or haphazard in terms of how their decisions are aligned with attention weights. This “consistency” mechanism is typical in models of decision-making tasks, such as the Iowa Gambling Task and the Balloon Analog Risk Task (Busemeyer & Stout, 2002; Wallsten et al., respectively). However, it is unclear whether decision-consistency will play a major role in the WCST, a task usually thought to measure executive function rather than decision-making.
To formalize decision-consistency, the predicted probability of choosing a particular pile is influenced by a decision-consistency parameter, d. Specifically, the predicted probability (P) of choosing pile k on trial t was defined as:
| (9) |
where mt,k denotes the match between the card that must be sorted on trial t and the pile k in which it could be placed (m′ simply denotes the transpose of m), and is a column vector with the element for each dimension i raised to the d power ( ). In the denominator of Equation 9, j ranges from 1 to 4 for the summation across all 4 piles. Dividing by the summation of piles forces Pt,k to add up to 1 across piles.
When d=1, the probability of choosing each pile is simply the sum of the elements of the attention vector that match that pile. For example, when d=1, the predicted probability of sorting to the far left pile in Figure 1A would be 2/3 because the card to be sorted matches that pile both in form (triangle) and number (one), and attention is currently 1/3 to form and 1/3 to number. As d becomes higher than 1, choices become more deterministic and constrained by attention. For example, when d=2, the predicted probability of sorting to the far left pile in Figure 1A would be .89. As d becomes lower, choices become more random and less consistent with attention. For example, when d=0.5, the predicted probability of sorting to the far left pile would be .59.
To assess the importance of the decision-consistency mechanism for explaining individual differences, models where d was free to vary were compared with models where d was constrained to equal 1. For parameter estimation purposes, when d was allowed to vary, it was constrained such that .01 ≤ d ≤ 5.
Attentional Focus
To illustrate the relevance of attentional focus, consider the example of Trial 2 in Figure 1B where the participant sorts on the basis of matching form but is told “wrong.” The feedback is ambiguous because either color or number could be the proper dimension to sort by. In ambiguous cases like this, the feedback signal s depends on a free parameter f that represents how focused or narrow attention is. As f approaches 0, representing no focus, the feedback signal is split evenly among all possible correct dimensions. In this example:
| (10) |
In this particular example, the ambiguity is not a drastic deterrent to learning, but in other situations, ambiguity could lead to increased error rates. Consider a case where a participant has correctly matched on the basis of color for several trials, and so attention to color has increased up to .9. Then, color is correctly chosen again, but this time the match is ambiguous, being consistent with both color and number. A low value of f will yield a feedback signal indicating that attention should be split between color and number. This signal would reduce attention to color for the next trial even though color is the correct dimension. Thus, a low f can increase the likelihood of errors after ambiguous feedback.
Higher values of f can avoid this problem. If f=1, s is split proportionally to current attention weights. For example, consider a case where current attention is weighted .60 to color, .20 to form, and .20 to number, and as in Figure 1B, the feedback is consistent with either color or number being the correct rule. In this particular example:
| (11) |
As f approaches infinity, the feedback signals the maximum attention element that is consistent with the feedback. Considering this same example:
| (12) |
More generally, the feedback signal for correct trial t on dimension i is:
| (13) |
For incorrect trials, the signal is:
| (14) |
where k is the chosen pile, mt,k,i is the element of the match vector mt,k at dimension i, and likewise, at,i is the element of attention vector at at dimension i. In the denominators of Equations 13 and 14, h ranges from 1 to 3 for the summation of all 3 dimensions. Dividing by the summation of dimensions forces the feedback signal to add up to 1 across dimensions. Note that Equations 13 and 14 simplify to Equations 3 and 4 when the feedback is unambiguous, and so the value of f is only relevant for trials with ambiguous feedback. For estimation purposes, the f parameter was constrained such that 0.01 ≤ f ≤ 5.
Attentional focusing mechanisms have been used in other models of the WCST (e.g., Amos, 2000). The potential value of this attentional focus mechanism is that, in addition to having feedback influence shifts of attention, the mechanism allows attention to influence the interpretation of feedback. To examine the importance of attentional focus in the WCST, three types of models were compared: Models where f⃗0 (no attentional focusing), where f=1 (focusing proportional to the attentional vector a; fixed across individuals), and where f was free to vary (attentional focusing differs across individuals).2
Model Comparison
The three model mechanisms (differential attention shifting for reward and punishment, different decision-consistencies across individuals, and attentional focus) were examined by considering different model constraints. These model constraints led to a factorial design of 12 models: p free vs. p=r crossed with d free vs. d=1 crossed with f free vs. f⃗0vs. f=1. In addition to the family of 12 models, a baseline model with zero free parameters was considered as a point of comparison. The baseline model assumed no attention shifting, just simple proportional matching. It predicted that the probability of choosing a particular pile was simply the number of dimensions matching between the pile and the current card, divided by 3. The baseline model was equivalent to having constraints r=0, p=0, and d=1, with f being irrelevant.
Modeling Substance Dependent Individuals
There are many possible reasons that substance dependent individuals (SDI) may have different estimated model parameters than healthy controls. We consider two prominent possibilities: first, that SDI will show a lower p parameter due to inattention to error signals and/or inhibitory failures, and second, that SDI will show a lower d parameter due to more haphazard decision-making.
Substance users often show decreased neural activity in regions specifically associated with errors. Anterior cingulate activation has been associated with the monitoring and prediction of errors in several tasks (e.g., Carter et al., 1998; 2000), including the WCST (Monchi et al., 2001, 2004). In attention shifting tasks, hypoactive anterior cingulate activation has been observed in substance users following errors (Kübler, Murphy, & Garavan, 2005; for a review, see Garavan & Stout, 2005). In addition to anterior cingulate activation, error responses (but not correct responses) on the WCST have been associated with a ventral lateral prefrontal cortex/striatal loop (Monchi et al., 2001, 2004). Loops between the frontal cortex and basal-ganglia structures are altered through substance use (Volkow et al., 1993; Willuhn, Sun, & Steiner, 2003).
A related finding is that substance users often fail to inhibit irrelevant information. In the WCST, inhibition would be most important in cases where a person had built up attention to a particular dimension (e.g., color), but then the feedback started to indicate that that dimension was wrong. Failure to inhibit this no longer relevant dimension would be associated with slower attention shifting following punished trials. A deficit in inhibiting irrelevant information has been observed in substance users, and specifically when performing switching tasks (Salo et al., 2005). Interestingly, an inhibitory deficit may be a precursor to drug use rather than the result of it, with poor inhibitory control at age 10–12 predicting substance use at age 19 (Tarter et al., 2003). Whatever the causal mechanism, though, the association between substance use and poor inhibitory control suggests that substance users may be slow to shift attention in response to punishing feedback.
These various findings can be summarized as two general patterns: substance use is associated with failures to fully use negative feedback and failures to inhibit previously relevant information. Both patterns would suggest that SDI will have a low p parameter relative to healthy controls.
Substance use is sometimes associated with random, inconsistent decisions on decision-making tasks. In the Iowa Gambling Task, substance users’ choices are less consistent with what they have learned on the task compared to the choices of healthy controls (Bishara et al., under review; Stout, Busemeyer, Lin, Grant, & Bonson, 2004). More generally, substance users’ behavior is often described as “impulsive” (see Jentsch & Taylor, 1999), though that word has several meanings (Evenden, 1999). Here, the interest is in the kind of impulsivity related to a lack of forethought that can lead to haphazard decisions. For example, substance users sometimes perform poorly due to rushed choices. This can occur even in tests of cognition not specifically intended to measure decision-making (Ersche, Clark, London, Robbins, & Sahakian, 2005). Therefore, substance users may make inconsistent decisions on the WCST, and thus display a lower d parameter.
Primary Questions
In this study, there were five questions of interest. First, in the family of models considered, which model would show the best quantitative fit to the data? This question was addressed primarily with the Bayesian Information Criterion, but also via nested comparisons with G2. Second, how well can the quantitatively best fitting model reproduce qualitative patterns in the data? This question was addressed by using estimated model parameters to simulate WCST performance, and then compare simulated performance to actual performance of SDI and controls. Third, would the model parameters relate to substance dependence even when controlling for traditional behavioral measures, such as perseverative errors (i.e., would the model parameters have incremental predictive validity)? This question was addressed by using logistic regression to predict group membership, with behavioral measures entered as predictors first, and model parameters entered second. Fourth, how would substance dependence be related to individual model parameters? This question was addressed via separate logistic regressions for each model parameter. Finally, would different types of drug users show different patterns of parameter values? This exploratory question was addressed by comparing SDI whose drug of choice was alcohol to SDI whose drug of choice was a stimulant (e.g., cocaine, crack, and methamphetamine).
Method
Participants
Table 1 shows demographic and other information about participants. Substance Dependent Individuals (SDIs) were recruited while undergoing or after having completed inpatient treatment at the Mid-Eastern Council on Chemical Abuse in Iowa City (see Bechara et al., 2001; Bechara & Damasio, 2002; Bechara, Dolan, & Hinders, 2002). Among SDI, the drug of choice was alcohol for 16 participants, stimulants for 22 participants, and unclear for 1 participant.
Table 1.
Participant demographics
| N | % Female | Age | Education | |
|---|---|---|---|---|
| Control | 49 | 49.0 | 33.6 (10.9) | 14.4 (2.2) |
| Substance Dependent | 39 | 56.4 | 34.1 (10.3) | 12.5 (1.8) |
| Stimulant | 22 | 68.2 | 30.3 (7.2) | 12.3 (1.5) |
| Alcohol | 16 | 37.5 | 39.9 (11.6) | 12.9 (2.2) |
Note. For Age and Education, the mean is shown with standard deviation in parentheses. “Stimulant” and “Alcohol” are drug preference subsets of the Substance Dependent group. Note that one individual did not report drug preference.
The selection criteria for SDIs were: (1) meeting the DSM-IV criteria for substance dependence; (2) absence of psychosis; and (3) no documented head injury or seizure disorder. Normal control subjects had no history of mental retardation, learning disability, psychiatric disorder, substance abuse, or any systemic disease capable of affecting the central nervous system. The Structured Clinical Interview for DSM-IV (First, Spitzer, Gibbon, & Williams, 1997) was used to determine a diagnosis of substance dependence. The interview was administered by a trained PhD candidate in clinical psychology.
For 3 subjects in the SDI group, the WCST was ended prematurely, which would bias the standard behavioral measures to be low. Accordingly, those 3 subjects were excluded from all analyses that involved standard behavioral measures.
Procedure and Materials
Participants were given the manual administration of the WCST using the Heaton et al. (1993) version. SDIs were tested after a minimum period of 15 days of abstinence from any substance use. SDIs were paid for their participation in the study with gift certificates with an hourly rate identical to that earned by normal controls.
Model Fitting and Analyses
Maximum Likelihood Estimation was used to estimate parameters separately for each model and each participant (see Appendix for further details). There were 12 models in the family of models of interest, and they consisted of every combination of the mechanisms tested: two p constraints (free p & p=r) by two d constraints (free d & d=1) by three f constraints (free f, f⃗0, & f=1). To adjust for differences in the number of parameters used for each model, the Bayesian Information Criterion (BIC) was used (Schwarz, 1978; see Appendix for further details). The BIC is based on asymptotic principles from Bayesian model comparison. Smaller BICs indicate better model performance. BIC allows all models to be put on a comparable metric of model performance. This is important, because many pairs of models considered here are non-nested. BIC was also chosen because, compared to other complexity corrections (e.g., Akaike Information Criterion), BIC tends to favor models with fewer free parameters. Using only a small number of free parameters encourages more independence among parameters and more precise estimation of those parameters.
G2 was also used to examine nested relationships, comparing all models to the baseline model. Additionally, to further test the model that had the smallest BIC, we compared that model to similar models via nested tests. The percentage of subjects where a parameter constraint led to a significant worsening of model fit was examined.
The best performing model was then used to simulate performance and compare it to actually observed performance. First, for each subject, the maximum likelihood parameter values were estimated from the observed data. Then, for each subject, the subjects’ parameter estimates and a1 were used to generate choice probabilities for trial 1, then simulate a choice in accord with those probabilities, then update a2 based on the simulated choice, and then start the process again using a2 and parameter estimates to generate choice probabilities for the trial 2. This process was repeated until the simulated sequence of choices produced 6 categories completed or 128 trials. Note that these simulations relied on one-step-ahead predictions using simulated choices, not actually observed choices, from the previous step.
Each subject’s simulated sequence of choices was analyzed with four standard behavioral measures. Categories Completed and Perseverative Errors were examined because these two measures are commonly reported in the literature. However, these two measures tend to be strongly correlated, and so two other scores were included: Nonperseverative Errors and Set Failures. These latter two scores were chosen because they sometimes load on two distinct factors in factor analysis, and these two factors are distinct from a more dominant factor that includes both Categories Completed and Perseverative Errors (Greve, Ingram, & Bianchini, 1998). To reduce within-subject noise, simulations were repeated 1000 times for each subject, and the standard behavioral measures were averaged across these 1000 repetitions.
Using the best fitting model, maximum likelihood estimates of parameters for each individual participant were analyzed. Logistic regression was used to analyze the relationship between estimated model parameters and groups so as to allow for other variables to be controlled for. Because of extremely non-normal parameter distributions, the Goodman-Kruskal γ correlation was used to indicate effect size for the relationships between subject groups and parameters. Like the Pearson correlation, γ ranges from −1 to 1, and 0 indicates no association.
Results
Quantitative Model Fit
The family of 12 attention shifting models generally fit the data better than the baseline model did. Table 2 displays the mean BIC across subjects for each model. All 12 models of interest had a significantly smaller mean BIC than the baseline model, as shown by pairwise t-tests, all ps < .001. Because all 12 models of interest were nested within the baseline model, comparisons to the baseline model were also analyzed with G2. G2 was computed separately for each subject and each model of interest. Significant improvement of the model of interest over the baseline model was assessed using the chi-squared distribution and df equal to the number of free parameters in the model of interest (because the baseline model had 0 free parameters). These analyses confirmed that the models of interest generally outperformed the baseline model. All models of interest fit significantly better than the baseline model for 86 out of the 88 subjects. The two remaining subjects were outliers in that they were the only two subjects to complete 0 categories.
Table 2.
Mean BIC as a function of model constraints.
| Model Constraints |
Baseline Model | ||||
|---|---|---|---|---|---|
| f free | f = 0 | f = 1 | |||
| p free | d free | 83.69 | 88.54 | 81.99 | 150.72 |
| d = 1 | 83.94 | 97.58 | 86.51 | ||
| p = r | d free | 84.39 | 88.95 | 82.79 | |
| d = 1 | 82.83 | 95.66 | 86.10 | ||
Comparing the BICs of the models of interest, two patterns were particularly noticeable in Table 2. First, BIC was higher when f was constrained to be 0 than when it was constrained to be 1 or was free to vary. Second, BIC was higher when both f and d were constrained to 1, or when both were free to vary. However, when only one was free to vary, BIC tended to be smaller. Thus, constraining f to 0 tended to hurt model performance, but constraining f to 1 was benign so long as d was free to vary.
Overall, the model with the lowest mean BIC had f constrained to 1 but allowed r, p, and d to vary freely. This model fit significantly better than 9 out of the 11 other models of interest, ps < .01. This model was not significantly different from the two remaining models, ps > .20. For additional analyses, we focus on this best fitting model, and denote it as rpd1 to indicate that r, p, and d are free to vary, whereas f is fixed at 1.
Nested comparisons and G2 were used at the subject level to further examine the performance of the rpd1 model. Using rpd1 as a point of reference, allowing f to vary freely failed to significantly improve the fit for 75% of the subjects (i.e., G2 < 3.84, the critical value for a chi-squared distribution with 1 df). In contrast, constraining d to equal 1 significantly worsened the fit for 53% of the subjects. Constraining p to equal r significantly worsened the fit for 34% of the subjects. Overall, the nested comparisons supported constraining f to equal 1 and allowing d to vary freely for the majority of subjects, but the usefulness of allowing p to vary freely was less clear.
Finally, we considered a variant of the rpd1 model where the assumption of equal attention weights on trial 1 was relaxed. Two additional free parameters were used for the initial attention weight to color and form (with the weight to number being determined by 1 minus the sum of the other weights). This variant of the rpd1 model was not well supported by the fit statistics. This variant had a worse BIC than the original rpd1 model for 94% of subjects. Furthermore, in nested comparisons, the variant’s improvement in fit relative to the original model was nonsignificant (G2(2) < 5.99) for 87% of subjects. The simplifying assumption of equal attention weights on trial 1 may work well enough because the attention weight vector often changes rapidly after the first trial.
Model Simulations of Standard Scores
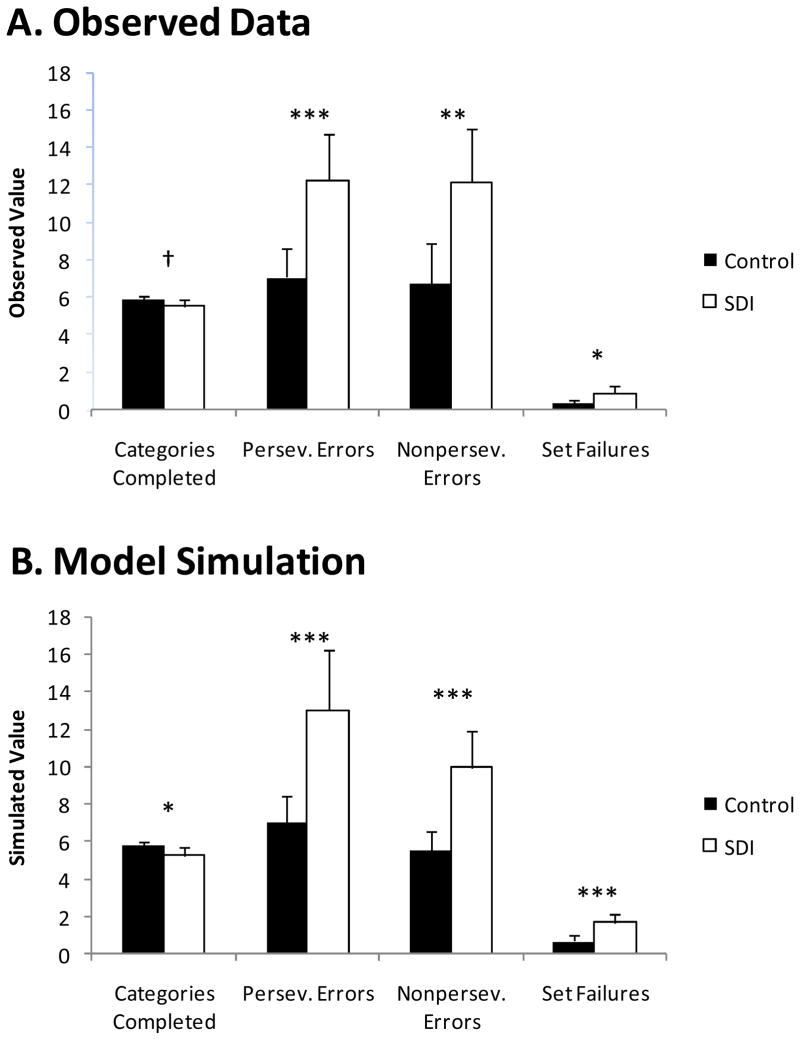
Figure 2A shows the observed standard behavioral scores for healthy controls and substance dependent individuals (SDI). As compared to healthy controls, SDI showed marginally fewer categories completed, t(83) = 1.87, p <.07, η2=.04, and significantly more perseverative errors, t(83) = 3.78, p < .001, η2=.15, nonperseverative errors, t(83) = 3.16, p < .01, η2=.11, and set failures, t(83) = 2.37, p < .05, η2=.06.
Figure 2.
Observed scores (A) and model simulated scores (B) for standard behavioral measures. Error bars show 95% confidence intervals of the mean. †p<.10, *p<.05, **p<.01, ***p<.001.
As shown in Figure 2B, model simulations generally reproduced the actual pattern of behavioral results. SDI had significantly fewer categories completed, t(83) = 2.58, p < .05, η2 = .07, and significantly more perseverative errors, t(83) = 3.81, p < .001, η2 = .15, nonperseverative errors, t(83) = 4.42, p < .001, η2 = .19, and set failures, t(83) = 3.86, p < .001, η2 = .15. Overall, the model could simulate the qualitative pattern of significant findings and directions of effects in the standard behavioral measures, however, the model did tend to underestimate nonperseverative errors and overestimate set failures. It should be noted that the model was not fit directly to the standard behavioral measures, for instance, by minimizing squared error between observed and simulated perseverative errors. Rather, the model’s maximum likelihood parameter estimates were used to re-simulate data.
Predicting Substance Dependence with Model Parameters
In order to determine whether the model provided predictive validity beyond the standard behavioral measures, a series of logistic regressions were performed with group (Control vs. SDI) as the dependent variable. In the initial analysis, in the first step, the behavioral measures (shown in Figure 2A) were entered as predictors, and in the second step, the model parameters r, p, and d were entered as predictors. Not surprisingly, the behavioral measures were significant, χ2(4) = 17.37, p < .01, sensitivity (to SDI) = 52.8%, specificity = 83.7%. However, even controlling for behavioral measures, the model parameters significantly improved prediction of group, χ2(3) = 15.05, p < .01, sensitivity = 63.9%, specificity= 77.6%. When the order of entry was reversed, with model parameters entered first and behavioral measures entered second, the model parameters were significant, χ2(3) = 30.28, p < .001, sensitivity = 58.3%, specificity = 79.6%, but the behavioral measures were not, χ2(4) = 2.14, p = .71. Thus, the model parameters were related to group even when controlling for standard behavioral measures, but not vice versa.
This general pattern of results was robust to several variations in the logistic regression analysis. In one analysis, demographic variables (gender, age, and education) were controlled for by being entered as predictors of group membership prior to entry of behavioral measures and model parameters. In another analysis, the rpd1 model parameters were replaced with the rd1 model parameters (constraining p to equal r). This was done because rd1 fit the data almost as well as rpd1. In yet another analysis, Categories Completed and Nonperseverative Errors were omitted from the behavioral measures step because those two scores were strongly correlated with Perseverative Errors in this study. Categories Completed and Nonperseverative errors might thereby cost the behavioral measures step two degrees of freedom in the logistic regression without providing much benefit. In every analysis, though, the pattern of results was the same. Model parameters significantly improved prediction beyond behavioral measures, but behavioral measures did not significantly improve prediction beyond model parameters.
In order to consider which parameter(s) contributed to the incremental predictive validity of the model, additional logistic regression analyses were performed again using the behavioral measures as predictors in the first step, but adding only a single parameter as a predictor in the second step. Adding r or p as a predictor for the second step did not significantly improve prediction of group membership, χ2(1) = 0.51, p > .10, and, χ2(1) = 0.22, p > .10, respectively. However, adding d lead to a significant improvement, χ2(1) = 9.22, p = <.01, sensitivity = 61.1%, specificity = 75.5%. Thus, although the set of all three model parameters provided incremental predictive validity over the traditional measures of WCST, this pattern was driven mainly by the decision consistency parameter.
Individual Parameter Analyses
As shown in Table 3, SDI was associated with declines in the p and d parameters, but not the r parameter, and this was true in both the means in medians. Compared to healthy controls, SDI had a significantly lower p parameter, χ2(1) = 16.20, odds-ratio = 8.7, p < .001, γ = −.44, and d parameter, χ2(1)=22.20, odds-ratio = 5.2, p <.001, γ = −.45. The r parameter was not significantly associated with substance dependence, χ2(1) = .26, p = .61.
Table 3.
Mean, median, and standard deviation of model parameter estimates.
| Group | Parameters |
||
|---|---|---|---|
| r | p | d | |
| Mean | |||
| Control | .82 | .78 *** | 1.70 *** |
| SDI | .85 | .42 | .25 |
| Stimulant | .92 * | .42 | .27 |
| Alcohol | .74 | .45 | .24 |
| Median | |||
| Control | .989 | .98 | .34 |
| SDI | .998 | .30 | .18 |
| Stimulant | .999 | .31 | .19 |
| Alcohol | .922 | .29 | .18 |
| Standard Deviation | |||
| Control | .25 | .35 | 2.11 |
| SDI | .27 | .42 | .20 |
| Stimulant | .20 | .41 | .22 |
| Alcohol | .32 | .44 | .18 |
Notes. SDI=Substance Dependent Individuals. Asterisks indicate significant differences between the Control and SDI groups, or between the Stimulant and Alcohol groups.
p<.05,
p<.001.
Comparing Stimulant and Alcohol groups in Table 3, the r parameter was higher in the stimulant group, but the p and d parameters were remarkably similar. Stimulant preference was associated with a significantly higher r parameter than alcohol preference, χ2(1) = 4.28, p < .05, odds-ratio = 15.0, γ = .35. Even when compared to the control group, the stimulant group’s r was marginally higher, χ2(1) = 3.03, odds-ratio = 8.9, p < .09, γ = .21. However, the alcohol and the control groups’ r parameters were not significantly different from one another, p > .30. There were no significant differences between the stimulant and alcohol groups in the p and d parameters, ps > .60.
General Discussion
Quantitative and qualitative analyses suggest that a three parameter sequential learning model can provide a reasonable fit to WCST data. Interestingly, the three processes implicated here are reminiscent of the processes that were speculated about six decades ago. Zable and Harlow speculated that WCST performance depended on the “rate of habit formation, rate of habit extinction, and response variability” (1946, p. 23), which are notably similar to attention shifting following reward, attention shifting following punishment, and decision-consistency. We arrived at our model independently of Zable and Harlow’s ideas, and so there are some differences in conceptualization. Most importantly, our formalization and model fitting provides psychometric precision to assessing such processes in the WCST.3
The model parameters suggest a nuanced interpretation of WCST performance in substance dependence, an interpretation that can be connected to a broader literature on cognition and decision-making. Compared to healthy controls, SDI showed slower attention shifting following punishment. This pattern is consistent with previous evidence of insensitivity to negative feedback and inhibitory failures in substance users (Garavan & Stout, 2005; Hester, Simões-Franklin, & Garavan, 2007; Salo et al., 2005). SDI also showed a lower decision-consistency parameter. This pattern is consistent with the haphazard decision-making observed in substance users on other tasks (e.g., Ersche et al., 2005).
Whereas the p and d parameters differed between SDI and controls, there was some evidence that the r parameter distinguished different kinds of SDI. Compared to the alcohol group, the stimulant group showed faster attention shifting following rewarded trials. It is possible that stimulant users are more sensitized to rewards because stimulants act more directly on the dopamine system than alcohol does (Grace, 2000).
The finding of lower decision-consistency in substance users on the WCST converges with findings from a cognitive model of the Iowa Gambling Task (IGT). Substance users often show lower consistency on that task when performance is analyzed via the Expectancy Valence Learning (EVL) model (Busemeyer & Stout, 2002; for discussion of decision-consistency and substance use, see Bishara et al., under review; Stout et al., 2004). Though the mathematics behind the d parameter here and the consistency parameter in the EVL model are similar, they are not identical. In the EVL model, consistency represents not just how decisions match learning, but how that changes over time. That is, the construct of decision-consistency may overlap only slightly across tasks and models (Bishara et al., under review).
Other parameters may overlap even less. There is a superficial similarity between the attention to losses parameter of the IGT and the r and p parameters of the WCST. However, the bases of these parameters most likely differ across the two tasks. The WCST involves an extradimensional shift of attention, whereas the IGT involves shifting valences within each deck, a process more akin to reversal learning (Fellows & Farah, 2005). Extradimensional and reversal shifts have been modeled via distinct mechanisms (Kruschke, 1996). Perhaps because of this distinction, the WCST tends to involve lateral areas of prefrontal cortex (Monchi et al., 2001) whereas the IGT tends to involve medial areas of prefrontal cortex (Bechara, Damasio, Damasio, & Anderson, 1994; also see Dias, Robbins, & Roberts, 1996). Thus, the EVL model and the WCST model used here might overlap in their assessment of decision consistency, but less so in their assessment of other parameters. Of course, more research is needed to directly compare the two models and tasks.
We have suggested that cognitive modeling is valuable because it allows for a nuanced theoretical analysis of WCST performance. That is, cognitive modeling provides incremental content validity to the WCST (see Haynes & Lench, 2003). However, perhaps an even greater contribution of the modeling is that it improves discrimination between SDI and healthy controls, i.e., the modeling provides incremental predictive validity. The model parameters here were able to significantly predict group membership even when controlling for traditional measures of the WCST, measures that had become popular in part because of their ability to distinguish clinical populations from controls. Of course, our logistic regression results should be interpreted with some caution. In order to provide stronger evidence of the incremental predictive validity of our model, larger samples would be desirable in future research, as well as separate calibration and validation samples.
Conclusion
The WCST is enormously popular in clinical neuropsychology. In one survey of neuropsychologists, 71% reported using the WCST with most of their patients, and the WCST was the most commonly used task to measure executive function (Butler et al., 1991). However, WCST interpretation is complicated because task performance can reflect multiple processes. Modeling approaches hold the promise of moving beyond simplistic “one task equals one process” interpretations, thereby improving the analytical and diagnostic capabilities of the WCST.
Acknowledgments
We thank Branden Sims, Kelly Sullivan, Kaitlyn Lennox, and Bethany Ward-Bluhm for assistance with coding data and other aspects of the research, Daniel Kimberg for sharing code and methodological details, and Daniel Fridberg, Sarah Queller, George Rebec, and Katie Whitlock for helpful feedback.
This research was supported in part by National Institute on Drug Abuse grant DA R01 014119, NIMH Research Training Grant in Clinical Science T32 MH17146, and National Institute of Mental Health Cognition and Perception Grant MH068346.
Appendix: Modeling Methods
All of the model evaluations are based on “one step ahead” predictions generated by each model for each individual participant. The accuracy of these predictions is measured using the log likelihood criterion. To be more specific, for a given subject, let yt be a t x 1 vector representing the sequence of choices up to and including trial t, and let xt be the corresponding sequence of “right” and “wrong” feedback. Let Pt+1,k|yt,xt be a model’s predicted choice probability for the next trial (t +1) and pile k given information about choices and feedback only up to trial t. Finally, let δt,k be the observed choice made by a decision maker on trial t for pile k, such that δt,k = 1 if k was chosen on trial t; else δt,k = 0. The log likelihood of the model (LLmodel) is determined by predictions for one trial ahead, summed across trials and piles:
| (A1) |
where v is the number of trials administered minus 1.
Because LL measures goodness of fit, −LL measures badness of fit. Parameters were estimated by minimizing −LL separately for each participant and each model. Estimation was implemented with the programming language “R” (R Development Core Team, 2006) using the robust combination of a simplex method (Nelder & Mead, 1965) and multiple quasi-random starting points.
BIC was also used to measure model performance:
| (A2) |
In the right side of Equation A2, the first expression represents badness of model fit. The second expression represents a penalty for model complexity, where u is the number of free parameters in the model, and v is the number of observations modeled for the participant (number of trials administered minus 1).
Footnotes
We examined over 30 variants of the models presented here, but for space considerations, only 12 models are reported in detail. For example, we examined models where attention shifting rates increased across trials. We do not to report these and other models due to extremely poor fits and/or unstable parameter estimates.
To approximate f⃗0, we used the constraint f=.0001.
Compared to Zable and Harlow’s conceptualization, ours is more cognitive, emphasizing an unobservable vector of attention weights. An additional difference is that our formalization treats r, p, and d as stationary across trials, whereas Zable and Harlow were speculating about rates of change across trials.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amos A. A computational model of information processing in the frontal cortex and basal ganglia. Journal of Cognitive Neuroscience. 2000;12:505–519. doi: 10.1162/089892900562174. [DOI] [PubMed] [Google Scholar]
- Batchelder WH. Multinomial processing tree models and psychological assessment. Psychological Assessment. 1998;10:331–344. doi: 10.1037//1040-3590.14.2.184. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H. Decision-making and addiction (part I): Impaired activation of somatic states in substance dependent individuals when pondering decisions with negative future consequences. Neuropsychologia. 2002;40:1675–1689. doi: 10.1016/s0028-3932(02)00015-5. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio AR, Damasio H, Anderson SW. Insensitivity to future consequences following damage to human prefrontal cortex. Cognition. 1994;50(1–3):7–15. doi: 10.1016/0010-0277(94)90018-3. [DOI] [PubMed] [Google Scholar]
- Bechara A, Dolan S, Denburg N, Hindes A, Anderson SW, Nathan PE. Decision-making deficits, linked to a dysfunctional ventromedial prefrontal cortex, revealed in alcohol and stimulant abusers. Neuropsychologia. 2001;39:376–389. doi: 10.1016/s0028-3932(00)00136-6. [DOI] [PubMed] [Google Scholar]
- Bechara A, Dolan S, Hindes A. Decision-making and addiction (part II): Myopia for the future or hypersensitivity to reward? Neuropsychologia. 2002;40:1690–1705. doi: 10.1016/s0028-3932(02)00016-7. [DOI] [PubMed] [Google Scholar]
- Berg EA. A simple objective technique for measuring flexibility in thinking. Journal of General Psychology. 1948;39:15–22. doi: 10.1080/00221309.1948.9918159. [DOI] [PubMed] [Google Scholar]
- Bishara AJ, Pleskac TJ, Fridberg DJ, Yechiam E, Lucas J, Busemeyer JR, Finn PR, Stout JC. Models of risky decision-making in stimulant and marijuana users. doi: 10.1002/bdm.641. under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bondi MW, Monsch AU, Butters N, Salmon DP. Utility of a modified version of the Wisconsin Card Sorting test in the detection of dementia of the Alzheimer type. Clinical Neuropsychologist. 1993;7(2):161–170. doi: 10.1080/13854049308401518. [DOI] [PubMed] [Google Scholar]
- Braff DL, Heaton RK, Kuck J, Cullum M. The generalized pattern of neuropsychological deficits in outpatients with chronic schizophrenia with heterogeneous Wisconsin Card Sorting Test results. Archives of General Psychiatry. 1991;48(10):891–898. doi: 10.1001/archpsyc.1991.01810340023003. [DOI] [PubMed] [Google Scholar]
- Burgess P, Alderman N, Evans J, Emslie H, Wilson B. The ecological validity of tests of executive function. Journal of the International Neuropsychological Society. 1998;4(6):547–558. doi: 10.1017/s1355617798466037. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Stout JC. A contribution of cognitive decision models to clinical assessment: Decomposing performance on the Bechara Gambling Task. Psychological Assessment. 2002;14:253–262. doi: 10.1037//1040-3590.14.3.253. [DOI] [PubMed] [Google Scholar]
- Butler M, Retzlaff PD, Vanderploeg R. Neuropsychological test usage. Professional Psychology: Research and Practice. 1991;22(6):510–512. [Google Scholar]
- Carter CS, Braver TS, Barch DM, Botvinick MM, Noll D, Cohen JD. Anterior cingulate cortex, error detection, and the online monitoring of performance. Science. 1998;280(5364):747–749. doi: 10.1126/science.280.5364.747. [DOI] [PubMed] [Google Scholar]
- Carter CS, Macdonald AM, Botvinick M, Ross LL, Stenger VA, Noll D, et al. Parsing executive processes: Strategic vs. evaluative functions of the anterior cingulate cortex. Proceedings of the National Academies of Sciences. 2000;97(4):1944–1948. doi: 10.1073/pnas.97.4.1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter JR. Unpublished doctoral dissertation. University of Western Ontario; 2000. Facial expression analysis in schizophrenia. [Google Scholar]
- Dehaene S, Changeux JP. The Wisconsin Card Sorting Test: Theoretical analysis and modeling in a neuronal network. Cerebral Cortex. 1991;1:62–79.3. doi: 10.1093/cercor/1.1.62. [DOI] [PubMed] [Google Scholar]
- Demakis GJ. A meta-analytic review of the sensitivity of the Wisconsin Card Sorting Test to frontal and lateralized frontal brain damage. Neuropsychology. 2003;17:255–264. doi: 10.1037/0894-4105.17.2.255. [DOI] [PubMed] [Google Scholar]
- Dias R, Robbins TW, Roberts AC. Dissociation in prefrontal cortex of affective and attentional shifts. Nature. 1996;380:69–72. doi: 10.1038/380069a0. [DOI] [PubMed] [Google Scholar]
- Ersche KD, Clark L, London M, Robbins TW, Sahakian BJ. Profile of executive and memory function associated with amphetamine and opiate dependence. Neuropsychopharmacology. 2005;31(5):1036–1047. doi: 10.1038/sj.npp.1300889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evenden JL. Varieties of impulsivity. Psychopharmacology. 1999;146(4):348–361. doi: 10.1007/pl00005481. [DOI] [PubMed] [Google Scholar]
- Fellows LK, Farah MJ. Different underlying impairments in decision-making following ventromedial and dorsolateral frontal lobe damage in humans. Cerebral Cortex. 2005;15(1):58–63. doi: 10.1093/cercor/bhh108. [DOI] [PubMed] [Google Scholar]
- First MB, Spitzer RL, Gibbon M, Williams JBW. Structured Clinical Interview for DSM-IV Axis I Disorders, Research Version, Non-patient Edition (SCID-I:NP) New York: Biometrics Research, New York State Psychiatric Institute; 1997. [Google Scholar]
- Garavan H, Stout JC. Neurocognitive insights into substance abuse. Trends in Cognitive Sciences. 2005;9:195–201. doi: 10.1016/j.tics.2005.02.008. [DOI] [PubMed] [Google Scholar]
- Grace AA. The tonic/phasic model of dopamine system regulation and its implications for understanding alcohol and psychostimulant craving. Addiction. 2000;95:S119–128. doi: 10.1080/09652140050111690. [DOI] [PubMed] [Google Scholar]
- Grant DA, Berg EA. A behavioral analysis of degree of reinforcement and ease of shifting to new responses in a Weigl-type card-sorting problem. Journal of Experimental Psychology. 1948;38:404–411. doi: 10.1037/h0059831. [DOI] [PubMed] [Google Scholar]
- Greve KW, Ingram F, Bianchini KJ. Latent structure of the Wisconsin Card Sorting Test in a clinical sample. Archives of Clinical Neuropsychology. 1998;13:597–609. [PubMed] [Google Scholar]
- Haynes S, Lench H. Incremental validity of new clinical assessment measures. Psychological Assessment. 2003;15(4):456–466. doi: 10.1037/1040-3590.15.4.456. [DOI] [PubMed] [Google Scholar]
- Heaton RK, Chelune GJ, Talley JL, Kay GG, Curtiss G. Wisconsin Card Sorting Test manual: Revised and expanded. Odessa, Fla: Psychological Assessment Resources Inc; 1993. [Google Scholar]
- Hester R, Simões-Franklin C, Garavan H. Post-error behavior in active cocaine users: Poor awareness of errors in the presence of intact performance adjustments. Neuropsychopharmacology. 2007;32:1974–1984. doi: 10.1038/sj.npp.1301326. [DOI] [PubMed] [Google Scholar]
- Jentsch JD, Taylor JR. Impulsivity resulting from frontostriatal dysfunction in drug abuse: Implications for the control of behavior by reward-related stimuli. Psychopharmacology. 1999;146(4):373–390. doi: 10.1007/pl00005483. [DOI] [PubMed] [Google Scholar]
- Kibby M, Schmitter-Edgecombe M, Long C. Ecological validity of neuropsychological tests: Focus on the California Verbal Learning Test and the Wisconsin Card Sorting Test. Archives of Clinical Neuropsychology. 1998;13(6):523–534. [PubMed] [Google Scholar]
- Kimberg DY, Farah MJ. A unified account of cognitive impairments following frontal lobe damage: The role of working memory in complex, organized behavior. Journal of Experimental Psychology: General. 1993;122:411–428. doi: 10.1037//0096-3445.122.4.411. [DOI] [PubMed] [Google Scholar]
- Kruschke JK. Dimensional relevance shifts in category learning. Connection Science. 1996;8:225–247. [Google Scholar]
- Kübler A, Murphy K, Garavan H. Cocaine dependence and attention switching within and between verbal and visuospatial working memory. European Journal of Neuroscience. 2005;21:1984–1992. doi: 10.1111/j.1460-9568.2005.04027.x. [DOI] [PubMed] [Google Scholar]
- Levine DS, Prueitt PS. Modeling some effects of frontal lobe damage: Novelty and perseveration. Neural Networks. 1989;2:103–116. [Google Scholar]
- Little A, Templer D, Persel C, Ashley M. Feasibility of the neuropsychological spectrum in prediction of outcome following head injury. Journal of Clinical Psychology. 1996;52(4):455–460. doi: 10.1002/(SICI)1097-4679(199607)52:4<455::AID-JCLP11>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- Mansouri FA, Matsumoto K, Tanaka K. Prefrontal cell activities related to monkeys’ success and failure in adapting to rule changes in a Wisconsin Card Sorting Test analog. Journal of Neuroscience. 2006;26:2745–2756. doi: 10.1523/JNEUROSCI.5238-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin RC, Caramazza A. Classification in well-defined and ill-defined categories: Evidence for common processing strategies. Journal of Experimental Psychology: General. 1980;109(3):320–353. doi: 10.1037//0096-3445.109.3.320. [DOI] [PubMed] [Google Scholar]
- Milner B. Effects of brain lesions on card sorting. Archives of Neurology. 1963;9:100–110. [Google Scholar]
- Monchi O, Petrides M, Doyon J, Postuma RB, Worsley K, Dagher A. Neural bases of set-shifting deficits in Parkinson’s disease. Journal of Neuroscience. 2004;24(3):702–710. doi: 10.1523/JNEUROSCI.4860-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monchi O, Petrides M, Petre V, Worsley K, Dagher A. Wisconsin card sorting revisited: Distinct neural circuits participating in different stages of the task identified by event-related functional magnetic resonance imaging. Journal of Neuroscience. 2001;21(19):7733–7741. doi: 10.1523/JNEUROSCI.21-19-07733.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monchi O, Taylor JG, Dagher A. A neural model of working memory processes in normal subjects, Parkinson’s disease and schizophrenia for fMRI design and predictions. Neural Networks. 2000;13:953–973. doi: 10.1016/s0893-6080(00)00058-7. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- Nelson HE. A modified card sorting test sensitive to frontal lobe defects. Cortex. 1976;12(4):313–324. doi: 10.1016/s0010-9452(76)80035-4. [DOI] [PubMed] [Google Scholar]
- Neufeld RWJ, editor. Advances in Clinical Cognitive Science: Formal Modeling of Processes and Symptoms. Washington, DC: American Psychological Association; 2007. [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. 2006 Retrieved from http://www.R-project.org.
- Rabin LA, Barr WB, Burton LA. Assessment practices of clinical neuropsychologists in the United States and Canada: A survey of INS, NAN, and APA Division 40 members. Archives of Clinical Neuropsychology. 2005;20:33–65. doi: 10.1016/j.acn.2004.02.005. [DOI] [PubMed] [Google Scholar]
- Rougier NP, O’Reilly RC. Learning representations in a gated prefrontal cortex model of dynamic task switching. Cognitive Science. 2002;26:503–520. [Google Scholar]
- Salo R, Nordahl TE, Moore C, Waters C, Natsuaki Y, Galloway GP, et al. A dissociation in attentional control: Evidence from methamphetamine dependence. Biological Psychiatry. 2005;57:310–313. doi: 10.1016/j.biopsych.2004.10.035. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Stout JC, Busemeyer JR, Lin A, Grant SJ, Bonson KR. Cognitive modeling analysis of decision-making processes in cocaine abusers. Psychonomic Bulletin & Review. 2004;11(4):742–747. doi: 10.3758/bf03196629. [DOI] [PubMed] [Google Scholar]
- Tarter RE, Kirisci L, Mezzich A, Cornelius JR, Pajer K, Vanyukov M, et al. Neurobehavioral disinhibition in childhood predicts early age at onset of substance use disorder. American Journal of Psychiatry. 2003;160:1078–1085. doi: 10.1176/appi.ajp.160.6.1078. [DOI] [PubMed] [Google Scholar]
- Volkow ND, Fowler JS, Wang GJ, Hitzemann R, Logan J, Schlyer DJ, et al. Decreased dopamine D2 receptor availability is associated with reduced frontal metabolism in cocaine abusers. Synapse. 1993;14:169–177. doi: 10.1002/syn.890140210. [DOI] [PubMed] [Google Scholar]
- Wallsten TS, Pleskac TJ, Lejuez CW. Modeling behavior in a clinically diagnostic sequential risk-taking task. Psychological Review. 2005;112(4):862–880. doi: 10.1037/0033-295X.112.4.862. [DOI] [PubMed] [Google Scholar]
- Willuhn I, Sun W, Steiner H. Topography of cocaine-induced gene regulation in the rat striatum: Relationship to cortical inputs and role of behavioural context. European Journal of Neuroscience. 2003;17:1053–1066. doi: 10.1046/j.1460-9568.2003.02525.x. [DOI] [PubMed] [Google Scholar]
- Yechiam E, Goodnight J, Bates JE, Busemeyer JR, Dodge KA, Pettit GS, et al. A formal cognitive model of the go/no-go discrimination task: Evaluation and implications. Psychological Assessment. 2006;18:239–249. doi: 10.1037/1040-3590.18.3.239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zable M, Harlow HF. The performance of rhesus monkeys on series of object-quality and positional discriminations and discrimination reversals. Journal of Comparative Psychology. 1946;39:13–23. doi: 10.1037/h0056082. [DOI] [PubMed] [Google Scholar]
- Zakzanis KK. The subcortical dementia of Huntington’s disease. Journal of Clinical and Experimental Neuropsychology. 1998;20(4):565–578. doi: 10.1076/jcen.20.4.565.1468. [DOI] [PubMed] [Google Scholar]