Quantitative Analysis of Synaptic Release at the Photoreceptor Synapse

Abstract

Exocytosis from the rod photoreceptor is stimulated by submicromolar Ca²⁺ and exhibits an unusually shallow dependence on presynaptic Ca²⁺. To provide a quantitative description of the photoreceptor Ca²⁺ sensor for exocytosis, we tested a family of conventional and allosteric computational models describing the final Ca²⁺-binding steps leading to exocytosis. Simulations were fit to two measures of release, evoked by flash-photolysis of caged Ca²⁺: exocytotic capacitance changes from individual rods and postsynaptic currents of second-order neurons. The best simulations supported the occupancy of only two Ca²⁺ binding sites on the rod Ca²⁺ sensor rather than the typical four or five. For most models, the on-rates for Ca²⁺ binding and maximal fusion rate were comparable to those of other neurons. However, the off-rates for Ca²⁺ unbinding were unexpectedly slow. In addition to contributing to the high-affinity of the photoreceptor Ca²⁺ sensor, slow Ca²⁺ unbinding may support the fusion of vesicles located at a distance from Ca²⁺ channels. In addition, partial sensor occupancy due to slow unbinding may contribute to the linearization of the first synapse in vision.

Introduction

Synaptic exocytosis from rod photoreceptors shows an unusually high affinity for calcium, with release evoked by submicromolar calcium (1,2). The shallow dependence of release rate on calcium in rods is consistent with fusion initiated by the binding of no more than three calcium ions to a sensor (1). This weak cooperativity may contribute to the linear relationship between calcium influx and release at photoreceptor synapses (1) and contrasts with release at other ribbon and conventional synapses, which show fourth- or fifth-order calcium dependence (3–6).

The mechanism(s) responsible for the unusual features of rod exocytosis is not clear. The conventional model of a calcium sensor that triggers release only after it binds four or five calcium ions fails to describe the rod data (1). One possibility is that photoreceptors use a unique sensor. Alternatively, they may use a conventional calcium sensor that behaves in an allosteric manner, triggering release with low cooperativity at low calcium levels, when fewer binding sites are occupied, and with higher cooperativity at higher calcium levels, when more of the binding sites are occupied (7). An allosteric sensor could thus potentially accommodate both the unusual properties of rod exocytosis and release at other synapses. Finally, rods might use a calcium sensor similar to that proposed to control asynchronous release at the calyx of Held, which has been modeled with only two calcium binding sites (8).

We tested a family of allosteric and conventional computational models to describe the final calcium binding steps of exocytosis from rod terminals. Measurements of release included exocytotic capacitance changes (1) and postsynaptic currents obtained during simultaneous whole cell recordings from photoreceptors and postsynaptic OFF bipolar and horizontal cells. Both were evoked by the abrupt elevation of intraterminal calcium produced by flash-photolysis of caged-calcium. The best descriptions of release were obtained with models in which two calcium binding sites were occupied. For all models, the sensor was more sensitive to calcium relative to other neurons by approximately an order of magnitude. This high sensitivity arose from an unusually slow rate of calcium unbinding. Thus, the photoreceptor calcium sensor exhibits properties that contribute to the unique features of photoreceptor synaptic transmission.

Methods

Recordings were obtained from retinal neurons of aquatic tiger salamanders (Ambystoma tigrinum; 18–25 cm in length). Animals were handled according to protocols approved by the UNMC Institutional Animal Care and Use Committee. The salamander was decapitated and the brain and spinal cord were rapidly pithed. Retinal slices were prepared as described previously (9). Slices were superfused at ∼1 mL/min with an oxygenated solution containing (in mM): 111 NaCl, 2.5 KCl, 1.8 CaCl₂, 0.5 MgCl₂, 10 HEPES, 5 glucose, 0.1 picrotoxin, 0.001 strychnine (pH 7.8). The use of HEPES minimized effects of vesicular protons (10,11).

Whole cell recordings were obtained from rods or cones and simultaneously from OFF bipolar or horizontal cells using 8–15 MΩ patch electrodes pulled from borosilicate glass (1.2 mm O.D., 0.95 mm I.D., with internal filament;, World Precision Instruments, Sarasota, FL) on a PP-830 micropipette puller (Narishige, East Meadow, NY). The pipette solution for second order neurons contained (in mM): 94 CsGluconate, 9.4 TEACl, 1.9 MgCl₂, 9.4 MgATP, 0.5 GTP, 0.5 EGTA, 32.9 HEPES (pH 7.2).

Photoreceptors were held at −70 mV using an Optopatch amplifier (Cairn Instruments, Faversham, UK). Bipolar cells were voltage clamped at −50 mV and horizontal cells at −60 mV using an Axopatch 200B (Axon Instruments, Foster City, CA). Recording pipettes were positioned with Huxley-Wall micromanipulators (Sutter Instruments, Novato, CA). Currents were acquired using Digidata 1320 interfaces and pClamp 8.1 software (Axon Instruments). Horizontal and OFF bipolar cells were distinguished by their response characteristics (12) and anatomically by sulfarhodamine B (0.5 mg/mL) added to the pipette solution. Charging curves for rods, cones, bipolar cells, and many horizontal cells could be fit by single exponentials, indicating compact electrotonic structures (9). The finding that a single exponential fitted the charging curves of most horizontal cells examined indicates that they were largely uncoupled from their neighbors in the retinal slice preparations used for these studies.

Flash photolysis of the photolyzable Ca²⁺ chelator, DM-nitrophen, allows rapid and spatially homogenous increases in intracellular Ca²⁺ throughout the terminal and gives the ability to estimate the Ca²⁺ concentration near the release site. The pipette solution for photoreceptors consisted of (in mM): 10 DM-nitrophen (Invitrogen, Carlsbad, CA), 5 CaCl₂, 4 MgCl₂, 26 CsGluconate, 7.8 HEPES, 6.5 TEACl, 11 Na₂ATP, 0.5 GTP, 0.5 Oregon Green BAPTA 6F (Invitrogen), (pH 7.4). DM-nitrophen was photolyzed by flashes of UV light derived from a Xenon arc flash lamp (Rapp Optoelectronic, Hamburg, Germany). Near maximal voltage settings (3 capacitors, 300 V) were used for most experiments. With these settings, photodiode measurements of flash lamp output reached peak intensity within ∼5 μs and lasted ∼1.5 ms total. Response latencies were often <1.5 ms, indicating that Ca²⁺ was uncaged rapidly after the flash reached its peak. Postsynaptic current latency was measured from a time point 100 μs after the flash reached its peak.

Photoreceptors were imaged with a confocal microscope containing a laser confocal scanhead (Ultraview LCI; Perkin Elmer, Waltham, MA), cooled CCD camera (Orca ER; Hamamatsu USA, Bridgewater, NJ), and upright compound microscope (E600 FN; Nikon, Melville, NY). Images were acquired at 60-ms intervals with single frame durations of 48–56 ms and pixel values were binned 2 × 2. Images were analyzed using UltraView Imaging Suite software (Perkin Elmer). To determine changes in Ca²⁺ with OGB-6F, we used the following formula (13):

$$\Delta \left[{\text{Ca}}_{\mathrm{i}}^{2+}\right]=\left({\left[{\text{Ca}}^{2+}\right]}_{\text{rest}}+K_{\mathrm{d}}\left(\Delta F/F\right)/{\left(\Delta F/F\right)}_{\max }\right)/1-\left(\Delta F/F\right)/{\left(\Delta F/F\right)}_{\max })\text{.}$$ (1)

ΔF/F represents the fractional change in fluorescence resulting from stimulation. (ΔF/F)_max was determined from the maximal fluorescence change produced by a 500-ms depolarization to −10 mV. We used the K_d of 3 μM for OGB-6F provided by Invitrogen. The resting Ca²⁺ concentration ([Ca²⁺]_rest) for each solution was determined ratiometrically using 0.2 mM Fura-2 as described previously (1). As a test of the Ca²⁺ measurements obtained with Eq. 1, we compared OGB-6F measurements with measurements made using a higher affinity dye, OGB-BAPTA 1 (K_d = 0.17 μM). Despite differences in the K_d, depolarizing test steps of −70 to −10 mV yielded similar intraterminal [Ca²⁺] measured with both dyes (14).

To mathematically model the calcium-dependence of both the rate and latency of exocytosis, calcium-dependent exocytosis was modeled as a series of calcium-binding steps followed by a calcium-independent fusion step (Fig. 1; see also Thoreson et al. (1), Heidelberger et al. (3), and Lou et al. (7)). The transitions between the steps were represented mathematically as a system whose dynamics are governed by a set of linear ordinary differential equations. For each model, an associated set of parameters was found using the Metropolis-Hastings algorithm (15). The range of parameters was restricted to physiologically realistic values (Table 1). In addition, possible values of α and β were further restricted such that α ≥ β, and I^∗f⁵ was restricted to values ≤6500 s⁻¹. Where indicated, a rate of 400 s⁻¹ at 10 μM calcium, adapted from Kreft et al. (16), was added to the rate versus calcium data set and given quadruple weighting. In addition, our estimated rate of spontaneous release was assigned a calcium concentration of 1 × 10⁻⁹ M, except where noted, and given quadruple weighting.

Figure 1.

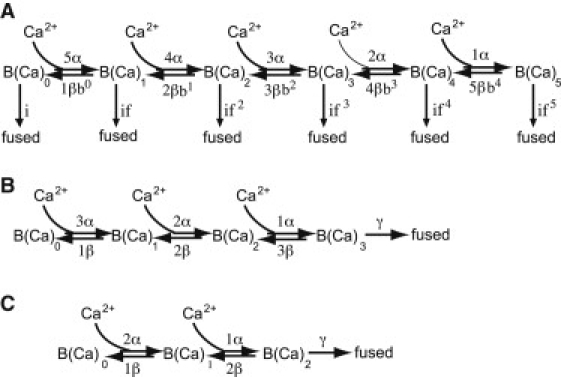
Schematic of models. (A) An allosteric model in which release can occur from any occupancy state of a calcium sensor with five calcium binding sites. (B) Conventional model with three Ca²⁺ binding sites. In this model, release is restricted to the fully-occupied sensor and there is no additional cooperativity between binding sites. (C) Conventional two-site model.

Table 1.

Parameter ranges

Range	α (M−1s−1)	β (s−1)	b	γ (s−1)	i (s−1)	f
Minimum	1 × 10−5	1 × 10−5	0.1	100	1 × 10−4	5
Maximum	1 × 109	1 × 109	1	10,000	5 × 10−3	40
Step size	3	3	0.1	10	6 × 10−4	1.2

Simulations were run in the MATLAB environment (The MathWorks, Natick, MA) on an Apple G5 dual-core Intel Xeon computer (2.66 GHz) or a Penguin computing high performance 64-bit architecture Beowulf cluster. Each simulation was initialized at six starting points chosen randomly and allowed to explore the parameter space for 1 × 10⁶ iterations. The sum of squared errors cost-function was used to simultaneously provide the best fit to the rate versus calcium and latency versus calcium data sets. In keeping with the literature on Metropolis-Hastings (15,17), ∼15–50% of the 1 × 10⁶ proposed parameters were kept by using a manually tuned step-size (Table 1). The range of permissible α- and β-values was much larger than the other parameters, so these two dimensions of the parameter space were explored in log-space. To visualize the multidimensional posterior distribution of parameter choices from Metropolis-Hastings, parameter sets were plotted using the parallel coordinates method and weighted by their goodness of fit (17). For α and β, the normalization was carried out in log-space.

The criterion for statistical significance was chosen to be p < 0.05 and evaluated with Student's t-tests. Variability is reported as ± SE.

Results

When exocytosis is evoked by the rapid and homogeneous photolytic release of caged-calcium, the measured change in spatially-averaged calcium is believed to reflect the local calcium concentration near release sites, whereas the kinetics of exocytosis reflect the calcium binding properties of the calcium sensor that triggers exocytosis (3,18). In rod photoreceptors, the elevation of intraterminal Ca²⁺ to submicromolar levels by flash-photolysis of caged-calcium stimulates capacitance changes consistent with exocytosis (1,2). This finding, along with the unusually shallow relationship between the rate of exocytosis and intraterminal calcium, raised the question of whether photoreceptors use a novel calcium sensor for driving neurotransmitter release. To address this question, we chose a quantitative modeling approach that required knowledge of both the calcium-dependence of the rate of release, obtained in our previous study (1), and new information about the calcium dependence of the latency to the first fusion event. Such information was difficult to obtain from the capacitance records due to their noise and slow rates of rise (1).

We measured the calcium-dependence of the latency to release by stimulating release from photoreceptors in retinal slices using flash-photolysis of caged-calcium and measuring the postsynaptic currents recorded simultaneously from horizontal or OFF bipolar cells. To visualize calcium changes in individual rod terminals in the retinal slice during paired recordings, we used a confocal microscope and the calcium-sensitive dye, Oregon Green BAPTA 6F (Fig. 2). In the experiment illustrated in Fig. 2, flash photolysis of the caged calcium compound, DM-nitrophen, caused an abrupt increase in intraterminal calcium levels from ∼100 nM to ∼900 nM and produced a postsynaptic current in the simultaneously recorded second order horizontal cell. Images of the rod before and after flash photolysis are shown above the graph.

Figure 2.

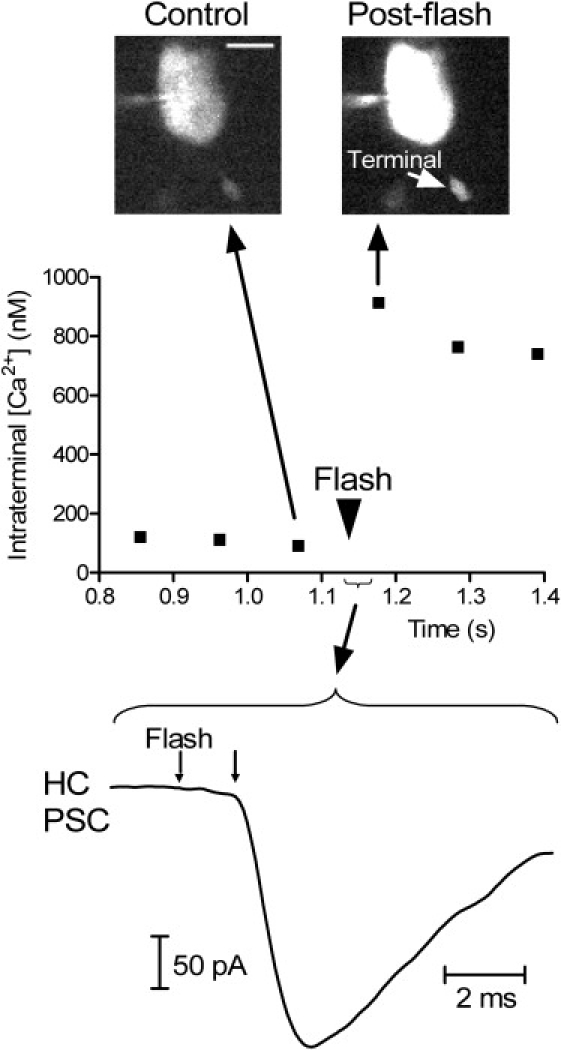
Example of latency measurements obtained with a paired recording from a rod and horizontal cell. Top graph shows intraterminal Ca²⁺ increase evoked by flash photolysis of DM-nitrophen. OGB-6F fluorescence was measured within the synaptic terminal of the rod shown in the control and postflash images above the graph. Scale bar = 5 μm. The trace at the bottom of the figure shows the postsynaptic current of the horizontal evoked by flash photolysis of caged Ca²⁺ in this rod. Latency was measured from the occurrence of flash to the beginning of the postsynaptic current indicated by the arrows.

We measured the latency from the flash to the initial inflection point of the excitatory postsynaptic current, i.e., the time to first vesicle fusion (Fig. 2, arrows). Fig. 3 A shows latencies measured from 26 rod/horizontal cell or rod/OFF bipolar cell pairs. Consistent with results from capacitance experiments (1,2), submicromolar Ca²⁺ levels evoked fast excitatory postsynaptic currents in second order neurons with a threshold for detectable postsynaptic currents of ∼400 nM. Response latency diminished with higher calcium levels, approaching 0.6 ms when calcium levels exceeded 1 μM. These are similar to the synaptic delays at conventional CNS synapses (19). The time required for the postsynaptic current to reach its peak after flash photolysis of caged Ca²⁺ also diminished with increasing Ca²⁺ levels (Fig. 3 B).

Figure 3.

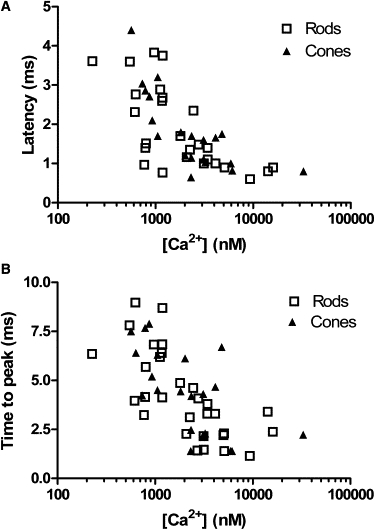
Ca²⁺ dependence of postsynaptic currents in OFF bipolar and horizontal cells evoked by flash photolysis of caged Ca²⁺ in rods. (A) Latency to beginning of postsynaptic versus intraterminal [Ca²⁺] measured using OGB-6F. (B) Latency to the peak of the postsynaptic current versus [Ca²⁺]. Squares, rods; triangles, cones.

Release from cones showed the same latency to fusion and time to peak as release from rods (Fig. 3 A) with a threshold of ∼400 nM and minimum latency of 0.65 ms (N = 21). These results are consistent with FM1-43 measurements (20) suggesting that release mechanisms in rods and cones have the same Ca²⁺ dependence.

To estimate the rate of spontaneous release from rods, we counted the number of individually distinguishable miniature excitatory post-synaptic currents recorded during the first 200 ms of responses to saturating 580 nm light flashes in OFF bipolar or horizontal cells (48.5 ± 7.7 v/s; N = 13; 8 OFF bipolar cells, 5 horizontal cells). We estimated the number of photoreceptors that contact each second order neuron by comparing the size of actual light-evoked currents to the size of postsynaptic currents evoked in the same OFF bipolar and horizontal cells by using a rod light response as the voltage clamp waveform in simultaneously recorded rods. The actual light-evoked current was 10.6 ± 1.7 times (N = 13; 9 horizontal cells, 4 OFF bipolar cells) larger than the postsynaptic current evoked by a light response waveform applied to a single rod suggesting that each second order neuron received inputs from ∼10 rods. Together, these results suggest release during a saturating bright light of ∼5 vesicles/rod/s. Assuming a total releasable pool size of 3500 vesicles (1), this corresponds to a release rate of ≈1.4 × 10⁻³ s (5 v s⁻¹/3500 v). This is an upper estimate of spontaneous release because it assumes that depolarization-associated release is entirely prevented by a saturating light flash. To depict results in log-space, the estimated spontaneous release rate was assigned a calcium value of 1 nM rather than 0.

Five-site allosteric model

To quantitatively examine the nature of the calcium sensor that drives release in the rod photoreceptor, we constructed mathematical models of the final calcium-dependent steps in the secretory pathway and compared the ability of these models to simultaneously simulate the calcium dependence of both the rate of exocytosis and the latency to first fusion event. In the five-site allosteric model (Fig. 1 A), release can occur from any occupancy state of a calcium sensor with five calcium binding sites. With zero calcium ions bound, there is a spontaneous release rate of i, and for each calcium ion that binds, the release rate becomes faster by a factor of f (7). With this model, the slope of the rate of fusion versus calcium relationship could range from zero to five, depending on the occupancy state of the calcium sensor. For the conventional models, release only occurs when all binding sites are occupied, and there is no term for spontaneous release.

For simplicity, we assumed that the calcium binding sites were equivalent and independent and modified the forward and backward rate constants, α and β, by the number of available binding sites. The parameter b, also called the cooperativity factor (3), was included in the backward (unbinding) direction. Values of b less than unity imply that there is something favorable about the fully-occupied state of the sensor that makes it more difficult for a calcium ion to dissociate, but as calcium ions begin to dissociate, it becomes progressively easier to remove the remaining ions.

The simulation with the five-site allosteric model that most closely matched both the rate and latency data is shown in Fig. 4, A and B, solid curve (see also Table 2). The on-rate, α, was 1.26 × 10⁸ M⁻¹ s⁻¹, comparable to the fastest on-rate reported for the calyx of Held, a conventional fast, spiking neuron (7). By contrast, the off-rate, β, of 145 s⁻¹ was approximately an order of magnitude slower than that of other neurons (3,5,6,8). The ratio of β/α, 1.15 μM, was indicative of a high-affinity receptor. Inspection of the posterior distribution of parameters (the conditional distribution of the parameters given the data) shows that the choice of α and β are tightly constrained by the data (Fig. 4 C, left). Parameter b was found to be close to 1.

Figure 4.

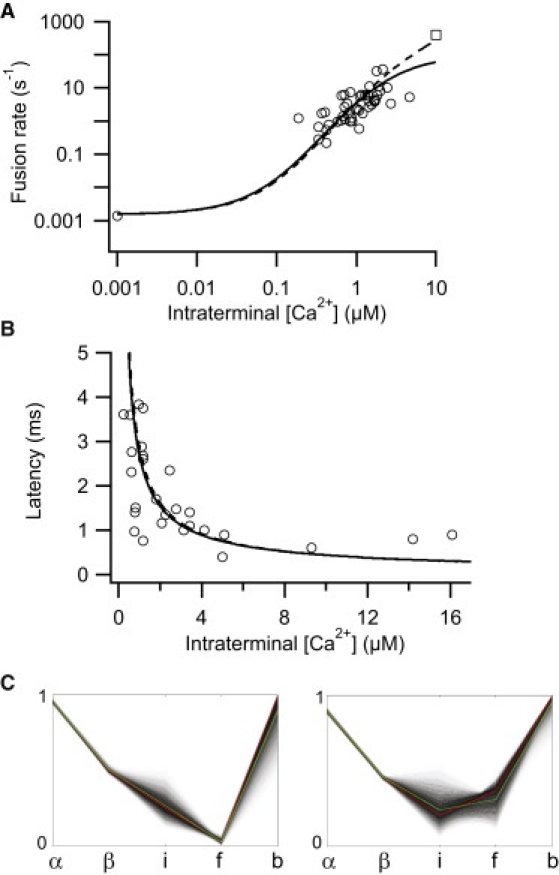
Simulations with the five-site allosteric model. (A) The rate of fusion plotted versus intraterminal [Ca²⁺]. Open circles represent rates of fusion derived from Thoreson et al. (1) and our estimate of spontaneous release. Open square depicts a weighted highpoint adapted from Kreft et al. (16). Shown are the best simulations to the data in the absence (solid curve) and presence (dashed curve) of the weighted highpoint (dashed curve). (B) Latency to postsynaptic current onset plotted against the intraterminal [Ca²⁺]. The best simulations using five-site allosteric model in the absence (solid curve) and presence (dashed curve) of a weighted high point. (C) Parallel coordinates plot of posterior distribution of normalized parameters in the absence (left) or presence of a weighted highpoint (right). Darker lines indicate better fits. Green and red lines are the mean and best fit, respectively.

Table 2.

Best parameter sets

Model	α (M−1s−1)	β (s−1)	b	i (s−1)	f	Maximum rate (s−1)	χ2
Five-site A	1.3 × 108	145	1.0	1.5 × 10−3	9.2	100	52
Five-site A∗	4.6 × 107	146	1.0	1.5 × 10−3	21.1	6490	68
Five-site A∗†	5.0 × 107	133	1.0	2.2 × 10−4	31.3	6448	76
Five-site A∗‡	4.2 × 107	148	1.0	5.0 × 10−3	16.7	5899	62
Five-site A§	1.5 × 108	161	1.0	1.4 × 10−4	14.7	100	60
Five-site A∗§	5.4 × 107	141	1.0	2.0 × 10−4	30.7	5369	77
Three-site C¶	2.3 × 107	54				2976	60
Three-site A	1.6 × 107	73	1.0	1.4 × 10−3	168	6453	42
Three-site A∗‖	3.3 × 107	151	1.0	1.2 × 10−3	129	2631	61
Two-site C¶	7.1 × 106	14				3634	40

A, allosteric model; C, conventional model.

^∗With weighted high point.

^†With spontaneous point at 2e⁻⁴.

^‡With spontaneous point at 5e⁻³.

^§With spontaneous point at 50 nM Ca²⁺.

^¶No weighted high point, no spontaneous point.

^‖b not well-defined, selected to be near 1.

The best simulation did not require that the rate of release continue to greatly rise as the Ca²⁺ concentration exceeded ∼5 μM (Fig. 4 A, solid curve). Accordingly, the slope of the rate versus calcium relationship did not rise above ∼2.5. To ascertain whether the rod photoreceptor might be capable of achieving a steeper relationship between rate and calcium at higher calcium concentrations, we needed data at higher calcium concentrations than we had attained. An earlier study suggested that increasing calcium >20 μM stimulated fusion at rates of ≈400 s⁻¹ in rod photoreceptors (16). Using this observation as a guide, we extended our data set by adding a single weighted data point at 10 μM calcium with a rate of 400 s⁻¹.

The best simulation obtained using the extended data set achieved a maximal rate of release at limiting calcium of 6490 s⁻¹ (Fig. 4, dashed curve; Table 2). This is comparable to the maximal rates reported for the calyx of Held (4–6,8). However, the slope of the rate versus calcium curve remained relatively shallow (Fig. 4 A). The preferred value for parameter b remained close to unity (Table 2). Inspection of the posterior distribution of parameters showed again that α and β are tightly constrained (Fig. 4 C, right). The on-rate, α, decreased with addition of the weighted high point; however, at 4.6 × 10⁷ M^-1s⁻¹, it was comparable to other estimates of neuronal on-rates (3,5,6). The value of β, 146 s⁻¹, was not appreciably affected by the addition of the weighted high point (Table 2), whereas the ratio β/α increased to ≈3.17 μM (Table 3).

Table 3.

Comparison with other neurons

Model	β/α (μM)	Time to leave fully-bound state (μs)	Off-rate of first Ca2+ to unbind (s−1)	Time for last Ca2+ to leave (ms)
Five-site A	1.15	1213	145	6.8
Five-site A∗	3.17	143	146	6.8
Five-site A∗†	2.61	165	141	7.1
Three-site A	4.69	150	73	13.7
Three-site A∗	4.5	325	148	6.6
Three-site C‡	2.32	319	54	18.5
Two-site C‡	1.98	273	14	71.4
Bipolar cell (3)	214	285	128	0.5
Hair cell (6)	77	508	55	0.465
Calyx five-site C (5)	105	103	37	0.105
Calyx five-site A (7)	40	138	250	0.25
Calyx dual sensor, fast (8)	38	164	23	0.172
Calyx dual sensor, slow (8)	44	160	130	7.69
Chromaffin cell three-site C (31)	≈10	700–2000	≈130	7.69

A, allosteric model; C, denotes conventional model.

^∗With weighted high point.

^†With spontaneous point at 50 nM Ca²⁺.

^‡No weighted high point, no spontaneous point.

To assess how the spontaneous release rate influences model parameters, the estimated spontaneous release rate in the extended date set was first decreased by approximately one order of magnitude to 2 × 10⁻⁴ s, the estimated spontaneous release rate at the calyx of Held (7). As expected, this caused a reduction in i in the model (Table 2), resulting in a compensatory increase in f, and a corresponding increase in if⁵, the maximal fusion rate. Importantly, the reduction in the rate of spontaneous release did not appreciably influence the forward and backward rate constants (α, β) or the cooperativity factor (b) (Table 2). The ratio of β/α decreased somewhat to 2.66 μM. We then asked how an increase in the estimated spontaneous release rate to 5 × 10⁻³ s⁻¹ would alter model parameters. This resulted in changes in both i and f as expected, and relatively minor changes in α and β (Table 2). β/α increased somewhat from 3.17 μM to 3.52 μM.

In the above simulations, we assumed that the estimated spontaneous release was calcium-independent. To determine how the simulations would be affected if the estimated spontaneous release were instead driven by basal calcium, we set the estimated spontaneous release rate at 50 nM calcium. For both our data set and the expanded data set, neither the forward and backward rate constants (α, β) nor b were greatly affected (Table 2). However, the spontaneous release rate, i, decreased by almost an order of magnitude, becoming virtually identical to that reported in the calyx of Held (7). This is consistent with the interpretation that our estimate of spontaneous release rate may include contributions from calcium-dependent release. The decrease in i was accompanied by a compensatory increase in f (Table 2).

Other models

Given the shallow slope of the data and the five-site allosteric model simulations, we asked whether a calcium sensor with three calcium binding sites would be sufficient to describe our data (see also Thoreson et al. (1)). We therefore coded a conventional three-site model (Fig. 1B) in which calcium-dependent release was restricted to the fully-occupied sensor and there was no interaction between binding sites (i.e., b = 1). The conventional three-site model does not explicitly provide for spontaneous, calcium-independent release, so we removed the spontaneous release rate datum from the data set.

The three-site conventional model provided an acceptable fit to both the rate and latency data (Fig. 5). The on-rate (α) was respectably fast for a neuron at 2.3 × 10⁷ M⁻¹s⁻¹. However, the off-rate, β, was unusually slow for a neuron at 54 s⁻¹ (2,4,5,8). The ratio of β/α was 2.32 μM. The maximal release rate, γ, for the best three-site simulation was ≈2976 s⁻¹, which is comparable to the maximal fusion rate in bipolar cells (3).

Figure 5.

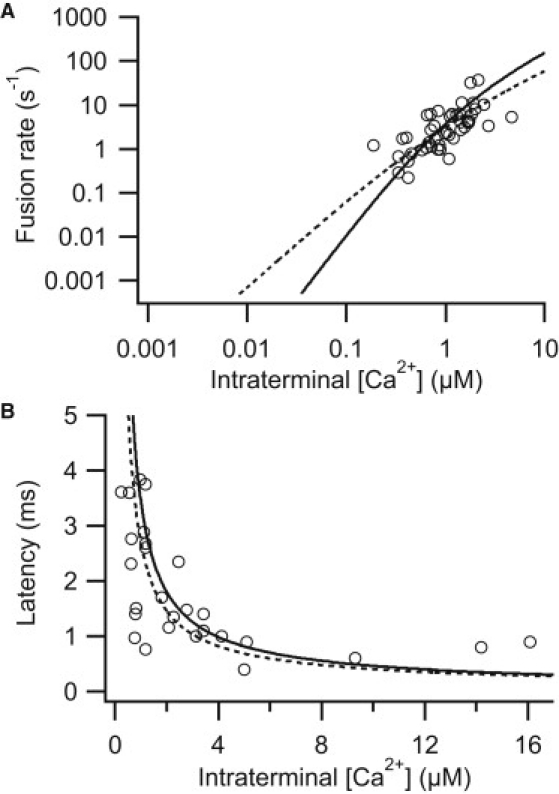
Simulations with two- and three-site conventional models. (A) Rate of fusion versus intraterminal [Ca²⁺] simulated with the three- (solid curve) and two-site (dashed curve) models. (B) Latency to the beginning of the postsynaptic current versus intraterminal [Ca²⁺] simulated with the three- (solid line) and two-site (dashed line) models.

For completeness, we also encoded a three-site allosteric model. We ran this model inclusive of the estimate of spontaneous release and also with the extended data set. As shown in Table 2, the parameter sets fall into the general pattern described for the previous two models. The on-rates were consistent with neuronal exocytosis, and the off-rates were unusually slow, indicative of a high-affinity binding site. The maximal release rates were also in the range typical of neurons (3,5,6,8).

It has been suggested recently that a neuron might contain both a traditional five-site calcium sensor and a second, unidentified two-site conventional calcium sensor (8). A two-site conventional model (Fig. 1 C) with the parameter set shown in Table 2 matched both the rate and latency data quite well (Fig. 5) and was better than the three-site model (Table 2). Both α and β were slower in the two-site model (Table 2). Interestingly, α was comparable to the on-rate suggested for the two-site sensor in the calyx of Held (8), whereas the off-rate was slower than that of the calyx by about an order of magnitude. The ratio of β/α was 1.98 μM, consistent with a high-affinity receptor. The maximal release rate, γ, was ≈3634 s⁻¹, similar to the maximal release rate of other neurons (3,5,6,8).

Discussion

At the photoreceptor synapse, light-evoked changes in membrane potential alter the likelihood of calcium channel opening. Unlike many synapses (21–25), both rod and cone photoreceptor synapses show a linear relationship between I_Ca and release (1,26). Although such linearity can arise from a linear relationship between the number of active release sites and number of open calcium channels (27–30), it may also arise at the level of the secretory machinery (1).

Our results indicate that a conventional two-site model, the most parsimonious model from a computational perspective, provides an excellent description of the physiological data. The data were also well-simulated with allosteric sensors with three or more calcium binding sites, but not conventional sensors with more than three binding sites. Interestingly, with all of the models, the rod photoreceptor sensor appeared unique among neurons in that it exhibited a profoundly slow rate of Ca²⁺ unbinding. These features are likely to contribute to the unusual linearity of this first synapse in vision.

Functional implications

The best simulations, irrespective of model form, share several features. For models of a similar form, the on-rates for Ca²⁺ binding predict that when given the appropriate Ca²⁺ stimulus, the photoreceptor release machinery is capable of driving release with minimal latencies that are comparable to other neurons, including a fast, spiking neuron, the calyx of Held (3,5,6,8). For most of the models, the simulated maximum fusion rates were also comparable among neurons. Thus, the photoreceptor Ca²⁺ sensor seems quite capable of rapidly signaling a change in illumination from light to dark.

The most profound finding is that each of the models predicted an unusually slow rate for the unbinding of Ca²⁺ from the rod sensor relative to other neurons (β, Table 2). However, the slow off-rate does not necessarily imply that release will be more asynchronous in photoreceptors than in other neurons. With the conventional models, if Ca²⁺ were to instantaneously fall to zero (31), the rate at which release ceases will be similarly rapid across neurons because the emptying of the fully-bound state is dominated by the forward fusion rate, rather than the backward rate, β (Table 3). For the conventional models, rod release would be predicted to cease within ≈300 μs. This contrasts with the high affinity sensor of the adrenal chromaffin cell, a nonneuronal secretory cell, which requires ∼1000 μs to turn off release (31). On the other hand, with the five-site allosteric model, cessation of release from the fully-occupied state could take as little as ≈150 μs or as long as ≈1000 μs, depending on the maximal fusion rate. However, if we accept the data point adapted from Kreft et al. (16), then the five-site allosteric model predicts a rapid cessation of release that is consistent with other neurons and the results of the conventional rod models (Table 3). That said, the rate at which release ceases under physiological conditions will be governed to a large extent by the rate at which the presynaptic calcium concentration falls below threshold for release.

The rate of unbinding of the first Ca²⁺ ion from the fully-loaded sensor is a function of the off-rate, β, and the cooperativity factor, b, which is raised to a power, the value of which depends on the model. Parameter b has a value close to one for the rod photoreceptor (Table 2) but is fractional for other neurons (3,5,6,8). In consequence, despite the profound difference in β between photoreceptors and other neurons, the unbinding rate of the first Ca²⁺ ion to unbind from the fully-loaded sensor is not appreciably slower for the rod (Table 3).

The consequence of the slow off-rate, β, is best appreciated when there are fewer bound Ca²⁺ ions, which diminishes the role of b. Our models indicate that the final one or two Ca²⁺ ions to leave the photoreceptor Ca²⁺ sensor do so relatively slowly (Table 3). Indeed, the last Ca²⁺ ion to leave the rod sensor can remain bound for up to tens of milliseconds. By contrast, for the bipolar cell, hair cell, and the calyx of Held, the last Ca²⁺ ion to unbind typically does so within a few hundred microseconds (Table 3). Furthermore, although the two-site sensor for the calyx of Held, believed to trigger asynchronous release, and the three-site sensor for hormone release in the adrenal chromaffin cell, show occupancy states of several milliseconds, photoreceptor models of a similar form suggest even longer occupancy times. According to the two-site model, during the tens of milliseconds, when a single Ca²⁺ binding site remains occupied, the binding of a single, additional Ca²⁺ ion could trigger release. Indeed, for any of the models, the longer Ca²⁺ ions remain bound, the fewer the number of additional Ca²⁺ ions needed to either trigger or increase the rate of release.

The slow off-rate might be particularly relevant during the dark, when Ca²⁺ is high at the base of the synaptic ribbon, a slow tonic release rate is observed and ribbon bases are depleted of vesicles (14,32,33). Slow off-rates may allow for partial occupancy of the sensors on the vesicles that are next in-line for fusion, contributing to linearization at the synapse. Slow-off rates have also been suggested to permit vesicles at a distance from an open Ca²⁺ channel to undergo fusion (8,34). Thus, the slow off-rate might allow a photoreceptor in the dark, which exhibits a loss of vesicles at the base of the synaptic ribbon and nearest the Ca²⁺ channels (33), to trigger the fusion of vesicles located a little farther up the ribbon or at nonribbon release sites (35,36). The slow off-rate may also promote the coordinated fusion of vesicles (37,38) by allowing vesicles at differing distances from a Ca²⁺ channel to attain suprathreshold Ca²⁺ levels at nearly the same time.

Molecular implications

The quantitative description of the photoreceptor Ca²⁺ sensor places some conditions on the candidate molecules. For example, the conventional sensors for fast neuronal exocytosis, synaptotagmins 1, 2, and 9, all have five calcium coordinating sites corresponding to the binding of three Ca²⁺ ions to the C2A domain and two Ca²⁺ ions to the C2B domain (reviewed by Rizo and Rosenmund (39) and Südhof and Rothman (40)). To accommodate the Ca²⁺-dependent properties of rod exocytosis described here, synaptotagmin molecules might act in an allosteric manner (see Fig. 1 A) or in a conventional manner with release ultimately triggered by the binding of Ca²⁺ ions to a single C2 domain. Support for the latter comes from the relative importance of the C2B domain, but not C2A domain, for fusion (41,42), the distinct energetics of the two C2 domains of synaptotagmin (43), and the suggestion that the C2A domain may be shielded by interdomain interactions until very late in the exocytotic process (44). Thus, an appealing interpretation is that a synaptotagmin-like molecule could trigger photoreceptor release in a manner that is less than fifth-order, depending on the availability of the C2 domains and/or local Ca²⁺ dynamics.

The K_d of each Ca²⁺ binding site predicted by our models is in the low micromolar range. By contrast, at other synapses, the K_d for Ca²⁺ at each binding site may range from micromolar to hundreds of micromolar, depending on β/α and the magnitude and power of the cooperativity factor b. One interpretation is that photoreceptors use a Ca²⁺ sensor with a higher affinity for Ca²⁺ than other neurons. Perhaps one of the high-affinity synaptotagmins, synaptotagmin 3 and 7, participates in release, as reported for neuroendocrine cells (45,46). Synaptotagmin 3 has been localized to ribbon synapses of the goldfish retina (47). Alternatively, the sensitivity of a conventional sensor might be modified. For example, a single point mutation in the C2A domain of the synaptotagmin can alter the apparent Ca²⁺ affinity of release (42). In addition, binding partners, such as complexins (48,49) can modulate the Ca²⁺ dependence of release, and complexin 3 and 4 isoforms are selectively localized to retinal ribbon synapses (50). Cysteine string protein-alpha also enhances the Ca²⁺ sensitivity of release (51); loss of this protein causes rapid degeneration of photoreceptor terminals (52).

Exocytosis at the photoreceptor synapse could involve a Ca²⁺ sensor other than a member of the synaptotagmin family. A ferlin protein with multiple Ca²⁺-binding C2 domains homologous to those of synaptotagmin 3 is found in the eye (53), and otoferlin has been proposed as the Ca²⁺ sensor for release from hair cells (54). Other proteins with C2 domains include Doc2 proteins, which bind Ca²⁺ with high affinity (55–57), and Munc13-1 (39). Ca²⁺ also binds to C2B domains on rabphilin, although the affinity seems too low (K_d ∼18 μM (58)) to account for release at photoreceptor synapses, unless modified. Finally, there is the unidentified sensor for asynchronous release at the calyx of Held (8) and cortical synapses (42), which exhibits a similarly shallow slope to that of the rod.

In conclusion, we find that photoreceptors use release mechanisms with three unusual properties: high Ca²⁺ affinity, an unusually slow off rate, and an unusually shallow relationship between rate of release and presynaptic Ca²⁺. These properties constrain candidate molecules and mechanisms of release at the photoreceptor synapse. They are also advantageous for improving the postsynaptic detection of small light responses by promoting linearity between Ca²⁺ influx and release, thereby enhancing the graded nature of synaptic signaling.