Relationships between Structural Dynamics and Functional Kinetics in Oligomeric Membrane Receptors

Abstract

Recent efforts to broaden understanding of the molecular mechanisms of membrane receptors in signal transduction make use of rate-equilibrium free-energy relationships (REFERs), previously applied to chemical reactions, enzyme kinetics, and protein folding. For oligomeric membrane receptors, we distinguish between a), the Leffler parameter α_L, to characterize the global transition state for the interconversion between conformations; and b), the Fersht parameter, ϕ_F, to assign the degree of progression of individual residue positions at the transition state. For both α_L and ϕ_F, insights are achieved by using harmonic energy profiles to reflect the dynamic nature of proteins, as illustrated with single-channel results reported for normal and mutant nicotinic receptors. We also describe new applications of α_L based on published results. For large-conductance calcium-activated potassium channels, data are satisfactorily fit with an α_L value of 0.65, in accord with REFERs. In contrast, results reported for the flip conformational state of glycine and nicotinic receptors are in disaccord with REFERs, since they yield α_L values outside the usual limits of 0–1. Concerning published ϕ_F values underlying the conformational wave hypothesis for nicotinic receptors, we note that interpretations may be complicated by variations in the width of harmonic energy profiles.

Introduction

Rate-equilibrium free-energy relationships (REFERs) date principally from early insights of Brønsted et al. (1, 2, 3). For any chemical reaction involving reactants (B) and products (A), the ratio of the forward and backward rate constants (^BAk and ^ABk, respectively) fixes the value of the equilibrium constant, K_eq = ^BAk/^ABk. Hence, changes in reaction conditions or the structures that alter K_eq must be reflected by corresponding changes in ^BAk and/or ^ABk. REFERs interpret the changes based on the nature of the transition state (TS). For a TS more closely resembling A than B, perturbations that change K_eq should be reflected by greater changes in ^BAk than ^ABk, because the perturbation alters the TS and A to a similar degree, leaving ^ABk largely unchanged, whereas the effect on B is different, leading to a greater change in ^BAk. Quantitatively, the TS is positioned on a hypothetical reaction coordinate, r_‡, between 0 (fully B-like) and 1 (fully A-like).

REFERs are based on the assumption that the TS position estimated from the slope of a plot of ΔG^‡ (activation energy) versus ΔG^o (reaction equilibrium), reflects the position on r_‡. This slope, ∂ΔG^‡/∂ΔG^o, had generally been designated by the Brønsted β, or the Leffler α (here designated α_L), or more recently by the Fersht ϕ (here designated ϕ_F). For oligomeric proteins, it is important to distinguish between α_L to characterize the global TS for interconversions between conformational states and ϕ_F to characterize the progression of particular residue positions at the TS. Each ligand molecule bound successively to equivalent sites of a homooligomeric protein will exert a similar effect on the conformational equilibrium by changing either forward or backward rate constants (or a combination of both), as indicated by the α_L value (4). In contrast, ϕ_F values, as originally applied to protein folding using mutational analysis at specific positions, indicate the degree of advancement of a particular residue at the TS (5, 6). Hence, a residue with ϕ_F > 0.5 is characterized as early, since it has advanced >50% of its trajectory toward the final state, whereas global conformational change with α_L > 0.5 is characterized as late (7), since the TS is more productlike than reactantlike. To maintain these distinctions, we employ here both α_L and ϕ_F.

REFERs have been applied to numerous classes of chemical reactions, including enzyme-catalyzed reaction, although residues directly in catalysis can produce irregular results (8), and protein folding (9). Interestingly, the formalism used in the analysis of the folding transitions can be applied to transitions of receptors from closed to open ion channels. Examples from protein folding can also clarify ϕ_F values <0 or >1 (10, 11), as well as inconsistent results for changes at neighboring positions along an α-helix (12). Insights into the implications of changes in the shape of energy profiles, as further developed in this article, can be useful (6).

Applications of REFERs to oligomeric proteins began with hemoglobin (7, 13) and were then applied, using α_L analysis, to characterize the rate changes for conformational interconversions as a function of agonist binding for normal nicotinic acetylcholine receptors (nAChRs) (4) and a myasthenic mutant (14). These applications were followed by an approach using ϕ_F analysis to characterize point mutations for nAChR in various regions of the nAChR molecule (15). Using the latter approach, researchers have produced novel results by introducing multiple replacements at the same residue position (16, 17), with marked variations in ϕ_F for different domains interpreted in terms of a hypothetical conformational wave (15). However, difficulties in interpretation are raised, notably for neighboring residues with markedly different ϕ_F values in the channel-lining M2 α-helix (17).

In this review, we develop distinctions between α_L and ϕ_F and explore other applications, initially using examples from nAChR presented in terms of free energy to use a linear scale that facilitates visualization. Indeed, REFERs are also commonly named linear free-energy relations (15, 18). We also examine harmonic energy profiles to represent the dynamic nature of protein conformations. Data from the literature are then examined to evaluate REFERs as criteria for kinetic models. Results for large-conductance, calcium-activated potassium channels (19) fit well to REFERs, but results for glycine and nicotinic receptors interpreted in terms of a novel flip state (20) are inconsistent with REFERs. Finally, the conformational wave hypothesis (15) for nAChR is critically examined based on distinctions between α_L and ϕ_F, and general conclusions are drawn.

Global TS characterization with α_L values

For oligomeric proteins with more than one conformational state, the Monod-Wyman-Changeux (MWC) model (21) provides a minimal functional description involving a preexisting equilibrium for the concerted transition between two states, designated T (constrained) and R (relaxed), with the assignment of R to the high-affinity, active state, as applied initially to allosteric enzymes and hemoglobin (21, 22, 23). However, for membrane receptors, confusion arises due to the practice of assigning R to the low-affinity, inactive resting state for receptors. Therefore, we adopted the terms basal (B) and active (A) in place of T and R, for the closed and open states, respectively, in the applications to ligand-gated channels (4), and these B and A designations are maintained here.

When A binds a ligand more strongly than B, a shift in the B-A equilibrium in favor of A with each ligand-binding event results from an increase in the B→A rate or a decrease in the A→B rate, or both. In early studies, without invoking REFERs, A→B rates were interpreted as progressively falling with ligand binding, both for an allosteric dehydrogenase, for which B→A rates were assumed to remain constant (24), and for hemoglobin, for which falling A→B rates were partially offset by increasing B→A rates (25). Subsequently, using REFERs for hemoglobin, the A→B rates were shown to decrease systematically with ligand binding, corresponding to α_L = 0.8 (13).

For the MWC model, each ligand-binding reaction is assumed to displace the equilibrium between the B and A states by ^BAc (21, 26), the ratio of the ligand dissociation constants for the two states, K_A and K_B, such that ^BAc = K_A/K_B < 1 for K_A < K_B. When expressed in terms of α_L, changes in the interconversion rate constants upon binding of the ith ligand molecule are fixed by (4)

$${}^{\mathrm{BA}}k_{i-1}/{}^{\text{BA}}k_i={\left({}^{\text{BA}}c\right)}^{{\alpha }_{\text{L}}}\text{and}{}^{\text{AB}}k_i/{}^{\text{AB}}k_{i-1}={\left({}^{\text{BA}}c\right)}^{\left(1-{\alpha }_{\text{L}}\right)}\text{.}$$ (1)

Hence, for α_L = 1, upon removal of the ith ligand, the B→A rate decreases by ^BAc, with the A→B rates unchanged. In contrast, for α_L = 0, upon addition of the ith ligand, the A→B rate decreases by ^BAc, with the B→A rates unchanged. For values of 0 > α_L > 1, the exact rates are given by Eq. 1.

In general, rate effects are more readily visualized on a linear scale of energies. Changes in the activation energy of the transition state, ΔΔG^‡, with respect to changes in the free energies of ligand binding to the two states, ΔG_A and ΔG_B, are given by (4)

$$\Delta \Delta G^{‡}={\alpha }_{\text{L}}\Delta G_{\text{A}}+\left(1-{\alpha }_{\text{L}}\right)\Delta G_{\text{B}}\text{.}$$ (2)

The diagram in Fig. 1 A illustrates the dependence of ΔΔG^‡ on ΔG_A and ΔG_B as a function of α_L. The B and A states are represented by energy ladders, with each rung set by the number of bound ligands (0, 1, or 2). Interconversion rates indicated by the TS heights also form a ladder, and the α_L value is directly related to the spacing of the TS rungs. For example, TS spacing equivalent to that of the B state corresponds to α_L = 0, whereas spacing equivalent to the A state corresponds to α_L = 1. In Fig. 1 A, the TS spacing is given by Eq. 2, with α_L = 0.8.

Figure 1.

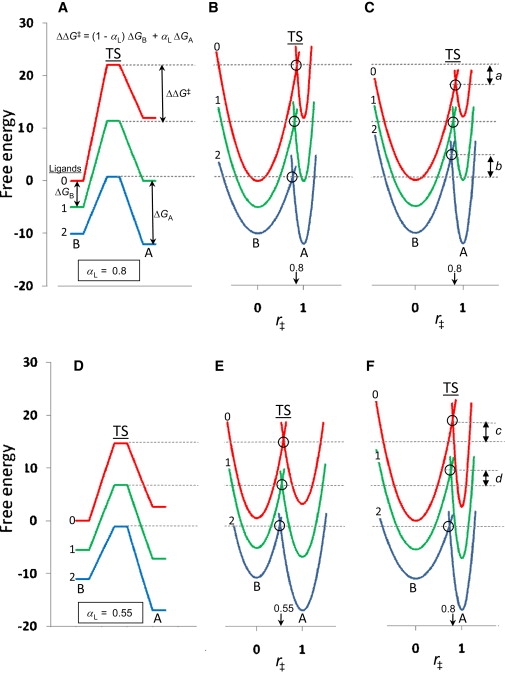
Static and dynamic energy diagrams for conformational isomerizations of normal (A–C) and mutant (D–F) nAChR with 0, 1, or 2 bound ligands. (A) Static energy diagram for normal nAChR based on published data analyzed previously, with α_L = 0.8 and L = 10⁹ (14). (In the original publication, the TS parameter was ^BAp, where ^BAp = 1 − α_L). (B) Dynamic representation of the diagram in A as profiles of free energy versus r_‡, with harmonic wells that broaden with ligand binding and the TS at intersection points (small open circles). (C) Dynamic representation as in B, but with profile widths that remain unchanged upon ligand binding; the double vertical arrows labeled a and b indicate the gap to the TS energy levels in B for unliganded and diliganded states, respectively. (D) Static energy diagram for nAChR myasthenic variant ɛT246P (49), as analyzed previously with α_L = 0.55 and L = 100 (14). (E) Dynamic representation of the diagram in D as energy profiles with harmonic wells, which broaden upon ligand binding. (F) Dynamic representation as in E, but with energy profiles as in B and with the open state shifted to lower energies corresponding to L = 10². The energies indicated by the double arrows labeled c and d indicate the gaps to the TS energy levels in E for unliganded and monoliganded states, respectively. Free-energy versus r_‡ profiles were computed from a general equation for harmonic wells: r_‡= k + ((x − h)²/(4p)), where h is the horizontal placement along r_‡ (h = 0 or 1); k is the vertical placement; and p is a flatness parameter. For profiles with minima at 0 and 1, the intersection value, r_‡^X is given by $r_{‡}^x=\left\{-p_0+\sqrt{p_0{p}_1\left[1-4\left(k_0+k_1\right)\left(p_0-p_1\right)\right]}\right\}/\left(p_1-p_0\right)$ Intersection points of B, C, E, and F occur at progressively lower values of r_‡ as the number of bound ligands increases (for example, in B, r_‡ = 0.85 for the unliganded state and 0.76 for the diliganded states, based on a value of α_L = 0.8 for the monoliganded state; in E, r_‡ = 0.51, 0.55, and 0.59 for the diliganded, monoliganded, and unliganded states, respectively). This progression to lower r_‡ values is a consequence of the geometry of the parabolic profiles.

To deduce the value of α_L in Fig. 1 A, for nAChR, REFERs were first applied to nAChR from Torpedo (4), a heteropentamer with a subunit composition of α₂βγδ, where each α subunit contributes the principal component of the ligand-binding sites at an interface with either a γ- or δ-subunit (27). Rates of channel opening and closing were deduced from single-channel data for diliganded receptors and monoliganded receptors from brief openings (28). With this information, the system is sufficiently defined to permit extrapolation to opening frequencies and lifetimes of unliganded receptors, regarding which data are very sparse (29). In this way, α_L = 0.8 was obtained for Torpedo muscle nAChR (4) and subsequently applied to data from human muscle receptors (14), as summarized in Fig. 1 A. The B and A states, corresponding to closed and open channels, respectively, can be considered to represent discrete structures, as would in principle be observed by x-ray crystallography (30, 31).

Adopting a simple TS, as in Fig. 1, provides a minimal representation, although more complex TS profiles for nAChR are possible (32, 33, 34). In addition, changes in the rate-constant prefactor could also play a role. Moreover, proteins are more accurately characterized as dynamic structures (35, 36), with population distributions of conformational states that may be shifted by bound ligands (37). To provide a simplified view with dynamic representation, the discrete energy levels of Fig. 1 A were replaced in Fig. 1 B by harmonic parabolic profiles (38), as might be produced by normal-mode analysis based on elastic network models (39, 40, 41, 42, 43), along the lines adopted for protein folding (6). We assume that the dynamics can be described with a simple mathematical expression to illustrate the basic principles, whereas more complex properties could be encountered. The six minima of the parabolic profiles in Fig. 1 B are fixed to correspond exactly to the energy levels in Fig. 1 A. In addition, the parabolic profiles are placed to intersect at energy levels corresponding exactly to the TS barriers in Fig. 1 A. For any pair of profiles, when the energy level of the product (Fig. 1, right) is lowered, the intersection point moves slightly to the left, which is known as the Hammond effect (44).

Although REFERs are based on the hypothesis that the reaction coordinate r_‡ is directly related to the α_L value, the parabolic profiles suggest that a range of r_‡ values apply. Moreover, to achieve agreement between the profiles in Fig. 1, A and B, the steepness of the profiles in Fig. 1 B was adjusted, since shifting only the profile heights produces insufficiently large changes in the intersection points, yielding differences in successive opening rates of only ∼50% of the values in Fig. 1 A. As illustrated in Fig. 1 C, the minima for each of the profiles corresponding to the same energy levels as in Fig. 1 B but with no change in profile shape, give intersection points that are higher or lower for the diliganded or unliganded states, respectively. This implies that a small progressive broadening of the profiles for both the closed and open states accompanies ligand binding. The origin of such changes in dynamics is unclear, but some clues are provided by the simulations of diphosphoglycerate binding to hemoglobin (37). Overall, the application of α_L may require adjustments for more precise data, but the principle of changes uniformly distributed between forward and backward rates is a reliable framework. Complexities in the system have been kept to a minimum here to highlight the general principles of Eq. 2 to provide guidelines for the examples considered in the following sections.

Applications of global TS characterization to mutant phenotypes

An important application of REFERs for nAChR concerns modifications of specific residues, either by site-directed mutations or by naturally occurring myasthenic mutations in the human population, which lead to major changes in functional properties in terms of both gain of function (45, 46) and loss of function (27, 47). With the MWC model, we can distinguish between K-phenotypes, which affect ligand binding sites, and L-phenotypes, which alter the equilibrium between states (48). The first abnormal nAChR studied using REFERs was a gain-of-function mutation myasthenic syndrome, ɛT246P (ɛ replaces γ in human adults), which exhibits three peaks in open-time distributions compared to the single peak observed for normal nAChR (49). These initially perplexing properties were represented by lowering the values of the allosteric constant, L, from 10⁸ to 10² and of α_L from 0.8 to 0.55 (14), as presented in Fig. 1 D as a static energy diagram. Although it reproduces three peaks of open times (14), the general agreement does not necessarily qualify as a perfect fit (50), but demonstrates how changes in basic parameters of the model could provide a general understanding of this unusual phenotype. More extensive data could alter the quantitative features, but showing how open times can be transformed from a unimodal to a trimodal distribution illustrates an important principle, and a description using harmonic profiles is presented in Fig. 1 E.

Compared to the properties of normal nAChR in Fig. 1 A, the mutant receptors are characterized by a more stable A state and lower kinetic barriers and α_L. For comparison, Fig. 1 F presents harmonic profiles using the values from Fig. 1 B, but with only the energy levels for the A state at lower values, to correspond to the decrease in the allosteric constant from L = 10⁹ to 10². In this case, an appropriate intersection for diliganded states is maintained, but for the monoliganded and unliganded states, intersection points correspond to TS values significantly above the values used to model the experimental data. Therefore, the mutant results cannot be represented satisfactorily without changing the steepness of harmonic profiles, as well as the levels of their minima, resulting in the shift of α_L from 0.8 to 0.55. Overall, the analysis of the ɛT246P nAChR receptors clearly illustrates how changes in the relative stability of conformational states, coupled with small changes in TS position, can produce striking differences in properties.

Tests of global TS characterization

Critical evaluations are possible using data obtained independently of REFERs that can subsequently be used to test the validity of α_L values. For example, for large-conductance calcium-activated potassium channels, Cox et al. (19) measured kinetic rate constants with 0–4 calcium ions bound. As shown in Fig. 2, these data are well-fit by REFERs with α_L = 0.65 to represent the increasing opening rates and decreasing closing rates as a function of bound calcium. Data that permit clear testing are rare, but were also available for hemoglobin due to the spectral signatures for the T and R states, which make it easier to follow conformational changes upon photodissociation of carbon monoxide or oxygen (13), and the appropriate α_L could then be used in the complete description of ligand-binding kinetics for hemoglobin (51). In comparison, earlier data analyses for hemoglobin without α_L usually produced inconsistent relationships between rate constants (52). Taken together, these applications to large-conductance potassium channels and hemoglobin illustrate that REFERs can provide coherence to mechanistic models.

Figure 2.

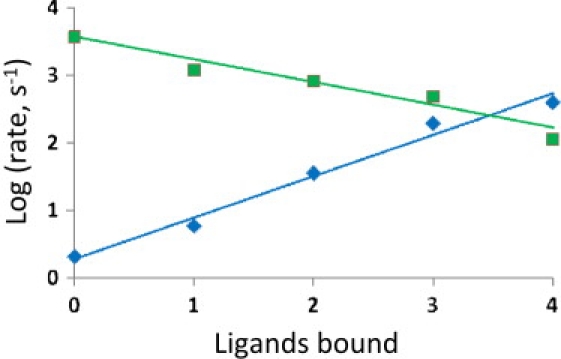
Progression of opening and closing rates of the large-conductance calcium-activated potassium channels according to the number of calcium ions bound (19). Each point represents the average of the three values for independent patches (presented in Table 3 of Cox et al. (19)), with blue diamonds for opening rates and green squares for closing rates. The straight lines are calculated using α_L = 0.65 from least-squares fitting of successive rates with Eq. 1, with ^BAc = 0.11, the average for successive L values obtained from the ratio of interconversion rates for each degree of ligand binding.

An extensive data set for glycine receptors (GlyR) and nAChR presented by Lape et al. (20) also provides an excellent opportunity to examine consistency with respect to REFERs, as analyzed here in detail, since these studies illustrate several relevant phenomena. The authors interpret their data in terms of a third state, flip (F), which intervenes between the closed (B) and open (A) states. Reduced access to F (but not to A) was proposed to explain partial agonism (20). However, these data display an unusual feature. In contrast to the standard pattern (Figure 1, Figure 2), with forward and backward reactions showing opposite dependence on ligand binding, the rate constants for activation of GlyR show marked deceleration (by >2 orders of magnitude) of both forward and backward rates for the B→F transition upon binding a third molecule of the partial agonist taurine (Fig. 3 A), corresponding to α_L = −13.1 (Fig. 3 B), well outside the usual limits of 0–1. Moreover, large acceleration (>1 order of magnitude) was reported for both forward and backward rates of the F→A transition (Fig. 3 A), corresponding to a value of α_L = 1.68 with taurine as the ligand (Fig. 3 B) or α_L = 4.7 with glycine as the ligand (data not shown). In a similar way, for nAChR in the same study (20), rate constants correspond to α_L values outside the usual 0–1 limits, with α_L = −3.9 for formation of F from B upon binding acetylcholine and α_L = 1.24 for formation of A from F upon binding of the partial agonist tetramethylammonium at −80 mV. These results raise questions regarding the exceptional nature of these α_L values.

Figure 3.

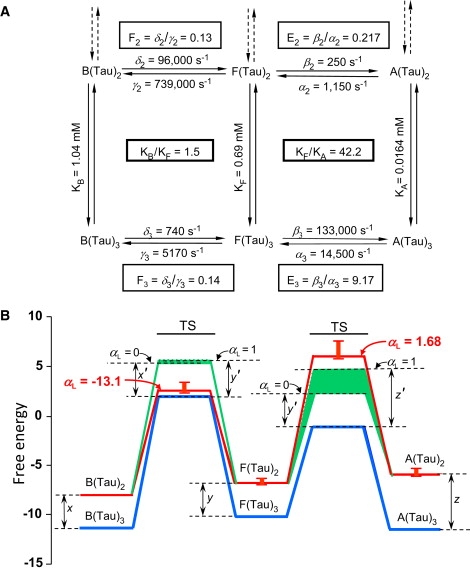
Application of REFERs to reactions of GlyR. (A) Reaction cycles with two or three molecules of taurine (Tau) bound. Rate constants and dissociation constants (K_B and K_F) are from Lape et al. (20). Binding of the third molecule of taurine stabilizes F relative to B by a factor of K_B/K_F = 1.5 and A relative to F by a factor of K_F/K_A = 42.2; their reciprocals give ^BFc and ^FAc, respectively, used in the calculations in B. A value for K_A was not presented by Lape et al., but was calculated from linkage relations. (B) Energy diagram for the reactions in A comparing predicted and observed energy barriers for the diliganded states (red, observed; green, predicted), based on the values reported for the triliganded states (blue). The calculated values are obtained from the data in A using Eq. 1. TS heights (kcal/mole) were calculated as described (4). Green areas correspond to the limits for δ₂ (A, left), with the lower TS barrier for x′ = x with α_L = 0 and with the upper barrier for y′ = y with α_L = 1 and for β₂ (A, right), with the lower TS barrier for y′ = y with a_L = 0 and with the upper barrier for z′ = z with a_L = 1. Error bars from estimates in Lape et al. are presented for the diliganded state only, since the errors are essentially within the thickness of the line for the triliganded states. Barrier heights may vary depending on specific assumptions of the TS theory (85), but the energy differences x = x′, y = y′, and z = z′ would remain unchanged.

For both GlyR and nAChR, better fits were reported when the mechanisms did not include direct ligand-binding reactions between open states (20). If the open states are not connected, partially liganded receptors can only add another ligand by returning to the flip state, which is surprising behavior for a multisite receptor (53), although specific ion effects cannot be excluded (54), as suggested for certain cases (55, 56, 57, 58, 59), with general applications to nonequilibrium phenomena also considered (60). Another issue involves the unusually high rate for the F→B reaction of GlyR with two molecules of taurine bound: γ₂ = 739,000 s⁻¹. Overall, the α_L values outside the limits of 0 and 1 for the postulated B→F and F→A transitions, and the exceptionally fast γ₂ rate constant, elicit concerns about the mechanism proposed and raise the question of whether alternative mechanisms might apply (61). Whatever the outcome in future studies of these receptors, REFERS should provide powerful criteria for evaluation of the mechanisms involved.

Residue progression at the TS probed with mutational analysis

An original and ambitious approach has been developed by Grosman and Auerbach and their colleagues for nAChR, focused initially on using diliganded receptors to investigate the role of individual residues in the kinetics and equilibria of the closed→open transition (15, 16, 17, 62). At various positions, ϕ_F values were obtained and used to interpret early and late changes. Since specific nAChR domains were ordered along an early-to-late scale, a novel interpretation was formulated of a conformational wave for the closed→open transition, beginning in the ligand-binding domain, where ϕ_F values approach 0.9, and continuing with a gradient of decreasing ϕ_F values to the ion channel, with values <0.3 (17).

Although this hypothesis provides a possible visualization of the conformational transition, an alternative scenario is that specific regions of the molecule could be characterized by different harmonic energy profiles. For example, along the M2 α-helix of the nAChR, α-subunit ϕ_F values for neighboring residues vary considerably, with ϕ_F = 0.63 for L250, but 0.26 for L251 (17), with similar values for the ɛ-subunit (63). Residues near the M2 C-terminal cap of the α-subunit also deviate from the pattern expected for a conformational wave, with ϕ_F reaching 0.9 (64).

The ϕ_F variations along M2 complicate explanations, since positions within a domain can show differences in ϕ_F of similar magnitude to those between domains, and may reflect principally the position on the transmembrane helix, as suggested by the fact that L251, the residue with the lowest ϕ_F value, is aligned with T254 on the next turn (ϕ_F = 0.35) on the surface of the helix facing the channel (30, 31, 65). This orientation may lead to a widening of the harmonic energy profile for the open state that produces lower ϕ_F values irrespective of a conformational wave, but this hypothesis implies rather homogenous behavior for all amino acid replacement residues tested at these positions (34)—with the exception of outliers, such as I254 (17). Although the channel environment may present unusual features, position-specific effects along helices have also been observed for nonchannel proteins, and for the energy profile, the possibility of asymmetric harmonic wells (6) could add additional complexity to this issue. Multiple shallow wells could further complicate the analysis (32), and possible speed limits for conformational isomerizations may have an impact on results (66). At this stage, conflicting arguments must be weighed concerning the validity of the conformational wave hypothesis.

A distinct REFER application was reported by Grosman, Auerbach, and colleagues involving the conformational transitions of unliganded nAChR (16, 67), which previously had been out of reach. The results were reported as ϕ_F values, but they correspond to α_L values according to the distinctions presented here, with the reported value of α_L ≅ 0.9 somewhat higher than, but consistent with, that of α_L = 0.8 reported previously (4), since higher r_‡ values can be expected for unliganded nAChR compared to diliganded nAChR (Fig. 1 B). The importance of distinguishing between α_L and ϕ_F is emphasized by the fact that ϕ_F for any residue position occurs within the context of the global TS characterized by α_L. Although precise values of α_L may vary somewhat depending on the experimental approach used, a consensus has emerged that the conformational TS of nAChRs strongly resembles the open state, with α_L ∼ 0.8.

General Considerations

For the applications reviewed here, REFERs are useful concepts for both wild-type and mutant oligomeric receptors. Global TS characterizations using α_L provide criteria for evaluating mechanistic models, since changes in conformational transition rates upon ligand binding that deviate from REFERS (values outside the limits of 0–1) can be subjected to added scrutiny. The use of ϕ_F values can also provide useful insights, although interpretations may be complicated by changes in harmonic profile steepness (6). In protein folding, the conformations of the unfolded and folded states are very different, and distinct domains can be readily characterized, although folding may involve competition between different folding pathways, with cooperative effects that can be influenced by changes in single residues (68). For ligand-gated channels, the transitions are more subtle, as illustrated by recent structural studies of bacterial homologs of nicotinic receptors (30, 31). For these systems, ϕ_F values for individual residues may reflect predominantly local stability differences that alter harmonic energy profiles rather than timing at the TS.

Applications of REFERs to other oligomeric proteins provide additional useful insights. In a novel application of REFERs, an abrupt ATP-dependent pathway switch was identified for the chaperonin GroEL (69). For the allosteric transition of calmodulin (70), free-energy profiles along the transition route provided new insights into the underlying conformational dynamics (71). Tetrameric glutamate or cyclic nucleotide receptors should also be studied with respect to REFERs. Because of the symmetry mismatch between the extracellular and membrane domains in this family (72), additional functional complexity may be expected, as for binding of a fluorescent cGMP analog to homotetrameric CNGA2 receptors with steps of both positive and negative cooperativity (73). For G-protein-coupled receptors, the availability of high-resolution structures (74) provides opportunities for studies on conformational dynamics (75, 76) and allosteric interactions (77).

These subjects emerge in the context of broader considerations of energy landscapes underlying protein function at all levels (78, 79, 80), including distinct time regimes (81). For ligand-gated channels, as shown here, the classical view of open-channel lifetimes from single-molecule recordings (82)—as the reflection of a homogenous process (83) based on standard stochastic kinetics (84)—is being refined to incorporate conformation dynamics of individual receptor molecules to open-channel lifetime distributions. Advances along these lines are now beginning to provide the long-awaited bridge between protein physical chemistry and electrophysiological recordings.

Editor: Eduardo Perozo.