Dynamics of Bacterial Swarming

Abstract

When vegetative bacteria that can swim are grown in a rich medium on an agar surface, they become multinucleate, elongate, synthesize large numbers of flagella, produce wetting agents, and move across the surface in coordinated packs: they swarm. We examined the motion of swarming Escherichia coli, comparing the motion of individual cells to their motion during swimming. Swarming cells' speeds are comparable to bulk swimming speeds, but very broadly distributed. Their speeds and orientations are correlated over a short distance (several cell lengths), but this correlation is not isotropic. We observe the swirling that is conspicuous in many swarming systems, probably due to increasingly long-lived correlations among cells that associate into groups. The normal run-tumble behavior seen in swimming chemotaxis is largely suppressed, instead, cells are continually reoriented by random jostling by their neighbors, randomizing their directions in a few tenths of a second. At the edge of the swarm, cells often pause, then swim back toward the center of the swarm or along its edge. Local alignment among cells, a necessary condition of many flocking theories, is accomplished by cell body collisions and/or short-range hydrodynamic interactions.

Introduction

Many flagellated bacteria have more than one mode of locomotion, moving independently in bulk liquid (swimming) or moving in association with other cells in a thin film of liquid over a moist surface (swarming). Both modes use the same mechanism of propulsion, with thrust generated by rotating helical flagella. In this study, we compare the movement of swarming cells of Escherichia coli to the movement of swimming cells. We begin with an overview of bacterial swimming and swarming, followed by a discussion of a related phenomenon, flocking.

Swimming

E. coli K-12 is a rod-shaped, peritrichously flagellated bacterium that is ∼1 μm in diameter by 2 μm long when grown in a dilute aqueous medium, i.e., when in the vegetative state. An isolated cell in such a medium swims at a speed of ∼30 μm/s, propelled by about four long, thin, helical filaments, each driven at its base by a rotary motor (1,2). When the motors spin counterclockwise (CCW), the filaments form a bundle that pushes the cell forward, it is said to run. If one or more motors spin clockwise (CW), the cell alters course, and it is said to tumble (3–7).

Swimming cells can purposefully move up or down chemical gradients, a phenomenon known as chemotaxis. By actively modulating the CCW/CW bias of their motors, cells control the run/tumble probability in response to changes in chemical concentrations. The biochemical pathway that allows this control is well understood (8–12). In short, an interacting group of receptor proteins and enzymes dynamically sets the phosphorylation level of a response regulator (CheY), which binds to a protein (FliM) in the switch complex at the base of the flagellar motor. This CheY-P/FliM binding determines motor bias (13), and hence chemotactic behavior (14,15).

Swarming

Swarming was distinguished from other forms of surface translocation by Henrichsen (16). When E. coli K-12 is placed on a moderately soft agar plate (0.45% w/v in our experiments) in a rich medium, cells elongate, produce more flagella, become multinucleate, and spread rapidly outward in a thin, highly motile layer (17–20). Swarming was characterized in E. coli and Salmonella by Harshey and Matsuyama (21). Unlike in most other swarming species, cells of laboratory strains of E. coli K12, including the strain used in this work, do not secrete surfactants (e.g., lipopeptides or glycolipids). Nevertheless, cells move over the surface of agar in a liquid film, under conditions in which they do not adsorb to the agar or stick to one other. Rauprich et al. (22) argued that such an environment is generated when bacteria extract water from the underlying agar, producing a thin lubrication layer.

Chemotaxis is not required for swarming in E. coli or in its close relative Salmonella. The clearest evidence for this is that strains deleted for cheY, whose motors spin exclusively CCW, fail to swarm, yet swarming is restored by mutations in fliM that generate motor reversals, which are thought to promote wetness by helping cells shed lipopolysaccharide (23). With CheY missing and FliM defective, the flagellar motors are uncoupled from the chemotaxis signaling pathway; nevertheless, the cells swarm. This suggests that swarming requires only flagellar propulsion and mechanical interactions; the fine control offered by the chemotaxis pathway is dispensable.

Flocking

Swarms typically produce large-scale swirling and streaming motions involving hundreds to millions or billions of cells (24–26). This is reminiscent of the coordinated motion of birds or fish, and indeed theoretical frameworks that were initially developed to describe flocking or schooling have been extended to the collective motion of bacteria. Starting with Vicsek et al. (27), flocking models usually assume that self-propelled particles move at a constant speed and align themselves with their local neighbors, subject to a certain amount of random noise in their orientation (28,29). Such models generally find that, provided the noise is not too strong, a sufficiently dense random collection of particles will spontaneously order so that all particles eventually move in the same direction (30–32). More biologically plausible models introduce attractive forces (to produce clustering) and/or repulsive forces (to prevent complete cluster collapse) (33–35). In two dimensions, such systems produce only short-range order (36,37), often involving swirling (31,38–40), in agreement with many theoretical predictions that the ordered phase is unstable and tends to break into large-scale swirls and jets (41–46).

A bacterial swarm evolves under physics consistent with many flocking theories, although under the particular conditions that: 1), the motion is coupled to an underlying fixed substrate (the agar plate); 2), the swarming cells are only approximately polar (they occasionally reverse direction); and 3), the cell number is not fixed (cells grow and divide while swarming). This study was designed to learn how cells move in this environment.

Materials and Methods

Bacteria

HCB1668 is a Tn5 fliC null derivative of AW405 (an E. coli strain that swims vigorously and is wild-type for chemotaxis (47)), in which FliC S353C is expressed on plasmid pBAD33 under control of the arabinose promoter. This strain was maintained by adding the antibiotics kanamycin (50 μg/mL) and chloramphenicol (34 μg/mL) to the culture media. Each week cells from a frozen stock were streaked on 2.0% w/v Difco Bacto agar plates containing LB broth (1% Bacto tryptone, 0.5% yeast extract, 0.5% NaCl, pH 7.5) and incubated overnight (16 h) at 30°C. A single colony from the plate was grown in T broth (1% Bacto tryptone, 0.5% NaCl) to saturation at 30°C, and aliquots of this culture were used to inoculate swarm plates.

Swarm plates

Swarm agar (0.45% Eiken agar (Eiken Chemical Co., Taito, Japan) in 1% Bacto peptone, 0.3% beef extract and 0.5% NaCl) stored in sterile aliquots of 100 mL was melted completely in a microwave oven and cooled to ∼60°C. Antibiotics were added at the concentrations used in liquid cultures and arabinose was added to a final concentration of 0.5%. Polystyrene petri plates (150 × 15 mm) were filled with 25 mL swarm agar, swirled gently to ensure complete wetting, and then cooled 15 min (without a lid) inside a large plexiglas box. The agar was relatively thin (1.4 mm) to allow phase-contrast imaging of the agar surface (see Phase-contrast video microscopy below). To grow swarms, a 2-μL drop of inoculant, diluted to 10⁻³, 10⁻⁵, or 10⁻⁶ from the saturated culture, was placed on the surface of different agar swarm plates, ∼3 cm from the rim. The inoculants were air dried for ∼5 min (in the plexiglas box) before the plates were covered and incubated overnight at 30°C and 100% relative humidity. By morning, the bacteria in the plate with the 10⁻³ inoculant typically grew to a colony of radius of at least 6 cm.

Phase-contrast video microscopy

Swarm plates were taken from the incubator and immediately placed on the stage of a Nikon Optiphot upright microscope held at the incubation temperature (30°C). Temperature control was maintained with a Lauda RM6 bath that circulated water through custom-made parts mounted underneath the stage and around the objective. The temperature was checked at the center of an agar plate placed beneath the objective. Imaging was with a 40× 0.65 n.a. bright-phase objective, an 8× relay lens, and a CCD camera (Marshall V1070, 30 frames/s, 2:1 interlace, Marshall Electronics, Culver City, CA) shuttered at 1/200 s and connected to a digital tape recorder (Sony GV-D1000, Sony, Montvale, NJ). The camera was oriented so that the edge of the swarm moved from left to right across the video frame. Thus, with the passage of time, the videotapes showed areas farther from the edge of the swarm. Times of observation were converted to distance from the swarm edge using the swarm expansion rate. Tapes for each swarm were surveyed by transferring one image every 5 s over a period of 5 min to a Mac G-3 using a Scion Image LG-3 video capture board, and the images were imported to Image-J for analysis. The bacteria in each image were counted using the Cell Counter plug-in available at the NIH Image website (written by Kurt De Vos, University of Sheffield, UK). Cells were excluded from counts when they were >50% out of the frame. In each of two swarms, five regions at varying distances from the swarm edge were selected for subsequent motion analysis. At the appropriate video frame (showing cells at a given region of the swarm) 1 s of video at 30 frames/s were analyzed by recording the positions of the head and the tail of each cell using an Image-J plugin (Manual Tracker, written by Fabrice Cordelires, Institut Curie, France, and adapted by Alan Stern, Rowland Institute at Harvard). These data were processed using MATLAB (The MathWorks, Natick, MA).

Data processing

• 1.The velocity-velocity correlation, defined as the mean of the cosine of the relative angle, is a function of vector distance Δr and the time lag Δt: $C\left(\Delta \mathbf{r},\Delta t\right)={\langle \cos \left({\theta }_{\text{i}}\left(\mathbf{r},t\right)-{\theta }_{\text{j}}\left({\mathbf{r}}^{\prime },t^{\prime }\right)\right)\rangle }_{{\mathbf{r}}^{\prime }-\mathbf{r}=\Delta \mathbf{r},{\mathrm{t}}^{\prime }-\text{t}=\Delta \text{t}}$. Here the average is over the velocity angles θ_i and θ_j corresponding to all cells i and j whose centers are separated by Δr and whose velocities are measured a time Δt apart. We computed separately the spatial correlation C(Δr,0) for zero time lag, and the temporal correlation C(|Δr| < 3 μm, Δt > 0) for positive time lags and small distances (<3 μm). Note that Δr is defined relative to the orientation of the target cell, so that the y axis corresponds to the cell's major axis with positive y in the direction of the cell's motion. The temporal autocorrelation compares the same cell's velocity at different times, regardless of position: $C\left(\Delta t>0\right)={\langle \cos \left({\theta }_{\text{i}}\left(\mathbf{r},t\right)-{\theta }_{\text{i}}\left({\mathbf{r}}^{\prime },t^{\prime }\right)\right)\rangle }_{{\mathrm{t}}^{\prime }-\text{t}=\Delta \text{t}}$. Given a cell whose center is at (0,0) and whose head points in the +y direction, the pair distribution function is the probability of finding a second cell centered on (x,y). This probability is normalized to the average density, so 0 corresponds to the mean probability of (surface cell density)⁻¹ and 1 to twice the mean probability.
• 2.The propulsion angle is the angle between the major axis of a cell body and its velocity vector. The vector body axis is constructed to point toward the head of the cell.
• 3.The curvature of a cell's trajectory is calculated from five consecutive positions, spanning 0.17 s of motion, which were fit to uniformly spaced points on a circular arc corresponding to a radius R and cell speed v. The curvature is ±1/R, with positive curvature assigned to clockwise motion. Short trajectories were difficult to fit reliably, so we required the five data points to span a 3-μm arc; this effectively restricted us to speeds >18 μm/s for curvature measurements. In addition, we also required that the root mean-square difference between measured and fit positions be ≥0.5 μm.

Results

Swarm structure overview

Most HCB1668 swarms had a similar structure, with cells spreading as far as 10 cm from the site of inoculation after overnight growth at 30°C. At the periphery of the colony, the advancing edge was a highly motile cell monolayer exhibiting classic wolf-pack style motility. The width of this monolayer varied from plate to plate and was usually <1 cm; however, it could be as large as 2–3 cm. Sometimes a narrow multilayer band formed immediately behind the edge, between the edge and the bulk monolayer. Farther from the edge, nearer the point of inoculation, the cells swirled in CW and CCW vortices, in stacks many cell layers deep. This swirling region extended over 3–4 cm. Toward the colony center, cell density slowly increased and the cells gradually lost the swarmer phenotype, becoming shorter and less motile, with complete loss of motility near the point of inoculation. Because the multilayer region was too dense for the motion of individual cells to be followed, we investigated the monolayer region, with particular emphasis on its leading edge.

Swarm monolayer

We videotaped seven HCB1668 swarms at 30°C (the incubation temperature) as the bacteria moved past a fixed microscope objective. Expansion rates tended to be higher for swarm fronts of higher densities (Table 1). The first two of these swarms were subjected to detailed analysis, but as the results were similar for both swarms, here we only report the results for swarm one. We selected five regions, as indicated by the closed symbols in Fig. 1, for tracking. Fig. 2 shows one video frame from each of these areas. Based on the average cell size (5.2 μm × 1 μm) a close-packed monolayer would contain ∼0.18 cells/μm². Within 100 μm of the swarm edge the observed cell density peaked at ∼2/3 of the close-packed density and then fell by about half to the plateau (Fig. 1).

Table 1.

Data for seven swarms of strain HCB1668 supplemented with arabinose

Expansion rate (μm/s)	Maximum density (cells/μm2)	Plateau density (cells/μm2)
3.7	0.118	0.050
2.6	0.072	0.028
5.2	0.121	0.048
4.4	0.129	0.065
4.5	0.149	0.076
2.4	0.106	0.044
3.7	0.067	0.034
3.8 ± 1.0∗	0.109 ± 0.030∗	0.049 ± 0.017∗

^∗Average over all seven individually measured swarms.

Figure 1.

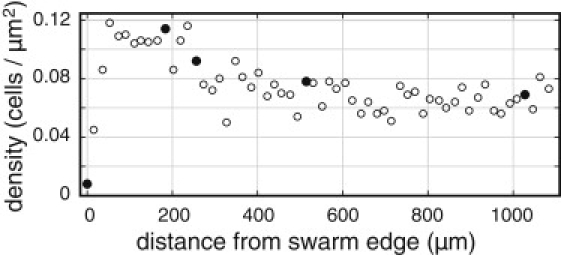
Swarm density profile. Cell-density profile for the first swarm from Table 1 (open symbols). Cells were counted in each video frame collected at 5-s intervals for a total of 300 s. Solid symbols denote the regions selected for further study, in the order (left to right) edge, peak, falloff, plateau 1, and plateau 2.

Figure 2.

Snapshots of an advancing swarm. Images of cells in regions corresponding to the solid symbols in Fig. 1. The field of view is (42 μm) × (57 μm). Scale bar = 10 μm. The cells are shown in the order and orientation appropriate for swarms moving from left to right.

Swarm cell tracking

Swarms one and two were analyzed by tracking the bacteria in a 30-frame (1-s) interval starting with the frames depicted in Fig. 2. Examples of the source video and tracking visualization are available as Supporting Material. Our goal was to understand how a typical swarm cell moves and how the motion of one cell is related to that of its neighbors. We calculated several measures of individual cell motility: cell length, speed and propulsion angle, and the curvature of the cell's trajectory. We also calculated several collective measures that relate different cells' motions: pairwise correlations between cells' orientations and velocities as a function of the cells' relative distance.

We examined all five areas (edge, peak, falloff, plateau 1, and plateau 2) separately, but for simplicity in presentation in Fig. 3, the peak and falloff areas are grouped together, as are the two plateaus.

Figure 3.

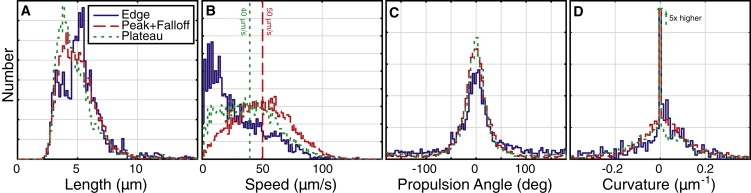
Population distributions. Distributions of body length, speed, propulsion angle, and curvature, each grouped by the location of the cells in the swarm: at the edge (solid blue), in the peak and falloff regions (dashed red), and in the two lower-density plateau regions (dotted green). Distributions of each type are normalized to the same area. Vertical lines on the speed distribution indicate mean values. The peaks at zero in the curvature distributions are truncated: they are 5× larger than pictured and contain ∼50% of the total distribution. Note that ∼40% of all measured trajectories were omitted from the curvature distribution because they failed to fit to an arc of a circle. See Methods for details.

Length

The cell bodies were of uniform width (∼1 μm) but of varying length, with 90% falling between 3.0 and 7.6 μm. The mean cell length was 5.2 μm and did not vary over the range of positions studied (≤1000 μm from the swarm edge) (Fig. 3 A). This length is about twice the mean length of cells from a swimming culture (our observation), as expected for a swarm phenotype in E. coli. Using cell length as the measure of differentiation, we saw no variation in phenotype within the outer 1000 μm studied here.

Speed

The mean cell speed (40 μm/s) was comparable to the velocity of cells grown in T-broth and tracked in motility medium at 32°C (36.4 ± 8.9 μm/s (48)). There was considerable variation in the average cell speeds of different swarms. Within each swarm, the speed distributions were very broad (Fig. 3 B), especially when compared with speed distributions for swimming cells: as judged by the normalized width (SD/mean), the width of the swarm cells' speed distribution was ∼60%, whereas that of a typical swimming culture is ∼25% (48). Although we only tracked cells for 1 s, within that limited time frame each cell sped up or slowed down considerably. That is, the width of the population speed distribution arose from variation in the speeds of individual cells over the course of the 1-s acquisition time, not from sampling over a heterogeneous population where each cell has a narrowly defined speed. All speed distributions showed a certain fraction of slow motion (<20 μm/s) as well as a large population of broadly distributed and significantly faster motion. As expected, because cells within a few body lengths of the edge are frequently stalled, the speed distribution near the edge showed an overabundance of slow cells; apart from this effect, within a swarm the mean speed decreased slightly with increasing distance from the edge.

Propulsion angle

Most propulsion angles were small (Fig. 3 C): the average was 0.7° and >50% fell within ±20°. This means that a cell tends to move in the same direction as its body axis. The typical cell moved in the straight-ahead direction, deviating now to the left, how to the right; that is, the population was not divided between left- and right-propelled cells. Propulsion-angle distributions were slightly flatter at the swarm edge, probably because of the large number of stalled cells at the edge subject to the jamming effect (see Correlations, below). Propulsion angle distributions were quite similar everywhere in the swarm interior. For a small fraction of cells, the propulsion angle was greater than 90°; these are cells that were caught in the process of reversing direction by exchanging the roles of head and tail. Though this phenomenon is infrequent, it uniquely allows cells to reverse away from jammed areas, as has been observed in Bacillus subtilis (49). By observing fluorescently labeled flagella in a swarmlike preparation, we find that when several flagellar motors reverse direction the cell body can back up, within a substantially intact bundle, until the leading end of the cell body becomes the lagging end; this phenomenon is addressed in detail in another publication (50).

Curvature

The majority of cells' paths had no appreciable left- or rightward curvature (Fig. 3 D). Of all the 0.17-s-long trajectories that were measured, ∼50% had a curvature of <0.01 μm⁻¹ or, equivalently, a radius >100 μm. We cannot reliably resolve larger radii in our limited field of view (∼50 μm square). Trajectories were broadly distributed between leftward and rightward curvature, with 90% falling within ±0.1 μm⁻¹; although, in most locations (and especially at the edge) the distribution was shifted slightly toward positive (clockwise) curvature. Averaging over all locations, the mean curvature was 0.003 μm⁻¹. This small curvature contrasts with the behavior of cells swimming close to a glass surface. Near glass, because the cell body and flagellar bundle rotate in opposite directions, any coupling to the surface produces oppositely-directed forces on the body and flagella, applying torque to the cell about an axis normal to the surface and making it swim in consistently clockwise spirals (as seen from above) of ∼25 μm radius (51). There are two possible explanations for the loss of clockwise bias in the swarm: 1), frequent collisions between tightly packed cells in the swarm might prevent them from curving; and 2), the upper (swarm/air) interface might exert an opposite torque on the cell from the lower (swarm/agar) interface, offsetting most or all of its effect. The upper interface appears to be stationary, covered by a surfactant monolayer pinned at its edges (52).

Correlations

We looked for relations between an individual cell's speed, length, and propulsion angle. Speed and length were not significantly correlated, nor were length and propulsion angle. Speed and propulsion angle were correlated only for faster motion; that is, fast-moving cells had consistently smaller propulsion angles than slower cells. The propulsion angle distribution was significantly different from a random, flat distribution for speeds >6 μm/s (at the 90% confidence level); at speeds lower than this, cells moved in completely random directions, uncorrelated with the cell body orientation (plots of these quantities are available in the Supporting Material). We suspect that this results from cell jamming: when cells are crammed together, they tend to move according to the forces applied by their neighbors rather than due to their own propulsive force, and therefore velocity and body orientation tend to be uncorrelated.

Temporal correlations among cells

The net motion of a cell depends not only on how fast it moves but also on how long it persists in moving in the same direction. Speed alone does not produce long-range transport if the direction of motion is randomized too quickly. For the population of tracked cells, the velocity-velocity time autocorrelation function declined with a time constant of 0.25 s (Fig. 4, upper curve). This is reasonably close to the decay time constant of 0.17 s associated with the velocity field of the swarm (Fig. 4, lower curve). When swimming cells run and tumble, directional changes occur via Brownian motion (over run intervals of order 1 s) or via active reorientation caused by the reversal of one or more flagellar motors (over tumble intervals of order 0.1 s) (53,54). The hallmark of a tumble is a relatively large change in direction (∼68° on average) within a short time (∼0.1 s), concomitant with a decrease in swimming speed. Due to the greater hydrodynamic coupling between cell and surface in a swarm, the importance of rotational Brownian motion is reduced. The velocity-velocity time autocorrelation function did not have any feature corresponding to the ∼0.1 s tumble lifetime. In addition, the greatest changes in body orientation did not correspond to the slowest cell speeds: for the 10% of events that had the largest change in body orientation (>50° over 0.1 s), the mean speed was only 3% slower than the population average (data not shown). Together, these observations suggest that collisions with adjacent cells, rather than active reorientation by flagellar reversal, are the dominant way that cells change direction while swarming. Sudden large changes in swimming direction do occur—for example, when looking at video tapes, one sees cells that back up—but these events do not have a large impact on the average cell behavior.

Figure 4.

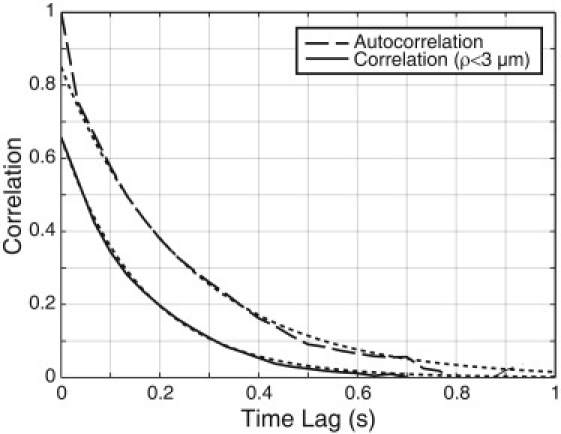
Temporal correlations. The velocity-velocity temporal correlation function (solid line, lower) represents the time over which the velocity of cells in a small (3 μm square) spatial region of the swarm becomes randomized. A 0.17 s exponential decay (dotted line) is included for reference. The correlation at t = 0 is <1 because the 3 μm spatial binning averages over several cells that are initially imperfectly aligned. Because the particular cells located within the 3 μm bins change over time, the temporal correlation function is a property of the swarm rather than of its individual cells. The velocity-velocity temporal autocorrelation function (dashed line, upper) represents the time over which an individual cell's velocity becomes randomized. A 0.25-s exponential decay (dotted line) is included for reference. Due to the finite size of our video frame, we are susceptible to sampling bias for times beyond a few tenths of a second (because cells that consistently move in the same direction tend to swim out of our field of view), so we are not confident in the long-time tail of the autocorrelation function. See Methods for formal definitions of correlation and autocorrelation functions.

Spatial correlations among cells

By eye, it appears that swarms contain dynamic packs or groups of cells whose swimming behavior (speed and direction) is similar. To quantify this observation, we examined the correlation between different cells as a function of the cells' separation. Fig. 5 A shows the correlation between cells' velocities as a function of the relative (vector) position of the cells. As expected, the correlation is left-right symmetric and extends over a few body lengths. The correlation extends significantly further behind the cell than in front of the cell: the cells behind the target cell were more likely to be moving in the same direction as the target cell than were the cells in front. Because the velocity of a cell is well aligned with its body, the body-body and body-velocity correlation (data not shown) are similar to the velocity-velocity correlation. The basic phenomenon—anisotropic objects forced into alignment due to high packing density—is also responsible for order in nematic liquid crystals and in flocking theory (55). However, a nematic liquid crystal is head-tail symmetric, whereas we see a difference in correlation lengths in front of and behind the swarm cell. We suspect that the fundamentally symmetrical collisional interaction between cells results in an asymmetrical correlation function because the history of the cells interactions is asymmetric. Because the cell is emerging from the region of the swarm behind it, it has had a greater opportunity to interact with cells in that area, and consequently it is more highly aligned with those cells. This is a simple mechanism to convert spatially symmetric collisional interactions into an effectively asymmetric correlation.

Figure 5.

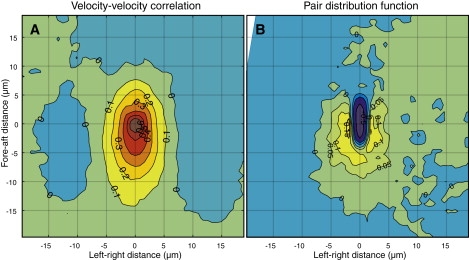
Spatial correlations. (A) The velocity-velocity spatial correlation function represents the degree of directional alignment between velocities of different cells as a function of distance. (B) The pair distribution function represents the probability of finding two cells a certain distance apart. The dark blue region of low probability around the origin is due to mutual exclusion by the 1 μm × 5 μm cell bodies. A second cell is ∼10% more likely than average to be located near the side and back of another cell. Outside of the exclusion zone, the error on the velocity-velocity correlation (A) is ∼0.015 and the error on the pair distribution function (B) varies from 0.03 to 0.02 with increasing distance from the origin. See Methods for definitions of these functions and of the coordinate system.

An alternative explanation for the head-tail asymmetry in the velocity-velocity correlation function is that the flagellar bundle, which usually trails behind the cell, influences neighbors in the cell's wake. We tend to disfavor this explanation because of the shape of the pair distribution function (Fig. 5 B). We see a symmetrical excess population to the left and right of the cell due to side-by-side packing of cells. The fore-aft distribution is not symmetric, however: there is a hole in front of the cell. This vacancy is what allows the cell to move forward. If the flagella were interacting significantly with the cells in the aft direction, we would also expect to see an excluded region there; on the contrary, we see an excess probability of cells in the rear, indicating that on average the flagellar bundle does not sterically hinder other cells.

Groups of cells

One of the striking features of a swarm of cells, clearly visible by eye, is the continuous formation and dissolution of groups of cells that tend to move together. This phenomenon proved difficult to define algorithmically, so we identified by eye groups of cells traveling in packs, drawn from the existing tracked-cell data. Comparing the behavior of cells in and out of groups, we found that cells were slightly closer together and more closely aligned when moving within a group but that their mean speeds were the same. The major difference was that cells in groups tended to swim in a given direction ∼3 times longer: the velocity-velocity temporal autocorrelation function declined linearly for short times with a time constant of 0.46 s for cells within groups versus 0.14 s for cells outside of groups. We conclude that cells in groups are not particularly fast, but the group as a whole travels more consistently in a straight line. This lesser rate of randomization of the cells' trajectories is presumably what is visible by eye when one observes a swarm.

Swarm edge

Cells encountering the swarm boundary (the junction of solid, fluid, and gas) moved in a distinctive way. A typical cell slowed as it neared the edge, stalled, and after a brief pause, moved away from the edge, either by completely reversing or by deflecting at a shallow angle, sometimes after traveling along the edge for some distance. We examined 66 such cells more closely, tracking them for a longer time (150 frames or 5 s). The majority (45/66) reversed their direction of motion and swam directly away from the edge back into the swarm, after spending an average of 1.21 s stalled at the edge. This probably underestimates the mean dwell time of a cell at the swarm edge, because some cells (11/66) remained at the edge for longer than our 5-s tracking time and others (9/66) turned and swam along the edge out of our field of view. The speeds of approach and departure for the cells were essentially identical (26 ± 17 μm/s); this is the same as the edge region population average of 26 μm/s. Because the majority of cells reversed their head-tail orientation, it is likely that flagellar motion aids swarm expansion by pumping fluid outward from the colony, allowing the swarm to expand.

Discussion

The advancing front of an E. coli swarm is a monolayer of moving cells that can extend >1 cm radially. This distance is enormous compared to the few micrometers size of a bacterium. The properties of the interior of the monolayer are different than the properties of its outer edge.

Swarm interior

Our swarm density and tracking data indicate that, with the exception of cells immediately adjacent to the swarm edge, the properties of the swarm monolayer are insensitive to location. Beyond a few 100 μm from the swarm edge, the swarm density profile is flat. At large distances another layer of cells forms on top of the monolayer, followed by successive new layers until the swarm eventually becomes very thick. Although we have carried out quantitative analysis only out to ∼1000 μm from the swarm edge, which is a small fraction of the width of a good monolayer, our impression is that swarm behavior within the constant-density plateau is uniform.

We examined two widely separated locations within the plateau in two different swarms. In both swarms, all the dynamic cell properties that we measured were consistent throughout the plateau. The distributions of cell speed, propulsion angle and curvature were substantially unchanged. Between the plateau and the swarm edge, the swarm surface density peaked ∼70% above the plateau density. Despite this increase, the propulsion angle and curvature distributions were unchanged; the speed distribution was shifted only slightly toward higher speeds and to a slightly different shape. In particular, the average cell speed peaked at moderately high local densities (∼0.1 cells/μm²). At low densities, speed dropped for unknown reasons; at very high density (approaching the close-packed density of 0.2 cells/μm²) cells jammed and speed dropped again. Directions of motion of different cells were correlated only over a limited distance; this correlation was not isotropic, being significantly shorter in the forward direction. The pair distribution function was also anisotropic, with a significant void in the forward direction.

Taken together, these observations lead us to the following description of motion in the interior of the swarm monolayer: each cell attempts to swim straight ahead, but is constantly jostled by its immediate neighbors. This jostling may involve either true collisions or mutually induced forces transmitted by the fluid. Because hydrodynamic interactions are screened by proximity to surfaces, they must be very short range. Whatever their origin, interactions are limited to the immediate neighbors of a cell and can therefore be thought of as collisions. The interaction itself tends to align bodies and velocities of the cells over a few cell lengths, and the movement of the cells transports this alignment from place to place. When a cell can move freely, it swims fast and straight ahead; when its progress is blocked it slows and tends to be pushed to either side. When many cells align they do not swim any faster but the group is deflected less easily and therefore moves straight ahead more consistently.

Swarm edge

At the edge of the swarm, cell motion looks quite different. Just inside the swarm boundary, a several-body-long layer of cells is nearly jammed. Just behind it, a narrow, motile, high-density ring of cells pushes on the jammed layer. When a cell manages to dart outward toward the edge, it rarely gets a full body length into virgin territory before stalling. Although a stalled cell looks immobile, its flagella must still be rotating, and they probably shift from pointing inward to pointing outward. Presumably, these outward pointing flagella pump fluid outward, contributing to swarm expansion. A second or so later, the swarm expands enough to release the stalled cell, which swims back into the interior or along the swarm edge. In a snapshot of the swarm boundary, it appears that a ring of nonmotile cells lines the edge, but these cells are fully motile once transported back into the swarm interior.

Beyond this mechanistic description of the swarm edge, what drives swarm expansion? Plausible important factors are depletion of nutrients (due to cell growth), wetness, and population pressure from the swarm interior (due to a combination of cell growth and cell motility). In swim plates, where cells move through a large-pore agar matrix, the population expands by following gradients generated by the consumption of nutrients (56). This contrasts with our case, where although nutrient availability might affect the bacterial growth rate, chemotaxis seems not to matter (57). Wetness must be important because an insufficiently wet plate (an agar concentration >0.45%) will not support swarming, but we do not know in detail how the swarm generates the concentric, expanding ring of wetness that precedes it onto the virgin agar. It might do so by sloughing off lipopolysaccharide and pumping fluid outwards. Population growth alone cannot explain swarm expansion because simple population pressure would produce a uniformly increasing cell density toward the colony interior, whereas we see an extended constant-density plateau. Because the plateau is not close-packed, the outward force may arise from collisions of billions of motile bacteria—a sort of bacterial gas pressure. Based on these arguments, we suspect that spreading depends principally on progressive wetting of the agar surface, and is driven by a combination of motility and cell density.

From the results obtained thus far, apart from modest gradual changes in average speed and density, it seems reasonable to treat all of the swarm monolayer (except the area within a few cell lengths of the edge) as a uniform collection of self-propelled particles drawn from a wide distribution of sizes and speeds, interacting over a range of a few cell lengths. The alignment that we have observed is left-right symmetric but not fore-aft symmetric, although we suspect that the observed asymmetry is not due to any fundamental asymmetry in cell-cell interactions. In contrast with most models of flocks, swarming cells do not move at constant velocity. The wide range of speeds is probably due to interactions with other cells, primarily because a cell's forward path is often blocked. At its most extreme, this results in an entire field of cells becoming jammed, as observed at the edges of the swarm monolayer. Within the swarm monolayer, the surface cell density stays close to 50% full coverage. There are plausible mechanisms for maintaining this density: a low density provides voids for neighboring cells to swim into, which bring the density back up, whereas a high density produces a jamming force that either dissipates the jam (for transient density fluctuations in the monolayer interior), forces the jam out onto virgin agar (at the swarm edge), or pushes cells out of the monolayer into a second layer (at the interior boundary of the monolayer). We see completely jammed, immobile monolayers only in swarms that fail, which is usually caused by surface dryness or a drop in incubation temperature. For modeling purposes, a swarming cell should probably be treated as a constant force object rather than a constant speed object.

A bacterial swarm is a spatially and temporally coordinated system composed of billions of individual cells. E. coli produces a regular swarm structure, including phenotypic variation as a function of position in the colony, without using cell-signaling molecules. This makes it a particularly simple model for understanding swarming because the (presumably) nonuniform concentration of quorum-sensing molecules, which governs the biological regulation of swarmer phenotype in other swarming species, is not a complicating factor. Based on the kinetic parameters we measured, the outer region, comprising the edge and a thin, highly motile layer, maintains a uniform microscopic structure while expanding. The monolayer is in dynamic equilibrium with both the colony edge (with its associated ring of wetness) and the colony interior (containing the majority of cells), so a quantitative understanding of the expansion of the swarm colony will necessarily incorporate the dynamics of the monolayer. Interpreted as a purely physical system, the swarm monolayer acts like a two-dimensional gas of self-propelled, substantially polar particles. We have measured the microscopic properties of the bacterial atoms of our gas, such as speed distributions and correlation functions, to facilitate comparison to the microscopic properties postulated in two-dimensional flocking theories.

Supporting Material

One figure and two movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00218-3.