Structure and Dynamics of Ribosomal Protein L12: An Ensemble Model Based on SAXS and NMR Relaxation

Abstract

Ribosomal protein L12 is a two-domain protein that forms dimers mediated by its N-terminal domains. A 20-residue linker separates the N- and C-terminal domains. This linker results in a three-lobe topology with significant flexibility, known to be critical for efficient translation. Here we present an ensemble model of spatial distributions and correlation times for the domain reorientations of L12 that reconciles experimental data from small-angle x-ray scattering and nuclear magnetic resonance. We generated an ensemble of L12 conformations in which the structure of each domain is fixed but the domain orientations are variable. The ensemble reproduces the small-angle x-ray scattering data and the optimized correlation times of its reorientational eigenmodes fit the ¹⁵N relaxation data. The ensemble model reveals intrinsic conformational properties of L12 that help explain its function on the ribosome. The two C-terminal domains sample a large volume and extend further away from the ribosome anchor than expected for a random-chain linker, indicating that the flexible linker has residual order. Furthermore, the distances between each C-terminal domain and the anchor are anticorrelated, indicating that one of them is more retracted on average. We speculate that these properties promote the function of L12 to recruit translation factors and control their activity on the ribosome.

Introduction

Proteins composed of multiple folded domains are common in nature (1,2). The lengths and conformational propensities of the linker regions have evolved to provide these proteins with structural and dynamic properties that determine their biological functions (3,4). Because of their inherent flexibility, multidomain proteins with disordered linkers are notoriously challenging to characterize in terms of their global structure and dynamics (4). The high degree of flexibility of these systems suggests that the relative domain orientations are best described in terms of conformational ensembles.

Recent developments in modeling flexible molecules (such as intrinsically disordered or denatured proteins), in terms of conformational ensembles, have been applied to yield agreement with experimental data (5–9). Continued progress in NMR methodology has improved the characterization of multidomain proteins and other inherently flexible systems in terms of both structure and dynamics (10,11). In favorable cases, the motions of individual domains can be deconvoluted from global tumbling, and quantitative descriptions of interdomain flexibility can be obtained by invoking specific dynamic models (12). Interpretation of relaxation rates using wobbling-in-a-cone (13) or two-site jump (14) models have been reported. However, in many cases the interpretation of relaxation data is restricted to qualitative models, because the analysis is hampered by the inherent coupling between the relative domain motions and global tumbling.

Ribosomal protein L12 is a two-domain protein that forms dimers mediated by its N-terminal domain (NTD) (15). A flexible 20-residue linker between the well-ordered N- and C-terminal domains gives L12 an overall topology resembling three loosely joined globular lobes (16–18) (see Fig. 1 a). Multiple copies of L12 are anchored to protein L10 on the ribosome via the NTD dimers; ribosomes from mesophilic and thermophilic bacteria contain two and three copies of the L12 dimer, respectively (19,20). The available x-ray structures of ribosomes do not include electron density for L12; this is due to its extensive flexibility. Indeed, the NMR spectrum of intact Escherichia coli ribosomes reveals that the C-terminal domains (CTD) of L12 undergo large-scale motions in their functional environment (17,21). The high degree of freedom of the CTDs is believed to enable their function to recruit translation factors (22) and control their activity on the ribosome, possibly by alternating extension and contraction of the linker (23,24).

Figure 1.

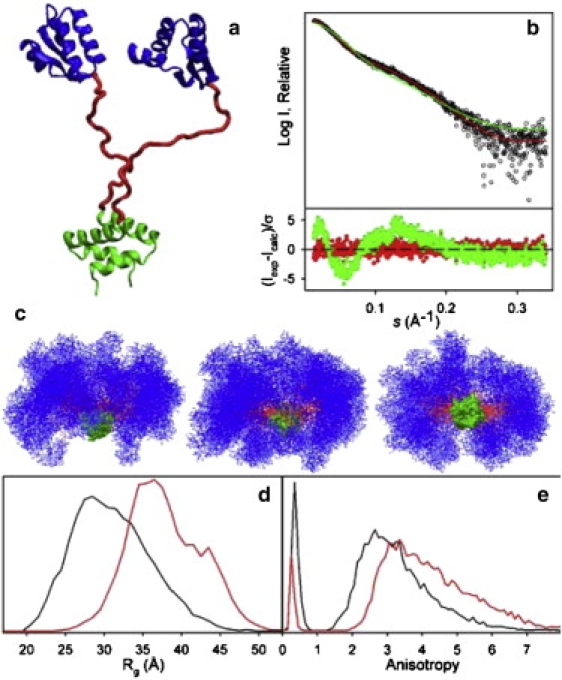
Ensemble optimization analysis of the SAXS profile measured for L12. (a) Cartoon of a single L12 conformation, 1rqu (16), showing the NTD dimer (green), the CTD (blue), and the linker (red). (b) Logarithm of the scattering intensity (black dots) as a function of the momentum transfer, s = 4πsin(θ)/λ. The fitted scattering profile of the optimized ensemble (OE), obtained by the EOM approach, is shown in red. The theoretical scattering curve of the random ensemble (RE, green line) is shown for comparison. The bottom panel displays the point-by-point error function for the two ensembles using the same color code. Both ensembles contain 10,000 independent conformers. (c) Three orthogonal views of a random subset (N = 50) of the OE; color code as in panel A. The orientation in the side view (left) is the same as in panel A. (d) Radius of gyration (R_g) and (e) anisotropy (A) distributions for the RE (black lines) and the OE (red lines). The sharp peaks at A < 1 correspond to oblate conformers with populations of 4.8% and 14.2% for the OE and RE, respectively.

The average solution structure of L12 has been determined by small-angle x-ray scattering (SAXS) (18), outlining the positions of the three globular domains. This static picture contrasts with the available evidence from NMR, which shows that L12 does not behave as a rigid body in solution; instead, it samples a range of relative domain orientations made possible by the flexible linker (17). Here, we reconcile these different views by presenting an ensemble model that agrees with experimental data from both SAXS and ¹⁵N relaxation measurements. Using reorientational eigenmode dynamics (iRED) analysis (25) of the SAXS-restrained ensemble, we model the domain motions in terms of eigenmodes and correlation times that agree with the experimental ¹⁵N spin relaxation data. The resulting ensemble model describes both the spatial distributions and reorientational dynamics of the L12 domains, revealing correlated motions of the NTDs and CTDs. The results help explain previous results on both isolated and ribosome-bound L12 in terms of its intrinsic conformational propensities.

Material and Methods

Ensemble generation

Monomeric L12 conformers were generated using the program PRE-BUNCH (7) by randomly assigning sterically allowed coordinates for the flexible linker (residues 31–52), which had been identified previously by NMR relaxation measurements (16,17). The dihedral angles of the linker residues were assigned randomly within the context of a C^α-C^α pseudo-Ramachandran space (7,26). Monomers were then randomly assembled into dimers, avoiding steric overlap. Fifty-thousand independent monomers were calculated to yield a pool of M = 10,000 dimeric conformers, which constitute a random ensemble (RE).

SAXS data collection and analysis

SAXS data were collected and processed as described previously (18). The final SAXS curve was analyzed based on either the full RE of conformers or an optimized ensemble (OE) that was obtained using the EOM strategy (7). The scattering profile was computed for each individual conformer of the RE using CRYSOL (27). Following the EOM protocol, N = 50 conformers/curves were selected by a genetic algorithm from the RE to minimize the deviation between the experimental and calculated SAXS curves,

$${\chi }_{\text{SAXS}}^2=\frac{1}{K-1}\sum _{j=1}^K{\left[\frac{\mu I\left(s_{\mathrm{j}}\right)-I_{\exp }\left(s_{\mathrm{j}}\right)}{\sigma \left(s_{\mathrm{j}}\right)}\right]}^2,$$ (1)

where I(s_j) and I_exp(s_j) denote the calculated and experimental scattering intensities, respectively, and I(s_j) is the average value calculated for the N conformers; s_j is the momentum transfer with index j running over all (K) experimental data points; σ(s_j) are the standard deviations; and μ is a scaling factor (7). The whole procedure, starting with the generation of a new RE, was repeated in 200 independent runs to generate an OE of 10,000 (i.e., 50 × 200) independent conformers. Although an ensemble size of 50 conformers generally is sufficient to reach agreement with the experimental SAXS data, the larger ensemble is necessary to account for the full conformational space consistent with the experimental data and to represent the ensemble in terms of smooth distributions of conformational parameters (see below), which can be compared directly with those of the RE.

Conformational analyses

The anisotropy parameter was calculated for each conformer: A = 2d1/(d2+d3), where d1, d2, and d3 are the eigenvalues of the radius of gyration tensor, defined such that d1 is the most different dimension (d1 ≥ d2 ≥ d3 or d1 ≤ d2 ≤ d3).

The interdomain distances were calculated from the center-of-mass of each domain. The relative domain positions and orientations were determined by diagonalizing the moment of inertia tensor for each domain (the two CTDs and the NTD dimer) in each conformer. The principal axes of the NTD inertia tensor define a coordinate system in which the location and orientation of the CTD principal axis system were determined. The eigenvectors were ordered by eigenvalue, i_x < i_y < i_z, so that I_x is pointing along the long axis of each domain. The center-of-mass positions as well as the I_x orientations of the CTDs relative to the NTD coordinate system were determined for each conformer.

Reorientational eigenmode dynamics analysis

Reorientational eigenmodes were extracted from the optimized SAXS ensemble following established protocols (25) implemented in C and MATLAB (The MathWorks, Natick, MA). The rank-2 M matrix, with elements M_kl = 〈P₂cosθ_kl〉, was calculated for the ¹⁵N-¹H vectors by averaging all pairs of blocks in the matrix that contain symmetry-related elements. Thus, the NTD1-CTD1 and NTD2-CTD2 blocks were replaced by their average, as were the NTD1-CTD2 and NTD2-CTD1 blocks. The M matrix was subsequently diagonalized, giving 15 eigenmodes with nonzero eigenvalues. The eigenvalues were used to calculate principal order parameter components $\delta A_{\mathrm{j},\mathrm{m}}^2$, which represent how much of the decay of the correlation function for residue j stems from mode m (25). Previous applications of iRED to analyze simulated trajectories have verified that the autocorrelation functions are monoexponential decays that can be described by mode-specific correlation times (25,28). First, we fitted the correlation times of the modes to the R₂/R₁ ratios using the nonlinear Levenberg-Marquardt algorithm (29), implemented in MATLAB. All pairs of degenerate modes (original modes 1-2, 4-5, 8-9, 10-11, and 12-13 for the RE, and original modes 8-9, 10-11, and 12-13 for the OE) were assigned a common correlation time. The experimental relaxation rates are obtained as averages over the two protomers in the dimer, because the domain reorientation is fast on the chemical shift and relaxation timescales (17). Hence, the experimental rates were fit against the average of the calculated relaxation rates of the two protomers. The trimmed mean (±1 standard deviation) of the R₂/R₁ ratios yielded effective correlation times of 5.4 ns for the CTD and 8.0 ns for the NTD dimer; these values were taken as starting values for the nonlinear fit. The correlation times of all modes were fitted simultaneously, because this procedure yielded the most stable results, as determined from simulated relaxation data. Subsequently, residue-specific order parameters were fitted to the full data set (R₁, R₂, and NOE), using the spectral density

$$J_{\mathrm{j}}\left(\omega \right)=S_{\mathrm{j}}^2\sum _{m=1}^{m_{\max }}\delta A_{\mathrm{j},\mathrm{m}}^2\frac{2{\tau }_{\mathrm{m}}}{1+{\omega }_2{\tau }_{\mathrm{m}}^2}+\left(1-S_{\mathrm{j}}^2\right)\frac{2{\tau }_{\mathrm{e}}}{1+{\omega }_2{\tau }_{\mathrm{e}}^2},$$ (2)

where $S_{\mathrm{j}}^2$ is the usual Lipari-Szabo order parameter for the intradomain local motion (30) with effective correlation times τ_e. To reduce the number of parameters, global τ_e values were used for each of the NTD and CTD. The chemical shielding anisotropy was set to –163 ppm (31) and the vibrationally averaged ¹⁵N-¹H bond distance was set to 1.04 Å.

In this model, the degrees of freedom include only the relative domain orientations, in which the structure of each domain is fixed. Thus, our approach is based on the assumptions that

• 1.The local motion of a given N-H vector in the molecular frame of its domain is uncorrelated with the domain reorientations, and
• 2.The relative domain reorientations occur on a timescale faster than, or comparable to the overall rotational diffusion of the entire L12 dimer.

The first assumption is the basis for the standard model-free approach (30) and holds as long as the individual domains are reasonably rigid, which is the case here. The second assumption is supported by the extensive flexibility of the linker (17).

The residuals of the fits were calculated as

$${\chi }_{\text{iRED}}^2=\sum _{k=1}^L{\left[\frac{Y_{\mathrm{k}}-Y_{\exp ,\mathrm{k}}}{{\sigma }_{\mathrm{k}}}\right]}^2,$$ (3)

where Y_k and Y_exp,k denote the calculated and experimental relaxation data (i.e., R₁/R₂, R₁, R₂, or NOE), respectively, with the index k running over all (L) residues in the protein; and σ_k is the standard deviation.

The apparent rotational diffusion tensor D of each domain was determined from the mode correlation times. The diffusion tensor thus obtained corresponds to that determined from a conventional fit to relaxation rates. We included only those modes that contribute significantly to the reorientation of a given domain (see below): modes 2, 3, 6, 7, 11, and 12 for the NTD, and modes 1, 2, 4, 5, 8–10 for the CTD. Thus, there are six correlation times for the NTD and seven for the CTD. Modes 1 and 2 affect the CTD identically, as does the pair 4 and 5. Therefore, we calculated two effective correlation times,

$$1/{\tau }_{1\prime }=0.5\left(1/{\tau }_1+1/{\tau }_2\right)$$

and

$$1/{\tau }_{4\prime }=0.5\left(1/{\tau }_4+1/{\tau }_5\right),$$

giving, in total, five correlation times for the CTD. Similarly, the correlation times of modes 2 and 3 were averaged for the NTD, as they are closely correlated in the NTD region. The five rank-2 correlation times of an anisotropically diffusing body are given by (32,33)

$$1/{\tau }_1=6D_{\mathrm{r}}-2\Delta ,$$

$$1/{\tau }_2=3D_{\mathrm{r}}+3D_1,$$

$$1/{\tau }_3=3D_{\mathrm{r}}+3D_2,$$

$$1/{\tau }_4=3D_{\mathrm{r}}+3D_3,$$

and

$$1/{\tau }_5=6D_r+2\Delta ,$$

with

$$D_{\mathrm{r}}=1/3\left(D_1+D_2+D_3\right)$$

and

$$\Delta ={\left(D_1^2+D_2^2{D}_3^2-D_1{D}_2-D_1{D}_3-D_2{D}_3\right)}^{1/2}\text{.}$$

The diffusion tensor components D_i were thus fitted to the five correlation times for each domain. Once the tensor components had been estimated, the harmonic mean correlation time was calculated as

$$1/{\tau }_{\mathrm{c}}=6D_{\mathrm{r}}=1/5{\sum }_{\mathrm{k}=1}^{5}1/{\tau }_{\mathrm{k}}\text{.}$$

The rotational diffusion anisotropy is defined as

$$A_{\mathrm{r}}=2D_3/\left(D_1+D_2\right)\text{.}$$

Results

RE and OE of L12

NMR relaxation data have shown that L12 does not behave as a rigid body in solution, and have further delineated the rigid domains from the flexible linker (17). However, the domain-specific rotational diffusion properties show that the domains cannot be treated as independently reorienting structures. The apparent correlation time and diffusion anisotropy of the CTD are τ_c = 5.9 ns and A_r = 1.84, respectively (17), which should be compared with the values expected from hydrodynamic calculations (34,35) for the isolated CTD, τ_c = 3.6 ns and A_r = 1.34. For the NTD dimer, the apparent correlation time was τ_c = 8.0 ns, compared to 3.8 ns from hydrodynamics calculations, whereas A_r could not be determined experimentally (17). These results provide evidence for motional coupling between the domains, although the exact degree of coupling remains elusive from this level of analysis using standard methods.

To construct a model that describes the overall rotational diffusion of L12 as well as the motional coupling between its domains, we initially tested whether an ensemble of random domain orientations can explain the available experimental data. We generated a 10,000-membered RE of L12 dimer structures with rigid domains and flexible linkers (see Material and Methods), which we analyzed using the iRED approach (25). The iRED analysis provides a view of the domain motions in terms of eigenmodes (Fig. S1 in the Supporting Material) and correlation times that could be optimized to reach good agreement with the experimental ¹⁵N spin relaxation data, with χ²_iRED = 4.72. To this extent, the RE provides a realistic representation of the domain reorientations experienced by L12 in solution. We further investigated whether the RE is consistent with SAXS data, but found that the quality of the fit was unsatisfactory, with χ²_SAXS = 4.44 and systematic deviations in the error function (Fig. 1 b).

To reach agreement with the SAXS data, we employed the EOM approach (7) to select from the RE a subensemble of domain orientations that optimally fit the SAXS scattering profile (Fig. 1 b). The mean-squared residuals of the fit are χ²_SAXS = 0.62 for the resulting OE and the error function is randomly distributed around zero for all momentum transfer values, s (Fig. 1 b). We verified that the iRED modes of the OE provide a representation of the conformational fluctuations that fits the experimental ¹⁵N relaxation data (χ_iRED² = 4.66) with physically reasonable correlation times (see below). The goodness of fit obtained for the OE is almost equivalent to that obtained for the RE, indicating the inability of NMR relaxation to distinguish between the two ensembles. A representative subset of conformers from the OE illustrates the intrinsic flexibility of L12 in solution (Fig. 1 c). Clearly, the CTDs sample a broad range of positions. Below, we present quantitative indicators of size, shape, and dynamics that together provide a comprehensive model of the domain fluctuations in solution.

Radius of gyration and anisotropy

Distributions of the radius of gyration (R_g) and the shape anisotropy (A; see Material and Methods) were calculated from the OE and compared with those obtained from the RE (Fig. 1, d and e). The broad distributions of R_g and A confirm that L12 is a highly flexible protein. Yet, both R_g and A are shifted toward greater values for the OE than for the RE, and the population of oblate conformations (A < 1.0) is reduced, indicating that L12 preferentially samples extended and prolate conformations.

Interdomain distances

The extension of L12 can be quantified in terms of interdomain distances (Fig. 2). As expected, there is a clear correlation between R_g and the interdomain distances, especially the CTD-CTD distance (Fig. 2, a and b). We observe enhanced separation between the NTD dimer and each of the two CTDs (Fig. 2, a, c, and d), as well as between the two CTDs (Fig. 2, b and c), in the OE compared to the RE. These results demonstrate that the CTDs preferentially sample the external shell of the available conformational space. Notably, the two CTDs are further apart than either of them is from the NTD dimer (Fig. 2, a–c), indicating a tendency for the CTDs to populate opposite locations in three-dimensional space, as also suggested by Fig. 1 c. Fig. 2 c highlights the structural differences between the OE and RE in terms of their NTD-CTD and CTD-CTD interdomain distances. Interestingly, the OE populates two separate regions, whereas the RE has a more unimodal distribution. The more extended conformation populated in the OE corresponds to an anticorrelation of the distances between the NTD dimer and the individual CTDs (NTD-CTD1 and NTD-CTD2), as shown in Fig. 2 d. Presumably, this anticorrelation is due in part to steric effects, because it is present in the RE, but it might also reflect different conformational states of the two linkers. In either case, the domain arrangement includes a significant population of asymmetric conformations in which one CTD is more retracted toward the NTD than is the other.

Figure 2.

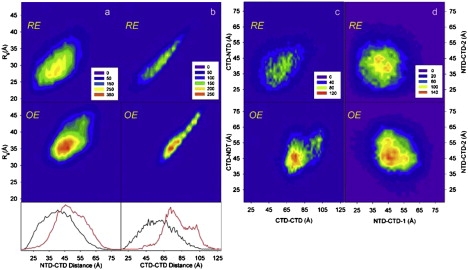
Structural characterization of the L12 ensemble. Contour maps of structural parameters for the optimized (bottom panel) and random (top panel) ensembles. The radius of gyration (R_g) is plotted versus the (a) NTD-CTD and (b) CTD-CTD interdomain distances, calculated from their respective center-of-mass. One-dimensional projections of the random (black solid line) and the optimized (red solid line) ensembles are shown along the horizontal axis; the corresponding projections onto the vertical axis are shown in Fig. 1d. The interdomain distances are here correlated: (c) NTD-CTD versus CTD-CTD, and (d) NTD-CTD1 versus NTD-CTD2. Panel c shows the average distance between the NTD and CTD, whereas panel d shows separate distances for the two CTDs.

Interdomain angles

To visualize the distributions of relative domain orientations in the derived model, we related the location and orientation of the CTD principal axis system to the principal axes of the NTD inertia tensor. The z axis of the NTD is pointing upwards in Fig. 1 a and the x axis of the CTDs is pointing from the N-terminus along the domain. Fig. 3, a and c, shows the angular coordinates (θ_com, ϕ_com) for the center-of-mass of each CTD, and Fig. 3, b and d, shows the angular coordinates (θ_x, ϕ_x) specifying the orientation of the CTD x axis. As seen in Fig. 3, a and c, the positions of the CTDs are much more constrained in the OE than in the RE, with clear peaks appearing at θ_com = 65° and ϕ_com = −140° and 30°. Although the orientation of the CTD is isotropic in the RE (the distribution approximately follows sin(θ_x); Fig. 3 b), the distribution in the OE is narrow and peaks at θ_x = 70° and ϕ_x = 45° (Fig. 3 d). Clearly, in this model the linker does not behave as a random coil, but exhibits considerable stiffness.

Figure 3.

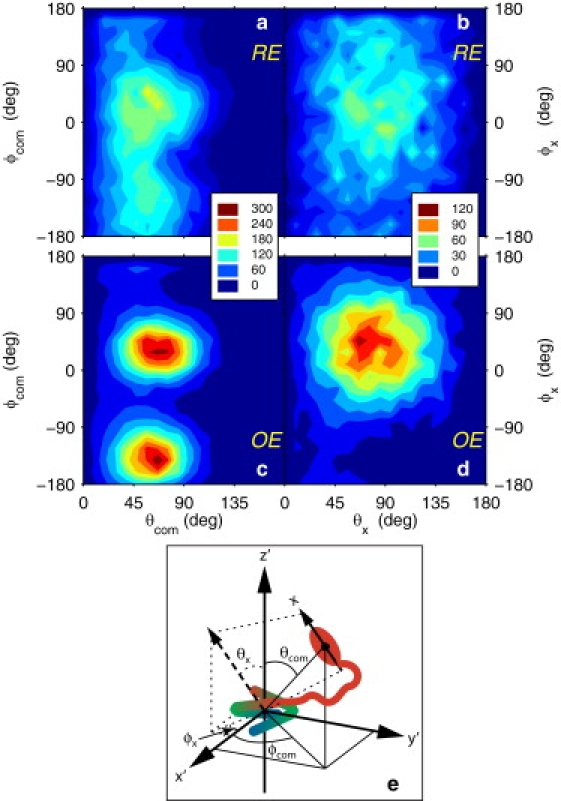
Distribution of relative domain positions and orientations in the L12 dimer. (a and c) The angles θ_com and ϕ_com specify the position of the CTD center-of-mass in the spherical coordinate system defined by the principal axes (x′, y′, z′) of the NTD inertia tensor (θ_com, angle from the z′ axis; ϕ_com, angle from the x′ axis). Results are included for both CTDs and shown for (a) the RE and (c) the OE. (b and d) The angles θ_x and ϕ_x specify the orientation of the x axis of the inertia tensor for CTD2 in the spherical coordinate system defined by the principal axes of the NTD inertia tensor (θ_x, angle from the z′ axis; ϕ_x angle from the x′ axis). For clarity, results are included for a single CTD (CTD2) and shown for (b) the RE and (d) the OE. In panel b, the θ_x distribution closely follows sinθ_x. The z axis (x axis) is associated with the largest (smallest) principal value of the inertia tensor. For reference, the z′ axis of the NTD dimer is pointing upwards in Fig. 1a. (e) Schematic depiction of the coordinate systems and angles. The NTD dimer has the same orientation as in Fig. 1a. The continuous color code of each NTD indicates the location of its N (blue) and C (red) termini. The red ellipse represents one of the two CTDs, depicting the center-of-mass and long axis x (associated with the smallest principal value of the inertia tensor). The dashed arrow and dashed projection lines shows the orientation of the CTD x axis, translated to the origin of the NTD coordinate system for clarity.

CTD order parameters

The restriction in the CTD orientations with respect to the NTD principal axes can be quantified by an order parameter (S²) that ranges between 0 for an isotropic distribution of orientations to 1 for a fixed orientation (36). The value obtained for the OE, S² = 0.17, reflects the extensive flexibility of L12, but is notably greater than that for the RE, S² = 0.02. Again, the structural constraints enforced by the SAXS data apparently select a subset of relative domain orientations.

Reorientational eigenmodes

Prompers and Brüschweiler (25) introduced the seminal concept of iRED analysis of molecular dynamics, which is applicable to a wide range of systems because it does not require separability between the overall tumbling and internal motions. Originally applied to trajectories from molecular dynamics (MD) simulations, the iRED method is equally applicable to any equilibrium ensemble of conformations. Based on the assumption that the SAXS-constrained OE serves as an adequate surrogate for the true equilibrium ensemble, we performed iRED analysis as a means of incorporating into the model the dynamic (timescale) information obtained from NMR relaxation. In this way, we achieve a complete model of the multidomain protein in terms of both structure and dynamics.

The iRED analysis of the L12 ensembles yields 15 eigenmodes with nonzero eigenvalues. In the case of the OE, three pairs of eigenmodes are degenerate because of the orientational symmetry between the two CTDs, resulting in 12 unique modes (Table 1). The eigenvalues (λ) are evenly distributed and do not exhibit any significant gap between the five largest values and the remaining seven, indicating that the eigenmodes do not separate into overall and internal motions (Fig. S2). Hence, all modes contribute to a similar extent to the rotational diffusion of L12, as might be expected from the high flexibility of the linkers (17).

Table 1.

Correlation times (τ_m), mode collectivities (κ), and eigenvalues (λ) of the 12 unique reorientational eigenmodes of the optimized ensemble

Mode∗	τm (ns)	κ (%)†	λ
1 (C)	5.4 ± 0.2	51.1	25.7
2 (C, N)	8.8 ± 0.3	66.6	25.5
3 (N, C)	8.2 ± 0.2	36.1	22.8
4 (C, N)	2.5 ± 0.1	49.5	17.2
5 (C)	7.3 ± 0.1	44.8	17.2
6 (N)	8.0 ± 0.3	22.2	15.9
7 (N)	8.1 ± 0.4	22.4	14.5
8 (C)	4.9 ± 0.1	35.0	9.8
9 (C)	7.3 ± 0.1	34.4	9.0
10 (C)	6.5 ± 0.1	30.7	5.6
11 (N)	7.7 ± 0.6	16.5	5.0
12 (N)	9 ± 2	11.0	3.4

^∗Letter within parentheses indicates which part of the peptide chain is most prominently affected by this mode: C = CTD, N = NTD. The correlation times were obtained by fitting a model that includes residue-specific order parameters to the full relaxation data set (see the Supporting Material).

^†Mode collectivity (κ) reports the percentage of N-H bond vectors that are significantly affected by this mode, as defined in the Supporting Material.

iRED order parameters

The principal order parameter components $\delta A_{\mathrm{j},\mathrm{m}}^2$ describe the contribution of mode m to the reorientations of the N-H vector of residue j. Fig. 4 shows the $\delta A_{\mathrm{j},\mathrm{m}}^2$ values of each residue for the 12 unique modes derived from the OE (see Fig. S1 for the RE results). Each of the 12 modes contributes significantly to the reorientation of a large number of amides in one or both domains. However, the individual modes contribute qualitatively different fluctuations to the different domains. Only a single mode (mode 2, see Fig. 4) has a significant effect on both the NTD and CTD, whereas another two modes (i.e., 3 and 4) predominantly reorient one domain and have a minor effect on the other domain. The remaining nine modes affect either the CTDs or the NTDs, but not both.

Figure 4.

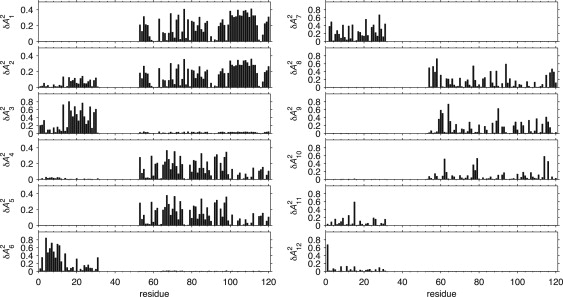
Backbone amide ¹⁵N-¹H bond vector principal order parameter components, $\delta A_{\mathrm{m}}^2$, obtained by rank-2 iRED analysis of the optimized ensemble of L12 structures obtained from SAXS data. Individual panels show order parameters associated with each of the 12 unique eigenmodes plotted versus residue number. The corresponding results for the RE are shown in Fig. S1.

Reorientational correlation times

Table 1 presents the mode-specific correlation times obtained by simultaneous fitting to the ¹⁵N relaxation data for each backbone amide in the NTD and CTD domains, as described under Material and Methods. The fit also includes residue-specific order parameters describing the internal motion of the backbone peptide planes in the molecular frame of the individual domains (see Fig. S3).

The dynamical model derived from the combined EOM/iRED analysis is significantly more detailed than the one arising from the classical diffusion tensor analysis of NMR relaxation data alone. The different reorientational eigenmodes have comparable correlation times, ranging between 4.9 and 9 ns (Table 1), indicating again that the global motion cannot be separated from the relative domain reorientations of the three lobes in the L12 dimer. We calculated the domain-specific values of τ_c and A_r from the iRED correlation times and compared them to the previous results. Our results yield diffusion tensors of the CTD and NTD dimer that are nearly axially symmetric, with values of A_r = 1.78 ± 0.06 and 1.08 ± 0.03, respectively, and apparent correlation times of τ_c = 5.8 ± 0.1 ns and τ_c = 8.2 ± 0.1 ns, respectively. The close agreement between our results and the previously determined classical domain-specific results (see above) demonstrates that the latter are embedded in the global eigenmode representation. Furthermore, the agreement verifies that the entire range of reorientational motion sampled by L12 is taking place on a rapid timescale of ≤9 ns.

Discussion

Structural modeling of highly flexible molecules is challenging, and is arguably best achieved using an ensemble description (8,9). In principle, ensembles can be generated by purely computational approaches, such as Brownian dynamics or MD simulations. However, limitations in the accuracy of the force fields and lengths of the simulations can severely bias the results, especially in cases such as ours, where the system undergoes large-scale conformational fluctuations on longer timescales. These problems make it virtually impossible to establish that a given set of MD trajectories represents a true equilibrium ensemble in the ergodic sense. As an alternative, it has proven highly valuable to model conformational ensembles using distributions that do not a priori reflect the underlying equilibrium, but do agree with experimental restraints obtained under equilibrium conditions. This approach has produced important insights into the nature of unfolded proteins (5,6). It should be kept in mind that this type of inverse problem, aiming at determining an optimal conformational distribution, is generally ill-posed due to the limited number of experimental data points. Nonetheless, the resulting underdetermined structural model, such as the one we present in this article, may generate insights into the biological function of flexible systems.

We reasoned that the significant flexibility observed for the L12 linker (16,17) would make it permissible for our purposes to generate a quasiequilibrium ensemble of domain orientations without taking into account either possible interactions between the domains or conformational propensities of the linker, even though indications of the latter exist (16,37). The fact that the OE reproduces the SAXS data suggests that it captures the equilibrium distance distribution of L12 in solution. Furthermore, the large size of the ensemble vouches for adequate sampling of the conformational space available within the experimental restraints.

Combined analysis of SAXS and NMR data has been employed previously to determine the structures of multidomain proteins with relatively fixed domain orientations (38–43), but has not aimed at characterizing their dynamics. SAXS experiments reflect the conformational distributions arising from such fluctuations, but do not yield any information on the motional timescales. Conversely, NMR relaxation is sensitive to the timescale, but cannot directly describe the relative domain fluctuations in highly flexible systems. Here, we have aimed to bridge this gap by extracting reorientational fluctuations from a SAXS-restrained quasiequilibrium ensemble to produce a unified picture of the domain dynamics in L12.

The RE and OE are notably different ensembles, as gauged by SAXS. In the present context, the combination of steric effects between individual domains and the distance distributions detected by SAXS apparently serve to define the domain orientations relatively well (Fig. 3). It should be noted, however, that the SAXS data are not a priori expected to provide any substantial restraint on the domain orientations, because the individual domains are not sufficiently asymmetric in shape to yield a significant influence of their orientations on the scattering curve. Indeed, the RE and OE exhibit similar reorientational eigenmodes that fit the experimentally measured relaxation rates equally well; compare Fig. 4 and Fig. S1. However, the increased spatial correlation in the OE compared to the RE (Figs. 2 and 3) is reflected in the correlation of the reorientational dynamics of the NTD dimer and CTDs, which is present only in the OE (Fig. 4 and Fig. S1).

Our results indicate that the conformational propensity of L12 is radically different from that expected for a three-lobe system with random-chain linkers. The combined EOM/iRED analysis confirms previous results from ¹⁵N spin relaxation data, which showed that the structured domains do not behave as independent bodies in solution, even though the linker is highly flexible (17). However, our approach goes significantly further by modeling the (quasi)equilibrium distributions and correlation times of the domain reorientations, which reveal correlated motions of the CTD and NTD dimer.

The domain distributions suggest that the linker is partially structured, in agreement with the high propensity for α-helical structure (44) predicted for the N-terminal part of the linker, which includes the ³⁴AAAAVAVAA⁴² region. Additional support for this interpretation includes NMR data suggesting transient helix formation in the linker (16), as well as the crystal structure of isolated L12, which shows the linker in α-helical conformation, albeit in a nonnative dimeric form (37). To this extent, the EOM analysis provides valuable insight into the linker behavior in solution, even though the conformational properties of the linker cannot be directly determined by SAXS. The superextension of the linker, beyond that expected for a random coil, should promote efficient recruitment of translation factors to the ribosome from the surrounding solution.

Furthermore, the results reveal an anticorrelation of the interdomain distances between the NTD dimer and each of the two CTDs: one CTD is extended away from the NTD dimer, whereas the other is located closer to the NTD dimer. Intriguingly, this arrangement agrees with previous observations of L12 bound to the ribosome, which showed that only two of the four CTDs extend away from the ribosome (17,21). The alternating extended and retracted positions suggests that L12's function to recruit translation factors and control different states of the ribosome during translation might be driven by this intrinsic conformational design (19,22,23,45).

In conclusion, we have derived an ensemble model to describe the structure and reorientational dynamics of the flexible multidomain protein L12, based on a combination of SAXS and NMR data. The SAXS data distinguish between ensembles that cannot be distinguished from NMR relaxation, allowing both local (from NMR) and global (from SAXS) dynamics to be characterized. Our approach should be applicable to other types of multidomain proteins, provided that the slowest significant reorientational modes contribute to NMR relaxation. With this limitation in mind, one could potentially use residual dipolar couplings instead of, or in combination with, SAXS data to constrain the conformational ensemble.

Supporting Material

Three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00263-8.