Comparison between Whole Distribution- and Average-Based Approaches to the Determination of Fluorescence Resonance Energy Transfer Efficiency in Ensembles of Proteins in Living Cells

Abstract

Current methods for analysis of data from studies of protein-protein interactions using fluorescence resonance energy transfer (FRET) emerged from several decades of research using wide-field microscopes and spectrofluorometers to measure fluorescence from individual cells or cell populations. Inherent to most measurements is an averaging of the distributions of FRET efficiencies over large populations of protein complexes, which washes out information regarding the stoichiometry and structure of protein complexes. Although the introduction of laser-scanning microscopes in principle could facilitate quantification of the distributions of FRET efficiencies in live cells, only comparatively recently did this potential fully materialize, through development of spectral- or lifetime-based approaches. To exploit this new opportunity in molecular imaging, it is necessary to further develop theoretical models and methods of data analysis. Using Monte Carlo simulations, we investigated FRET in homogenous and inhomogeneous spatial distributions of molecules. Our results indicate that an analysis based on distributions of FRET efficiencies presents significant advantages over the average-based approach, which include allowing for proper identification of biologically relevant FRET. This study provides insights into the effect of molecular crowding on FRET, and it offers a basis for information extraction from distributions of FRET efficiencies using simulations-based data fitting.

Introduction

Fluorescence resonance energy transfer (FRET) is a process of nonradiative transfer (via dipole-dipole coupling) of energy from an excited donor molecule (D) to an unexcited acceptor molecule (A) located in close proximity of each other (typically <10 nm). When both molecules are fluorescent, the term fluorescence resonance energy transfer is used, although the energy is not actually transferred by fluorescence (1). If fluorescent probes are attached to known sites of two macromolecules of interest or of the same macromolecule, FRET efficiency measurements allow one to evaluate inter- and intramolecular distances or changes. FRET can be detected using both fluorescence lifetime imaging (2–10) and fluorescence intensity measurements (7,8,11–18). In biological applications, FRET has been used to investigate, e.g., the structure of proteins or protein complexes (9,16,19,20), conformational molecular changes (18,21), interactions between molecules (7,8,11–15,17,22,23), and as a powerful indicator of biochemical events (24,25). Those, as well as other applications, are discussed more extensively in review articles and books (1,10,26,27).

Provided that the usual distance and orientation conditions are fulfilled (see below), FRET may occur both between monomers within functional complexes (that may be either long- or short-lived) and noninteracting molecules expressed in high concentrations inside biological cells. In the latter case, the donor- and acceptor-tagged proteins need not associate with each other to exchange excitation energy; only their concentration needs to be high enough so that the average distance between them is of the order of the Förster distance. This undesired energy transfer, known as stochastic FRET, may generate background noise in FRET studies aimed at identifying functional interactions. For example, it has been claimed that stochastic FRET has contaminated the results of relevant biological interactions in several studies of bioluminescence resonance energy transfer in oligomers of G-protein coupled receptors (28). This problem, which is generally assumed to be relevant also to FRET measurements, has been investigated theoretically by several investigators, either analytically or numerically (29–34).

Early FRET-based investigations of protein-protein interactions used wide-field microscopes or spectrofluorometers to measure average intensity of the fluorescence from individual cells, cell populations, or solutions of fluorescent molecules. The data in such experiments have been normally analyzed by plotting the average FRET efficiency of individual cells, synthetic vesicles, or even entire cell populations against the acceptors and donors concentrations or their ratios, and interpreting the results in light of models for functional and/or stochastic FRET (1,13,35,36). Although this approach has been successful in detecting global properties of molecular interactions, when applied to spatial distributions of molecular complexes in cells or cellular regions of interest, it poses two kinds of difficulties. First, the average-based approach makes the explicit or implicit assumption that the distribution of molecules inside the cell is homogeneous, although, for instance, cytoplasmic proteins may be excluded from regions occupied by organelles or other macromolecular complexes, whereas membrane proteins may be sequestered within cytoskeletal cages or lipid microdomains (also known as rafts). Such heterogeneity may lead to significant changes in the average FRET efficiency, which may not be distinguished from changes in the distance between monomers within a protein complex. Second, the process of averaging of a distribution of FRET efficiency values washes out the rich information otherwise contained in a distribution of FRET efficiencies; this includes relative contributions of stochastic and functional FRET, as well as contributions by different pathways for energy transfer that may be present in protein complexes containing more than one donor and one acceptor.

The comparatively recent advent of laser-scanning microscopes, such as confocal and two-photon microscopes (1,37,38), provided opportunities for measuring fluorescence emission from thin sections of cells, thereby avoiding the averaging of fluorescence data along the z axis. However, quantitative interpretation of FRET data obtained with scanning microscopes is often done in terms of cellular averages of FRET efficiencies; in many cases when pixel-level data are obtained, the analysis remains mostly qualitative, e.g., in the form of the so-called ratiometric FRET, instead of FRET efficiency (13,26,39,40). This situation is perhaps reminiscent of several decades of evolution of the FRET theory within the framework created by the classical technology. In addition, unresolved technological challenges in laser-scanning microscopy have prevented investigators from obtaining all the information necessary to estimate the FRET efficiency at pixel level in a time shorter than that of molecular diffusion (16).

Laser-scanning microscopes for lifetime or intensity measurements allow one to detect the signal from very small focal volumes of the sample. Under physiological expression levels of the proteins of interest, the small focal volumes contain only a few (ideally, only one) molecules or molecular complexes and therefore the information contained in each image pixel is mostly single-molecule- or single-molecular-complex-level. To take full advantage of the opportunities introduced by laser-scanning microscopes, theoretical models and methods of data analysis need to be further developed. Analytical calculations of energy transfer between multiple donors and acceptors are rather complex and require numerous simplifying assumptions. Förster (34) derived an expression for FRET efficiency for very low concentrations of excited donors distributed at random in mixtures with acceptors. Similar calculations for FRET efficiency were done by Eisenthal (33) and Wolber and Hudson (32) for FRET efficiency in two dimensions. Analytical expressions have been also derived for oligomeric complexes containing arbitrary numbers of monomers (41). Many practical situations are still more conveniently tackled using numeric approaches.

Numerical Monte Carlo simulations (MCS) have been used to calculate the FRET efficiency between chromophores constrained in various geometries. Snyder and Freire (31) examined the quenching of donor chromophores distributed in two dimensions. Demidov (42) used MCS to calculate energy transfer using the mean of randomly generated decay rates. Berney and Danuser (30) included competition between donors for the same acceptors to examine the transfer between fluorescent probes distributed on a surface. Corry et al. (29) used MCS to calculate FRET efficiency for an ensemble of linked pairs of acceptors and donors and pentameric structures. Frazier et al. (43) used FRET to investigate the domain formation in sphingomyelin/cholesterol/palmitoyl oleoyl phosphatidyl choline mixtures and used MCS to interpret their experimental results. Towles et al. (44) applied MCS to study the effect of membrane microheterogeneity and domain size on FRET. Kiskowski and Kenworthy (45) examined resonance energy transfer for disk-shaped membrane domains, relevant to FRET studies of lipid rafts.

In this work, we used MCS to compare FRET efficiency results between homogeneous and inhomogeneous spatial distributions of molecules. In all the cases investigated, the results were comparatively analyzed in terms of average FRET efficiencies for an entire image area as well as distributions of FRET efficiencies for that area, as if the data were obtained from wide-field and scanning optical microscopes, respectively. The main goals of this study are: i), to understand the effect of molecular crowding on functional interactions at concentrations commensurate with those encountered in experiments; and ii), to establish a procedure for FRET data simulations that can be used for information extraction from distributions of FRET efficiencies obtained experimentally. These results should be relevant to both intensity-based and fluorescence lifetime imaging-based investigations, as our simulations rely only on the Förster radius and intermolecular distances and make no assumption regarding the manner in which the pixel-level FRET efficiencies are obtained experimentally.

Theoretical Background

The problem of determining the efficiency of nonradiative energy transfer for systems of donors and acceptors distributed at random in two or three dimensions has been dealt with by several investigators (29,30,32–34,46). Drawing on those studies, in this section, we will outline a general method, used in this work, for numerical simulations of FRET efficiency for distributions of donors and acceptors on Euclidian as well as fractal lattices (see below). Fractal lattices are represented here by a well-known fractal object called Sierpinski's carpet (26,47). The main assumptions made are as follows: i), the distribution of molecular species (i.e., dimers, donors, and acceptors) is random and uniform in the available space; however, for fractal lattices the distributions are nonuniform (relative to the Euclidian space), due to the inhomogeneous character of the lattice itself; ii), the rate of donor excitation by light is very low, so that no more than one donor is excited at any single time (i.e., during the lifetime of the donor's excited state) in each focal spot; this ensures that excited donors do not compete for acceptors with other donors in their neighborhood; and iii), the orientation factor, which enters the Förster radius, R₀ (1), is independent of time on the timescale of the fluorescence lifetime. The third approximation implies that the timescale for rotational diffusion of the donors and acceptors is either much shorter (i.e., dynamic averaging) or much longer (i.e., static averaging) than the lifetime of the donor's excited state.

Under the above approximations, the rate of de-excitation of a donor surrounded by N acceptors located at arbitrary distances R_j (where j = 1, 2,… N) is given by (33,34,41):

$$k\equiv {\tau }_{\text{DA}}^{-1}={\tau }_{\text{D}}^{-1}\left[1+\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{j}}}\right)}^6\right],$$ (1)

where τ_DA and τ_D are the lifetime of the excited donor in the presence and absence of acceptors, respectively, and R₀ is the Förster radius, which depends on a number of physical parameters, such as the relative orientation of the transition dipoles of the donor and the acceptor (1). If the probability density, P(t) of the donor being excited at t = 0 is P(0) = 1, then the probability density for the donor to still be excited at a time t must satisfy the differential equation:

$$-\frac{dP\left(t\right)}{dt}=kP\left(t\right)={\tau }_{\text{D}}^{-1}\left[1+\sum _{\text{j}=1}^N{\left(\frac{R_0}{R_{\text{j}}}\right)}^6\right]P\left(t\right)\text{.}$$ (2)

Integration of Eq. 2 gives:

$$P\left(t\right)=e^{-\raisebox{1ex}{$\text{t}$}\!\left/ \!\raisebox{-1ex}{${\tau }_{\text{D}}$}\right.}\prod _{\text{j}=1}^{\text{N}}\exp \left[-\left(\frac{t}{{\tau }_{\text{D}}}\right){\left(\frac{R_0}{R_{\text{j}}}\right)}^6\right]\text{.}$$ (3)

In the absence of resonance energy transfer, the sum in Eq. 2 becomes zero, and the survival probability density for the excited state is $P_0\left(t\right)=e^{-\text{t}/{\tau }_{\text{D}}}$.

If P(t − t′)dt′ denotes the probability that a donor excited at t′ remains excited at time t (with P(0) = 1), then the relative quantum yield measured in a fluorescence experiment is given by:

$$\frac{Q^{\text{DA}}}{Q^{\text{D}}}=\frac{{\int }_{-\infty }^{\text{t}}P\left(t-t\prime \right)dt\prime }{{\int }_{-\infty }^{\text{t}}{P}_0\left(t-t\prime \right)dt\prime }=\frac{{\int }_0^{\infty }P(t\prime )dt\prime }{{\int }_0^{\infty }{P}_0(t\prime )d{t}^{\prime }},$$ (4)

where P₀(t − t′) is the probability density function analogous to P(t − t′) when no FRET occurs, whereas Q^D and Q^DA are the donor quantum yields in the absence and presence of the acceptor (i.e., of FRET), respectively.

Substituting Eq. 3 into Eq. 4 and using$P_0(t\prime )=e^{-\text{t}\prime /{\tau }_{\text{D}}}$, we get:

$$\frac{Q^{\text{DA}}}{Q^{\text{D}}}=\frac{1}{1+\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{j}}}\right)}^6}\text{.}$$ (5)

Because the FRET efficiency, E, is related to the two quantum yields by E = 1 − Q^DA/Q^D (26,41), Eq. 5 becomes:

$$E=\frac{\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{j}}}\right)}^6}{1+\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{j}}}\right)}^6}\text{.}$$ (6)

In the case of M donors and N acceptors distributed in a small excitation area (equal to the focal spot area in a confocal or two-photon microscope), the FRET efficiency is obtained as the average over all FRET efficiencies, E_i, defined by Eq. 6, namely:

$$E=\frac{1}{M}\sum _{\text{i}=1}^{\text{M}}{E}_{\text{i}}=\frac{1}{M}\sum _{\text{i}=1}^{\text{M}}\frac{\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{ij}}}\right)}^6}{1+\sum _{\text{j}=1}^{\text{N}}{\left(\frac{R_0}{R_{\text{ij}}}\right)}^6}\text{.}$$ (7)

This equation applies to homogeneous as well as inhomogeneous distributions of molecules on Euclidian as well as fractal lattices.

Methods

We generated random distributions of molecules on two different planar surfaces: i), a planar Euclidian surface (i.e., a square), which allows for donors and acceptors to be distributed uniformly; and ii), a well-characterized fractal lattice called Sierpinski's carpet (26,47), which has a fractional dimension and therefore confines the monomers and dimers to certain allowed areas (Fig. 1). All simulations were carried out using the software package Mathematica 6.0 (Wolfram Research, Champaign, IL). The electronic file comprising our simulation algorithm may be provided on request to those interested, and it essentially follows the steps described below.

Figure 1.

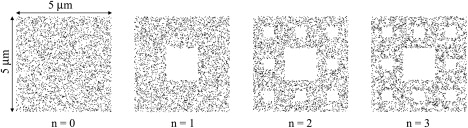
Different stages in the generation of a fractal distribution of molecules embedded in an Euclidian square. The stage represented by n = 0 is identical to the Euclidian square surface, whereas cases for n ≥ 1 represent different stages in the construction of the fractal structure. The model represents the Sierpinski carpet, which has a fractal dimension 1.893. For n → ∞, the surface area tends to zero (26,47).

First, a lattice of area 25 μm² was defined, which is comparable to the area of a small-to medium-size biological cell (such as yeast, erythrocyte, etc.). This is called herein the total excitation area. To populate the two-dimensional lattices with donors, acceptors, and/or dimers, random pairs of coordinates were generated by the program; these coordinates defined the positions of each molecule. In the case of dimeric complexes, two pairs of coordinates were generated. The coordinates corresponding to the position of the donor were generated first, and then the associated acceptor was constrained to have any random coordinates within a circle of 6 nm radius centered on the donor coordinates. Because a Förster distance of 5 nm was assumed for all calculations (that is typical for several combinations of green fluorescent protein variants, which are often used in experiments), this radius corresponds to a FRET efficiency E_d ∼0.25. To create a fractal distribution of molecules, such as the one corresponding to stage n = 1 in Fig. 1, additional steps were required to constrain the coordinates of all monomers or dimers to fall within the allowed areas of the Sierpinski carpet (Fig. 1), by using the following procedure:

• 1.The coordinates of a monomer or a dimer were generated as described above.
• 2.As it is well known, the Sierpinski carpet is generated by dividing each side of the large square by a factor of 3, removing the middle square, and then repeating the process n times for each remaining square. The values of the monomer or dimer coordinates were therefore expanded by a factor of 3, which is the scaling factor of the Sierpinski carpet. Thus, if L is the length of the carpet, the minimum possible value that the expanded x (or y) coordinate could take was zero, whereas the maximum value was 3L.
• 3.Next, the expanded x (or y) coordinate was divided by the length of the carpet, L, to obtain the reduced coordinate, ξ, . A function, Floor[ξ], was used to find the greatest integer that was ≤ξ, where ξ is a real number. For example, for ξ = 2.4, Floor[ξ] = 2.
• 4.If, for a particular molecule (or dimer) ξ ∈ (1,2), then Floor[ξ] = 1, and that molecule was not considered any further in the simulations (because it fell in the excluded square of the first stage of the Sierpinski carpet); otherwise, the molecule was retained for subsequent determinations of FRET efficiency.
• 5.Steps 1 through 4 were repeated until the desired number of monomers and dimers were placed on Sierpinski's carpet.

To generate distributions of monomers and/or dimmers for the nth stage of the Sierpinski's carpet, we used the same procedure described above (by steps 1–5), except that each procedure was applied to a subcarpet of length (L/3)ⁿ⁻¹ (with n > 1) instead of L.

To determine the distribution of FRET efficiencies, the excitation area occupied by monomers and/or dimers was divided into smaller areas of 0.25 × 0.25 μm², each of which being roughly equal to the area of a diffraction-limited focal spot of a focused light beam in a laser-scanning microscope. Depending on the total number of donors (M) and acceptors (N) distributed in each lattice, it was possible to have zero, one, or more of each type of molecule (i.e., donors, acceptors, and dimers) in every focal spot. Therefore, an average FRET efficiency was computed for each focal spot using Eq. 7. When dimers were present, one term of the sum in Eq. 7 accounted for the fixed distance between a donor and an acceptor within the dimer. In general, there exists a low but finite probability that the donor and the acceptor of the same dimer fall in separate but adjacent focal spots. To avoid such situations, a simple subroutine checked whether the coordinates of the donor and acceptor of each dimer fell in the same focal spot, and only those dimers for which the condition was fulfilled were kept in the computer memory.

After choosing appropriate bin ranges for FRET efficiency values, the average FRET efficiency value for each focal spot was placed in an appropriate bin, and histograms were prepared using the accumulated bin counts, to generate the statistical distribution of FRET efficiencies for the total excitation area. Such distributions are expected to be obtained from measurements with laser-scanning microscopes. The average FRET efficiency, E_ave, for an entire excitation area (as it would be obtained from wide-field microscopy) was also computed.

Results and Discussion

Whereas the simplified classical picture of donors surrounded by uniform distributions of acceptors (32,46) has been a useful first approximation to solutions of interacting molecules, more elaborate models are often required for biological cells (29,30,43–45), which are characterized by an inhomogeneous distribution of material. For instance, cytoplasmic proteins may be excluded from regions occupied by other molecular complexes (such as the ribosomes) or by membrane-bound cellular organelles (e.g., the nucleus, or the mitochondria), whereas membrane proteins may be sequestered within cytoskeletal cages or lipid microdomains. Therefore, depending on their degree of inhomogeneity, most biological systems present two types of molecular distributions, or combinations thereof: i), donors and acceptors confined to disconnected oligomers or larger assemblies (i.e., microdomains); and ii), bicontinuous, percolative (26,48) distributions of donors and acceptors.

In this study, we used two-dimensional simulations to determine the FRET efficiency for molecules distributed on excitation areas of size comparable to that of biological cells, both for Euclidian and for (incomplete) fractal structures obtained for a finite number of steps in the construction of Sierpinski gasket (47) (Fig. 1). The donors and acceptors were distributed at random on the fractal lattices, the only restriction being that they occupied an allowed area of the structure. The average FRET efficiency per donor was calculated using Eq. 7 for each focal spot (of area 0.25 × 0.25 μm²) comprising the total excitation area, as described in the Methods section.

The first case investigated was that of a random distribution of noninteracting molecules tagged with donors and acceptors. Despite the lack of physical interaction between the tagged molecules, a type of energy transfer, known as stochastic FRET, may still occur between the donor and acceptor tags (32). As seen in Fig. 2, for both types of lattices investigated, most FRET efficiencies assumed values close to zero, with just a small fraction of excitation areas showing nonvanishing FRET efficiencies. This was true for any proportion of donors and acceptors investigated, even though the total concentration considered (4800 mol/25 μm²) corresponded to as many as 332,160 molecules dispersed in a relatively small cell (with a volume of ∼125 μm³).

Figure 2.

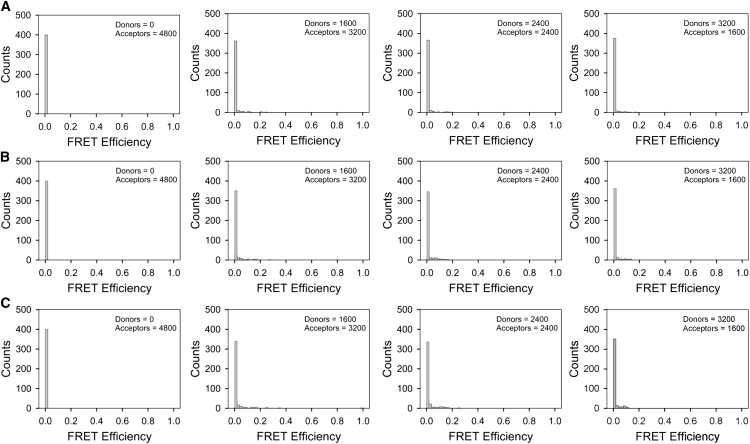
Histograms showing the distribution of FRET efficiencies for donors and acceptors randomly scattered on lattices of the type shown in Fig. 1. (A) Euclidian (i.e., uniform) distribution of molecules. (B) Fractal distribution with n = 5. (C) Fractal distribution with n = 7. The total number of 4800 donors and acceptors per whole excitation area (25 μm²) corresponds to 12 molecules per focal spot of area 0.25 × 0.25 μm².

The distributions of FRET efficiencies shown in Fig. 2 were characterized by very small average values (Fig. 3); these values are typical for measurements carried out using a wide-field microscope. We concluded that stochastic FRET is not a major source of signal, even when relatively large average concentrations of interacting molecules are present. Furthermore, local increases in concentration, caused by the large exclusion areas of the fractal lattices, failed to enhance the FRET efficiency to a significant extent. This weak effect stems from the fact that FRET is a nonlinear process, in which the efficiency of energy transfer dies out rather rapidly with the distance between donors and acceptors (as R⁻⁶). We have only obtained large values of FRET efficiencies for concentrations of donors and acceptors much larger than physiological expression levels of most proteins in the cell.

Figure 3.

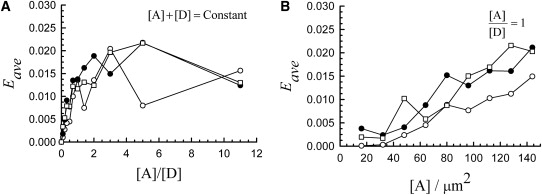
Dependence of the average FRET efficiency for distributions of monomeric donors and acceptors on (A) the ratio of acceptor to donor concentrations, [A]/[D] (for [A] + [D]= constant), and (B) the concentration of acceptors, [A] (for [A]/[D] = constant), for Euclidian and fractal distributions of molecules. The significance of the symbols is: ○, n = 0; •, n = 5; □, n = 7.

Next, we investigated whether stochastic FRET may contribute significantly to the FRET efficiency of distributions of functional heterodimers. Herein, we define heterodimers as both long-lived (or constitutive) and transient associations of molecules tagged with donor and acceptor chromophores. We placed heterodimers at various concentrations on Euclidian as well as fractal lattices, and calculated the FRET efficiency for all donors present in each focal spot of the excitation beam. Eq. 7 was again used for this purpose, in which one term of the sum over summation variable j accounted each time for the fixed distance between a donor and an acceptor within the dimer (see Methods).

As it can be seen in Fig. 4, the main bar in each of the histograms (corresponding to a value E_d ∼0.25 for the FRET efficiency) was due to the presence of the dimers themselves, with some broadening of the distribution toward larger values occurring due to an occasional exchange of energy between donors and acceptors belonging to different dimers. This broadening effect reflected the stochastic FRET component, which was only marginally stronger for the inhomogeneous distribution corresponding to the Sierpinski carpet, compared to the Euclidian lattice. In addition to these features, most histograms also presented sizable bars corresponding to cases when no FRET occurred. It is worth noting here that, although instances with zero-FRET efficiency were rare for Euclidian distributions, such occurrences were always observed in fractal distributions, even for relatively high dimer concentrations. This is because, there are always regions within the Sierpinski carpet from which dimers are excluded.

Figure 4.

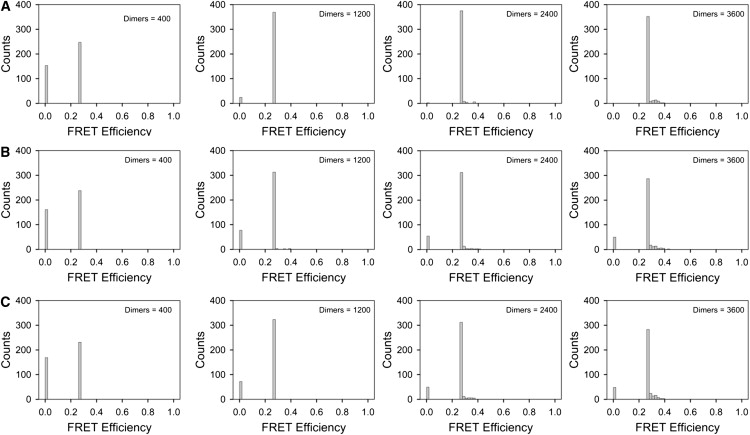
Histograms showing the distribution of FRET efficiencies for dimers distributed at random on lattices of the type shown in Fig. 1. (A) Euclidian (i.e., uniform) distribution of dimers. (B) Fractal distribution with n = 5. (C) Fractal distribution with n = 7. The first concentration in each row (i.e., 400 dimers per whole excitation area) corresponds to 1 dimer per focal spot, whereas the last concentration represents 9 dimers per focal spot.

The presence of bare spots in the fractal lattice leads to significant differences between the average efficiencies of fractal and Euclidian distributions, as seen in Fig. 5. This finding pertains to the experimental situation where an average cellular FRET efficiency is calculated for cells containing protein complexes that do not spread uniformly throughout the cell (such as membrane proteins), which leads to an underestimate of the efficiency. In addition, it seems from Fig. 5 that the average efficiency does depend on the total number of heterodimers (that is the same with that of acceptors, for [A]/[D] = 1), even though each dimer is expected to contribute a constant FRET efficiency portion to the average value. This is because, at low concentrations of dimers (that are actually similar to protein expression levels of practical interest), the presence of excitation spots with no dimers at all decreases the average efficiency; an increase in concentration leads to a decrease in the number of bare spots, hence, the observed increase in the average FRET efficiency.

Figure 5.

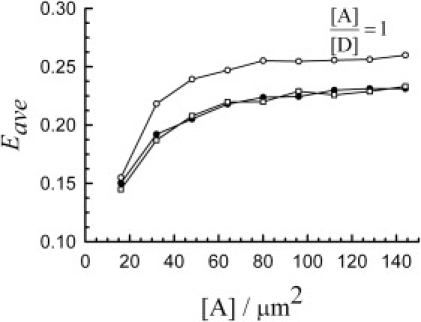
Dependence of the average FRET efficiency for distributions of dimers on the concentration of acceptors, [A] (for [A]/[D] = 1), for the for Euclidian and fractal distributions of molecules. The significance of the symbols is: ○, n = 0; •, n = 5; □, n = 7.

We next investigated the behavior of heterodimers in the presence of various concentrations of free donors and acceptors. Such mixtures may be relevant to several biological situations, such as, for instance, the case where there exist populations of free donors and acceptors, some of which may interact to form short-lived dimers. Another example is when donor- and acceptor-tagged proteins only exist as dimeric complexes, but either the donor or the acceptor tag takes a longer time to become mature and hence fluorescent. This may be described as either a mixture of dimers and donors, or dimers and acceptors, depending on which tag takes longer to become mature. Typical results from these simulations are shown in Fig. 6 for Euclidian as well as fractal distributions (as defined in Fig. 1). Although the FRET efficiency value corresponding to dimers (E_d ∼ 0.25) appeared in all histograms, the distribution of values was broader than expected for purely dimeric populations. This can be accounted for by the following two mechanisms. First, the slight broadening of the distribution of efficiencies toward larger values was due to the stochastic FRET between dimers as well as between donors in the dimers and monomeric acceptors. Second, a more pronounced broadening of the distribution of FRET efficiency values toward values lower than the dimer FRET efficiency value, E_d, was accompanied by a decrease in the number of instances when the E_d value was detected. The occurrence of FRET efficiencies lower than E_d was caused by the fact that free donors, present in a focal spot alongside with dimers, contributed a value less than E_d (even zero) to the sum in Eq. 7, but increased the total number of donors, M, in that spot. This reduction in FRET efficiency represents a type of stochastic FRET whose importance has been less appreciated before, and which is not due to a real interaction between donors and acceptors but to the increase in M caused by the mere presence of free donors in the excitation spot. It is to be remarked also that, although the broadening of the distributions of FRET efficiencies toward higher values is somewhat more prominent for fractal lattices compared to Euclidian ones (compare Fig. 6, B and C, to Fig. 6 A), a more obvious difference is the presence of bars of sizable height at zero FRET efficiency for fractal distributions, even for very high concentrations of dimers. The latter effect leads to systematically lower values of the average fret efficiency for fractal lattices (Fig. 7).

Figure 6.

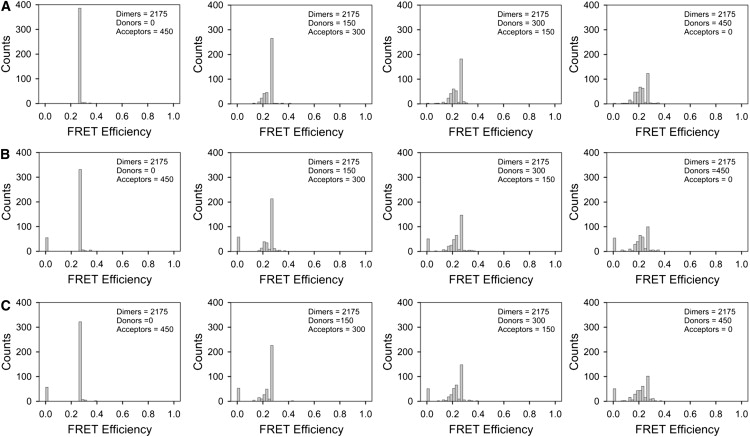
Histograms showing the distribution of FRET efficiencies for mixtures of dimers, donors, and acceptors distributed at random on lattices of the type shown in Fig. 1. (A) Euclidian (i.e., uniform) distribution of dimers, donors, and acceptors. (B) Fractal distribution with n = 5. (C) Fractal distribution with n = 7.

Figure 7.

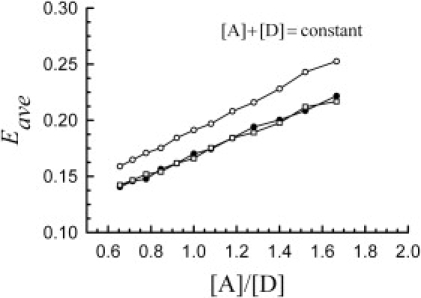
Dependence of the average FRET efficiency for distributions of dimers, donors, and acceptors on the ratio of total acceptor/total donor concentrations, [A]/[D] (for [A] + [D]= constant) for the three molecular distributions shown in Fig. 1. The significance of the symbols is: ○, n = 0; •, n = 5; □, n = 7.

Experimental observation of distributions of FRET efficiencies similar to those shown in Fig. 6 has been reported in a recent study (16) on an artificial dimeric construct formed by two green fluorescent protein variants (49) linked by two amino acids, whereby the acceptor (yellow fluorescent protein) is known to take a somewhat longer time to become mature and fluoresce. Whereas in the histogram representation of FRET efficiencies one remains able to distinguish between stochastic and functional FRET for mixtures of dimers and free monomers, the average cellular efficiency hardly provides any usable information (Fig. 7). This difficulty is caused by the dependence of the average FRET efficiency on the ratio of donor to acceptor concentrations, which needs to be determined from separate measurements. An additional difficulty is caused by the fact that the average efficiency depends on whether the spatial distribution of molecules is homogeneous or inhomogeneous. This becomes apparent when comparing the results obtained for the fractal case to those obtained for Euclidian lattices (Fig. 7).

We also note that the discriminating power of the distribution-based analysis decreased gradually with the ratio of free donors to total donor concentrations, as manifested by a reduction in the height of the bar corresponding to E_d = 0.25 in Fig. 6. This reduction may cause difficulties in separating between stochastic and functional FRET by mere visual inspection of the histogram when free donors represent more than 20% of the total donor population (data not shown). However, even in that unfavorable case it may still be possible to separate functional (i.e., dimeric) FRET from the stochastic FRET background by performing detailed analyses of the histograms. Notwithstanding possible complications caused by the point-spread function of the microscope (50), this kind of analysis could be done by recognizing that the FRET efficiencies in the histograms corresponding to values less than E_d represent various combinations of dimers and free donors, and therefore contain information about E_d, which could be extracted by fitting the simulated curves to experimental distributions.

Conclusion

The experimental approach based on average FRET efficiencies has been used widely in FRET studies. Our numerical simulations described above indicated that the inherent inhomogeneity of any biological cell, together with the presence of a form of stochastic FRET (not involving true interactions between donor- and acceptor-tagged molecules), may markedly diminish the practical utility of the average-based approach. By contrast, a distribution-based (or pixel-level) approach afforded by laser-scanning microscopes should allow one to fully quantify the information regarding the distribution of FRET efficiencies. Admittedly, this first modeling attempt to investigate an important problem in FRET, as described above, required some simplifications regarding the size of the oligomers as well as the ideality of the point-spread function of the optical instrument (50), which was considered to map a point-object onto a point-image. However, a careful evaluation of the physical situation indicates that, although future studies will likely incorporate useful refinements, the main conclusions of this study should remain valid for any oligomer size (such as trimers and tetramers) and for more realistic point-spread functions. We believe that this analysis will offer a basis for extraction of structural and stoichiometric information from whole distributions of FRET efficiencies by using simulation-based fitting of experimental FRET data.