Gas-phase water-mediated equilibrium between methylglyoxal and its geminal diol

Abstract

In aqueous solution, aldehydes, and to a lesser extent ketones, hydrate to form geminal diols. We investigate the hydration of methylglyoxal (MG) in the gas phase, a process not previously considered to occur in water-restricted environments. In this study, we spectroscopically identified methylglyoxal diol (MGD) and obtained the gas-phase partial pressures of MG and MGD. These results, in conjunction with the relative humidity, were used to obtain the equilibrium constant, K_P, for the water-mediated hydration of MG in the gas phase. The Gibbs free energy for this process, ΔG^°, obtained as a result, suggests a larger than expected gas-phase diol concentration. This may have significant implications for understanding the role of organics in atmospheric chemistry.

Atmospheric aerosols are a major topic of current atmospheric studies, given the important, but not fully understood, role that aerosols play in the Earth’s radiative balance (1). Aerosols affect global radiative forcing directly by absorbing or scattering radiation and indirectly by enhancing cloud albedo (1). Because of their changing chemical composition, aerosol optical and physiochemical properties vary, which greatly complicates the quantification of their global radiative forcing. Efforts at modeling aerosol effects on climate, as assessed by the Intergovernmental Panel on Climate Change (1), are primarily based on sulfate aerosol studies, though there is growing evidence that organic aerosols play an important role in climate change (2–4). Organic molecules formed by the oxidation of biogenic and anthropogenic organic emissions have been identified as important components of atmospheric aerosols (2, 5). The formation pathways of these secondary organic aerosols (SOA) remain highly speculative, leading to uncertainties in predictions of atmospheric models (6–8). A large SOA source is missing from models as illustrated by simultaneous field measurements of volatile organic compounds (VOCs) and aerosol particles (6, 7, 9, 10).

Organic acids, especially oxalic and pyruvic acid, are found in SOA, though the origin of these acids is not predicted correctly by the gas-phase chemistry considered in models (11–14). Recent studies suggest that these acids are made in the aqueous phase, particularly in cloud water, by the oxidation of aldehydes (e.g., glyoxal and methylglyoxal) with hydroxyl radicals and other aqueous radical species (14–17). Methylglyoxal (MG) is one of the most abundant α-dicarbonyls present in the atmosphere and is produced from VOCs of both biogenic and anthropogenic origin (14, 18–20).

Water-mediated aldehyde chemistry is expected to have important consequences to the formation of SOA. For example, laboratory studies of MG hydration performed using theoretical (21) and spectroscopic techniques (14, 22–24) suggest that in aqueous environments MG can become hydrated to form methylglyoxal diol (MGD) via reaction 1 and undergo further reactions to form oligomers (14, 21, 24). Like other aldehydes and ketones in aqueous solution, MG hydrates through proton addition to the aldehyde carbonyl and reaction to form MGD (21–23, 25–27). MG has both an aldehydic and ketonic C = O and it was determined computationally that the aldehydic C = O is more favorably hydrated in solution (ΔG = -1.4 kcal mol^-1) than the ketonic C = O (ΔG = +2.5 kcal mol^-1) (21). In solution, MG is present primarily as MGD (60% diol to 40% tetrol) with the aldehydic group forming a geminal diol (21, 23). MGD has a lower vapor pressure than MG, which allows the molecule to partition more easily into the particle phase, lending to the formation of SOA.

R1

Although the hydration of small aldehydes in aqueous solutions is known to be extensive, gas-phase hydration of carbonyls has not yet been considered in atmospheric models because it is commonly believed that there is not enough water present to make such reactions favorable. Gas-phase studies of glyoxylic acid performed in our laboratory observed hydration of glyoxylic acid and allowed for the identification of the gem diol through IR spectroscopy, suggesting this chemistry can occur in water restricted environments (28). In a CCl₄ matrix with restricted water present, similar results were obtained for the hydration of pyruvic acid.

In this IR spectroscopic study, we identify and assign the vibrational features of gas-phase MGD and characterize the water-mediated gas-phase equilibrium between MG and MGD. The equilibrium constant, K_P, is calculated using spectroscopically determined concentrations of MG, MGD, and water. This study shows gas-phase hydration to be significant even under relatively dry environmental conditions. This affects the gas-phase/aqueous particle partitioning of MG and could provide insight into the discrepancy between measured and modeled amounts of SOA (29, 30).

Results and Discussion

Spectral Identification of MG and MGD.

Fundamental gas-phase spectra MG and MGD.

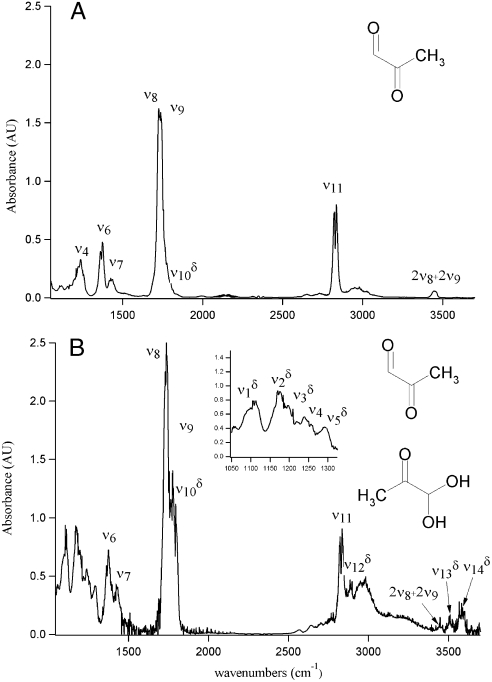
The fundamental gas-phase IR spectrum of MG has been previously observed (31) and provides the basis for determining the presence of MGD in this study (Fig. 1). In the lower energy region of the MG spectrum (Fig. 1A), from 1,050 to 1,500 cm^-1, there are three distinguishable bands which are assigned to the CCC asymmetric stretch at 1,240 cm^-1 (ν₄), the CH bend (ν₆) at 1,373 cm^-1, and the CH₃ bends (ν₇) in the 1,415 to 1,440 cm^-1 region (Table 1). MG contains a ketonic and aldehydic C = O, which are present in the MG spectrum at 1,723 cm^-1 (ν₈) and 1,741 cm^-1 (ν₉), respectively (Fig. 1A). The CH stretching vibration of MG has been previously assigned (31) and occurs at 2,835 cm^-1 (ν₁₁). The MG CH stretch is very prominent and was used to compare the MG and MGD spectra and to identify MGD. The peak at 3,450 cm^-1, which normally corresponds to the OH stretching region, we assign to the first overtone, 2ν₈ and 2ν₉, of the ν₈ and ν₉ C = O stretches as seen in Fig. 1A. This peak has been previously observed, but not assigned (31).

Fig. 1.

Fundamental gas-phase spectra from 1,050 cm^-1 to 3,600 cm^-1 of (A) MG and (B) MG and MGD. MGD frequencies are labeled with δ.

Table 1.

Theoretical and observed experimental frequencies for MG and MGD with vibrational modes assignments

Theoretical frequency, cm-1	Theoretical intensity , km mol-1	Experimental frequency, cm-1	Mode assignments
1,099	182	1,088		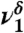Hb C-O stretch
1,185	73	1,173		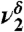COH wag
1,180	18	1,199		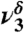CCC stretch
1,207	22	1,240	ν4	CCC stretch
1,275	48	1,292		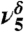Hb COH bend
1,335	2	1,373	ν6	CH bend
1,366–1,415	—	1,415–1,440	ν7	3 × CH3 bend
1,754	132	1,723	ν8	C = O stretch
1,774	114	1,741	ν9	HC = O stretch
—	—	1,780		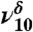Diol
2,811	72	2,835	ν11	CH stretch
2,838	43	2,895		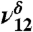CH stretch
3,497	—	3,443	2ν8	C = O overtone
3,530	—	3,458	2ν9	C = O overtone
3,478	86	3,505		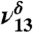Hb OH stretch
3,623	55	3,585		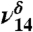Fr OH stretch

B3LYP/6-31 + G(d,p) theoretical frequencies were scaled using wavenumber linear scaling method. δ, MGD vibration; Hb, hydrogen bonding; Fr, free OH.

The addition of water to the MG sample hydrates MG to form MGD (Fig. 1B). The spectrum in Fig. 1B shows both MG and MGD features under very low relative humidities. In the absence of literature assignments, theoretical frequency and intensity calculations aided in assigning MGD vibrational modes (Table 1). The formation of MGD can be observed by the coincidence of the distinct MGD vibrational modes that appear in the lower energy region from 1,050 to 1,500 cm^-1 (Fig. 1B, Inset), the decrease in the ν₉ intensity relative to ν₈ intensity, and the appearance of OH stretching vibrations at 3,505 cm^-1 (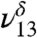) and 3,585 cm^-1 (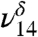) (Fig. 1B) with the addition of water vapor. With water present, the CH stretching mode of MGD is observed at 2,895 cm^-1 (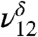). Because the lower energy region of the spectra from 1,050 to 1,500 cm^-1 becomes increasingly complex due to overlapping bands from the addition of water, the intensities of the ν₈, ν₉, 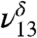, and 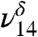stretches were used to quantify and follow the formation of MGD.

C = O fundamental and overtone stretching region.

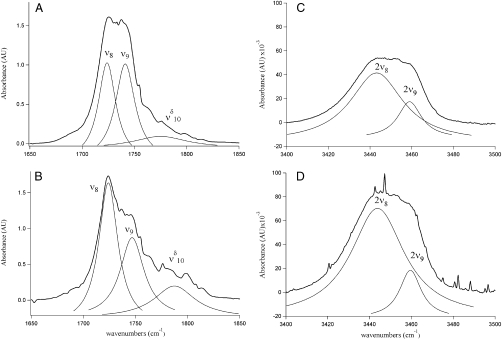
With the addition of trace amounts of water, the C = O stretching region is altered by the decrease in intensity of ν₉ relative to the ν₈, presumably due to the formation of MGD. To better understand these changes in the fundamental C = O stretching region, the intensity and peak width (FWHM) of the fundamental and overtone C = O stretches for MG and MGD were modeled by two Lorenzian curves. The fundamental MG C = O stretching region shows ν₈ and ν₉ with roughly the same intensity (Fig. 2A). As MG is hydrated to form MGD, the aldehydic C = O is hydrated to form the gem diol, which can be observed spectroscopically by the decrease in the relative intensity of ν₉ in Fig. 2B, intensity ν₈∶ν₉ = 1.0∶0.75. In addition to the MG and MGD fundamental C = O stretches near 1,730 cm^-1, there is a third peak around 1,780 cm^-1 (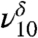), which is attributed to the diol because of its intensity increase mirroring the increase in partial pressure of water. The MG and MGD C = O first overtone region near 3,450 cm^-1 has the ketonic C = O overtone at 3,443 cm^-1 (2ν₈) and the aldehydic C = O overtone at 3,458 cm^-1 (2ν₉). In both MG and MGD spectra, the intensity of the first overtone C = O stretches drops by at least a factor of 10 from the intensity of the fundamental C = O stretches. In the MG C = O first overtone spectrum in Figure 2C, the relative intensity of 2ν₈∶2ν₉ = 1.00∶0.23, whereas in Figure 2D it is 1.00∶0.17. This relative intensity decrease seen for ν₉ in Figure 2D is consistent with the decrease in the fundamental C = O, reinforcing the suggestion that the fundamental aldehydic C = O intensity is decreasing because of hydration of the carbonyl to generate diol.

Fig. 2.

Fundamental C = O stretching region of (A) MG and (B) MGD and the first overtone, 2ν₈ and 2ν₉, of (C) MG and (D) MGD showing a decrease in the relative intensity of ν₉ in (B) when compared to (A) and a decrease in the 2ν₈ and 2ν₉ aldehydic peak in (D) when compared to (C).

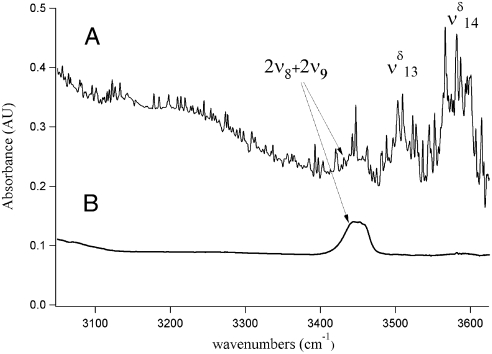
OH stretching region of MGD.

In the MGD spectrum (Fig. 3), there are two OH vibrational stretching modes, with the δ denoting MGD vibration, located at 3,505 cm^-1 (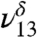) and 3,585 cm^-1 (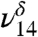), in addition to the 3,450 cm^-1 peak assigned to 2ν₈ and 2ν₉. The first OH vibrational stretch at 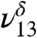is attributed to the hydrogen-bonded OH of MGD and the 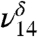is attributed to the free OH of MGD. Our theoretical frequency puts the 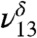at 3,478 cm^-1, which is slightly red shifted compared to the experimental value of 3,505 cm^-1. This discrepancy between the theoretically and experimentally derived frequencies is consistent with results from other studies (28, 32–35). The 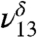and 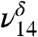could also have a contribution from tetrol OH stretching vibrations which all fall near to those of MGD, making it difficult to distinguish or model them. In solution, the ratio of diol to tetrol is approximately 60/40 (23). Although this ratio has not been measured for the gas phase, at much lower water concentration in our gas-phase experiments we expect MGD to be favored over the tetrol. The 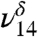stretch is present in very small amounts even in our lowest relative humidity MG spectrum. The 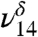stretch increases in intensity in response to increasing the partial pressure of water in the experiments.

Fig. 3.

The 3,000 cm^-1 to 3,650 cm^-1 region of (A) MGD and (B) MG, showing the appearance of water clusters (3,100 cm^-1 to 3,350 cm^-1), the 2ν₈ and 2ν₉ of C = O, and the 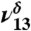and 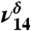of MGD.

The region from 3,100 to 3,350 cm^-1 contains water clusters and hydrated complexes of MG and MGD. The long red shift relative to computations and very broad appearance of these features are consistent with observations and predictions of hydrogen-bonded water clusters (28, 32–34, 36, 37). The broad and overlapping features in this region make it difficult to qualitatively and quantitatively identify these clusters.

Determination of MG, MGD, and Water Partial Pressures.

Based on the spectroscopic identification of MGD, we quantified the amount of MG, MGD, and water present in each spectrum as outlined below. Spectra that were saturated were not used in the calculation of partial pressures, but were useful in making MG and MGD mode assignments.

Partial pressure of water.

Experimentally observed spectroscopic water lines were compared with high-resolution transmission molecular absorption database (HITRAN) water lines and line strengths to determine the partial pressure of water (Table 2), P_H2O, and percent relative humidity, RH%, in each experiment. Three water lines at 1,550; 1,918; and 3,920 cm^-1 were isolated and analyzed. Each observed water line was integrated and the H₂O number density (N/v) was determined via Eq. 1:

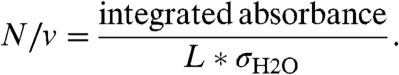[1]

The path length of the cell, L, was 71 cm and σ_H2O (cm molecule^-1) is the HITRAN line strength for each waterline. The P_H2O was determined using the average N/v from the three water lines and converted to %RH using the ideal gas law and the vapor pressure of water.

Table 2.

Partial pressure of water

Experiment	Int abs 1,550 cm-1	Int abs 1,918 cm-1	Int abs 3,920 cm-1	Avg N/v, molecule cm-3	PH2O, atm
1	0.003	0.003	0.002	1.3 × 1015	5.4 × 10-5
2	0.003	0.003	0.002	1.3 × 1015	5.4 × 10-5
3	0.003	0.003	0.002	1.3 × 1015	5.4 × 10-5
4	0.008	0.006	0.005	3.2 × 1015	1.3 × 10-4

Partial pressures, P_H2O, of water determined from experimental spectra and HITRAN. Integrated absorbance (Int abs) for each experimental water line was taken. Water lines at 1,550; 1,918; and 3,920 cm^-1 had the following cross-sections: 2.88 × 10²⁰, 2.93 × 10²⁰, and 2.61 × 10²⁰ cm molecule^-1 (55).

Partial pressure of MG.

The partial pressure of MG, P_MG, was determined spectroscopically using the integrated absorbance of the MG CH stretch at 2,835 cm^-1 (Table 3) and a theoretically calculated MG cross section, σ_MG, of 1.19 × 10^-17 cm molecule^-1 (Table 1). The theoretical and literature value for σ_MG were compared: There is a discrepancy, with the literature value being higher (31). In this work we chose to use the theoretically calculated σ_MG because of the agreement of the calculated and experimental frequencies and intensities (Table 1). For consistency, the theoretical σ_MG was used to determine the K_P from these experiments. The MG N/v was determined for each experiment using Eq. 1, and the P_MG was then determined using the ideal gas law.

Table 3.

Partial pressures of MG

Experiment	Int abs, cm-1	N/v, molecule cm-3	PMG, atm
1	26.05	3.08 × 1016	1.25 × 10-3
2	25.93	3.07 × 1016	1.24 × 10-3
3	25.66	3.04 × 1016	1.23 × 10-3
4	33.15	3.92 × 1016	1.59 × 10-3

Partial pressures of MG, P_MG, determined from experimental spectra. Integrated absorbance (Int abs) for the MG CH stretch at 2,835 cm^-1 was taken. Theoretical calculated σ_MG of 1.19 × 10^-19 cm molecule^-1 is used.

Partial pressure of MGD.

The partial pressure of MGD, P_MGD, was determined spectroscopically using the MGD OH stretching vibration at 3,585 cm^-1 (Table 4). This peak was used because of its presence in each of the spectra containing MGD and its response to water. It is assumed that this peak contains only MGD (although it may also contain a small tetrol contribution) and this feature was integrated to obtain an integrated absorbance. The integrated absorbance along with the theoretically determined cross-section, σ_OH, of 9.14 × 10^-18 cm molecule^-1, which is in agreement with a typical alcohol cross-section (34, 38, 39), was used in Eq. 1 to determine MGD N/v. The P_MGD was then determined using Eq. 1 and ideal gas law. The experimentally obtained partial pressures are shown in Table 5.

Table 4.

Partial pressures of MGD

Experiment	Int abs, cm-1	N/v, molecule cm-3	PMGD, atm
1	0.172	2.65 × 1014	1.08 × 10-5
2	0.169	2.60 × 1014	1.06 × 10-5
3	0.171	2.63 × 1014	1.07 × 10-5
4	0.505	7.78 × 1014	3.16 × 10-5

Partial pressures of MGD, P_MGD, determined from experimental spectra. Integrated absorbance (Int abs) for the MGD Fr OH stretch at 3,585 cm^-1 was taken. Theoretically calculated σ_OH of 9.14 × 10^-18 cm molecule^-1 is used.

Table 5.

Experimental equilibrium constant and gibbs free energy

Experiment	PMGD, atm	PH2O, atm	PMG, atm	KP	ΔG°, kcal mol-1
1	1.08 × 10-5	1.25 × 10-3	5.40 × 10-5	159	-3.13
2	1.06 × 10-5	1.24 × 10-3	5.40 × 10-5	157	-3.12
3	1.07 × 10-5	1.23 × 10-3	5.40 × 10-5	161	-3.13
4	3.16 × 10-5	1.59 × 10-3	1.29 × 10-4	154	-2.98

Experimentally determined gas-phase water-mediated equilibrium constant, K_P, values calculated using Eq. 2 for reaction R1 between MG and MGD and the experimentally determined Gibbs free energy, ΔG^°, values calculated using Eq. 3. Temperature was 298 K. K_P values have an error of ± 13.0 and ΔG^° values have an error of ± 0.05 kcal mol^-1.

Water-Mediated Gas-Phase Equilibrium Constant.

Previous MG hydration studies have been primarily performed in the solution phase (21, 22). There have been few thermodynamic studies of the hydration of MG and none performed in the gas phase. As shown in Table 5, under very dry conditions like those used in this study (RH% < 5%), easily detectable quantities of MGD are formed. Assuming that this reaction involves equilibrium R1, and that the tetrol formation is inefficient under conditions like those in our investigation, the equilibrium constant K_P can be derived from the partial pressures extracted from our spectra using Eq. 2.

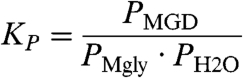[2]

The K_P values for the four experiments (Table 5) fall within the range of 154–161 (± 13.0) and reflect MGD production. The low relative humidity conditions of the experiments did not allow for the water concentration to be varied over a large range and there was little clustering observed by FTIR. As noted previously, there was a discrepancy between the theoretical and literature σ_MG, which leads to ∼11% discrepancy in the K_P values determined using the same spectra, with the theoretical values being slightly higher than the literature K_P values.

The Gibbs free energy (ΔG^°) was calculated from K_P using Eq. 3

[3]

Our experimentally determined ΔG^° values, which range from -2.98 to -3.10 kcal mol^-1 (± 0.051) (Table 5) reflects production of MGD in the gas phase. These values for MGD formation are significantly more favorable than theoretical predictions, even ones made in the aqueous phase (21, 40).

Experimental.

Sample preparation.

MG(CH₃COCHO) in aqueous solution (40 wt%) (Sigma-Aldrich) was dried and distilled before use. A 20 mL sample of MG solution was attached to a vacuum line at around 15 m torr and gently heated and stirred at 313 K for ∼12–15 h. Under these conditions, the solution became increasingly viscous. An equimolar amount of P₂O₅ was added to the sample, which was heated to 393 K and put under vacuum. Two condensers were employed in the distillation, each cooled with cold water, similar to Gurnick et al. (41). A liquid nitrogen bath was used to trap the purified MG. The MG solution was orange-brown in color in contrast to the pure MG, which is bright yellow-green, and MGD, which is colorless. The MG was put under nitrogen and kept frozen so it would remain in its aldehydic form until the experiment. The MGD was prepared in situ, by introducing small amounts of water to the sample in the spectroscopic cell, and allowing MG and water vapor to equilibrate over a period of about 10–30 min.

Fourier transformation infrared spectra.

The mid-IR absorption spectra of MG and MGD were measured between 1,000 and 8,000 cm^-1 using FTIR spectroscopy at 0.5 cm^-1 resolution in a static cell. A Bruker IFSv 66 spectrometer equipped with a globar source, KBr beamsplitter, and mercury cadmium telluride or MCT detector was used for optimal mid-IR absorption spectroscopy. This setup has been described previously (42, 43). The spectroscopic cell was both pressure- and temperature-controlled and was pumped down to approximately 15 m torr and then closed off to the pump. The MG sample was introduced to the cell and water vapor was subsequently added and allowed to equilibrate. All experiments were performed at 298 K.

Theoretical calculations.

The structures and fundamental vibrational mode frequencies of MG and MGD were calculated using the hybrid density functional theory method of B3LYP (44, 45) with the 6 - 31 + G(d,p) basis set (46–50) using the Gaussian 03 program (48). The anharmonic frequencies using the perturbation theory developed by Barone (51) using the B3LYP method is reported along with the intensity calculated by the double harmonic approximation. The optimized structures indicate that trans-MG is the most stable structure of MG, with the cis-MG structure being 4.9 kcal mol^-1 higher in energy. Calculations also confirmed that MG would hydrate at the aldehydic group. The theoretical frequencies and intensities along with the experimental frequencies are presented in Table 1.

Conclusion

MG is a known product of VOC oxidation and is prevalent in the atmosphere. In this work, we obtain and assign the gas-phase IR spectrum of MGD and find that the gas-phase hydration of MG is possible at low relative humidity (RH% < 5%). One of the consequences of this gas-phase water-mediated chemistry is a change in the electronic state of the molecule, eliminating the n → π^∗ transition of the aldehyde carbonyl which is well known to undergo near-UV photochemistry (52–54). Instead, the OH vibrational chromophore of the diol may react through excitation of the OH vibrational overtone in the near IR to form new products by dehydration, decarboxylation, and decarbonylation, as suggested recently for a number of alcohols and acids (32, 55–58). Using MG and MGD spectral features, we determine the gas-phase water-mediated equilibrium K_P. This K_P suggests that the gas-phase formation of the diol in the atmosphere is possible and could be expected to affect gas-particle partitioning of MG and its potential to form SOA.