Integration of biomechanical compliance, leverage, and power in elephant limbs

Abstract

The structure and motion of elephant limbs are unusual compared with those of other animals. Elephants stand and move with straighter limbs (at least when walking), and have limited speed and gait. We devised novel experiments to examine how the limbs of elephants support and propel their mass and to explore the factors that may constrain locomotor performance in these largest of living land animals. We demonstrate that elephant limbs are remarkably compliant even in walking, which maintains low peak forces. Dogma defines elephant limbs as extremely “columnar” for effective weight support, but we demonstrate that limb effective mechanical advantage (EMA) is roughly one-third of that predicted for their size. EMA in elephants is actually smaller than that in horses, which are only one-tenth their mass; it is comparable to human limb values. EMA drops sharply with speed in elephants, as it does in humans. Muscle forces therefore must increase as the limbs become more flexed, and we show how this flexion translates to greater volumes of muscle recruited for locomotion and hence metabolic cost. Surprisingly, elephants use their forelimbs and hindlimbs in similar braking and propulsive roles, not dividing these functions among limbs as was previously assumed or as in other quadrupeds. Thus, their limb function is analogous to four-wheel-drive vehicles. To achieve the observed limb compliance and low peak forces, elephants synchronize their limb dynamics in the vertical direction, but incur considerable mechanical costs from limbs working against each other horizontally.

Elephants have unusual limb structure and function. They use walking footfall patterns, have seemingly straightened limbs, and lack an aerial phase in their stride throughout their speed range (1–7). However, at faster speeds, they switch to biomechanical running (i.e., bouncing; refs. 8, 9), without a discrete gait transition (4–7, 10). Elephants also seem unable to exceed speeds of ~7 ms⁻¹ (15 mph) (1–5). These odd features relate to elephants’ massive size and thus have broader comparative relevance, but they remain unexplored in a deeper biomechanical context. These features suggest that elephants do not use their limbs in the same mechanical ways as typical quadrupeds do, perhaps involving considerable limb compliance (11–13). In the present study, we examined how elephant forelimbs and hindlimbs function across a wide range of speeds, and compared these mechanical functions with those of other animals.

Furthermore, elephants are particularly relevant to a major biomechanical concept regarding the relationship of body size and the limbs’ effective mechanical advantage [EMA; the amount of ground reaction force (GRF) generated at the foot per unit muscle force, or simply “overall leverage”] (Fig. 1A). EMA is proportional to the moment arm of each joint's muscle force divided by the moment arm of the GRF about that joint (14–16). Larger animals tend to increase their EMA mainly by straightening their limbs, thereby reducing GRF moment arms. This helps maintain bone stresses roughly constant across a wide range of animal sizes (14–16). At very large sizes, two solutions remain viable. First, EMA could be maximized by continuing scaling trends from smaller animals. Second, athletic performance, such as peak GRFs attainable (and thus faster speeds and gaits), might be reduced. As the largest living land animals, elephants provide an exciting case study of this phenomenon: Do they use one or both of the two aforementioned mechanical strategies? Reduced athletic performance has been strongly indicated by previous studies of elephants (1–7, 10), but EMA has not been quantified for animals larger than horses. We aimed to resolve this mystery.

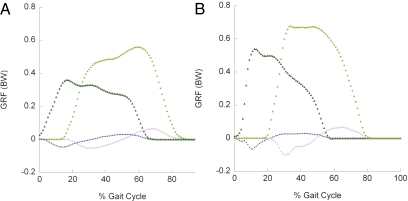
Fig. 1.

GRFs on individual Asian elephant limbs, normalized to body weight in Newtons (BW), for normal walking (A) and running (B) at dimensionless speeds [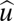= v (g l)^−0.5, where v is velocity in ms⁻¹, g = 9.81 s⁻², and l is hip height] of 0.30–0.35 and 0.75–1.3 (n = 6 individuals, 48 strides) and velocities of ~1.2 and 2.9–4.8 ms⁻¹, respectively. GRF traces begin with hindlimb contact (compare Fig. 4) and are for the horizontal (F_x: positive, propulsive; open purple squares, forelimb; blue circles, hindlimb) and vertical (F_y: light-green diamonds, forelimb; dark-green triangles, hindlimb) components. See also Figs. S1 and S2.

To achieve our two main aims, we analyzed elephant limb mechanics with a novel array of 16 force platforms and seven infrared cameras, supplemented with quantitative dissections of elephant cadavers (Tables S1 and S2). We recorded biomechanical data for 168 steady-state strides from six Asian elephants (Elephas maximus Linnaeus 1758), at speeds of 0.64–4.83 ms⁻¹.

Results and Discussion

Faster speeds (>2 ms⁻¹) had bouncing center of mass (CoM) dynamics indicating running (8–10), confirming previous predictions that elephants run according to the modern biomechanical definition (4, 6), although the timing of any gait transition remains ambiguous (4–7, 10). However, here we focus on individual limb mechanics, which reveal the deeper mechanisms that support and power locomotion. The four limbs had generally similar GRF profiles at all speeds, including roughly two-peaked vertical force traces, although these irregular peaks for the forelimbs vanished at the fastest speeds (Fig. 1). Such peaks are considered to be indicative of walking, but not exclusive to walking (11–13).

As expected, and consistent with most other quadrupedal mammals, peak vertical GRFs were ~50% higher for the forelimbs than for the hindlimbs (corresponding to a weight distribution of ~60% on the forelimbs) (10). The two vertical GRF peaks were observed at ~25% and 55% of the stance time of each limb. The timing of the maximal GRF peak differed between limbs, however; maximal vertical GRF peaks were at ~55% of the stance phase for the forelimbs and at ~25% of the stance phase for the hindlimbs. Maximal vertical GRFs were <1 body weight (BW) for each forelimb and <0.7 BW for each hindlimb. If observed increases of these peak GRFs were to continue to the near-maximal speeds of ~7 ms⁻¹ (4, 5) then they should reach about 1.1 BW and 0.98 BW, respectively (Fig. S1). The horizontal and mediolateral GRF components remained <0.1 BW for all speeds and limbs. Mediolateral GRFs were especially low, with a slight lateral bias for the forelimbs and a medial bias for the hindlimbs (Fig. S2).

The peak vertical GRFs were low relative to most other running quadrupeds (>1 BW), as expected given the slower relative speed, high duty factors, and evenly spaced footfall patterns of elephants (4, 5). Such low forces also are reflective of another factor: limb compliance. This is because compliant limbs dampen impact accelerations and keep peak GRFs low (13).

We found surprising compliance in elephant limbs, matching previously observed gradual changes of duty factor (decreases) and limb flexion (increases) with speed (5, 7). One correlated factor is the EMA, the ratio of GRFs to “antigravity” (e.g., extensor) muscle forces. More compliant, crouched limbs must incur decreased EMA for their benefit of reduced peak GRFs (13, 14), and thus may require greater antigravity muscle forces per unit GRF despite having smaller peak GRFs.

We find that elephants, even during relatively stiff-legged walking (Fig. 2), have average or poor EMA compared with other large, upright animals, such as humans and horses. Mean EMA in normal walking (dimensionless speed 0.33) was 0.68 ± 0.046, with generally smaller values (~0.5) for the ankle and wrist joints (Table S3). Scaling data predict a limb EMA of ~1.75 for an animal of a body mass of 3,000 kg (14–16), leaving elephant EMA values about one-third of those expected (Table S3). These EMA values are similar to or substantially less than those in much smaller animals, such as walking humans (0.71 ± 0.028) (15) and trotting horses (~1.0) (15).

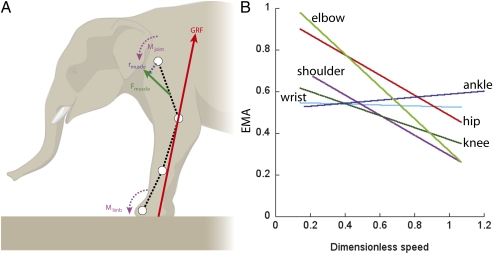
Fig. 2.

Inverse dynamics analysis (8) of Asian elephant limbs. (A) GRF and muscle force (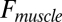) vectors, limb and joint moments (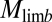and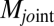), and muscle moment arm (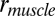) in a representative forelimb's walking pose from one individual (early stance phase; approximate marker positions shown by circles connected by black dashed lines). (B) Changes in individual joint EMA with increasing dimensionless speed (n = 306 total steps for all joints). Data and regression line equations for joints, with further explanations, are provided in Table S3 and Fig. S3.

Our results thus support the inference that there is an upper limit to EMA in large land animals, a limit requiring differential scaling of the musculoskeletal system in animals with a body mass exceeding ~300 kg (15, 16). Horse limbs are already almost as straight as feasible (15, 17), and thus have an EMA near the probable limit. Orientation of the GRF vector and position of the center of pressure are other important components of EMA. These components have been factored into our calculations as well as calculations of others; limb posture (with muscle moment arms) is the critical determinant of EMA. Elephants seem to have reached a similar limit for slow walking (maximal joint EMA ~1.0) even as 100-kg babies, which have the same limb orientations as adults (7).

An equally important aspect of EMA is that it decreases dramatically with increasing speed in elephants (Fig. 2 and Fig. S3), by ~1.5- to 2-fold for the more proximal joints, to mean values of 0.48 ± 0.036 (all joints) at the fastest speeds recorded. Running humans (mean EMA, 0.52 ± 0.016) (14) show a very similar pattern of reduced EMA that shares the same underlying postural basis, but with a more discrete shift of posture and gait. In contrast, other quadrupeds exhibit a nearly constant EMA across measured speeds (15, 16). We predict that this pattern of declining EMA with speed is common to animals that have relatively continuous gait transitions involving limbs that gradually increase their flexion with speed (13, 18, 19). If limb flexion were to increase gradually with speed, then such a continuous change of limb compliance could smooth out other normally discontinuous kinematic and kinetic shifts, thereby blurring any gait transition. This blurring should be expected, particularly in quadrupeds that spread their footfalls evenly across a stride as elephants do, but it is evident in running birds as well (18, 19). It may circumvent the decrease of stability that could accompany a discontinuous gait transition, or may prevent jarring loads (13). We also speculate that elephant EMA will plateau at faster speeds (~5–7 ms⁻¹) than measured here, because their duty factors (5) and joint angles (7) seem to approach asymptotes at such speeds.

The unexpectedly low EMA values in elephants are explained not only by an increase in joint flexion as elephants locomote faster (4–7), but also by the small muscle moment arms of elephants, which are about 36%–69% of those predicted for their size (Table S3). Furthermore, elephants’ relatively long proximal limb segments (2, 3) exacerbate the decreases of EMA with speed, because even small increases in limb flexion move the knee and elbow joints further from the resultant GRF vector, incurring greater external moments for all but the most distal joints.

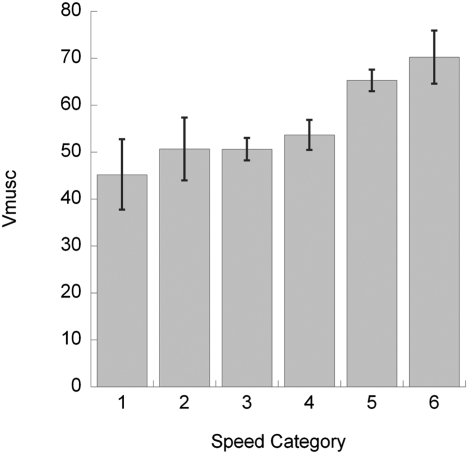
Relatively poor muscle leverage in running elephants has a direct impact on the metabolic cost of locomotion (Fig. 3). The normalized muscle volume recruitment (V_musc; 45–70 cm³ kg⁻¹ m⁻¹) in elephants is relatively 2- to 4-fold greater than in humans but comparable to estimates for other quadrupeds (15, 20, 21). Walking elephants move as cheaply as expected for their size (22), but our estimates of the muscle volume needed to support elephant limbs increase with speed (and reduced EMA). This increase parallels the trend observed in humans (14). Indeed, by combining our data with published metabolic data (22), we find a strong correlation between normalized muscle recruitment and metabolic costs (net cost of transport in mL of O₂ kg⁻¹ m⁻¹ = 0.0030 V_musc − 0.0944; R² = 0.88), with a slope identical to that seen in other species (fig. 2d in ref. 21). Our data indicate that elephants, lacking a discrete gait shift that could potentially lower costs as in other quadrupeds, should experience linearly increasing locomotor costs as speed increases past normal walking speeds. Thus, we surmise that running elephants sustain markedly higher metabolic costs and may suffer reduced endurance. Wild elephants may walk long distances to cover their home ranges and migrate, but seldom run and seemingly only for short distances, which might be explained by poor endurance. Certainly other factors, such as mechanical fatigue of musculoskeletal tissues, could be involved.

Fig. 3.

Changes in active limb muscle volumes (V_musc; in cm³ kg⁻¹ m⁻¹) with increasing dimensionless speed in Asian elephants. Speed categories 1–6 are dimensionless speeds (n = 48 steps): 1, slow (<0.3); 2, normal (0.30–0.35); 3, medium-fast (0.35–0.50); 4, fast (0.50–0.75); 5, very fast (0.75–1.0); and 6, >1.0. Error bars are ±SEM.

The mechanical costs of moving the CoM help determine the metabolic costs of locomotion. Therefore, we analyzed the individual limb power and work of elephant limbs to distinguish how the dynamics of the CoM measured previously (6, 10) are generated by the limbs (Fig. 4 and Figs. S4 and S5). Most strikingly, we ascertain that the forelimbs and hindlimbs do not fulfill drastically different functional roles. This is in contrast to our previous assumptions (6) that elephants would sharply divide mechanical functions between their limbs as other quadrupedal mammals do in walking and running gaits (23–26). The individual limb work needed to propel and brake the CoM was relatively constant with speed, with the forelimbs doing about double the work of the hindlimbs (Fig. S4). Both pairs of limbs thus contributed substantially to braking and propulsion. In other quadrupedal mammals, the forelimbs function primarily as brakes, and the hindlimbs function primarily as motors (23–26).

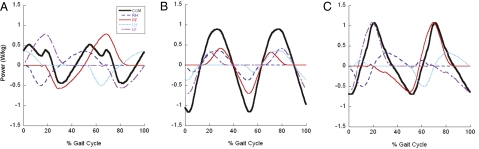
Fig. 4.

Individual limb power measurements (mean, normalized to W kg⁻¹ body mass) for normal walking (dimensionless speed 0.30–0.35) in Asian elephants (n = 30 strides). Horizontal (A) and vertical (B) components are shown, followed by the total mechanical power (C). Forelimb traces are represented by solid red (right forelimb) and dashed-dotted purple (left forelimb) lines, hindlimb traces are represented by dashed dark-blue (right hindlimb) and finely dashed light-blue (left hindlimb) lines, and CoM power traces (component or total) are represented by thick black lines. See Fig. S4 for data on work patterns and Fig. S5 for data on running.

The individual limb work (Fig. S4) done to move the CoM horizontally showed increasing fluctuations with speed; however, the limb work done to move the CoM vertically decreased with speed. The latter decrease indicates a reduced vertical motion of the CoM with increased speed in elephants, although vertical motions are small even at slow speeds (6, 10). The hindlimbs performed a relatively larger fraction of this work at slower speeds. The mediolateral component of individual limb work (and power) was highly variable and very small relative to the other components.

We conducted a novel 3D analysis of individual limb power (Fig. 4) to investigate two questions: (i) how does the relative timing of mechanical work by individual limbs influence total CoM dynamics? and (ii) what does individual limb power reveal about limb function in elephants? Previous studies have focused on limb impulses (force-time integrals) (23, 26), which are less informative than our limb power method, because impulses do not directly gauge the influence of limb forces on CoM velocity.

At all speeds, elephant limbs produced and absorbed a substantial amount of simultaneous positive and negative power during double and triple support, between both contralateral and ipsilateral limbs. This strategy incurs mechanical and, presumably, metabolic costs that conventional “combined limbs” force platform analyses (8, 10) cannot account for (27). Opposing limb power production in elephants could provide critical enhancements to overall stability (24). The timing of forelimb and hindlimb power in the horizontal component (Fig. 4A) often was in phase with total power requirements, but because the forelimbs’ power contributions were absolutely larger, they generated more net power for moving the CoM. The vertical components of power (Fig. 4B) were produced by smoothly synchronized bursts, typically from two forelimbs and one hindlimb during walking and from one forelimb and hindlimb during running, with little simultaneous positive and negative power usage. Examination of only total CoM power (Fig. 4C and Fig. S5) reinforces these conclusions. In particular, the forelimbs’ power contributions closely correspond to the total mechanical power, whereas the hindlimbs’ power contributions often are out of phase with total power.

Remarkably, elephant limbs exhibit a compression and rebound of each limb during the stance phase, with alternating cycles of negative and positive power production, indicating substantial limb compliance at all speeds, not just in running. This conclusion is firmly reinforced by evidence from duty factors, CoM dynamics, and joint kinematics (5–7, 10). Such compliance is in accordance with recent demonstrations that walking and running do not involve fundamentally different compliance (or other mechanics), but rather are different shades of a continuous spectrum (28). Thus, although elephants demonstrate normal vaulting CoM mechanics during walking but bouncing mechanics during running, their underlying limb mechanics remain compliant. This compliance persists despite the mechanical changes seen with speed, defying a dichotomy between stiff, “columnar” limbs in walking and compliant, spring-like limbs in running (4, 17, 28). The similarity in forelimb and hindlimb compliance in elephants again reinforces that the functions of these limbs are not as distinct as was previously assumed (4–6, 10).

Our present analysis has uncovered aspects of elephant gait mechanics that our previous kinematic (1–7) and kinetic (6, 10) studies could not, overturning some ideas and revealing that elephant locomotion is even stranger than previously imagined. In particular, we found less division of labor between limbs than expected. Elephant limbs operate analogously to four-wheel-drive vehicles. Although the four limbs share qualitatively equivalent mechanical functions (i.e., their contributions to braking and propulsion are proportionately similar, not skewed toward one or the other), elephant locomotor mechanics are dominated by the forelimbs, which do more work and contribute more power to the CoM. This is not only because they support more weight (as in other mammalian quadrupeds), but also because of the timing of their mechanical power output is better synchronized with total mechanical power. Curiously, the hindlimbs are less critical, especially in the fore–aft direction, although this discordance diminishes with increasing speed (Figs. S1 and S4). The reduced division of labor between the limbs stands in contrast to interlimb differences in such areas as joint kinematics (7) and anatomy (2). Functional equivalence of all four limbs is in contradiction to our previous findings (4–6), which assumed some functional similarity between the limbs of elephants and other mammals (23–26). This equivalence seems to be a unique specialization of elephants that relates to their unique size, range of habitats, and evolutionary history.

Our innovative measurements of mechanical work by individual limbs provide more insights than the classical combined limb method (8, 10), which tends to greatly underestimate mechanical work (27). We find that the individual limb method calculates mechanical work in elephants to be on average almost double that estimated by the combined limb method (Table S4). Our elephant individual limb work and power data are the first such comprehensive measurements for quadrupeds, opening new directions for reexamining the comparative mechanical costs of moving the CoM and revising classical scaling theories about locomotor costs and efficiency. We also find that our muscle recruitment–based estimates of locomotor cost have stronger correlations with published metabolic costs compared with measurements of individual limb or CoM (combined limb) work (Table S4).

Our study reveals that elephants have quite compliant limbs, not as stiff and columnar as previously envisaged (1–4, 17), that give a smooth ride to the CoM (6) and keep peak GRFs low (11–13). To achieve the observed limb compliance and low peak GRFs, elephants synchronize their limb dynamics in the vertical direction, but they incur considerable mechanical costs from limbs working against each other horizontally (27). The limbs also exhibit some continuous speed-related mechanical patterns that blur distinctions between walking and running.

Our measurements of EMA complement the rather low peak GRFs measured; the limited low EMA (and small distal muscles; Table S3) of elephants could prevent the achievement of high speeds and this high peak GRFs. This relates to the second major question raised in our introduction; elephant EMA is modest, not maximized. Thus, their peak locomotor performance is reduced relative that of to smaller animals; for example, elephants are not fast runners (3, 4). Furthermore, the limited EMA of elephant limb muscles must incur the metabolic cost of large recruited muscle volumes during running, ultimately constraining their endurance. Exciting questions remain, such as which joints or which tissues most limit speed and the timing of peak stresses in stride.

Our findings illustrate how locomotion in elephants diverges in critical ways from that of other animals. Elephants also elucidate fundamental size-related mechanical principles underlying critical constraints on gait choice, speed, and limb design. Elephants’ remarkable integration of limb compliance, leverage, and power allows them to support and move their large mass at relatively low cost (22). We speculate that this suite of locomotor specializations is central to elephants’ efficiency, safety, and stability, which are under uniquely stringent constraints imposed by the demands of natural selection because of their giant size. Nonetheless, elephants are able to use walking and running mechanisms while adopting noncolumnar, compliant limb poses with surprisingly modest leverage. Thus, their locomotor repertoire is broader than might be expected from conventional hypotheses regarding size-related constraints. This increases the possibility that other giant tetrapods, such as sauropod dinosaurs, likewise might have been more than stiff-legged walkers, or that locomotor diversity in the past might have been greater than the present might suggest.

Materials and Methods

Experimental Protocol.

Six juvenile Asian elephants (mean age, 8.5 ± 3.0 years; mean mass, 2,291 ± 669 kg; mean hip height, 1.52 ± 0.19 m; Table S1) served as the subjects in this study. All of our noninvasive experimental measurements were approved by The Royal Veterinary College's Animal Welfare and Ethics Committee and the Forest and Industry Organization of Thailand. The elephants were ridden or guided by their mahouts at a steady speed across a straight, level, 50-m path, across their entire comfortable range of speeds. At the fastest speeds, positive food awards and other benign reinforcement techniques were used. A seven–infrared camera (Qualisys) motion analysis system was used to capture the 3D elephant limb marker motions at 240 Hz. A set of 16 custom-made 1 × 1-m strain gauge-based force platforms (Arsalis) (10) were arrayed in a 2 × 8 grid mounted flush in the middle of the walkway to record the 3D GRFs and moments exerted on the elephant limbs at 100 Hz (minimum frequency 200 Hz for the fastest trials). The Qualisys motion analysis system and the force platforms were synchronized through digital signals. Measurements were conducted outdoors during cloudy or twilight periods, to reduce sunlight interference with the multicamera system. Infrared-reflective hemispherical markers were firmly attached to the animals’ skin using double-sided tape over palpable landmarks representing limb joints and segments using the same marker configuration reported previously (7).

Limb Footfall Timings and Forward Speed.

Individual limb touchdowns and liftoffs were determined using the vertical force component of the force platform data, with a threshold of 3% of the peak vertical force, and only for trials in which only one limb landed on one force platform. The forward velocity of an elephant for each stride was measured by calculating the averages of the hip and shoulder marker velocities. Steady-state trials were defined as those in which the variation between the forward velocities at two consecutive touchdowns was <10% of the average forward velocity. The data were divided into component strides based on the right hindlimb touchdowns. Froude numbers and dimensionless speeds were used to normalize the velocities to enable comparison between elephants of different sizes (4–7).

Individual Limb Mechanical Analysis.

The mechanical work and power contributions of each individual limb to the whole-body CoM motion were analyzed using an individual-limb power analysis (27). The mechanical limb power, P_limb, was calculated as the dot product of the limb force vector,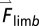, and the whole-body CoM velocity vector, ,

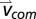The components of the dot product at different directions were used to measure the limb mechanical power contributions to propel the animal body forward [positive horizontal component, 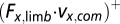], decelerate the body [negative horizontal component, 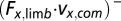], or lift the body upward [positive vertical component, 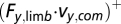]. Slightly different from the conventional usage of mechanical work, here we decompose the dot product into its three components in the three independent directions. This helps dissect the individual limb contributions to moving the whole-body CoM in different directions. Finally, the whole-body CoM mechanical power was calculated as the dot product of the sum of all of the supporting limb forces and whole-body CoM velocity. Further details on these calculations are given in SI Materials and Methods.

Our inverse dynamics analyses for calculating EMA and active muscle volume followed conventional methods (14–16, 20, 21, 29). Specific details are given in SI Materials and Methods.