Dynamic Nucleotide Mutation Gradients and Control Region Usage in Squamate Reptile Mitochondrial Genomes

Abstract

Gradients of nucleotide bias and substitution rates occur in vertebrate mitochondrial genomes due to the asymmetric nature of the replication process. The evolution of these gradients has previously been studied in detail in primates, but not in other vertebrate groups. From the primate study, the strengths of these gradients are known to evolve in ways that can substantially alter the substitution process, but it is unclear how rapidly they evolve over evolutionary time or how different they may be in different lineages or groups of vertebrates. Given the importance of mitochondrial genomes in phylogenetics and molecular evolutionary research, a better understanding of how asymmetric mitochondrial substitution gradients evolve would contribute key insights into how this gradient evolution may mislead evolutionary inferences, and how it may also be incorporated into new evolutionary models. Most snake mitochondrial genomes have an additional interesting feature, 2 nearly identical control regions, which vary among different species in the extent that they are used as origins of replication. Given the expanded sampling of complete snake genomes currently available, together with 2 additional snakes sequenced in this study, we reexamined gradient strength and CR usage in alethinophidian snakes as well as several lizards that possess dual CRs. Our results suggest that nucleotide substitution gradients (and corresponding nucleotide bias) and CR usage is highly labile over the ∼200 m.y. of squamate evolution, and demonstrates greater overall variability than previously shown in primates. The evidence for the existence of such gradients, and their ability to evolve rapidly and converge among unrelated species suggests that gradient dynamics could easily mislead phylogenetic and molecular evolutionary inferences, and argues strongly that these dynamics should be incorporated into phylogenetic models.

Introduction

In vertebrate mitochondrial (mt) genomes there exists an intriguing link between genome structure and genome-wide nucleotide evolution due to the asymmetrical replication of the mitochondrial genome [Clayton, 1982; Bielawski and Gold, 2002; Faith and Pollock, 2003; Krishnan et al., 2004a; Raina et al., 2005; Jiang et al., 2007]. This asymmetry leads to gradients of mutational bias across the genome that are governed predominantly by the distance between any given nucleotide site and the origins of genome replication. Variation in this strand-asymmetric replication process appears to have contributed substantially to variation in substitution rates and patterns across the mitochondrial genome [Bielawski and Gold, 2002; Faith and Pollock, 2003; Raina et al., 2005].

The strand-asymmetric replication mechanism has been thought to expose different regions of the parental heavy strand to varying amounts of time in the single-stranded state during replication (D_ssH) [Tanaka and Ozawa, 1994], depending on the distances of the regions from the origins of heavy strand (O_H) and light strand (O_L) synthesis. There is some controversy over the classical mt genome replication mechanism based on the research of Holt and colleagues, mostly concerning the asymmetry of the process, the role of the putative origin of light strand replication, and whether the replicating DNA spends substantial amounts of time single-stranded [Yang et al., 2002; Reyes et al., 2005; Yasukawa et al., 2005]. Therefore, to take a neutral position, we refer to the time that a gene or nucleotide is predicted to spend in an asymmetric mutagenic state (T_AMS), rather than the predicted duration of time that the heavy strand spends single-stranded (D_ssH); the calculation of these statistics are identical [Tanaka and Ozawa, 1994; Reyes et al., 1998; Faith and Pollock, 2003]. We note that the evolutionary genetic evidence is highly compatible with and provides extremely strong evidence for the classic replication model (or something like it), while there is no known mechanism by which the Holt models could have produced the asymmetric substitution patterns observed in vertebrate mitochondria.

Single-stranded DNA is particularly prone to deaminations, especially deaminations of cytosine (C) and adenine (A), which cause respective transitions to thymine (T) and guanine (G) on the heavy strand [Tanaka and Ozawa, 1994; Reyes et al., 1998; Faith and Pollock, 2003]. Since transition rates are much greater than transversion rates, these excess transitions lead to elevated G/A and T/C ratios, which accounts for most of the asymmetry in synonymous substitutions in vertebrate mt genomes [Bielawski and Gold, 1996; Rand and Kann, 1998; Reyes et al., 1998; Frank and Lobry, 1999; Faith and Pollock, 2003; Krishnan et al., 2004a, 2004b; Raina et al., 2005]. On the heavy strand, C→T substitutions occur at a very high rate [Frederico et al., 1990], and the T/C ratio quickly plateaus at low T_AMS [Faith and Pollock, 2003]. The deamination of A→hypoxanthine (leading to A→G mutations after replication) occurs at a slower rate, and in vertebrates the A→G heavy strand substitutions at 4-fold and 2-fold redundant 3rd codon positions increase linearly with increasing T_AMS [Faith and Pollock, 2003; Krishnan et al., 2004a]. Consequently, A→G substitutions and the resultant A/G nucleotide frequency gradient are good predictors of T_AMS [Faith and Pollock, 2003; Raina et al., 2005; Jiang et al., 2007].

What is known about the evolution of this gradient in vertebrates comes from an analysis of primate mitochondria [Raina et al., 2005]. In the primates, the gradients are ancestrally weak, and have convergently evolved from weak to strong in at least 2 lineages [Raina et al., 2005]. It is notable, however, that mitochondrial genome size and gene order are highly conserved across primates (and mammals in general), whereas other vertebrate groups demonstrate more diversity of mitochondrial genome size and structure. Thus, primate gradient evolution may not be fully representative of gradient evolution in other groups with more extensive mitochondrial genome structural diversity. Further study of diverse vertebrate mitochondria would provide a more inclusive perspective on the degree to which gradients vary among vertebrate species, particularly when changes in mitochondrial genome structure and gene order occur. Although mitochondrial gene sequences are extensively used for phylogenetic inference and studies of molecular evolution, mitochondrial nucleotide gradients and their ability to change through time have never been incorporated into phylogenetic models (partly due to a lack of understanding about how such gradients evolve through time). Thus, in-depth understanding of mitochondrial gradients and their evolutionary dynamics are important for appreciating how current evolutionary inferences may be biased by not accounting for such mutational dynamics, and also how future development of nucleotide models may appropriately account for the existence and evolution of gradients.

In this study we focus on the mitochondrial genomes of squamate reptiles (snakes and lizards). In contrast to primates, squamate mitochondrial genomes possess numerous examples of structural rearrangements, including the duplication of the mitochondrial control region (CR) thought to contain the O_H. In most snakes, and some lizards, the control region is duplicated and the 2 copies evolve by concerted evolution, resulting in the 2 identical or nearly identical duplicates in a given mitochondrial genome. Additionally, compared to the relatively shallow evolutionary divergence of the primate clade, the squamates in this study span a much greater depth of evolutionary divergence (∼200 m.y.). Previously, we analysed the mitochondrial genomes of several snake species with dual CRs and found evidence, based on nucleotide gradients, that both CRs may act as heavy strand origins in many species, although the actual gradients themselves were never characterized and compared. Recently, the number of squamate mitochondrial genomes available has increased substantially, including many new snake species with dual CRs, and including lizard species with dual CRs.

We also analyze the diversity of mutational gradients in squamate mitochondrial genomes, including 2 new snake species added in this study, to develop a greater understanding of the evolution of these gradients in a clade of vertebrates that demonstrates substantial diversity in mitochondrial genome structure. Using this example, we address the following questions: (1) What is the overall diversity of gradients observed in squamates and how does this compare to that previously reported for the primates? (2) How rapidly do these gradients appear to evolve? (3) Could convergent evolution of gradients potentially mislead phylogenetic inference? And (4), how rapidly does the preference for one CR over the other evolve in mitochondria with dual control regions?

Material and Methods

Mitochondrial Genome Sequencing and Annotation

Complete mitochondrial genomes of 2 new snake species, Micrurus fulvius (‘eastern coral snake’; Elapidae) and Causus defilippii (‘snouted night adder’; Viperidae), were sequenced to complement existing sampling of alethinophidian snakes. Laboratory and annotation protocols follow Jiang et al. [2007], but briefly, total DNA was isolated from frozen liver tissue and the mitochondrial genomes were amplified in 6 large overlapping fragments [Jiang et al., 2007]. These fragments were cloned and the clones were sequenced by primer walking on a Beckman CEQ8000 automated sequencer. Contigs were assembled using the commercial program Sequencher, and tRNAs were identified using tRNAscan [Lowe and Eddy, 1997] and homology was verified manually based on sequence similarity and anticodon. The tRNAs were used to identify approximate boundaries of protein coding genes, control regions, and ribosomal RNAs, which were then confirmed and fine tuned by manual inspection of homology with previously annotated snake mitochondrial genomes [Slack et al., 2003]. The 2 genomes were submitted to GenBank under accession numbers GU045452 (Causus) and GU044553 (Micrurus).

Gradient Analyses

Complete mitochondrial genome sequences from squamate species available in GenBank (September, 2008) were retrieved and combined with the 2 newly sequenced snake species to form our starting data set of 51 species (table 1). For analyses of gradients, the sequences and genome coordinates for all 13 mitochondrial protein-coding genes were extracted. The heavy strand origins of replication (O_H) were estimated as the center of the annotated control regions (recall that many snakes have 2 control regions), and the light strand of replication (O_L) was estimated as the center of the annotated O_L sequence. In cases where no O_L was identified in the GenBank annotation, the center of the region between the tRNA-Asn and tRNA-Trp gene annotations, the normal O_L location, was used. Two additional snake species of special interest (representatives of the poorly sampled blind snakes) with nearly complete mitochondrial genomes were also included in this study (bringing the total to 53 taxa): Ramphotyphlops australis and Typhlops mirus. For these 2 species, complete mitochondrial genomes of congeneric species are known, and genome size, gene coordinates, and origin locations were estimated by aligning these incomplete genomes to the complete genomes of congeneric species, and then substituting the missing sequence data from the completed genomes to obtain estimates of genome length, and gene coordinates.

Table 1.

GenBank accession numbers for species used

GenBank	Species	Family	Tetrapod group
NC_006284	Amphisbaena schmidti	Amphisbaenidae	Lizards
NC_006285	Geocalamus acutus	Amphisbaenidae	Lizards
NC_006287	Bipes biporus	Bipedidae	Lizards
NC_006288	Bipes canaliculatus	Bipedidae	Lizards
NC_006286	Bipes tridactylus	Bipedidae	Lizards
NC_006282	Rhineura floridana	Rhineuridae	Lizards
NC_006283	Diplometopon zarudnyi	Trogonophiidae	Lizards
NC_005958	Abronia graminea	Anguidae	Lizards
EU747729	Ophisaurus attenuatus	Anguidae	Lizards
NC_005959	Shinisaurus crocodilurus	Xenosauridae	Lizards
NC_008774	Coleonyx variegatus	Gekkonidae	Lizards
NC_007627	Gekko gecko	Gekkonidae	Lizards
NC_008772	Gekko vittatus	Gekkonidae	Lizards
NC_007008	Teratoscincus keyserlingii	Gekkonidae	Lizards
NC_009683	Calotes versicolor	Agamidae	Lizards
NC_009421	Chlamydosaurus kingii	Agamidae	Lizards
NC_006922	Pogona vitticeps	Agamidae	Lizards
NC_008065	Xenagama taylori	Agamidae	Lizards
NC_008777	Furcifer oustaleti	Chamaeleonidae	Lizards
NC_010972	Anolis carolinensis	Iguanidae	Lizards
NC_002793	Iguana iguana	Iguanidae	Lizards
NC_005960	Sceloporus occidentalis	Phrynosomatidae	Lizards
NC_005962	Cordylus warreni	Cordylidae	Lizards
NC_008328	Lacerta viridis	Lacertidae	Lizards
NC_008773	Takydromus tachydromoides	Lacertidae	Lizards
NC_000888	Eumeces egregius	Scincidae	Lizards
NC_008775	Lepidophyma flavimaculatum	Xantusiidae	Lizards
NC_008776	Heloderma suspectum	Helodermatidae	Lizards
NC_008778	Varanus niloticus	Varanidae	Lizards
NC_010974	Varanus salvator	Varanidae	Lizards
NC_007400	Acrochordus granulatus	Acrochordidae	Snakes (Alethinophidia)
NC_001945	Dinodon semicarinatus	Colubridae	Snakes (Alethinophidia)
NC_010200	Enhydris plumbea	Colubridae	Snakes (Alethinophidia)
NC_009769	Pantherophis slowinskii	Colubridae	Snakes (Alethinophidia)
NC_010225	Naja naja	Elapidae	Snakes (Alethinophidia)
GU 045453	Micrurus fulvius	Elapidae	Snakes (Alethinophidia)
NC_009768	Agkistrodon piscivorus (LA)	Viperidae	Snakes (Alethinophidia)
EF669477	Agkistrodon piscivorus (FL)	Viperidae	Snakes (Alethinophidia)
NC_010223	Deinagkistrodon acutus	Viperidae	Snakes (Alethinophidia)
NC_007397	Ovophis okinavensis	Viperidae	Snakes (Alethinophidia)
GU045452	Causus defilippii	Viperidae	Snakes (Alethinophidia)
NC_007402	Xenopeltis unicolor	Xenopeltidae	Snakes (Alethinophidia)
FJ755180	Anilius scytale	Aniliidae	Snakes (Alethinophidia)
NC_007398	Boa constrictor	Boidae	Snakes (Alethinophidia)
NC_007401	Cylindrophis ruffus	Cylindrophiidae	Snakes (Alethinophidia)
NC_007399	Python regius	Pythonidae	Snakes (Alethinophidia)
NC_012573	Tropidophis haetianus	Tropidophiidae	Snakes (Alethinophidia)
NC_005961	Leptotyphlops dulcis	Leptotyphlopidae	Snakes (Scolecophidia)
NC_010196	Ramphotyphlops braminus	Typhlopidae	Snakes (Scolecophidia)
NC_010971	Typhlops reticulatus	Typhlopidae	Snakes (Scolecophidia)
AM236346	Ramphotyphlops australis	Typhlopidae	Snakes (Scolecophidia)
AM236345	Typhlops mirus	Typhlopidae	Snakes (Scolecophidia)
NC_004815	Sphenodon punctatus	Sphenodontidae	Sphenodontia (outgroup)

We implemented a slightly modified version of the MCMC approach in Raina et al. [2005] to estimate the likelihoods of the slope and intercept of the G/A ratio gradient depending on the calculated T_AMS at every site. These analyses were run on 4-fold degenerate sites. The calculation of T_AMS differs depending on whether CR1 or CR2 is functional, but only for the genes that are in between the 2 control regions [Jiang et al., 2007]; for the alethinophidian snakes with 2 control regions, these genes include the 2 rRNAs and ND1. The G/A ratio in the ND1 gene was used in such species to predict activity of CR1 or CR2 in initiating heavy strand replication. To do this, slope and intercept calculations were made based on the T_AMS from CR1 and CR2 separately, and together as a weighted average in a Markov chain Monte Carlo (MCMC) analysis [Raina et al., 2005]. Other than the addition of the weighting parameter, all details of the Markov chain were as in Raina et al. [2005]. Relative support levels for alternative control region usage hypotheses were determined using the Akaike Information Criterion (AIC) and Akaike weights [Akaike, 1973, 1983], as in Jiang et al. [2007]. The Akaike weights for the alternative individual models provide a measure of the degree to which a control region is exclusively functional, while the weight parameter in the mixed model represents the time-averaged effect of mixed control region usage on the G/A ratios.

Quantitative Analyses of the Evolutionary Rate and Phylogenetic Consistency of the G/A Gradient

To estimate the approximate rate of change of gradient slope and intercept over time, we reconstructed the ancestral G/A gradient slope and intercepts at all nodes by treating the gradient parameter MLEs from the tip sequences as continuously-valued characters and reconstructing the most likely states by ML under a Brownian motion model. This was done using the R-module APE [Paradis et al., 2004]. We measured the relationship between changes in slope and intercept (as estimated via the Brownian motion ancestral reconstruction) versus temporal divergence (as assessed via linear regression analyses). To statistically estimate the degree of phylogenetic association of the slope and intercept estimates, we conducted randomization tests in which the slope and intercept assignments were randomly permuted among different tips to assess the correspondence of gradient parameters with the phylogeny. The distributions of likelihood scores were examined across 1000 such permutations, after maximizing the parameters of the model by ML, to estimate the significance of the phylogenetic association.

Clustering of Gradients Using Mixture Models

To identify groupings of mt genomes with similar nucleotide gradients, we applied MCMC-based mixture models, as described in Raina et al. [2005]. In brief, a Markov chain was run on all squamate mt genomes (4-fold degenerate sites only) simultaneously using a series of mixture models with different numbers of mixture classes (from 2 to a total of 20 classes in the mixtures). Genome membership in classes was determined according to full Bayesian posterior probabilities. To determine whether larger numbers of classes were justified, we considered the relative likelihood maxima between runs with different numbers of mixture classes (the likelihood ratio test), as well as the degree of mixed membership in different classes according to full Bayesian posterior probabilities [Raina et al., 2005]. Previous experience has shown that the p < 0.05 cutoff in the likelihood ratio test is a good predictor of when genomes will have mixed membership according to empirical Bayesian posteriors, whereas the 0.001 cutoff is a better predictor of when membership will be mixed according to full Bayesian posteriors [Raina et al., 2005]; interestingly, the results in this study were consistent with this observation, although there is no guarantee that this will always be so.

Phylogeny and Divergence Time Estimates

Phylogenetic inference or divergence dating, per se, is not a main goal of this study, although we did utilize a reasonable estimate of the phylogeny and divergence times to place aspects of gradient evolution into a coarse temporal and phylogenetic framework. To infer phylogenetic relationships among the species of squamates used in the gradient analysis, we analyzed the nucleotide alignments of the 12 protein-coding mitochondrial genes encoded on the heavy strand of each mt genome. These sequences were aligned based on their amino acid sequence, using ClustalX [Thompson et al., 1997], reverse-translated back to their nucleotide sequences using a perl script, and concatenated. This automated alignment was verified manually, and modified only slightly to exclude a small number of ambiguously aligned positions (mostly at the 5′ and 3′ end of genes).

We simultaneously inferred phylogenetic relationships and divergence times using Beast 1.4.8 [Drummond and Rambaut, 2007]. Previous studies have shown evidence of strong selection and molecular convergence in the mitochondrial genome that can lead to misleading estimates of phylogenetic relationships [Castoe et al., 2008, 2009]. Because of this potential problem we constrained several nodes that represent a better consensus of the phylogenetic relationships among squamates [Vidal and Hedges, 2005; Castoe et al., 2009]. Thus, we constrained the monophyly of iguania (iguanids, chamaeleonids and agamids), the monophyly of Toxicofera [Vidal and Hedges, 2005] and the monophyly of Scolecophidia. We partitioned the entire dataset by gene and codon position and implemented a different GTRΓI model for each partition and unlinked parameters estimation across partitions. We used the relaxed clock method assuming uncorrelated lognormal rates among branches and a birth-death process of speciation. For the treeModel.rootHeight parameter we used a normal distribution prior with mean = 250 and SD = 15 based on the suggested origin of squamates (online supplementary table S1, www.karger.com/doi/10.1159/000295342). We used 5 fossil cali-brations across the entire tree and implemented lognormal priors with SD = 0.2 for all of them (online supplementary table S1).

We initiated 4 independent runs in Beast with random starting trees, and ran each for 10 million generations. Chains were sampled every 1000 generations, and convergence and stationarity were verified by examining the ESS values for parameter estimates using the program Tracer 1.4. Based on examination of trial runs we discarded the first 3 million generations as burn-in period. The posterior probabilities for nodal support were obtained after combining the post burn-in samples from the 4 independent runs.

Results

Results of Genome Annotation and Phylogeny Estimation

The mitochondrial genome of M. fulvius contained 17,506 bp, and that of C. defilippii 17,342 bp. As expected for alethinophidian snakes, the genomes of both newly sequenced species contain dual control regions that are nearly identical to one another within each genome. In both cases, the location of the control regions follows the typical alethinophidian snake pattern, with CR1 in the standard vertebrate placement, between CYTB and 12s rRNA (excluding the intervening tRNAs), and the duplicate CR2 located between ND1 and ND2 (again excluding intervening tRNAs). In Causus, CR1 is 1,144 bp in length, whereas CR2 is 1,134 bp, missing 10 bp from the 3′ end of CR1. In Micrurus, CR1 is 1,194 bp and CR2 is 40 bp shorter, missing these last 40 bp from the 3′ end. These genomes also possess the translocated tRNA^LEU common to all alethinophidian snakes yet sequenced. The only notable structural difference between the 2 genomes is that Causus has its tRNA^PRO located upstream of CR2 (as in other viperid species) compared to Micrurus, in which it is located upstream of CR1 (as in most colubroid species).

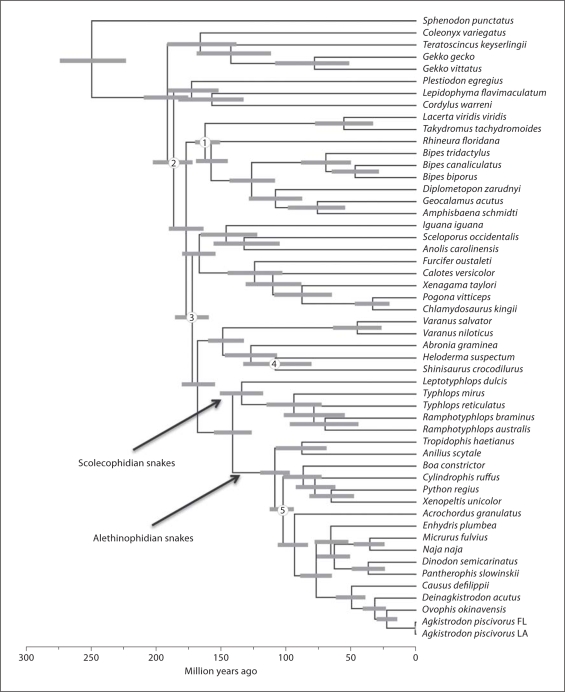
Our estimates of phylogeny and divergence times, based on analyses of the mitochondrial genome data are shown in figure 1. We note that there is some controversy over the taxonomic classification of the fossil we use as calibration point number 1 [fig. 1; Gao, 1997], but we observed no notable differences in divergence time estimates with or without this calibration point. Thus, regardless of the resolution of this controversy, it does not appear to have any appreciable effect on our estimates of divergence times, especially for the purposes we employ them in this study. Our estimates of divergence times are broadly consistent with other studies [Vidal and Hedges, 2005; Castoe et al., 2009; Hedges and Vidal, 2009], and place the 2 new species with other members of their respective families (Causus: Viperidae; Micrurus: Elapidae) in the tree (fig. 1).

Fig. 1.

Phylogenetic tree of squamate species used in this study, with divergence times for nodes estimated. This Bayesian tree was estimated using nucleotide sequences of 12 mitochondrial protein-coding genes, estimated simultaneously with divergence times. Numbers on the tree indicate nodes at which fossil calibrations were applied for the estimation of divergence times (details in online suppl. table S1).

Estimate of CR Usage in Dual CR Genomes

To test for mutational evidence that one CR has been preferred over another, or for dual CR usage, we applied our MCMC analysis [Raina et al., 2005] to fit alternative models of exclusive CR1 or CR2 usage, or mixed control region effect. This included analysis of dual CR mt genomes of all 17 alethinophidian snakes, as well as the analyses of 5 lizard mt genomes with dual CR that appear to be homogenized by some type of concerted evolution (table 2).

Table 2.

Results of likelihood-based hypothesis tests for CR usage in dual CR squamates

Species name	CR1 MLE	CR2 MLE	2(ΔLnL) CR1-v-CR2	Dual CR MLE	2(ΔLnL) CR1-v-Dual	2(ΔLnL) CR2-v-Dual	CR1 Weight	Null slope significance
Lizards
Chlamydosaurus kingii	-1,133.68	-1,132.35	-2.65	-1,132.36	1.32	-0.01	0.001
Pogona vitticeps	-1,137.02	-1,135.98	-2.10	-1,135.66	1.37	0.32	0.337
Gekko vittatus	-1,329.36	-1,329.36	0.00	-1,329.36	0.00	0.00	0 13	∗∗
Takydromus tachydromoidei	-1,437.87	-1,437.87	0.00	-1,437.87	0.00	0.00	0.202
Varanus niloticus	-1,367.60	-1,367.60	-0.01	-1,367.60	0.01	0.00	0.18
Snakes
Acrochordus granulatus	-1,238.85	-1,235.32	-7.07∗∗	-1,235.33	3.53	-0.01	0.012	∗∗
Agkistrodon piscivorus FL	-1,129.65	-1,128.79	-1.72	-1,128.79	0.86	0.00	0.006
Agkistrodon piscivorus LA	-1,172.20	-1,171.04	-2.31	-1,171.05	1.14	-0.01	0.012
Anilius scytale	-1,253.17	-1,252.61	-1.12	-1,252.59	0.58	0.02	0.201
Boa constrictor	-909.13	-908.53	-1.19	-908.41	0.72	0.12	0383	∗
Causus defilippii	-1,472.59	-1,472.87	0.55	-1,472.48	0.11	0.39	0.706
Cylindrophis ruffus	-1,127.81	-1,130.63	5.64	-1,127.82	0.00	2.82	0 999	∗∗
Deinagkistrodon acutus	-1,199.89	-1,199.04	-1.69	-1,199.05	0.83	-0.01	0.017
Dinodon semicarinatus	-1,159.34	-1,158.35	-1.97	-1,158.30	1.04	0.05	0 223	∗
Enhydris plumbea	-1,173.55	-1,172.52	-2.06	-1,172.52	1.03	-0.01	0.004
Micrurus fulvius	-1,312.30	-1,310.72	-3.17	-1,310.73	1.58	-0.01	0.003
Naja naja	-1,168.36	-1,169.27	1.82	-1,168.36	-0.01	0.90	0.997
Ovophis okinavensis	-1,246.36	-1,246.19	-0.33	-1,246.12	0.24	0.07	0.445
Pantherophis slowinskii	-1,153.63	-1,153.13	-0.98	-1,152.85	0.77	0.28	0.46	∗∗
Python regius	-1,130.98	-1,126.94	-8.07	-1,126.95	4.03	0.00	0 001	∗∗
Tropidophis haetianus	-1,188.30	-1,188.67	0.74	-1,188.31	-0.01	0.36	0.987
Xenopeltis unicolor	-1,149.35	-1,148.97	-0.75	-1,148.61	0.74	0.37	0 529	∗∗

Dual CR models were compared to null-slope models to test the significance of the gradient, and the significance levels of these tests (based on likelihood ratio tests) are indicated with ^∗ (p < 0.05) or ^∗∗ (p < 0.01). Based on the dual CR model, the weighting parameter of CR1 is given; the CR2 weighting parameter is 1 minus this value.

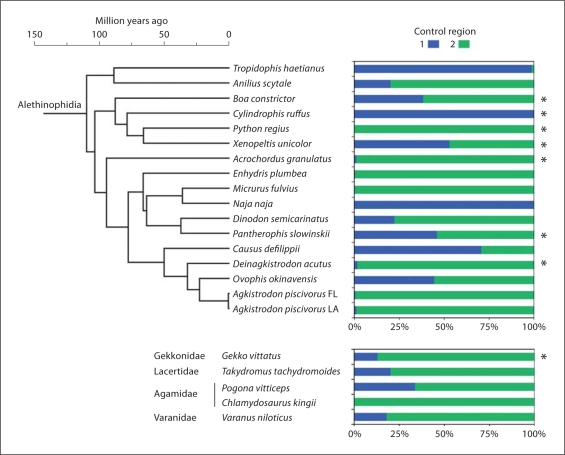
Among the dual CR lizards, 3 appear to have almost no preference among the individual CR or dual CR models: Gekko vittatus, Takydromus tachydromoides, and Varanus niloticus. In contrast, the 2 agamid lizards, Pogona vitticeps and Chlamydosaurus kingii, show a stronger preference for individual CR2 usage or dual CR models, but not strong enough to significantly reject either of the individual CR models (table 2). Only in 2 snake species, Acrochordus granulatus and Python regius, was the CR1 model significantly rejected (at p < 0.05) in favor of the individual CR2 usage model. To determine the overall significance of the gradient within these models tested, we compared the likelihood of the G/A gradient models with the same model but with a slope of zero (but freely varying intercept). In the case of mt genomes with dual CRs, we used the dual CR model as the alternative hypothesis. One lizard, G. vittatus, of the 5 dual CR lizard species had significant slopes, as did 7 of the 17 alethinophidian snakes (table 2; fig. 2).

Fig. 2.

Weighted estimates of the time-averaged effect of differential control region usage in species with 2 control regions (maintained in concerted evolution) from a linear G/A gradient mixture model of dual control region usage. An asterisk indicates species with significant gradient slopes based on comparison with a constrained zero slope gradient model (p < 0.05). The snakes are shown with a dated phylogeny adjacent to the CR usage data to visualize the degree to which CR preference evolves over time.

Since the nucleotide sequence of duplicate control regions is nearly identical within each genome, it is also reasonable to assume that both control regions are probably functional, and that a mixed CR usage model is most appropriate as a hypothetical null model. From this perspective, the weight parameter in the mixed model represents the time-averaged effect of mixed control region usage on the G/A ratios (table 2; fig. 2). Based on the weighting parameter of CR usage from the dual CR model, CR2 usage was strongly preferred over CR1 as an explanation of the data in the lizard Chlamydosaurus, and the Python, Acrochordus, Deinagkistrodon, Agkistrodon, Enhydris, and Micrurus snakes. Only the Tropidophis, Cylindrophis, and Naja snakes show strong preference for CR1 (fig. 2). The remaining lizards and snakes show intermediate preference for both control regions. In the mixed dual CR model, the average control region effect tends to mirror the preferences for one CR over another in the individual CR models. The results of the dual CR model analyses (together with the individual CR2 analyses) provide evidence that CR2 plays a functional role in replication in some and perhaps most species. The patterns of CR preference, however, appear to be highly species-specific, and change rapidly over time (fig. 2).

Gradient Analysis Results from Single CR Species

The results of the G/A gradient model analyses are provided in table 3, along with the results of hypothesis tests for the existence of a gradient (based on a null zero slope gradient model). Considering all squamate mt genomes analysed (including the dual CR mt genomes), the null gradient model was significantly rejected in favor of the free-parameter models (based on LRTs at p < 0.05) in 17 out of the total 52 tested mt genomes. None of the gradients from the 5 scolecophidian (one CR) snakes were significant. Among the 24 lizards with a single CR, 9 were able to reject the null gradient model. There was considerable variation among genomes in both slope and intercept, and values for many pairs of species were apparently meaningfully different from one another in that they lay outside their respective 95% credible intervals.

Table 3.

Results of G/A gradient analyses, including MLE and confidence intervals for slope and intercept, and the p value of the likelihood ratio test comparing the null (zero slope) model with the free-slope models

Species	CR Model	Slope			Intercept			p value
		MLE	CI (5%)	CI (95%)	MLE	CI (5%)	CI (95%)
Lizards
Abronia graminea	Single	0.10	-0.30	0.48	1.30	1.04	1.60	0.712
Amphisbaena schmidti	Single	0.93	0.40	1.52	1.54	1.20	1.94	0.022
Anolis carolinensis	Single	0.33	0.10	0.56	0.72	0.57	0.90	0.052
Bipes biporus	Single	0.26	-0.66	1.12	2.72	2.13	3.53	0.693
Bipes canaliculatus	Single	0.76	-0.87	2.20	3.57	2.68	4.82	0.470
Bipes tridactylus	Single	0.08	-0.44	0.63	1.93	1.57	2.38	0.837
Calotes versicolor	Single	0.45	0.08	0.82	1.23	1.00	1.53	0.115
Chlamydosaurus kingii	Dual	-0.48	-1.13	0.28	2.47	1.91	2.99	0.249
Coleonyx variegatus	Single	0.30	-0.33	0.92	2.19	1.76	2.70	0.531
Cordylus warreni	Single	0.83	0.23	1.39	1.72	1.36	2.16	0.050
Diplometopon zarudnyi	Single	0.29	-0.02	0.56	1.03	0.84	1.25	0.189
Furcifer oustaleti	Single	0.10	-0.21	0.43	1.18	0.95	1.45	0.681
Gekko gecko	Single	0.81	0.47	1.13	0.91	0.72	1.14	0.001
Gekko vittatus	Dual	0.37	0.19	0.54	0.47	0.37	0.60	0.004
Geocalamus acutus	Single	0.47	0.12	0.78	1.01	0.82	1.25	0.044
Heloderma suspectum	Single	0.39	0.21	0.58	0.52	0.40	0.66	0.005
Iguana iguana	Single	2.96	1.80	4.07	2.31	1.76	3.06	0.001
Lacerta viridis	Single	0.46	0.16	0.76	0.91	0.73	1.13	0.034
Lepidophyma flavimaculatum	Single	0.87	0.29	1.38	1.57	1.26	1.96	0.024
Plestiodon egregius	Single	0.63	0.12	1.11	1.52	1.24	1.91	0.085
Pogona vitticeps	Dual	-0.98	-1.86	-0.06	2.99	2.39	3.68	0.107
Rhineura floridana	Single	0.63	0.02	1.21	1.62	1.29	2.04	0.129
Sceloporus occidentalis	Single	0.24	-0.30	0.84	1.89	1.51	2.34	0.560
Shinisaurus crocodilurus	Single	-0.13	-0.48	0.20	1.40	1.15	1.70	0.602
Takydromus tachydromoides	Dual	0.35	0.11	0.59	0.83	0.67	1.01	0.055
Teratoscincus keyserlingii	Single	0.89	0.45	1.32	1.19	0.94	1.49	0.004
Varanus niloticus	Dual	0.04	-0.40	0.47	1.69	1.38	2.06	0.887
Varanus salvator	Single	0.86	0.13	1.56	2.16	1.74	2.77	0.094
Xenagama taylori	Single	0.28	-0.27	0.77	1.62	1.30	2.02	0.470
Snakes (Scolecophidia)
Leptotyphlops dulcis	Single	1.19	-0.42	2.86	3.97	2.98	5.33	0.316
Ramphotyphlops australis	Single	-0.11	-0.60	0.32	1.90	1.59	2.31	0.741
Ramphotyphlops braminus	Single	0.17	-0.33	0.67	1.86	1.51	2.28	0.664
Typhlops mirus	Single	0.04	-0.30	0.36	1.25	1.02	1.51	0.869
Typhlops reticulatus	Single	0.36	-0.14	0.86	1.61	1.29	2.01	0.311
Snakes (Alethinophidia)
Acrochordus granulatus	Dual	0.63	0.39	0.93	0.73	0.56	0.91	0.000
Agkistrodon piscivorus FL	Dual	0.56	-0.16	1.29	2.37	1.89	2.96	0.212
Agkistrodon piscivorus LA	Dual	0.43	-0.19	0.96	2.11	1.75	2.65	0.240
Anilius scytale	Dual	0.38	0.05	0.78	1.25	1.01	1.54	0.117
Boa constrictor	Dual	1.05	0.42	1.81	1.81	1.39	2.33	0.026
Causus defillipii	Dual	0.38	0.03	0.69	1.21	1.01	1.50	0.122
Cylindrophis ruffus	Dual	0.87	0.34	1.30	1.29	1.06	1.69	0.013
Deinagkistrodon acutus	Dual	0.39	-0.20	0.95	2.07	1.72	2.60	0.285
Dinodon semicarinatus	Dual	0.69	0.27	1.16	1.36	1.07	1.71	0.027
Enhydris plumbea	Dual	0.38	-0.10	0.87	1.69	1.38	2.09	0.208
Micrurus fulvius	Dual	0.33	-0.08	0.64	1.39	1.17	1.74	0.157
Naja naja	Dual	-0.39	-0.76	0.27	2.21	1.72	2.56	0.332
Ovophis okinavensis	Dual	0.46	-0.03	0.98	1.84	1.50	2.25	0.217
Vantherophis slowinskii	Dual	0.69	0.32	1.09	1.07	0.84	1.33	0.012
Python regius	Dual	1.30	0.71	1.92	1.61	1.26	2.03	0.001
Tropidophis haetianus	Dual	-0.15	-0.45	0.23	1.35	1.07	1.61	0.537
Xenopeltis unicolor	Dual	0.85	0.40	1.29	1.30	1.04	1.64	0.008

p values less than 0.05 are printed in bold.

Comparisons and Phylogenetic Trends of G/A Gradients

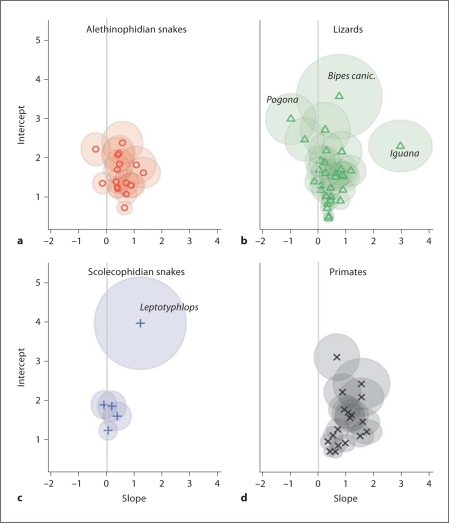
To demonstrate the broad taxonomic trends in G/A gradient characteristics, we first plotted the MLEs of the slopes and intercepts by taxonomic grouping; gradients previously calculated for the primates [Raina et al., 2005] were included for comparative purposes (fig. 3). The primates tend to have on average higher G/A slopes than squamate groups, although the variation observed in some squamate species far exceeds the range of the primate gradients. As a group, the lizard gradients tend to have lower slopes than the primate and alethinophidian snake gradients. Of the 4 taxonomic groupings (fig. 3), the alethinophidian snakes contain the least overall variation and tightest clustering of gradients, followed by the primates. Although the lizard and snake mitochondrial gradients tended to have lower slopes and often lower intercepts than those estimated for the primates, several species within the squamates stand out as having particularly extreme outlying values for gradient slopes and/or intercepts. The iguana (Iguana iguana) mitochondrial genome is estimated to have an extremely high slope (MLE = 2.96), and the amphisbaenian lizard Bipes canaliculatus had an extremely high intercept (MLE = 3.57). The blind snake Leptotyphlops also has an extremely high intercept (MLE = 3.97) and slope (MLE = 1.19), especially in comparison to the other 4 scolecophidian snake mt genomes included.

Fig. 3.

Plots of mitochondrial G/A gradient slope and intercept estimates, separated by taxonomic group. Slope and intercepts are shown as the maximum likelihood estimates (MLEs), with the shaded ovals representing the 95% confidence interval around the MLEs.

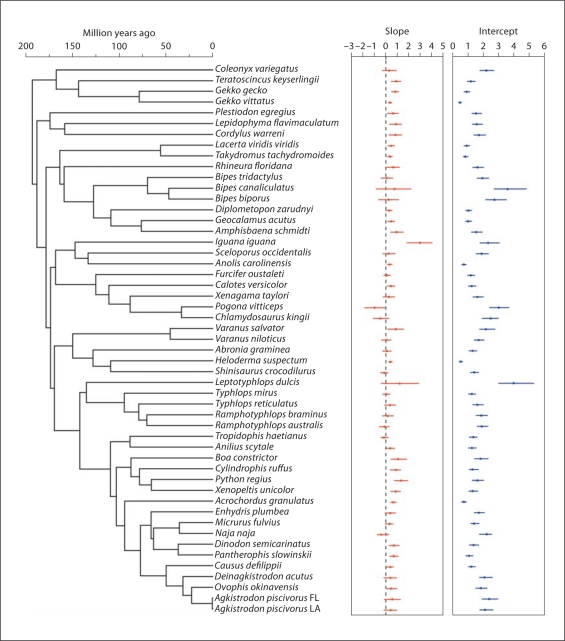
Visualization of the G/A gradient slope and intercept estimates in the context of the inferred phylogeny (and divergence timescale) provides further insight into the evolutionary dynamics of the G/A gradient characteristics (fig. 4). Overall, the estimated intercept values are more highly variable across the tree than the slope. In terms of phylogenetic conservatism, the intercept is also less phylogenetically consistent than the slope (fig. 4). From this visualization it is clear that substantial increases and decreases in the slope and intercept have occurred multiple times over the course of squamate evolution, and even within the more evolutionarily shallow snake clade (fig. 4).

Fig. 4.

Among-species variation in the G/A gradient slope and intercept presented in the context of the dated phylogeny of species analyzed. Slope and intercept values are presented as the MLE value (dot) and 95% confidence interval (lines).

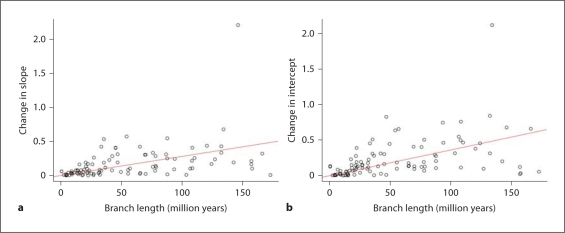
To quantitatively assess how rapidly the slope and intercept evolved, and statistically evaluate how consistent changes in the G/A gradient were with the phylogeny, we analysed the relationship between evolutionary distance (in time) and change in gradient characteristics. We reconstructed the ancestral G/A gradient slope and intercepts at all nodes, and regressed the change in gradient parameters versus evolutionary divergence (in millions of years). From these estimates, we infer that the gradient slope changed on average approximately 0.0028 units per million years, whereas the intercept parameter evolved more rapidly (0.0036 units per million years; fig. 5). In each plot, there is a single major outlier observed (fig. 5) – this outlier is the Iguana, which is extreme in both slope and intercept compared to the other squamates (e.g. fig. 3).

Fig. 5.

Plots of inferred change in G/A gradient slope (a) and intercept (b) versus divergence time (in millions of years), based on ancestral reconstructions of gradient characteristics from a Brownian motion model of G/A gradient slope and intercept evolution over the squamate tree. The slope of the regression line for the change in slope per time analysis (a) is 0.0028x, and for the change in intercept per time (b) is 0.0036; R² values for the change in slope (a) = 0.42, and change in intercept (b) = 0.50.

Although the regressions in figure 5 clearly indicate a linear relationship between the evolution of mutation gradient parameters and evolutionary time, a substantial amount of variation remains in the data (R² = 0.42 for slope; R² = 0.50 for intercept). We therefore conducted a randomization test in which the slope/intercept assignments were randomly permuted among different tips to assess the correspondence of gradient parameters with the phylogeny. The observed distribution of slope assignments was more likely than 998/1000 permutations, giving a p value of 0.002 for phylogenetic association of the gradient data. The observed distribution of intercept data was also significantly associated with the phylogeny, but had a larger p value (p = 0.021).

Clustering of Gradients and Relation to Phylogeny

Based on likelihood ratio tests of significance for adding model classes to the mixture models, a total of 11 model classes were highly justified (p < 0.01; table 4). After 7 or 8 classes, however, the posterior assignments of mt genome gradients to a particular class became progressively less certain, and the ability to visualize the clustering of similar gradients became more difficult. Because our primary goal was to generally explore the groupings of different gradients in relation to phylogeny, we decided to show the detailed results of the 6-class mixture model because with more classes, class assignments became weaker (based on posterior probability estimates) and more difficult to meaningfully interpret. The 6-class mixture model also was the model with the highest number of classes that was significant at p < 0.001 (table 4).

Table 4.

Results of mixture model clustering of squamate mitochondrial genome G/A gradients under different numbers of classes

Number of classes in mixture model	Mean likelihood of 6 runs	Maximum likelihood estimate (MLE)	2(ΔLnL)	p value
2	-62,986.31	-62,986.30
3	-62,761.78	-62,761.74	449.12	<0.01%
4	-62,627.20	-62,623.19	277.09	<0.01%
5	-62,548.66	-62,545.08	156.23	<0.01%
6	-62,521.17	-62,518.90	52.35	<0.01%
7	-62,508.57	-62,506.36	25.07	<1%
8	-62,498.46	-62,496.62	19.49	<1%
9	-62,491.22	-62,490.55	12.13	<1%
10	-62,486.05	-62,485.26	10.58	<1%
11	-62,482.73	-62,480.12	10.28	<1%
12	-62,479.70	-62,476.80	6.65	<2%
13	-62,478.85	-62,476.22	1.16	>5%
14	-62,478.85	-62,476.67	-0.92	>5%
15	-62,478.34	-62,475.57	2.20	>5%
16	-62,478.22	-62,476.20	-1.25	>5%
17	-62,478.42	-62,476.15	0.10	>5%
18	-62,478.98	-62,476.46	-0.62	>5%
19	-62,479.19	-62,476.69	-0.46	>5%
20	-62,481.26	-62,477.38	-1.38	>5%

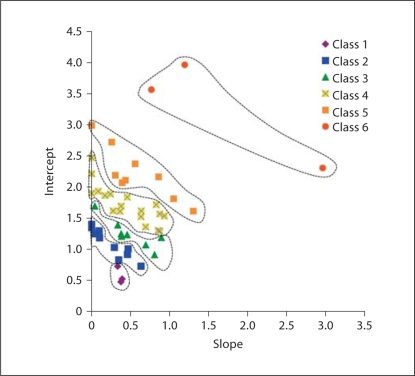
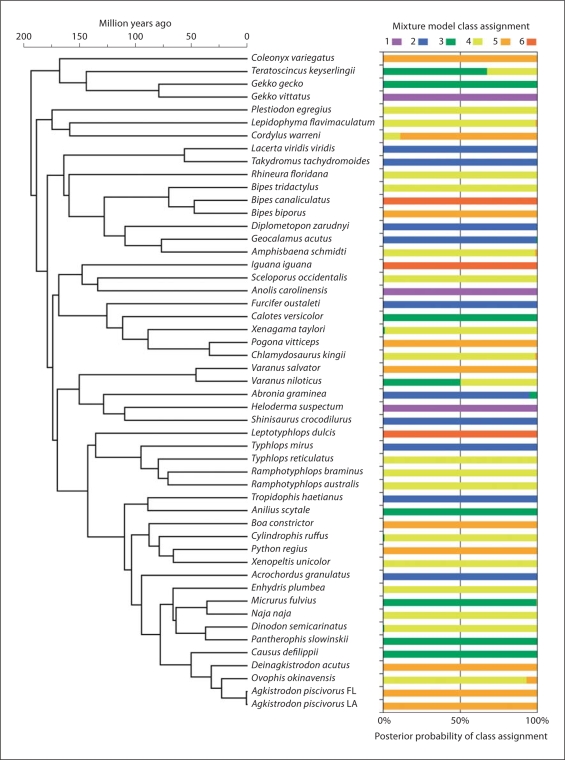
The clusters identified by the 6-class mixture model (fig. 6) are readily separated, and visualized as discrete groupings that tend to separate out as layers of increasing slope and intercept. When the mixture class assignments are visualized in the context of the squamate phylogeny, a striking number of examples of distantly related lineages with similar gradients are observed (fig. 7). These results highlight the degree to which gradient characteristics (represented by classes in this case) can converge among distantly related lineages, and also diverge substantially between some relatively closely related species.

Fig. 6.

Plot of the MLE slope and intercept estimates for squamate mitochondrial G/A gradients, clustered according to the results of a 6-class mixture model. Slope MLEs that were negative (and were not significant based on the null, zero slope model) were set to zero in this figure.

Fig. 7.

Phylogenetic distribution of G/A gradient classes, based on gradient class assignments from a 6-class mixture model, demonstrating widespread convergence of gradient characteristics across the phylogeny.

Discussion

Vertebrate mitochondrial genome sequences are important systems and heavily utilized for molecular evolutionary studies, phylogenetics, and taxonomy. A thorough understanding of nucleotide substitution gradients in vertebrate mitochondrial genomes is thus important for making advances in evolutionary model construction, accurate evolutionary inferences, and providing basic insight into the biology of the mitochondria. The results of this study provide new details on the evolution of the response of the G/A mutational gradient to the asymmetrical process of mitochondrial replication. We refer to evolution of this response as ‘gradient evolution’ and the combined slope and intercept as the ‘response curve’ [Faith and Pollock, 2003]. Building on previous work in the evolutionarily-shallow primate clade [Raina et al., 2005], our results here provide a novel perspective on gradient evolution and diversity over a much broader, evolutionarily deep scale in the squamate reptiles.

In the squamates, as with the primates, there is evidence that components of the response curve (i.e., slope and intercept) are for the most part phylogenetically consistent for closely related species and groups. In squamates, the family taxonomic level, for example, seems to often contain groupings of fairly similar gradients. We have also found, however, several extreme cases in which the response curve changed substantially between fairly close relatives; examples of this include comparisons between the extreme response curves of Iguana, Leptotyphlops, and Bipes, and their sister taxa. Despite the tendency for related species to have similar response curves, we find many examples where close relatives do not share similar response curves and sister taxa (in our tree) have response curves that do not cluster together.

As with the evolutionary variation in gradient characteristics, we found further evidence of substantial variation in the inferred usage of multiple control regions in snake and lizard species that possess dual CRs. Duplicate control regions, homogenized via concerted evolution, have evolved at least 4 times in squamates, with no evidence of being lost after their origin in any of these lineages; alethinophidian snakes, for example, have stably maintained dual CRs since they evolved in the ancestral alethinophidian lineage ∼100 million years ago (fig. 1). This is consistent with dual CRs conveying a selective functional advantage, possibly in either genome replication and/or transcriptional decoupling [Jiang et al., 2007]. Although the molecular details of how dual CRs may behave are not yet clear, our mixture model results suggest that many species may utilize both CRs to varying extents to initiate mitochondrial genome replication. In one species of lizard (Chlamydosaurus) and several lineages of snakes (Python, Acrochordus, Deinagkistrodon, Agkistrodon, Enhydris, Micrurus) there is evidence of a strong preference for the duplicate CR copy (CR2) in genome replication (fig. 2), implying that this duplicate copy does play an important functional role in at least some species.

To an even greater extent than previously documented for the primates [Raina et al., 2005], we observed substantial convergence in gradient characteristics between distantly related lineages of squamate reptiles. Since changes in equilibrium base frequencies are the necessary outcome of evolution of the mutation spectrum, and because evolution of base frequencies can dramatically mislead phylogenetic analyses, these results may explain some difficulties encountered inferring phylogenies of squamates using mt genomic data. In addition to interfering with phylogenetic inference, other effects of these gradients and their evolution that should be considered are the potential effect they have had on amino acid substitutions, whether they can be incorporated into codon-based models, and whether they substantially affect our ability to detect selection and adaptation in mitochondria using synonymous versus nonsynonymous substitution ratios. Gradients, and their evolutionary dynamics, may also affect how synonymous and nonsynonymous ratios are used in population genetics to understand how selection affects polymorphism levels.

Evidence for mitochondrial substitution gradients is extensive, and their ability to evolve rapidly through time is now even clearer, however, accounting for these gradients in the context of phylogenetic models of DNA evolution has not been accomplished. Our results demonstrate a degree of phylogenetic conservatism in gradient evolution, while also providing many examples of the exact opposite, including rapid radical changes and widespread convergence of the response curve. Thus, there is evidence that a gradient-based phylogenetic model that allowed for modifications of the gradient across branches would be reasonable. Based on our current analysis, incorporation of a gradient evolution model directly into phylogeny-based likelihood analysis would seem necessary to obtain accurate estimates and variances for topology, divergence time, and molecular evolutionary inferences.

This study provides important baseline information about how diverse gradients may be on a broad taxonomic scale, and how rapidly aspects of the gradient may evolve through time. Our evaluations of how gradients change through time and among species provide an important first step towards developing new phylogenetic evolutionary models that would reasonably account for the existence and evolutionary dynamics of gradients. Despite their evolutionary labiality, our findings also show that there is some phylogenetic component (i.e., heritability of gradients) of gradient characteristics; collectively these results suggest gradient evolution could feasibly be incorporated into a dynamic phylogenetic model. Although challenging, the development of such models would provide a major expected increase in the power and accuracy of evolutionary inferences for mitochondrial genomic data.

Supplementary Material

Supplemental Table S1

Fossil constraints utilized in this study. All priors were implemented. The Amphisbaenian calibration point is somewhat controversial, but it does not have any appreciable effect on our estimates of divergence times.