The Role of Plasmalemmal-Cortical Anchoring on the Stability of Transmembrane Electropores

Abstract

The structure of eukaryotic cells is maintained by a network of filamentous actin anchored subjacently to the plasma membrane. This structure is referred to as the actin cortex. We present a locally constrained surface tension model for electroporation in order to address the influence of plasmalemmal-cortical anchoring on electropore dynamics. This model predicts that stable electropores are possible under certain conditions. The existence of stable electropores has been suggested in several experimental studies. The electropore radius at which stability is achieved is a function of the characteristic radii of locally constrained regions about the plasma membrane. This model opens the possibility of using actin-modifying compounds to physically manipulate cortical density, thereby manipulating electroporation dynamics. It also underscores the need to improve electroporation models further by incorporating the influence of trans-electropore ionic and aqueous flow, cortical flexibility, transmembrane protein mobility, and active cellular wound healing mechanisms.

1 INTRODUCTION

In the presence of an externally applied pulsed electric field (PEF) of appropriate duration and intensity, a cell membrane will develop aqueous defects, or electropores [1–4]. This phenomenon, known as electroporation, has been widely used in medicine and biomedical research, for instance, to destroy unwanted cells through the induction of both apoptotic [5–7] and necrotic death [8–11]. While generation of transmembrane electropores can result in cell death, cells in a transiently electroporated state are competent for the transfer of behavior-modifying macromolecules such as peptides, full-length proteins, small interfering RNA (siRNA), messenger RNA (mRNA), and DNA [4, 12, 13]. Application of electroporation as a gene delivery technique was first pioneered in 1982 by Neumann and coworkers [14] and is now a standard method for gene transfection in both bacterial and eukaryotic cell lines [12].

The sustained and growing interest in electroporative gene delivery is in part due to the myriad advantages electroporation holds over other delivery techniques. For instance, viral gene delivery methods, while providing high efficiency, may induce immune reactions, cause genetic mutations, and are limited to delivering only shorter strands of genetic material [15, 16]. Gene delivery techniques involving nonvirally condensing DNA circumvents problems associated with viral delivery. However, the use of these condensation reagents provides poor delivery efficiency. In contrast, electroporation provides nonviral and relatively efficient delivery directly to the cytosol in a wide variety of cell types [16–21].

In instances where molecular delivery is intended to control or behaviorally modify cells, cells must remain viable. With regard to electroporative gene and drug delivery, maintenance of cell viability is predicated upon the ephemerality of transmembrane electropores. However, the factors governing electropore development, stability and closure remain elusive. Elucidation of these governing factors is required to advance electroporation towards high-efficiency gene and drug delivery.

Interest in improving our understanding of electropore dynamics served as the impetus for a number of electroporation modeling studies over the last few decades. The theory that transient aqueous pores develop in bilayer membranes as a result of PEF exposure was first described by Chizmadzhev and coworkers in a series of papers [22–28] published in 1979. This transient aqueous pore theory suggested a combined roll of thermal fluctuations and the locally induced electric fields across the membrane. This model was later expanded to include electrostatic effects as well as the role of a dynamic transmembrane potential [29]. Numerical models were later developed based on the Smoluchowski equation [30–31] in order to quantitatively predict dynamic parameters associated with electropore development. These theoretical models described an evolution of the distribution of electropores with different radii under the combined influence of thermal fluctuations, electropheretic forces from the applied electric field, and mechanical stresses within the cell membrane.

Joshi and Schoenbach [32] later described a dynamical electroporation model, also based on the Smoluchowski equation, which went beyond addressing electropore formation by investigating the important issue of electropore closure. Until that point, pore closure was only described as a one-step random process [33] requiring a number of potentially invalid approximations. Joshi and Schoenbach’s treatment of electropore growth, expansion, and closure was controlled by drift and diffusion in radius space and was subject to the influence of a temporally dynamic transmembrane potential. This model predicted a pulsewidth-dependant distribution in electropore radii where, during pulse application, electropores would grow in radius. Upon pulse cessation, electropores would have fates dependent on their radius relative to a threshold radius. Specifically, if pores remained under ~20 nm in radius, energetics would favor pore closure. If pores expanded beyond ~20 nm, pores would continue to expand even after pulse termination. This model was an important advance in theoretically understanding the nature by which electropores evolved and sealed.

In a later simulation study, Joshi, Schoenbach and coworkers [34] predicted that electropore resealing would consist of an initial fast process, followed by a relatively slower closure. With this model, they predicted a 0.1 ms time-window in which electropores remained mostly open for a cell exposed to a 4 μs, 10 kV/cm PEF. However, we have previously reported experimental evidence in HL60 human leukemia cells of stable electropores lasting for hundreds of seconds after exposure to a single, square 40 μs PEF. The electropores exhibited large enough radii to internalize approximately 88 million propidium iodide (PI) molecules per cell [35] (PI molecular weight is 668.4 Da). In three other recent studies [36–38], Pakhomov and coworkers also reported membrane permeabilization lasting hundreds of seconds using a novel patch-clamp technique in order to measure plasma membrane conductance. In [36], membrane ionic permeability was reported to last hundreds of seconds in GH3, PC-12, and Jurkat cells after exposure to single 60 ns square PEFs. They also reported the development of stable, long-lasting membrane conductance pores in GH3 and HeLa after exposure to single 60 ns PEFs and trains of 60 ns PEFs [37]. Note that no PI uptake was detected in these experiments until well after PEF exposure. Finally, in [38], long-lasting membrane conductance was reported in GH3 and CHO cells using both single 60 ns and single 600 ns PEFs.

In light of the experimental evidence substantiating the existence of prolonged, stable electroporation, Joshi and coworkers updated their electroporation model to include the dynamic effects of pore population, pore density, variable surface tension about the plasma membrane, dynamic transmembrane potential, and the finite conductivity of electropores [39,40]. This improved model allowed for dynamic self-adjustment of pore energy to changes in the pore density distribution, wherein, under certain conditions, stable electropores would develop. Here, we continue to explore the conditions contributing to electropore stability with a modified electroporation model that includes some of the structural complexities of the cell. Namely, we explore the possibility that anchoring of the plasma membrane to the actin cortex alters the dynamics of pore expansion in a manner contributing to electropore stability.

2 MODELING DETAILS

2.1 THE SMOLUCHOWSKI EQUATION-BASED MODEL

A generally accepted theoretical model of electroporation describes the evolution of the distribution of pores with different radii under the combined influences of thermal fluctuations, electrophoretic forces from an applied electric field, and mechanical stresses within the membrane. This model generally uses a form of the convection-diffusion-resection equation known as the Smoluchowski equation, and has been successful in predicting electrical parameters required for electroporative initiation as well as estimates of fractional aqueous area, changes in membrane capacitance, and the mean pore separation [30, 31].

The Smoluchowski equation describes the temporal evolution of the statistical distribution of membrane pores of different radii. It models pore distribution evolution as a diffusive process in pore radius space. The equation for the pore density distribution function u at time t for pores with radius r can be expressed as

$$u_t-D_{\text{p}}{\partial }_r\left(\frac{{\psi }_r}{k_{\text{B}}T}u+u_r\right)=S$$ (1)

where D_p is the pore diffusion constant in radii space, Ψ_r is the pore energy, k_B is the Boltzmann constant, and T is the absolute temperature. The pore generation rate, S, has been given as

$$S(r)=\frac{v_c{h}_{\text{m}}}{k_{\text{B}}T}{U}_{r}exp\left(-\frac{u}{k_{\text{B}}T}\right)-v_{\text{d}}H(r^{\ast }-r)$$ (2)

where v_c is the attempt rate density, h_m is the thickness of the lipid membrane, U is the hydrophobic pore energy, v_d is the frequency of lipid fluctuation, and r^* is the radius at which pores transition from hydrophobic to hydrophilic pores [29]. In [41], it has been shown that equations (1) and (2) can be reduced to the boundary problem when pore radius r is larger than the hydrophilicity transition radius r^*,

$$u_t-D_{\text{p}}{\partial }_r\left(\frac{{\epsilon }_r}{k_{\text{B}}T}u+u_r\right)=\frac{v_{\text{c}}{h}_{\text{m}}}{k_{\text{B}}T}{U}_{r}exp\left(-\frac{u}{k_{\text{B}}T}\right)$$ (3)

with the absorbing boundary condition u(r^*,t) = 0. Here ε is the hydrophilic pore energy as opposed to the hydrophobic pore energy, u in equation (2) as our interests are in hydrophilic pores, which can become large enough to facilitate the internalization of foreign molecules of interest (i.e., genes and drugs). In previously published models, the hydrophilic pore energy is expressed as the sum of four parts:

$$\epsilon ={\epsilon }_{\text{LT}}+{\epsilon }_{\text{ST}}+{\epsilon }_{\text{SR}}+{\epsilon }_{\text{EL}}$$ (4)

where ε_LT is the pore line tension energy, ε_ST is the membrane surface tension energy, ε_SR is the energy associated with the steric repulsion between lipid heads lining the pore, and ε_EL is the capacitive energy in the presence of a transmembrane potential arising from an applied electric field.

For pores with radii of several nanometers or larger, the energy due to steric repulsion between lipid heads is at least two orders of magnitude smaller than the energies associated with line tension and surface tension [42]. Therefore, this contribution to the total pore energy is generally neglected. The line tension energy around the circumference of a pore is modeled as:

$${\epsilon }_{\text{LT}}=2\pi r\gamma$$ (5)

where γ is the pore line tension energy (given as 1.8 × 10⁻¹¹ J/m in [31]). The surface tension energy can be described with the equation:

$${\epsilon }_{\text{ST}}=-\pi r^2\mathrm{\Gamma }$$ (6)

where Γ is the local surface tension of the cell membrane in the vicinity of the pore.

2.2 A LOCALLY CONSTRAINED SURFACE TENSION MODEL

In previous studies, Γ has been described with a global cell membrane surface tension model

$${\mathrm{\Gamma }}_{\text{global}}=2{\sigma }^{\prime }\left[1-{\left(\frac{1}{\frac{A_{\text{m}}^{\text{global}}}{A_{\text{p}}^{\text{global}}}-\frac{A_0^{\text{global}}}{A_0^{\text{global}}}}\right)}^2\right]$$ (7)

where σ′ is the interfacial energy per area of the hydrocarbon-water interface (0.02 J/m²) [34]. In equation (7), A_p^global is the cumulative membrane area filled by pores, A_m^global represents the global membrane area for a cell under zero electric field, and the cell’s global membrane surface area when the resting surface tension is zero is given as

$$A_0^{\text{global}}=4\pi R^2$$ (8)

where R is the cell’s radius. A conventional approach is to model the non-porated membrane using the estimate of A_m^global/A₀^global = 81/80 as this produces a resting equilibrium surface tension of 0.001 J/m². This appears to model the resting state cell membrane mechanics with reasonable accuracy [34].

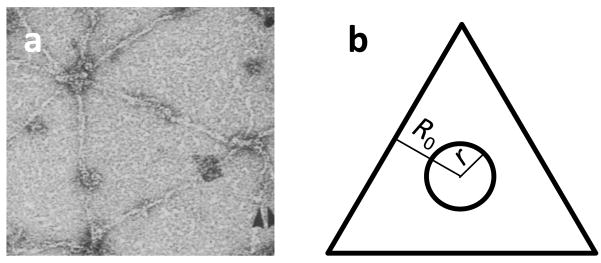
A challenge with this particular set of model assumptions is that it fails to predict the existence of stable, persistent pores once the externally applied electric field is terminated and the transmembrane potential returns to its equilibrium level. As described in the introduction, pores with radii less than a critical size will drift towards smaller radii until they reseal, while larger pores will increase in size without limit until the cell membrane’s integrity is lost [34, 43]. The reason for this can be seen through the examination of equations (5) through (7) which represent the dominant mechanical stress expressions for a cell membrane after electric field termination. The inability of the model to predict the existence of stable pore equilibria is due to the lack of a transition from a surface tension state to a surface compression state in equation (7), unless the total pore area becomes such a large percentage of the total membrane area that cell membrane integrity is impossible to maintain. We attribute this to the fact that in the conventional model for cell membrane surface tension, the local surface tension in the vicinity of a pore is determined through a calculation involving the global area of the membrane and the cumulative global area of the pores. However, in eukaryotic cells, there is a dense cross-linked network of filamentous actin (F-actin) subjacent to the plasma membrane [44]. This network, referred to as the actin cortex, is a critical structure for cell motility and the maintenance of cell morphology [45,46]. Requisite in these functions is the anchoring of the actin cortex to the plasma membrane which is achieved through linking and anchoring proteins [47,48]. An electron micrograph of the cytosolic face of an erythrocyte’s plasma membrane is provided in Figure 1a detailing anchoring proteins (dark punctuations) and filaments of the cell cortex (branches) [49].

Figure 1.

(a) An electron micrograph of the cytosolic face of an erythrocyte’s plasma membrane detailing anchoring proteins (dark puntations). Adapted and reprinted with authors’ permission from Figure 3 in [49]. (b) An illustration of the geometry used in the locally-constrained surface tension model. R₀ is the characteristic size of the triangular locally constrained region and r is the radius of the electropore.

The anchoring of the actin cortex to the plasma membrane is expected to constrain the membrane’s mechanical stress state. In fact, the plasma membrane is highly proteinaceous, composed of nearly 50% protein by mass. The existence of these transmembrane proteins, particularly those involved in cortical anchoring, likely have an effect on electropore dynamics. Therefore, we propose a locally constrained surface tension model to describe the local mechanical stress state arising from cortical anchoring on the evolutionary dynamics of electropores. This is an effective model that seeks to capture the basic observed phenomena with a simplified mathematical representation. Using Figure 1a as motivation, we model the cell’s elastic membrane as being locally constrained by a lattice of triangular regions with rigid boundaries with a nominal size A₀^local. Therefore, in the presence of a membrane pore, the elastic surface tension within one of these local triangular regions is modeled as

$${\mathrm{\Gamma }}_{\text{local}}=2{\sigma }^{\prime }\left[1-{\left(\frac{1}{\frac{A_{\text{m}}^{\text{local}}}{A_{\text{p}}^{\text{local}}}-\frac{A_0^{\text{local}}}{A_0^{\text{local}}}}\right)}^2\right]$$ (9)

Using the illustration in Figure 1b, we take $A_0^{\text{local}}=3\sqrt{3}{R}_0^2$ and $A_{\text{p}}^{\text{local}}=\pi r_{\text{pore}}^2$. We retain the approximations of σ′ = 0.02 J/m² and A_m^local/A₀^local = 81/80 to describe the at-rest (pore-free) membrane surface tension, due to their success in prior applications of the Smoluchowski equation model for electroporation.

3 RESULTS AND DISCUSSION

3.1 CONDITIONS FOR ELECTROPORE STABILITY

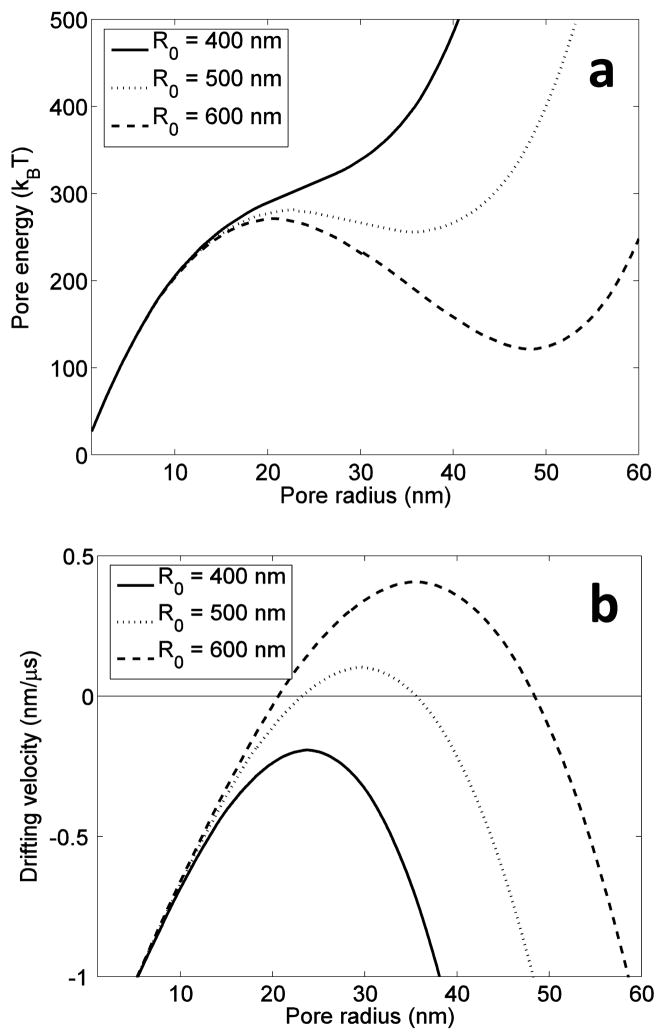
Figure 2 shows the calculated pore energy and drifting velocity as the locally constrained area is varied by choosing R₀ values of 400, 500, and 600 nm. In Figure 2a, for the case where R₀ is chosen to be 400 nm, pore energy monotonically increases with pore radius, precluding the possibility of a stable pore. That is, there are no energy suprema (minima or maxima) for the R₀ = 400 nm case. This can also be seen by inspecting Figure 2b where the pore drift velocity is non-zero for all radii. However, when R₀ is increased to 500 nm, it can be seen that there are two radii at which pore drift velocity is zero. At the first zero crossing (r ≈ 22 nm), while drift velocity is zero, the pore energy is at a local maximum and thus in only a metastable state. Small perturbations such as lipid thermal fluctuations will destabilize the pore. However, the next zero crossing (at r ≈ 38 nm) is at a local minimum on the pore energy plot, or, in an energy equilibrium state (see Figure 2a). Therefore, only large perturbations may destabilize the pore. For the case where R₀ = 600 nm, similar stability dynamics occur though at different radii. For instance, the first zero drift velocity occurs at r ≈ 19 nm (see Figure 2b). At this pore radius, the energy vs. pore radius curve (Figure 2a) indicates a metastable state for which small perturbations would destabilize the pore. However, again, at the next zero drift velocity point (r ≈ 50 nm), there is an energy equilibrium state and therefore the likelihood of a stable electropore.

Figure 2.

(a) Pore energy and (b) pore drift velocity as a function of pore radius for three different locally constrained surface tension areas associated with R₀ = 400, 500, and 600 nm.

The equilibrium points in Figure 2 can be explained physically. After electropore creation and cessation of the applied electric field, there are two dominating, dynamic forces governing electropore evolution. The first is the contractile force associated with the line tension energy while the second is the expansive force associated with membrane surface tension. Equilibrium points arise when these opposing forces are equal. Electropore line tension energy is provided in equation (5) and is linearly proportional to the pore radius, r. Therefore, the contractile force associated with the pore line tension energy is constant and independent of pore radius, r (force is the gradient of energy). The force associated with membrane surface tension energy can be derived in a similar manner and importantly, can be equal to the contractile force associated with pore line tension energy at multiple radii, depending on the size of the locally constrained surface area A₀^local (which is a function of R₀). For instance, when R₀ = 600, these opposing forces are equal at two radii: at approximately 19 nm and 50 nm. The first radius experiencing force equality is associated with the transition in the dominant forces: from contractile pore line tension force to the expansive force associated with membrane surface tension. At this radius, stability will never be achieved since small perturbations in energy will either shift the pore radius to a smaller value where it will continue to contract or shift the pore radius to a larger value where it will expand towards the larger radii. Thus, this equilibrium radius will be referred to as the metastable radius. The second equilibrium radius is associated with a reduction in the expansive membrane surface tension force due to a relief in surface tension within the locally constrained area. At this radius, however, smaller and larger radii move the pore radius back towards the equilibrium radius, resulting in a stable electropore. That is, smaller radii are subject to net expansive or tensile forces while larger radii are subject to net contractile or compressive forces, resulting in a stable radius.

For larger locally constrained regions (that is, larger values of R₀), similar dynamics will manifest. For these larger values of R₀, the stable radius will be larger. In previous models where a globally dependent surface tension is employed, this theoretical stability is still a possibility. However, when using a using a globally dependent surface tension, the stable radius would be too large for the cell to maintain proper function. When the locally constrained surface tension model is employed, the stable radius is significantly reduced to radii that may be biophysically realizable.

3.2 CONSISTENCY WITH EXPERIMENTS

The model presented here suggests that anchoring of the actin cortex to the plasma membrane alters electropore dynamics in a manner that allows for electropore stability. Prolonged electropores have been reported in several experimental studies [35–38] using different metrics, for a variety of different cell types, and using a variety of different PEF parameters. In each of these experimental studies, electropores were reported to recover after hundreds of seconds. Though not included in this model, it is possible that this resealing is aided by active wound-healing mechanisms. Eukaryotic cells posses the ability to actively repair membrane and cytoskeletal damage in a calcium-dependent process [50–52]. This active repair response initiates within seconds of membrane damage, allowing normal membrane function to recover after several minutes [53–55]. Because this active repair response corresponds to timeframes similar to those observed for prolonged electroporation [35–38], it is likely a factor governing electropore persistence and closure.

The stable electropore radii predicted in our simulation results (Figure 2) suggest that prolonged uptake of molecules such as PI is possible. In fact, this prolonged uptake was experimentally observed in [35]. However, the relatively large stable electropore radii predicted in these simulations would also allow for prolonged uptake of larger molecules such as peptides, proteins, and DNA. While this could be very advantageous in regard to high efficiency gene and drug delivery, prolonged uptake of such molecules has not yet been reported. It is important to note that this study was a theoretical exercise geared towards developing an electroporation model based on cellular structures that predicts the development of stable electropores. This model introduces an important parameter—the characteristic area of a locally constrained region (represented by the parameter R₀)—that, in part, governs the radius at which an electropore would stabilize.

The data presented here suggest that the generation of electropores smaller than a metstable radius will collapse whereas electropores larger than that radius will expand to a larger stable radius. The model does not account for the widely reported phenomenon of electropores expanding beyond recovery. However, in regard to irrecoverable electroporation, we believe the modified electroporation model presented here is, in part, qualitatively consistent experimental observations. For instance, in a recent experimental study [35], we reported a four-stage, electric-field-dependent progression in observable electroporative PI uptake: (i) at low electric field values, no PI uptake was observed; (ii) at higher electric fields, a low-level decelerating uptake was observed, lasting for hundreds of seconds before terminating; (iii) at even higher fields, low-level uptake was observed followed by abrupt onsets of accelerated uptake that are delayed sometimes hundreds of seconds after PEF exposure; and (iv) at extreme field intensities, immediate, high-level, accelerating uptake was observed.

Uptake signature (i) can be explained by either the absence of electroporation or by the development of electropores that are too small and short-lived to result in detectible amounts of internalized PI (i.e., if electropores develop, they have radii smaller than the metastable radius). Uptake signature (ii) can be explained by the development of electropores with radii greater than the metastable radius, resulting in prolonged and detectible PI uptake. In this case, the relatively low electric field intensity avoids irrecoverable damage and/or membrane poration is not overly extensive allowing the cell to recover (possibly with the aid of active wound-healing mechanisms). For uptake signature (iii), stable electropores develop, resulting in prolonged molecular uptake. Abrupt, delayed increases in molecular uptake may be influenced by a number of factors including electropore coalescence, cytoskeletal damage, damage to would healing apparatuses, and the inability of the cell to maintain ionic gradients about the membrane. All of these factors are more likely when using higher electric field strengths. Finally, uptake signature (iv) is likely due to extreme electropore expansion during electric field exposure, perhaps beyond the bounds of the locally constrained surface tension regions about the plasma membrane. This would result in electropore dynamics unbound by locally constrained surface tensions, allowing for electropore expansion beyond recovery and immediate, high-level molecular uptake. It is also likely that severe electric field exposure and the development of very large transmembrane pores would impede active wound-healing.

3.3 USE OF ACTIN-MODULATORY AGENTS

The actin cortex is a key cellular component in resisting external stresses [56] and setting the plasma membrane tension. In fact, in addition to differences in anchoring and transmembrane protein density, it is likely that differences in the actin cortex (and therefore differences in the initial plasma membrane surface tension), is a reason why electroporation dynamics are reportedly so different for different cell types. The actin cortex may be readily manipulated using actin-modulatory compounds such as latrunculin and jasplakinolide. Latrunculin, for instance, reduces cellular filamentous actin (F-actin) by inhibiting actin monomer polymerization. This is achieved by its competitive binding to free actin monomers [57]. Therefore, the actin cortex density is significantly reduced through latrunculin treatment. Jasplakinolide, on the other hand, stabilizes actin microfilaments by binding to the negative end of F-actin, preventing actin filament disassembly [58]. It also enhances actin nucleation, thus increasing actin cortical density. Xenopus oocytes treated with latruculin or jasplakinolide are noticeably squishy or firm, respectively, when compressed using forceps [59].

These actin-modulatory compounds may be useful in controlling electropore dynamics and therefore the electroporative delivery of molecules to cells. For example, if the anchoring and rigidity of the actin cortex is increased through jasplakinolide treatment, the stable electropore radius would be reduced to radii that may be more manageable by the cell’s active would-healing mechanisms. On the other hand, treatment of cells with latrunculin may result in unmanageably large electropores by increasing the effective sizes locally-constrained surface tension regions. This would make the cell less likely to survive electroporation. This could be pragmatically applied to more efficiently killing unwanted cells such as cancers and contaminants such as bacteria.

While the possibility of manipulating the radius of stable electopores is exciting in that is may lead to regulated electroporative gene and drug delivery efficiency, several considerations are not addressed here. First, much remains unknown on how the actin cortex is regulated and how it is specifically attached to the plasma membrane [47]. Also, though transmembrane anchoring proteins are responsible for this attachment, much remains unknown regarding the movement of transmembrane proteins in biological membranes [60]. Research is now reinforcing the idea that molecular movement within biological membranes is much more complex than the traditional fluid mosaic model [61]. Knowledge of these specifics is required to improve the current model. While these above issues will be difficult to model accurately, they should be taken into account when comparing model predictions and experimental observations.

3.4 OTHER FACTORS INFLUENCING ELECTROPORE STABILITY

In addition to plasmalemmal-cortical anchoring, a number of other factors may influence electropore stability. For instance, it is likely that the pressure differential across the plasma membrane will induce aqueous flow through electropores once they have developed. This trans-electropore flow may contribute pneumatic forces to the model described here. Additionally, the ionic differential across the plasma membrane will induce ionic flows, or electrical currents, through electropores. These currents would likely contribute electro-repulsive forces to the model described here. Incorporation of these contributions will be the focus of future work.

4 SUMMARY AND CONCLUSIONS

A number of recent experiments support the idea that for certain conditions, electropores can remain stable and open for significant intervals of time (i.e., minutes) after the application of a pulsed electric field. The conventional Smoluchowski model of electroporation does not allow a mathematical solution consistent with this observed phenomenon. However, we have shown that a small modification to this model, gained by introducing a locally constrained surface tension, instead of a surface tension determined by the cell’s global membrane area and total pore area, allows for stable electropores. This locally constrained surface tension model is inspired by the physical mechanism by which a eukaryotic cell maintains its structure—the anchoring of the plasma membrane to the actin cortex. Calculations indicated that the area of locally constrained surface tension determines the electropore radius at which an electropore would remain stable. This model leaves open exciting possibilities for manipulating electroporative dynamics by altering cortical density through the use of actin-modulatory agents such as latrunculin and jasplakinolide. While this model represents a step forward in understanding how the complexities of cellular structures influence electroporation dynamics, several considerations remain neglected. Namely, the role of trans-electropore aqueous and ionic flow, cortical flexibility, the specific dynamics of transmembrane protein motility, and the active wound healing mechanisms of the cell are topics for future investigations.

Biographies

Stephen M. Kennedy (S’04) received the B.S. (with distinction) and M.S. degrees in electrical engineering from the University of Wisconsin, Madison, USA, in 2004 and 2006, respectively. He is currently pursuing the Ph.D. degree in electrical engineering at the University of Wisconsin, Madison, as a National Institutes of Health (NIH) Predoctoral Fellow. He was with Science Applications International Cooperation (SAIC) from 2000–2002 and with General Electric Medical Systems (GEMS) from 2003–2004. His research interests include electrically inspired techniques for regulating gene and drug delivery and electromagnetic approaches for directing cell behaviors and interactions important in stem-cell-based tissue engineering. Mr. Kennedy was the recipient of the National Institutes of Health (NIH) Ruth L. Kirschstein National Research Service Award (NRSA) in 2008, the 2008 Wisconsin Interdisciplinary Stem Cell Fellowship in Bioengineering, the 2008 University of Wisconsin Gerald Holdridge Award for Excellence in Teaching, and multiple scientific paper competition awards. He is a member of the Bioelectromagnetics Society and Tau Beta Pi engineering honor society.

Zhen Ji (S’02 M’07) received the B.S. degree from Tsinghua University, Beijing, China, in 1994, the M.S. degree from Rose-Hulman Institute of Technology, Terre Haute, IN, in 2001, and the Ph.D. degree from the University of Wisconsin, Madison, USA, in 2007, all in electrical engineering. He is currently a research associate with the Department of Medical Physics at the University of Wisconsin School of Medicine and Public Health, Madison. Dr. Ji’s research interests include biological applications of computational electromagnetics, pulsed-electric-field-induced biological cell membrane dynamics, and fetal cardiac electromechanical function analysis.

Nicole B. Rockweiler was born in Madison, WI. USA, Ms. Rockweiler is currently pursuing the B.S. degrees in biomedical engineering and mathematics from Washington University, Saint Louis, MO. Her research interests include biochemistry and molecular biophysics. Ms. Rockweiler was the recipient of the Washington University Dean’s Honorary Scholarship.

Adam R. Hahn was born in Madison, WI. USA, He is currently pursuing the B.S. degrees in electrical engineering and chemistry at the University of Wisconsin, Madison. His research interests include applications of electroporation. Mr. Hahn was the recipient of a 2009 Wisconsin Hilldale Undergraduate Research Fellowship, the 2008 Fred W. and Josephine Colbeck Scholarship, the University of Wisconsin Grainger Textbook Scholarship, and the 2008 Claude and Dora Richardson Engineering Scholarship.

John H. Booske (S’82-M’85-SM’93-F’07) received the Ph.D. degree in nuclear engineering from the University of Michigan, Ann Arbor, USA, in 1985. He was a Research Scientist at the University of Maryland, College Park, from 1985 to 1989, researching magnetically-confined hot ion plasmas and sheet-electron-beam free electron lasers. In 1990, he joined the University of Wisconsin’s Electrical and Computer Engineering faculty, where he currently holds the title of Duane H. and Dorothy M. Bleumke Professor of Engineering. From 2001 to 2005, he served as a Director of the University of Wisconsin’s Interdisciplinary Material Science Program. His research interests include the experimental and theoretical study of coherent electromagnetic radiation sources and their applications, spanning the RF, microwave, millimeter-wave and THz regimes. Recent research activities include vacuum electronics, microfabrication of millimeterwave and THz-regime sources and components, and biological applications of electromagnetic fields. He has been the Guest Editor of the IEEE Transactions on Plasma Science, a co-editor of the book Microwave and Radio Frequency Applications (American Ceramic Society, Westerville, OH, 2003), and coeditor of the book Microwave and Millimeter-Wave Power Electronics (IEEE/Wiley, 2005). Professor Booske received the University of Wisconsin Vilas Associate Award for research and the U.S. National Science Foundation (NSF) Presidential Young Investigator Award. He has received many teaching awards, served as co-Director of a U.S. DoD MURI99 consortium on Innovative Microwave Vacuum Electronics, and is Director of a U.S. DoD MURI04 consortium on cathode field emission and RF window breakdown in high power microwave sources.

Susan C. Hagness (S’91-M’98-SM’04-F’09) received the B.S. (with highest honors) and Ph.D. degrees in electrical engineering from the Northwestern University, Evanston, IL, in 1993 and 1998, respectively. While working toward the Ph.D. degree, she was a National Science Foundation (NSF) Graduate Fellow and a Tau Beta Pi Spencer Fellow. Since August 1998, she has been at the University of Wisconsin, Madison, USA, where she currently holds the title of Philip D. Reed Professor in Electrical and Computer Engineering, and is also a faculty affiliate of the Department of Biomedical Engineering. Her research interests in bioelectromagnetics include microwave imaging, sensing, and thermal therapy techniques, ultrawideband radar, dielectric spectroscopy, inverse scattering, electroporative uptake kinetics, and finite-difference time-domain (FDTD) theory and applications in biology and medicine. Dr. Hagness was an elected member of the IEEE Antennas and Propagation Society (AP-S) Administrative Committee from 2003 to 2005 and an Associate Editor for the IEEE Antennas and Wireless Propagation Letters from 2002 to 2007. She is currently the Chair for Commission K of the United States National Committee (USNC) of the International Union of Radio Science (URSI) and the Chair of the New Technology Directions Committee for the IEEE AP-S. She was the recipient of the Presidential Early Career Award for Scientists and Engineers presented by the White House in 2000. In 2002, she was named one of the 100 top young innovators in science and engineering in the world by the Massachusetts Institute of Technology (MIT) Technology Review Magazine. She received the University of Wisconsin Emil Steiger Distinguished Teaching Award in 2003. She received the IEEE Engineering in Medicine and Biology Society Early Career Achievement Award in 2004, the URSI Isaac Koga Gold Medal in 2005, the IEEE Transactions on Biomedical Engineering Outstanding Paper Award in 2007, and the IEEE Education Society’s Mac E. Van Valkenburg Early Career Teaching Award in 2007.