Evidence for equilibrium iron isotope fractionation by nitrate-reducing iron(II)-oxidizing bacteria

Abstract

Iron isotope fractionations produced during chemical and biological Fe(II) oxidation are sensitive to the proportions and nature of dissolved and solid-phase Fe species present, as well as the extent of isotopic exchange between precipitates and aqueous Fe. Iron isotopes therefore potentially constrain the mechanisms and pathways of Fe redox transformations in modern and ancient environments. In the present study, we followed in batch experiments Fe isotope fractionations between Fe(II)_aq and Fe(III) oxide/hydroxide precipitates produced by the Fe(III) mineral encrusting, nitrate-reducing, Fe(II)-oxidizing Acidovorax sp. strain BoFeN1. Isotopic fractionation in ⁵⁶Fe/⁵⁴Fe approached that expected for equilibrium conditions, assuming an equilibrium Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation factor of +3.0 ‰. Previous studies have shown that Fe(II) oxidation by this Acidovorax strain occurs in the periplasm, and we propose that Fe isotope equilibrium is maintained through redox cycling via coupled electron and atom exchange between Fe(II)_aq and Fe(III) precipitates in the contained environment of the periplasm. In addition to the apparent equilibrium isotopic fractionation, these experiments also record the kinetic effects of initial rapid oxidation, and possible phase transformations of the Fe(III) precipitates. Attainment of Fe isotope equilibrium between Fe(III) oxide/hydroxide precipitates and Fe(II)_aq by neutrophilic, Fe(II)-oxidizing bacteria or through abiologic Fe(II)_aq oxidation is generally not expected or observed, because the poor solubility of their metabolic product, i.e. Fe(III), usually leads to rapid precipitation of Fe(III) minerals, and hence expression of a kinetic fractionation upon precipitation; in the absence of redox cycling between Fe(II)_aq and precipitate, kinetic isotope fractionations are likely to be retained. These results highlight the distinct Fe isotope fractionations that are produced by different pathways of biological and abiological Fe(II) oxidation.

1 Introduction

Iron redox cycling is a significant process in many aquatic and terrestrial environments and plays a key role in determining the fate of nutrients (e.g., P, N), metal ions (e.g., arsenate and chromate), and organic compounds (Ehrlich, 2008; Zachara et al., 2001; Neubauer et al., 2008). At neutral pH, Fe(III) is poorly soluble and mostly present in the form of iron (hydr)oxides such as ferrihydrite (Fe(OH)₃), goethite (FeOOH), hematite (Fe₂O₃), and magnetite (Fe₃O₄) (Cornell and Schwertmann, 2003). Fe(II) is stable under anoxic conditions and present either as dissolved species or in the form of iron(II) minerals such as Fe-carbonate (e.g., siderite, FeCO₃) or Fe-phosphate (e.g., vivianite, Fe₃(PO₄)₂). Abiotic pathways of Fe redox cycling include chemical reduction of Fe(III) (e.g., by sulfide) and chemical oxidation of Fe(II) (e.g., by O₂). Iron redox cycling may also be driven by biologically catalyzed processes (Kappler and Straub, 2005; Weber et al., 2006). Microorganisms are known to be able to respire Fe(III) minerals by transferring electrons stemming from oxidation of hydrogen or organic electron donors to Fe(III) (Lovley, 2004). Additionally, neutrophilic, aerobic Fe(II)-oxidizing microorganisms can compete with chemical oxidation of Fe(II) by O₂ (Emerson and Moyer, 1997). Even under neutrophilic anoxic conditions, bacteria can grow via oxidation of Fe(II) either by using light as an energy source for CO₂-fixation (phototrophic Fe(II) oxidation; Widdel et al., 1993; Ehrenreich and Widdel, 1994), or by using nitrate as an electron acceptor (nitrate-dependent Fe(II) oxidation; Straub et al., 1996; Hafenbradl et al., 1996).

Both aerobic and anaerobic iron-oxidizing microorganisms that oxidize Fe(II) at circumneutral pH face the problem of the extremely poor solubility of Fe(III), one of the end products of their metabolism. At circumneutral pH, the ambient concentration of dissolved Fe(III) in solution is typically in the nM to μM range (Stumm and Morgan 1995), and at this pH, the Fe(III) minerals formed during precipitation are positively charged due to their high points of net zero charge (pzc ~7.9 for ferrihydrite and pzc ~9.0–9.4 for goethite; Schwertmann and Cornell, 2000; pzc ~8.5 for hematite; Jeon et al., 2004). If formed by microbial Fe(II) oxidation, Fe(III) ions, Fe(III) colloids and Fe(III) minerals would therefore be expected to adsorb to the cell surface, which is in general negatively charged due to a high content of carboxylic, phosphoryl and/or hydroxyl groups. This could lead to cell encrustation, potentially limiting the diffusion of substrates and nutrients to the cell, impairing uptake of these compounds across the membrane, and, as a consequence, leading to stagnation of cell metabolism and eventually to cell death.

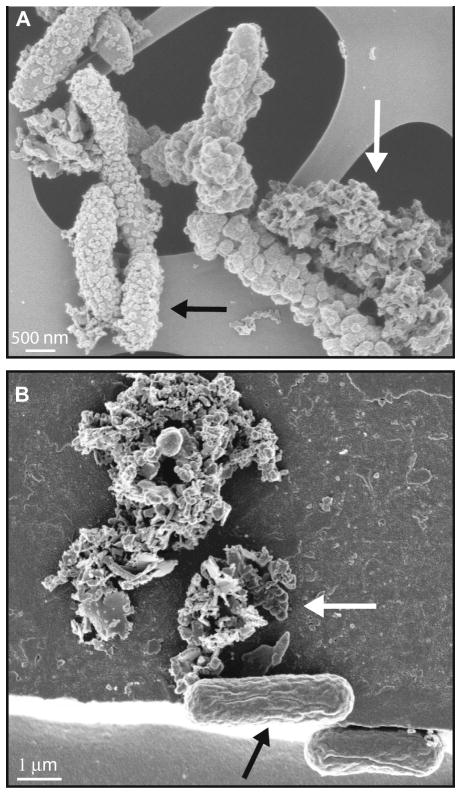
For stalk- or sheath-forming aerobic Fe(II)-oxidizing bacteria of the genera Gallionella and Leptothrix, it was suggested that microbially produced and excreted organic matrices are used for extra-cellular precipitation/binding of Fe(III) minerals produced during aerobic Fe(II) oxidation (Hanert 1981; Emerson and Revsbech 1994). This, however, still leaves open the questions i) where is Fe(II) oxidized (in the cytoplasm, in the periplasm, or at the cell surface?), and ii) in the case of intracellular oxidation, how is Fe(III) transported from the cytoplasm to the cell surface and the organic templates? Abiologic Fe(II) oxidation is often envisioned to occur at circum-neutral pH via a “two-step-model”, where Fe(II) oxidation generates an intermediate Fe(III) species that then precipitates in a second step as an Fe(III) mineral, but it remains unknown if neutrophilic Fe(II)-oxidizing bacteria follow the same path. Recent studies indicate that different strains of neutrophilic Fe(II)-oxidizing microorganisms utilize different mechanisms and exhibit different biomineralization patterns, particularly with respect to the importance of dissolved Fe(III) (Kappler and Newman, 2004; Kappler et al., 2005; Hegler et al., 2008; Miot et al., 2009, Schaedler et al., 2009). For example, the nitrate-reducing, iron-oxidizing β-proteobacterial strain BoFeN1 becomes encrusted with Fe(III) minerals as iron oxidation proceeds (Kappler et al., 2005; Schaedler et al., 2009; Miot et al., 2009; Fig. 1), whereas the photosynthetic iron-oxidizing purple bacteria Rhodobacter ferroxidans strain SW2 (Ehrenreich and Widdel, 1994) and Thiodictyon sp. strain F4 (Croal et al., 2004; Fig. 1) do not encrust, even after complete oxidation of Fe(II) (Kappler and Newman, 2004; Schaedler et al., 2009). It has been suggested that this is related to differences in Fe(II) oxidation and Fe(III) stabilization (solubilization) mechanisms, yet the exact mechanisms accounting for these two distinct phenotypes are still poorly understood.

Fig. 1.

Comparison of scanning electron micrographs of circum-neutral pH Fe(II)-oxidizing bacteria. A) Nitrate-reducing Fe(II)-oxidizing Acidovorax sp. strain BoFeN1 cells heavily encrusted in iron(III) (hydr)oxides (black arrow) plus extracellular Fe(III) mineral precipitates (filaments – white arrow). B) Phototrophic Fe(II)-oxidizer Thiodictyon sp. strain F4 (black arrow) associated with, but not encrusted in iron(III) (hydr)oxides (white arrow). Thiodictyon sp. strain F4 was used in the Fe-isotope study of phototrophic Fe(II)-oxidizers by Croal et al. (2004).

Bacterial species may use several strategies to avoid encrustation of the cell surface with the Fe(III) minerals they produce, although these are only speculative (Schaedler et al., 2009). It was suggested that phototrophic Fe(II)-oxidizing bacteria oxidize Fe(II) at the cell surface (Ehrenreich and Widdel, 1994), allowing Fe(III) minerals to fall away from the cell surface, but this does not explain how the electrons are then transported from the outside to the inside of the cell and why the positively charged Fe(III) minerals do not bind to the negatively charged cell surface. Recently it was proposed that Fe(II) oxidation by the photoautotrophic strains “Rhodobacter ferrooxidans” strain SW2 and Rhodopseudomonas palustris strain TIE-1, occurs in the periplasm of the cells (Croal et al. 2007; Jiao et al. 2007). Because cell encrustation was not observed in these strains (Kappler and Newman 2004; Jiao et al. 2005; Schaedler et al., 2009), it remains unclear how Fe(III) is transported after periplasmic Fe(II) oxidation to the cell exterior and then away from the cells. The possibility of a low-pH microenvironment was suggested for strain SW2 (Kappler and Newman 2004), as well as for neutrophilic aerobic Fe(II)-oxidizers (Sobolev and Roden 2001). A lower pH would potentially keep Fe(III) in solution in close cell proximity and lead to controlled Fe(III) mineral precipitation at a certain distance from the cell surface. A role for organic ligands as complexing and solubilization agents has also been postulated (Croal et al. 2004), although no evidence for such molecules has been found so far.

Isotopic studies have great potential for providing insight into bacterial redox cycling, as has been demonstrated, for example, using S and Fe isotopes (e.g. Farquhar and Wing, 2003; Johnson et al., 2004a; Johnson et al., 2004b). In most low-temperature aqueous environments, the largest Fe isotope fractionations occur between Fe(III) and Fe(II) species (e.g. Schauble et al., 2001; Welch et al., 2003). In addition, chloride speciation may change Fe isotope fractionations on the order of 0.2 ‰/M Cl⁻ in ⁵⁶Fe/⁵⁴Fe ratios (e.g., Hill and Schauble, 2008), and isotopic fractionations up to 1 ‰ are predicted or measured between aqueous Fe and Fe complexed by organic ligands (e.g., Domagal-Goldman and Kubicki, 2008; Dideriksen et al., 2008). Iron isotope fractionation during bacterial Fe(II) oxidation has been investigated in experiments on anaerobic photosynthetic Fe(II)-oxidizing bacteria at circum-neutral pH, where CO₂ was the terminal electron acceptor (Croal et al., 2004). The Fe isotope fractionations produced by bacterial Fe(II) oxidation in acidic and oxic conditions have been studied by Balci et al. (2006), where O₂ was the terminal electron acceptor and significant quantities of dissolved Fe(III) were produced. In the experiments of Croal et al. (2004) and Balci et al. (2006), the ferric hydroxide precipitates did not encrust the cells, and in the case of the work by Balci et al. (2006), Fe(II) oxidation clearly occurred via a two-step process of oxidation of Fe(II) to Fe(III), followed by precipitation of Fe(III) as Fe(OH)₃. Croal et al. (2004) inferred oxidation and precipitation via a two-step process, but the presence of dissolved Fe(III) was not detected in the ambient solution. Because isotopic exchange between Fe(III)_aq and Fe(II)_aq is very rapid (Johnson et al., 2002; Welch et al., 2003), where complete isotopic exchange may occur in less than one minute, isotopic equilibrium is expected to be maintained between aqueous Fe species even under conditions of extremely rapid oxidation, although kinetic fractionations produced upon precipitation may still occur (Beard and Johnson, 2004), indicating the overall isotopic fractionation between ferric oxide/hydroxide precipitates and Fe(II)_aq may be dependent upon precipitation rates.

The goal of the current study was to determine the Fe isotope fractionations produced via biological oxidation of Fe(II) by a recently isolated nitrate-dependent Fe(II)-oxidizing strain (Acidovorax sp. strain BoFeN1; Kappler at al, 2005). Relative to the previous studies of Croal et al. (2004) and Balci et al. (2006), where the cells did not become encrusted with ferric hydroxide mineral products, oxidation of Fe(II) by Acidovorax forms crusts of iron(III) (hydr)oxides in the periplasm and at the cell surface as Fe(II) oxidation proceeds, suggesting a potentially different pathway for Fe(III) mineral formation compared to previous studies (Miot et al. (2009)). The results reported here indicate that different Fe isotope fractionations may be produced by a variety of microbial Fe(II) oxidation processes, and these may depend on the extent of Fe redox cycling in intra-cellular micro environments.

2 Methods

2.1. Media and growth conditions

Acidovorax sp. strain BoFeN1 was cultivated as described previously (Kappler et al., 2005). The anoxic medium was buffered at pH 6.8 with bicarbonate (30 mM). Vitamin and trace-element solutions (1 ml each) and a vitamin B₁₂ solution (1 ml) were added anoxically under a gas stream of N₂:CO₂ (v:v, 80:20) (for details and concentrations see Ehrenreich and Widdel, 1994). The medium was transferred into an anoxic glove box, and 5–10 ml of an anoxic 1 M FeCl₂ stock solution were added followed by precipitation of a whitish-grey precipitate, which, based on earlier work (Croal et al., 2004), probably consisted of vivianite and siderite that formed from phosphate and bicarbonate present in the medium. After 24 h the medium was filtered (0.2 μm, cellulose nitrate, Millipore), leaving a clear solution that contained ~2–6 mM of aqueous Fe(II). In uninoculated controls, no further precipitation was observed for the duration of the incubations. This method allowed isotope analysis of the Fe(III) precipitates formed by the Fe(II)-oxidizing bacteria in the absence of Fe(II) precipitates in the background, which is critical for determining the actual Fe(II)_aq-ferric oxide/hydroxide fractionation factors. The medium (25 ml) was transferred anoxically into 58-ml serum bottles that were closed with butyl rubber stoppers, crimped and flushed with N₂-CO₂ (v:v, 80:20). Acetate (2 mM final concentration) as organic co-substrate and nitrate (5 mM final concentration) as electron acceptor were added from anoxic stock solutions (see also Kappler et al., 2005). Cultures were incubated at 16 and 30°C for 21 days.

Iron speciation analysis for the filtered medium was calculated using Geochemists Workbench 6.05 (minteq database). The calculation yielded [Fe(H₂O)₆]²⁺ (81.6%), [FeHCO₃]⁺ (10.1%), FeSO_4aq (5.6%), [Fe-acetate]⁺ (1.6%), [FeCl]⁺ (0.4%), [FeHPO₄]_aq (0.4%), [FeH₂PO4]⁺ (0.2%), and [FeOH]⁺ (0.1%) as the main aqueous Fe species present. These calculations indicate that the Fe isotope effects due to variable aqueous speciation were negligible, and the measured Fe(II)_aq - ferric oxide/hydroxide fractionations may be assumed to be equal to [Fe(H₂O)₆]²⁺ - ferric oxide/hydroxide fractionations. Although the second most abundant species is [FeHCO₃]⁺, we infer only small fractionations between [FeHCO₃]⁺ and [Fe(H₂O)₆]²⁺ based on the small (+0.5 ‰) fractionation in ⁵⁶Fe/⁵⁴Fe between [Fe(H₂O)₆]²⁺ and siderite (FeCO₃) at room temperature (Wiesli et al., 2004), suggesting an effect of <0.05 ‰ given the proportion of [FeHCO₃]⁺. The effects of Cl⁻ and acetate speciation on the measured Fe isotope fractionations have been calculated by Hill and Schauble (2008) and Ottonello and Vetuschi Zuccolini (2008) and these are insignificant at the levels that existed in the experiments.

2.2. Wet chemical and spectrophotometrical Fe(II) and Fe(III) analysis

For analysis of dissolved iron (Fe(II)_aq), a 200 μl culture suspension was withdrawn in an anoxic glovebox with a syringe and filtered through Nylon (0.22 μm) filter tubes (Costar, Corning, NY). The filtrate was acidified with 1 M HCl to stabilize the solutions and analyzed spectrophotometrically outside the glove box for total dissolved Fe and dissolved Fe(II) using Ferrozine assay after incubation in the presence or absence of the reducing agent hydroxylamine hydrochloride (Stookey, 1970). For analysis of total iron, a 100 μl suspension was added in the glove box to 900 μl 6 M HCl, and incubated for 1 h. After filtration through 0.22 μm Nylon filter tubes (Costar, Corning, NY) in the glove box, total Fe and Fe(II) concentrations were determined as above. All iron measurements by the Ferrozine assay were done in triplicate. The standard deviation (SD) for these triplicate measurements was usually smaller than the SD calculated for different independent experiments. Dissolved Fe(III) may be estimated as the difference between total dissolved Fe and dissolved Fe(II); in all cases total Fe and Fe(II) contents were identical within uncertainty of the calibration curves, indicating that dissolved Fe(III) contents were insignificant. Sorbed Fe(II) contents were determined from the solids collected after centrifugation of 1-ml aliquots of culture suspension. The pellets were washed twice in anoxic water (in the anoxic glove box), followed by extraction using a solution of 0.5 M sodium acetate (NaAc) and acidification by 1 M HCl prior to spectrophotometric analysis outside the anoxic chamber, which stabilized the solutions. Total and Fe(II) contents were determined on the water washes, and these contained several μM Fe(II) and Fe(III), which likely reflects small amounts of sorbed Fe(II) and Fe(III) precipitates, but these quantities were insignificant. Measurement of total Fe and Fe(II) contents of the NaAc extractions indicated that all Fe in these extracts was Fe(II). The percent oxidation for each sample was calculated based on the sum of Fe(II)_aq and Fe(II)_sorb, relative to the initial FeCl₂ contents (after removal of the carbonate and phosphate precipitates); because the sorbed Fe(II) comprises only a minor portion of the total Fe(II) abundance, the calculated percent oxidation is not dependent upon the efficiency of the sorbed Fe(II) extraction.

2.3. Mineral analyses and microscopy

Powder X-ray diffraction

Samples of culture suspensions were withdrawn at the end of the experiment with a syringe in an anoxic glove box and centrifuged to recover the precipitates. Remaining dissolved Fe(II) was removed from the microbially produced precipitates to avoid oxidation and formation of significant amounts of non-biogenic secondary Fe(III) precipitates through washing with water that had been degassed under vacuum, flushed with N₂ and equilibrated under an anoxic atmosphere for several days. After spreading on a glass disk, the precipitates were dried inside an anoxic glove-box. XRD spectra were obtained on a Scintag Pad V X-ray Powder Diffractometer using Cu-Kα radiation operating at 35 kV and 30 mA with a θ-2θ goniometer equipped with a germanium solid-state detector. Each scan used a 0.04° step size from 10° to 80° with a counting time of 2 seconds per step. Structures were identified by comparison to spectra in the PCPDFWIN program, © JCPDS-International Centre for Diffraction Data, 1997, (Newton Square, Pennsylvania), as well as to reference spectra obtained of synthetic ferrihydrite and goethite.

2.4. Electron microscopy

For light and scanning electron microscopy (SEM), 1 ml of a culture was taken with sterile syringes that had been flushed with N₂/CO₂. Light microscopy images of the samples were taken with a Zeiss AxioVison microscope equipped with an oil immersion objective lens. For SEM imaging, samples were chemically fixed using a half-strength Karnovsky solution, placed on holey carbon-coated EM-copper-grids, dehydrated in subsequent steps with an increasing concentration of isopropanol and finally dried in a Critical Point Dryer Bal-Tec CPD030 (for details see Schaedler et al. 2008). Dried samples were mounted on aluminium stubs using double-sided carbon tape. For enhanced electrical conductivity, the edges of the EM grids were painted with conductive silver paste. Samples which showed strong surface charging were coated in a Balzers sputter coater SCD 40 (Bal-Tec, Balzers, Liechtenstein) with a thin layer of Au/Pd (90%/10% w/w). The coating thickness was approximately 20 nm, as determined in focused ion beam cross-sections and by a surface texture analyzer (results not shown).

Imaging was performed with Zeiss Gemini 1550VP FE-SEM, Zeiss Gemini 1540XB FIB/FE-SEM, and Zeiss Ultra 55 SEM-FEG microscopes. Microscopes were equipped with Everhart-Thornley SE detectors and in-lens detectors and were optimized to a lens aperture of 30 μm. Images were recorded in a format of 1024 × 768 pixels, at integration times between 15 μs and 45 μs per pixel.

2.5. Fe isotope analyses

Iron phase separation and wet-chemical analysis

Over the course of the microbial Fe(II) oxidation experiment, subsamples were taken from each culture and abiotic control and were separated under O₂-free conditions in an anoxic glove box into solid and aqueous Fe fractions by a series of centrifugation, washing, and extraction steps as follows. At each time point, two 0.5 ml culture suspension aliquots were withdrawn in an anoxic glove box and centrifuged to separate dissolved Fe from precipitated Fe. The supernatant was separated, filtered (0.22 μm Nylon microcentrifuge tubes, Costar, Corning, NY, USA), and frozen in the closed centrifuge tubes at −18°C prior to Fe isotope analysis (see below). The remaining pellet was washed and centrifuged twice with 1 ml of anoxic water in the glovebox in order to remove loosely attached Fe leaving behind a pellet of Fe precipitates with sorbed Fe(II). The water used as wash solution for the Fe(III) precipitates contained several μM Fe(II) and about 2–4 times as much Fe(III), which probably reflects the presence of Fe(III) colloids or nano-particles in the water wash. The sorbed Fe(II) was separated for Fe isotope analysis from the pellet by extraction using a solution of 0.5 M sodium acetate (NaAc). The remaining Fe(III) pellet was frozen at −18°C until processed for Fe isotope analysis.

Iron isotope measurements

All Fe(II)_aq and solid pellet fractions were converted to FeCl₃ upon repeated dry down in ambient laboratory conditions, followed by purification using anion-exchange chromatography. This procedure is identical to that used in previous biological experiments (e.g., Croal et al., 2004; Crosby et al., 2007; Wu et al., 2009), and produces accurate Fe isotope compositions regardless of the presence or absences of organics. Isotopic measurements were made using a multi-collector inductively coupled plasma mass spectrometer, as previously described (Beard et al., 2003). Data are reported as ⁵⁶Fe/⁵⁴Fe ratios relative to the average of igneous rocks in standard δ notation, in units of per mil (‰):

$$\delta {}^{56}Fe=\left[\frac{{}^{56}Fe/{}^{54}F{e}_{\mathit{sample}}}{{}^{56}Fe/{}^{54}F{e}_{\mathit{IgRxs}}}-1\right]{10}^3$$ [1]

δ⁵⁷Fe values may be defined in an analogous manner using the ⁵⁷Fe/⁵⁴Fe ratio. The Fe isotope fractionation between two phases or species A and B is defined as:

$$\mathrm{\Delta }{}^{56}F{e}_{A-B}=\delta {}^{56}F{e}_A-\delta {}^{56}F{e}_B$$ [2]

following standard practice. Measured external precision in δ⁵⁶Fe values is ±0.05‰ (1σ, SD) based on replicate analyses and standards. On the igneous rock scale, the δ⁵⁶Fe value of the IRMM-014 standard is −0.09‰ (Beard et al., 2003).

3 Results

3.1. Fe(II) oxidation and cell encrustation by the nitrate-reducing Fe(II)-oxidizing strain BoFeN1

Strain BoFeN1 oxidizes Fe(II) mixotrophically, where iron oxidation occurs with oxidation of small amounts of acetate to CO₂, coupled to the reduction of nitrate (Kappler et al., 2005). During and after Fe(II) oxidation, strain BoFeN1 becomes heavily encrusted in Fe(III) minerals (Fig. 1). In separate, but generally analogous experiments, Miot et al. (2009) demonstrated that Fe(III) minerals are present both in the periplasm as well as at the cell surface as Fe(II) oxidation proceeds; Fe(III) minerals first form in the periplasm, when no minerals are present at the cell surface. This suggests that the periplasm is the site of Fe(II) oxidation. As time passes, Fe(III) mineral precipitates in the BoFeN1 cultures associate with extracellular filaments (Fig. 1), which Miot et al. (2009) identified as polysaccharides. This contrasts with the studies of Straub et al. (1996) and Schaedler et al. (2008), who showed that another nitrate-reducing, autotrophic Fe(II)-oxidizing (enrichment) culture contained only cells that are not encrusted but associated with Fe(III) minerals.

Analysis of the Fe(III) solids by XRD produced no strong signal (not shown), indicating that the Fe(III) minerals produced were either amorphous or very finely crystalline. EDX spectra showed only Fe and O peaks, indicating that no significant quantities of Fe phosphates were formed as were found in the experiments of Miot et al. (2009). This is consistent with the relatively low phosphate contents of the medium used in the current study (approximately 40 μM after filtration of the Fe(II)-carbonates and Fe(II)-phosphates formed upon Fe(II)Cl₂ addition to the medium). The absence of carbonates in STXM analysis of the experiments of Miot et al. (2009) also suggests that during the co-metabolic acetate oxidation and CO₂ production, no Fe(II) carbonates precipitated during the course of Fe(II) oxidation. The products of Fe(II) oxidation in the current study, run at 16 °C and 30 °C, are similar to those observed by Kappler et al. (2005), who studied Fe(II) oxidation by strain BoFeN1 at 30 °C in cultures that were inoculated with cells that were pre-grown using acetate/nitrate and Fe(II)/acetate/nitrate. In the acetate/nitrate cultures, Kappler et al. (2005) determined a BET surface area of 158 m² g⁻¹ for the Fe(III) products and found no XRD signals, suggesting a mixture of ferrihydrite and nano-crystalline goethite, whereas the Fe(II)/acetate/nitrate cultures produced clear evidence of nano-crystalline goethite, based on XRD spectra. Mössbauer spectroscopy of Fe(III) solids produced by acetate/nitrate BoFeN1 cultures in experiments similar to the current study suggests a mixture of nano-crystalline goethite and/or ferrihydrite (Hohmann et al., 2010). We conclude that the Fe(III) minerals produced in our experiments likely consisted of large amounts of ferrihydrite and/or nano-crystalline goethite. If the products were mixtures of ferrihydrite and/or nano-crystalline goethite, it is likely that the proportions of these minerals change over time; based on the results of Kappler et al. (2005) and Hohmann et al. (2010), we would expect the proportion of nano-crystalline goethite to be higher in the later time points, where the probability of phase conversion of poorly crystalline Fe(III) hydroxides would be greatest. In the present study, we will use “Fe(OH)₃” in a generic sense to describe a variety of poorly crystalline ferric hydroxides such as ferrihydrite, as well as minerals such as schwertmannite and akaganeite, which were produced in some of the experiments of Balci et al. (2006).

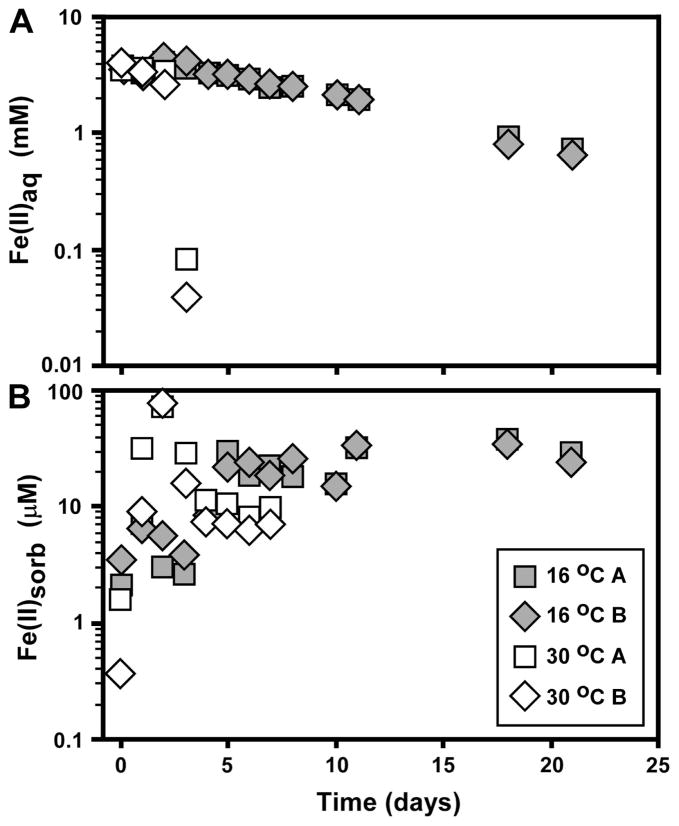
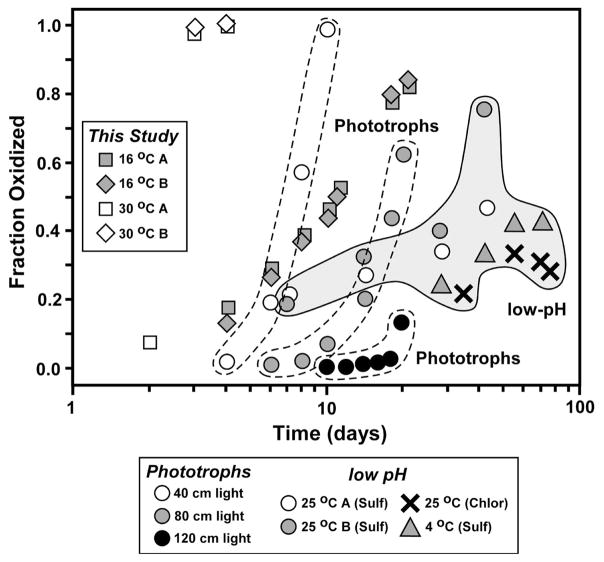
In the present study, we observed that approximately 80% of the Fe(II) initially present was oxidized by strain BoFeN1 at 16°C by 21 days (Fig. 2). The average oxidation rates in the strain BoFeN1 experiments at 16°C lie between those observed by Croal et al. (2004) for phototrophic Fe(II) oxidation at 40 and 80 cm light distances (40W light source) at room temperature, but significantly higher than the rates observed at 120 cm light distances by Croal et al. (2004) (Fig. 3). The average oxidation rates observed in the 16 °C strain BoFeN1 experiments were much higher than those observed by Balci et al. (2006) in their low-pH bacterial Fe(II) oxidation experiments. The average oxidation rates of the 30°C strain BoFeN1 experiments were very fast, where complete oxidation occurred within 4 days (Fig. 2 and 3). Sorbed Fe(II) contents for the 16 °C experiments increased in the first five days and then levelled off (Fig. 2), suggesting no major changes in the sorption capacity of the Fe(III) minerals. In contrast, sorbed Fe(II) contents in the 30 °C experiments increased dramatically in the first few days, where oxidation rates were very fast, but decreased after 3 days, levelling off to the end of the experiment (Fig. 2); this may suggest a decrease in surface area of the Fe(III) minerals, possibly reflecting conversion to larger crystals, or conversion of ferrihydrite to crystalline ferric hydroxides such as goethite. Additionally, decreasing Fe(II)_sorb contents can be a result of the depletion of Fe(II) in solution.

Fig. 2.

Temporal changes in aqueous Fe(II) (A) and sorbed Fe(II) (B) during Fe(II) oxidation by the nitrate-reducing bacterium Acidovorax sp. strain BoFeN1 at 16°C and 30°C. Symbols for sorbed Fe plotted as average of two extractions (Table 1). Data for uninoculated controls not shown (see Table 1).

Fig. 3.

Comparison of oxidation rates measured in microbial experiments in the current study of Acidovorax sp. strain BoFeN1 (Table 1), Fe(II)-oxidizing phototrophs at circumneutral pH (Croal et al., 2004), and low-pH Fe(II)-oxidizing bacteria (Balci et al., 2006). The study of Croal et al. (2004) was conducted at room temperature, whereas those of Balci et al. (2006) and the current work were conducted at different temperatures, as noted.

3.2. Fe isotope fractionation by the nitrate-reducing Fe(II)-oxidizing strain BoFeN1

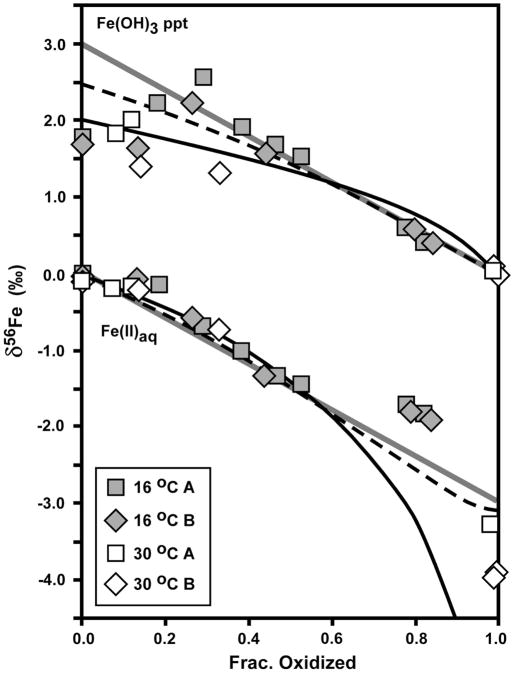
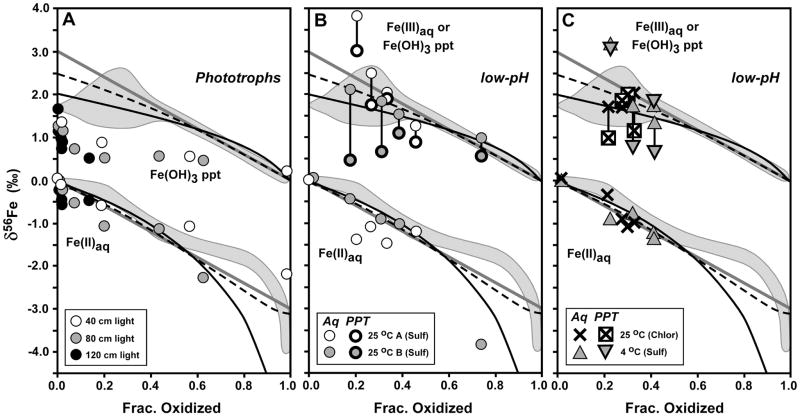
The δ⁵⁶Fe values for Fe(II)_aq and the Fe(OH)₃ precipitate produced in the strain BoFeN1 experiments varied systematically as a function of fraction oxidized (Fig. 4). As is the case with all biological or abiological Fe(II) oxidation experiments to date, the isotopic variations may be described by two end-member models, one involving continuous isotopic equilibrium in a closed system, and one involving Rayleigh fractionation using a kinetic or equilibrium fractionation factor but where the solid is prevented from re-equilibrating with Fe(II)_aq after precipitation (e.g., Bullen et al., 2001; Beard and Johnson, 2004; Johnson et al., 2004a; Croal et al., 2004; Balci et al., 2006; Dauphas and Roxell, 2006). The δ⁵⁶Fe values for the Fe(OH)₃ precipitate at low fraction oxidized scatter between a trend described by Rayleigh fractionation using a Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation factor of +1.5 to 2.0 ‰ (solid black curve in Fig. 4 shown for +2.0 ‰ fractionation) and a trend that accounts for partial isotopere-equilibration between Fe(OH)₃ and Fe(II)_aq. Partial isotopic re-equilibration of the precipitate was modeled using the mass-balance equations of Crosby et al. (2007), assuming precipitates that initially formed through Rayleigh fractionation (Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} = +2.0 ‰) maintained isotopic equilibrium between a 1 nm-thick reactive Fe(III) layer on the surface of a 10 nm-diameter spherical precipitate, sorbed Fe(II), and aqueous Fe(II) (see Fig. 4 caption for details); if the thickness of the reactive Fe(III) layer is increased, or the dimensions of the particle changes such that the ratio of surface atoms to total atoms increases (e.g., rod-shaped goethite), the partial re-equilibration model will move toward a closed-system equilibrium model (solid diagonal grey lines in Fig. 4). In contrast, for the data for the 16 °C experiments, the δ⁵⁶Fe values for the Fe(OH)₃ precipitate follow a closed-system equilibrium trend after ~30 % oxidation using an equilibrium Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation factor of +3.0 ‰ (Fig. 4). From 0 to 40 % oxidation, the δ⁵⁶Fe values for the Fe(OH)₃ precipitate in the 30 °C experiments appear to be better described by a Rayleigh fractionation process (Fig. 4), which would be more likely at the higher oxidation and precipitation rates of the higher temperature experiments.

Fig. 4.

Isotopic data for Fe(II)_aq and Fe(OH)₃ precipitate produced by Fe(II) oxidation by Acidovorax sp. strain BoFeN1, as a function of fraction oxidized (Table 1). δ⁵⁶Fe values normalized to a system value of zero. Reference curves shown for a) Rayleigh fractionation using a net Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation of +2 ‰ (black curve), b) the Rayleigh fractionation curve modified to account for partial isotopic re-equilibration (dashed black curve), and c) closed-system equilibrium fractionation for Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} = +3 ‰ (straight grey line). Partial isotopic re-equilibration calculated assuming a reactive Fe(III) surface layer of 1 nm thickness (10 nm diameter spherical particle) maintains isotopic equilibrium with Fe(II)_aq. δ⁵⁶Fe value for Fe(II)_aq calculated in the partial re-equilibration model at increments of 1 % oxidation, using the isotope mass balance equation (eq. 4) from Crosby et al. (2007), modified to ignore sorbed Fe(II).

The δ⁵⁶Fe values for Fe(II)_aq from 0 to 60% oxidized decrease with progressive oxidation, but, as noted by Croal et al. (2004), at low extents of oxidation the isotopic composition of Fe(II)_aq during oxidation is not sensitive to a particular fractionation model such as Rayleigh or equilibrium fractionation (Fig. 4). We stress that the Rayleigh models shown in Fig. 4 are primarily for illustrating potential processes that may explain the isotopic data, and a variety of Fe(OH)₃ – Fe(II)_aq fractionation factors between +1 and +3 ‰ may describe the results at the early stages of oxidation where the scatter is greatest for any particular time point. The δ⁵⁶Fe values for Fe(II)_aq in the 16 °C experiments at ~80 % oxidation appear to be anomalously high, relative to any fractionation model that fits the data at smaller degrees of oxidation. Although it is possible that anomalously high δ⁵⁶Fe values for Fe(II)_aq could be produced by contamination by Fe(OH)₃ precipitates, great care was taken to ensure complete separation of solid and aqueous components. The δ⁵⁶Fe values for Fe(II)_aq in the 30°C experiments at complete- or near-complete oxidation lie between those expected for a Rayleigh or equilibrium fractionation trend (Fig. 4).

4 Discussion

The new results presented here for strain BoFeN1, when combined with previous studies of Fe isotope fractionation by Croal et al. (2004) and Balci et al. (2006), provide a broad view of Fe isotope fractionation during biological Fe(II) oxidation via a variety of pathways that utilize different electron acceptors. Important issues arising from these studies include the measured or inferred abundance of aqueous Fe(III), the degree of isotopic equilibrium between Fe(II)_aq and ferric hydroxide precipitates, and kinetic isotope effects upon precipitation.

4.1. Fe isotope fractionation by chemical and biological Fe(II) oxidation

In all cases of biological Fe(II) oxidation, ferric hydroxide precipitates have higher δ⁵⁶Fe values than coexisting Fe(II)_aq (Fig. 5), consistent with the expected relative fractionation based on experimental (Johnson et al., 2002; Skulan et al., 2002; Welch et al., 2003) and theoretical (Polyakov and Mineev, 2000; Schauble et al., 2001) studies. The degree of fractionation between Fe(OH)₃ and Fe(II)_aq among these studies, however, is variable. Relative to the results obtained here, the fractionation between Fe(OH)₃ and Fe(II)_aq measured for phototrophic Fe(II) oxidation (Croal et al., 2004) is significantly less (Fig. 5A). Microbial oxidation of Fe(II) at low-pH (Balci et al., 2006) produced a wide range of δ⁵⁶Fe values for Fe(OH)₃, overlapping with the range measured in this study, but also producing higher and lower δ⁵⁶Fe values (Figs. 5B and 5C). In addition, microbial oxidation of Fe(II) at low pH produces significant quantities of Fe(III)_aq, and Balci et al. (2006) noted that the δ⁵⁶Fe values for Fe(III)_aq were always greater than those of co-existing Fe(II)_aq (Figs. 5B and 5C), as expected from abiological experiments and theoretical predictions.

Fig. 5.

Comparison of Fe isotope variations of the current study (grey fields, from Fig. 4) with phototrophic Fe(II) oxidation (panel A, from Croal et al., 2004) and low-pH Fe(II) oxidation (panels B and C, from Balci et al., 2006). δ⁵⁶Fe values normalized to a system value of zero for all studies to allow direct comparison. Reference curves shown from Fig. 4 for a) Rayleigh fractionation using a net Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation of +2 ‰ (black curve), b) the Rayleigh fractionation curve modified to account for partial isotopic re-equilibration (dashed black curve), and c) closed-system equilibrium fractionation for Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} = +3 ‰ (straight grey line). For low-pH experiments of Balci et al. (2006) (panels B and C), δ⁵⁶Fe values for aqueous Fe(III) and Fe(II) shown with thin line for symbols, and δ⁵⁶Fe values for ferric hydroxide precipitates shown with thick line for symbols.

In Figure 6 we compare the Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionations measured in the current study (Fig. 6A), with those determined for phototrophic Fe(II) oxidation (Fig. 6B), and low-pH Fe(II) oxidation (Fig. 6C), as well as the Δ⁵⁶Fe_{Fe(III)aq – Fe(II)aq} fractionations measured for low-pH microbial oxidation where significant quantities of Fe(III)_aq were produced (Fig. 6D). As initially proposed by Beard and Johnson (2004) and Johnson et al. (2004b), and expanded upon by Dauphas and Rouxell (2006), the overall fractionation between Fe(OH)₃ precipitate and Fe(II)_aq during Fe(II) oxidation can be approximated by the relation:

$$\mathrm{\Delta }{}^{56}\text{F}{\text{e}}_{\text{Fe}(\text{OH})3-\text{Fe}(\text{II})\text{aq}}\approx \mathrm{\Delta }{}^{56}\text{F}{\text{e}}_{\text{Fe}(\text{III})\text{aq}-\text{Fe}(\text{II})\text{aq}}+\mathrm{\Delta }{}^{56}\text{F}{\text{e}}_{\text{Fe}(\text{OH})\text{3}-\text{Fe}(\text{III})\text{aq}}$$ [3]

if Fe(III)_aq is present as an intermediate component; this approximation is valid where the proportion of Fe(III)_aq is ≤5% of the total aqueous Fe. At larger proportions of Fe(III)_aq, such as the experiments of Balci et al. (2006), the overall Fe(OH)₃ – Fe(II)_aq fractionation may deviate from equation 3 by up to ~1 ‰, producing a smaller net Fe(OH)₃ – Fe(II)_aq fractionation for a given set of values for Δ⁵⁶Fe_{Fe(III)aq – Fe(II)aq} and Δ⁵⁶Fe_{Fe(OH)3 – Fe(III)aq} (Beard and Johnson, 2004).

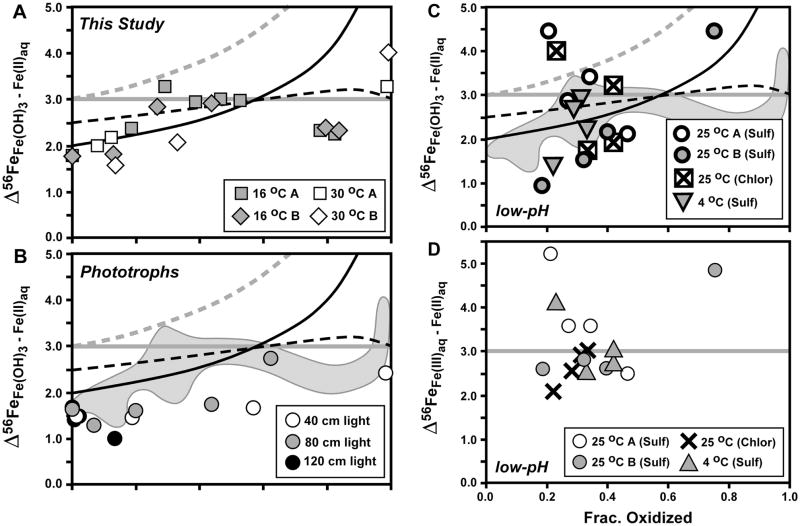
Fig. 6.

Comparison of isotopic fractionations between ferric hydroxide precipitate (Fe(OH)₃) and Fe(II)_aq (panel A: current study (Table 1); panel B: study of Croal et al., 2004; panel C: study of Balci et al., 2006), as well as between Fe(III)_aq and Fe(II)_aq from the study of Balci et al. (2006) (panel D). Reference curves for panels A–C shown from Figs. 4 and 5 for Rayleigh fractionation using a net Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation of +2 ‰ (black curve), the Rayleigh fractionation curve modified to account for partial isotopic re-equilibration (dashed black curve), and closed-system equilibrium fractionation for Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} = +3 ‰ (straight grey line). In addition, a Raleigh curve for an equilibrium Δ⁵⁶Fe_{Fe(III)aq – Fe(II)aq} fractionation of +3 ‰, followed by quantitative sequestration of Fe(III)_aq to Fe(OH)₃, is shown in grey dashed line (panels A–C). Reference curve for closed-system equilibrium fractionation for Δ⁵⁶Fe_{Fe(III)aq – Fe(II)aq} = +3 ‰ (straight grey line) shown for panel D. Grey field in panels B and C shows outline of data from panel A.

The measured Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionations during the initial stages of oxidation for strain BoFeN1 are consistent with a Rayleigh trend using an overall Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation factor of ~+2.0 ‰, as well as possible partial isotopic re-equilibration (Fig. 6A), which we interpret to reflect initial precipitation that combines an equilibrium Δ⁵⁶Fe_{Fe(III)aq – Fe(II)aq} fractionation of ~+3.0 ‰ and a kinetic Δ⁵⁶Fe_{Fe(OH)3 – Fe(III)aq} fractionation of ~ −1.0 ‰, assuming a two-step oxidation and precipitation model (Beard and Johnson, 2004). It is certainly possible that different net Fe(OH)₃ – Fe(II)_aq fractionation factors may be chosen to explain different time points at <20% oxidation, consistent with the overall conclusion that a combination of equilibrium Fe(III)_aq – Fe(II)_aq fractionation, but variable kinetic Fe(OH)₃ – Fe(III)_aq fractionation, is responsible for the observed net Fe(OH)₃ – Fe(II)_aq fractionations for the early time points. Between ~20 and 60 % oxidation, however, the overall Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation appears to lie along a fractionation line of +3.0 ‰, which could reflect an equilibrium fractionation factor, assuming a near-zero Δ⁵⁶Fe_{Fe(OH)3 – Fe(III)aq} fractionation factor; the Fe(OH)₃ – Fe(III)_aq fractionation factor has not been measured experimentally, nor predicted from theory, and possible values for this fractionation factor are discussed in the next section. At ~60–80 % oxidation, the Fe(OH)₃ – Fe(II)_aq fractionation at 16 °C decreases to ~ +2.2 ‰, and this is caused by an increase in the δ⁵⁶Fe value for Fe(II)_aq relative to that predicted by a Rayleigh fractionation or closed-system equilibrium relation at a constant fractionation factor (Fig. 4), possibly reflecting a change in the nature of the Fe(III) precipitate (from ferrihydrite to goethite, see above, or potential changes in crystallinity of the formed ferrihydrite and goethite). The +3 to +4 ‰ Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation at the end of the 30 °C experiment may be explained in part by a Rayleigh process, which produces high fractionations when Fe(II)_aq contents become very small (Fig. 6).

The overall Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionation measured for phototrophic Fe(II) oxidation (Fig. 6B) is generally less than that measured for strain BoFeN1 (current study). Croal et al. (2004) noted that the relatively small fractionation measured for phototrophic Fe(II) oxidation may reflect 1) a unique equilibrium Fe isotope fractionation via binding to biological ligands, and/or 2) a two-step fractionation involving an equilibrium Fe(III)_aq – Fe(II)_aq fractionation combined with a kinetic Fe(OH)₃ – Fe(III)_aq fractionation upon precipitation; subsequent studies have demonstrated the importance of a two-step, equilibrium-kinetic process associated with abiological Fe(II) oxidation (Beard and Johnson, 2004; Johnson et al., 2004b), and we therefore prefer the second interpretation for the Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionations observed by Croal et al. (2004). Although there was no measurable ambient Fe(III)_aq in the experiments of Croal et al. (2004), it is possible that local decreases in pH at the cell interface allowed Fe(III)_aq to exist (Kappler and Newman, 2004), which would permit a two-step oxidation mechanism. Additionally, the existence of an intracellular ligand that controls the Fe(III)_aq pool cannot yet be excluded.

A range in overall Δ⁵⁶Fe_{Fe(OH)3 – Fe(II)aq} fractionations was measured by Balci et al. (2006) during low-pH microbial Fe(II) oxidation (Fig. 6C). As noted by Balci et al. (2006), the net Fe(OH)₃ – Fe(II)_aq fractionation probably reflects a significant Fe(OH)₃ – Fe(III)_aq fractionation upon precipitation, in addition to Fe(III)_aq – Fe(II)_aq fractionation, which will decrease the net Fe(OH)₃ – Fe(II)_aq fractionation if the Δ⁵⁶Fe_{Fe(OH)3 – Fe(III)aq} fractionation factor is negative. Based on regression of Fe isotope data for Fe(II)_aq, Balci et al. (2006) inferred a net Fe(OH)₃ – Fe(II)_aq fractionation of +2.2 ‰. Balci et al. (2006) noted that, based on direct measurement of Fe(III)_aq and Fe(II)_aq, their results were broadly consistent with the equilibrium Fe(III)_aq – Fe(II)_aq fractionation of +3.0 ‰ measured in abiologic experiments and predicted by theory (e.g., Anbar et al., 2005; Domagal-Goldman and Kubicki, 2008; Johnson et al., 2002; Welch et al., 2003).

4.2. The effects of kinetic fractionations upon precipitation

We suggest that any variations in the measured overall Fe(OH)₃ – Fe(II)_aq fractionation must reflect variable kinetic effects on the Fe(OH)₃ – Fe(III)_aq fractionation upon precipitation. As noted in Section 2.1, the effects of aqueous speciation on the Fe isotope fractionations will be small in the experiments, <0.1 ‰ in ⁵⁶Fe/⁵⁴Fe. Based on the temperature dependence determined by Welch et al. (2003), Anbar et al. (2005), and Domagal-Goldman and Kubicki (2008), the Fe(III)_aq – Fe(II)_aq fractionation should be ~0.3 ‰ less at 30 °C than it is at 16 °C. We have compiled the data available for ferric oxide/hydroxide – Fe(III)_aq fractionations in Figure 7, drawing from the studies of Skulan et al. (2002) and Balci et al. (2006). There have been no studies that have determined the equilibrium fractionation between ferrihydrite and Fe(III)_aq, because even for nm-size crystals, isotopic exchange between these components is limited to surface atom sites (Poulson et al., 2005). The equilibrium fractionation between hematite and Fe(III)_aq has been estimated by Skulan et al. (2002) based on experiments that underwent >80 % exchange (determined by ⁵⁷Fe-enriched tracer studies). These experiments, however, were run at temperatures above the stability range for goethite, and therefore extrapolation to room temperatures requires some assumptions. Nevertheless, the equilibrium Fe₂O₃ – Fe(III)_aq fractionation at room temperature is estimated to lie between 0.0 and +0.4 ‰ (Fig. 7). Skulan et al. (2002) measured a kinetic Fe₂O₃ – Fe(III)_aq fractionation between −1.0 and −1.5 ‰ that approximately followed a Rayleigh process (Fig. 7).

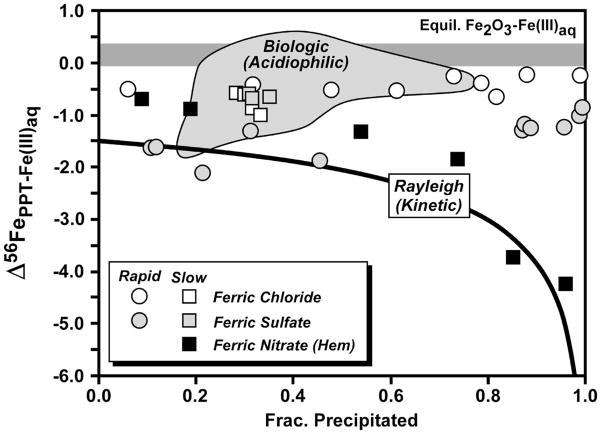
Fig. 7.

Compilation of fractionations measured between ferric oxide/hydroxide and Fe(III)_aq from the studies of Skulan et al. (2002) and Balci et al. (2006). Skulan et al. estimated a slightly positive equilibrium hematite – Fe(III)_aq fractionation at 98 °C (horizontal dark grey field, and determined a kinetic hematite – Fe(III)_aq fractionation at 98°C (black squares) that can be described by a Rayleigh process and a Δ⁵⁶Fe_{Hematite – Fe(III)aq} fractionation between −1 and −1.5 ‰ (black curve shown for −1.5 ‰). The fractionation between ferric hydroxide precipitates and co-existing Fe(III)_aq shown for abiologic precipitation experiments (symbols) and measured in biologic oxidation experiments (light grey field) also shown from the study of Balci et al. (2006).

Balci et al. (2006) investigated the fractionation between ferric hydroxide precipitates and Fe(III)_aq in a range of abiologic and biologic experiments, and in almost all cases found a negative fractionation (Fig. 7), which can also be observed in Figures 5B and 5C through comparison of data for the precipitate and Fe(III)_aq. The differences in Fe(OH)₃ - Fe(III)_aq fractionation for ferric chloride and ferric sulfate observed by Balci et al. (2006) (Fig. 7) may in part reflect differences in the precipitate that was produced, where ferric sulfate solutions produced schwertmannite and ferric chloride solutions produced akaganeite. As noted by Balci et al. (2006), it is difficult at this time to infer the equilibrium Fe(OH)₃ – Fe(III)_aq fractionation factor. If we assume that the equilibrium Fe(OH)₃ – Fe(III)_aq fractionation is approximately equal to the equilibrium Fe₂O₃ – Fe(III)_aq fractionation, then the negative Fe(OH)₃ – Fe(III)_aq fractionations in Figure 7 may reflect kinetic effects. We suggest that the equilibrium Fe(OH)₃ – Fe(III)_aq fractionation factor is probably close to zero, but it is important to stress that this fractionation factor is not well constrained by experiments, nor has it been calculated from theory.

4.3. Implications for biological Fe(II) oxidation mechanisms

The observation that the Fe(OH)₃ – Fe(II)_aq isotope fractionations during oxidation of Fe(II)_aq by strain BoFeN1 approach those expected for equilibrium conditions between ~20 and 60 % oxidation (Fig. 6A) suggests that the oxidation pathway must permit redox cycling between Fe(OH)₃ and Fe(II)_aq. Fig. 8A shows the three different locations where Fe(OH)₃ precipitation was observed after oxidation of Fe(II)_aq by strain BoFeN1 (Miot et al., 2009), i.e. in the periplasm, at the cell surface or at a distance to the cells (e.g. at exopolysaccharides). The proportion of oxides that is formed in the periplasm versus the fraction of mineral that is formed extracellularly is unknown. As discussed above, unidirectional oxidation of Fe(II)_aq to Fe(III)_aq, followed by precipitation of Fe(III)_aq to Fe(OH)₃, tends to produce overall Fe(OH)₃ – Fe(II)_aq isotope fractionations that are less than those expected for equilibrium conditions, and this probably reflects the very low rates of isotopic exchange between Fe(III)_aq and Fe(III) oxides or hydroxides. For example, Poulson et al. (2005) noted that only ~26 % isotopic exchange occurred between Fe(III)_aq and 3 nm-size ferrihydrite in 10 days at room temperature, with little subsequent exchange up to the end of the 85 day experiment. Skulan et al. (2002) noted that 150 days were required to attain ~80 % isotopic exchange between Fe(III)_aq and 200 nm-size hematite at 98 °C. In contrast, Handler et al. (2009) noted that 100 % isotopic exchange occurred between Fe(II)_aq and 100 nm-long goethite at room temperature within ~15 days. These observations suggest that equilibrium Fe isotope fractionation upon Fe(II) oxidation will most likely be attained when Fe(II)_aq and Fe(III) oxide/hydroxides remain in close contact, with low Fe(III)_aq contents, to permit a continuous state of coupled Fe atom and electron exchange between Fe(II)_aq and Fe(III) precipitates. High Fe(III)_aq contents would be expected to inhibit aqueous-oxide isotopic exchange.

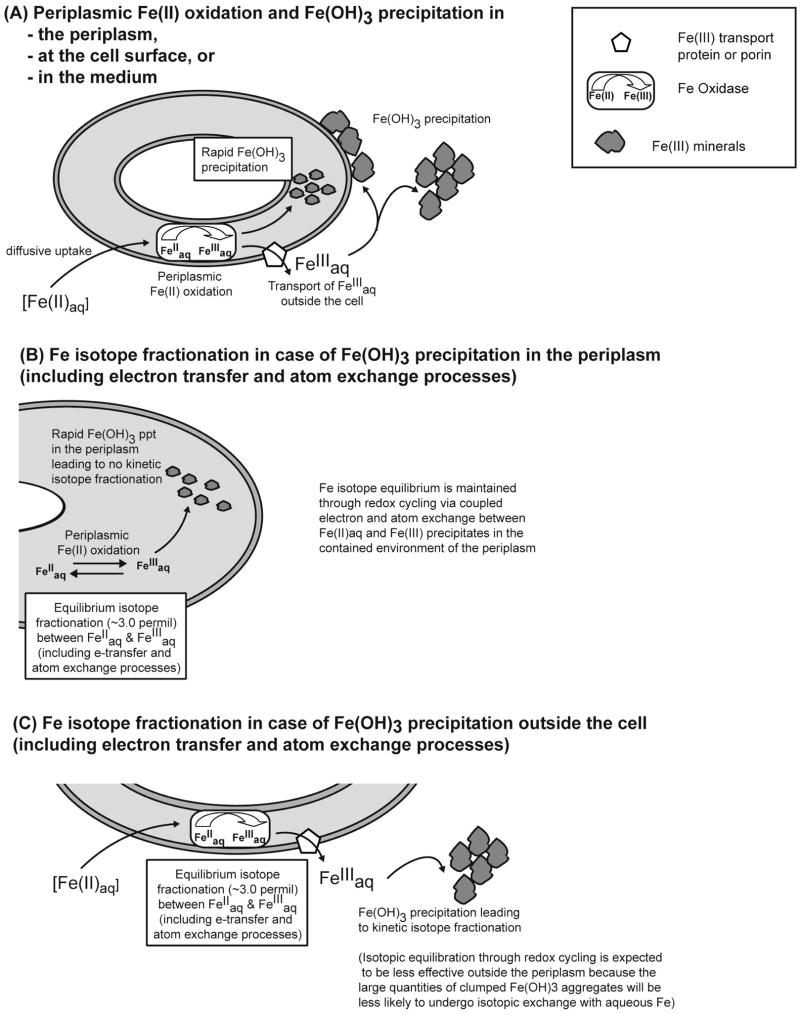
Fig. 8.

Cartoon illustrating periplasmic oxidation of Fe(II) by Acidovorax sp. strain BoFeN1 followed by Fe(OH)₃ precipitation either in the periplasm, at the cell surface or extracellularly (A) and potential Fe isotope fractionations expected in case of periplasmic (B) and extracellular (C) Fe(OH)₃ precipitation.

Unidirectional oxidation of Fe(II)_aq to Fe(III)_aq, and attendant equilibrium isotope fractionation, followed by quantitative precipitation to Fe(OH)₃ with no fractionation, is an alternative pathway that would reflect equilibrium conditions among aqueous species but no isotopic exchange between aqueous Fe and Fe(OH)₃. Such a pathway is modeled using a Rayleigh process with a net Fe(OH)₃-Fe(II)_aq fractionation factor of +3 ‰ for ⁵⁶Fe/⁵⁴Fe (Figs. 6A–6C). It is clear, however, that such a process does not fit the observed data, and, in particular, cannot explain the ~+3 ‰ Fe(OH)₃ – Fe(II)_aq fractionations at intermediate stages of oxidation. We therefore conclude that Fe(II)_aq – Fe(OH)₃ redox cycling is the best explanation for the observed isotopic fractionations.

In their study of Fe(II) oxidation by strain BoFeN1, Miot et al. (2009) concluded that Fe(II) oxidation began in the periplasm, producing Fe(III) precipitates that resulted in cell encrustation. An important finding in the study by Miot et al. was the observation that a consistent Fe(II)/Fe(III) precipitate ratio existed in the periplasm of the cells at any given time, independent of the degree of encrustation of individual cells, suggesting a continual state of redox equilibrium between the periplasm and the ambient conditions in the culture. Miot et al. (2009) concluded that active Fe(II) – Fe(III) redox cycling occurred in the periplasm during Fe(II) oxidation by strain BoFeN1. This suggests that Fe isotope equilibrium is likely to be maintained between Fe(II)_aq and Fe(III) precipitates in the periplasm (for illustration see Fig. 8B), consistent with the ~3 ‰ Fe(OH)₃ – Fe(II)_aq isotope fractionation measured for samples that reflect ~20 to 60 % oxidation in the 16 °C experiments; as noted above, the lower fractionations at <20 % oxidation are interpreted to reflect kinetic effects during the early stages of Fe(II) oxidation, when the rates of oxidation were highest. Isotopic equilibration through redox cycling is expected to be less effective outside the periplasm (Fig. 8C) because the large quantities of clumped Fe(OH)₃ aggregates observed outside the cells (Miot et al., 2009; Schaedler et al., 2009) will be less likely to undergo isotopic exchange with aqueous Fe, as compared to the restricted environment of the periplasm where smaller Fe(OH)₃ particles with high surface-per volume ratios are present (Miot et al., 2009). We conclude that microbial Fe(II) oxidation that involves oxidation and Fe(III) mineral precipitation in the periplasm is most likely to produce an equilibrium Fe isotope fractionation relative to Fe(III) mineral precipitation that occurs extracellularly, as in the studies of Croal et al. (2004) and Balci et al. (2006). It should be noted, however, that the scenarios presented in Fig. 8B and C reflect two extremes of either periplasmic or extracellular Fe(OH)₃ precipitation following periplasmic Fe(II) oxidation. In reality the process will probably reflect a combination of these scenarios at different time points of Fe(II) oxidation. As a consequence, in future experiments the proportion of Fe(III) oxides that forms in the periplasm of BoFeN1 relative to the total amount of Fe(III) oxides present should be determined during the course of Fe(II) oxidation.

We speculate that the decrease in Fe(OH)₃ – Fe(II)_aq fractionation at ~80 % oxidation in the 16 °C experiments reflects an increase in the proportion of well-crystallized goethite in the Fe(III) precipitates. Polyakov and Mineev (2000) predicted that the δ⁵⁶Fe values of goethite should be 2.1 ‰ lower than those of hematite at room temperature, which would decrease the Fe(III) oxide/hydroxide – Fe(II)_aq fractionation to ~ +1 ‰. If well-crystallized goethite preferentially exchanged with the remaining Fe(II)_aq at ~80 % oxidation via a Fe(II)-promoted phase transformation, the overall Fe(III) precipitate – Fe(II)_aq isotope fractionation would decrease, as observed (Fig. 6A).

Alternatively, the decrease in Fe(OH)₃ – Fe(II)_aq fractionation at ~80 % oxidation in the 16 °C experiments could indicate that some Fe(II) is oxidized chemically (and extracellularly) by nitrite without reaching the 3 per mil equilibrium fractionation. Such a contribution of abiotic Fe(II) oxidation was suggested to occur at the end of the Fe(II) oxidation in BoFeN1 cultures by Kappler et al. (2005) and Miot et al. (2009). Additional uncertainties exist for the 30 °C experiments because the fast oxidation and precipitation kinetics would make it less likely to produce equilibrium isotopic fractionations.

5. Conclusions

Microbial Fe(II) oxidation coupled to reduction of CO₂, O₂, or NO₃⁻ consistently produces positive Fe isotope fractionations between Fe(III) oxide/hydroxide precipitates and aqueous Fe(II). In many cases, the measured Fe(OH)₃ – Fe(II)_aq fractionations at low extent of oxidation, where fractionations are not strongly dependent upon closed-system equilibrium or Rayleigh models, are less than the ~ +3 ‰ fractionation estimated to reflect equilibrium conditions at room temperature. Based on the rapid rates of isotopic exchange between Fe(II)_aq and Fe(III) oxide/hydroxide (Handler et al., 2009), relative to the slow rates of exchange for Fe(III)_aq, (Poulson et al., 2005; Skulan et al., 2002), we propose that equilibrium Fe isotope fractionation during biological Fe(II) oxidation is most likely to be produced under conditions of continuous electron and atom exchange, in environments that promote redox cycling. These conditions may be satisfied when Fe(II) oxidation and initial Fe(III) mineral precipitation occur in the periplasm, as they do for Acidovorax sp. strain BoFeN1. We hypothesize that the isotopic fractionations produced by biological oxidation pathways that involve initial Fe(III) mineral precipitation outside the cell, such as the neutrophilic phototroph Thiodictyon sp. (Croal et al., 2004), or the acidophilic Fe(II) oxidizer Acidothiobacilus sp. (Balci et al., 2006), or abiological oxidation of Fe(II)_aq (Bullen et al., 2001), are unlikely to reflect equilibrium conditions because Fe(II) – Fe(III) oxide/hydroxide redox cycling may be inhibited where significant quantities of Fe(III)_aq exist, or where much larger quantities of Fe(III) precipitates exist in the ambient environment. Determining the proportion of Fe(III) oxides that first form in the periplasm of BoFeN1, relative to the total amount of Fe(III) oxides that eventually encrust the cell, is a priority for future research.

Although uncertainties remain with regard to the equilibrium Fe(OH)₃ – Fe(II)_aq isotope fractionation factor, which is important for comparison to biological Fe(II) oxidation, the results of the current study demonstrate that distinct Fe isotope fractionations may be produced by different oxidative pathways. The rapid rates of isotopic exchange between Fe(II)_aq and Fe(III)_aq suggests that these species should always be in isotopic equilibrium even under conditions of very rapid Fe(II) oxidation. The isotopic effects of sorption are difficult to estimate for experiments that produced ferrihydrite because the equilibrium Fe(II)_sorb – Fe(II)_aq fractionation has not been determined for ferrihydrite substrates. Under conditions of isotopic equilibrium, however, fractionations between aqueous and sorbed Fe(II) will not affect the overall Fe(OH)₃ – Fe(II)_aq fractionation. Kinetic fractionation upon precipitation of Fe(OH)₃, therefore, is the most likely explanation for measured Fe(OH)₃ – Fe(II)_aq fractionations at low extent of oxidation that are less than ~ +3 ‰.

Table 1.

Concentration and isotopic data. The data is given for two (abiotic, i.e. cell-free) control bottles A and B as well as for two bottles (A and B each) for Fe(II)-oxidizing Acidovorax cultures grown at 16°C and 30°C (labelling #1 – #18 represents different time points (in days) of sampling.

Sample	Day	Fe(II) mM	Percent oxidation	Analysis	δ56Fe	2SE/1SD	δ57Fe	2SE/1SD
Control - Bottle A
CtrlA-#0-1 Aq	0	3.94		1	0.33 ±	0.06	0.54 ±	0.08
				2	0.33 ±	0.07	0.54 ±	0.04
				Avg	0.33 ±	0.00	0.54 ±	0.00
CtrlA-#1-1 Aq	1	3.65
CtrlA-#2-1 Aq	2	4.46		1	0.40 ±	0.07	0.59 ±	0.07
				2	0.36 ±	0.04	0.53 ±	0.02
				Avg	0.38 ±	0.03	0.56 ±	0.04
CtrlA-#3-1 Aq	3	4.10
CtrlA-#4-1 Aq	4	4.27		1	0.40 ±	0.06	0.57 ±	0.09
				2	0.34 ±	0.04	0.54 ±	0.03
				Avg	0.37 ±	0.05	0.55 ±	0.03
CtrlA-#5-1 Aq	5	4.03
CtrlA-#6-1 Aq	6	4.14		1	0.28 ±	0.06	0.44 ±	0.07
				2	0.41 ±	0.05	0.62 ±	0.08
				3	0.28 ±	0.04	0.44 ±	0.03
				Avg	0.32 ±	0.07	0.50 ±	0.10
CtrlA-#7-1 Aq	7	4.07
CtrlA-#8-1 Aq	8	4.07
CtrlA-#10-1 Aq	10	4.00
CtrlA-#11-1 Aq	11	4.15
CtrlA-#18-1 Aq	18	4.19
Control - Bottle B
CtrlB-#0-1 Aq	0	4.08
CtrlB-#1-1 Aq	1	3.55
CtrlB-#2-1 Aq	2	4.03
CtrlB-#3-1 Aq	3	3.71
CtrlB-#4-1 Aq	4	4.21
CtrlB-#5-1 Aq	5	3.87
CtrlB-#6-1 Aq	6	4.21
CtrlB-#7-1 Aq	7	4.01
CtrlB-#8-1 Aq	8	4.12
CtrlB-#10-1 Aq	10	4.00
CtrlB-#11-1 Aq	11	4.20
CtrlB-#18-1 Aq	18	4.29
Bottle 16A - 16 °C
16A-#0-1 Aq	0	3.54	0.0	1	0.32 ±	0.04	0.41 ±	0.06
				2	0.34 ±	0.04	0.65 ±	0.08
				Avg	0.33 ±	0.02	0.53 ±	0.17
16A-#0-1 Sorb		0.0021
16A-#1-1 Aq	1	3.11	0.0
16A-#1-1 Sorb		0.0070
16A-#2-1 Aq	2	3.89	0.0	1	0.30 ±	0.04	0.48 ±	0.04
				2	0.24 ±	0.04	0.30 ±	0.05
				Avg	0.27 ±	0.04	0.39 ±	0.13
16A-#2-1 Sorb		0.0030
16A-#2-1 Precip				1	2.08 ±	0.05	3.18 ±	0.04
16A-#3-1 Aq	3	3.60	7.4
16A-#3-1 Sorb		0.0026
16A-#4-1 Aq	4	3.19	17.8	1	0.18 ±	0.04	0.27 ±	0.05
				2	0.20 ±	0.05	0.21 ±	0.07
				Avg	0.19 ±	0.02	0.24 ±	0.05
16A-#4-1 Sorb		0.0085
16A-#4-1 Precip				1	2.60 ±	0.05	4.07 ±	0.08
				2	2.53 ±	0.03	3.89 ±	0.04
				Avg	2.56 ±	0.05	3.98 ±	0.13
16A-#5-1 Aq	5	3.03	21.4
16A-#5-1 Sorb		0.0294
16A-#6-1 Aq	6	2.77	28.3	1	−0.33 ±	0.08	−0.57 ±	0.08
				2	−0.35 ±	0.04	−0.61 ±	0.06
				Avg	−0.34 ±	0.01	−0.59 ±	0.02
16A-#6-1 Sorb		0.0176
16A-#6-1 Precip				1	2.84 ±	0.07	4.40 ±	0.11
				2	2.98 ±	0.02	4.51 ±	0.03
				Avg	2.91 ±	0.10	4.46 ±	0.08
16A-#7-1 Aq	7	2.41	37.5
16A-#7-1 Sorb		0.0221
16A-#8-1 Aq	8	2.40	37.8	1	−0.70 ±	0.06	−1.02 ±	0.08
				2	−0.64 ±	0.04	−0.89 ±	0.06
				Avg	−0.67 ±	0.04	−0.96 ±	0.09
16A-#8-1 Sorb		0.0183
16A-#8-1 Precip				1	2.27 ±	0.04	3.37 ±	0.03
				2	2.25 ±	0.04	3.38 ±	0.03
				Avg	2.26 ±	0.02	3.37 ±	0.01
16A-#9-1 Aq	10	2.10	45.6	1	−0.98 ±	0.04	−1.44 ±	0.04
16A-#9-1 Sorb		0.0160
16A-#9-1 Precip				1	2.01 ±	0.03	2.96 ±	0.05
16A-#10-1 Aq	11	1.86	51.4	1	−1.13 ±	0.05	−1.66 ±	0.08
				2	−1.08 ±	0.03	−1.61 ±	0.03
				Avg	−1.10 ±	0.04	−1.64 ±	0.04
16A-#10-1 Sorb		0.0307
16A-#10-1 Precip				1	1.90 ±	0.04	2.81 ±	0.03
				2	1.83 ±	0.07	2.75 ±	0.11
				Avg	1.87 ±	0.05	2.78 ±	0.04
16A-#11-1 Aq	18	0.87	76.7	1	−1.36 ±	0.03	−2.01 ±	0.04
16A-#11-1 Sorb		0.0358
16A-#11-1 Precip				1	0.95 ±	0.05	1.44 ±	0.04
16A-#12-1 Aq	21	0.70	81.3	1	−1.48 ±	0.04	−2.14 ±	0.04
16A-#12-1 Sorb		0.0285
16A-#12-1 Precip				1	0.76 ±	0.05	1.04 ±	0.08
Bottle 16B - 16 °C
16B-#0-1 Aq	0	3.85	0.0	1	0.30 ±	0.03	0.48 ±	0.07
16B-#0-1 Sorb		0.0038
16B-#0-1 Precip				1	2.02 ±	0.04	2.96 ±	0.06
16B-#1-1 Aq	1	3.43	10.7
16B-#1-1 Sorb		0.0089
16B-#2-1 Aq	2	3.84	0.1	1	0.27 ±	0.05	0.37 ±	0.04
16B-#2-1 Sorb		0.0059
16B-#2-1 Precip				1	2.06 ±	0.05	3.18 ±	0.05
				2	2.09 ±	0.05	3.16 ±	0.04
				Avg	2.08 ±	0.03	3.17 ±	0.01
16B-#3-1 Aq	3	4.14	0.0
16B-#3-1 Sorb		0.0039
16B-#4-1 Aq	4	3.35	12.7	1	0.17 ±	0.03	0.27 ±	0.03
16B-#4-1 Sorb		0.0104
16B-#4-1 Precip				1	1.97 ±	0.03	2.96 ±	0.03
16B-#5-1 Aq	5	3.11	18.6
16B-#5-1 Sorb		0.0224
16B-#6-1 Aq	6	2.83	25.9	1	−0.24 ±	0.05	−0.31 ±	0.06
				2	−0.27 ±	0.05	−0.39 ±	0.04
				Avg	−0.25 ±	0.02	−0.35 ±	0.06
16B-#6-1 Sorb		0.0239
16B-#6-1 Precip				1	2.55 ±	0.03	3.79 ±	0.04
16B-#7-1 Aq	7	2.62	31.5
16B-#7-1 Sorb		0.0180
16B-#8-1 Aq	8	2.44	35.9
16B-#8-1 Sorb		0.0261
16B-#9-1 Aq	10	2.17	43.2	1	−1.00 ±	0.05	−1.41 ±	0.04
16B-#9-1 Sorb		0.0152
16B-#9-1 Precip				1	1.90 ±	0.05	2.87 ±	0.06
16B-#10-1 Aq	11	1.93	49.0
16B-#10-1 Sorb		0.0317
16B-#11-1 Aq	18	0.78	78.9	1	−1.50 ±	0.03	−2.24 ±	0.04
				2	−1.43 ±	0.05	−2.14 ±	0.04
				Avg	−1.46 ±	0.05	−2.19 ±	0.07
16B-#11-1 Sorb		0.0340
16B-#11-1 Precip				1	0.91 ±	0.03	1.32 ±	0.03
16B-#12-1 Aq	21	0.63	83.0	1	−1.56 ±	0.03	−2.28 ±	0.07
16B-#12-1 Sorb		0.0239
16B-#12-1 Precip				1	0.75 ±	0.03	1.07 ±	0.03
Bottle 30A - 30 °C
30A-#0-1 Aq	0	3.73	0.0	1	0.31 ±	0.04	0.37 ±	0.06
				2	0.32 ±	0.05	0.59 ±	0.06
				Avg	0.32 ±	0.01	0.48 ±	0.15
30A-#0-1 Sorb		0.0016
30A-#1-1 Aq	1	3.30	10.7	1	0.19 ±	0.05	0.25 ±	0.05
30A-#1-1 Sorb		0.0314
30A-#1-1 Precip				1	2.38 ±	0.07	3.45 ±	0.04
				2	2.31 ±	0.04	3.35 ±	0.04
				Avg	2.35 ±	0.05	3.40 ±	0.07
30A-#2-1 Aq	2	3.46	5.3	1	0.14 ±	0.04	0.11 ±	0.07
				2	0.15 ±	0.03	0.20 ±	0.03
				Avg	0.15 ±	0.01	0.16 ±	0.07
30A-#2-1 Sorb		0.0715
30A-#2-1 Precip				1	2.23 ±	0.03	3.30 ±	0.05
				2	2.10 ±	0.04	3.11 ±	0.04
				Avg	2.17 ±	0.09	3.20 ±	0.13
30A-#3-1 Aq	3	0.08	97.1	1	−2.91 ±	0.05	−4.18 ±	0.04
				2	−2.91 ±	0.07	−4.37 ±	0.05
				Avg	−2.91 ±	0.00	−4.28 ±	0.13
30A-#3-1 Sorb		0.0280
30A-#3-1 Precip				1	0.42 ±	0.08	0.62 ±	0.11
				2	0.37 ±	0.04	0.55 ±	0.03
				Avg	0.39 ±	0.03	0.58 ±	0.05
30A-#4-1 Precip	4			1	0.41 ±	0.04	0.59 ±	0.03
				2	0.39 ±	0.03	0.51 ±	0.06
				3	0.30 ±	0.09	0.34 ±	0.09
				Avg	0.36 ±	0.06	0.48 ±	0.12
Bottle 30B - 30 °C
30B-#0-1 Aq	0	3.94	0.0	1	0.25 ±	0.03	0.32 ±	0.05
30B-#0-1 Sorb		0.0004
30B-#1-1 Aq	1	3.41	13.2	1	0.17 ±	0.03	0.23 ±	0.04
30B-#1-1 Sorb		0.0094
30B-#1-1 Precip				1	1.75 ±	0.04	2.63 ±	0.04
30B-#2-1 Aq	2	2.64	30.8	1	−0.39 ±	0.02	−0.56 ±	0.04
30B-#2-1 Sorb		0.0864
30B-#2-1 Precip				1	1.67 ±	0.08	2.49 ±	0.04
30B-#3-1 Aq	3	0.04		1	−3.56 ±	0.03	−5.20 ±	0.03
				2	−3.61 ±	0.05	−5.29 ±	0.04
				Avg	−3.59 ±	0.04	−5.25 ±	0.06
30B-#3-1 Sorb		0.0016
30B-#3-1 Precip				1	0.44 ±	0.04	0.66 ±	0.05
30B-#4-1 Precip	4			1	0.33 ±	0.04	0.48 ±	0.03
				2	0.32 ±	0.04	0.47 ±	0.04
				Avg	0.33 ±	0.00	0.48 ±	0.01