The influence of initial outlines on manual segmentation

Abstract

Purpose: Initial outlines are often presented as an aid to reduce the time-cost associated with manual segmentation and measurement of structures in medical images. This study evaluated the influence of initial outlines on manual segmentation intraobserver and interobserver precision.

Methods: Three observers independently outlined all pleural mesothelioma tumors present in five computed tomography (CT) sections in each of 30 patient scans. After a lapse of time, each observer was presented with the same series of CT sections with the outlines of each observer superimposed as initial outlines. Each observer created altered outlines by altering the initial outlines to reflect their perception of the tumor boundary. Altered outlines were compared to original outlines using the Jaccard similarity coefficient (J). Intraobserver and interobserver precision of observer outlines were calculated by applying linear mixed effects analysis of variance models to the J values. The percent of minor alterations (alterations that resulted in only slight changes in the initial outline) was also recorded.

Results: The average J value between pairs of observer original outlines was 0.371. The average J value between pairs of observer outlines when altered from an identical initial outline was 0.796, indicating increased interobserver precision. The average difference between J values of an observer’s segmentation created by altering their own initial outline and when altering a different observer’s initial outline was 0.476, indicating initial outlines strongly influence intraobserver precision. Observers made minor alterations on 74.5% of initial outlines with which they were presented.

Conclusions: Intraobserver and interobserver precision were strongly dependent on the initial outline. These effects are likely due to the tendency of observers to make only minor corrections to initial outlines. This finding could impact observer study design, tumor growth assessment, computer-aided diagnosis system validation, and radiation therapy target volume definition when initial outlines are used as an observer aid.

INTRODUCTION

Manual segmentation of a structure in medical images is often required in both the research and clinical settings. A typical segmentation task involves manually outlining the structure in each section of, for example, a computed tomography (CT) scan. This sequence of outlines that defines the segmented structure is then analyzed to derive size, shape, density, positional, and other quantitative information. In many scans, these structures span tens or hundreds of sections and demonstrate complex morphology so that manual segmentation is not practical in terms of time and effort (Fig. 1).

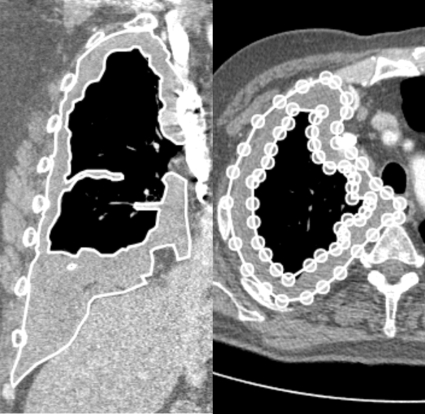
Figure 1.

Left: Mesothelioma tumor (white outline) illustrated on a coronal CT section. The tumor spans 260 axial sections. Right: Manually segmented tumor on axial CT section (white outline). The outlines are created using a computerized system by manually placing vertices of the polygon (white circles). Note that the tumor demonstrates complex topology and nested outlines are used to create an annulus.

One method to reduce the time-cost associated with manual segmentation is to present an observer with an initial outline for modification rather than force the observer to create a new outline. In practice, such initial outlines likely would be generated by a computerized system. The fundamental assumption when using initial outlines to facilitate manual segmentation is that the presence of an initial outline will not adversely influence (bias) an observer, so that the observer’s resulting manual outlines will be similar with or without initial outlines present.

An extensive amount of previous work has investigated the variability, bias, and reproducibility of observer measurements, the impact of previous information on detection and diagnosis, and the effect of the order in which information is presented to an observer. Schwartz et al.¹ demonstrated that the coefficient of variation was reduced by half when using an automated contouring method to measure tumor size instead of digital or electronic calipers. Monsky et al.² measured decreased intraobserver variability using edge contouring for tumor size measurement but were unable to demonstrate statistical significance. Geets et al.³ demonstrated an average Jaccard similarity value (see definition below) of 0.4 between manual observer outlines of pharengolaryngeal tumors. Wormanns et al.⁴ performed semiautomated volume measurements of lung nodules and found a mean intraobserver variability of 0.9% and interobserver variability of 0.5%. Gietma et al.⁵ performed a similar study and demonstrated a correlation of 99% between observer measurements. Bolte et al.⁶ demonstrated a significant difference between lung tumor volumes measured by experienced observers vs inexperienced observers; a significant difference was not measured when semiautomated methods were utilized. Meyer et al.⁷ examined the application of manual and semiautomated volume measurement methods to lung nodules; they found that interobserver variability contributed 40.4% to the total volumetric variance and the choice of method contributed 31.1% to the total volumetric variance. Armato et al.⁸ performed semiautomated linear measurements of mesothelioma using several different algorithms and demonstrated reduced interobserver variability vs fully manual measurements.

Zheng et al.⁹ demonstrated a slight decrease in observer performance when low-sensitivity∕high-false-positive computerized systems provided cues concurrently with the observer read relative to observer performance when presented with cues after an initial independent read. Gilbert et al.¹⁰ found a significant relationship between both the presence and size of a computerized cue placed on mammograms and the decision to recall a patient. Finally, Bergus et al.¹¹ demonstrated that the order in which information is presented to a physician (history followed by diagnostic tests and vice versa) can influence diagnosis. These studies demonstrate the influence of information presented to observers in the interpretation of medical images and the extraction of information from these images; however, none has directly investigated how the presence of an initial outline influences a human observer in the task of lesion segmentation.

The purpose of this study was to quantitatively measure the influence of an initial outline on an observer when manually segmenting a structure. This study differs from previous works in three ways. First, previous studies did not specifically consider the impact of an initially presented outline on the observer. Second, this study evaluates observer variability based on the segmented structures directly instead of on geometric features (e.g., volume estimates) derived from the segmentations. By examining the segmentation results directly, the analysis in this study includes positional information that is lost when only size estimates such as area or volume are used. Finally, the majority of previous studies concentrated on lung nodules which are small, compact, and roughly spherical. The structure segmented in this study (malignant pleural mesothelioma tumor) has an especially complex morphology and may be large enough to compress large portions of the lung.

MATERIALS AND METHODS

Database characteristics

The database for this study consisted of 30 diagnostic thoracic helical CT scans acquired from patients with malignant pleural mesothelioma. These patients (25 males and five females; age range 50–83 yr; mean 68 yr) had been enrolled in a variety of chemotherapy clinical trials and no scan was acquired specifically for this study. The CT scans were acquired on the Philips (Philips Medical Systems, Cleveland, OH) Brilliance 16 slice scanner (n=3), Brilliance 16P scanner (n=19), Brilliance 40 slice scanner (n=1), and Brilliance 64 slice scanner (n=7) at our institution. The scans were acquired with slice thicknesses of 1 (n=28), 2 (n=1), or 3 mm (n=1), and pixel spacing ranged from 0.559 to 0.951 mm (mean: 0.727±0.085 mm). Each CT section was axially reconstructed as a 512×512 pixel image matrix.

Visualization and segmentation system

An in-house computer software system was developed for the visualization and manual segmentation of structures in medical images (Figs. 12). This system allows window and level changes, magnification, and viewing of adjacent CT sections within the same patient scan. Segmentation was performed through the manual placement of points along the perceived boundary of the structure (tumor) using the mouse. As points were placed along the structure boundary, a line connected the sequential points to form a polygon that became the outline of the structure. Neither the placed points (vertices of the polygon) nor the connecting lines were restricted to the pixel coordinates of the image.

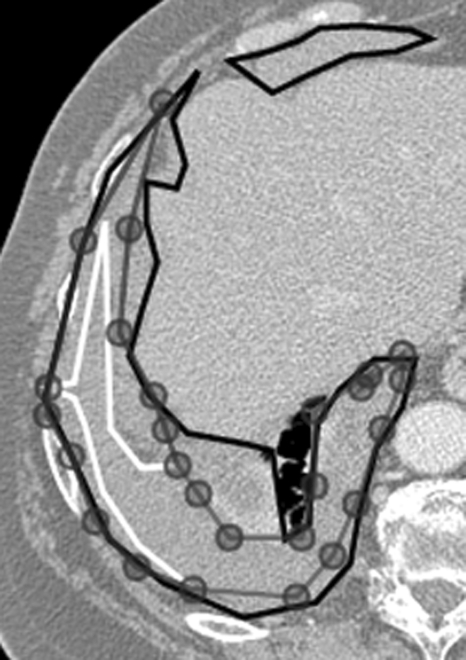
Figure 2.

Impact of an initial outline on intraobserver precision. Observer A’s Phase 1 outline (A_p1; white outline), Observer B’s Phase 1 outline (B_p1; black outline), and Observer A’s Phase 2 outline created by altering Observer B’s Phase 1 outline (A_p2B_p1; gray outline). Observer A’s Phase 2 (altered) outline is closer to, but still substantially different than, Observer A’s Phase 1 (original) outline.

Experimental setup and data collection

Phase 1: Segmentation without initial outlines present

Three observers independently outlined five randomly selected sections in each of the 30 patient scans. The observers consisted of two attending radiologists (Observers A and C) and one resident with radiological training specific to mesothelioma (Observer B). All observers were trained to use the computer interface. Observers could view the entire patient scan but could only create outlines on the predefined sections. Observers were instructed to outline all mesothelioma tumor present in each of the 150 selected sections or to make no outlines if no disease was present in a section. The window and level settings were set to the default in the DICOM header of each image, but the observer could modify the window and level according to their own preference. The choice to allow window∕level changes was made both to simulate a clinical setting and to facilitate an observer’s ability to accurately localize low-contrast structure boundaries. No restrictions were placed on ambient lighting, computer hardware, or completion time.

Phase 2: Segmentation with initial outlines present

After a one-month period had lapsed to reduce the impact of observer memory, each observer was presented with the same 150 predefined CT sections; however, in this phase of the study, each of the outlines created by each of the observers in Phase 1 was anonymously superimposed on the section as an initial outline. The observer had the ability to view all sections from the entire scan, but only that one section had an initial outline visible. The observer then created a Phase 2 (altered) outline in the section by accepting the initial outline without changing, deleting∕adding an outline, or altering the initial outline by moving, adding, or deleting vertices of the outline. When the observer was satisfied with the altered outline on a section, a new section∕initial outline combination was presented. This process was repeated for all five sections in each of the 30 patients and for each of the three Phase 1 (original) outlines (450 total alteration tasks for each observer). Thus, every Phase 1 outline created by every observer was viewed for alteration by each of the observers in Phase 2. This resulted in a total of 1350 Phase 2 outlines created in this study. Instructions and restrictions were identical to those described in the Phase 1 study.

Data analysis

Comparisons between outlines were quantified by the Jaccard similarity coefficient (J) defined as J(S,T)=Area(S∩T)∕Area(S∪T), where S and T are the two outlined regions being compared and Area() is the number of pixels contained within an outline. This metric creates a single number between 0 (no overlap between outlines S and T) and 1 (outlines S and T are identical). The J values were calculated on a section-by-section basis between various combinations of original and altered outlines.

Denote the Phase 1 outlines of Observer X as X_p1, where Observer X represents Observer A, B, or C, and denote n as the number of selected sections. Average J values between the Phase 1 outlines of different observers were used to quantify interobserver variability without initial outlines present (Table 1).

Table 1.

Expressions for calculating average J values for Phase 1 outlines and the corresponding values with 95% CI.

	A vs B	A vs C	B vs C
Phase 1 expressions	(∑nJ(Ap1,Bp1))∕n	(∑nJ(Ap1,Cp1))∕n	(∑nJ(Bp1,Cp1))∕n
J	0.325	0.496	0.291
(CI)	(0.251–0.398)	(0.422–0.569)	(0.217–0.365)

Denote the Phase 2 outline of Observer Y as derived by altering the Phase 1 outline of Observer X as Y_p2X_p1. The influence of initial outlines on intraobserver precision was quantified by calculating average J values over all sections between an observer’s Phase 1 (original) outlines and the Phase 1 (original) outlines of other observers altered by that observer (Table 2, columns 2 and 3). Conceptually, these average J values measure the extent to which an observer is biased by the initial presentation of an independent outline. These values were also compared to the average J values between an observer’s Phase 1 outlines and that same observer’s Phase 2 outlines when altering their own Phase 1 outlines (Table 2, column 1). Recall that the initial outlines were presented to the observer anonymously. This comparison also demonstrates the influence of initial outlines on intraobserver precision because the only difference between the two sets of J values (i.e., Table 2, column 1 and Table 2, columns 2 and 3) is whether an observer altered their own Phase 1 outlines as the initial outlines or a different observer’s Phase 1 outlines as the initial outlines.

Table 2.

Expressions for calculating the average J for analysis of intraobserver precision and the corresponding values with 95% CI.

Phase 2 intraobserver precision calculations	(∑nJ(Ap1,Ap2Ap1))∕n	(∑nJ(Ap1,Ap2Bp1))∕n	(∑nJ(Ap1,Ap2Cp1))∕n
J	0.957	0.481	0.559
(CI)	(0.916–0.999)	(0.428–0.533)	(0.507–0.611)
Phase 2 intraobserver precision calculations	(∑np1J(Bp1,Bp2Bp1))∕n	(∑nJ(Bp1,Bp2Ap1))∕n	(∑nJ(Bp1,Bp2Cp1))∕n
J	0.860	0.345	0.320
(CI)	(0.802–0.917)	(0.293–0.397)	(0.268–0.372)
Phase 2 intraobserver precision calculations	(∑nJ(Cp1,Cp2Cp1))∕n	(∑nJ(Cp1,Cp2Ap1))∕n	(∑nJ(Cp1,Cp2Bp1))∕n
J	0.916	0.519	0.388
(CI)	(0.865–0.966)	(0.465–0.572)	(0.335–0.441)

Average J values over all sections between the Phase 2 (altered) outlines of Observers A and B, Observers A and C, and Observers B and C when the altered outlines were derived from a common initial outline (Table 3). These J values were then compared to the J values calculated between Phase 1 observer outlines (Table 1) to evaluate the impact of initial outlines on interobserver precision.

Table 3.

Expressions for calculating the average J for analysis of interobserver precision and the corresponding values with 95% CI.

	A vs B	A vs C	B vs C
Phase 2 interobserver precision calculations	$\left({\sum }_n\begin{array}{c}J\left(A_{p2}{A}_{p1},B_{p2}{A}_{p1}\right)+\hfill \\ J\left(A_{p2}{B}_{p1},B_{p2}{B}_{p1}\right)+\hfill \\ J\left(A_{p2}{C}_{p1},B_{p2}{C}_{p1}\right)\hfill \end{array}\right)∕3n$	$\left({\sum }_n\begin{array}{l}J\left(A_{p2}{A}_{p1},C_{p2}{A}_{p1}\right)+\hfill \\ J\left(A_{p2}{B}_{p1},C_{p2}{B}_{p1}\right)+\hfill \\ J\left(A_{p2}{C}_{p1},C_{p2}{C}_{p1}\right)\hfill \end{array}\right)∕3n$	$\left({\sum }_n\begin{array}{l}J\left(B_{p2}{A}_{p1},C_{p2}{A}_{p1}\right)+\hfill \\ J\left(B_{p2}{B}_{p1},C_{p2}{B}_{p1}\right)+\hfill \\ J\left(B_{p2}{C}_{p1},C_{p2}{C}_{p1}\right)\hfill \end{array}\right)∕3n$
J	0.763	0.824	0.802
(CI)	(0.712–0.814)	(0.780–0.868)	(0.756–0.848)

The extent that observers altered the initial outlines was quantified by identifying the percentage of outlining tasks in Phase 2 where only minor alterations were made by the observer. A minor alteration was defined for the purposes of this study as an alteration that created a Phase 2 outline such that the Jaccard similarity coefficient between the original and altered outline [J(Phase 2,Phase 1)] was greater than 0.9.

Repeated measures analysis of variance models were used to analyze the data.¹² In each model, J value was the response variable and observer combination was the fixed effect. Correlation between multiple sections in each patient was considered by including a patient as a random effect. Finally, an unstructured correlation matrix was used to account for the correlation among multiple J values calculated from different combinations of observer outlines for each section. Estimates, confidence intervals (CIs), and p-values based on these models are reported. Analyses were performed using SAS 9.2 software.

The complexity of a tumor outline was quantified by its maximal entropy^{13, 14}E=log₂(2L∕C), where L is the length of the outline and C is the length of the convex hull of the outline. Maximal entropy is 1 (when the outline is convex) and increases to infinity as the length of the curve increases without a corresponding change in the convex hull. The relationship between outline complexity and whether or not an outline was altered was determined by applying the Wilcoxon sum-rank test between the maximal entropy of Phase 1 outlines that were not altered and the maximal entropy of Phase 1 outlines that were altered.

RESULTS

Analysis was performed on 118 (n) of the original 150 sections. Seventeen sections were excluded from analysis because all three observers agreed that no mesothelioma tumor was present in those sections, and 15 additional sections were excluded from analysis because only one observer identified and outlined tumor in those sections. The average J values calculated between observers’ Phase 1 outlines are recorded in Table 1. A statistically significant decrease in the J value existed in measurements involving Observer B (the resident). The J value for the two attending radiologists (A and C) was, on average, 0.188 higher than the J values involving measurements by Observer B, and this difference was statistically significant (p<0.01).

The average J values over all sections between the Phase 2 outlines of Observers A and B, Observers A and C, and Observers B and C were calculated when the altered outlines were derived from a common initial outline. These values (Table 3) were substantially higher (p<0.001 for all comparisons) than the average J values calculated between observers’ Phase 1 (original) outlines (Table 1), implying an increased interobserver precision between observers when the same initial outline is presented to all observers.

The average J value over all sections ranged between 0.320 and 0.559 when an observer’s Phase 1 (original) outlines were compared to that observer’s Phase 2 outlines altered from the Phase 1 outlines of a different observer (Table 2, columns 2 and 3). The average J value over all sections when an observer altered their own Phase 1 outlines (Table 2, column 1) ranged from 0.860 to 0.957 and were significantly higher than J values resulting from alteration of another observer’s Phase 1 outlines (p<0.001 for each of the comparisons). Comparing Table 2, column 1 to Table 2, columns 2 and 3 implies that the presence of an initial outline alters an observer’s perception of the structure boundary (Fig. 2).

The percentage of altered outlines where observers made only minor alterations to the initial outlines with which they were presented [defined as J(Phase 1,Phase 2)>0.90] are presented in Table 4. The relationship between tumor complexity and observer alteration was quantified by applying the Wilcoxon rank-sum test. The median maximal entropy of Phase 1 outlines that were and were not altered in Phase 2 was 1.1721 and 1.2108, respectively. The distribution of the two groups differed significantly (p=0.016).

Table 4.

Percent of alteration tasks where only minor alterations were made by the observer [J(Phase 1,Phase 2)<0.9].

	Observer A	Observer B	Observer C
	Phase 1 outline (%)	Phase 1 outline (%)	Phase 1 outline (%)
Observer A altering	91.5	50.8	65.3
Observer B altering	78.8	78.0	70.3
Observer C altering	88.1	65.3	82.2

DISCUSSION

The time-consuming nature of segmenting a structure of interest by manually drawing outlines limits the utility of the technique in both research and clinical settings. One approach for time-cost reduction is to initialize scans with outlines that the observer can manually adjust as necessary; however, the results of this study imply that manual outlines created when initial outlines are present are substantially different from those created without initial outlines present. Time requirements were not a direct consideration in our study, and all observers were encouraged to create or modify tumor outlines to reflect their best interpretation of tumor margins irrespective of time. Even though time data were not captured, the essential finding of this study is that the differences between observers’ original outlines and the modified outlines they created from presented initial outlines were so substantial that any realistic time savings would be far outweighed by this bias, despite the practical willingness to tolerate some loss of accuracy to gain some savings in time.

The interobserver variability in manual outlines of large structures (i.e., mesothelioma tumor) observed in this study was consistent with findings in the small and compact pharengolaryngeal tumors measured by Geets et al.³ The presence of an initial outline substantially influenced both the intraobserver and interobserver variability. Mathematically, implementing initial outlines as an observer aid causes the manual segmentation to become a function of both the observer and the initial outlines presented to the observer. Agreement between observer outlines (as measured by J) was substantially increased when observers altered a common initial outline. Comparing corresponding values in Tables 1, 3 demonstrates that outlines created in the presence of a common initial outline will be more precise (i.e., a higher degree of agreement exists among observers) than outlines created without initial outlines present. The increase in interobserver precision, as measured by interobserver variability (Tables 1, 3), and dependence of intraobserver precision on the initial outline, as measured by calculating J between an observer’s Phase 1 outlines and outlines altered by that same observer in Phase 2 (Table 2), are related by the extent that initial outlines were altered by the observers. The majority of alterations made by observers were minor, thus producing high average J values between the initial and altered outlines (Table 4) and consequently higher agreement between observers when altering a common initial outline (i.e., increased interobserver precision). Similarly, intraobserver precision was decreased because the Phase 1 outlines of different observers demonstrated substantial differences, and the minor alterations often made by an observer failed to transform the Phase 1 outline of a different observer into a close approximation of the Phase 1 outline of the altering observer.

Mesothelioma tumor outlines may exhibit a range of complexities. The results of the Wilcoxon sum-rank test indicated that there was a significant difference between the complexities of Phase1 outlines that were altered in Phase 2 and the complexities of Phase 1 outlines that were not altered in Phase 2. Outlines that were altered in Phase 2 were significantly less complex (based on the maximal entropy feature) than those that were not altered. The lower complexity for outlines that were subsequently altered has two possible causes. First, a less complex outline is simpler to alter because it is composed of fewer vertices per unit length of the outline. Second, when the boundary between tumor and surrounding tissue is not well defined, the observer must estimate the placement of outline vertices. This estimation is likely to result in less complex outlines because the observer will essentially interpolate between adjacent image areas where the tumor boundary is more clearly defined. These observer-estimated portions of the outline are more likely to be altered in Phase 2 because they are less clearly defined within the image.

Three limitations of this study should be noted. First, a large number of patients and sections were presented to the observers for Phase 1 outlining. This resulted in a large set of Phase 2 alteration tasks for each observer to review and alter. However, only three observers provided Phase 1 and 2 outlines. Further, the less experienced observer created Phase 1 outlines that were significantly different from the more experienced observers. Future work will increase the number of observers and allow for a stratification of findings by experience level. Second, the purpose of allowing observers to alter existing outlines is to mitigate the time-cost necessary to segment a structure of interest. The amount of time necessary to alter initial outlines (and thus the time-cost improvement by implementing such a strategy) will be directly influenced by both the structure being outlined and the accuracy of the initialization. Third, the frequency and extent of observer alteration may be a function of the subtlety of the tumor boundary. The mesothelioma tumors used in this study often demonstrate both high-contrast boundaries (tumor∕lung interface) and low-contrast boundaries (tumor∕chest wall interface) within the same tumor. Future research should focus on structures that can be classified as either low or high contrast to determine the impact of subtlety on alteration frequency and extent.

This study investigated the influence of an initial outline on the manual segmentation of structures in medical images. The results of this study indicate that observers tend to make only small alterations to initial outlines, even when those initial outlines are quite different from their own independent outlines, and thus observers are substantially influenced by the presence of an initial outline. Accordingly, the presence of initial outlines may be detrimental to specific clinical tasks such as tumor volume calculations, tumor response assessment, and subsequent patient management decisions, although such targeted clinical impact was not directly investigated in this study. The decision to implement initial outlines (such initializations often being created by a computerized method) to facilitate clinical tasks such as volumetric measurements must be determined on a task-by-task basis. Factors such as the accuracy of the method creating the initial outlines, the intraobserver precision of competing measurement methodologies (e.g., diameter vs area vs volume), and the necessity of multiple observer measurements (and their interobserver precision) should be considered when determining whether to implement previous outlines into existing measurement and evaluation schemes.