Computer-aided measurement of liver volumes in CT by means of geodesic active contour segmentation coupled with level-set algorithms

Abstract

Purpose: Computerized liver extraction from hepatic CT images is challenging because the liver often abuts other organs of a similar density. The purpose of this study was to develop a computer-aided measurement of liver volumes in hepatic CT.

Methods: The authors developed a computerized liver extraction scheme based on geodesic active contour segmentation coupled with level-set contour evolution. First, an anisotropic diffusion filter was applied to portal-venous-phase CT images for noise reduction while preserving the liver structure, followed by a scale-specific gradient magnitude filter to enhance the liver boundaries. Then, a nonlinear grayscale converter enhanced the contrast of the liver parenchyma. By using the liver-parenchyma-enhanced image as a speed function, a fast-marching level-set algorithm generated an initial contour that roughly estimated the liver shape. A geodesic active contour segmentation algorithm coupled with level-set contour evolution refined the initial contour to define the liver boundaries more precisely. The liver volume was then calculated using these refined boundaries. Hepatic CT scans of 15 prospective liver donors were obtained under a liver transplant protocol with a multidetector CT system. The liver volumes extracted by the computerized scheme were compared to those traced manually by a radiologist, used as “gold standard.”

Results: The mean liver volume obtained with our scheme was 1504 cc, whereas the mean gold standard manual volume was 1457 cc, resulting in a mean absolute difference of 105 cc (7.2%). The computer-estimated liver volumetrics agreed excellently with the gold-standard manual volumetrics (intraclass correlation coefficient was 0.95) with no statistically significant difference (F=0.77; p(F≤f)=0.32). The average accuracy, sensitivity, specificity, and percent volume error were 98.4%, 91.1%, 99.1%, and 7.2%, respectively. Computerized CT liver volumetry would require substantially less completion time (compared to an average of 39 min per case by manual segmentation).

Conclusions: The computerized liver extraction scheme provides an efficient and accurate way of measuring liver volumes in CT.

INTRODUCTION

More than 7300 liver transplantations are performed each year in the U.S.¹ Evaluating total and segmental liver volumes is crucial because graft size is a major predictor of success for both donor and recipient. A liver remnant volume of 30%–40% of the original volume is required for the donor to survive, whereas a minimum of 40% of the standard liver mass is required by the recipient.² Therefore, accurate, noninvasive liver volumetry is necessary^{3, 4, 5, 6} for planning liver transplantation. Manual tracing of the liver boundary on each CT image is the current “gold-standard” technique for liver volume calculation. Although manual tracing provides accurate results, it is very time consuming and subjective. It takes more than 30 min, on the average, to determine the liver volume for one patient.⁷ In addition, manual volumetry has relatively large intra- and interobserver variations. With new, advanced technology, computerized liver volumetry could replace the current gold-standard manual liver volumetry for accurate calculation of liver volumes. To this end, the accuracy of computerized volumetry must be comparable with manual volumetry.

Researchers have developed computerized liver extraction schemes in CT. Bae et al.⁸ developed an automated liver segmentation scheme based on thresholding. They evaluated their scheme with four cases by comparing the liver area in each slice with that drawn by a radiologist. Gao et al.⁹ developed an automated liver segmentation scheme based on thresholding and morphological filtering and tested their scheme on ten cases. Nakayama et al.⁷ developed an automated liver segmentation method based on thresholding, feature analysis, and region growing. They compared the liver volumes estimated by their scheme for 35 cases to those obtained by manual tracing by a radiologist and achieved a correlation coefficient of 0.883 between them. Selvera et al.¹⁰ developed a three-stage automated liver segmentation scheme that employs preprocessing for excluding neighboring structures, k-means clustering, and multilayer perceptron for classification, and postprocessing for removing mis-segmented objects and smoothing liver contours. They tested their scheme on 20 cases. Okada et al.¹¹ developed an automated scheme based on a probabilistic atlas and a statistical shape model, and they tested their scheme on eight cases. The above computerized liver extraction schemes employed thresholding and morphologic filtering, region growing, k-means clustering, or a statistical shape model for extracting the liver. Although the above papers stated that their automatically determined volumes were comparable to gold-standard volumes manually determined by a radiologist, there is still room for improvement in the accuracy of the liver extraction. In other areas, researchers reported the advantages of active contour models and level-set algorithms over conventional segmentation techniques such as thresholding,¹² morphologic filtering,¹³ and region growing.^{13, 14} There is a potential for improving the liver extraction accuracy with new techniques such as geodesic active contour models and level-set algorithms.

Our purpose of this study was to develop a computerized liver extraction scheme based on a geodesic active contour segmentation technique coupled with level-set algorithms for measuring liver volumes in hepatic CT. (We use the term “extraction” instead of “segmentation” here to avoid potential confusion for abdominal radiologists because segmentation is a specific term used by abdominal radiologists for segmentation of liver segments. We still use the term segmentation for image segmentation techniques because it is a well-accepted standard term for such techniques in the pattern-recognition community.) We evaluated our scheme on 15 prospective liver donors under a liver transplant protocol with a multidetector CT system, and we compared computerized volumetry to gold-standard manual volumetry.

MATERIALS AND METHODS

The Institutional Review Board (IRB) approved this retrospective study. Informed consent for the use of cases in this study was waived by the IRB because patient data were deidentified. This study complied with the Health Insurance Portability and Accountability Act, and it met all standards for good clinical research according to the National Institutes of Health’s (NIH) and local IRB’s guidelines.

Hepatic CT database

Our database consisted of dynamic contrast-enhanced hepatic CT scans of 15 prospective living liver donors. Scans were obtained under a liver transplant protocol with a multidetector CT system with a 16-, 40-, or 64-channel detector scanner (Brilliance, Philips Medical Systems, The Netherlands). Contrast medium was administered to the patients for acquisition of arterial-phase and portal-venous-phase CT images. The CT scanning parameters included collimation of 3 mm (n=11) or 4 mm (n=4) and reconstruction intervals of 2.5 mm (n=2) or 3.0 mm (n=13). Each reconstructed CT slice had a matrix size of 512×512 pixels, with an in-plane pixel size of 0.5–0.8 mm.

A board-certified abdominal radiologist (specializing in liver imaging) traced the contour of the liver on each CT slice very carefully. The number of slices in each case ranged from 52 to 77 (average: 62.3). The time required to complete the manual tracing was recorded. To calculate the entire liver volume for each case, we summed the volumes obtained by multiplying the areas of the manually traced regions in each slice by the reconstruction interval. [We do not use the terms slice thickness or collimation because they do not always equal a reconstruction interval (or distance between slices.)] Liver volumes obtained by use of our computerized liver extraction scheme were compared to manual liver volumes, used as the “current gold standard.”

Computer-aided measurement scheme for liver volumes in CT

We developed a computerized liver volumetry scheme in CT that is based on fast marching and geodesic active contour segmentation¹⁵ coupled with level-set contour evolution,¹⁶ as shown in Fig. 1. The scheme was applied to portal-venous-phase images in order to maximize the intensity difference between liver parenchyma and nonliver tissue.

Figure 1.

Flow chart for our computer-aided measurement scheme for liver volumes in hepatic CT.

Preprocessing for extraction

To accurately segment the liver from a series of axial, portal-venous-phase CT images using a level-set-based methodology, the images must first be preprocessed by filters that reduce noise and enhance anatomic structures. Subsequent to combining the series of CT images into a 3D volume, f(x,y,z), the volume was passed through a noise-reduction filter employing an anisotropic diffusion algorithm¹⁷ to obtain a noise-reduced CT image, f_N(x,y,z). This denoising filter smoothes noise in the image while preserving structures such as liver vessels and liver boundaries. The anisotropic diffusion filter follows a differential equation called a modified curvature diffusion equation,¹⁸

$$\frac{\partial f}{\partial t}=\left|\nabla f\right|\nabla \cdot c\left(\left|\nabla f\right|\right)\frac{\nabla f}{\left|\nabla f\right|},$$ (1)

where ∇ is the gradient operator,

$$c\left(\left|\nabla f\right|\right)=e^{-{\left(\left|\nabla f\right|∕K\right)}^2}$$ (2)

is the diffusion coefficient, and K is a user-specified conductance parameter (set to 3.0 in this scheme) to control the filter’s sensitivity to edge contrast.

Subsequent to the anisotropic diffusion noise reduction, a scale-specific gradient magnitude filter was applied to the noise-reduced CT images to enhance the liver boundaries for the succeeding level-set-based segmentation. The scale of enhancing edges is controlled by the standard deviation σ of a Gaussian filter, which is applied prior to a differential operator, represented by

$$f_G=f_N\ast f_g\left(\sigma \right)=f_N\ast \frac{1}{{\left(2\pi \right)}^{1∕2}\sigma }{\text{exp}}^{-\left(x^2+y^2+z^2\right)∕2{\sigma }^2},$$ (3)

where  ^* denotes a convolution operator. The standard deviation σ was set to 0.5 in this scheme. The following differential operator was used for calculating the magnitude of the image gradient at each voxel:

$$f_M=\left|\nabla f_G\right|=\sqrt{{\left(\frac{\partial f_G}{\partial x}\right)}^2+{\left(\frac{\partial f_G}{\partial y}\right)}^2+{\left(\frac{\partial f_G}{\partial z}\right)}^2}.$$ (4)

Receiving the gradient magnitude image, f_M(x,y,z), as input, a nonlinear grayscale converter enhanced the contrast of the liver parenchyma as a final preprocessing step prior to level-set-based segmentation. This converter was based on a sigmoid function, represented by

$$f_S=\frac{1}{1+{\text{exp}}^{\left\{-\left(f_M-\beta \right)∕\alpha \right\}}},$$ (5)

where α is a parameter specifying the intensity range to be enhanced and β is a parameter specifying a value at the center of the intensity range. α and β were −1.5 and 4.0 in this scheme, respectively. The voxel intensities of this enhanced volume were then normalized to floating point intensity values ranging from 0 to 1. This normalized volume was used as a speed function for the succeeding level-set-based segmentation.

Liver extraction

Extracting the liver from an abdominal CT volume was accomplished by use of a two-step approach involving a geodesic active contour model¹⁵ with a level-set methodology.¹⁶ The fast-marching level-set algorithm¹⁹ was used to estimate an initial rough contour of the liver; then, a geodesic active contour level-set algorithm¹⁵ was used to refine this initial approximation.

For generating an initial contour that roughly estimates the shape of the liver, a fast-marching level-set algorithm¹⁹ was employed in this scheme. This algorithm is a simplified, efficient version (or a special case) of general level-set algorithms. In the fast-marching level-set algorithm, the evolution of a closed contour (or curve) is expressed as a function of time t, with speed, F(p), in the normal direction at a point, p, on the contour. The time at which the contour crosses a point, p, is obtained by solving the following partial differential equation, called the Hamilton–Jacobi equation,

$$\frac{d\psi }{dt}=-F\left(p\right)\left|\nabla \psi \right|,$$ (6)

where ψ(p,t) is a level-set function, with the initial level set at t=0 given by

$$\psi \left(\mathbf{p},t=0\right)=\Gamma ,$$ (7)

and Γ a closed contour (curve) in R² space. The fast-marching algorithm requires one or more seed points from which the initial contour can be generated. Naturally, the seed points (5–10 points for each case with a median of 7; it took about 15 s for each case to put seed points) in our scheme were placed by the radiologist within the borders of the liver; this allowed the fast-marching algorithm to expand outward toward the anatomic borders of the liver. The output of the fast-marching algorithm is a time-crossing map that indicates, for each pixel, how much time it would take for the front representing the contour to arrive at the pixel location. The level-set evolution stops if the maximum number of iterations is reached. Because the front (i.e., the contour) propagates continuously over time, it is desirable to stop the process once a certain time has been reached. The maximum number of iterations was set to 100 in this scheme.

Next, a geodesic active contour level-set segmentation refined the initial contour (i.e., the initial level set) determined by the fast-marching algorithm to approximate the liver boundaries more precisely. The evolution of a geodesic active contour level-set function, ψ(p,t), is controlled by the following partial differential equation:

$$\frac{d\psi }{dt}=-\alpha \mathbf{A}\left(\mathbf{p}\right)\cdot \nabla \psi -\beta F\left(\mathbf{p}\right)\left|\nabla \psi \right|+\gamma Z\left(\mathbf{p}\right)\kappa \left|\nabla \psi \right|,$$ (8)

where A is an advection vector function, F is an expansion (or speed) function, and Z is a spatial modifier function for the mean curvature κ. The user-defined scalar constants α, β, and γ allow us to determine the extent to which each of the three functions (advection, expansion, and curvature) affect the change, dψ∕dt, of the contour of the level set, ψ. In this scheme, α=1.0, β=0.5, and γ=5.0. The spatial modifier term acts as a smoothing term where areas of high curvature, assumed to be due to noise, are smoothed out. This algorithm requires an initial level set that represents a rough estimate of the actual contour of the liver. We used the initial contour determined by the fast-marching algorithm as the initial level set. In this way, the level-set algorithm only refines the initial contour according to the partial differential equation [Eq. 8]. This algorithm used the liver-parenchyma-enhanced image as the speed (or expansion) term for evolution of the front (i.e., contour). With this image, the expansion speed of the front is very low close to high image gradients, whereas it moves rather fast in low-gradient areas. This arrangement makes the contour expand rapidly until it reaches the edges of anatomic structures in the image and then slow down rapidly as these edges are approached. The level-set evolution stops if the convergence criterion is reached. The convergence criterion is defined in terms of the root-mean-square (RMS) change in the level-set function. The evolution has converged if the RMS change is below a user-specified threshold, determined as 0.02 in this scheme.

After the geodesic active contour level-set segmentation algorithm generated a refined contour of the liver, thresholding was employed for converting the output level set to a binary liver segmentation image. For eliminating potential anomalies—particularly impulse noise that could result from an imperfect extraction of the liver—a median filter was applied to the extracted liver. Then, connected-component labeling^{20, 21} was applied to the binary liver images for the calculation of the area of each extracted liver region. Finally, the liver volume was calculated by summing up of the areas of the liver region in each slice.

Evaluation of the computer-aided measurement scheme

The computer-estimated liver volumes were compared to the gold-standard manually determined liver volumes with respect to the mean and difference in the liver volume. Agreement between computer-estimated volumetry and the manual volumetry was evaluated by using the intraclass correlation coefficient.^{22, 23} Analysis of variance was performed to obtain the F-statistics. Linear association was also evaluated by using Pearson’s product-moment correlation coefficient as additional information. A t-test for the significance of the coefficient was performed. Figure 2 shows a schematic diagram for evaluating a computer-estimated liver region compared to the gold-standard manually drawn liver region. We determined true-positive (TP) segmentation, false-negative (FN) segmentation, false-positive (FP) segmentation, and true-negative (TN) segmentation for detailed analysis. TP was defined as an overlapping area (the number of pixels) between a computer-estimated region, C, and a gold-standard manual region, G, represented by TP=C∩G. FN was represented by FN=G−C∩G. FP was represented by FP=C−C∩G. TN was represented by TN=I−C∪G, where I is the entire image. We defined the accuracy, sensitivity, and specificity of the extraction as

$$\text{accuracy}=\left(\text{TP}+\text{TN}\right)∕I,$$ (9)

$$\text{sensitivity}=\text{TP}∕G=\text{TP}∕\left(\text{TP}+\text{FN}\right),$$ (10)

$$\text{specificity}=\text{TN}∕\left(\text{TN}+\text{FP}\right),$$ (11)

respectively. We also defined the percent (absolute) volume error between the computer volume and the manual volume E as

$$E=\left|\left(\text{FN}+\text{FP}\right)∕G\right|.$$ (12)

Figure 2.

Schematic diagram for evaluating a computer-estimated region compared to a “gold-standard” manually drawn region.

In order to examine the robustness of our scheme against seed point changes, we conducted an experiment to move the seed points selected by a radiologist systematically. We moved all of the original seed points by a certain distance d. The locations of new seed points were determined randomly, i.e., each new seed point was on a circle with a radius of d, the center of which was at the location of the original seed point. We changed the distance between the original seed points and the new seed points, d, from 3 to 12 mm at a step of 3 mm, because it is not likely that one person will select new seed points that are different from the seed points selected by another person by more than 10 mm, on the average. We created five different sets of new seed points with each distance (i.e., 20 sets of new seed points in total). We applied our scheme with the 20 sets of new seed points and evaluated the performance.

RESULTS

Figure 3 illustrates the intermediate images taken from each step of our scheme for an example case. The noise in the original CT image in Fig. 3a was reduced by the anisotropic diffusion filter, while maintaining the liver structures such as the portal vein and the liver border, as shown in Fig. 3b. A scale-specific gradient magnitude filter was applied to the noise-reduced image to enhance the liver boundary, as shown in Fig. 3c. The nonlinear grayscale converter enhanced the liver boundary for the use of the subsequent geodesic active contour segmentation, as shown in Fig. 3d. Finally, the liver was extracted by using the fast-marching and geodesic active contour level-set segmentation, as shown in Fig. 3e. After the extraction, the median filter was applied for removal of impulse noise in the extracted liver. Liver volumes were calculated using the extracted liver regions.

Figure 3.

Illustration of the resulting images at each step in our scheme. (a) Original CT image. (b) Anisotropic diffusion noise reduction. (c) Scale-specific gradient magnitude calculation. (d) Nonlinear grayscale conversion. (e) Geodesic active contour segmentation.

The mean liver volume obtained by use of our scheme was 1504 cc, with a standard deviation of 407 cc (range: 956–2381 cc), whereas the mean gold-standard manual volume was 1457 cc with a standard deviation of 357 cc (range: 984–2439 cc), with a mean absolute difference of 105 cc (7.2%), as shown in Table 1. The relationship between the computer-estimated volumes and the gold-standard manual volumes is shown in Fig. 4. The two volumetrics reached excellent agreement (the intraclass correlation coefficient was 0.95), with no statistically significant difference for variance (F=0.77; p(F≤f)=0.32). Pearson’s product-moment correlation coefficient was 0.96 at a nonstatistically significant level (p=11.8). The average accuracy, sensitivity, specificity, and percent volume error were 98.4%, 91.1%, 99.1%, and 7.2%, respectively, as shown in Table 2. Figure 5 shows the results of the robustness study for our scheme in terms of seed point changes. When the distance between the new seed points and the original seed points was less than or equal to 9 mm, the ICC between computer-estimated volumes with new seed points and the gold-standard manual volumes was comparable to the original ICC. Any combinations of ICCs did not achieve a statistical significance difference (p=0.15–0.49). Figure 6 illustrates computerized liver extraction and gold-standard manual liver extraction for a case with a high accuracy (99.2%). The computerized liver extraction agrees almost perfectly with the gold-standard manual liver extraction for a slice through the superior portion of the liver, as Fig. 6b shows. There is a small FN segmentation (a tip of the liver) and a small FP segmentation (a portion of the vena cava) in a slice of the inferior liver of the same case, as Fig. 6d shows.

Table 1.

Comparison between computer-estimated volume and gold-standard manual volume.

	Average	Standard deviation
Computer volume (cc)	1504	407
Manual volume (cc)	1457	357

Figure 4.

Relationship between computer-estimated volumes and “gold-standard” manual volumes. The two volumetrics reached an excellent agreement (the intraclass correlation coefficient was 0.95), with no statistically significant difference for variance (F=0.77;p(F≤f)=0.32).

Table 2.

Summary of quantitative evaluation of computerized liver extraction compared to gold-standard manual liver extraction.

	Average	Standard deviation
Accuracy (%)	98.4	0.8
Sensitivity (%)	91.1	5.0
Specificity (%)	99.1	0.5
Percent volume error (%)	7.2	4.9

Figure 5.

Robustness of our scheme against seed point changes. All of the original seed points were randomly moved by a distance d. The error bar indicates the standard deviation of ICCs between computer-estimated volumes with new seed points and gold-standard manual volumes in 5 runs.

Figure 6.

Illustrations of computerized liver extraction and “gold-standard” manual liver extraction for a case with a high accuracy (99.2%). (a) Original CT image from the case. (b) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). (c) Original CT image (different slice) from the same case. (d) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). Note that the contrast of the images in (b) and (d) is reduced so that the contours can be seen well. Note also that a manual contour (thin dashed contour) cannot be seen when it overlaps a computer contour (thick solid contour).

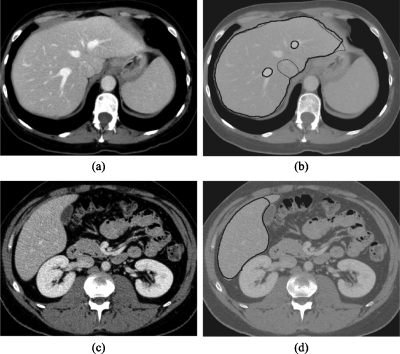
Figure 7 illustrates two cases with more typical results (i.e., accuracies close to the average value). Overall, the computerized scheme extracted the liver accurately, although there were FP and FN extractions. There is an FP extraction due to the vena cava abutting the liver and FN extractions due to the portal veins in the case shown in Fig. 7b. Although the exclusion of the portal veins was considered as FN extractions, this consideration is controversial. We discuss this point in Sec. 4. In Fig. 7d, a FN extraction representing a small tip of the liver is shown. This error occurred because the level-set segmentation stopped before it reached the liver boundary, which is likely due to the high noise level in this particular case. Figure 8 illustrates examples of FP and FN extractions. Major FP sources included the vena cava, heart, and kidney—all which abut the liver. Major FN sources included a low-contrast liver boundary, a high-intensity-value artifact, an artifact due to the partial volume effect, and density inhomogeneity secondary to focal fat deposition. Note that the same window∕level display setting was applied to all cases in Figs. 678.

Figure 7.

Illustrations of computerized liver extraction and “gold-standard” manual liver extraction for two cases with accuracies (98.5% for the upper case; 98.6% for the lower case) close to the average accuracy (98.4%). (a) Original CT image from one of the cases. (b) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). (c) Original CT image from the other case. (d) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). Note that the contrast of the images in (b) and (d) is reduced so that the contours can be seen well. Note also that a manual contour (thin dashed contour) cannot be seen when it overlaps a computer contour (thick solid contour).

Figure 8.

Illustrations of major FP and FN sources. (a) Original CT image from one case. (b) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). There is an FP due to the heart (a), an FN due to a high-intensity region (b), and an FP due to the vena cava (c). (c) Original CT image from another case. (d) Computerized liver extraction (thick solid contour) and “gold-standard” manual liver extraction (thin dashed contour). There are FPs due to the skeletal muscles (mainly, intercostal muscles) (d), an FP due to part of the vena cava (e), and an FP due to part of the right kidney (f). Note that the contrast of the images in (b) and (d) is reduced so that the contours can be seen well. Note also that a manual contour (thin dashed contour) cannot be seen when it overlaps a computer contour (thick solid contour).

The processing time by the computerized scheme was 2–5 min per case on a PC (Intel, Xeon, 2.7 GHz), whereas that by manual extraction was 28–48 min per case with an average of 38.8 min per case (standard deviation=5.4 min).

DISCUSSION

Although we achieved an excellent agreement between computer-estimated liver volumes and gold-standard manual liver volumes (the intraclass correlation coefficient was 0.95), there are still occasional FPs and FNs because the liver often abuts other organs of similar density. In addition, inaccurate extraction was often the result of the variable liver density across different studies∕patients, as density depends on acquisition timing and contrast material characteristics. Therefore, accurate computerized liver extraction is very challenging. In the future, we will need to eliminate such FP and FN sources to improve the accuracy further. One way to eliminate FP sources such as the vena cava, kidney, heart, and intercostal muscles would be to develop and incorporate a separate method of segmenting each specific FP source. For example, ribs have relatively consistent CT values and are easy to identify. If we were to use ribs as landmarks, the intercostal muscles located between the ribs could be excluded.

Although our scheme achieved an excellent correlation with gold-standard manual liver volumes (Pearson’s product-moment correlation coefficient was 0.96), this does not reach the level of the variation between expert radiologists [the interobserver correlation between two radiologists’ manual volumes was 0.997 (Ref. ²⁴)]. There are FP and FN extractions that require manual correction. This can, however, be accomplished rapidly with routine manipulations. The substantial amount of time saved by using the computerized volumetric methodology may justify the small error rate (average volume error E=7.2%) compared to the manual process, which averages approximately 39 min per case.

We considered the exclusion of hepatic vessels to be FN extractions in this study because manual CT liver volumetry includes hepatic vessels. Studies^{4, 7} have shown, however, that CT liver volumetry overestimates the liver volumes when compared to actual liver volumes measured after resection. One possible explanation for this phenomenon is that actual liver volumes are measured with less blood in the hepatic vessels. Therefore, the exclusion of major hepatic vessels may be “desirable” FN extractions.

In order to examine the seed point dependence on the performance of our scheme, we performed an experiment with seed points selected by a different person. An imaging scientist selected an independent set of seed points for our scheme because a radiologist may not always select seed points, but a radiologic technologist or imaging scientist may do this in an actual clinic. This should be a more severe test for evaluating the robustness of our scheme, compared to a study with a different radiologist, because variation between a radiologist and a radiologic technologist (or imaging scientist) is expected to be larger than that between radiologists. We employed our scheme with the independent set of seed points and evaluated the performance. The ICC between the computer-estimated volumes with the independent seed point set and the gold-standard manual volumes was 0.95. The interobserver agreement was an ICC of 0.95.

A limitation of this study is the use of a small number of cases. We used 15 cases for evaluating our scheme, whereas other studies used 4 cases,⁸ 35 cases,⁷ 20 cases,¹⁰ 10 cases,⁹ and 9 cases.¹¹ In general, a small number of cases limit the variations among cases. In computerized liver extraction studies, however, case variations would be relatively small, compared to studies involving abnormal cases such as computer-aided diagnosis^{25, 26} because prospective donors have normal livers. Nonetheless, we will need to increase the number of cases for evaluation.

A limitation of the evaluation in this study is that the gold-standard manual volumes were determined by a single expert radiologist. Ideally gold-standard manual volumes are determined by multiple expert radiologists who have sufficient experience in liver diagnosis. This ideal evaluation would not be feasible at all institutions because not many institutions have a number of such radiologists who are sufficiently experienced in liver diagnosis. Although researchers evaluated their automated liver extraction schemes with gold-standard manual volumes in their studies,^{7, 8, 9, 10, 11} none of the studies used gold-standard volumes determined by multiple radiologists, probably for the above reason. We used manual volumes determined by a single experienced radiologist (more than 15 years of experience in liver diagnosis) as gold standard because we thought that volumes determined manually by a mixture of inexperienced and experienced radiologists or by multiple inexperienced radiologists might not be reliable, compared to volumes determined very carefully manually by a single experienced radiologist. More importantly, because the interobserver variation in CT volumetry is considered to be small (the interobserver correlation between two radiologists’ manual volumes was 0.997 in a study²⁴), volumes determined by multiple radiologists and those by a single radiologist would not differ much. Although this single radiologist’s gold standard may have some deviation (or bias) in accuracy in liver volumetry, we believe that such a deviation would be minimal because the interobserver variation is usually small,²⁴ living liver donor cases (as opposed to cases with disease) were used in this study, and the manual volumes were obtained by careful tracing by a radiologist who has substantial experience in liver diagnosis.

There are several parameters to adjust in this scheme. We first used the original parameter values recommended or used in the original papers; then, we adjusted the parameters by empirical analysis with several trials. Thus, the parameters were not optimized. In the future, we will need to optimize the parameters by using a larger number of cases.

We cannot compare our scheme with other schemes in literature directly because the cases used were different for each study, but we discuss advantages and limitations of the schemes. There are thresholding-based schemes,^{7, 8, 9} a classifier-based scheme,¹⁰ and a statistical model-based scheme¹¹ for extracting the liver in literature. Although the thresholding-based schemes provide a simple, efficient way to extract the liver, they may not be robust against variations in liver CT density across different studies∕patients, and they may include other organs of similar density in the extraction region. whereas our scheme based on the active-contour level-set method would be relatively robust against such variations, but would not be robust against noise because the active-contour level-set method relies on noise-sensitive edge information instead of the gray-level information used in thresholding. To minimize this shortcoming of the edge-information-based method, we employed an edge-preserving noise-reduction technique called anisotropic diffusion. Both classifier-based schemes and statistical model-based schemes generally require a relatively large number of training cases to determine the free parameters of the model (or classifier) adequately, whereas thresholding-based schemes and the active-contour level-set-based scheme have a smaller number of free parameters to be determined.

The liver extraction scheme developed in this study can be used as a first and necessary step in computer-aided diagnosis for the detection of liver tumors in hepatic CT. FN extractions by the liver extraction scheme may decrease the overall sensitivity in the detection of liver tumors by a computer-aided diagnostic scheme, whereas FP extractions may decrease the overall specificity (or increase the FP rate). For such applications, we will need to test our scheme with abnormal cases including those with liver tumors. Consequently, we may need to adjust the parameters to include liver tumors within the extracted liver volumes.

CONCLUSION

We developed a computer-aided measurement scheme employing a fast-marching and geodesic active contour segmentation coupled with level-set algorithms for measuring liver volumes in CT. CT liver volumetrics determined by our computerized scheme agreed excellently with gold-standard manual volumetrics, and they required substantially less completion time. Our computerized scheme provides an efficient and accurate way of measuring liver volumes in CT; thus, it would be useful for radiologists in their measurement of liver volumes.