Abstract
This paper presents a novel perspective of Robotic Stem Cells (RSCs), defined as the basic non-biological elements with stem cell like properties that can self-reorganize to repair damage to their swarming organization. “Self” here means that the elements can autonomously decide and execute their actions without requiring any preset triggers, commands, or help from external sources. We develop this concept for two purposes. One is to develop a new theory for self-organization and self-assembly of multi-robots systems that can detect and recover from unforeseen errors or attacks. This self-healing and self-regeneration is used to minimize the compromise of overall function for the robot team. The other is to decipher the basic algorithms of regenerative behaviors in multi-cellular animal models, so that we can understand the fundamental principles used in the regeneration of biological systems. RSCs are envisioned to be basic building elements for future systems that are capable of self-organization, self-assembly, self-healing and self-regeneration. We first discuss the essential features of biological stem cells for such a purpose, and then propose the functional requirements of robotic stem cells with properties equivalent to gene controller, program selector and executor. We show that RSCs are a novel robotic model for scalable self-organization and self-healing in computer simulations and physical implementation. As our understanding of stem cells advances, we expect that future robots will be more versatile, resilient and complex, and such new robotic systems may also demand and inspire new knowledge from stem cell biology and related fields, such as artificial intelligence and tissue engineering.
Keywords: robot team, self-reconfiguration, regeneration, tissue engineering, self-organization, self-healing, morphallaxis, wound healing, morphogenesis, pattern formation, multi-agent systems
Introduction
Patterns are ubiquitous in the universe. They exist in biological organisms (e.g., animals, plants), physical entities (e.g., sand dunes or galaxies), as well as artifacts designed and constructed by humans. Robots are such artifacts and they may form patterns or configurations to accomplish the desired goals, tasks, and functions. When a swarm of robots suffer from damage, the remaining robots may reform their configuration and continue to function. In an analogy to regeneration in biology, we name this process as self-organization, self-healing, or self-regeneration, to emphasize the fact that this process is autonomous and free from any external triggers, commands or helps preset by the designers. In physics, chemistry, and computational theories, this process is also broadly referred as “self-organization.”
Self-organization, self-healing, and self-regeneration are pervasive in biology. Besides healing by growing new cells to replace the lost or damaged body parts, many organisms can self-repair by reorganizing the existing/remaining cells into a new whole without the addition of new cells or parts. This phenomenon of healing-by-reorganizing is historically labeled “morphallaxis” in biology. The extraordinary aspect of healing-by-reorganizing is that it is both scalable and distributed. The healing can start from any subset and recover the original whole with a less number of cells. In addition, individuals can reconstruct the global arrangement by their local and distributed knowledge in the new situation even if the original global pattern has become completely obsolete.
To understand self-organization and duplicate it in artifacts is a highly desired goal for science and engineering. Although computer science alone can make many advances in designing and building such systems, the best approach is probably still to learn directly from nature. The DNA based life systems have continued to survive and thrive in the dynamic and often hazardous environments on earth. Organisms and species have adapted to unexpected disasters (change of climate, volcano, meteorites, glacier, etc.) and evolved mechanisms to heal, repair and regenerate from unexpected injuries from the environment or predators. The ability to cope with these injuries is fundamental to the survival of individual organisms as well as their species. Over millions of years of evolution, different healing strategies have been evolved in different animals. In the search for a systematic technology for self-regeneration, it would be wise to learn from these strategies. Specifically, we ask, what are the biological mechanisms of self-regeneration? Can we mathematically model the entire self-regeneration process? Can we build artificial systems to demonstrate such a process?
This paper presents a new computational and robotic model to address these challenging questions. In computer simulations, robot-like elements from a random swarm can first (re)-construct a global coordinate system, and then form an organization with the desired spatial, visual, and temporal patterns. When damaged, the remaining elements will recover the same organizational patterns but in a scale proportional to the number of elements available. These elements exhibit properties similar to those of stem cells, for they dynamically change their behaviors, location, features, and function, based on the nature and the scale of the damage. Since the underlying mechanisms for this model are selected and developed purely from computational point of view, they might inspire interesting new research directions for stem cell biology and other related research fields.
From application point of view, the purpose of this dual research in robotics and stem cell biology is to develop new system architectures, representations, algorithms, and theories that will enable future information or networked systems or robots to learn and regenerate themselves in response to unforeseen errors and/or attacks, and automatically improve their ability to deliver critical services. Through this exercise, we wish to develop a new theory for self-organization and self-assembly as a foundation for building future self-regenerative and self-healing systems as well as for understanding the essence of such systems.
This paper is organized as follows. Section 2 introduces different strategies of regeneration in several animal models. Section 3 describes a list of features of stem cells that are critical for self-healing and self-organization. Section 4 proposes the concept of robotics stem cells in terms of their functional requirements, critical design features, communication, collaboration, topology discovery, and monitor and detection mechanisms which decide when and how self-healing should take place. Section 5 presents a new computational and robotic model for self-healing and self-organization in both computer simulation and physical prototypes. This model integrates positional information and pattern formation in both spatial and temporal domains. Section 6 introduces an example of a physical prototype of robotic stem cells called “SuperBot” whose modules are designed for self-reconfiguration, self-assembly, self-healing, and self-regeneration. Section 7 concludes the paper with a list of future research topics, with a precaution that the concept raised in this paper is at its early stage and there are still a lot to build upon.
Strategies of regeneration in animals
In single cellular organisms (analogous to the single robot in the following section), the fate of an organism is tied with the cell. In multi-cellular organisms (analogous to a team of multi-robots) such as the sponge, it is more like a pile of cells living tightly together with somatic and reproductive function. The differentiation of cell types is not obvious and there is no apparent blueprint for body plan. Therefore there is no clear cut spatial organization which has to be re-established following damages. In hydra, the animal has evolved two layers for body wall and has established a clear body plan with a head and a trunk. When a hydra is bisected, the existing cells in each separated half can reorganize and form a complete hydra with the original shape and structure, but in a scale proportional to the number cells that are available (Bode 2003). Hydra can even self-heal into a new whole from a piece or a collection of tissues as small as 1/100th the original body size (Shimizu et al., 1993). Yet the regenerative ability gradually becomes more restricted as animals become more complex. In vertebrates, they can not regenerate the other half of their bodies if unfortunately bisected. However, some amphibians and lizards can regenerate a limb or tail upon the loss of these appendages (Brockers and Kumar, 2005). In mammals, the ability to regenerate digits is limited to embryonic time or during the newborn period (Han et al., 2003). On the other hand, hairs undergo molting and regenerative cycles repetitively throughout their adult lives.
Analyses of these regenerative processes in animal models lead to the concept of stem cells. Stem cells are defined as cells that can undergo self-renewal, have the ability of changing differentiated cell types, and the ability to position themselves correctly. In the case of the hydra, the majority of cells in an individual have the ability to regenerate into a whole hydra. Therefore, in a broad way, the cells in a hydra behave as if they are stem cells. In the amputated amphibian limb, cells undergo de-differentiation to generate stem cells that can re-differentiate into different cell types. In organs such as hairs and feathers, they perform regeneration as a physiological process. The organs have special locations that contain stem cells that are activated to enter regeneration upon each molting cycle or plucking injury (Chuong et al., 2006).
Based on whether there is new cell proliferation, regeneration has been categorized as morphallaxis and epimorphosis in the classical literature (Table 1) (see discussion in Agata et al., 2007). In morphallaxis, organisms such as the hydra cope with injury by reorganizing the remaining cells into a new whole without adding new cells. In epimorphosis, organisms rely on cell proliferation to add new cells to replace the lost / damaged body parts. Cells activated to proliferate may be differentiated cells which have been de-differentiated (e.g., amputated amphibian limb), or niched stem cells (e.g., hairs and feathers). Indeed in the regeneration of most animals, activation of stem cells leads to a group of transient amplifying cells to generate enough “raw materials” for making new tissues.
TABLE 1.
COMPARISON OF BIOLOGICAL SYSTEMS AND ROBOTS IN REGENERATION BEHAVIOR
| Essentials | Morphallaxis | Epimorphosis | Current robots | Future robots |
|---|---|---|---|---|
| Proliferation (self-renewal) | No | Yes | No | ? |
| Multi-potentiality | No | Yes | No | possible |
| Topological configuration | Yes | Yes | Yes | Yes |
| Special stem cell niche | No | Yes | No | ? |
In Agata et al., 2007, the authors discussed the idea of doing away of the morphallaxis and epimorphosis terminology, since the authors consider that how positional identity is rearranged is the key issue of regeneration. Although the paper mentioned that it is possible to re-organize positional information of cells in the stump region after amputation of amphibian limb, no detailed mechanism was provided for how such positional information is updated and self-organized. In this paper, we propose and demonstrate such a mechanism using computer simulation. Whether our mechanism is the same as that used in the biological regenerative systems is an interesting topic for future research, but it is indeed possible for robotic elements to self-reassign their relative positions and roles in the process of self-healing and self-organization.
As for the terminologies of morphallaxis vs epimorphosis, since it is not yet practical with current technology for robots to dynamically produce new parts/elements in the field, the distinction of a regenerative model with and without the addition of new cells is still critical. Therefore, this paper will still use the term morphallaxis and focus more on the patterning of stem cells without new cell proliferation at the current stage.
Pattern formation of stem cells is based on cell rearrangement, i.e. change of cell adhesion, and can occur in the following two scenarios. (1) In development, a group of progenitor cells, all equivalent to begin with, can form periodically arranged primordia positioned between inter-primordial cells. The process can occur through Turing model (Turing, 1952; Meinhardt and Giere, 2000) and has been shown in the formation of feathers (Jiang et al., 2004) and hairs (Maini et al., 2006). Based on this, earlier we have developed “digital hormone model” for a team of robots in a field to form clustered or stripe configuration (Shen et al., 2004) and demonstrated the novel utility of this model in controlling self-reconfigurable robotic systems (Shen et al., 2002). (2) In regeneration, a patterned organism such as hydra encounter the loss of a body part, the rest of the cells undergo morphallaxis to redistribute the remaining cells and reform the hydra. In this paper, we would like to develop and demonstrate systems and algorithms so that a team of configured robots, when damaged, can regroup and reform the lost functional configuration even if the scale of the configuration is smaller than before.
In the following part, we will emphasize the morphallaxis type of regenerative patterning. However, in the proposed mechanism for self-healing and self-organizing, the positional information is useful for self-regeneration in general, regardless of the distinctions between morphallaxis and epimorphosis. It would also be interesting to study the phenomena in depth and further investigate the internal mechanism to see how a seemingly regular cell can become a stem cell when needed (Fröbius1 et al., 2003). Although the exact biological mechanism for such a complex process is still under active investigation, we can postulate the functional requirements of regeneration based on their adaptive behaviors. This challenging task is multidisciplinary in nature. From biology, one must learn from the latest research results about stem cells, including the key differences between stem cells and regular cells.
The essence of stem cell concept
Morphallaxis is a biological self-healing process by which organisms can restore either a part or the whole body from a fragment without cell proliferation. This process of tissue reorganization is observed in many lower animals following severe injury, such as bisection of the animal, and involves the movement of organs, and re-differentiation of tissues. The result is usually a smaller but complete individual, derived entirely from the tissues of part of the original animal. It is believed that such a reorganization process is the most efficient way for simple organisms to self-heal and self-regenerate. Hydra is a typical example of this sort, and observations suggest that the regular cells in Hydra have abilities similar to that of stem cells. One interesting question then is whether any regular cell has the potential to become a stem cell under the proper conditions. In other words, whether a regular cell can “de-differentiate” and then differentiate again for different functions. We now will examine what are the essential properties of stem cells that allow them to have the self-healing, self-regenerative, and self-organizing ability.
Biological stem cells have remarkable capabilities that are different from regular cells. The following list attempts to capture these capabilities in terms of their functions. The list is by no means complete, but serves as a departure point for capturing the key capabilities of stem cells that could be implemented using modern non-biological technologies.
Stem cells have a mechanism for deciding what new functions they must adapt into. The decision process seems distributed and collaborated among many cells and the cells involved in this process are “communicating” and “collaborating” to determine the “context” of their surroundings and the roles they must play in that context.
Stem cells have a triggering mechanism to know when they must start a new differentiation process. This seems to be the result of collaborative communication among neighboring cells.
Stem cells have an executing mechanism to know how to differentiate into a new type of cells in the current context.
Stem cells have a connecting mechanism for them to physically connect to other cells to form new organs or body-parts that exhibit spatial and temporal patterns and regulations.
Stem cells have all the above mechanisms integrated in a coherent way, and these mechanisms may be intertwined and executing in parallel.
Evidence for the above list comes from both morphogenesis and morphallaxis. In morphogenesis, recent studies show that biological self-building and self-healing, such as initial formation of feathers, is a distributed and collaborative result of many cells, without any apparent leaders. New results in feather formation and development provide an interesting example of this type (Jiang et al., 2004). In feather experiments, when skin cells are disturbed from their original configuration and distribution in embryos of chicken, they still grow into the regular feather buds. This suggests that such cells have no predetermined molecular addresses, and that the periodic patterning process of feather morphogenesis is likely a self-organizing process based on physical-chemical properties and reactions between cells.
Robotic stem cells
Inspired by the biological counterparts, we have developed the new concept of “robotics stem cells” for robotics and engineering. Robotic stem cells are defined as any non-biological basic elements that possess the capabilities of dynamically deciding what, when, and how to adapt their own functions and relationship for self-organizing into a new organization or self-healing a damaged organization. These elements may or may not grow new elements, but they can autonomously change their functions and relationship during the adaptation process. In the discussion below, we will focus on the functional requirements of robotic stem cells that are independent from any particular implementation. The implementation may take advantage of chemistry, physics, computers, or any modern technology that exists. The scale of implementation is also independent. It can be large as stars or small as nano-parts.
At the functional level, a robotic stem cell is an autonomous, reconfigurable and evolvable building block that can self-organize with others to form new systems or heal damage in the current system. They are also capable of learning from experience and evolve their capabilities over a long period of time. Most importantly, they adapt their functions depending on the needs and they can renew themselves for reuse.
Robotic stem cell must have some basic structures (Table 2). We expect each RSC to have a “Gene Controller” which contains core information, i.e. equivalent to a genome (DNA). At certain times, the gene controller can selectively activate and inhibit the receptors and thus change the functional properties of the cell dynamically. The choice of which program to use depends on “Program Selectors”, i.e., the equivalent of transcriptome (mRNA). It is through the change of receptors that a RSC will adapt its behaviors. The gene activations determine which receptors are activated and which are inhibited. The types and the numbers of receptors in each RSC may be innate but their activations are regulated by the gene controller. Furthermore, the control “software” inside the gene controller may be evolved over the lifetime of a cell. Finally, unlike elements in engineering systems, computers, or the Internet, robotics stem cells will not rely on global names or unique identifiers to distinguish among themselves.
TABLE 2.
COMPARISON OF STEM CELLS AND ROBOTIC STEM CELLS
| Stem Cells | Robotic Stem Cells | |
|---|---|---|
| Basic properties | ||
| Gene Controller | Genomic DNA | Gene Controller |
| Program Selector | Transcribed mRNA | Selected programs |
| Executors | Translated proteins Secreted proteins, membrane receptors | Sensors, connectors actuator, receptors, signals |
| Basic behaviors | ||
| Communication | Yes | Yes |
| Triggering mechanism | Yes | Yes |
| Execution mechanism | Yes | Yes |
| Topological information | Self-organizing | Topological recovery |
| Environment | Extracellular matrix Signaling molecules | Physical and chemical environment in the field |
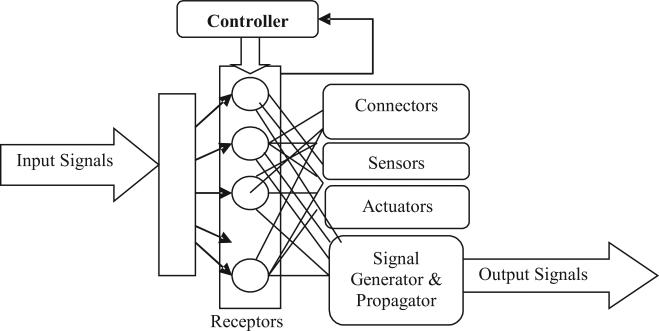
Fig 1 shows the internal structure of an RSC. The receptors are the basic sensory and triggering units of RSC. They are activated and inhabited by the gene controller. Each activated receptor will be triggered by four factors: (1) the local topology or positional information in which the cell is located in the current organization. This information is dynamic and must be monitored and discovered by the cells; (2) the received incoming signals and their types and values; (3) the current readings of local sensors; and (4) the internal state of RSC, which includes the status of the gene controller, the actuators, and others. At a higher level, the receptors can be viewed as a state machine that maps the above four inputs to two types of outputs: (1) the control of actuators and sensors, and (2) the messages to be propagated to its neighbors. Different from normal state machines, the receptors can be dynamically modified by the gene controller.
Fig. 1. Functional diagram of a robotic stem cell (RSC).
Each RSC has its own controllers, receptors, sensors, connectors and actuators. The controller activates and inhabits the receptors. The connectors support dynamic connection and disconnections with other cells. The actuators enable movement or other actions of the cell. RSCs communicate using signals similar to hormones or neurotransmitters among biological cells. Each RCS has a dynamic set of receptors that will react to incoming signals and trigger local actions. The local actions include activating and controlling local sensors and actuators, connecting and disconnecting with other RSCs, and generating and sending signals to other RSCs.
Before we define a complete system view of RSCs, we must define some terminologies such as connectors, links, paths, configurations, topological types, messages, receptors, global action vectors, behaviors, environments, observations, and goals.
Each robotic stem cell is an autonomous basic unit for decision-making and actions. Each RSC has a finite number of connectors that can be dynamically controlled to change the connections with other RSCs. The concept of connector is general. In biology, it may represent the synapse of a neural cell or a binding between neighboring cells. In a computer network, it represents the interface such as Ethernet ports/cables or a wireless communication channel. In a self-reconfigurable robot, it represents the mechanism to allow robotic modules to connect and disconnect with other modules. We assume that every RSC has sensors to monitor the status of its connectors. Two RSCs can form a link l (cix, cjy) by joining their connectors cix and cjy if the connectors are free. For example, if each RSC has n different connectors, then there are n2 possible directed-links between two RSCs. A RSC can disconnect an existing link by disjoining its connector from the link. When this happens, the RSC at the other end of the link will sense the change immediately. RSCs can autonomously join or leave (e.g., when damaged) the network, and links can be dynamically formed or disconnected by the RSCs. A path is a list of directed-links that are connected by RSCs.
A configuration of a system made by robotics stem cells at time t can be defined as: Ct = (Mt, Lt), where Mt and Lt denote the RSCs and links, respectively, in the network at time t. A configuration of a system can be interpreted in several ways. The physical interpretation is that it represents the structure or shape of the system. The connectivity interpretation is that it is a communication network of RSCs, with the expectation that the connections may change dynamically and unexpectedly. The control implication is that global functions do not depend on any single RSC but are distributed and embedded in multiple RSCs in the network. RSCs must use their location in the topology to select and execute local actions. In this representation, self-organization and self-healing can occur at two levels. At the configuration level, the topology of configuration can be changed, and at the RSC level, a RSC's software or even hardware can also be changed. To ensure the distributed nature, RSCs do not know their configuration at the outset and they must discover it dynamically.
A topological type(d) of a RSC represents its local topology and reflects how it is connected to its neighbors in the configuration. The parameter d is the size or radius of the neighborhood. For example, type(0) considers a cell by itself with no neighbors, type(1) considers the connections of the immediate neighbors, and type(2) considers the connections of neighbors that are two steps/links away, and so on. Semantically, a RSC's topological type represents the RSC's role and position in the configuration. For example, in a snake configuration, if a RSC has only one immediate neighbor and its back connector is connected to the front connector of that neighbor, represented as type(1)=[(front, back)], then this RSC is the head of the snake. Similarly, if a RSC's type(1)=[(back,front)], then it is the tail of the snake. If its type(1)=[(front,back),(back,front)], then it is a part of the snake body, because such a RSC has two immediate neighbors and its front connector is linked to the back connector of one neighbor and its back connector is linked with the front connector of another neighbor. Notice that in more complex configurations, RSCs may have to look into larger neighborhood in order to determine its relative position in the current organization. The concept of topological types can be generalized to any finite number of connectors. Using the topological types, RSCs can identify their location in a configuration without requiring unique global identities. This is very different from any classical computational models where components and functions must be indexed by unique names. After all, biological cells do not have unique names, yet they can determine its desired function based on their topological locations. Topological types is one way to describe the positional information of cells, other approaches may involves a coordinate system that is dynamically negotiated by cells. We will describe such an approach in the next section.
The communication signals between RSCs are analogous to the chemicals between biological cells. They can be either hormone or neural-transmitter signals that bind with the receptors of the receiving cells and trigger their actions. In computational models, we may allow these signals to contain numbers. We are aware of that in biological systems, cellular communication may or may not be based on numbers.
A global action vector of a configuration is defined as the current actions by all actuators in all RSCs in the configuration, denoted as a vector ACtt = < a1,..., ai,..., ac >, where ai is the current action by RSCi in the configuration. A global action has a duration in which RSCs can perform their actions synchronously or asynchronously. Based on this, a behavior of a configuration is defined as a sequence of global action vectors of the configuration: BCts = < ACtt1, ACtt2, ..., ACttj >. The time and synchronization is implied by the sequence, where one global action can trigger the next. A single configuration can have many different behaviors.
An environment is defined as the current surrounding of the system. It is reflected in the system's perceived consequences of its actions. An observation is a vector containing the current values of all sensors in all RSCs in the network. It is a snapshot of all sensors. A goal (or a mission) can be defined as a targeted observation. For example, a goal for a climbing robot can be defined as an observation in which the elevation sensor values are above a certain threshold.
Finally, in a given environment, the same configuration may be good for one goal but bad for another. For example, on a slope, a ball configuration is good for going down but bad for going up. For a given goal, a system can change behaviors in the same configuration, or change configurations completely. The tradeoff is very interesting and depends on the cost of changing and the urgency of the goal. For example, to reach an object at the far end of a table, one can stand up and walk around the table (changing behaviors from sitting/reaching to walking/grasping), or simply form a longer arm to reach the object by concatenating the left arm with the right arm. This is to change the configuration but using the same “reaching” behavior. This is sometimes a much better, easier, or only choice for accomplishing certain goals in certain environment, and it is certainly a critical feature of stem cells.
Figure 2 presents a graphic view of the terms defined above, we now describe regeneration as a process. In biology, Bryant et al., 2002 has proposed to divide the regeneration process into three stages: wound healing, de-differentiation and re-development. Upon injury, a multi-cellular organism first has to sense damage (Singer and Clark, 1999). Through communication among cells, extracellular matrix, and humoral factors, it will decide the response. Different thresholds of stimuli will trigger different response: a local clotting, a call for white blood cells to migrate in, or a signal to send the whole body in alert. During wound healing, cells migrate in to repair and stem cells are activated. Then there is a decision to make on whether the tissue will be simply padded or a patterning process will initiate. Corresponding to these stages, the following subsections describe the ability we assign to RSC in parallel order: ability to communicate, sense the damage and trigger the response, execution, and the ability to recover original topological order or positional values.
Fig. 2. The organizational diagram of robotic stem cells.
It shows the organizational view of the robotic stem cells. Each cell is shown as a small cylinder and a set of connectors. In terms of their relationship, they can connect to each other using the connectors, or they disconnect from other cells. Similar to biological cells, RSCs do not have any names or globally unique identifiers and they are free to come and go in an organization. Unlike biological cells, RSCs may not die by themselves.
Programming and communication
To program RSCs, we propose a distributed language that can facilitate RSCs to change receptors for differentiation and evolution, and propagate signals through links to trigger actions by topological types. This language is for functional programming with syntax similar to Erlang (http://www.erlang.org/), but it uses no global identifiers and is based on the concept of hormone-inspired control (Shen et al., 2002).
The RSC programming language contains basic objects (constants, compound terms, and variables) and functions. It represents a receptor as a process explicitly created by a message:
create_receptor(CellType; [fH(H), fT(T), fS(S), fV(V)]; [action1(Args1), ..., actionJ(ArgsJ)]).
This message will create a new receptor at a receiver RSC if that receiver's topological type matches CellType. The newly created receptor will behave as follows. Whenever it is evoked, it will first evaluate the four matching functions, [fH(H), fT(T), fS(S), fV(V)], with parameters H (the expected hormone), T (the expected local topology), S (the expected local sensor values), and V (the expected local state). When these matches are successful, the receptor will bond to the hormone and execute the actions: action1(Args1), , actionJ(ArgsJ). The actions can affect the behaviors of a RSC in terms of sensors, actuators, gene controllers, communication, or deletion and insertion of receptors.
Communication is accomplished by propagating messages among RSCs. When a message is propagated in the system, the path of the message will be appended with the message. As we defined before, a path is a list of links through which the message has been propagated. A newly created message has an empty Path. If the message is propagated through a link x→ y where x and y are connectors, then its Path = [(xy) | Path]. If a message has no effect on the receiving RSC, the message will be automatically propagated to its neighbors.
All RSCs have the same basic and innate process that runs as long as it is alive. This process is illustrated below and it maintains a Mailbox for received messages, a Buffer for propagating messages, a LocalClock for timing, and ConnectorStatus for its connectors.
RSC_innate_process(ClockCycle):
Loop_forever {
For each msg(_, [(xy)|Path]) in Mailbox, do {
Remove the message from Mailbox;
ConnectorStatus[y] = x;
Execute all active receptors triggered by the message;
Insert the newly created messages into Buffer;
}
For each message msg(_, [(z_)|Path]) in Buffer, do {
Remove the message from Buffer
Send the message through the z connector;
If sending fails (e.g., no receiver at the z connector);
then set ConnectorStatus[z] = 0;
}
LocalClock = mod(LocalClock + 1, ClockCycle);
}
As we can see, this process constantly receives message and invokes local receptors to perform actions. It also monitors the status of each connector so that the cell can dynamically update its local topology information whenever there is a change in the local links. This local topology will be used to discover the local structure of the network in a distributed fashion and the results will be used to detect unexpected damage in the network.
This language can be used to program a network of RSCs to perform actions (Shen et al., 2002). To trigger an action of the network, a message is created and propagated. Such a message may be given by an external source (e.g., an injected hormone), or created by an existing cell that is triggered by a local sensor input. This mechanism is scalable and can be independent from the network's shape and size because cells are not required to know the entire configuration and they may decide their actions based on local information. Since such a mechanism is entirely characterized by the receptors of the cell, one can use it to modify the gene controller so that the receptors of cells can also be evolved over time. A machine learning approach can be applied here to change the gene controller over the experience of the cell.
Triggering mechanisms
The next question is when to trigger a self-healing process in a timely fashion. Because damage can occur anytime, RSCs must constantly monitor the changes in the topology. RSCs accomplish this by periodically sending out “probe” messages to their connectors. For any given connector, there are four possible cases: (1) there is a connection and a probe succeeds; (2) there is no connection and a probe fails; (3) there is no connection but a probe succeeds; and (4) there is a connection and a probe fails. For the first two cases, no action is needed. For the third case, the procedure of RSC_innate_process will update the status of the connector as there is a new connection just discovered. The last case is special because it indicates that there is an unexpected discrepancy between the established topology and communication. The RSC has discovered a fault and it will report the error to all the RSCs in the system. The system will stop its normal behavior and start planning reconfiguration for self-healing. To avoid false alarms caused by random communication errors, a RSC will report a fault only when it has detected this case for several times consecutively.
Notice that the probing mechanism can be used not only for connectivity, as we described above, but also for functionality. For example, a RSC may probe its neighbors for questions such as: can you move? What is your state? How much power do you have? These types of probes may be necessary to detect functional failures rather than connection failures.
Execution mechanisms
To illustrate how RSCs execute the self-organization process, consider an example of reconfiguring a lizard-like robot to a snake-like robot. As we mentioned before, a single message will be sufficient to trigger and change one configuration to another, and there is no need for individual low-level instructions for individual RSCs. The basic sequence is as follows: the lizard-like robot first connects its tail to a foot, and then disconnects the leg from the body so that the leg becomes a part of the tail. This action is repeated until every leg is “absorbed” into the tail. A reverse of this sequence would reconfigure a snake to “grow” new legs by converting a part of the tail into a leg.
This sequence can be implemented using the above mechanism as follows. One (anyone) RSC in the lizard configuration is first triggered to generate a message to call for changing legs to snake. This message is propagated to all RSCs, but only the RSCs at the tip of a leg have the relevant receptors to react. Those RSCs will in turn generate and propagate another message. This second message will cause only the RSC at the end of the current tail to react. The tail will select a leg and conduct the actions of bending, aligning, docking the tail to the foot and disconnecting the leg from the body. When these actions are accomplished, then the new tail will start another leg absorption. This process will repeat until all legs are absorbed regardless of how many legs are there in the initial configuration. If this reconfiguration sequence were stopped unexpectedly or prematurely, the process can resume itself correctly after the interruption is over.
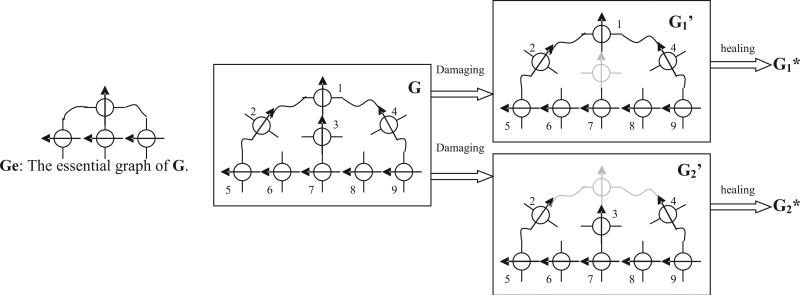
Mathematically speaking, when a fault is detected, planning for self-healing occurs in two cases. In a given configuration, a RSC is trivial if it matters only to the size of the structure (e.g., the length of a chain), and a RSC is essential if it is critical for the structure (e.g., at the shoulder location). Shown in Fig. 3, for example, RSCs 2, 3, 4, 6, 8 are trivial, and 1, 5, 7, 9 are essential. We say that two configurations are structurally equivalent if and only if their essential configurations are the same. For example, any two snakes are structurally equivalent, but a starfish is structurally different from a snake. Thus, self-healing can be defined as an execution process that accomplishes the following: Given a graph G and a damaged graph G’ (e.g., G1’ or G2’ in Fig. 3), reconfigure G’ into a new graph G* that is structurally equivalent to G.
Fig. 3. The trivial and essential RSCs and structural equivalence.
If the damaged RSC is trivial (e.g. RSC 3 in G1’), then its good neighbor RSC (e.g. 1) will disconnect from it and search and dock with the other good neighbor (e.g., 7). If the damaged RSC is essential (e.g. RSC 1 in G2’), then the good neighbors will select a replacement for the lost essential RSC. The selected RSC will conduct the healing process by forming the essential structure around itself with the collaboration of the good neighbors. For example, to replace a damaged RSC 1 in G2’, the good neighbors 2, 3, and 4 may select 3 as the new essential RSC, and RSC 3 will connect to 4 and 2 respectively to recover the lost structure. This process can be used to repair multiple damages. For example, if a starfish has lost three tentacles, then this approach will first redistribute the body RSCs to form three new short tentacles and then adjust the lengths of five tentacles by moving RSCs around. The repaired starfish will be smaller in size but equivalent in structure.
Topology recovery
We mentioned earlier that the function of a RSC is completely defined by the current set of active receptors. Thus, the mechanism to change the function of a RSC is to change the activation of the receptors. This is the task for the gene controller, which activates or inhibits the receptors based on the cell's current spatial and temporal location in the organization. In other words, for a different spatial and temporal location, the gene controller will turn on or off different set of receptors. So the question is how does a RSC determine its current spatial and temporal location? This is a task of topological discovery or location discovery.
To support self-organization and self-healing, RSCs must have a way to memorize the desired topology and compare it with the current topology. Since topology is global while RSCs are distributed, it is a challenge to decide how to distribute the global topology among the RSCs. At one extreme, if every RSC keeps a copy of the entire topology, then this will be an information explosion for individual RSCs if the configuration is large. At the other extreme, if each RSC keeps only unique information to itself (no redundancy), then critical information will be lost forever if any single RSC is lost.
A good solution to the problem would automatically balance the tradeoff between the two extremes. The main idea is to let each RSC to discover its local neighborhood topology as a bi-product of receiving hormone messages. Recall that RSCs can discover and maintain their type(1) information in the local variable ConnectorStatus[x], where x is the name of a connector. The information is discovered as soon as a RSC receives a hormone from the connector x. To discover type(d) information, where d>1, we notice that each received hormone contains a Path that lists the links through which the hormone has been propagated. This Path information can be used to determine the receiver RSC's type(d) values. For example, if a RSC receives a hormone with Path=(back-front, back-front), then this path information will be inserted into its type(2) value. So, by accumulating the path information for the received messages, a RSC can discover the value for type(d), with d=0, d=1, d=2, ..., and so on. These discovered values will determine the current location of the cell in the current organization. When d is big enough, the location value will be unique.
Based on this method, each RSC will keep a topology that is local to its neighborhood, and each RSC will discover and remember a part (not the whole) of the global topology. No RSC will need to be burdened by the entire global topology unless such a RSC has received hormones from every RSC in the entire network (this is very unlikely to happen). Since the range of neighborhood is determined by the propagation of hormones, this approach will keep the topological information distributed yet redundant enough. If a RSC is damaged, the RSCs in the same neighborhood will have sufficient information to reproduce the lost information. The approach will prevent information explosion because not every RSC has to remember the entire topology.
Given the topological information of a RSC, the gene controller will select a set of receptors to be active, which in turn defines the current function of the cell. The mappings from topology to receptors inside the gene controller may be innate to the cell, but these mappings may also be changed just as the DNA and RNA would change in the biological cells.
A model for scalable self-organization and self-healing
Based the terms defined above, we now present and demonstrate a simplified model of RSC for healing-by-reorganization that is both scalable and distributed. It is scalable because its self-healing can start from any subset and recover the original whole with a smaller size. Furthermore, individuals in this model can self-organize into a new global coordinate/positional system if and when the original one is damaged or obsolete. We define this type of self-healing as scalable self-organization and self-healing. To demonstrate this, we show that elements that are randomly placed in a swarm can first (re)-construct a global coordinate system, and then self-organize into a structure of desired spatial, visual, and temporal patterns. When damaged, the remaining elements will autonomously recover these patterns in a scale proportional to the number of elements available. Notice that elements in this model exhibit similar properties found in stem cells, for they dynamically change their behaviors, location, features, and function, based on the nature and the scale of the damage. Notice also that this model does not require growth or addition of new cells but can incorporate new elements into the structure if they are provided. In this sense, this scalable self-healing model is applicable to both morphallaxis and epimorphosis.
The elements in this model are defined as a simple version of RSC that can move in the environment, sense the distance to its neighbors (no other sensors), exchange coded information with neighbors, and change its behaviors or features (e.g. color), based on their receptors. These simple RSCs have no unique names or identifiers, nor any pre-determined global coordinate system. The position of an element is not given but must be globally negotiated with others. This is similar to a stadium crowd at a football game without tickets for seating. Individuals can move and change seats, change the color of their outfits (e.g., to change color patterns in the audience), and synchronize their actions with neighbors (e.g., to generate “wave patterns”). Each of these aspects: spatial, visual, and temporal, can be thought of as one facet for the robotic stem cells, so that they can be combined to form complex self-organizing and self-healing capabilities in time-space. One unique advantage of this model is that all the essential aspects, such as self-coordinating, self-orientating, self-shaping, self-coloring, and self-timing are intertwined and integrated automatically and coherently.
The elements in this model autonomously negotiate a consistent global coordinate system so that they can determine their individual position in the potential organization. We have developed a new method based on trilateration (Grabowski and Khosla 2001; Mirisola 2003; Borg 2005; Cheng et al., 2005) for this purpose. The basic idea is as follows: every element first guesses its own position xself = (x1, x2, ..., xN), where N is the dimension of the environment, and senses the real distance dj to the j element in the neighborhood. Then, all elements continue to modify and exchange their guessed positions until the following function becomes zero:
| (1) |
This function reflects the summed difference between the real distance and the guessed distance (computed based on their currently guessed positions) for every neighbor. When this function reaches zero (or below a threshold), then the individual positions are consistent among elements and they can be used as a coherent global coordinate system.
If every element can communicate to every other element (i.e., each element has as many connectors as needed), then a cell's neighborhood would be big enough to include all other elements and we can prove that the above process will converge to zero for all elements. However, when communication is local (i.e., each element has only a few connectors) and neighborhoods are small, then this function may not be able to converge to zero due to local minimums. This can be seen, without loss of generality, in a simple example in a one-dimension (1D) environment where elements are located along a single line (Arbib 1969). With local communication, elements near one end of the line may not know the existence of the elements at the other, thus the agreed coordinate near one end may be inconsistent with that near the other. This will trouble the elements in the middle because they may not be able to assign their positions that satisfy the both ends. In this case, the global coordinate will not be able to converge into a straight line, but a line that is folded in the middle.
To overcome this difficulty, we added an extra term in the equation as follows:
| (2) |
where is a smoothing force in an extra N+1 dimension. In our 1D example, this is a force to unfold the line in the 2D space. Using this technique, we have experimentally verified in both 1D and 2D environments that a consistent global coordinate can be reached even if elements have no sense of direction and can only talk to a subset of the organization. The rate of convergence is proportional to the percentage of communication range or the size of the neighborhood.
Because elements negotiate a global coordinate on the fly, the orientation of the resulting organization may vary. An element can determine its orientation by making two orthogonal movements and computing the orientation based on the result positions. We view this as evidence for being consistent with the self-healing phenomena in nature, and that no global information is used.
The above process is also used for elements to determine their “current time”, which is automatically advanced in step with the computer simulation. All elements continue to modify and exchange their guessed current time tself until it agrees with the averaged current time in the neighborhood. This process is simpler than other synchronization methods (Mirollo and Strogatz, 1990) for elements can communicate values.
Once the global coordinate is negotiated, an element can determine its global position and its position in the current organization. The spatial shape of the organization is given to the elements as a mathematical function fshape. For example, a flower shape of four petals is specified as r=2+cos(4φ+1), where 0≤φ≤2π. In general, the shape function can be arbitrary, but our current model uses only smooth and positive polar functions.
Although the shape of organization is given, its scale must be dynamically determined to be proportional to the number of available elements. Our model approximates the scale by the longest distance, smax, of the elements that are farthest from the agreed origin, and iteratively identifies this value by local communication and propagation among elements.
The behaviors of elements are governed by internal functions. To self-organize and self-heal, every element uses an internal function
| (3) |
that repeatedly calculates, and moves into the negative direction of the surface normal of the scaled shape function relative to its own position. If a collision is detected, it will move randomly. Such movements will cause the elements to form the appropriately scaled shape in space. To exhibit colors, every element uses another internal function,
| (4) |
to repeatedly calculate and change its color.
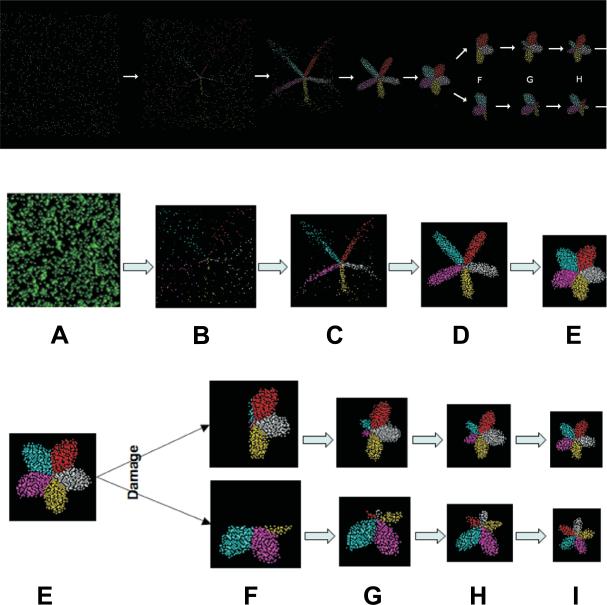
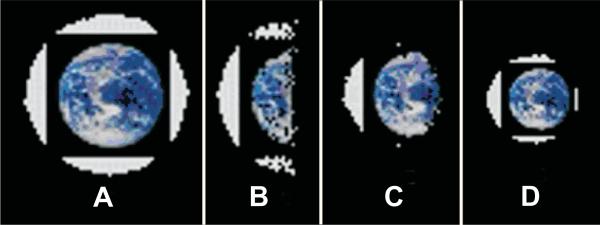
The above model has been demonstrated in computer simulation. The equations (2)-(4) described above allow a swarm of robots to exhibit scalable self-healing and pattern formation. Fig. 4 shows a typical example of this model. Initially, a swarm of randomly placed RSCs can self-form the desired shape of a “starfish” (Fig. 4 A-E). Between Fig. 4 E and F, the self-formed starfish is cut in half and the halves are separated beyond communication range. The RSCs continue to move in accordance of the self-healing equations, and in Fig. 4 F-I, the separated halves independently re-form into two new but smaller starfishes.
Fig. 4. Self-healing starfish shape formation and recovery after damage and separation.
(A-E). A random swarm of elements self-organize into a coherent global position system and a starfish with individually colored limbs. (E-I) A self-formed starfish is cut and separated in two halves, and each half self-heals into a complete, new, but smaller starfish.
In addition to spatial patterns, a swarm of individually colored RCS can also differentiate, display, and self-heal a color pattern upon the self-formed shape. Each RCS can display and change its individual color, and the global color pattern can be simple, such as the starfish in Fig. 4 where each arm has a different color, or complex as a picture of the earth shown in Fig. 5. In general, the color pattern can arbitrary. When the swarm is damaged, as the robots move to reform the damaged shape, they will also change their individual colors in order to re-form the desired pattern. The new pattern will automatically re-size to fit the original pattern upon the new smaller swarm, as shown in Figures 4 and 5.
Fig. 5. Self-healing complex color patterns upon spatial patterns.
The initial RSCs first self-form a picture of the earth, then a half of the RSCs are removed from the picture. The remaining elements self-heal the picture of earth into a smaller scale.
Fig. 6 shows the synchronization of the RSCs in time. A swarm of RSC not only display a pattern but the pattern can be time varying. Figure 6A shows a “scrolling text” displayed on a swarm holding a circle shape. As with the self healing pattern, this time varying pattern will also recover from damage, and scale to the size of the swarm, as shown in Fig. 6B. Similar behaviors can also be applied to the form of a movie.
Fig. 6. Self-healing temporal patterns with a scrolling text over a circular swarm of elements.
(A) Images of a circular swarm during increasing time, showing the text scrolling across the swarm. (B) Scrolling text swarms before damage (left), after damage once (center), and after damage twice (right).
Physical prototypes and SuperBot
In addition to mathematical modeling and computer simulations, physical prototypes of RCS can also be designed and built. The most related are modular self-reconfigurable robots (Mackenzie 2003; Yim et al., 2007). Here we describe one of these robots called SuperBot (Salemi et al. 2006). Fig. 7 shows the mechanical design of a module of SuperBot. Each module is a complete robot by itself and has its own power, sensors, actuators, and can move with its three degree-of-freedom locomotion capability. The module's software implements the controllers and the receptors. Each module also has six reconfigurable connectors that allow them connect or disconnect with other modules to form different configurations. Fig. 8 shows several examples of such configurations. The communication among modules is accomplished in two ways: IR for short distance and wireless radio for long distance. The IR can also be used to guide the alignment between two RSCs for autonomous docking. The radio communication can be useful for searching for other RSCs, for remote control and negotiation and collaboration among RSCs in distance.
Fig. 7. SuperBot as a candidate mechanical platform for Robotic Stem Cells.
A single SuperBot module with three degrees of freedom, electronics, power, computer, sensors, actuators and connectors.
Fig. 8.
Example configurations of robotic stem cells based on SuperBot modules.
The physical prototypes of RSC can demonstrate many aspects of RSC described in this paper. For example, SuperBot modules can “differentiate” their receptors and connect with other modules to form different configurations with multiple functions. Fig. 9 shows some examples of this multifunction. For example, six SuperBot modules can form a rolling track and roll a long distance on flat terrain or climb a steep sand dune. Three modules can form a “rope climber” with two short arms and move on a horizontal rope across two high buildings, or climb a vertical rope to the top of a six-floor building. Four modules can form a chain and move like a caterpillar on the beach or on carpet. Four modules can form a four-legged robot with a very low center of gravity to climb over steep obstacles such as a concrete riverbank of 45 degrees incline. Six modules can form a human-shaped robot and walk on two legs. A snake made of seven modules can move as a sidewinder on carpet. Three modules can form a scorpion shape and move with a gait similar to butterfly stroke in swimming. In addition to these, SuperBot modules can form a roller skate and carry a payload up to 530% of their own weight. They can carry wireless camera and be remotely controlled for surveillance or performing jobs that are too risky or expensive for humans. These configurations are interchangeable via reconfiguration. For details of these multi-functional behaviors of SuperBot, please see (Shen et al., 2006) and many movies at http://www.isi.edu/robots. Since these functions are implemented as software receptors inside module, they can be viewed as the results of differentiating the robotic stem cells proposed in this paper. In addition, RSCs can be easily re-differentiated (i.e., go back to the state of stem cell even after they are already differentiated), so that they can be differentiated again.
Fig. 9. Multifunctional examples of robotic stem cells based on SuperBot modules.
From top-left to bottom-right: (1) a rolling track composed of six modules, (2) a rope climber of three modules, (3) an “inchworm” formed by four modules, (4) a slope climber with four modules, (5) a “humanoid” formed by six modules, (6) a sidewinder “snake” configured by seven modules, (7) a “caterpillar” of three modules and (8) a “scorpion” with four modules.
The above capacities are useful to many different applications, such as search and rescue, military or civilian operations in dangerous environments, space or deepwater exploration, and self-assembling large structures in space. For example, a long chain configuration with several branches can serve as a crane to lift and move objects in space or unloading equipment from a Lander. The modules in the configuration can then reconfigure into mobile robots with legs and limbs so that they can climb slopes that are too steep for wheeled robots. A single module can be connected with a thruster to fly in micro-gravity environment for inspection. For applications of self-assembly in micro-gravity environment, please see (Shen et al., 2003; Everist et al., 2004; Suri et al. 2006) for details.
Summary and future research directions
Our long-term goal is to build a resilient multi-element system that can self-organize, self-heal, and self-regenerate. We adopt a nature-inspired approach based on the analysis of different strategies used by animals for regeneration. To be practical and useful for the current robotic technology, we focus on the morphallaxis type of regeneration and patterning in this paper. The comparison of robotic stem cells with stem cells is summarized in Table 2.
A key for self-regeneration, regardless if it is based on morphallaxis or epimorphosis, is to self-reorganize their patterning information. This paper proposes two possible mechanisms. One is to incrementally discover the local topology based on the connections between RSCs, and the other is to use trilateration to dynamically negotiate a global coordinate system. Both approaches can be used to support the scalable self-healing.
In this paper, we assign RSCs to possess a copy of the fshape information at birth (the Gene Controller), even though it does not know where and what role it will end up in the original swarming organization. If the original organization was damaged, the overall organization will reform and an individual RSC has the ability to assume different positions even though it is likely to be different from the original role. The ability of RSC to sense the environment and communicate is coupled with the flexibility of Program Selector, and allows patterned organization to be executed in a distributed fashion.
One of the open questions is how stem cells communicate and with what information. In our simulation, our RSCs communicate with numbers. In biological cells, they may communicate with difference concentrations of signaling molecules. Furthermore, the range of communication among RSCs determines the quality of the negotiated coordinate or positional information. In tissue interactions, communication can be carried out via direct cellular contacts, short and long range diffusible signaling molecules, or elongated filapodia. It would be interesting to set up different routes of communications among RSCs for different types of regenerative pattern formation and self-healing.
The amazing abilities of stem cells fascinate scientists and engineers. Stem cells and morphallaxis are especially attractive because they imply that a future system may be able to repair its structure and function without any external additional supplies. Such capabilities are critical and may be used in space, deep water, fire-fighting, disaster areas, thrombus cleaning nano-bots, micro-robots for engineering biotic tissues, or other applications where access to the environment is extremely expensive and difficult, and the required functions are diverse and time-critical.
Perhaps the most challenging issue related to RSC is–whether they can learn with time and experience. For a robot to accomplish a new task in a new environment, it must find a good behavior. If such a behavior is not supported by its current configuration, then the robot must find a better configuration. In biology, how the stem cells find a satisfying configuration and behavior for a given task and environment is still an open problem. We propose to let the RSCs learn from their experience and self-evolve the configuration and behavior. We plan to investigate two approaches for this problem, a symbolic algorithm for learning from experience, and a genetic algorithm for co-evolving configuration and behavior based on feedback received from the environment. The first approach uses a surprise-based learning algorithm (Shen 1994) that detects and analyzes “surprises” and extracts critical information from the surprises to improve the configuration and behavior. For example, when a robot that walks well on ground steps on ice, it will be surprised that its normal gait cannot make the expected progress. By analyzing the surprise, the robot may notice that the friction between its feet and the ice is too low, so it would reduce the force exerted on its feet and try it again. The genetic algorithm approach will generate and test many generations of configurations and behaviors based on the evaluation of the previous configurations and behaviors (Bongard et al., 2006). In both approaches, the configuration changes are represented by the “configuration graphs” and the behaviors changes are represented by the “receptors” of cell RSCs. The dynamics of DNA, RNA and proteins on a biological cell are recapitulated in the Gene Controller, Program Selector, RSC Executor, and their ability to “differentiate.” Analogous to the effort to reset a somatic cell back to stem cell status in the pursuit of stem cell biology, a differentiated robotic cell can be reset back to new robotic stem cell status if all the evolved “receptors” are cleared and program reset. We will investigate the significance and implications of such renewable stem cells.
We hope the exercise in this paper, although speculative and preliminary, has provided useful insights in two aspects. One is to have distilled our understanding of the functional aspects and principles of regenerative behavior of stem cells in biological systems. The other is to have inspired new designs for future engineering systems that can perform self-organization, self-healing and even self-evolving.
Acknowledgement
This work is supported by grants in part by NASA's Cooperative Agreement NNA05CS38A, ARO grants W911NF-04-1-0317 and W911NF-05-1-0134, and AFOSR grant FA9550-06-1-0336. The work is also supported by grants from NIA and NIAMS to CM Chuong. The views, opinions, and/or findings contained in this report are those of the author(s) and should not be construed as an official sponsors’ position, policy, or decision, unless so designated by other documentation. The authors are also grateful to other members of the Polymorphic Robotics Laboratory at USC/ISI for their useful comments on the earlier drafts of this paper.
Abbreviations used in this paper
- RSC
robotic stem cell
References
- AGATA K, SAITO Y, NAKAJIMA E. Unifying principles of regeneration I: Epimorphosis versus morphallaxis. Dev. Growth Differ. 2007;49:73–78. doi: 10.1111/j.1440-169X.2007.00919.x. [DOI] [PubMed] [Google Scholar]
- ARBIB MA. Towards a Theoretical Biology. Edinburgh University Press; 1969. Self-reproducing automata: some implications for theoretical biology. [Google Scholar]
- BODE HR. Head regeneration in Hydra. Dev. Dynamics. 2003;226:225–36. doi: 10.1002/dvdy.10225. [DOI] [PubMed] [Google Scholar]
- BONGARD J, ZYKOV V, LIPSON H. Resilient machines through continuous self-modeling. Science. 2006;314:1118–1121. doi: 10.1126/science.1133687. [DOI] [PubMed] [Google Scholar]
- BORG I. Modern Multidimensional Scaling: Theory and Applications. Springer Series in Statistics. 2005:3–59. [Google Scholar]
- BROCKES JP, KUMAR A. Appendage regeneration in adult vertebrates and implications for regenerative medicine. Science. 2005;310:1919–1923. doi: 10.1126/science.1115200. [DOI] [PubMed] [Google Scholar]
- BRYANT SV, ENDO T, GARDINER DM. Vertebrate limb regeneration and the origin of limb stem cells. Int J Dev Biol. 2002;46:887–896. [PubMed] [Google Scholar]
- CASTANO A, SHEN W-M, WILL P. Towards Deployable Robots with Inter-Robot Metamorphic Capabilities. Autonomous Robots. 2000;8:309–324. CONRO. [Google Scholar]
- CHENG J, CHENG W, NAGPAL R. Robust and Self-repairing Formation Control for Swarms of Mobile Agents. Proceedings of the Twentieth National Conference on Artificial Intelligence. 2005:59–64. [Google Scholar]
- CHUONG CM. New hair from healing wounds. Nature. 2007;447:265–266. doi: 10.1038/447265a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CHUONG CM, RICHARDSON MR. Pattern formation today. Int. J. Dev. Biol. 2009 doi: 10.1387/ijdb.082594cc. doi: 653-658 (10.1387/ijdb.082594cc) [DOI] [PMC free article] [PubMed] [Google Scholar]
- CHUONG C-M, WU P, PLIKUS MV, JIANG TX, WIDELITZ RB. Engineering Stem cells into organs: Topobiological transformations demonstrated by beak, feather and other ectodermal organ morphogenesis. Curr Topics Dev Biol. 2006;72:237–274. doi: 10.1016/S0070-2153(05)72005-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- EVERIST J, MOGHAREI K, SURI H, RANASINGHE N, KHOSHNEVIS B, WILL P, SHEN W-M. A System for In-Space Assembly.. Proc. 2004 IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems; Sendai, Japan. 2004. pp. 2356–2361. [Google Scholar]
- FRÖBIUS1 AC, GENIKHOVICH G, KÜRN1 U, ANTON-ERXLEBEN F, BOSCH TCG. Expression of developmental genes during early embryogenesis of Hydra. Dev Genes Evol. 2003;213:445–455. doi: 10.1007/s00427-003-0344-6. [DOI] [PubMed] [Google Scholar]
- GRABOWSKI K, KHOSLA P. Localization Techniques for a Team of Small Robots.. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS'01).2001. pp. 1067–1072. [Google Scholar]
- HAN M, YANG X, FARRINGTON JE, MUNEOKA K. Digit regeneration is regulated by Msx1 and BMP4 in fetal mice. Development. 2003;130:5123–5132. doi: 10.1242/dev.00710. [DOI] [PubMed] [Google Scholar]
- JIANG T-X, WIDELTZ RB, SHEN W-M, WILL P, WU DY, LIN CM, JUNG JS, CHUONG CM. Integument pattern formation involves genetic and epigenetic controls operated at different levels: Feather arrays simulated by a digital hormone model. Int. J. Dev. Biol. 2004;48:117–135. doi: 10.1387/ijdb.041788tj. [DOI] [PMC free article] [PubMed] [Google Scholar]
- JUNG H-S, FRANCIS-WEST F, WIDELITZ RB, JIANG T-X, TING S, TICKLE C, WOLPERT L, CHUONG C-M. Local inhibitory action of BMPs and their relationships with activators in feather formation: Implications for periodic patterning. Dev Biol. 1998;196:11–23. doi: 10.1006/dbio.1998.8850. [DOI] [PubMed] [Google Scholar]
- MAINI PK, BAKER RE, CHUONG CM. The Turing model comes of molecular age. Science. 2006;314:1397–1398. doi: 10.1126/science.1136396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MACKENZIE D. Shape shifters tread a daunting path toward reality. Science. 2003;301:754–756. doi: 10.1126/science.301.5634.754. [DOI] [PubMed] [Google Scholar]
- MEINHARDT H, GIERER A. Pattern formation by local self-activation and lateral inhibition. Bioessays. 2000;22:753–760. doi: 10.1002/1521-1878(200008)22:8<753::AID-BIES9>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- MIRISOLA L. Thesis. Carnegie Mellon University; 2003. The Localization Problem on Sensor Networks. [Google Scholar]
- MIROLLO R, STROGATZ S. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 1990;50:1645–1662. [Google Scholar]
- NYE HL, CAMERON JA, CHERNOFF EA, STOCUM DL. Regeneration of the urodele limb: a review. Dev Dyn. 2003;226:280–294. doi: 10.1002/dvdy.10236. [DOI] [PubMed] [Google Scholar]
- RANASHINGHE N, SHEN W-M. Surprise-Based Developmental Learning and Experimental Results on Robots.. Proceedings of the IEEE 8th International Conference on Development and Learning; Shanghai, China. 2009. (ICDL 2009) [Google Scholar]
- SALEMI B, MOLL M, SHEN W-M. A Deployable, Multi-Functional, and Modular Self-Reconfigurable Robotic System.. Proc. 2006 IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems; Beijing, China. 2006. SUPERBOT. [Google Scholar]
- SHEN W-M. Autonomous Learning from the Environment. Computer Science Press, W.H. Freeman; N.Y., USA: 1994. [Google Scholar]
- SHEN W-M, KRIVOKON M, RUBENSTEIN M, EVERIST J, CHIU H, VENKATESH J. Multimode Locomotion for Reconfigurable Robots. Autonomous Robots. 2006;20:165–177. [Google Scholar]
- SHEN W-M, WILL P, KHOSHNEVIS B. Self-Assembly in Space via Self-Reconfigurable Robots.. Proc. 2003 IEEE Intl. Conf. on Robotics and Automation; Taiwan. 2003. pp. 2516–2521. [Google Scholar]
- SHEN W-M, WILL P, GALSTYAN A, CHUONG C-M. Hormone-inspired self-organization and distributed control of robotic swarms. Autonomous Robots. 2004;17:93–105. [Google Scholar]
- SHEN W-M, SALEMI B, WILL P. Hormone-Inspired Adaptive Communication and Distributed Control for CONRO Self-Reconfigurable Robots. IEEE Transactions on Robotics and Automation. 2002;18:700–712. [Google Scholar]
- SHIMIZU H, SAWADA Y, SUGIYAMA T. Minimum tissue size required for hydra regeneration. Dev. Biol. 1993;155:287–296. doi: 10.1006/dbio.1993.1028. [DOI] [PubMed] [Google Scholar]
- SINGER AJ, CLARK RA. Cutaneous wound healing. N Engl J Med. 1999;341:738–746. doi: 10.1056/NEJM199909023411006. [DOI] [PubMed] [Google Scholar]
- SURI H, WILL P, SHEN W-M. System Design of Robots for Application to In-Space Assembly.. Proc. 2006 IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems; Beijing, China. 2006. [Google Scholar]
- TURING A. The chemical basis of morphogenesis. Philos. Trans. R. Soc. London B. 1952;237:37–72. [Google Scholar]
- YIM M, SHEN W-M, SALEMI B, RUS D, MOLL M, LIPSON H, KLAVINS E, CHIRIKJIAN GS. Modular Self-Reconfigurable Robot Systems — Challenges and Opportunities for the Future. IEEE Robotics and Autorotation Magazine. 2007:43–53. [Google Scholar]