Quantitative analysis of cryo-EM density map segmentation by watershed and scale-space filtering, and fitting of structures by alignment to regions

Abstract

Cryo-electron microscopy produces 3D density maps of molecular machines, which consist of various molecular components such as proteins and RNA. Segmentation of individual components in such maps is a challenging task, and is mostly accomplished interactively. We present an approach based on the immersive watershed method and grouping of the resulting regions using progressively smoothed maps. The method requires only three parameters: the segmentation threshold, a smoothing step size, and the number of smoothing steps. We first apply the method to maps generated from molecular structures and use a quantitative metric to measure the segmentation accuracy. The method does not attain perfect accuracy, however it produces single or small groups of regions that roughly match individual proteins or subunits. We also present two methods for fitting of structures into density maps, based on aligning the structures with single or groups of regions. The first method aligns centers and principal axes, whereas the second aligns centers and then rotates the structure to find the best fit. We describe both interactive and automated ways of using these two methods. Finally, we show segmentation and fitting results for several experimentally obtained density maps.

1. Introduction

Density maps obtained by cryo-electron microscopy give much insight into the structure and function of molecular machines [1-5]. An important task in the analysis of such maps is segmentation, which aims to identify regions belonging to individual proteins or subunits. Segmentation is a hard problem, and it is still mostly accomplished interactively. It has been a widely studied subject, for example in computer vision [6] and medical image analysis [7]. Approaches to segmentation include edge detection [8], active contours [9], level sets [10], graph partitioning [11,12], random walks [13], mean-shift [14,15] and watershed [16]. Scale-space filtering has been used along with some of these methods; it involves smoothing, and reduces the number of segmented contours or regions while retaining salient features [17-23].

For the segmentation of cryo-EM density maps into individual proteins or subunits, several of these methods have been used, for example the level set and watershed methods. The level-set method [24] heavily depends on prior placement of seed points in each region to be segmented. Automatic classification of seed points is yet an unsolved problem, and hence this method still depends extensively on user guidance. The watershed method is very effective in lower-resolution density maps, and requires very little user guidance [25,26]. However it typically produces too many regions, an effect often referred to as oversegmentation. Methods for dealing with oversegmentation include grouping of regions based on topological persistence [27] or varying the step size in the immersive approach [25]. They generally do not produce accurate segmentations because the metrics they use are based on local information, which is unreliable in the presence of noise.

Since accurate automated segmentation methods remain elusive, segmentation of cryoEM density maps is still mostly performed manually. Software tools for interactive segmentation of cryo-EM density maps allow users to trace out regions interactively [28-30]. This is a labor-intensive task that can take many hours to accomplish, and requires a lot of prior knowledge and skill.

In recent work, we used a multi-scale segmentation approach, which applies the immersive watershed algorithm to progressively smoothed maps [31]. It produces regions that roughly match proteins or subunits, and requires very little user interaction. In this paper we present a similar method, which also uses the immersive watershed method, but then groups the regions using progressively smoothed maps. The process of progressively smoothing an input signal is known as scale-space filtering [17].

Grouping of regions by scale-space filtering does not require watershed calculations on smoothed maps, as the method in [31] did, and is consequently faster. The segmentation accuracy is also slightly better. As in our prior work, we apply the method to density maps generated from structures obtained from the Protein Data Bank (PDB), and quantitatively measure its accuracy. We compare the accuracies obtained with both methods to each other and also to the highest accuracies attainable by grouping watershed regions. Recognizing that this method is incapable of finding perfect segmentations, we also augment this computational approach with interactive grouping and ungrouping of regions, allowing the researcher to manually modify the results obtained with cryo-EM maps based on any additional information they may have.

We also present two methods for fitting molecular structures into density maps, based on alignment of the structures with segmented regions. Previously reported fitting methods include manual placement [28,32,33], exhaustive search, e.g. EMFIT [34], DOCKEM [35], SITUS [36], URO [37], Foldhunter [38], FRM [39], and ADP_EM [40], and matching of feature points [41], or surfaces, e.g. 3SOM [42,43]. These methods can produce good fits, however they also have limitations. For example, manual placement is tedious and prone to error. Exhaustive search can take several minutes on even small maps, and the running time scales poorly with map size. Methods based on matching features can be faster, however they can be less reliable since features can be affected by noise.

The fitting methods we present are based on the alignment of structures with segmented regions, either by alignment of centers and principal axes, or by alignment of centers followed by rotational search. The resulting alignments are locally refined so as to optimize the cross-correlation score. The method that aligns principal axes is extremely fast, however it doesn't always find the right fit; rotational search is more reliable, however it too might fail if the shapes of the structure being fit and the region it is aligned with are considerably different. Despite this, these fitting methods are especially useful in an interactive setting. For example, the user can select a structure and a region to align it with, and the fit is achieved in only a few seconds.

Both the segmentation and fitting methods have been implemented in a software tool, Segger [44], which is publicly available as a plug-in to the molecular visualization software Chimera [45].

2. Methods

2.1 Segmentation

2.1.1 Watershed segmentation

We use the immersive watershed algorithm to segment a density map [46]. The algorithm is illustrated in Figure 1 in with a 1-dimensional map. For a 3D density map, the process is the same: all density values in the density map are first sorted, and then considered in descending order. For each density value, if the corresponding voxel is not adjacent (26-connected) to any voxels in an existing region, it is assigned to a new region. If it is adjacent to one or more voxels from a single region, it is assigned to that region. If it is adjacent to voxels from two or more regions, the adjacent regions are sorted by the number adjacent voxels in each region in decreasing order, and the voxel being considered is assigned to the first region in the list. Each resulting region contains a number of adjacent voxels, and the boundaries between regions are the points with the lowest densities between local maxima.

Figure 1.

From left to right, the images illustrate the first three and the last step during the immersive watershed algorithm for a 1D map. The smooth curve represents the underlying density function, which is discretized at evenly spaced grid points. Each point is drawn at a height proportional to its density value. The algorithm considers each point in order of decreasing density value: the point is added to a new region when none of its adjacent points are already in an existing region, or it is added to an existing region if it is adjacent to a point already in that region. In the end, two regions result in this example, containing either the points labeled with red triangles or the points labeled with green squares. Each region thus corresponds to a local density maximum (circled in the right-most image), which is the first point added to it. The points on the boundaries between the regions are points with the lowest density between local maxima.

2.1.2 Grouping of regions by scale-space filtering

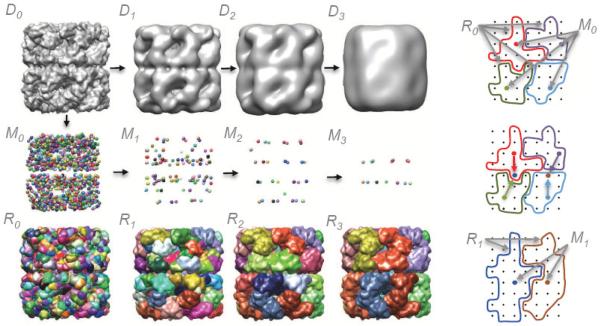
The process of successively smoothing a signal is known as scale-space filtering [17]. Here we apply it to a density map, in order to group regions obtained using the watershed method. The process is illustrated in Figure 2. The density map to be segmented is labeled D₀. The density map D_i, where i=1..3, is obtained by smoothing D_i-1. The regions in R₀ are given by the watershed method applied to the map D₀, and M₀ is the set of points corresponding to the local maxima. Once the smoothed map D₁ is obtained, each of the points in M₀ are moved by steepest ascent from their original positions to the local maxima in D₁. When two or more points converge to the same local maximum, they are replaced by a single point at that position, and the corresponding regions are grouped. When two or more regions are grouped, they are drawn using a single enclosing surface, so that they appear as a single region. The updated positions in M₀ become M₁, and the grouped regions become R₁. The same process is repeated for the positions in M₁, yielding M₂ and R₂, and so on.

Figure 2.

The watershed segmentation of a density map, D₀, is a set of regions, R₀, with regions corresponding to points positioned at every local density maxima, M₀. Density maps are shown using iso-surfaces, regions are drawn using smooth surfaces that enclose contained voxels, and points of local density maxima are drawn using spheres. Grouping by scale-space filtering moves the points in M₀ by steepest ascent to local density maxima in D₁, yielding new points M₁. When two or more points in M₁ coincide, the corresponding regions are grouped, as shown in the images on the right, producing R₁. R₃ results after two more smoothing and grouping steps, in which each region corresponds to a single protein. The illustrated density map was generated from PDB:1xck at 10Å resolution.

2.1.3 Segmentation procedure and parameters

Three parameters are used for the segmentation and grouping procedures: a segmenting threshold, a smoothing step size, and the number of smoothing steps. The threshold affects the resulting regions much like it affects the iso-surface visualization of the density map. At higher thresholds, the denser inner regions are segmented. In particular, in high resolutions maps, at high threshold values, the backbone and secondary structures are typically seen. At lower thresholds, a more complete envelope of each protein or subunit is segmented.

The smoothing step size specifies the standard deviation of the Gaussian kernel used to smooth the density map, and thus determines how much smoothing is performed at each step. For example, a step size of ~3Å produces a small decrease in the number of local density maxima and small changes in their locations. Smaller step sizes are preferred, since they produce more gradual changes, however larger steps may sometimes be desired to deal with noisy maps, since more smoothing suppresses more noise.

Grouping by scale-space filtering is performed for a number of specified smoothing steps. Optionally, the user can have the process stop if the number of regions drops below a given number (e.g. fro GroEL, the user might enter 14, since it contains 14 proteins). The ideal result is such that regions correspond to individual proteins or subunits. If too many steps are taken, the results may be such that single regions span more than one protein or subunit. In this case, the user can backtrack to a previous set of regions, where small groups of regions correspond to single proteins or subunits. From there, regions corresponding to the same protein or subunit can be interactively grouped, or grouped based on structures aligned to groups of regions, as will be further detailed below.

2.2 Fitting of structures into density maps

Fitting of a structure into a density map involves positioning and orienting the structure so that it best overlaps a corresponding component in the density map. In this paper we only consider rigid-body fitting, which assumes that the structure being fit, which might have been obtained for example by X-ray crystallography, has approximately the same conformation in the cryo-EM density map. Moreover, the methods we present assume that the structure being fit has roughly the same shape as the regions it is aligned with. The fitting methods will likely to fail if these assumptions do not hold, and also in the presence of reconstruction artifacts, such as a missing wedge in tomography.

2.2.1 Density cross-correlation metric

During the fitting process, a metric that reflects the quality of the fit is optimized, with the assumption that the correct fits are given by position and orientation parameters that globally maximize this score. Several metrics are possible, with the most common being the density cross-correlation score [47]. This score is computed between a simulated map of the structure being fitted, translated and rotated by the transform T, and the reference density map, using the formula:

$$\mathit{cc}\left(T\right)=\frac{\overrightarrow{u}\cdot \overrightarrow{v}}{\left|\overrightarrow{u}\right|\left|\overrightarrow{v}\right|}=\frac{{\displaystyle \underset{i=1}{\overset{n}{\Sigma }}}{u}_i{v}_i}{\sqrt{{\displaystyle \underset{i=1}{\overset{n}{\Sigma }}}{u_i}^2}\sqrt{{\displaystyle \underset{i=1}{\overset{n}{\Sigma }}}{v_i}^2}},$$ (1)

In the above, $\overrightarrow{u}$ and $\overrightarrow{v}$ are vectors containing n scalar values. The vector $\overrightarrow{u}$ contains density values above a threshold, which can be set by the user, at grid points in the density map generated from the structure being fit, after application of the transform T. The vector $\overrightarrow{v}$ contains density values from the reference density map in which the structure is being fit, calculated by trilinear interpolation at the positions from which the density values in $\overrightarrow{u}$ are taken.

2.2.2 Local refinement

Local refinement adjusts the position of the structure so as to increase the cross-correlation score. We use the fit in map function provided by Chimera [28], which translates and rotates the structure in the direction of the density gradient. Other local refinement methods have been reported, for example, Monte-Carlo random search [48]. We use the gradient-based method in Chimera because we found it to be robust and fast.

2.2.3 Alignment of structures with regions

The local refinement process locally maximizes the cross-correlation, and thus if the initial placement of the structure is not close to a global maximum, an incorrect fit is produced. To produce placements of the structure in the density map, we align it to a single region or a small group of regions produced by segmentation and grouping by scale-space filtering. Two methods are described here for creating such alignments: the first aligns centers and principal axes, and the second aligns centers and then exhaustively rotates the structure to find the best fit.

2.2.3.1 Principal-axes transform

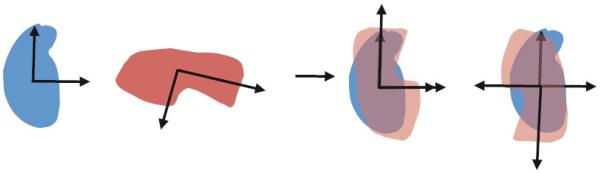
The principal axes of a structure are computed directly from its atomic positions. The first moment of these points is their center of mass, and the 3 eigenvectors and eigenvalues of the second moment tensor give the principal axes and their relative lengths. The principal axes of the region(s) that the structure is being aligned to are also computed in the same way, but using the positions of all the voxels in the region(s). The transform aligns the centers of mass and principal axes in order of decreasing relative lengths. The principal axes are coarse shape descriptors and are affected very little by noise or small differences in the structure and region being aligned.

The alignment of 2 shapes using the principal axes transform is illustrated for 2D shapes in Figure 3. The signs of the vectors defining the principal axes are ambiguous, which leads to 2 possible alignments in 2D and 4 possible alignments in 3D. In each of the 4 alignments for 3D shapes, either none or two of the 3 principal axes are reversed. Reversing one or three axes results in a reflection, which is not a valid alignment. Each of the 4 alignments is first locally refined, producing 4 possible fits of the structure in the map. The fit with the highest cross-correlation score is kept.

Figure 3.

Illustration of the principal axes transform for 2D shapes. The transform aligns centers of mass and principal axes. The signs of the principal axes are ambiguous; thus two alignments are possible in this 2D example.

2.2.3.2 Rotational search

The principal-axes transform can be expected to yield correct fits for structures that are asymmetric (i.e. not spherical, or rod-shaped). When the principal-axis alignment method doesn't produce a good fit, as indicated by visual inspection and a low cross-correlation score, an alternate alignment method can be used. This method first aligns the centers of mass of the structure and region(s), and then coarsely samples rotational space. Each rotated alignment is first locally refined, and the resulting fit with the highest cross-correlation score is kept. This method is more thorough and thus also more reliable, although slower, since more alignments are considered. It is similar to exhaustive search except that only rotational degrees of freedom are discretized.

2.2.4 Interactive fitting of structures to regions

One way to determine which region or group of regions that a structure should be aligned with is for the user to interactively select them. The alignment is then performed using the principal-axes transform first, since it is faster than rotational search. If the resulting fit does not look right, or if the cross-correlation score is low, rotational search can be used to see if a better fit is found. When the structure is to be aligned with a group of regions, and the user is not sure which group gives the best fit, a single region can be selected, and groups of adjacent regions can be generated automatically starting with that region. The structure is then aligned to all groups of regions and the resulting fit with the highest cross-correlation score is kept. Again the principal axes transform is used first, followed by rotational search if necessary. The automatic generation of groups is described below.

2.2.5 Automated alignment of structures to regions

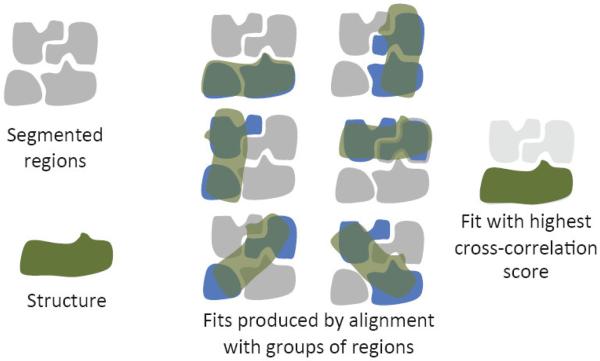
The structure can also be aligned to groups of regions that are automatically generated from all segmented regions. Again, the principal-axes alignment method is used first, followed by rotational search if the resulting fits do not appear to be correct or produce low cross-correlation scores. After aligning a structure to all groups, the resulting fits are sorted in order of decreasing cross-correlation score, and the first n fits are kept, where n is the number of times the structure is expected to appear in the density map. The number n can be determined by inspecting the cross-correlation scores, since cross-correlation scores of incorrect fits tend to be much lower than cross-correlation scores of correct fits. For the fits kept, the regions overlapping the fitted structure are grouped, to create single regions corresponding to the fitted structure. This process is illustrated in Figure 4.

Figure 4.

A structure is aligned with automatically generated groups of segmented regions, producing many potential fits. The fit with the highest cross-correlation score is taken.

2.2.6 Generation of groups of adjacent regions

The goal in this process is to consider all possible groups of adjacent regions, so that when the structure is aligned with one or more of these groups, the correct fit is found. An exhaustive enumeration of all possible combinations of regions could generate a very large number of groups. However, we require that the groups contain adjacent regions, and since each region is adjacent to only a small number of other regions, the number of possible groups is drastically reduced. Two regions are considered adjacent if at least one voxel in one region is adjacent to a voxel in the other region. In a group of adjacent regions, every region is adjacent to at least one other region. For generality, it is also possible for a group to consist of a single region.

To automatically generate groups of adjacent regions, a recursive algorithm based on a queue is used. Each element of the queue is a group of adjacent regions remaining to be processed. The queue is initialized either with a single group containing the region selected by the user, or the same number of groups as segmented regions, with each group containing a different segmented region. In the former case, all groups generated include the selected region, and in the latter, the groups generated include every segmented region. At each step, a group is removed from the front of the queue and processed. The algorithm stops when the queue becomes empty.

In parallel, a list of resulting groups is maintained. This list of groups is initially empty. A group is added to this list only if is different than any of the groups already in the list. When a group is removed from the queue, it is ignored if it is the same as a group currently in the list. Otherwise it is added to the list. Furthermore, if the volume of the group is smaller than the volume of the structure to be fit, further regions are considered for addition to the group. First, all regions that are adjacent to at least one region in the group are listed. All possible combinations of these adjacent regions are added to the group to create new groups, and all these new groups are added to the queue.

2.2.7 Filtering of groups based on volume and bounding-radius ratios

When considering a structure for alignment to groups of regions, the groups are first filtered to remove groups that are not similar to the structure, and thus which would not create a correct fit. Considering fewer groups for each structure reduces the number of alignments, and thus makes the automated process faster. The groups are filtered using two metrics: the ratio of volumes and ratio of bounding radii.

The bounding radius of a structure is the largest distance from its center to any of the atoms it contains. The bounding radius of a group of regions is the largest distance to any of the voxels in any of the regions, from the center of all the voxels in every region in the group. The volume of a group of regions is the number of combined voxels from all the regions in the group, multiplied by the volume of each voxel. The volume of a structure is computed from a density map generated from its atomic coordinates: it is the number of voxels with density values above a threshold, multiplied by the volume of each voxel. The threshold can be adjusted by the user, with the goal of making the iso-surface look similar to segmented regions. This would also make the volume of the structure and the volume of the group of regions it correctly aligns with similar, which would mean that this group would not be eliminated by filtering.

To compute the volume ratio, the difference between the volume of the structure and the volume of the combined regions in a group is first calculated. The absolute value of this difference is then divided by the volume of the structure to get the ratio. If this ratio is greater than a cut-off value, (we use 0.75), the group is ignored. The above process is the same for the bounding radius, with a cut-off of 0.3. These values were determined by starting with small values, and increasing them until all the correct fits were found for the structures considered here. They can be set to different values by the user if necessary. Decreasing them speeds up the process but increases the risk that the correct fit may not be found, while increasing them will make the process take more time but increases the chances that the correct fits will be found.

2.3 Segger

The multi-scale segmentation and fitting procedures are performed using the Segger software [44], available as a plug-in to Chimera [45]. The plug-in is written mostly in Python, making extensive use of routines already implemented in Chimera. The immersive watershed algorithm was compiled in C++ for speed. The smoothing is performed using the Gaussian filter method in Chimera, which performs the operation in Fourier space for efficiency.

2.4 Generating a density map from a structure

A density map is generated from a structure using the molmap command in Chimera. A grid is created around the structure, and the values of Gaussian functions centered at each atom position are added at each grid point. The standard deviation of every Gaussian function is set to 0.187r, with r being the desired resolution. This formulation makes the Fourier transform of each Gaussian half its maximum at wavenumber 1/r, similar in principle to the FSC_0.5 criterion used to determine the resolution of an experimentally-obtained density map [49].

2.5 Segmentation accuracy

The segmentation accuracy is quantitatively measured by applying the segmentation method to density maps generated from X-ray structures. The maps are masked using atomic positions in each individual protein or subunit. We call these protein-masked regions if the masking structure is of a protein, or subunit-masked regions if the structure is of a subunit (e.g. ribosome subunit). The regions obtained with the watershed method and grouping by scale-space filtering are compared to protein-masked or subunit-masked regions to determine the segmentation accuracy.

To generate a protein-masked region or a subunit-masked region, all voxels in the density map that are closer than 2.0Å to any atom in the protein or subunit keep their density values, and all others are given density values of 0. The value of 2.0Å is chosen because it is close to what the radius of an atom is when drawing a molecular surface for a structure. The voxels in the density map with density value lower than the threshold used to segment the map are also given density values of 0. The remaining voxels with non-zero density value represent the protein-masked or subunit-masked region.

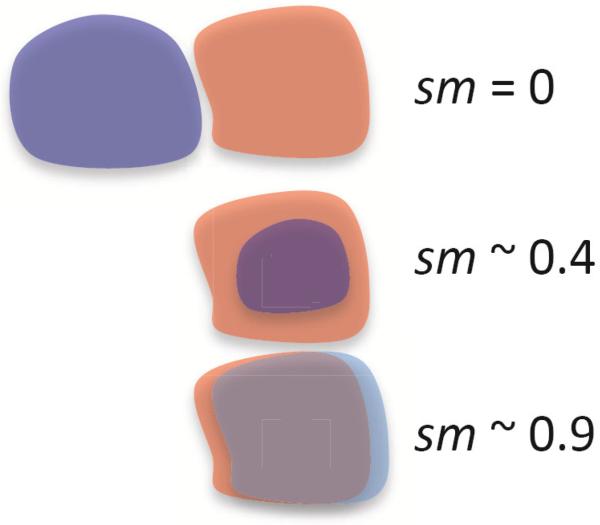
2.5.1 Shape-match score

Segmented regions are compared to protein-masked or subunit-masked regions using a shape-match score. Similar to the segmentation accuracy metric used in [50], this score is defined as follows:

$$\mathit{sm}=\frac{\mathit{volume}(R\cap G)}{\mathit{volume}(R\cup G)}$$ (2)

In the above equation, volume(R ∩ G) is the volume of the intersection of regions R and G, and volume(R ∪ G) is the volume of the union of the two regions. The shape-match score will be 0 if the two regions do not match at all (the intersection will have 0 volume), and it will be 1 if they match exactly (the volumes of the intersection and the union will be the same). Figure 5 illustrates this metric for 2D shapes. Both regions being compared are defined by voxels on the same grid, so the intersection and union operations are performed directly on these sets of voxels.

Figure 5.

Illustration of the shape-match score, which is used to quantitatively measure the difference between two regions. The score is 0 when the regions are disjoint, and 1 only when they cover exactly the same area.

2.5.2 Maximum accuracy for watershed segmentation

We also measure what is the most accurate grouping attainable for watershed regions in R₀, obtained from the non-smoothed map D₀ (Figure 2). The regions in R₀ are grouped based on which protein-masked or subunit-masked region they overlap the most. The resulting regions are compared to the protein-masked or subunit-masked regions using the shape-match score. This score will tell us how well the scale-space grouping method performs, and how much better it could potentially do.

2.6 Accuracy of fitting method

To measure the accuracy of the fitting methods, we use them to fit structures of individual proteins or subunits into density maps generated from the entire structure. For example, in the structure of GroEL (PDB:1xck), there are 14 proteins, represented by 14 chains labeled A,B,…,P. All chains have the same primary amino acid sequence and approximately the same conformation. The segmentation of the entire map produces 14 regions, or one region for each protein. We fit the structure of chain A to each of the regions, which results in 14 fitted structures. We then measure the RMSD between the positions of the atoms in each of the 14 fitted structures and the positions of the atoms in the closest chain from the entire structure. The RMSD is computed as follows:

$$\mathit{RMSD}=\sqrt{\frac{{\displaystyle \underset{i=1}{\overset{n}{\Sigma }}}{\Vert {\overrightarrow{r}}_i-{{\overrightarrow{r}}_i}^0\Vert }^2}{n}}$$ (3)

In the above, ${\overrightarrow{r}}_i$ are the positions of atom i, for i=1..n, in one of the fitted structures (where n is the total number of atoms in the fitted structure), and ${{\overrightarrow{r}}_i}^0$ are the positions of the atoms in the chain from the entire structure that is closest to the fitted structure. When an RMSD score low, the fit is accurate.

3. Results and Discussion

All results described below were obtained on a 2.8 GHz Intel Core 2 Duo processor, with 4GB DDR3 memory, using UCSF Chimera version 1.4 running on Mac OS 10.5.8, and Segger version 1.4.

3.1 Segmentation of density maps generated from PDB structures

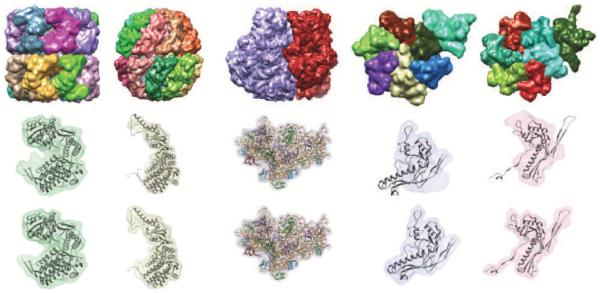
Density maps of 5 structures were generated at 10Å resolution, using the Chimera molmap command, sigmaFactor 0.187, grid spacing 2.0Å. The segmenting threshold was 0.2, and a smoothing step size of 3.0Å was used. The map dimensions, # of regions segmented, number of steps taken and running times are listed in Table 1. For the first 5 cases, the final number of regions matched the number of proteins or subunits. The resulting regions for these maps are shown in Figure 6. The regions are shown in Figure 6. For the remaining 2, the number of regions obtained did not match the number of proteins. These are shown in Figure 10.

Table 1.

Results of segmentation and grouping of regions by scale-space filtering, in maps generated from structures from the protein data bank (PDB). All maps were generated at a resolution of 10Å, the smoothing step size used for all of them was 3.0Å.

Structure	PDB ID	Map size	# proteins or subunits	# regions obtained	# steps	Time(s)
GroEL	1×ck	108×106×108	14	14	20	21
Thermosome	1q3s	109×109×112	16	16	17	20
Ribosome subunits	2avy,2aw4	139×155×161	2	2	68	114
HK97 procapsid	2gp1	94×102×73	7	7	4	4
HK97 mature	1ohg	56×108×133	7	7	9	6
GroEL+GroES	1aon	102×102×130	21	35	9	16
Ribosome proteins	2avy,2aw4	139×155×161	49	293	1	26

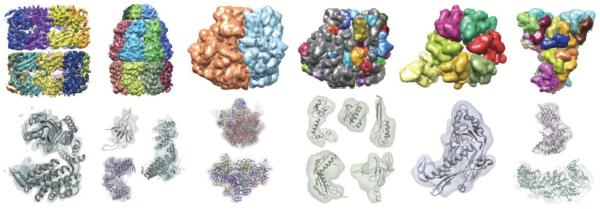
Figure 6.

Segmented regions in 5 simulated density maps are shown on the top row; from left to right, they are GroEL, thermosome, Ribosome subunits, HK97 procapsid asymmetric unit (ASU), and HK97 mature capsid ASU. On the middle row, a single segmented region from each map is shown using a transparent surface, along with the structure of the corresponding protein or subunit shown as a ribbon. The bottom row shows regions resulting from grouping regions R₀ based on which protein-masked or subunit-masked region they overlap the most, and hence giving the maximum accuracy that could be attained by grouping watershed regions.

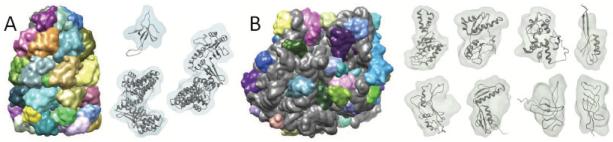
Figure 10.

(A) Segmented regions from the simulated density map of GroEL+GroES (PDB:1aon) are shown. In the barrel-section (GroEL), groups of 2-3 regions correspond to single proteins, whereas in the lid section (GroES), single regions correspond to each protein. Three of the resulting regions (transparent surfaces) and corresponding proteins, chains A, H, and O (ribbons) are shown. (B) Segmented regions from the density map of the E-coli ribosome (PDB:2aw4,2avy) are shown, using random colors for regions corresponding each of the 45 correctly fitted proteins, and grey for all remaining regions. 8 of these fitted proteins (ribbons) and corresponding regions (transparent surfaces) are also shown. The top row shows 2avy chains B,C,D,J, and bottom row shows 2aw4 chains F,G,P,R).

3.1.1 Segmentation accuracy

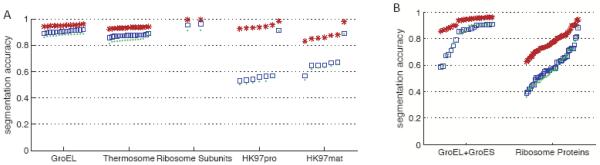
Segmentation accuracies for each protein or subunit were measured by computing the shape-match scores between segmented regions and protein/subunit-masked regions. The scores are plotted in Figure 7A. Good segmentation accuracies were obtained for GroEL (0.86-0.89), thermosome (0.81-0.88), and the ribosome large and small subunits (0.97, 0.98), but lower accuracies (0.50-0.89) for HK97. For the components segmented with high accuracy, the segmented regions closely match the protein/subunit-masked regions and the corresponding structures of each component or subunit, as seen in Figure 6.

Figure 7.

(A) Segmentation accuracies for the 5 simulated density maps shown in Figure 6. (B) Segmentation accuracies for simulated density maps of GroEL+GroES and Ribosome. Accuracies obtained with the grouping by scale-space filtering method are plotted with blue squares, accuracies obtained with the smoothing and sharpening method [31] are shown with green dots, and maximum accuracies attainable by grouping watershed regions are plotted with red asterisks. The same parameters were used for the two smoothing-based methods; the grouping method presented in this paper achieves slightly better segmentation accuracies.

Figure 7 also plots the accuracies obtained with the previous method described in [31], which involved application of the watershed algorithm on every smoothed map and then sharpening the regions in the most smoothed map. The present approach obtains slightly better accuracies.

The maximum accuracies attainable using watershed regions, as described in section 2.5.2, are also plotted in Figure 7. All the maximum watershed accuracies for each component are high, indicating that the watershed method could be used to produce very accurate segmentations. These accuracies however are not 1, because the protein-masked regions approximate the molecular volume of each protein, whereas the regions resulting from grouping watershed regions are limited by the watershed method and the resolution of the density map.

3.1.2 Cause of low accuracies

The accuracies obtained by the scale-space method are lower than the maximum watershed accuracies. They are very close for the GroeL, thermosome, and ribosome complexes, however they are lower for the HK97 asymmetric units. Figure 6 shows that narrow segments in the proteins of HK97 were not captured correctly in the regions produced by the multi-scale method, and hence the segmentation accuracies for these components were low (0.5-0.6). This happens because the regions corresponding to these protruding segments are grouped with regions corresponding to the nearby proteins they interact with. They appear as separate regions in less-smoothed maps, however during the grouping process, the local density maxima move towards the maxima corresponding to the nearby protein. We tried improving the grouping process by taking into account local metrics such as density values between regions, however we didn't find that this consistently improved the accuracy, perhaps because the local metrics are easily influenced by noise and discretization error.

The segmentation accuracies plotted in Figure 7(A) also show that one of the proteins in HK97 has substantially higher segmentation accuracy than the other six. The units with lower accuracies are part of a 6-fold ring-like symmetric arrangement where each protein interacts with two others. The protein with the higher accuracy is part of a 5-fold symmetric arrangement that is formed with proteins from 4 other asymmetric units. The segmentation of this protein was more accurate because the two neighbors it has in adjacent asymmetric units are not present in the asymmetric unit.

3.1.3 Interactive ungrouping and regrouping of regions

Since the accuracies obtained with the scale-space method cannot be expected to be perfect, Segger allows the user to manual ungroup the resulting regions. When ungrouping a region, it is split up into the groups of regions that were grouped at the previous smoothing step. Thus, if several smoothing steps were used (rather than just one, for example), the results will typically be a small number of regions. Each ungrouped region could be further ungrouped as necessary, to get even smaller regions. The regions from the initially segmented map, D₀ in Figure 1, cannot be further ungrouped. The ungrouped regions can be regrouped or added to other regions, as the user sees best fit. When this process is guided by other information, for example, a fitted structure, better segmentations can be obtained, overcoming limitations of the scale-space method.

3.1.4 Dependence of computation time on map size and resolution

The running time for the watershed algorithm is dominated by the sorting of the density values, and thus is O(nlogn), where n is the total number of voxels to be segmented. The running time thus scales favorably with map size. The smoothing operation is performed by a Chimera function, which performs the operation in Fourier space, and thus its running time also scales well with n. However n itself scales poorly with map dimension d, by O(d³). Lastly, the total running time is also affected by the number of regions produced by the watershed method, since the same number of points as regions are then updated by steepest ascent (this number decreases as regions merge). Maps at higher resolution tend to produce more regions, and thus grouping by scale-space filtering will take longer on them compared to maps at lower resolution.

3.1.5 Memory requirements and map size limits

The watershed segmentation method, as presently implemented, requires at most 6 times the size of the density map in available memory, in order to 1) store the map, 2) create a list of voxels sorted by density value (the list includes density values and voxels indexed with 3 integers), and 3) store a label for each voxel indicating what region it belongs to. The list in 2) does not typically include all voxels in a map, so that the memory requirements are typically smaller than the 6x bound. Since this program currently runs externally, and the map is also open in Chimera simultaneously, realistically 7x the memory is actually needed. Once the segmentation is finished, the list of sorted voxels is no longer needed, and this memory is used instead to store the smoothed map.

Size limits are dictated by the amount of physical memory that is available and can be accessed on the system. With 4GB of memory, the maximum map size along one dimension is (2³²/7)^1/3, so it should be possible to process a map of at most ~850×850×850. With 8GB, and 16GB of physical memory, maps of roughly 1000×1000×1000, and 1300×1300×1300 respectively can be processed. However in practice, not all physical memory is available to the program due to library code, stack space, architecture, and operating system limits, and thus the maps sizes that can be actually processed may be smaller.

Visualization of the density map and the segmentation results (which are shown as smooth surfaces for each region) must also be taken into account. For example, within Chimera, performance decreases considerably if more than 2000 surfaces are shown. If more than this number of regions are segmented, only the largest 2000 of them are shown. As scale space grouping reduces the number of regions, eventually a segmentation of the entire map can be produced.

3.2 Segmentation accuracy vs. resolution

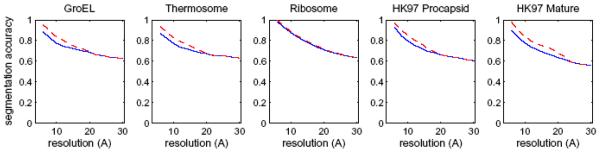
An important question in the analysis of cryo-EM density maps is how accurately components can be identified at different resolutions. We try to answer this question using density maps generated from a molecular structure at a range of resolutions (6Å - 30Å, in steps of 2Å ) for GRoEL, thermosome, Ribosome, HK97 procapsid and HK97 mature capsid. The map at every resolution was segmented and the resulting regions were grouped, specifying only an initial threshold for each map, the number of proteins or subunits to be segmented, and a smoothing step size of 2.0Å. In all cases, a large number of smoothing steps were specified (99), and the scale-space filtering process automatically stopped when this number was reached. The number of steps actually taken varied and depended on map and the resolution – at lower resolutions, fewer smoothing steps were required, since the map was smoother to start with. In all cases, the number of regions produced was the same as the number of proteins or subunits.

In Figure 8, the highest segmentation accuracy (blue lines) obtained with the scale-space method and highest maximum watershed segmentation accuracy (dashed red lines) in each density map is plotted vs. resolution. The plots show that accuracies are high for high-resolution density maps, and decrease with resolution, but stay above 0.6 even at the lowest resolution of 30Å. At lower resolutions, the grouping of regions using the scale-space approach produces the same accuracy as the maximum accuracy possible with the watershed method, since the two lines coincide. This is because at lower resolutions, there are fewer watershed regions to group, and hence it becomes somewhat easier to group the correct regions.

Figure 8.

Segmentation accuracies for 5 density maps simulated at various resolutions (6Å-30Å, every 2Å). The highest segmentation accuracy (blue lines) and highest maximum watershed segmentation accuracy (dashed red lines) amongst all components in each density map is plotted vs. resolution. The plots show that segmentation accuracies drop as the resolution increases, and that at low resolutions, the accuracies obtained by multi-scale grouping are the same as the maximum watershed accuracies.

To illustrate the effect of resolution on segmented regions, a single protein from GroEL is shown in Figure 9. The regions shown are the protein-masked region and the regions produced by the scale-space method applied to simulated maps at different resolutions. At high resolution, the segmentation closely resembles the ground-truth region. At lower resolutions, the segmented regions have increasingly smooth surfaces compared to the protein-masked region. However, even at low resolutions, the segmented region still closely, if roughly, captures the shape of the protein.

Figure 9.

Protein-masked region and segmented regions corresponding to a single protein in simulated maps of GroEL at different resolutions. The protein-masked is the first from the left. The remaining segmented regions are from maps with resolutions of (left to right) 6Å, 10Å, 20Å, and 30Å.

3.3 Accuracy of fitting methods

To measure the accuracy of the fitting methods, structures of individual proteins or subunits were aligned with single segmented regions in the first 5 simulated density maps in Table 1. The automated procedure was used, and since each region corresponds to a single protein or subunit, the groups generated consisted of only one region each. Hence the procedure was extremely fast, taking less than a minute for each of the density maps. The RMSD between the atoms in each fitted structure and the corresponding atoms in the structure from which the density maps was simulated were all less than 1Å, indicating that the fits were correct. The principal-axes alignment method produced the correct fits for all structures. The fitting method was also tested with simulated maps at lower resolutions. Correct fits were obtained for density maps simulated at up to 30Å resolution.

3.3.2 GroEL + GroES

A density map of the structure (PDB:1aon) was generated at 10Å resolution. The segmenting threshold was 0.2, and a smoothing step size of 3.0Å was used. After 9 smoothing and grouping steps, 35 regions were obtained. Taking more stepsSingle regions correspond to proteins in the lid (GroES) section, and groups of 2 regions correspond to proteins in the barrel (GroEL) section, as shown in Figure 10A.

The 3 different protein structures (chains A, H, and O) were fitted by alignment with the segmented regions. Using the interactive approach, each protein structure was aligned with interactively selected regions, taking only a few seconds per structure. Using the automated approach, 215 groups were considered for chain A, and alignment took ~8min; 65 groups were considered for chain H, with alignment taking ~2min, and 28 groups were considered for chain O, with alignment taking ~1min. The principal-axes transform produced correct fits for proteins in the barrel section (chains A and H), but not in the lid section, where rotational search was required to find the correct fits. The RMSD scores computed for each fitted structure were all less than 1.0Å, indicating that the correct fits were found. Segmentation accuracies for the resulting regions are plotted in Figure 7B; good accuracies are obtained for regions in the barrel section (0.83-0.90), but lower accuracies for regions in the lid section (0.58-0.72).

3.4.2 Ribosome

For the simulated map of the E-coli ribosome, as shown in Figure 6, the scale-space grouping procedure was able to produce single regions for the large and small subunits after many steps. In less-smoothed maps (1 steps of size 3.0Å), a total of 602 regions result. Each of the 49 protein structures were aligned to automatically generated groups of regions, and 43 of them were fitted correctly. The principal axes method found the correct fit for most of the proteins, however rotational search was required for some. Due to the numerous regions, the number of groups generated were very large, but only the 1000 most similar groups (by volume ratio) were considered. Alignment took ~10 minutes per protein when using the principal axes method, and ~30 minutes with rotational search.

All RMSD scores computed for the fitted structures were lower than 1Å, indicating the correct fits were found. Eight of the resulting regions and corresponding protein structures are shown in Figure 10B. Segmentation accuracies for the 43 proteins fitted correctly are plotted in Figure 7B, and range between 0.38 and 0.88. Some of the accuracies are quite low, since the boundaries between proteins and RNA can be quite dense, and thus hard to segment.

3.5 Results for experimental density maps

A total of 5 experimental density maps from the electron microscopy data bank (EMDB) [51] were segmented, and structures of individual components obtained from the PDB were fitted by alignment with segmented regions. The results are shown in Figure 11, and shape-match scores between the regions and protein-masked and subunit-masked regions are plotted in Figure 12. For the fitting procedure, maps for the structures of each protein or subunit were generated at the same resolution as the reported resolution of the cryo-EM map and at the same grid spacing. The cross-correlation scores are not reported here since they vary depending on the thresholds used in the density maps. Details are summarized in Table 2.

Figure 11.

Segmented experimental density maps, from left to right: GroEL, GroEL+GroES, ribosome large/small subunits, ribosome RNA/proteins, bacteriophage lambda, and rice dwarf virus. The top row shows regions after segmentation, grouping by scale-space filtering, and finally grouping based on fitted structures when fitted structures overlap more than one region. The bottom row shows single regions as transparent surfaces and corresponding fitted structures as ribbons. The structures are, from left to right, PDB:1xck chain A, PDB:1aon chains A, H, and O, PDB:2avy and PDB:2aw4 all chains, PDB:2avy chains M,I,J (top) and PDB:2aw4 chains G,P (bottom), PDB:3bqw, and PDB:1uf2 chains A and C.

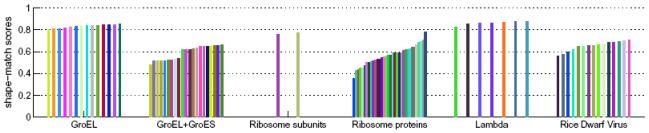
Figure 12.

Shape-match scores between segmented regions for 5 cryo-EM density maps and protein/subunit masked regions. The cryo-EM map of the ribosome was segmented twice, first into larger and small subunits, and then into proteins and RNA.

Table 2.

Results of segmentation and grouping of regions by scale-space filtering in experimental density maps from the electron microscopy data bank (EMDB).

Density map (EMDB id)	Resoluti on (Å)	Map size	# proteins or subunits	Step size (Å)	# steps	# regions obtained	Time(s)
GroEL (5001)	4.2	200×200×200	14	8	3	14	33
GroEL+GroES (1180)	7.7	192×192×192	21	5	3	37	30
Ribosome (1056)	9.0	130×130×130	2 subunits	5	32	2	30
Ribosome (1056)	9.0	130×130×130	49 proteins	n/a	0	897	9
Lambda (1507)	14.5	192×192×96	7 per ASU	6	4	236	128
Rice dwarf virus (1060)	6.8	279×279×140	15 per ASU	3	1	1553	56
Rice dwarf virus ASU	6.8	152×196×212	15	4	4	43	13

3.5.1 GroEL

The density map for GroEL at 4.2Å resolution [52] (EMDB:5001) was segmented at a thresholdof 1.0. After 3 steps of size 8.0Å, 14 regions were obtained, with each region corresponding with a single protein. Chain A from PDB:1xck was aligned with automatically generated groups of regions using the principal axes transform. Only 28 groups were generated, and the fitting procedure was thus very fast, taking only ~20 seconds. The shape-match scores between each of the 14 segmented regions and corresponding protein-masked regions (generated from each fitted protein structure) were quite high, ranging between 0.81 and 0.86. The scores for each region are not the same even though the map has 14-fold symmetry, because the segmentation method does not impose symmetry on the resulting regions, nor does it use any type of symmetry information. The scores are slightly lower than for the analogous simulated density map, signifying lower segmentation accuracy (perhaps due to noise), and/or slight difference between crystal and cryo-EM structures.

3.5.2 GroEL+GroES

The density map for GroEL+GroES at 7.7Å resolution [1] (EMDB:1180) was segmented at a threshold of 0.8. A total of 3 smoothing and grouping steps of size 5Å were used, resulting in 37 regions. The 3 different protein structures (chains A,H,O) in PDB:1aon were fitted into the map by alignment to regions, with both interactive and automated approaches. The structures from chains A and H were fitted correctly by alignment to groups of 2 regions each, using the principal axes transform. The regions corresponding to each protein were grouped to yield regions corresponding to single proteins. Chain O was fitted correctly by alignment with single regions, using rotational search. The interactive fitting was very fast, taking only several seconds for chains A and H using the principal axes transform, and about 20 seconds for chain O using rotational search. Using the automated approach, 568, 255, and 49 groups were generated respectively, taking ~15, ~10, and ~14 minutes.

The shape-match scores, comparing the regions to protein-masked regions, were between 0.49 and 0.54 for chain A, 0.65 and 0.67 for chain O, and 0.52 and 0.64 for chain H. All these scores are quite low, and by visual inspection, the cause appears to be that the density map is very noisy.

3.5.3 Ribosome

The density map of the E-coli ribosome at 9Å resolution [2] (EMDB:1056) was segmented at a threshold of 43.4. A total of 32 smoothing and grouping steps of size 5.0Å were performed. This produces only two regions corresponding to the large and small subunits. The structure of the large (PDB:2aw4) and small (PDB:2avy) subunits were fitted correctly by alignment to the corresponding regions using the principal-axes transform, taking less than 10 seconds for each structure. The shape-match scores between the segmented regions and subunit-masked regions were 0.79 and 0.77.

Each of the 49 protein structures in the two subunits were also fitted into the density map using the automated procedure. About 1000 groups were considered for each structure, and the alignment process took about 10 minutes using the principal-axes transform, or about 30 minutes using rotational search for each structure. The rotational search was used when the best fit obtained using the principal axes transform was not correct. To decide whether the fit for a structure was correct, the RMSD between the fitted protein structure and the corresponding protein structure in the entire fitted subunit was measured. The correctly fitted structures produced low (<5Å) RMSDs whereas the incorrect fits produced much higher RMSDs, >15Å. The cross-correlation scores of the correct fits were also significantly higher than those of incorrect fits. Of the 49 proteins, 33 were correctly fitted. The shape-match scores computed for the regions and the protein-masked regions ranged between 0.436 and 0.784. For the proteins that weren't fitted correctly, the potential cause is that the protein-RNA boundary in the density is perhaps more difficult to discern for some proteins than others, and regions obtained for some of the proteins may not have been produced at all.

3.5.4 Bacteriophage lambda

The density map of bacteriophage lambda at 14.5Å resolution [3] (EMDB:1507) contains a symmetric half of the T=7 icosahedral lattice, and thus about 30 asymmetric units(ASU) - a full capsid contains 60 ASUs, and each ASU consists of only 7 proteins in this case. The map was segmented at a threshold of 4.0, and the resulting 6,688 regions were grouped with 4 steps of size 6Å. In total, 236 regions were produced, and single regions corresponded to individual proteins.

The 7 regions making up an ASU were interactively selected and extracted from the rest of the regions. The structure of a single protein (PDB:3bqw) was aligned to automatically generated groups. Only 12 groups were considered, and the process took about 20 seconds. All the correct fits were produced using the principal-axes transform. The shape match scores computed between segmented regions and protein-masked regions were quite high, ranging between 0.84 and 0.89.

3.5.5 Rice dwarf virus (RDV)

The density maps of the rice dwarf virus at 6.8Å resolution [4] (EMDB:1060) was segmented at a threshold of 2.5, resulting in 17,195 regions. This map contains a symmetric half of the entire capsid along with enclosed DNA. At the threshold of 2.5, only the capsid is segmented, since the DNA region has lower density values. The map was smoothed with 1 step of size of 3.0Å, and grouping resulted in 1,553 regions. Individual proteins in the outer capsid could be seen in this segmentation, corresponding with groups of 2 regions each.

The crystal structure of the asymmetric unit (PDB:1uf2) is composed of 13 proteins that form 4+1/3 trimers in the outer capsid, and 2 proteins in the inner capsid. The structure of one of the trimer proteins (chain C), was fitted into the map by alignment with two of the segmented regions, which were selected interactively. The structure of the entire asymmetric unit was fitted into the density map by aligning the corresponding chain in the structure to the structure fit by alignment to the group of 2 regions. The cryo-EM map was masked using this structure, thus extracting a map the asymmetric unit alone. This was done to simplify further segmentation and fitting of structures.

The map of the asymmetric unit was then segmented alone, with the segmentation of the non-smoothed map producing 1,113 regions. It was smoothed with 4 steps of size 4.0Å, and after grouping of reiongs, 43 regions resulted. Groups of 2 regions corresponded to proteins in the outer capsid, and groups of 5 regions to proteins in the inner capsid. Structures of each protein (chains A, B, and C) from PDB:1uf2 were fitted by selecting regions interactively and aligning the structures with them, taking only a few seconds per structure. All three structures were correctly fitted using only the principal-axes transform. The shape match scores between the resulting regions and protein-masked regions were between 0.57 and 0.71. These scores are quite low, signifying lower segmentation accuracy and/or more substantial differences between crystal and cryo-EM structures.

4. Conclusions

We've presented a segmentation method based on the immersive watershed algorithm and scale-spaced grouping of the resulting regions. The method is very easy to use and requires little prior structural knowledge. The method yields reproducible results given only three parameters: the initial threshold, the smoothing step size, and the number of smoothing steps. The results are typically such that either single regions or small groups of regions correspond to individual components. The segmentation accuracy was measured using a shape-based metric. Good segmentation accuracies were obtained for some complexes, although narrow protruding segments tend to be incorrectly segmented, resulting in low accuracies for other complexes. In the Segger interface, manual ungrouping and regrouping of regions is possible, and thus through some interactive effort on the part of the user, segmentations can be improved.

We also showed that structures of individual components can be rigidly fit into a density map through the alignment of structures to segmented regions. A correct fit can be found for a single structure in as little as a few seconds. When structures are aligned with multiple, automatically generated groups of regions, in cases where each structure corresponds to a single region, the fitting of all structures is again extremely fast, taking only tens of seconds. When each structure corresponds to multiple regions, the number of generated groups is higher, and thus longer times are required.

On top of thoroughly measuring the accuracies of these methods, we have also aimed to make the methods presented here easy to use and widely accessible to the public [44]. Continued effort in this direction should lead to improved tools allowing us to more quickly and accurately extract important biological information from density maps obtained by the increasingly popular cryo-EM method.