Evaluation of different tests based on observations for external model evaluation of population analyses

Abstract

Purpose

To evaluate by simulation the statistical properties of normalized prediction distribution errors (NPDE), prediction discrepancies (pd), standardized prediction errors (SPE), numerical predictive check (NPC) and decorrelated NPC (NPC_dec) for the external evaluation of a population pharmacokinetic analysis, and to illustrate the use of NPDE for the evaluation of covariate models.

Methods

We assume that a model M_B has been built using a building dataset B, and that a separate validation dataset, V is available. Our null hypothesis H₀ is that the data in V can be described by M_B. We use several methods to test this hypothesis: NPDE, pd, SPE, NPC and NPC_dec. First, we evaluated by simulation the type I error under H₀ of different tests applied to the four methods. We also propose and evaluate a single global test combining normality, mean and variance tests applied to NPDE, pd and SPE. We perform tests on NPC and NPC_dec, after a decorrelation. M_B was a one compartment model with first order absorption (without covariate), previously developed from two phase II and one phase III studies of the antidiabetic drug, gliclazide. We simulated 500 external datasets according to the design of a phase III study.

Second, we investigated the application of NPDE to covariate models. We propose two approaches: the first approach uses correlation tests or mean comparisons to test the relationship between NPDE and covariates; the second evaluates NPDE split by category for discrete covariates or quantiles for continuous covariates. We generated several validation datasets under H₀ and under alternative assumptions with a model without covariate, with one continuous covariate (weight), or one categorical covariate (sex). We calculated the powers of the different tests using simulations, where the covariates of the phase III study were used.

Results

The simulations under H₀ show a high type I error for the different tests applied to SPE and an increased type I error for pd. The different tests present a type I error close to 5% for for the global test appied to NPDE. We find a type I error higher than 5% for the test applied to classical NPC but this test becomes close to 5% for NPC_dec.

For covariate models, when model and validation dataset are consistent, type I error of the tests are close to 5% for both effects. When validation datasets and models are not consistent, the tests detect the correlation between NPDE and the covariate.

Conclusion

We recommend to use NPDE over SPE for external model evaluation, since they do not depend on an approximation of the model and have good statistical properties. NPDE represent a better approach than NPC, since in order to perform tests on NPC, a decorrelation step must be applied before. NPDE, in this illustration, is also a good tool to evaluate model with or without covariates.

INTRODUCTION

The Food and Drugs Administration (FDA) performed a survey to evaluate the impact of population pharmacokinetic (PK) and/or pharmacodynamic (PD) analyses on drug approval and labelling decisions between 2000 and 2004 and an article concerning evolution and impact of pharmacometrics at FDA (1). They pointed out in their survey that, in order for the information resulting from a population analysis to be useful during regulatory assessment, the analysis needs to be of sufficient quality so that the final model can be judged to be a good description of the data and that the results ensuing from the population analysis can be considered valid. The guideline of the European Agency of Evaluation of Medicinal Products (EMEA) on reporting the results of population pharmacokinetic analyses, in 2006, recommends to use model evaluation procedures to demonstrate that the final model is robust and is a sufficiently good description of the data so that the objective(s) of the analysis can be met (2). The FDA guidelines on population analyses also fully supports the use of population PK and/or PD modeling during drug development process, and stresses the need for model evaluation. Two types of model evaluation can be performed (3). The first is internal evaluation, which compares an original dataset used for the model building (called learning dataset); in the following here, we only consider the second one, more stringent, external evaluation, which refers to a comparison between a separate dataset (usually called validation dataset) and the predictions from the model built from the learning dataset using dosage regimen information and possibly covariates from the validation dataset. The validation dataset is not for model building or for parameter estimation. However evaluations methods described here could be applied for internal model evaluation too.

Mentré and Escolano developed a new model evaluation method, called prediction discrepancies (pd), and showed that pd exhibit have better statistical properties than standardized prediction errors SPE (usually called weighted residual or WRES), the most frequently used metric according to a survey investigating PK/PD analyses in 2005 and 2006 (4), but that multiple observations per subject increased the type I error of the test (5).

In a recent paper, we defined and illustrated metrics for external evaluation of a population model (6). In particular, we proposed an improved version of pd. This improved version presents better theoretical statistical properties with multiple observations per subject by taking into account correlations and was called Normalized prediction errors (NPDE) (6).

In the present paper, we now evaluate in a simulation study the properties of different tests applied to NPDE; we compare these results to those obtained both with the historical method, SPE, and with the pd from which the NPDE were derived, to see the benefit of taking into account correlations within an individual. We also compare NPDE with a related statistic based on the visual predictive check (VPC). VPC are a graphical comparison between the observations and the simulated predictive distribution. The simulated data used for the VPC can be used to derive a related statistic, called numerical predictive check (NPC) (8). We apply two tests, a Student test and a binomial exact test, to test whether the percentage of observations in a given prediction interval match the theoretical coverage. We evaluate and compare using simulations the properties of these two tests on the classical NPC, and on an extension to this NPC developed here: the decorrelated numerical predictive check (NPC_dec).

The model used to perform simulations under H₀ in order to evaluate the type I error of different tests applied to SPE, NPDE, pd, NPC and NPC_dec was a population pharmacokinetic model of gliclazide, built from concentrations measured in two phase II studies and one phase III study (9). The validation datasets are simulated using the design of a real phase III study.

We then extend the application of NPDE to evaluate different models with a covariate by generating several validation datasets under alternative assumptions: without covariate, with one continuous covariate, with one categorical covariate.

POPULATION PHARMACOKINETIC MODEL OF GLICLAZIDE

Data

We used four clinical studies, which were performed during the clinical development of a modified release formulation of gliclazide (gliclazide MR), an oral antidiabetic agent. They were part of a larger dataset analyzed by Frey et al.(9), who studied the relationship between the pharmacokinetics of gliclazide and its long-term PD effect. The first phase II study (N = 40 patients, 18 observations per subject) was a ascending-dose study of gliclazide MR. The second one (N = 169 patients, 6 observations per subject) was a dose ranging, monocentric study of gliclazide MR. The two phase III studies (N = 462 patients and 351, respectively, 3 observations per subject for each study) were clinical comparative trials of gliclazide MR with the currently formulation of gliclazide in different countries, with a titration period of 4 months, a maintenance period of 6 months and a follow up period of 2 months. At the end of these phases III studies, all patients received gliclazide MR. The designs of these four studies have been described in details by Frey et al(9).. Gliclazide plasma concentrations were measured using high-performance liquid chromatography with ultaviolet detection.

Basic model building

We developped the population pharmacokinetic model for gliclazide MR, from the two phase II studies and the first phase III study, in a total of 642 Type II diabetic patients with 5931 plasma concentrations of gliclazide. The last phase III study was used as an external validation dataset for model evaluation.

During model building, we tested a zero order or a first order absorption model with or without a lag time. We assumed an exponential random-effect model to describe inter-individual variability. For residual variability, three error models were tested: additive, proportional and combined error model. The existence of a correlation between the PK parameters was also tested. Model selection was based on comparison of the objective function. The decision to include a parameter in the model was based on the Likelihood ratio test (LRT). The objective function obtained in NONMEM is up to a constant equal to −2 log likelihood. The difference in objective function (likelihood ratio) between two nested models (i.e. the larger model can be reduced to the smaller) is approximately chi square distributed, with degrees of freedom (df) equal to the difference in the number of parameters. Based on this, the improvement here in model fit from the inclusion (or deletion) of a model parameter can be assigned a significance level; 3.84 corresponds to nominal p value of <0.05 (df=1). Non-nested models were compared using the Akaike criterion (AIC).

During model building, values below the quantification limit (BQL), with a quantification limit (QL) which was equal to 0.05 mg/l, were treated in one of the standard ways by imputing the first BQL measurement to QL/2 and omitting subsequent BQL measurements during the terminal phase (10). The symmetrical reverse procedure was applied to BQL measurements during the absorption phase.

Covariate model building

From the final basic model, the effects of covariates on the Empirical Bayes Estimates (EBE) of each individual random effects, were tested using non parametric tests: a Wilcoxon Mann-Whitney test for categorical variables and a Spearman correlation test for continuous variables. Non parametric statistical tests were carried out to identify potential covariates of interest to save time during covariate model building. The tested covariates were: age, sex, race, weight, body mass index, creatinine, creatinine clearance (calculated from the Cockcroft and Gault formula), total plasma protein, alcohol habit, hepatic disease, drug interaction and dose. For drug interaction, as the principal routes of gliclazide metabolism are catalysed by CYP2C9 and CYP2C19 enzyme, categorical covariates were defined for each co-administratered substrate, inhibitor or inducer of these enzymes. These covariates took the value of 1 in case of co-administration, and 0 otherwise.

The covariate model was then built with the covariates which were found to have a significant effect in this first step (p<0.05). The population models corresponding to all the combinations of these candidate covariates were evaluated. Let θ_i be an individual PK parameter of the i^th subject, θ the population PK parameter and θ_COV a covariate effect on θ. For a continuous covariate, COV_i was the covariate value in the i^th patient and MEAN_COV the arithmetic mean. For categorical covariates, COV_i was an indicator variable of the i^th patient, with a value of 1 when the characteristic was present in the i^th patient, 0 otherwise. η_i represents the vector of random effect of individual i. For a continuous covariate, the covariate model was implemented with the equation:

$${\theta }_{\text{i}}=[\theta +{\theta }_{\text{COV}}\times ({\text{COV}}_{\text{i}}-{\text{MEAN}}_{\text{COV}})]\times exp({\eta }_{\text{i}})$$ (1)

The equation for the covariate model of a categorical covariate was:

$${\theta }_{\text{i}}=[\theta \times (1+{\theta }_{\text{COV}}\times {\text{COV}}_{\text{i}})]\times exp({\eta }_{\text{i}})$$ (2)

The decision to include a covariate in the model was also based on the LRT. From the best model with the smallest AIC, a backward elimination procedure was then used to test whether all covariates selected should remain in the final model using a LRT with a value of p = 0.005.

The population analysis of the two phase II studies and the one phase III study was performed using NONMEM software version V (University of San Francisco) with the FO method.

Results

Data, which are normalized for a dose of 30 mg, are dispayed in figure 1; the 90% predicted interval, obtained as the 5^th and 95^th percentiles of 1000 simulations are surimposed on the observations on the top plot and the 10^th, 50^th and 90^th percentiles of 1000 simulations are superimposed on the 10^th, 50^th and 90^th percentiles of the observations on the bottom plot. We decided here in the second plot to represent the percentiles of the observations and not the observations themselves; there is less need for displaying the observations as the percentiles will reveal where the information in data is rich and where it is sparse. This VPC was satisfactory concerning the 90% predicted interval but less satisfactory for the median. The basic model was found to be a one compartment model with a first order absorption with a lag time, and a first order elimination. It was parameterized with the apparent volume of distribution (V/F), the apparent clearance (CL/F), the absorption rate constant (k_a) and a lag time (T_lag). A correlation between CL/F and V/F and between k_a and T_lag was estimated. A proportional error model was found to best describe the residual error model. The estimated population parameters are given in Table I.

Figure 1.

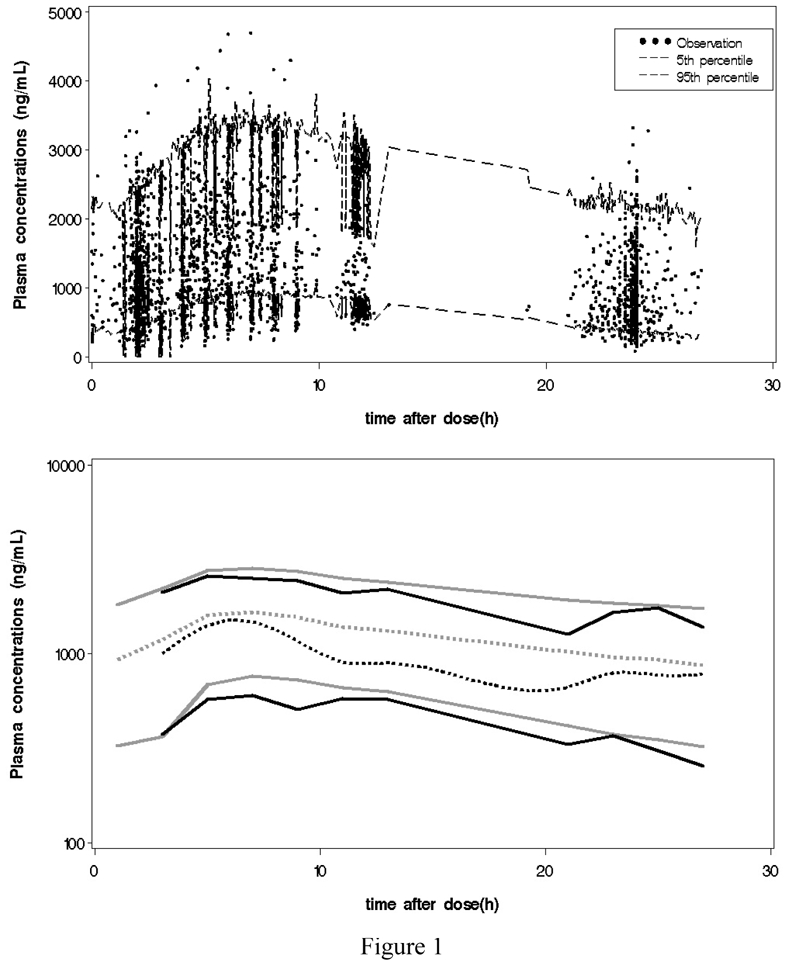
Gliclazide plasma concentration normalized for a dose of 30 mg versus time. On the top plot, the black dots represent the observations and the dashed lines the 5^th and 95^th percentiles of 1000 simulations. On the bottom plot, the black lines represent the 10^th, 50^th and 90^th percentiles of 1000 simulations. The gray lines represent the 10^th, 50^th and 90^th percentiles of the observations.

Table I.

Estimated population pharmacokinetic parameters of gliclazide MR for the basic and the final models (estimate and relative standard error of estimation, RSE).

Population parameters	Basic model		Final model
	Estimate	RSE (%)	Estimate	RSE (%)
CL/F (L/h)	0.91	2.3	0.88	2.0
V/F (L)	19.7	10.9	27.0	5.9
θweight	-	-	0.21	22.2
ka (h−1)	0.32	20.0	0.38	9.1
Tlag (h)	1.3	7.3	1.2	5.9
ω2CL/F	0.19	6.3	0.19	6.3
ω2V/F	0.12	13.9	0.07	16.4
ω2ka	0.31	22.1	0.31	19.1
ω2Tlag	0.60	29.1	0.60	30.1
Cov(V-CL)	0.10	12.1	0.09	12.3
Cov(ka-Tlag)	0.29	23.7	0.31	22.5
σ2	0.04	15.4	0.03	17.6

From that basic model, significant effects of the covariates on the individual estimates of the random effects were found for age, sex, race, weight, creatinine clearance, total plasma protein and alcohol habit. The final model with the lowest AIC, after performing backward elimination of the covariates included only a weight effect on V/F. The estimates of the population parameters of the final model are given in Table I. Goodness-of-fit plots are not shown here but were satisfactory.

EVALUATION BY SIMULATION: MODEL WITHOUT COVARIATE

Simulation design

We used the design of the second phase III study (number of subjects = 351 and number of observations = 973), the basic model and the parameters of Table I to simulate validation datasets (V). The null hypothesis (H₀) is that data in the validation dataset V can be described by the model. We simulated 500 datasets V under the null hypothesis H₀ in order to evaluate the type I error of different tests applied to several metrics or approaches. Simulation data were treated as the observations concerning BQL values.

Metrics evaluated under H₀

We applied five metrics to each of the simulated datasets under H₀.

The first metric is SPE, which are frequently used to evaluate nonlinear mixed effect models because they were computed in the main software used in population PKPD analyses, NONMEM(11), where they are reported under the name weighted residuals (WRES). SPE are defined as the difference between the observations and the predictions, standardized by the variance-covariance matrix of the observations. For each individual, the mean value and variance are computed using the first-order approximation around the mean of the model like in the first order linearization approach used in NONMEM. Under H₀ and assuming the first-order approximation holds, the prediction errors SPE_ij, for a j^th observation of a i^th subject, should have a normal distribution with mean 0 and variance 1. SPE were computed under the name WRES using NONMEM for the validation datasets.

We evaluated the second metric, pd, for each simulated dataset. pd are computed as the percentile of each observation in the simulated predictive distribution under H₀. Figure 2 shows graphically how pd are obtained. For each observation (Y_ij), we perform Monte Carlo simulations to obtain the posterior predictive distribution and we compute the percentile of an observation in the whole marginal predictive distribution. When the distribution of the pd is represented as a histogram, we expect a uniform distribution under H₀.

Figure 2.

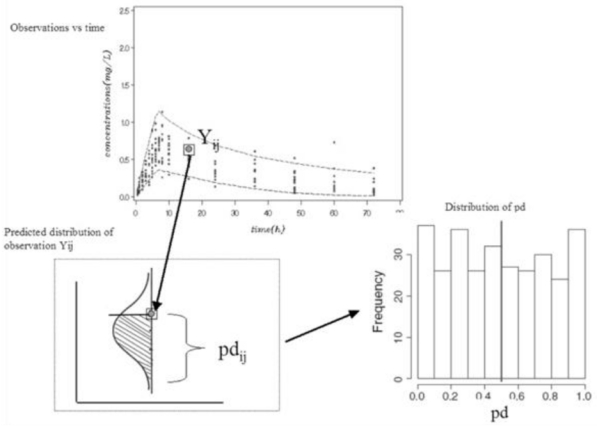
Illustration of how to compute prediction discrepancies (pd), also used to compute NPDE. In the left top plot, dots represent observed plasma concentrations versus time and the dashed lines represent the 90% predicted interval, obtained as the 5^th and 95^th percentiles of simulations. In the left bottom plot; the predicted distribution of an observed concentration (Y_ij) is represented in order to define the pd. In the right bottom plot, the distribution of pd is represented.

The third metric, NPDE, are obtained in a similar way as the pd, but using decorrelated and centered simulated and observed data(6). The empirical mean and variance of the simulated data for each subject are used for the decorrelation. By construction NPDE_ij follow a N(0, 1) distribution under H₀ without any approximation.

Finally, we considered NPC, which compares the observations with their prediction intervals obtained by simulation. Observed data are often compared against different simulated predicted intervals obtained by simulation (8). We considered here classical NPC and another case developed here called NPC_dec by taking into account correlations within individuals. The NPC_dec approach consists in decorrelating and centering simulations and observations just before performing NPC as it is performed for the NPDE computation(6).

Several tests can be used in combination to test that a metric follows the N(0, 1) distribution: we use a Wilcoxon signed-rank test to test whether the mean is significantly different from 0, a Fisher test to test whether the variance is significantly different from 1, a Shapiro-Wilks test (SW) to test the normality assumption. We also define a global test, which consists in rejecting H₀ if at least one of the three tests (mean, variance, normality) is significant with a Bonferroni correction (p=0.05/3). These four tests were applied to SPE and NPDE but also to the pd after a normalization step.

In order to compare NPC with the first three metrics, we propose to test if the percentage of observations outside a prediction interval was significantly different from the expected one. We use a Student test and a binomial exact test. From the 1000 simulations, the 5^th, 10^th, 25^th, 75^th, 90^th and 95^th simulated percentiles for each observation were calculated and we computed the percentage of observations outside the 90%, 80% and 50% prediction intervals (PI). We tested if these percentage of obsevations outside the different PI were not different from the expected one (under H₀).

For all the tests applied to these metrics, the type I error computed by simulation corresponds to determine the percentage of reject of H₀, when H₀ is true.

The simulation of the 500 validation datasets and the simulations used for pd, NPDE and NPC were performed with NONMEM version V. We performed 1000 simulations to implement the evaluation of pd, NPDE and NPC for each of the 500 simulated validation datasets V. SPE were computed with NONMEM (WRES item). The final computation of NPDE (and pd) was performed using R version 2.3.1. The statistical software SAS version 9.1 and R were used to perform statistical analyses.

Results

The type I errors evaluated for the different tests on the 500 replications for the three metrics (SPE, pd and NPDE) are reported in Table II, while the results for NPC and NPC_dec are given in Table III. The performances of the different tests were very poor for SPE. The type I errors were close to 100% for the normality and variance tests for SPE. The Wilcoxon signed rank test was the only one which has a type I error close to 5% (4.2%). As a result, the global test presented a type I error close to 100% for the SPE.

Table II.

Type I error under H₀ (in %) of the global test, Wilcoxon test, the Fisher test and the Shapiro-Wilks test (SW), for the standardized prediction errors (SPE), the prediction discrepancies (pd) and the normalized prediction errors (NPDE), evaluated on 500 simulated datasets.

TEST	METRICS
	SPE	pd*	NPDE
Wilcoxon	4.2%	19.9%	3.0%
Fisher	100%	15.4%	8.6%
SW	100%	16.1%	6.2%
Global	100%	24.6%	5.8%

^*after normalization

Table III.

Type I error under H₀ (in %) of the Student test and the exact Binomal test applied to NPC and NPC_dec approaches, evaluated on 500 simulated datasets.

PI	NPC		NPCdec
	Student test	Binomial test	Student test	Binomial test
90%	12.0	13.0	7.4	6.2
80%	14.0	13.2	7.8	6.8
50%	13.4	13.4	4.6	4.6

The type I errors of all tests were higher than 5% (around 20%) for the pd after normalization. By taking into account correlation within individuals, the type I error of the global test based on the NPDE was close to 5%, confirming the good statistical properties of this metric. There was however a little increase of the type I error for the variance test (8.6%) and a slight decrease (3.0%) for the signed rank test.

The figure 1 is an illustration of a NPC with a 90% PI. In Table III, for the classical NPC, the percentage of observations outside the 90%, 80% and 50% PI was significantly different from the theoretical PI, in around 13% of the datasets for all the different percentiles (for both Student and exact Binomial tests). When we took into account correlations within individuals by performing NPC_dec, we found a slight increase of the type I error of the Student test, but a type error close to 5% for the exact Binomial test. Thus the high type I error of the classical VPC approach can be explained by the correlation between observations.

Only NPDE and NPC_dec presented good statistical properties with these simulations. As NPC_dec are very close to NPDE by computation, we decide in the following to extend only the application of NPDE to evaluate different models with a covariate.

EVALUATION BY SIMULATION: MODELS WITH COVARIATES

Simulation design

As previously we used the design and the real covariate values of the second phase III study (number of subjects= 351 and number of observations=973) to simulate different validation datasets in order to evaluate the type I error and the power of different tests applied to NPDE for model with covariates. The final model only had a weight effect on V/F, but we chose to simulate a continuous covariate (weight) effect on V/F, or a categorical covariate (sex) effect on CL/F in order to evaluate models with different type of covariate (continuous and discrete). We generated external validation datasets under alternative assumptions, with different models: (i) M₀, the basic model without covariate; (ii) M_WT with a weight effect of 50% on V/F (a weight effect was simulated on V/F using equation (1) with θ = 27 and θ_COV = 0.6; this corresponds to a 50% change of V/F between weight at the first quartile and at the third quartile); (iii) M_SEX with a sex effect of 50% on CL/F.; (a sex effect on CL/F was simulated using equation (2) with θ = 0.71 and θ_COV = 1.5 to obtain the same mean (θ = 0.88) than in Table I, and an increase of 50% of CL/F in women). For the other parameters of the models, we took the estimates obtained with the final model given in Table I.

Thus we simulated 1500 validation datasets for each of three different assumptions with M₀, M_WT and M_SEX to obtain these validation datasets: (i) 500 V₀, without covariate; (ii) 500 V_WT, with a weight effect on V/F; (iii) and 500 V_SEX with a sex effect on CL/F.

Evaluation of models with covariates using NPDE

For each of the 1500 validation datasets, we computed NPDE as previously using 1000 simulations with the different models M₀, M_WT and M_SEX. If the validation dataset and the model with which we computed NPDE were the same (V₀ and M₀, V_WT and M_WT, V_SEX and M_SEX), the number of times the model was rejected even though it was true was defined as the type I error. If the validation dataset and the model did not correspond (model misspecification), we defined the power as the number of times we rejected the model being tested.

We propose two approaches based on NPDE to evaluate a model with or without covariates with a validation dataset. The first approach consists in using a Spearman correlation test for continuous variables, to test the relationship between NPDE and weight, and a Wilcoxon test for categorical variables, to test the relationship between NPDE and sex. If the model and validation datasets agree, there should be no relationship between NPDE and covariates and the test should not be significant. Scatterplots of NPDE versus the continuous covariate and box-plots of the NPDE split by the categorical covariate can be performed to display the link between NPDE and covariates.

The second approach consists in testing whether the NPDE follow a N(0, 1) distribution after splitting them by covariates. If the covariate is continuous, we discretize it in several classes according to the quantiles. We choose here to categorize the weight effect into 3 classes: below first quartile (< Q₁), between first and third quartiles (Q₁–Q₃) and above third quartile (> Q₃). Again, we expect that NPDE does not significantly differ from a N(0, 1) distribution in any of the categories, if the model and validation datasets agree. Graphs of the cumulative density function (cdf) of NPDE can be plotted with the theoretical cdf overlaid, in order to visualize any departure of the NPDE distribution from the N(0, 1) distribution in each category or after splitting by quantiles. To test the N(0, 1) distribution of the NPDE, we consider the global test with a Bonferroni correction to take into account the number of covariate classes, since we found a type I error close to 5% for this test in the first series of simulations. NPDE were computed on the different validation datasets in order to evaluate the power of the different tests under the alternative assumptions.

Results

In the phase III study used to simulate the different validation datasets, the median value and the interquartile ranges for the covariate weight were respectively 85 (76–93) kg for men and 74 (64–83) kg for women. There were 61% of men and 39% of women.

When model and validation dataset are consistent (M₀ and V₀), we found a type I error close to 5% for both approaches (5.4% and 6.6% respectively). Results are summarised in table IV for Spearman and Wilcoxon tests and in table V for the global test split by covariate. We obtained the same results for M_WT and V_WT, and M_SEX and V_SEX, i.e. under H₀.

Table IV.

Percentage of significant Spearman test for weight and Wilcoxon test for SEX applied to NPDE, evaluated on 500 simulated datasets.

Validation dataset	Model	Weight (Spearman)	Sex (Wilcoxon)
V0	M0	5.4%*	5.4%*
V0	MWT	52.0%	-
VWT	M0	61.6%	-
V0	MSEX	-	100%
VSEX	M0	-	100%

^*Type I error under H₀

Table V.

Percentage of significant global test applied to NPDE, evaluated on 500 simulated datasets.

Validation dataset	Model	Weight	Sex
V0	M0	6.6%*	6.6%*
V0	MWT	52.8%	-
VWT	M0	67.0%	-
V0	MSEX	-	99.2%
VSEX	M0	-	99.6%

^*Type I error under H₀

Concerning the 500 validation datasets without covariate (V₀), when we computed NPDE with a model with a weight effect (M_WT), we found a power around 50% for the Spearman test. Figure 3 displays the box-plots between the NPDE and the weight effect categorized into 3 classes for one of the 500 V₀. When NPDE were performed with a model with a sex effect (M_SEX), we found a power of 100% for the Wilcoxon test. Figure 4 displays the box-plots of the NPDE with respect to sex. We found the same results with the global tests split by covariates. We found the same results with the global tests split by covariates. We found a departure from a N(0, 1) distribution for sex and weight, especially for weight <Q₁. Figure 5 displays an example of the cdf of the NPDE with the theoretical cdf overlaid, split by sex.

Figure 3.

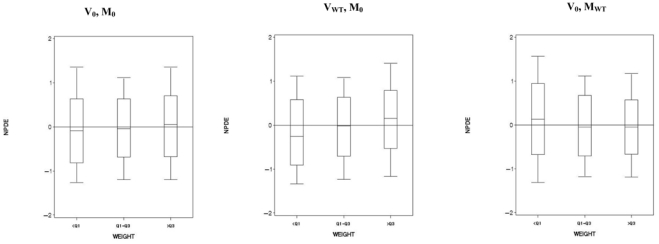
Box-plots of the Normalized Prediction Distribution Errors (NPDE) versus a continuous covariate (weight) categorized into 3 classes. V₀ denotes a dataset simulated under H₀ with the model M₀ and V_WT a dataset simulated assuming an effect of weight on V/F (model M_WT). In the left hand plot, NPDE were computed for V₀ with simulations under M₀; in the middle plot, NPDE were computed for V_WT with simulations under M₀; in the right hand plot, NPDE were computed for V₀ with simulations under M_WT.

Figure 4.

Box-plots of the Normalized Prediction Distribution Errors (NPDE) versus a categorical covariate (sex) with M for male and F for female. V₀ denotes a dataset simulated under H₀ with the model M₀ and V_SEX a dataset simulated assuming an effect of SEX on CL/F (model M_SEX). In the left hand plot, NPDE were computed for V₀ with simulations under M₀; in the middle plot, NPDE were computed for V_SEX with simulations under M₀; in the right hand plot, NPDE were computed for V₀ with simulations under M_SEX.

Figure 5.

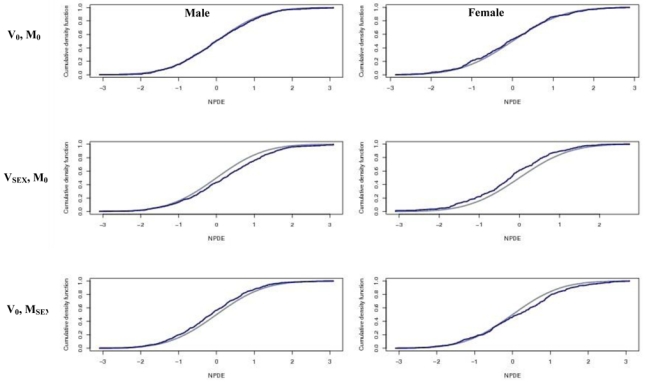
Cumulative density function (cdf) plots of the Normalized Prediction Distribution Errors (NPDE) split by sex. In the top plots NPDE were computed for V₀ with simulations under M₀; in the middle plots, NPDE were computed for V_SEX with simulations under M₀; in bottom plots, NPDE were computed for V₀ with simulations under M_SEX.

Concerning the 500 validation datasets with a weight effect (V_WT), when we computed NPDE with a model without covariate (M₀), we found a power around 60% with the Spearman test, and slightly higher (67%) with the global test after splitting. For the 500 validation datasets simulated with a sex effect (V_SEX), we found for both approaches a high power to reject that the data came from M₀.

DISCUSSION

Evaluation through prediction errors on observations, for instance using SPE, or WRES with NONMEM, were the most frequently used metrics for internal and external evaluation of PK and/or PD models. However commonly used diagnostics (like WRES based diagnostics) may falsely indicate that a model is inadequate (12).

In the present paper, we first compared through simulations the statistical properties of recent metrics based on observations (NPDE, NPC_dec) to SPE, pd and NPC.

The computation of the SPE computed in NONMEM relies on a linear approximation of the mixed-effect model around the mean as in the first order estimation method. It is however known that the linearisation around the mean is poor if the model is highly nonlinear or if the inter-patient variability is large, and then the distribution of SPE_ij under H₀ is no longer normal, which can explain the high type I error for the global test. This has already been shown by Mentré and Escolano when they showed the better performance of pd over SPE (5). We nonetheless evaluated SPE also here, because this metric is one of the most used to assess the performance of a model through goodness of fit plots so that we wanted to compare NPDE with SPE. It is obvious from the present study that SPE should not be used as a model evaluation tool. Hooker et al. proposed computing another metric that they called conditional WRES (CWRES) in which the FOCE approximation is used for the computation of the mean and the variance of the model instead of the FO approximation (13). We did not evaluate CWRES, although they are indeed a better approach than the usual WRES Thus, a formal comparison of the performances of CWRES and NPDE in the same setting would be interesting.

To test H₀ using NPDE, we proposed to perform a mean test, a variance test, a normality test or a global test combining all three. We found here, using simulations, that the global test presented a type I error close to 5%, confirming the good theoretical statistical properties of the NPDE and providing a single p-value for model evaluation. The NPDE metric does not require any assumption on the distribution of the observations, and, when computed with a large number of simulations, has a known theoretical distribution which can be tested. In a previous work, Mentré and Escolano showed that prediction discrepancies presented a type I error close to 5% when there were one observation per patient but a higher value if there were more than one observation per patient(5). We found the same conclusions here by finding a type I error for all the tests higher than 5% (around 20%) for the pd. These results for pd show the need to decorrelate the NPDE.

The VPC have been applied in several PK and/or PD analyses. A few extensions and/or application of classical VPC have been proposed to falicitate evaluation (3, 14). As this method is subjective, the evaluation of model adequacy depends on the appreciation of the modeller. The related statistic of VPC, NPC is also applied in model evaluation (8). Therefore, we propose here to use a test, which consists in a comparison between the percentage of observations outside a simulated prediction intervals and the theoretical expected value. This test on classical NPC however shows a significantly higher type I error (13%) than the nominal level expected, due to the correlations introduced by multiple observations within subjects. Consequently we defined NPC_dec, to take into account these correlations. We then obtained a type I error close to 5% using the exact binomial test for NPC_dec. We observed that the type I error was slightly higher using the Student test despite the large number of observations, which should have made the normal approximation valid. The disadvantage of using NPC_dec is that we need to choose a prediction interval to perform the test, or combine results from several prediction intervals, whereas with NPDE we obtain a single p-value taking into account the full distribution of the NPDE. An extension of VPC called the Quantified Visual predictive check (QVPC) presents the distribution of the observations as a percentage, thus regardless the density of the data, above and below the predicted median at each time point. However this technic is only visual and no test were performed or proposed (14).

In the second part of this paper, we examined the application of NPDE to the evaluation of covariate models. During the building of the covariate model in a population analysis, plots are often generated to check potential covariate relationships (for example, plots of the posterior Bayes estimates of the parameters versus potential covariables, or the posterior Bayes estimate of the random effects versus potential covariates). The EMEA, in the guideline on reporting the results of population pharmacokinetic analyses, indicate that a conclusion of no covariate effect based solely upon inspection of graphical screening plots is usually not acceptable.

Several methods are available to evaluate a model with covariate during the building process and during the final internal evaluation process. In this paper, we propose here, within the framework of external evaluation, to use NPDE. We suggest two approaches with tests based on NPDE to evaluate a model with or without covariates with a validation dataset. The first approach consists in using a Spearman correlation test for continuous variable, and a Wilcoxon test for categorical variable to test the relationship between NPDE and covariates. The second approach consists in testing whether the NPDE follow a N(0, 1) distribution with a global test after splitting them by covariates. Regarding all the tests applied to the different metrics, the null hypothesis is that the model is correct, so we can only invalidate a model when we reject H₀, never accept it.

For covariate models, when model and validation dataset were consistent, type I error of the tests were close to 5% for both type of covariates used in the simuation (discret, continuous). When validation datasets and models were not consistent, the tests presented a high power to detect the correlation between NPDE and sex but only a power around 60% for NPDE and weight. This difference may reflect the simulation conditions we chose, i.e. the size of the weight effect relative to the of sex effect and the variability on the parameters. Graphs of parameters versus covariates showed only a small trend for both effects, but the power to detect relationships was high, partly because of the large number of observations in the validation dataset (n=351).

A current limitation of npde concerns BQL concentrations, which the present version of npde does not handle properly. Recently, estimation methods that handle censored data by taking into account their contribution to the log-likelihood were implemented in Nonmem and Monolix (15), making them readily available to the general user. In the next extension to npde, we therefore plan to propose and implement a method to handle BQL data for models using these estimation methods. In the meanwhile, we suggest to remove times for which too many observations are BQL before computing npde, since otherwise they might bias the results of the tests.

The population model developped here with an oral antidiabetic agent, gliclazide was used for all the simulations. The FO method is known to behave poorly during model building It was used here only to provide estimates for the model used for simulation. However, the final model fits should be performed using FOCE or FOCE_INTER as appropriate.

The example chosen here was a pharmacokinetic one. Of course these different approaches and in particular NPDE could be apply for different PK and/or PD models. No modification of implementation and interpretation concerning NPDE are expected. An example of NPDE application with a PD model was presented in (16).

In conclusion, we recommend to use NPDE over SPE for external model evaluation (and therefore for internal model evaluation), since they do not depend on an approximation of the model and have good statistical properties. Moreover, NPDE are not as subject to interpretation as NPC, which also suffer from not accounting for within subject correlation. The exact binomial test applied to NPC_dec may be an alternative to compute a statistic, but leaves the modeller with the choice of the prediction interval(s). An add-on package for the open source statistical package R, designed to compute NPDE, is available at www.npde.biostat.fr and discussed in Comets et al. (17). In that paper, its is also discussed the importance of choosing the number of simulation for NPDE computation. NPDE are also automatically computed with MONOLIX v2.4, a new software for population PK and/or PD analyses, which implements the SAEM algorithm (18).