Effect of Implantation Accuracy on Ankle Contact Mechanics with a Metallic Focal Resurfacing Implant

Abstract

Background:

Talar osteochondral defects can lead to joint degeneration. Focal resurfacing with a metallic implant has shown promise in other joints. We studied the effect of implantation accuracy on ankle contact mechanics after focal resurfacing of a defect in the talar dome.

Methods:

Static loading of seven cadaver ankles was performed before and after creation of a 15-mm-diameter osteochondral defect on the talar dome, and joint contact stresses were measured. The defect was then resurfaced with a metallic implant, with use of a custom implant-bone interface fixture that allowed fine control (in 0.25-mm steps) of implantation height. Stress measurements were repeated at heights of –0.5 to +0.5 mm relative to an as-implanted reference. Finite element analysis was used to determine the effect of implant height, post axis rotation, and valgus/varus tilt over a motion duty cycle.

Results:

With the untreated defect, there was a 20% reduction in contact area and a 40% increase in peak contact stress, as well as a shift in the location of the most highly loaded region, as compared with the values in the intact condition. Resurfacing led to recovery of 90% of the contact area that had been measured in the intact specimen, but the peak contact stresses remained elevated. With the implant 0.25 mm proud, peak contact stress was 220% of that in the intact specimen. The results of the finite element analyses agreed closely with those of the experiments and additionally showed substantial variations in defect influences on contact stresses across the motion arc. Talar internal/external rotations also differed for the unfilled defect. Focal implant resurfacing substantially restored kinematics but did not restore the stresses to the levels in the intact specimens.

Conclusions:

Focal resurfacing with a metallic implant appears to have the potential to restore normal joint mechanics in ankles with a large talar osteochondral defect. However, contact stresses were found to be highly sensitive to implant positioning.

Clinical Relevance:

Resurfacing a talar osteochondral defect with an implant that restores the joint contour, that provides immediate stability, and that reproduces normal joint mechanics, without requiring biological potential, offers advantages over existing resurfacing techniques; however, restoration of normal joint mechanics is highly dependent on precise surgical implantation.

It is widely accepted that a persistent osteochondral defect, particularly if it is large and at a weight-bearing site, can lead to chronic degeneration of adjacent and/or apposing cartilage¹. The associated secondary osteoarthritis often leaves patients with a painful and dysfunctional joint. The accelerated rate of cartilage degeneration associated with this pathological condition has been empirically linked to chronic abnormality of joint contact mechanics, which has been attributed to altered articular geometry. Biological resurfacing techniques have emerged as a means of restoring the articular surface contour with hyaline (or at least hyaline-like) cartilage^2-11.

Both clinical and laboratory studies have demonstrated that age is a significant factor in outcomes following these resurfacing procedures^4,12,13. Resurfacing an articular defect with an implant that does not rely as heavily on biological potential; that restores the joint contour, providing immediate stability; and that reproduces normal joint mechanics would in many ways be preferable to existing treatments. Focal resurfacing with use of a metallic cap has been shown to be a promising alternative approach with which to avoid or delay joint replacement in middle-aged and older patients^14-19. However, recent animal studies have suggested that articular damage can be associated with these implants^20-22, especially in the case of surface-proud implantation.

Only a few basic-research studies have addressed the biomechanical effects of focal resurfacing on adjacent and/or apposing cartilage^20-25. Potential aberrant implant-on-cartilage contact stress is of substantial clinical concern, particularly in the case of focal resurfacing by a metallic cap, whose mechanical properties are markedly different from those of articular cartilage. Becher et al.¹⁴ measured contact stress redistribution in the human knee following implantation of a metallic resurfacing cap. They reported elevated contact stresses associated with device implantation that was 1 mm proud but did not test less proud implants. The central bearing surface of the knee is arguably a forgiving site for implantation because of both the thickness of its cartilage and the regularity of its articular surface topography. Contact stress aberrations associated with articular defects have been studied with finite element analysis, although almost exclusively in the knee^26-28. The focus of these studies was primarily on the healing of defects left untreated or treated with biological resurfacing.

The superior-medial aspect of the talar dome is a common site for implantation in ankles with this pathological condition. Interestingly, the ankle often fares well in the presence of an articular defect. Excision and curettage alone have been reported to provide good-to-excellent results in 60% to 80% of cases²⁹, but that leaves 20% to 40% that do not do well and require further treatment. Because of the geometric complexity of the ankle and the relative thinness of its cartilage³⁰, the use of focal resurfacing implants to treat talar osteochondral defects presents challenges with regard to implant design, selection, and surgical placement that are greater than those associated with joint surfaces with a quasi-spherical contour (e.g., the femoral head and the humeral head) or with relatively simple morphology and thicker cartilage (e.g., the femoral condyles and the patellar groove).

The purpose of this study was therefore to determine the effect of implantation accuracy on cartilage contact mechanics in the human ankle after focal resurfacing with a metallic cap intended for the treatment of talar dome lesions.

Materials and Methods

Cadaver Experiment

Seven fresh-frozen human cadaver ankles were obtained at autopsy from one male and six female donors who ranged in age from seventy-three to ninety-four years at the time of death. After thawing at room temperature, each specimen was dissected free of skin, muscles, and tendons. Gross inspection revealed no morphological abnormalities and verified that every specimen had a passive physiologic motion arc (from at least 10° of dorsiflexion to 30° of plantar flexion). The midparts of the tibial and fibular shafts as well as the body of the calcaneus were secured in separate polymethylmethacrylate blocks. To afford access to the talar dome during implantation and testing, the ankle was disarticulated just prior to testing. The integrity of the articular cartilage was then inspected visually. Careful attention was paid to keeping the articular cartilage moist during preparation and testing.

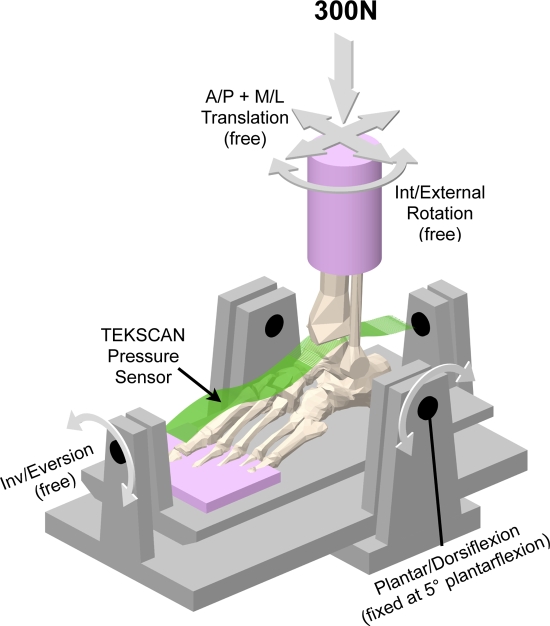
A custom ankle loading fixture (Fig. 1) was utilized for testing³¹. This fixture was mounted in a servohydraulic materials testing machine (Bionix, model 858.20; MTS, Eden Prairie, Minnesota) used to apply a prescribed axial compressive force to specimens held at a predetermined amount of ankle flexion. Translations in the anterior-posterior and medial-lateral directions as well as inversion-eversion and internal-external rotations were unrestricted during load application. A custom-designed contact stress sensor (Tekscan, model 5033; Tekscan, South Boston, Massachusetts)³² was utilized to measure local contact stresses in the talocrural joint. The sensors are very thin (0.1 mm) and flexible, thus allowing conformation to curved joint surfaces. The active sensing area measures 27 mm (in the medial-lateral direction) by 39 mm (in the anterior-posterior direction) and incorporates a uniformly distributed thirty-two by forty-six array of sensing elements (sensels), thus yielding contact stress data from 1472 distinct sites, at a spatial resolution of 0.694 mm² per sensel. The insert size was chosen to fully cover a typical talocrural joint. This custom “ankle” sensor has been used in a number of previous studies^31,33-38.

Fig. 1.

This schematic shows the physical testing setup used to load the cadaver ankles and the Tekscan pressure sensor used to measure talocrural contact stress. A/P = anterior/posterior and M/L = medial/lateral.

To collect baseline data regarding specimen-specific contact stress distributions, each ankle was first tested in an intact condition (i.e., with the talar dome undisturbed). The specimen was mounted on the loading device and held in 5° of plantar flexion, such that the most typical location of medial talar osteochondral lesions (the central-to-posterior aspect of the talar surface)^39,40 was principally engaged. To maintain physiologic ankle joint apposition without relying on the transected periarticular ligaments, the ankle was aligned relative to the MTS loading axis both mediolaterally and anteroposteriorly, such that moments associated with axial loading could be minimized. Contact stresses in the talocrural joint were measured with the specimen axially loaded to 300 N, simulating bipedal standing. This somewhat nonphysiologic loading configuration (quasi-static loading at a single degree of ankle flexion, with relatively low loads compared with those experienced during gait) was chosen to protect the integrity of the cadaveric tissues during the extended mechanical testing period.

Next, a 15-mm-diameter cylindrical osteochondral defect was created on the medial edge of the talar dome. The anterior-posterior location was set slightly posterior, at the approximate center of the contact patch prevailing when the ankle was in 5° of plantar flexion. The defect was then resurfaced with a metallic implant (HemiCAP; Arthrosurface, Franklin, Massachusetts), with the manufacturer's regular implantation protocol supplemented with a custom implant-bone interface fixture (Fig. 2, A) that allowed very fine (0.25-mm-increment) control of implantation height along its post axis. Within this fixture, a bone surrogate material consisting of medium-density closed-cell polyurethane foam (model FR-7140; General Plastics, Tacoma, Washington) was utilized to replicate the effect of the implant-bone interface as well as to minimize the potential influence of inconsistency in bone quality, as natural talar cancellous bone in cadaver specimens from elderly donors can be much more porotic than would be expected in the intended-use population⁴¹.

Fig. 2.

A: The modular implantation approach involved use of bone cement, a metallic outer sleeve, a height-adjusting collar, and a bone surrogate housing. B: Precise variations in implant proudness and recession, relative to the baseline implantation height, were achieved by substituting different height-adjusting collars.

An experienced surgeon (Y.T.) made all surgical decisions, including selection of a “best fit” metallic surface component (cap) and the datum reference height of implantation, according to the manufacturer's guidelines (with the cap slightly recessed with respect to the adjacent articular surface). These decisions required subjective judgment, with the decision regarding implantation height made at the time that the implant post was advanced into the bone and final minor adjustments made as needed prior to definitive placement of the cap.

Contact stress measurements were then repeated at five implant heights (–0.5, –0.25, 0, +0.25, and +0.5 mm with respect to the datum reference implantation height; Fig. 2, B) as well as without placement of the metallic cap (i.e., a nonresurfaced-defect control). For the experiments, the cap was first seated onto the post and the bone surrogate-implant construct was removed from the talus between tests, with the appropriate height-adjusting collar placed prior to replacement of the construct. The full series of tests was repeated three times for each ankle, with the order of testing randomized. The reproducibility of measurements was confirmed on repeat load applications. The maintained integrity of the cartilage surfaces was likewise confirmed throughout the series of tests. Contact stress measurements were thus obtained under seven different articular surface conditions (including the baseline, intact state) for each ankle.

The “best available” implantation height was defined as the height at which the original contact stress distribution (that in the intact specimen) was most closely restored in each ankle. This determination was based on visual assessment of the Tekscan contact stress data for each ankle. Typically, this occurred as the implant's superior surface just began to carry load, relative to the surrounding cartilage surface. This load uptake was accompanied by a decrease in the contact stress elevation (that had occurred after defect creation) in the adjacent anterocentral articular cartilage.

The values of peak local contact stress and of contact area were determined for each specimen, at each articular surface condition. Differences in peak local contact stress and contact area across specimen conditions were assessed with a one-way analysis of variance. Pairwise comparisons were performed only when this test was positive. P values of <0.05 were regarded as indicating significant differences.

Computational Simulation

Complementary contact finite element modeling was performed to independently determine the effect of implant height (amenable to cadaver validation), implant rotation about its post axis, and implant valgus/varus tilt in a single ankle over a motion duty cycle. As part of a prior study, a cadaveric ankle joint was disarticulated, and the cartilage surfaces of the tibia and talus were imaged with a highly accurate (± 2 μm) stereophotography system³⁰. The cartilage was then dissolved in a 5% sodium hypochlorite solution, and the denuded subchondral bone surfaces were imaged. The resulting point cloud data were saved in digital format to disk. For the present model, those geometric data (paired subchondral bone and cartilage surfaces of the tibia and talus) were imported into the Geomagic Studio software environment (Geomagic, Research Triangle Park, North Carolina), where the tibial and talar surfaces were placed in a neutral load-bearing apposition. Next, a 15-mm-diameter cylindrical osteochondral defect was modeled on the medial edge of the talar dome, to correspond with the location used in the cadaveric testing, and a computer-aided design model of an appropriately sized and contoured metallic resurfacing implant (from manufacturer inventory) was placed within the modeled defect.

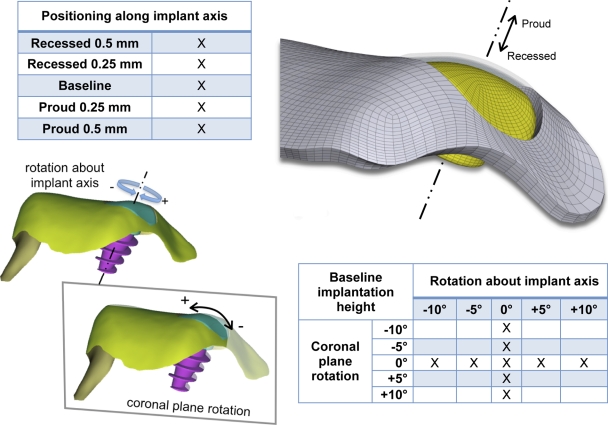
The geometries of the intact specimen, nonresurfaced-defect control specimen, and specimen with the implant cap were then transferred in digital format to a structured finite element meshing program (TrueGrid; XYZ Scientific Applications, Livermore, California). The meshing procedure that was implemented enabled parametric variation in the positioning of the implant cap along its post axis (from a 0.5-mm-recessed position to a 0.5-mm-proud position, as tested experimentally), in the rotation of the cap (±10°) about its post axis, and in the rotation of the cap (±10°) about an axis aligned with the medial edge of the talar dome (Fig. 3). The latter two parametric studies worked from the baseline-height implantation case.

Fig. 3.

The influences of positioning of the implant along its axis (studied experimentally and computationally), of implant coronal plane rotation (studied computationally), and of rotation about the implant axis (studied computationally) on the contact mechanics were parametrically investigated.

The ankle contact finite element modeling approach was based on previous work⁴², with bone treated as rigid material and cartilage treated as linear elastic material. The resurfacing implant was included as an additional rigid surface. Contact was modeled between cartilage surfaces as well as between the superior cap surface and the apposing tibial surface, and between the cap sides and the adjacent talar cartilage surface. The coefficients of friction assigned for cartilage-on-cartilage contact (μ = 0.01) and implant-on-cartilage contact (μ = 0.1) were derived from the literature^43-46. A vertical load of 300 N, corresponding to that used experimentally, was applied to the model in neutral apposition, with the talus free to seat itself according to its mating with the apposing tibial articular surface. Next, the tibia was rotated about the talus through an arc from neutral to 10° of plantar flexion, back through neutral to 10° dorsiflexion, and then finally back to neutral. While these tibial rotations were applied, the 300-N load was continuously directed toward the talus, with the talus free to rotate (internal/external rotation and inversion/eversion) and translate (anterior/posterior and medial/lateral) in response to the tibia articulating over the talar dome. Medial/lateral translation was resisted by a spring (stiffness = 100 N/mm) to represent the resistance to translation provided by the fibula, which was not explicitly modeled.

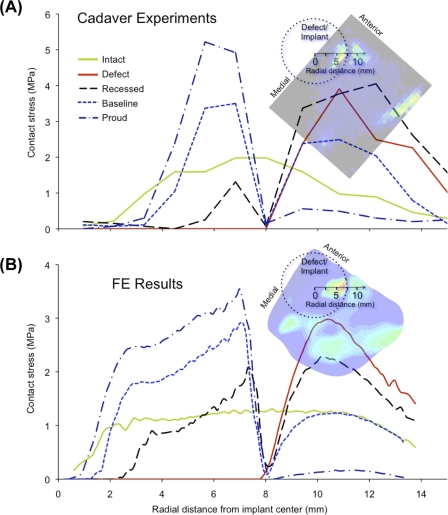
Data analysis of the finite element modeling results focused on computed contact stress distributions and the associated talocrural kinematics. The maximum contact stresses and contact areas computed, with the finite element modeling, at 5° of plantar flexion, for all heights of implant positioning, were compared with those measured experimentally, to establish the validity of the computational approach. In addition, profiles of contact stress were generated along a radial line emanating from the center of the implant cap along an anterolateral direction chosen to intercept the local maxima, to establish general replication of the physically measured contact stress distributions in the near vicinity of the defect.

Source of Funding

This research was supported by grants from Arthrosurface, Inc. (Franklin, Massachusetts), and by the National Institutes of Health/National Institute of Arthritis and Musculoskeletal and Skin Diseases Grant P50 AR055533. The funding sources did not play a role in the investigation.

Results

Cadaver Experiment

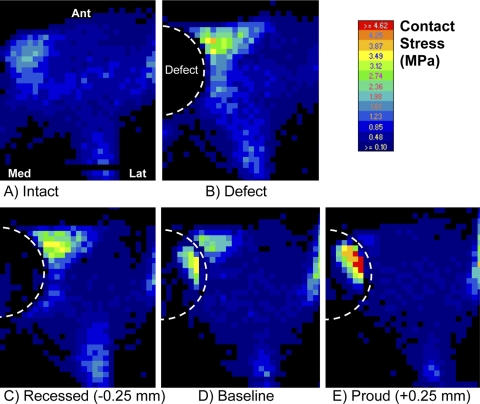
In the intact state, contact stresses were distributed relatively uniformly across the articular surface (Fig. 4, A). Local contact stress values were typically below 2.0 MPa, with the peak values averaging 2.1 ± 0.6 MPa (mean and standard deviation) (Fig. 5, A). The average contact area was 431 ± 26 mm² (Fig. 5, B). Following the introduction of a (nonresurfaced) defect, the peak contact stress values averaged 2.9 ± 1.2 MPa, which was 1.4 times higher than that in the intact ankles (p = 0.047). These elevated contact stresses were observed at the anterior-central region near the border of the defect (Fig. 4, B). The contact area decreased to 81% ± 11% of the contact area in the intact configuration (p = 0.005).

Fig. 4.

Representative pressure-sensor contact stress mappings are shown for the loaded cadaver ankles under the five conditions as labeled.

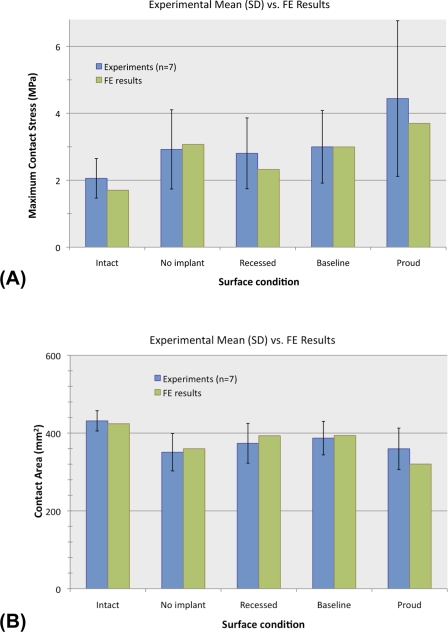
Fig. 5.

Peak contact stress (A) and contact area (B) in the experimental cadaver study and the finite element (FE) analysis for each of the five test groups. The error bars indicate one standard deviation (SD).

The “best available” implantation height (the height that best restored contact stress to the levels in the intact ankles) was at the datum reference height (corresponding to the surgeon's decision based on the manufacturer's recommendation) in four of the seven specimens and was within 0.25 mm of the datum reference height in the other three specimens. The best available implantation heights thus selected were considered the baseline implantation state for subsequent analysis. In the baseline implantation state, the contact area increased to 90% ± 11% of that in the intact condition, which was significantly different from that associated with the defect alone (p = 0.027) but not significantly different from that in the intact condition (p = 0.058). However, the mean peak local contact stress was significantly elevated (3.0 ± 1.1 MPa, 1.5 times that in the intact ankles; p = 0.044), to a level indistinguishable from the mean peak value in the nonresurfaced-defect condition (p = 0.745). In four of the seven ankles, the peak values were associated with elevated contact stresses in the implant-on-cartilage contact zone, rather than the peak remaining located at the anterior-central cartilage-on-cartilage contact region (Fig. 4, D).

When the implant was placed 0.25 mm proud (with respect to the baseline implantation height, specific to each ankle), the mean peak contact stress value was elevated to 4.4 ± 2.3 MPa—i.e., 2.2 times that in the intact surface condition (p = 0.028). The changes with proud implantation were characterized by elevation of implant-on-cartilage contact stresses (Fig. 4, E), as evidenced by a mean peak value that was 1.6 ± 0.3 times higher than that associated with the baseline implantation height (p = 0.012). The contact area was decreased slightly in six of the seven ankles (p = 0.07). With the implant recessed 0.25 mm (Fig. 4, C), the peak values of implant-on-cartilage contact stress decreased (to 0.5 ± 0.3 times those associated with the baseline implantation height), while peak values in the cartilage-on-cartilage contact region increased in six of the seven ankles (p = 0.10).

Computational Simulation

The contact stress distributions computed with finite element analysis agreed closely with those measured in the cadaver experiments (Fig. 5), with the computed values of peak contact stress and contact area falling well within one standard deviation of the experimental means in all cases. The trends observed experimentally with advancement of implant height were closely mirrored by the contact stress distributions computed in the finite element analysis (Fig. 6).

Fig. 6.

Spatial profiles of contact stress are plotted along a ray emanating from the center of the implant axis, for the cadaver experiments (A) and the finite element (FE) analyses (B).

The finite element simulations of duty cycle ankle motion showed substantial variations in the computed contact stress distributions across the motion arc, with different levels of influence of the defect at different stages in the cycle (see Appendix). Specifically, while contact stresses were only mildly altered in terminal dorsiflexion (peak contact stress, 94% of that in the intact ankles), they were substantially elevated in plantar flexion (peak contact stress, 230% of that in the intact ankles), as the defect edge was engaged. The different cases of implant positioning also behaved differently over the duty cycle. While implant proudness consistently elevated contact stress over the implant (the peak contact stress over the duty cycle averaged 205% of that in the intact ankles), the baseline and recessed cases both restored contact stresses toward those in the intact state (average peaks of 149% and 121%, respectively, of that in the intact ankles), with both cases exhibiting closer agreement in dorsiflexion (baseline, 116% of that in the intact ankles; recessed, 95% of that in the intact ankles) than in plantar flexion (baseline, 162%; recessed, 137%).

Whereas computational simulations showed smooth and regular motion across the duty cycle in the intact state, in the presence of a nonresurfaced defect there was dramatically increased talar external rotation with ankle plantar flexion (a net change of 3.4° of external rotation in the defect state, compared with 1.0° of internal rotation in the intact state, as the ankle plantar flexed from neutral to 10°; see Appendix). Furthermore, there was a striking, 200% elevation in cartilage stress on the talar dome directly adjacent to the defect at the higher angles of plantar flexion (see Appendix), reflecting an absence of buttressing of cartilage at the defect lip. The modeled implantation of a resurfacing device substantially restored the natural kinematics (talar internal/external rotation restored to a <1° difference compared with that in the intact state across all flexion angles) but did not uniformly restore stresses to levels found in the intact ankles.

Variations in cap orientation about the implant axis substantially altered contact stress values between the cap and the apposing cartilage surface (with peak contact stress values of 120% to 334% of that in the intact condition), with little effect away from the cap (see Appendix). In fact, when the implant was rotated –5° about its axis, the contact stress values showed closer agreement with the values in the intact ankles (between 120% and 144% of the values in the intact ankles) than did those in the baseline case (between 148% and 190% of the values in the intact ankles), in all but the largest degrees of dorsiflexion, while kinematics were restored comparably well. Coronal plane cap orientation about the medial edge of the talar dome more dramatically influenced contact stress levels over the implant surface (with as high as a 958% increase relative to the values in the intact ankles), with the effect centrally in many ways analogous to changes observed with variation of the implant cap height (see Appendix). Cap orientations that effectively resulted in prominence against the apposing medial malleolar surface of the tibia were likewise associated with elevations in contact stress, particularly in ankle dorsiflexion.

Discussion

In the present study, cartilage contact stress distributions in the human ankle with a metallic focal resurfacing implant were explored in complementary cadaveric and computational models. Given that stability in axially loaded human ankles relies primarily on the tibial-talar joint geometry^31,47,48, the contribution of ligamentous restraint to ankle stabilization in this study was assumed to be minimal. Previous experimental studies^31,47,48 established that, during normal gait, the periarticular ligaments contribute little with regard to dictating talar motion, acting to resist talar motion only at the extremes of joint motion. Had ligaments been included in the finite element model, it would undoubtedly have undergone less talar motion, but there would still be an underlying tendency for this motion.

In the intact ankles, peak contact stress values were consistent with similarly acquired measurements in ankles with intact major ligaments^31,37. Contact areas measured in the intact ankles were also consistent with those reported in the literature for similarly configured loadings^49-53. However, reduced (subfunctional) loads were applied in the present experiments, in the interest of protecting the integrity of the cadaveric tissues. Thus, extrapolation of the observed contact mechanics to full dynamic ankle loads must be done with caution because of the inherent nonlinearity between load and contact area.

An osteochondral defect created on the medial talar dome surface caused a substantial (20%) reduction in ankle contact area, and finite element duty cycle simulations also indicated altered kinematics. Given the primary role of joint surface geometry in ankle stabilization^31,48, these findings seem reasonable.

In the present study, both reduced contact area and altered kinematics associated with the introduction of an osteochondral defect were somewhat restored by focal resurfacing, suggesting the capacity of the metallic cap to alleviate some of the biomechanical abnormality in clinical situations. However, peak contact stresses near the border of the nonresurfaced defect were elevated to 140% of the levels in the intact condition and remained elevated to similar levels following implantation of a metallic resurfacing implant at baseline (best available) height. Moreover, with the implant only 0.25 mm proud (as were three of the implants that were supposed to be at the best available height in the cadaver ankles, despite the carefully controlled bench setting for implantation, including disarticulation), peak implant-on-cartilage contact stress was further elevated to 220% of the values in the intact condition. These findings support a somewhat recessed placement of the implant. Restoration of contact stress levels must of course be balanced against the restoration of normal ankle kinematics, and the results of the finite element analysis suggest that slightly recessed implantation does also restore motion.

Clinically, metallic cap implantation involves several surgical perturbations other than implantation height, and some directly influence implant-on-cartilage contact stresses. Finite element simulation showed a high degree of sensitivity to the insertion angle of the post screw and rotational positioning of the articular surface component.

In addition to implantation accuracy, implant selection is critical to the success of this treatment approach. In current resurfacing operations, although a “best fit” implant is selected on the basis of intraoperative measurement of local articular surface morphology, the final decision depends on the surgeon's subjective visual evaluation, rather than on quantitative measurement. It is also possible that the most appropriate implant surface contour for restoring regional functional biomechanics of the articular surface differs from the most anatomical surface contour.

Going forward, the ankle contact finite element model lends itself to addressing several questions not practical for experimental investigation. For example, the use of finite element analysis as presented could inform selection of the best implant design to balance restoration of the ankle kinematics against the risk of increased contact stress at the implant-cartilage interface. Parametric analysis, such as to identify the surface contour most forgiving of small perturbations in implant positioning, could be helpful for optimizing implant surface designs. The finite element modeling approach also has utility as a vehicle with which to study the influence of other resurfacing options, whether they be osteochondral plugs or other implant designs, on ankle contact mechanics.

In conclusion, focal resurfacing with a metallic implant appears to hold promise as a means to restore more quasi-physiologic contact mechanics in ankles with a large talar osteochondral defect, appreciably reducing biomechanical aberrations presumed to be responsible for whole-joint cartilage degeneration. However, it did not fully restore the contact stress distributions of the intact surface under any specific implantation condition that we investigated. While peak contact stresses were not significantly reduced, an optimally positioned implant shifted the site of peak contact stress onto the implant itself (Fig. 4, D), thus restricting these peak cartilage stresses to the tibia, effectively sparing the talus. This is in contrast to the case for a nonresurfaced defect, where high contact stresses persist in the talar cartilage near the defect (Fig. 4, B), which is arguably a more deleterious situation. Cartilage contact stresses after focal resurfacing were sensitive to proud implantation, even with small amounts of proudness (0.25 mm). The contact mechanics were likewise sensitive to small variations in implant cap orientation. In clinical situations, the poroelastic characteristics of articular cartilage, along with active tissue remodeling, may over time somewhat offset small incongruities in the implant-cartilage interface. Bone and/or cartilage remodeling also may allow longer-term accommodation. However, it seems that, to minimize the risk of excessive cartilage contact stresses acutely after focal resurfacing, even a small degree of proud implantation should be carefully avoided, as should deviations from the preferred orientation of the implant.

Appendix

Supplementary illustrations depicting additional results of the finite element analysis are available with the electronic version of this article on our web site at jbjs.org (go to the article citation and click on “Supporting Data”).