Modeling Torque Versus Speed, Shot Noise, and Rotational Diffusion of the Bacterial Flagellar Motor

Abstract

We present a minimal physical model for the flagellar motor that enables bacteria to swim. Our model explains the experimentally measured torque-speed relationship of the proton-driven E. coli motor at various pH and temperature conditions. In particular, the dramatic drop of torque at high rotation speeds (the “knee”) is shown to arise from saturation of the proton flux. Moreover, we show that shot noise in the proton current dominates the diffusion of motor rotation at low loads. This suggests a new way to probe the discreteness of the energy source, analogous to measurements of charge quantization in superconducting tunnel junctions.

The bacterial flagellar motor is a molecular machine that rotates a helical filament and thereby powers the swimming of bacteria like E. coli [1]. Motor rotation is typically driven by H⁺ ions that generate torque by passing into the cell via the motor, down an electrochemical gradient called the proton motive force (PMF). Although much work has been devoted to understanding proton translocation and its coupling to torque generation, biochemical details are lacking and many questions remain unanswered. An important one is whether ion translocation is cooperative, i.e., whether protons translocate individually or in groups. Here, we present a minimal physical model for torque generation (Fig. 1) that not only explains a variety of previous experimental observations, but also suggests a way to measure the cooperativity of proton translocation. Specifically, the model predicts that at low loads, motor diffusion is dominated by proton shot noise with a strong (quadratic) dependence on proton cooperativity.

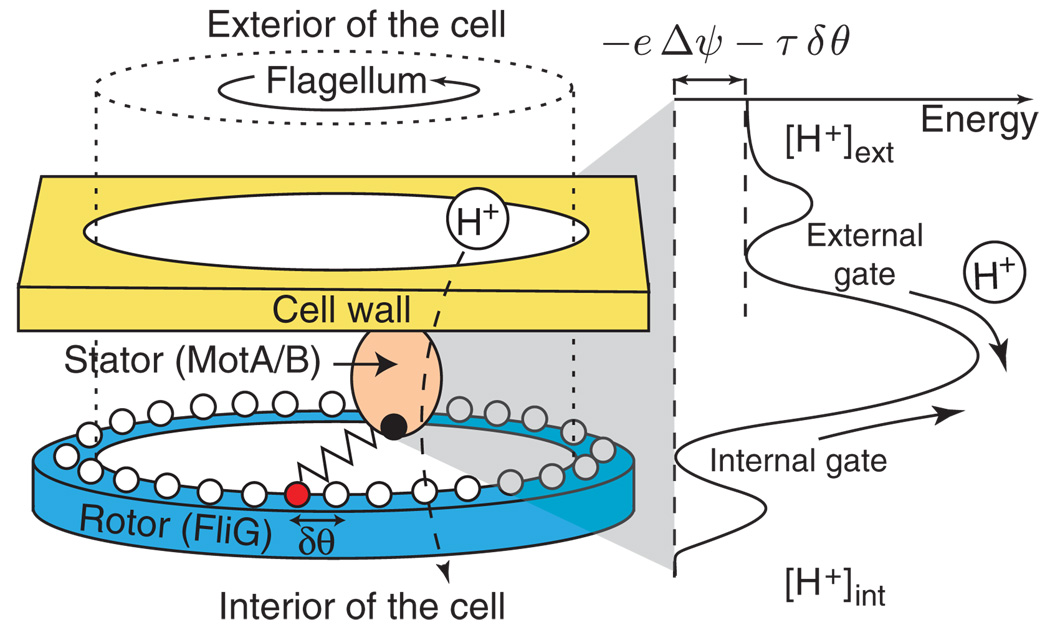
FIG. 1.

(color). Schematic model of the bacterial flagellar motor. Left: The passage of a proton, or possibly a group of protons, through a torque-generating unit (a MotA/B stator—only one stator of about 10 is shown) causes a protein spring to stretch to its next attachment site, represented by circles, on the rotor. Right: To translocate, a proton must pass through an external gate, over a barrier, and finally through an internal gate, with all the steps assumed to be reversible. The net energy difference driving proton translocation is the electrical potential energy, −eΔψ, minus the work, τδθ, necessary to stretch the protein spring by δθ, where τ is the torque applied by the spring to the rotor.

The flagellar motor operates with near-perfect efficiency at low speeds [2]. As the speed is increased, e.g., by reducing the load, the torque and efficiency initially remain high—the “plateau” of the torque-speed relationship (TSR)—and then drop abruptly at a “knee” (cf. Fig. 2). This knee occurs at higher speeds as temperature is increased. Despite much experimental [3–6] and modeling progress [6–11], the origin of the knee is still poorly understood. In [11,12], the cause of the knee was argued to be the gating of proton translocation by the relative position between stator and rotor. In [9], a detailed model of motor kinetics was proposed in which the knee arises from the crossover between two time scales, one governing mechanical relaxation and the other proton translocation. In our model, proton translocation, which is assumed to be the rate-limiting step, is modeled by a barrier crossing event as in [11], with the difference that the barrier height depends on the mechanical tension between stator and rotor. The knee in the TSR then arises from the kinetically limited rate of proton translocation. Importantly, our model fully incorporates proton thermodynamics and yields the separate dependence of the TSR on the electrical and chemical parts of the PMF.

FIG. 2.

(color). The torque-speed relationship (TSR) of the E. coli flagellar motor. Rotation speed is measured with beads of various loads (data points) attached to a flagellar stub, under different pH conditions (colors) [5]; solid curves: model fits. Inset: Total torque vs speed from [6], normalized by the number of stators. Data collapse indicates that stators contribute independently and additively to the total torque. Solid curve: model TSR for a single stator using the same parameters as in the main figure and Fig. S2 [17], with the temperature fit as 21 °C and the stall torque fit as 300 pN · nm.

Three ingredients underlie our model. (i) Each torque-generating unit (MotA/B stator) contributes independently and additively to the total torque, in agreement with experimental observations 2 [13]. (ii) The torque from each MotA/B stator is applied to the rotor by a protein spring. Proton translocation into the cell causes the stretching of a protein spring to its next attachment site (Fig. 1) [10,14]. This assumption enforces the tight coupling between proton current and rotation speed [2]. (iii) Assuming a cooperativity index of n, translocation occurs through three reversible steps: first n protons load into an external gate, then all n cross an energy barrier to an internal gate, and finally all n are released into the cell. The barrier crossing event is the rate-limiting step. The external and internal gates are necessary to explain the nonlinear dependence of the TSR on proton concentrations [Fig. 2]. (We define the distance between two attachment sites as nδθ so that the average displacement per proton is δθ.)

The external and internal gates are assumed to be in fast equilibrium with the external and internal proton concentrations, respectively. Their dissociation constants are denoted by K_ext and K_int so that the occupancy of the external gate is $H_{\text{ext}}^n/(K_{\text{ext}}^n+H_{\text{ext}}^n)$, where H_ext is the proton concentration outside the cell, and similarly for the internal gate. The energy difference between the internal and external gates is n[eΔψ + τδθ + k_BT log(K_int/K_ext)]. Δψ is the transmembrane electric potential (ψ_int − ψ_ext), and τ δθ is the work necessary to stretch the protein spring. When Δψ = 0 and τ = 0, the energy barrier per proton to inward translocation is $U_{\text{in}}^0$, and the barrier to outward translocation is $U_{\text{out}}^0$, with $U_{\text{in}}^0-U_{\text{out}}^0=k_{B}T\text{log}(K_{\text{int}}/K_{\text{ext}})$. In general, some fraction α of the electric potential and some fraction β of the work contribute to the inward barrier so that the barriers per proton to inward and outward translocations are, respectively, $U_{\text{in}}=U_{\text{in}}^0+\alpha e\mathrm{\Delta }\psi +\beta \tau \delta \theta \text{and}{U}_{\text{out}}=U_{\text{out}}^0-(1-\alpha )e\mathrm{\Delta }\psi -(1-\beta )\tau \delta \theta$. For simplicity, we have neglected any dependence of K_int,ext on Δψ and τ. Then the rate of inward proton translocations is

$$J_{\text{in}}=n{J}_0\frac{H_{\text{ext}}^n}{K_{\text{ext}}^n+H_{\text{ext}}^n}\frac{K_{\text{int}}^n}{K_{\text{int}}^n+H_{\text{int}}^n}\text{exp}\left(-n\frac{U_{\text{in}}}{k_{B}T}\right),$$ (1)

J₀ is a kinetic constant (in Hz), and the other prefactors represent the occupancies of the external and internal gates. The outward rate J_out is given by a similar expression so that the net inward proton flux is

$$J_{\text{in}}-J_{\text{out}}=n{J}_0{e}^{-n{U}_{\text{in}}^0/k_{B}T}\frac{H_{\text{ext}}^n}{K_{\text{ext}}^n+H_{\text{ext}}^n}\frac{K_{\text{int}}^n}{K_{\text{int}}^n+H_{\text{int}}^n}\times e^{-n(\alpha \mathrm{\Delta }\psi +\beta \tau \delta \theta )/k_{B}T}\left[1-\text{exp}\left(n\frac{e\mathrm{\Delta }p+\tau \delta \theta }{k_{B}T}\right)\right].$$ (2)

Δp := Δψ + (k_BT/e) log(H_int/H_ext) is the PMF composed of the electrical and chemical potential differences. Its value is approximately −150 mV in normal conditions. To account for the data, we assume that the height of the barrier may depend on temperature, and we expand the prefactor to linear order in temperature: $J_0{e}^{-U_{\text{in}}^0(T)/k_{B}T=}{\tilde{J}}_0{e}^{\eta (T-T_0)}$, where T₀ = 17.7 °C, is chosen as a reference temperature.

Rotation is then described by coupled stochastic equations for the angular position of the rotor θ and the stretching of the protein springs i = 1, …, N, where N is the number of stators, each exerting a torque τi on the rotor

$$\frac{d\theta }{\mathit{\text{dt}}}=\frac{1}{\nu }{\displaystyle \sum _{i=1}^N{\tau }_i+\xi (t),}$$ (3)

$$\frac{d{\tau }_i}{\mathit{\text{dt}}}=k({\tau }_i)\left[-\frac{d\theta }{\mathit{\text{dt}}}+\mathrm{\Omega }({\tau }_i)+{\xi }_i^{\tau }(t)\right].$$ (4)

ν is the frictional drag coefficient of the load, and k(τ) is the spring constant of the (possibly non-Hookean) protein springs. The spring constant need not be specified as none of the observables computed below depend on it. In the second equation, each spring relaxes as the rotor moves (backreaction of the rotor onto stators, −dθ/dt), but gets restretched by proton translocations (Ω(τ_i) := (J_in − J_out)δθ). ξ(t) is the thermal noise on the load and satisfies the Einstein relation: 〈ξ(t)ξ(t′)〉 = 2(k_BT/ν)δ(t − t′). ${\xi }_i^{\tau }$ is the shot noise at each stator i, due to the randomness of proton translocation events. To obtain the average speed ω and torque per stator τ = 〈τ_i〉, we solve Eqs. (3) and (4), at steady state (dτ_i/dt = 0) with no noise, yielding: ω = dθ/dt = Nτ/ν and τ_i = τ, with Ω(τ) = ω. Along with Eq. (2), this gives a closed set of equations from which we obtain the TSR. Note that the resulting expression depends separately on the electrical and chemical potential for protons. At stall (ν→∞), the system is in equilibrium. The energy necessary for a protein spring to move to its next attachment site, which is proportional to the torque τ it exerts on the rotor, is matched by the PMF, τδθ + eΔp = 0. Consequently, the total torque grows linearly with the PMF, Nτ = −NeΔp/δθ, and the efficiency near stall is ≈100%, in agreement with experiments [15,16].

Our model with no cooperativity (n = 1) can fit all existing measured TSR of the E. coli motor. Some our model’s parameters are fixed properties of the motor and thus are fit by single values: (δθ = 4.6°, K_int = 1.2 × 10⁻⁸, K_ext = 2 × 10⁻⁷, J͂₀ = 670 Hz, α = 0.2, β = 0.078, η = 0.11 K⁻¹) while others depend on conditions (T, H_int,ext, Δψ, number of stators N), and may or may not have been measured in the experiments.

Figure 2 shows fits of TSRs measured under various pH conditions [5]. The electric potential Δψ was not measured and so was used as a fitting parameter for each set of pH conditions. Our fit indicates that |Δψ| increases with pH (Fig. S1 [17]), consistently with previous measurements [18,19].

Electrorotation experiments [3,7] have been used to apply an external torque on the load via an oscillating field. When the motor is driven backwards (upper-left quadrant of the TSR), the internal torque is approximately equal to its stall value up to speeds of−100 Hz [7]. When the motor is driven to speeds larger then the maximum operating speed (lower-right quadrant of the TSR), the motor resists rotation, resulting in a negative internal torque. In this regime, the slope of the TSR remains approximately the same as for positive torques beyond the knee [3]. Our model agrees with measurements in both regimes. The absence of a barrier to backward rotation follows from the reversibility of proton translocation. For negative torques, the model predicts an inflection of the TSR, as seen for the red curve in Fig. 2.

Within our model, the proton flux is limited by the loading of the external and internal gates and by the barrier crossing. This limitation on flux accounts for the knee of the TSR. In Fig. 2, the position of the knee strongly depends on pH values: as the internal proton concentration increases, the internal gate gets saturated, preventing protons from translocating inwards, and thus limiting the stretching of stator springs and the applied torque.

Our model also accounts quantitatively for measurements of the TSR at different temperatures (Fig. S2 [17]) [4], as well as for measurements with different numbers of stators [Inset of Fig. 2] [6]. We compared the model to earlier measurements at different temperatures [3] (data reported in [4]), with no additional fitting parameters, and found excellent agreement (Fig. S3 [17]).

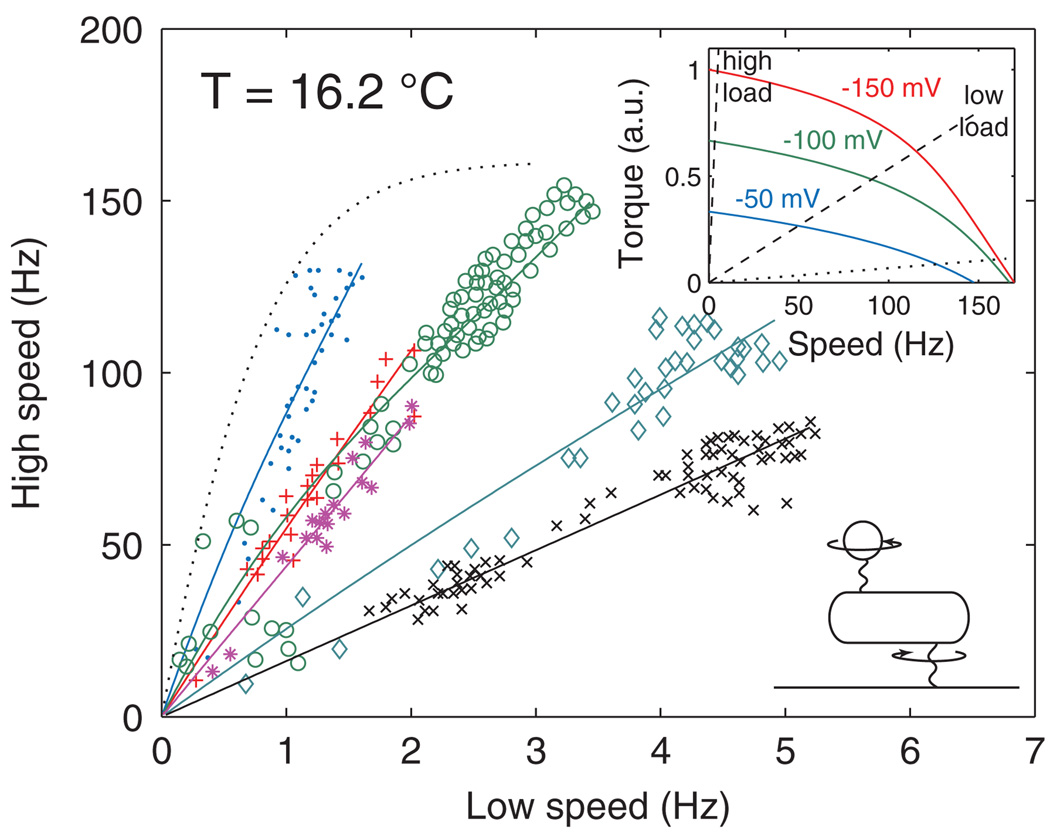
Experiments by Gabel and Berg (Fig. 3) [20] have been interpreted to imply that the rotation speed is proportional to PMF, even at high speeds beyond the knee of the TSR. Our model predicts that speed is proportional to PMF at low speeds, in the plateau region of the TSR. However, at high speeds, the torque is limited by the proton flux, and therefore both torque and speed grow sublinearly with PMF. Nevertheless, our model (with n = 1) is fully consistent with the measurements reported in [20]. Experimentally, speeds were simultaneously recorded for two motors of the same cell, one rotating the cell itself (high load) and the other rotating a small polystyrene bead (low load), as shown schematically in the lower inset of Fig. 3. These two loads correspond to the two dashed lines in the upper inset of Fig. 3. As cells were deenergized by the introduction of a respiratory poison, the PMF Δp regressed from −150 mV to 0, and the motors slowed, with the two speeds approximately proportional to each other, even at low temperature where the low-load, high-speed motor was in the kinetically limited regime. We fitted the data for each cell, using N/ν_cell and N/ν_bead as free parameters, and assuming that during deenergization the electric and chemical parts of the PMF regressed in fixed ratio to each other. The model fits are consistent with the data, both at 24 °C (Fig. S6 [17]) and at 16.2 °C (Fig. 3). However, a further reduction of the low load would be predicted to lead to a strong deviation from proportionality (dotted line in Fig. 3).

FIG. 3.

(color). Relationship between the high-speed (low-load) and low-speed (high-load) regimes of the E. coli flagellar motor, as the PMF varies from −150 mV to 0, at temperature T = 16.2 °C. Symbols: Experimental data from individual cells [20]. Solid curves: model fits with the same parameters as in Fig. 2. Dotted curve: the model predicts loss of proportionality at very low loads. Lower inset: schematic of the experiment [20]. Upper inset: model TSR for PMFs of −150, −100, and −50 mV; the dashed lines show the low- and high-load lines of the cell represented by ◊ in the main panel, and the dotted line is the load line corresponding to the dotted curve in the main panel.

Adding cooperativity (n>1) to the model still captures the general shape of the TSR, as well as its temperature dependence (Fig. S4 [17]), but agrees poorly with the observed pH dependence (Fig. S5 [17]), as it implies a stronger dependence of proton current on ion concentrations. The model with n>1 is consistent with the Gabel-Berg data for most cells (Fig. S7 [17]), although it breaks down for the two cells with the largest high speeds.

Although n = 1 appears to best explain the data, measurements of average rotation speeds do not allow us to discriminate with certainty the proton cooperativity. In contrast, our model predicts that diffusion of the rotor angle at low loads should depend very strongly on proton cooperativity. The discrete nature of proton translocations implies the existence of shot noise ${\xi }_i^{\tau }(t)$ in the stretching of the protein spring at each stator i. We can approximate the shot noise as Gaussian white noise: $\langle {\xi }_i^{\tau }(t){\xi }_i^{\tau }(t\prime )\rangle =2D_{\text{shot}}\delta (t-t\prime )$, with D_shot = (1/2)(J_in + J_out)nδθ² (this approximation is valid for times much larger than $J_{\text{in}}^{-1}\text{and}{J}_{\text{out}}^{-1}$). Solving Eqs. (3) and (4), including shot noise ${\xi }_i^{\tau }(t)$ and thermal noise ξ(t), we find an exact expression for the effective diffusion coefficient of the rotor angle:

$$\begin{array}{cc}{D}_{\text{eff}}\hfill & :=\underset{t\to \infty }{\text{lim}}\frac{1}{2t}(\langle \theta {(t)}^2\rangle -\langle \theta {(t)\rangle }^2)\hfill \\ \hfill & =\frac{k_{B}T}{\nu }{\left(1-\frac{N\mu }{\nu +N\mu }\right)}^2+\frac{D_{\text{shot}}}{N}{\left(\frac{N\mu }{\nu +N\mu }\right)}^2,\hfill \end{array}$$ (5)

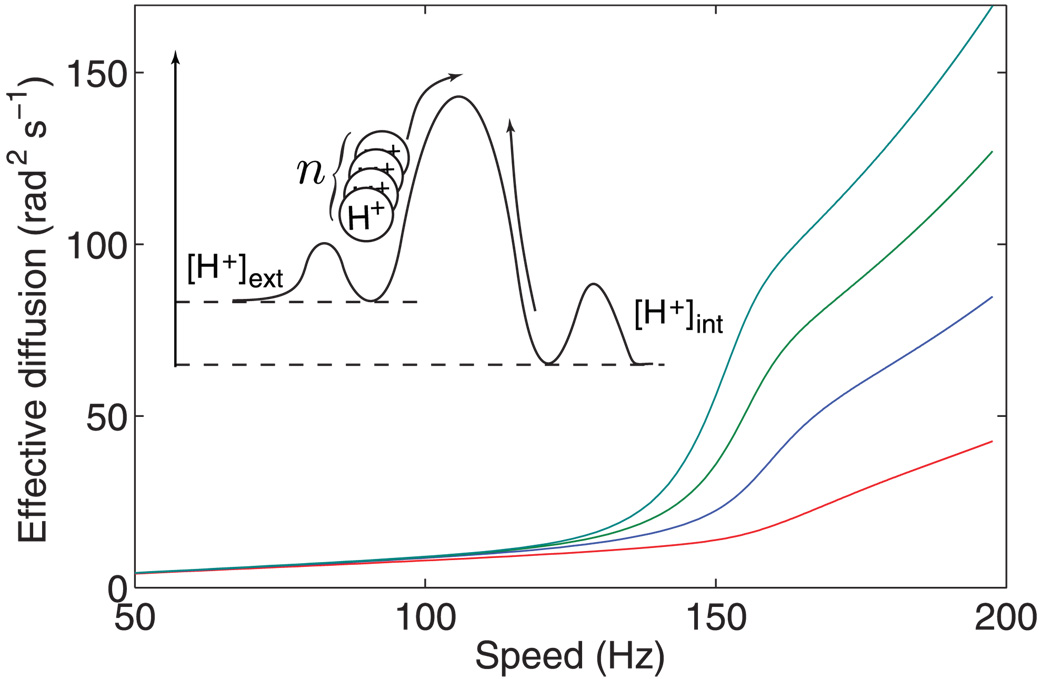
where N is the number of stators and µ(τ) = −(dΩ/dτ)⁻¹ is minus the local slope of the TSR. Figure 4 shows the effective diffusion coefficient as a function of motor speed for different proton cooperativities. Parameters were chosen so that the speed at zero torque is 200 Hz.

FIG. 4.

(color). Effective diffusion as a function of rotation speed for a single stator (N = 1), with different ion translocation cooperativities n = 1, … , 4 (bottom to top). Inset: schematic of cooperative ion translocation.

At high loads (ν ≫ µ), diffusion is entirely due to thermal noise: D_eff ≈ k_BT/ν. However, at low loads (ν ≪ µ), diffusion is dominated by shot noise: D_eff ≈ D_shot/N. In fact, the thermal noise is completely suppressed in the low-load limit: e.g., a small thermally induced backward jump in rotor angle causes the stretching of all springs, which then rapidly pull the rotor forward, thus canceling the jump. Notice that in the low-load limit, the shot-noise contribution is inversely proportional to the number of stators. Intuitively, a small jump in the angular stretch Δθ_i of one protein spring ultimately only causes the rotor to move Δθ_i/N because the rotor is equally coupled to all N stators. The variance per jump is therefore (Δθ_i/N)², and with N independent stators, the resulting diffusion scales as 1/N.

Equation (5) could be used to infer n experimentally. In the low-load limit, we have J_in ≫ J_out, and therefore n ≈ 2D_eff/(ωδθ). δθ can be determined by measuring the torque per stator and the PMF at stall: δθ = −eΔp/τ.

Our analysis of rotor diffusion suggests a novel experimental test to investigate the cooperativity of proton translocation. Some rotational diffusion measurements have already been made [21,22], but not in the regime of very low load, where shot noise is expected to dominate. Although we have derived the expression for diffusion in the specific framework of our minimal spring model, the same approach is generalizable to more detailed models of the bacterial flagellar motor.